Understanding the Temporal Variability of Rainfall for Estimating Agro-Climatic Onset of Cropping Season over South Interior Karnataka, India
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Meteorological Data
2.3. Analysis of Trend in Rainfall
2.3.1. Mann-Kendall (M-K) Test
2.3.2. Modified Mann-Kendall (MMK) Test
2.3.3. Sen’s Slope Estimator
2.3.4. Shifting Pattern in the Rainfall Distribution
2.3.5. The Estimation of the Agro-Climatic Onset of Cropping Season
- Start date (calendar date): An estimated date of meteorological onset of rainfall, used to start the simulation of agro-climatic onset.
- Rainfall threshold (mm): the minimum amount of rainfall required to sow the crop.
- Dry day threshold (mm): the minimum amount of soil moisture required to meet soil evaporation.
- Dry spell threshold (days): the maximum number of days that crop can sustain even after reaching the dry day threshold. That is, if the crop undergoes moisture stress even up to 10 days, there will not be considerable yield losses.
- Dry spell search period (days): this is decided based on the concept the ability of that particular crop to sustain after germination. If the dry spell occurs before the end of this search period, the model postpones the sowing date to the next moisture abundance period. If not, the first day of the search period will be considered.
2.3.6. GIS Mapping
3. Results
3.1. Trend in Monthly, Seasonal and Annual Rainfall
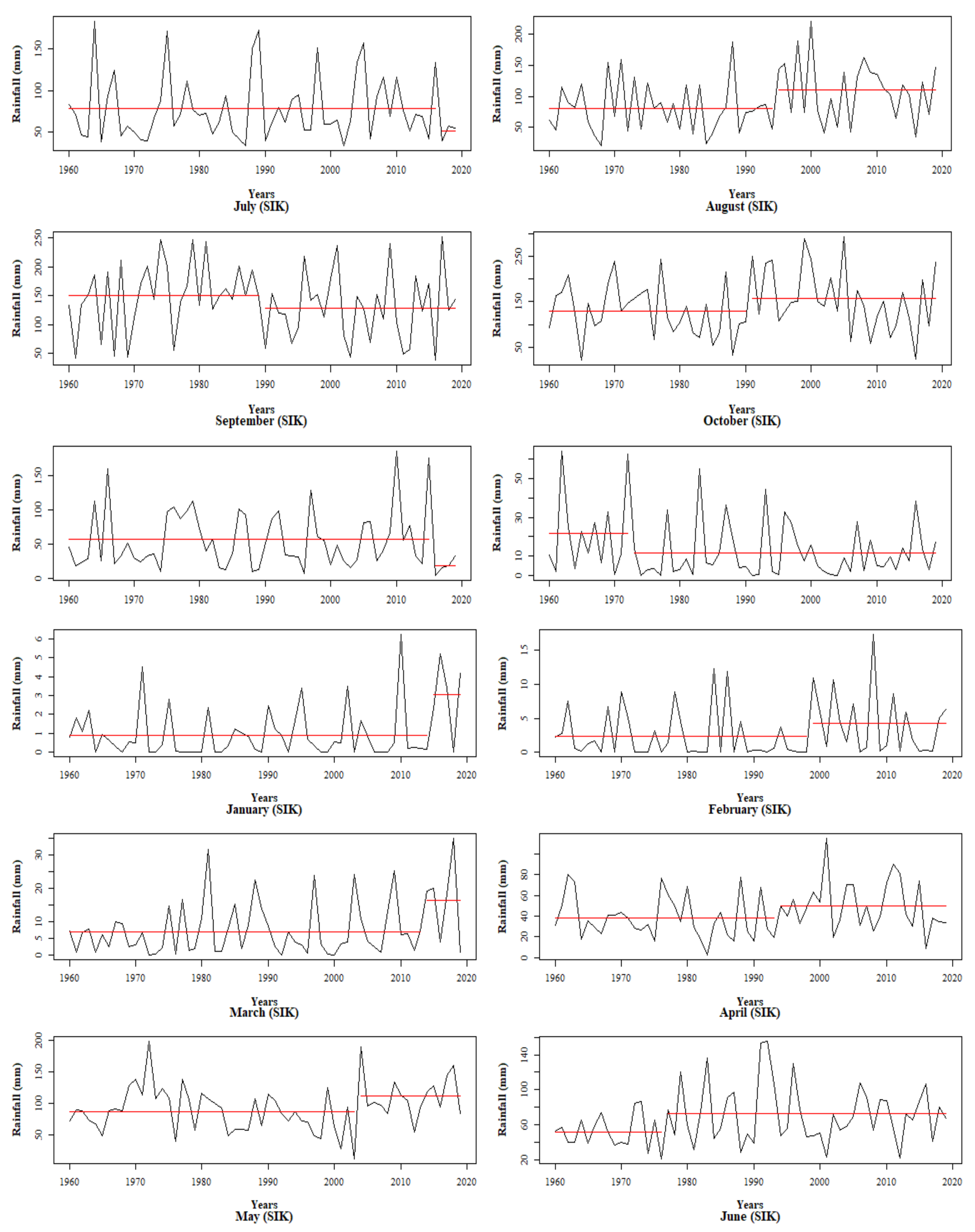
3.1.1. Trend in Month-Wise Rainfall
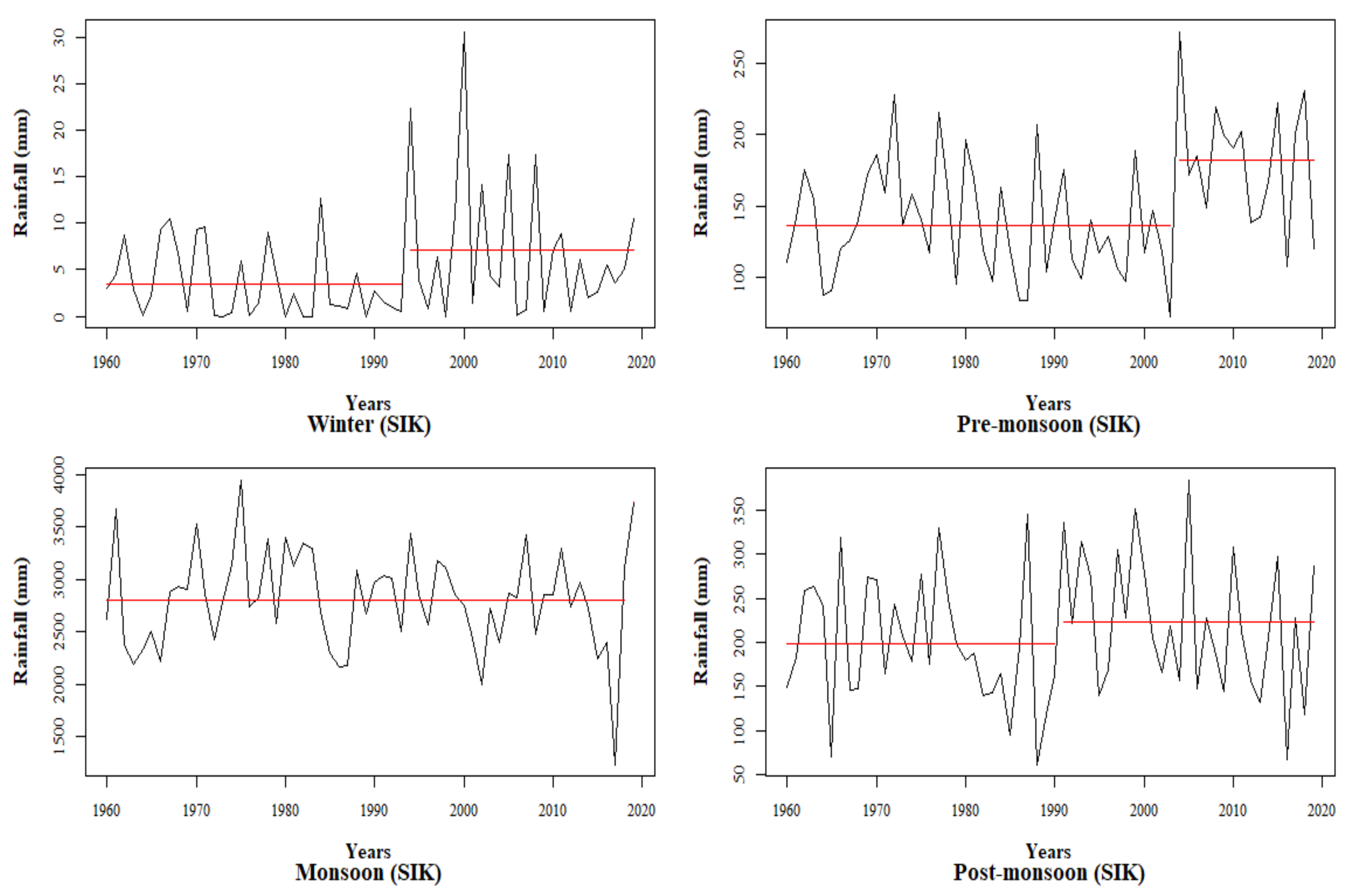
3.1.2. Trend in Seasonal Rainfall
3.1.3. Trend in Annual Rainfall
3.2. Shift in Rainfall Distribution Pattern
3.2.1. Shifting Pattern in Month-Wise Rainfall Distribution
3.2.2. Shifting Pattern in Seasonal Rainfall Distribution
3.2.3. Shifting Pattern in Annual Rainfall Distribution
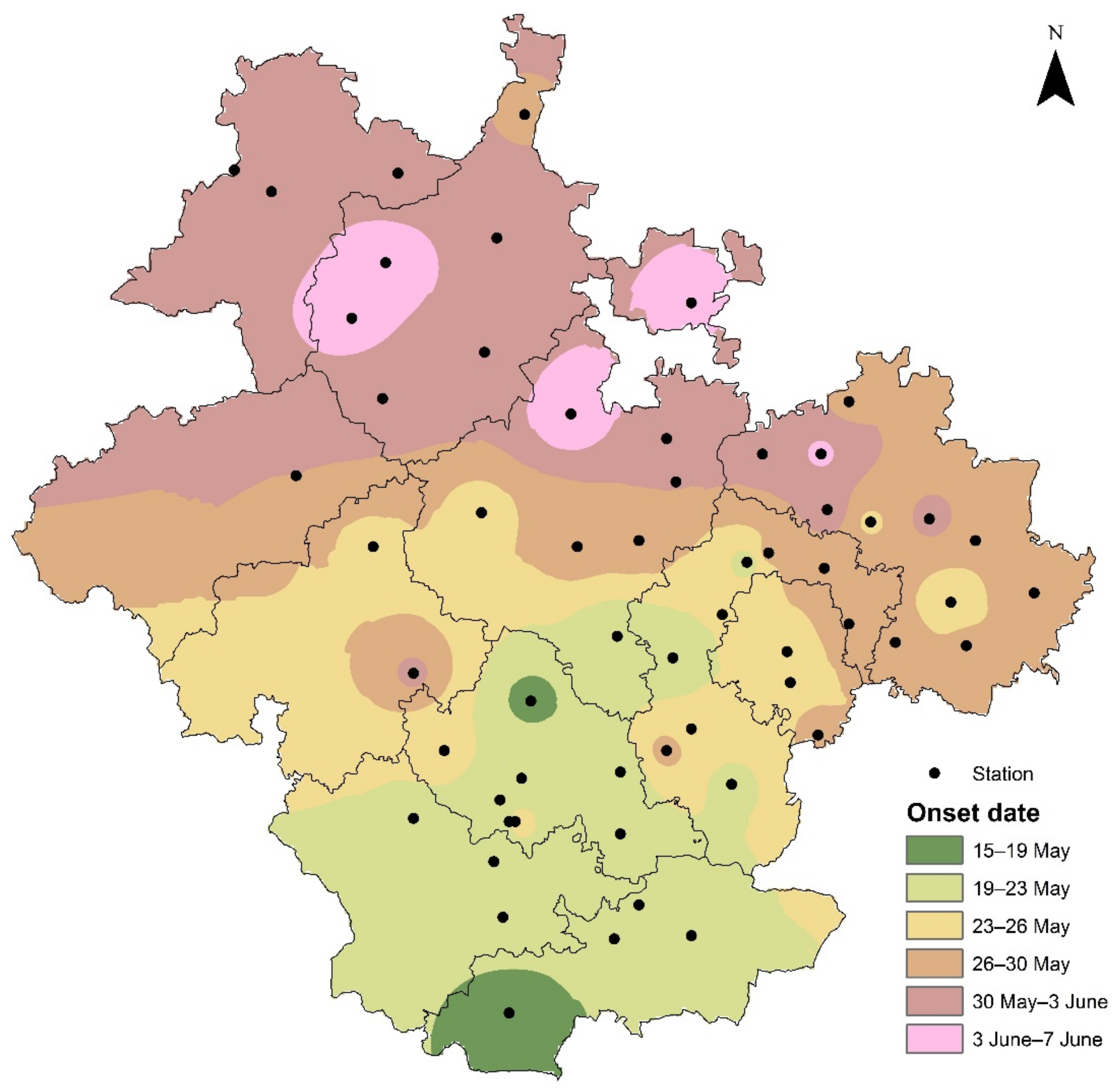
3.2.4. Agro-Climatic Onset of Cropping Season in SIK
CDZ
EDZ
SDZ
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krishnan, R.; Zhang, C.; Sugi, M. Dynamics of breaks in the Indian summer monsoon. J. Atmos. Sci. 2000, 57, 1354–1372. [Google Scholar] [CrossRef]
- Mccarthy, J.; Canziani, O.; Leary, N.; Dokken, D.; White, K. Climate Change 2001: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; pp. 19–25. [Google Scholar]
- Khanday, M.Y.; Javed, A. Impact of climate change on land use/land cover using remote sensing and GIS in Chopal watershed, Guna, Madhya Pradesh (India). J. Envnt. Res. Dev. 2008, 2, 568–579. [Google Scholar]
- IPCC. Summary for policymakers. In Climate Change 2007: The Physical Sciences Basis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Subash, N.; Sikka, A.K.; Ram Mohan, H.S. An investigation into observational characteristics of rainfall and temperature in central northeast India: A historical perspective 1889–2008. Theor. Appl. Climatol. 2011, 103, 305–319. [Google Scholar] [CrossRef]
- Vijaya Kumar, P.; Bal, S.K.; Subba Rao, A.V.M. All India Coordinated Project on Agrometeorology, Annual Report (2018–19); ICAR Central Research Institute for Dryland Agriculture: Hyderabad, India, 2019; pp. 1–144. [Google Scholar]
- Delitala, A.; Cesari, D.; Chesa, P.; Ward, M. Precipitation over Sardinia (Italy) during the 1946–1993 rainy season and associated large scale climate variation. Int. J. Climatol. 2000, 20, 519–541. [Google Scholar] [CrossRef]
- Indian Meteorological Department (IMD). 2015. Available online: http://www.imd.gov.in (accessed on 26 November 2020).
- Prasad, V.S. Onset and withdrawal of Indian summer monsoon. Geophys. Res. Let. 2005, 32, L20715. [Google Scholar] [CrossRef]
- Goswami, B.N.; Wu, G.; Yasunari, T. The annual cycle, intra seasonal oscillations, and roadblock to seasonal predictability of the Asian summer monsoon. J. Clim. 2006, 19, 5078–5099. [Google Scholar] [CrossRef]
- Taniguchi, K.; Koike, T. Comparison of definitions of Indian summer monsoon onset: Better representation of rapid transitions of atmospheric conditions. Geophys. Res. Let. 2006, 33, L02709. [Google Scholar] [CrossRef]
- Fasullo, J.; Webster, P.J. A hydrological definition of Indian Monsoon onset and withdrawal. J. Clim. 2003, 16, 3200–3211. [Google Scholar] [CrossRef]
- Rajagopalan, B.; Molnar, P. Combining regional moist static energy and ENSO for forecasting of early and late season Indian monsoon rainfall and its extremes. Geophys. Res. Let. 2014, 41, 4323–4331. [Google Scholar] [CrossRef]
- Wang, B.; Ding, Q.; Joseph, P.V. Objective definition of the Indian summer monsoon onset. J. Clim. 2009, 22, 3303–3316. [Google Scholar] [CrossRef]
- Stolbova, V.; Surovyatkina, E.; Bookhagen, B.; Kurths, J. Tipping elements of the Indian monsoon: Prediction of onset and withdrawal. Geophys. Res. Let. 2016, 28, 3982–3990. [Google Scholar] [CrossRef]
- Flatau, M.K.; Flatau, P.J.; Rudnick, D. The dynamics of double monsoon onsets. J. Clim. 2001, 14, 4130–4146. [Google Scholar] [CrossRef]
- Dore, M.H.I. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef]
- Bhowmik, M.; Das, N.; Ahmed, I.; Debnath, J. Rainfall frequency analysis to predict flood in west Tripura district, Tripura, north-east India. Int. J. Geomat. Geosci. 2017, 7, 310–320. [Google Scholar]
- Karim, T.H.; Keya, D.R.; Amin, Z.A. Temporal and spatial variations in annual rainfall distribution in Erbil province. Outlook Agric. 2018, 47, 59–67. [Google Scholar] [CrossRef]
- Husak, G.J.; Michaelsen, J.; Funk, C. Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications. Int. J. Climatol. 2007, 27, 935–944. [Google Scholar] [CrossRef]
- Venkatesh, H.; Shivaramu, H.S.; Rajegowda, M.B.; Rao, V.U.M. Agroclimatic Atlas Karnataka. 2016, p. 211. Available online: https://www.uasbangalore.edu.in/index.php/research-en/agrometerology-en (accessed on 21 January 2021).
- Pulakeshi, H.B.P.; Patil, P.L.; Dasog, G.S.; Radder, B.M.; Bidari, B.I.; Mansur, C.P. Mapping of nutrients status by geographic information system in Mantagani village under northern transition zone of Karnataka. J. Agric. Sci. 2012, 25, 332–335. [Google Scholar]
- Sivakumar, M.V. Predicting rainy season potential from the onset of rains in southern Sahelian and Sudanian climatic zones of West Africa. Agric. For. Meteorol. 1988, 42, 295–305. [Google Scholar] [CrossRef]
- Maracchi, G.; Bacci, L.; Cantini, C.; Haimanot, M.T. Effect of water deficit in vegetative and post-flowering phases on pearl millet grown in controlled environment. Agric. Med. 1993, 123, 65–71. [Google Scholar]
- Ingram, K.T.; Roncoli, M.C.; Kirshen, P.H. Opportunities and constraints for farmers of west Africa to use seasonal precipitation forecasts with burkina- faso as a case study. Agric. Syst. 2002, 22, 331–349. [Google Scholar] [CrossRef]
- Barbier, B.; Yacouba, H.; Karambiri, H.; Zorome, M.; Some, B. Human vulnerability to climate variability in the Sahel: Farmers’ adaptation strategies in northern Burkina Faso. J. Environ. Manag. 2009, 43, 790–803. [Google Scholar] [CrossRef] [PubMed]
- Steward, J.I. Principles and performance of response farming. In Climatic Risk in Crop Production. Models Management for the Semi-Arid Tropics and Sub-Tropics; Ford, W., Muchow, R.C., Bellamy, Z.A., Eds.; CAB International: Wallinford, UK, 1991. [Google Scholar]
- Sivakumar, M.V. Empirical analysis of dry spells for agricultural applications in West Africa. J. Clim. 1992, 5, 532–539. [Google Scholar] [CrossRef]
- Omotosho, J.B.; Balogun, A.A.; Ogunjobi, K. Predicting monthly and seasonal rainfall, onset and cessation of the rainy season in West Africa using surface data. Int. J. Climtol. 2000, 20, 865–880. [Google Scholar] [CrossRef]
- Traore, S.B.; Alhassane, A.; Muller, B.; Kouressy, M.; Somé, L.; Sultan, B.; Oettli, P.; Ambroise, C.; Siéné, L.; Sangaré, S.; et al. Diop, M.; Dingkuhn, M.; Baron, C. Characterizing and modelling the diversity of cropping situations under climatic constraints in West Africa. Atmos. Sci. Lett. 2010, 12, 89–95. [Google Scholar] [CrossRef]
- Walter, M.W. Length of rainy season in Nigeria. Niger. Geogr. J. 1967, 10, 123–128. [Google Scholar]
- Omotosho, J.B. Onset of thunderstorms and precipitation over northern Nigeria. Int. J. Climtol. 1990, 10, 849–860. [Google Scholar] [CrossRef]
- Bacci, L.; Cantini, C.; Pierini, F.; Marachi, G.; Reyniers, F.N. Effects of sowing date and nitrogen fertilization on growth, development and yield of a short day cultivar of millet (Pennisetum glaucum L.). Eur. J. Agron. 1999, 10, 9–21. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. The West African monsoon dynamics—The “pre-onset” and “onset” of the summer monsoon. J. Clim. 2003, 16, 3407–3427. [Google Scholar] [CrossRef]
- Birch, H.F. The effect of soil drying on humus decomposition and nitrogen availability. Plant Soil. 1958, 10, 1–31. [Google Scholar] [CrossRef]
- Sparling, G.P.; Ross, D.J. Microbial contribution to the increased nitrogen mineralization after air-drying of soils. Plant Soil. 1988, 105, 163–167. [Google Scholar] [CrossRef]
- Badiane, A.N. Le Statut Organique d’un Sol Sableux de la Zone Centre-Nord du Sénégal. Ph.D. Dissertation, Institut National Polytechnique de Lorraine, Lorraine, France, 1993. [Google Scholar]
- Andrews, D.J. Effects of date of sowing on photosensitive Nigerian sorghums. Exp. Agric. 1973, 9, 337–346. [Google Scholar] [CrossRef]
- Stoop, W.A.; Pattanayak, C.M.; Matlon, P.J.; Root, W.R. A Strategy to Raise the Productivity of Subsistence Farming Systems in the West African Semi-Arid Tropics. Proceedings Sorghum in the Eighties; ICRISAT: Patancheru, India, 1981; Volume 2, pp. 519–526. [Google Scholar]
- Vaksmann, M.; Traoré, S.B.; Niangado, O. Le photo-périodisme des sorghos africains. Agric. Dév. 1996, 9, 13–18. [Google Scholar]
- Agriculture in Karnataka. Economic Survey Report 2018–2019; Directorate of Economic and Statistics: Karnataka, India, 2019; pp. 2–5.
- Kodandarama, S.R. Forecasting of Rainfall in Meteorological Subdivisions of Karnataka Using Non-Linear Statistical Models. Master’s Thesis, University of Agricultural Sciences, Bagalore, India, 2020; pp. 21–50. [Google Scholar]
- Sonali, P.; Nagesh Kumar, D. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–222. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann–Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Res. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Mondal, A.; Kundu, S.; Mukhopadhyay, A. Rainfall trend analysis by Mann-Kendall test: A case study of north-eastern part of Cuttack district, Orissa. Int. J. Geol. Earth Environ. Sci. 2012, 2, 70–78. [Google Scholar]
- Hinkley, D.V. Inference about the change point in a sequence of random variables. Biometrika 1970, 57, 1–17. [Google Scholar] [CrossRef]
- Chen, J.; Arjun, K.G. Parametric Statistical Change Point Analysis: With Applications to Genetics, Medicine, and Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hawkins, D.M. Testing a sequence of observations for a shift in location. J. Am. Stat. Assoc. 1977, 72, 180–186. [Google Scholar] [CrossRef]
- Marteau, R.; Benjamin, S.; Vincent, M.; Agali, A.; Christian, B.; Traore, S.B. The onset of the rainy season and farmers’ sowing strategy for pearl millet cultivation in southwest Niger. Agric. For. Meteorol. 2011, 151, 1356–1369. [Google Scholar] [CrossRef]
- Marteau, R.; Moron, V.; Philippon, N. Spatial coherence of monsoon onset over western and central Sahel (1950–2000). J. Clim. 2009, 22, 1313–1324. [Google Scholar] [CrossRef]
- Narayanan, P. Trend analysis and forecast of pre-monsoon rainfall over India. Weather 2016, 71, 94–99. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality. Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Semenov, M.A.; Porter, J.R. Climatic variability and the modelling of crop yields. Agric. For. Meteorol. 1995, 73, 3–4. [Google Scholar] [CrossRef]
- Corte-Real, J.; Qian, B.; Xu, H. Regional climate change in Portugal: Precipitation variability associated with large-scale atmospheric circulation. Int. J. Climatol. 1998, 18, 619–635. [Google Scholar] [CrossRef]
- Chakraborty, S.; Pandey, R.P.; Chaube, U.C.; Mishra, S.K. Trend and variability analysis of rainfall series at Seonath river basin, Chhattisgarh (India). Int. J. Appl. Sci. Eng. Res. 2013, 2, 425–443. [Google Scholar]
- Adarsh, S.; Reddy, J.M. Trend analysis of rainfall in four meteorological subdivisions of southern India using nonparametric methods and discrete wavelet transforms. Int. J. Climatol. 2015, 35, 1107–1124. [Google Scholar] [CrossRef]
- Ruth, K.; Darshini, R.; Tashinae, S. Local adaptation strategies in semi-arid regions: Study of two villages in Karnataka, India. Clim. Dev. 2015, 9, 1–15. [Google Scholar]
- Ramachandrappa, B.K.; Thimmegowda, M.N.; Krishnamurthy, R.; Srikanth Babu, P.N.; Savitha, M.S.; Srinivasarao, C.H.; Gopinath, K.A.; Ravindra Chary, G. Usefulness and impact of agromet advisory services in eastern dry zone of Karnataka. Indian J. Dryland Agric. Res. Dev. 2018, 33, 32–36. [Google Scholar] [CrossRef]
- Amrutha, H.R.; Shreedhar, R. Study of rainfall trends and variability for Belgaum district. Int. J. Res. Eng. Technol. 2014, 3, 148–155. [Google Scholar]
- Rajegowda, M.B.; Muralidhara, K.S.; Murali, N.M.; Kumar, T.N.A. Rainfall shift and its influence on crop sowing period. J. Agrometeorol. 2000, 2, 89–91. [Google Scholar]
- Davey, E.G.; Mattei, F.; Soloman, S.I. An Evaluation of Climate and Water Resources for the Development of Agriculture in the Sudano-Sahelian Zone of West Africa; WMO Publication: Geneva, Switzerland, 1976; p. 304. [Google Scholar]
- Iyengar, R.N. Application of principal component analysis to understand variability of rainfall. Proc. Indian Acad. Sci. 1991, 100, 105–126. [Google Scholar]
- Stern, R.D.; Dennett, M.D.; Garbutt, D.J. The start of the rains in West Africa. J. Climatol. 1981, 1, 59–68. [Google Scholar] [CrossRef]
- Morris, R.A.; Zandstra, H.G. Land and climate in relation to cropping patterns in rainfed lowland rice. In Proceedings of the International Rice Research Conference, Los Banos, Philippines, 15 February 1975. [Google Scholar]
- Shukla, P.R.; Sharma, K.K.; Amit, G. NATCOM Emission scenarios and Carbon Emissions projections for India. V&A Workshop Scenar. Future Emiss. 2003, 27, 1–16. [Google Scholar]
- Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.S.; Xavier, P.K. Increasing trend of extreme rain events over India in a warming environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef]
- Subash, N.; Singh, S.S.; Priya, N. Variability of rainfall and effective onset and length of the monsoon season over a sub-humid climatic environment. Atmos. Res. 2001, 99, 479–487. [Google Scholar] [CrossRef]
- Rajeevan, M.; Bhate, J.; Jaswal, A.K. Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys. Res. Let. 2008, 35, 1–6. [Google Scholar]
- Patra, P.K.; Behera, S.K.; Herman, J.R.; Maksyutov, S.; Akimoto, H.; Yamagata, Y. The Indian summer monsoon rainfall: Interplay of coupled dynamics, radiation and cloud microphysics. Atmos. Chem. Phys. 2005, 5, 2181–2188. [Google Scholar] [CrossRef]
- Ravindrababu, B.T.; Rajegowda, M.B.; Janardhana gowda, N.A.; Girish, J. Weekly, monthly and seasonal rainfall at Bengaluru in Karnataka. J. Agrometeorol. 2010, 12, 263–265. [Google Scholar]
- Reddy, V.C.; Babu, B.T.R.; Yogananda, S.B. Growth and flowering behaviour of groundnut varieties in relation to sowing dates during kharif season. Curr. Res. 2000, 29, 163–165. [Google Scholar]
- Sharanappa, K.; Shivaramu, H.S.; Thimmegowda, M.N.; Yogananda, S.B.; Prakash, S.S.; Murukannappa. Effect of row spacing, varieties and sowing dates on growth and yield of pigeonpea. Int. J. Curr. Microbiol. Appl. Sci. 2018, 7, 1125–1128. [Google Scholar]
- Rao, C.S.; Gopinath, K.A. Resilient rainfed technologies for drought mitigation and sustainable food security. Mausam 2016, 67, 169–182. [Google Scholar]
- Sridhara, S.; Gopakkali, P.; Nandini, R. Rainfall probability analysis for crop planning in Shivamogga block of Karnataka. J. Agrometeorol. 2016, 18, 168. [Google Scholar]
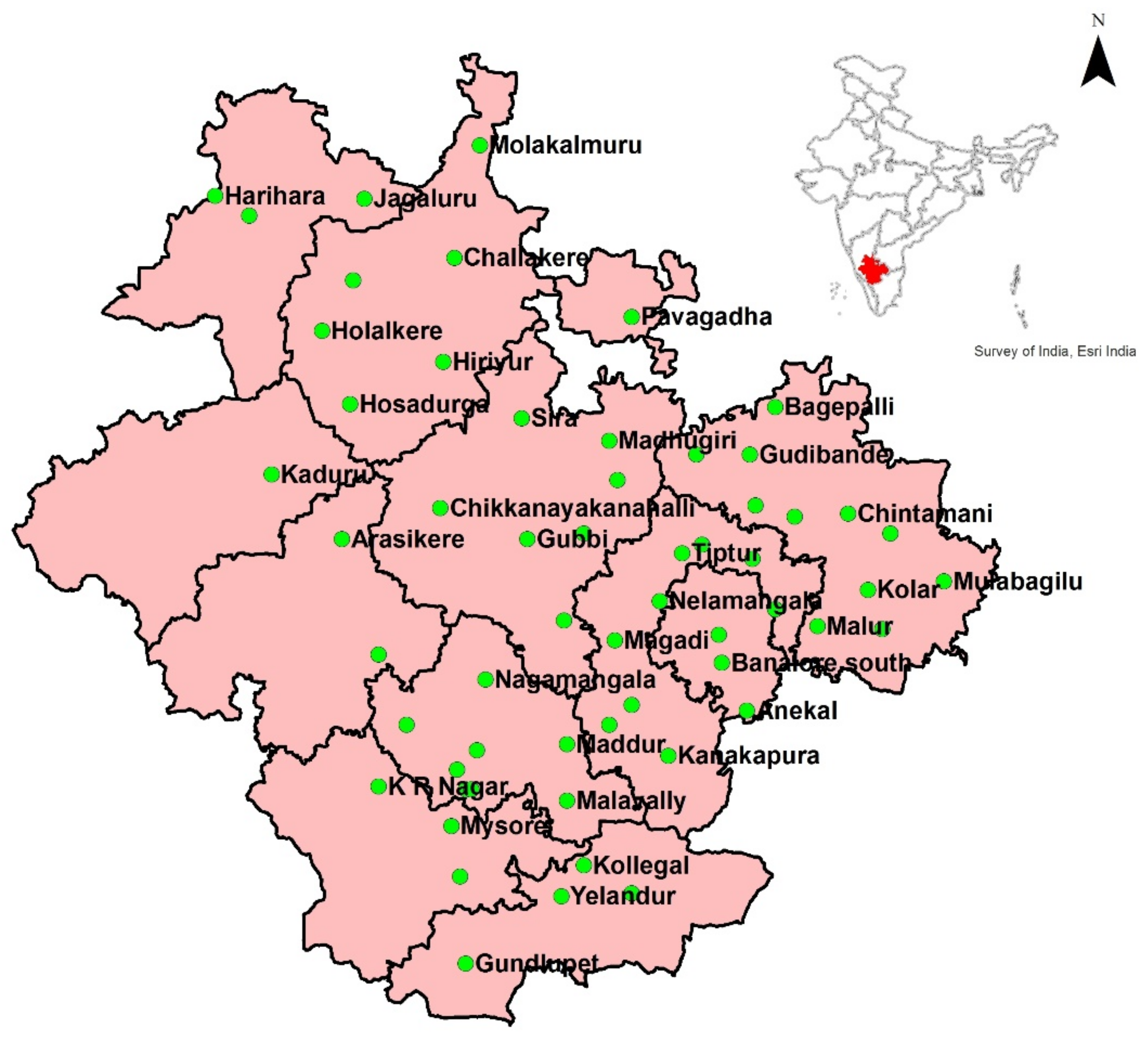

| Zone | District | Blocks (Location of Rain Gauge) |
|---|---|---|
| CDZ | Chitradurga | Chitradurga, Hosadurga, Challakere, Molakalmuru, Holalkere, Hiriyuru |
| Davanagere | Davanagere, Harihara, Jagaluru | |
| Tumakuru | Madhugiri, Pavaghadha, Sira, Chikkanayakanahalli | |
| Chikkamagaluru | Kaduru | |
| EDZ | Tumakuru | Gubbi, Koratagere |
| Bangalore (rural) | Devanahali, Doddaballapura, Nelamangala, Hosakote | |
| Ramnagara | Ramnagara, Magadi, Kanakapura, Channapattana | |
| Bangalore (urban) | Bangalore (north), Bangalore (south), Anekal | |
| Kolar | Kolar, Maluru, Bangarapete, Shrinivasapura, Mulabagilu | |
| Chikkaballapur | Chikkaballapur, Shiddalaghatta, Chintamani, Gudibande, Gouribidanuru, Bagepalli | |
| SDZ | Mandya | Mandya, Madduru, Malavalli, S. pattana, Pandavapura, K R Pete, Nagamangala |
| Mysore | Mysore, K R Nagar, T Narasipura, Nanjanagudu | |
| Chamrajnagar | Chamrajnagar, Yalanduru, Gundlupet, Kollegala | |
| Tumakuru | Tumakuru, Kunigal, Tipaturu | |
| Hassan | Channarayapattana, Arasikere |
| Station | Lat. (°N) | Long. (°E) | RF (mm) | Station | Lat. (°N) | Long. (°E) | RF (mm) |
|---|---|---|---|---|---|---|---|
| CDZ (average annual rainfall 608.8 mm) | |||||||
| Chitradurga | 14.23 | 76.29 | 641.7 | Harihara | 14.53 | 75.8 | 640.4 |
| Hosadurga | 13.79 | 76.28 | 687.7 | Jagaluru | 14.52 | 76.33 | 555.8 |
| Challakere | 14.31 | 76.65 | 620.9 | Madhugiri | 13.66 | 77.2 | 693.3 |
| Molakalmuru | 14.71 | 76.74 | 552.9 | Pavagadha | 14.1 | 77.28 | 596.2 |
| Holalkere | 14.05 | 76.18 | 750.5 | Sira | 13.74 | 76.89 | 666.0 |
| Hiriyur | 13.94 | 76.61 | 590.0 | CK halli | 13.42 | 76.6 | 715.4 |
| Davanagere | 14.46 | 75.92 | 626.3 | Kaduru | 13.42 | 76.6 | 715.4 |
| EDZ (average annual rainfall 776.7 mm) | |||||||
| Gubbi | 13.31 | 76.91 | 792.8 | Anekal | 12.7 | 77.69 | 860.1 |
| Koratagere | 13.31 | 76.91 | 792.8 | Kolar | 13.13 | 78.12 | 774.9 |
| Devanahalli | 13.24 | 77.71 | 815.5 | Malur | 13.13 | 77.94 | 745.5 |
| Doddaballapur | 13.29 | 77.53 | 819.2 | Bangarpet | 12.99 | 78.17 | 695.4 |
| Nelamangala | 12.72 | 77.28 | 874.0 | Shrinivasapura | 13.13 | 77.94 | 745.5 |
| Hoskote | 13.06 | 77.79 | 820.1 | Mulabagilu | 13.16 | 78.39 | 804.3 |
| Ramanagara | 12.72 | 77.28 | 874.0 | Chikkaballapur | 13.43 | 77.72 | 752.9 |
| Magadi | 12.95 | 77.22 | 925.2 | Siddalaghatta | 13.39 | 77.86 | 682.9 |
| Kanakapura | 12.54 | 77.41 | 813.9 | Chintamani | 13.4 | 78.05 | 781.1 |
| Chanapattana | 12.65 | 77.2 | 823.9 | Gudibande | 13.61 | 77.7 | 671.2 |
| Bangalore north | 12.97 | 77.59 | 962.6 | Gouribidanur | 13.61 | 77.51 | 717.3 |
| Bangalore south | 12.92 | 77.59 | 962.6 | Bagepalli | 13.78 | 77.79 | 648.5 |
| SDZ (average annual rainfall 753.4 mm) | |||||||
| Mandya | 12.56 | 76.73 | 683.0 | Nanjanagud | 12.11 | 76.67 | 776.4 |
| Maddur | 12.58 | 77.05 | 770.5 | Chamarajnagar | 11.55 | 76.56 | 787.6 |
| Malavally | 12.38 | 77.05 | 687.7 | Yelandur | 12.04 | 77.03 | 817.9 |
| SR pattana | 12.42 | 76.69 | 683.3 | Gundlupet | 11.80 | 76.69 | 758.1 |
| Pandavapura | 12.49 | 76.66 | 708.1 | Kollegal | 12.15 | 77.11 | 768.1 |
| Krishnarajpete | 12.65 | 76.48 | 768.2 | Tumkur | 13.33 | 77.11 | 864.6 |
| Nagamangala | 12.81 | 76.76 | 785.3 | Kunigal | 13.02 | 77.04 | 816.4 |
| Mysore | 12.29 | 76.64 | 776.2 | Tiptur | 13.26 | 77.46 | 711.2 |
| K R Nagar | 12.43 | 76.38 | 675.9 | CR pattana | 12.9 | 76.38 | 687.5 |
| T Narasipura | 12.42 | 76.71 | 763.0 | Arasikere | 12.9 | 76.38 | 687.5 |
| Month | M-K Test | MM-K Test | Sen’s Slope | |||||
|---|---|---|---|---|---|---|---|---|
| Tau | P | Trend # | Tau | C.F | P | Trend # | ||
| January | 0.02 NS | 0.15 | - | 0.02 NS | 0.1 | 0.05 | - | 0.00 |
| February | 0.08 NS | 0.39 | - | 0.08 ** | 0.1 | 0.01 | ↑ | 0.003 |
| March | 0.15 NS | 0.08 | - | 0.15 ** | 0.37 | 0.01 | ↑ | 0.08 |
| April | 0.09 NS | 0.32 | - | 0.09 * | 0.19 | 0.02 | ↑ | 0.16 |
| May | 0.06 NS | 0.47 | - | 0.06 NS | 0.4 | 0.31 | - | 0.16 |
| June | 0.17 NS | 0.06 | - | 0.17 ** | 0.2 | <0.01 | ↑ | 0.37 |
| July | 0.03 NS | 0.25 | - | 0.03 NS | 0.06 | 0.16 | - | 0.05 |
| August | 0.15 NS | 0.1 | - | 0.15** | 0.08 | <0.01 | ↑ | 0.56 |
| September | −0.07 NS | 0.44 | - | −0.07 NS | 0.16 | 0.05 | - | −0.38 |
| October | 0.02 NS | 0.86 | - | 0.02 NS | 0.19 | 0.7 | - | 0.08 |
| November | −0.03 NS | 0.75 | - | −0.03 NS | 0.09 | 0.29 | - | −0.07 |
| December | −0.04 NS | 0.65 | - | −0.04 NS | 0.31 | 0.41 | - | −0.03 |
| Season | M-K Test | MM-K Test | Sen’s Slope | |||||
|---|---|---|---|---|---|---|---|---|
| Tau | P | Trend # | Tau | CF | P | Trend # | ||
| Winter | 0.07 NS | 0.47 | - | 0.07 ** | 0.07 | 0.01 | ↑ | 0.02 |
| Pre-monsoon | 0.15 NS | 0.1 | - | 0.15 ** | 0.32 | <0.01 | ↑ | 0.58 |
| Monsoon | 0.11 NS | 0.23 | - | 0.11 ** | 0.13 | 0.001 | ↑ | 0.92 |
| Post-monsoon | −0.02 NS | 0.84 | - | −0.02 NS | 0.12 | 0.57 | - | −0.12 |
| Annual | 0.11 NS | 0.21 | - | 0.11 ** | 0.09 | <0.01 | ↑ | 1.47 |
| Month | Shifting Year | Average RF (mm) | Change in RF (mm) | Shifting Nature # | Normal RF (mm) | |
|---|---|---|---|---|---|---|
| Before | After | |||||
| January | 2014 | 0.9 | 3.0 | 2.2 | ↑ | 1.8 |
| February | 1998 | 2.3 | 4.2 | 2.0 | ↑ | 3.5 |
| March | 2013 | 7.1 | 16.3 | 9.2 | ↑ | 5 |
| April | 1993 | 35.0 | 50.2 | 12.1 | ↑ | 41 |
| May | 2003 | 56.9 | 112.8 | 25.9 | ↑ | 96 |
| June | 1976 | 51.5 | 72.5 | 21.1 | ↑ | 64 |
| July | 2016 | 78.5 | 50.5 | −27.9 | ↓ | 79 |
| August | 1994 | 80.0 | 109.6 | 29.6 | ↑ | 81 |
| September | 1989 | 151.0 | 128.9 | −22.1 | ↓ | 135 |
| October | 1990 | 128.5 | 156.5 | 28.0 | ↑ | 146 |
| November | 2015 | 57.0 | 15.3 | −38.7 | ↓ | 50 |
| December | 1972 | 21.5 | 11.4 | −10.1 | ↓ | 14 |
| Season | Shifting Year | Average RF (mm) | Change in RF (mm) | Shifting Nature # | Normal RF (mm) | |
|---|---|---|---|---|---|---|
| Before | After | |||||
| Winter | 1993 | 3.5 | 7.1 | 3.7 | ↑ | 5.0 |
| Pre-monsoon | 2003 | 136.5 | 182.2 | 45.7 | ↑ | 145.0 |
| Monsoon | 1970 | 322.7 | 387.9 | 65.1 | ↑ | 359.0 |
| Post-monsoon | 1990 | 198.0 | 222.9 | 24.9 | ↑ | 210.0 |
| Annual | 1968 | 662.0 | 753.2 | 91.2 | ↑ | 719.00 |
| Input. | Value Fixed | Rationale for Consideration |
|---|---|---|
| Start date | April 1 | To take into account of pre monsoon showers in the region. |
| Rainfall threshold (mm) | 20 mm | Sufficient for sowing of major dryland crops such as finger millet, pigeonpea and other crops [64]. |
| Dry day threshold (mm) | 2.5 mm | Minimum amount of soil moisture to meet the daily evaporation need of soil in study area (red sandy loams). |
| Dry spell threshold (days) | 10 days | Maximum number of days that crop can sustain even after reaching the dry day threshold. |
| Dry spell search period (days) | 20 days | Majority of dryland crops have ability to sustain up to 20 days with minor amounts of soil moisture. |
| Block | DASD | ACOD | Block | DASD | ACOD |
|---|---|---|---|---|---|
| CDZ | |||||
| Chitradurga | 38 | 09-May | Harihara | 34 | 04-June |
| Hosadurga | 32 | 17-May | Jagaluru | 32 | 02-June |
| Challakere | 34 | 18-June | Madhugiri | 35 | 05-June |
| Molakalmuru | 30 | 21-May | Pavagadha | 36 | 21-May |
| Holalkere | 37 | 22-May | Sira | 39 | 24-May |
| Hiriyur | 32 | 17-May | Chikkanayakanahhalli | 25 | 10-May |
| Davanagere | 33 | 17-Jun | Kaduru | 25 | 10-May |
| EDZ | |||||
| Gubbi | 29 | 14-May | Anekal | 28 | 13-May |
| Koratagere | 29 | 14-May | Kolar | 23 | 24-May |
| Devanahalli | 30 | 15-May | Malur | 29 | 30-May |
| Doddaballapur | 28 | 13-May | Bangarpet | 28 | 13-May |
| Nelamangala | 30 | 15-May | Shrinivasapura | 28 | 13-May |
| Hoskote | 30 | 15-May | Mulabagilu | 30 | 15-May |
| Ramanagara | 25 | 10-May | Chikkaballapur | 34 | 04-June |
| Magadi | 19 | 20-May | Siddalaghatta | 26 | 10-June |
| Kanakapura | 22 | 23-May | Chintamani | 32 | 16-June |
| Chanapattana | 29 | 30-May | Gudibande | 36 | 06-June |
| Bangalore North | 23 | 08-May | Gouribidanur | 33 | 03-June |
| Banalore south | 23 | 08-May | Bagepalli | 30 | 14-June |
| SDZ | |||||
| Mandya | 22 | 23-May | Nanjanagud | 22 | 23-May |
| Maddur | 20 | 05-May | Chamarajnagar | 19 | 20-May |
| Malavally | 20 | 05-May | Yelandur | 19 | 20-May |
| Shrirangapattana | 19 | 20-May | Gundlupet | 15 | 16-May |
| Pandavapura | 20 | 05-May | Kollegal | 26 | 11-May |
| Krishnarajpete | 25 | 26-May | Tumkur | 30 | 15-May |
| Nagamangala | 17 | 18-May | Kunigal | 19 | 20-May |
| Mysore | 22 | 23-May | Tiptur | 21 | 22-May |
| K R Nagar | 22 | 07-May | Channarayapattana | 32 | 17-May |
| T Narasipura | 27 | 12-May | Arasikere | 26 | 11-May |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanjeevaiah, S.H.; Rudrappa, K.S.; Lakshminarasappa, M.T.; Huggi, L.; Hanumanthaiah, M.M.; Venkatappa, S.D.; Lingegowda, N.; Sreeman, S.M. Understanding the Temporal Variability of Rainfall for Estimating Agro-Climatic Onset of Cropping Season over South Interior Karnataka, India. Agronomy 2021, 11, 1135. https://doi.org/10.3390/agronomy11061135
Sanjeevaiah SH, Rudrappa KS, Lakshminarasappa MT, Huggi L, Hanumanthaiah MM, Venkatappa SD, Lingegowda N, Sreeman SM. Understanding the Temporal Variability of Rainfall for Estimating Agro-Climatic Onset of Cropping Season over South Interior Karnataka, India. Agronomy. 2021; 11(6):1135. https://doi.org/10.3390/agronomy11061135
Chicago/Turabian StyleSanjeevaiah, Shivaramu Huchahanumegowdanapalya, Kodandarama Shettygowdanadoddi Rudrappa, Mohankumar Thavakadahalli Lakshminarasappa, Lingaraj Huggi, Manjunatha Melekote Hanumanthaiah, Sowmya Dadireddihalli Venkatappa, Nagesha Lingegowda, and Sheshshayee M. Sreeman. 2021. "Understanding the Temporal Variability of Rainfall for Estimating Agro-Climatic Onset of Cropping Season over South Interior Karnataka, India" Agronomy 11, no. 6: 1135. https://doi.org/10.3390/agronomy11061135
APA StyleSanjeevaiah, S. H., Rudrappa, K. S., Lakshminarasappa, M. T., Huggi, L., Hanumanthaiah, M. M., Venkatappa, S. D., Lingegowda, N., & Sreeman, S. M. (2021). Understanding the Temporal Variability of Rainfall for Estimating Agro-Climatic Onset of Cropping Season over South Interior Karnataka, India. Agronomy, 11(6), 1135. https://doi.org/10.3390/agronomy11061135






