Fluid Dynamic Approaches for Prediction of Spray Drift from Ground Pesticide Applications: A Review
Abstract
:1. Introduction
2. Key Factors Influencing Spray Drift
2.1. Droplet Size
2.2. Meteorological Conditions
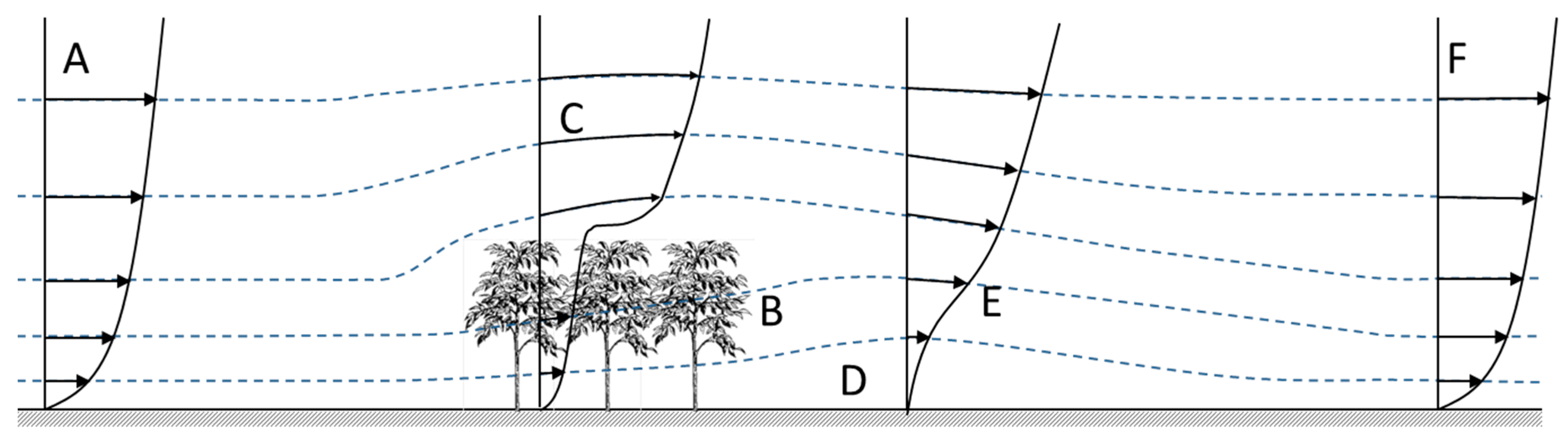
2.3. Plant Canopy
3. Early Models for Spray Drift Prediction
3.1. Plume Models and Droplet Trajectory Models
3.2. Empirical Models
4. Fluid Dynamic Considerations for Modelling Ground Pesticide Applications
4.1. Air Jets and Entrained Air Currents
4.2. Droplet Release
4.3. Turbulent Air Flows in a Plant Canopy and a Crop Field
4.4. Spray Droplet Retention by Plant Canopies
4.5. Wind Field and Downwind Spray Drift
5. Computational Fluid Dynamics Approaches
5.1. Modelling Considerations in CFD Prediction of Spray Drift
5.2. Experimental Validation
5.3. Promising Uses of CFD Applications
6. Discussion and Future Research Trends
- A process-based modelling, as one of the solutions to complex phenomena, which can offer more comprehensive understanding and easier interpretation of the spray drift than detailed numerical models.
- Improving spray retention models in relation to realistic features of leaf-airflow interactions. Leaves flutter or vibrate in wind and turbulence, resulting in spray retention and impact behaviours [130].
- Promoting validation of spray drift models along with enhanced measuring technologies. Most spray drift models were validated by data measured in limited environmental and operational conditions due to difficulties of the field experiment.
- Using new computational technologies to import three-dimensional field images consisting of crops and terrains as boundary conditions and real-time local weather data as the initial inputs into the simulation models.
- Including sprayer physical parameters and spray cloud patterns along with sprayer travel conditions in the computer simulations to demonstrate real-time droplet trajectories.
- Assessing environmental risks and mitigation measures using the fluid-mechanical computer simulations for users and regulatory authorities [135].
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farooq, M.; Salyani, M. Modeling of spray penetration and deposition on citrus tree canopies. Trans. ASAE 2004, 47, 619–627. [Google Scholar] [CrossRef]
- Delele, M.A.; Jaeken, P.; Debaer, C.; Baetens, K.; Endalew, A.M.; Ramon, H.; Nicolai, B.M.; Verboven, P. CFD prototyping of an air-assisted orchard sprayer aimed at drift reduction. Comput. Electron. Agric. 2007, 55, 16–27. [Google Scholar] [CrossRef]
- Salyani, M.; Cromwell, R. Spray drift from ground and aerial applications. Trans. ASAE 1992, 35, 1113–1120. [Google Scholar] [CrossRef]
- Van den Berg, F.; Kubiak, R.; Benjey, W.; Majewski, M.; Yates, S.; Reeves, G.; Smelt, J.; Van der Linden, A. Emission of pesticides into the air. In Fate of Pesticides in the Atmosphere: Implications for Environmental Risk Assessment; Springer: Berlin, Germany, 1999; pp. 195–218. [Google Scholar] [CrossRef]
- USEPA. Introduction to Pesticide Drift. Available online: https://www.epa.gov/reducing-pesticide-drift/introduction-pesticide-drift (accessed on 5 January 2021).
- Yarborough, D.E. Minimizing Off-Target Deposition of Pesticide Applications; Fact Sheet No. 303; University of Maine Cooperative Extension: Orono, ME, USA, 2002; Available online: http://extension.umaine.edu/blueberries/factsheets/integrated-crop-management/minimizing-off-target-deposition-of-pesticide-applications/ (accessed on 5 January 2021).
- Ware, G.; Apple, E.; Cahill, W.; Gerhardt, P.; Frost, K. Pesticide drift. II. Mist-blower vs. aerial application of sprays. J. Econ. Entomol. 1969, 62, 844–846. [Google Scholar] [CrossRef]
- Teske, M.E.; Thistle, H.W.; Schou, W.C.; Miller, P.C.H.; Strager, J.M.; Richardson, B.; Ellis, M.C.B.; Barry, J.W.; Twardus, D.B.; Thompson, D.G. A Review of Computer Models for Pesticide Deposition Prediction. Trans. ASABE 2011, 54, 789–801. [Google Scholar] [CrossRef]
- Ryan, S.D.; Gerber, A.G.; Holloway, A.G.L. A Computational Study on Spray Dispersal in the Wake of an Aircraft. Trans. ASABE 2013, 56, 847–868. [Google Scholar] [CrossRef]
- Walklate, P.J.; Weiner, K.L.; Parkin, C.S. Analysis of and experimental measurements made on a moving air-assisted sprayer with two-dimensional air-jets penetrating a uniform crop canopy. J. Agric. Eng. Res. 1996, 63, 365–377. [Google Scholar] [CrossRef]
- Weiner, K.-L.; Parkin, C. The use of computational fluid dynamic code for modelling spray from a mistblower. J. Agric. Eng. Res. 1993, 55, 313–324. [Google Scholar] [CrossRef]
- Zhu, H.; Reichard, D.; Fox, R.; Brazee, R.; Ozkan, H. Simulation of drift of discrete sizes of water droplets from field sprayers. Trans. ASAE 1994, 37, 1401–1407. [Google Scholar] [CrossRef]
- Gil, Y.; Sinfort, C. Emission of pesticides to the air during sprayer application: A bibliographic review. Atmos. Environ. 2005, 39, 5183–5193. [Google Scholar] [CrossRef]
- Reichard, D.; Zhu, H.; Fox, R.; Brazee, R. Wind tunnel evaluation of a computer program to model spray drift. Trans. ASAE 1992, 35, 755–758. [Google Scholar] [CrossRef]
- Reichard, D.; Zhu, H.; Fox, R.; Brazee, R. Computer simulation of variables that influence spray drift. Trans. ASAE 1992, 35, 1401–1407. [Google Scholar] [CrossRef]
- Teske, M.E.; Bird, S.L.; Esterly, D.M.; Curbishley, T.B.; Ray, S.L.; Perry, S.G. AgDrift®: A model for estimating near-field spray drift from aerial applications. Environ. Toxicol. Chem. Int. J. 2002, 21, 659–671. [Google Scholar] [CrossRef]
- Zhu, H.; Reichard, D.; Fox, R.; Ozkan, H.; Brazee, R. DRIFTSIM, a program to estimate drift distances of spray droplets. Appl. Eng. Agric. 1995, 11, 365–369. [Google Scholar] [CrossRef]
- Smith, R.; Miller, P. Drift predictions in the near nozzle region of a flat fan spray. J. Agric. Eng. Res. 1994, 59, 111–120. [Google Scholar] [CrossRef]
- Brazee, R.; Fox, R.; Reichard, D.; Hall, F. Turbulent jet theory applied to air sprayers. Trans. ASAE 1981, 24, 266–272. [Google Scholar] [CrossRef]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolai, B.M.; Verboven, P. Modelling pesticide flow and deposition from air-assisted orchard spraying in orchards: A new integrated CFD approach. Agric. For. Meteorol. 2010, 150, 1383–1392. [Google Scholar] [CrossRef]
- Al Heidary, M.; Douzals, J.; Sinfort, C.; Vallet, A. Influence of spray characteristics on potential spray drift of field crop sprayers: A literature review. Crop Prot. 2014, 63, 120–130. [Google Scholar] [CrossRef]
- Bonds, J.A.S.; Leggett, M. A Literature Review of Downwind Drift from Airblast Sprayers: Development of Standard Methodologies and a Drift Database. Trans. ASABE 2015, 58, 1471–1477. [Google Scholar] [CrossRef]
- Hilz, E.; Vermeer, A.W.P. Spray drift review: The extent to which a formulation can contribute to spray drift reduction. Crop Prot. 2013, 44, 75–83. [Google Scholar] [CrossRef]
- Jensen, P.K.; Olesen, M.H. Spray mass balance in pesticide application: A review. Crop Prot. 2014, 61, 23–31. [Google Scholar] [CrossRef]
- Bartzanas, T.; Kacira, M.; Zhu, H.; Karmakar, S.; Tamimi, E.; Katsoulas, N.; Lee, I.B.; Kittas, C. Computational fluid dynamics applications to improve crop production systems. Comput. Electron. Agric. 2013, 93, 151–167. [Google Scholar] [CrossRef]
- Matthews, G.A.; Thornhill, E. Pesticide Application Equipment for Use in Agriculture: Manually Carried Equipment; Food & Agriculture Organization: Rome, Italy, 1994; Volume 112. [Google Scholar]
- Gu, J.B.; Zhu, H.P.; Ding, W.M.; Jeon, H.Y. Droplet Size Distributions of Adjuvant-Amended Sprays from an Air-Assisted Five-Port Pwm Nozzle. At. Sprays 2011, 21, 263–274. [Google Scholar] [CrossRef] [Green Version]
- Katzman, D.; Bohbot-Raviv, Y.; Dubowski, Y. Does polyacrylamide-based adjuvant actually reduce primary drift of airborne pesticides? Sci. Total Environ. 2021, 775, 145816. [Google Scholar] [CrossRef] [PubMed]
- Baetens, K.; Nuyttens, D.; Verboven, P.; De Schampheleire, M.; Nicolai, B.; Ramon, H. Predicting drift from field spraying by means of a 3D computational fluid dynamics model. Comput. Electron. Agric. 2007, 56, 161–173. [Google Scholar] [CrossRef]
- Miller, P.; Ellis, M.B.; Lane, A.; O’sullivan, C.; Tuck, C. Methods for minimising drift and off-target exposure from boom sprayer applications. Asp. Appl. Biol. 2011, No.106, 281–288. [Google Scholar]
- Gil, Y.; Sinfort, C.; Brunet, Y.; Polveche, V.; Bonicelli, B. Atmospheric loss of pesticides above an artificial vineyard during air-assisted spraying. Atmos. Environ. 2007, 41, 2945–2957. [Google Scholar] [CrossRef]
- Yates, W.; Akesson, N.; Coutts, H. Drift hazards related to ultra-low-volume and diluted sprays applied by agricultural aircraft. Trans. ASAE 1967, 10, 628–632. [Google Scholar] [CrossRef]
- Hong, S.; Lee, I.; Hwang, H.; Seo, I.; Bitog, J.; Kwon, K.; Song, J.; Moon, O.; Kim, K.; Ko, H.; et al. CFD modelling of livestock odour dispersion over complex terrain, part II: Dispersion modelling. Biosyst. Eng. 2011, 108, 265–279. [Google Scholar] [CrossRef]
- Fritz, B.K. Meteorological effects on deposition and drift of aerially applied sprays. Trans. ASABE 2006, 49, 1295–1301. [Google Scholar] [CrossRef]
- Chen, Y.; Ozkan, H.E.; Zhu, H.; Derksen, R.C.; Krause, C.R. Spray Deposition inside Tree Canopies from a Newly Developed Variable-Rate Air-Assisted Sprayer. Trans. ASABE 2013, 56, 1263–1272. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, H.; Ozkan, H.E.; Derksen, R.C.; Krause, C.R. Spray Drift and Off-Target Loss Reductions with a Precision Air-Assisted Sprayer. Trans. ASABE 2013, 56, 1273–1281. [Google Scholar] [CrossRef] [Green Version]
- SDTF. A Summary of Airblast Application Studies; Stewart Agricultural Research Services; Spray Drift Task Force: Macon, MO, USA, 1997. [Google Scholar]
- Raupach, M.; Briggs, P.; Ahmad, N.; Edge, V. Endosulfan transport: II. Modeling airborne dispersal and deposition by spray and vapor. J. Environ. Qual. 2001, 30, 729–740. [Google Scholar] [CrossRef] [PubMed]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. In Boundary-Layer Meteorology 25th Anniversary Volume, 1970–1995; Springer: Berlin, Germany, 1996; pp. 351–382. [Google Scholar] [CrossRef]
- Schou, W.C.; Forster, W.A.; Mercer, G.N.; Teske, M.E.; Thistle, H.W. Building canopy retention into AGDISP: Preliminary models and results. In Proceedings of the American Society of Agricultural and Biological Engineers (ASABE) Annual International Meeting, Louisville, Kentucky, 7–10 August 2011; p. 1. [Google Scholar]
- Dorr, G.J.; Kempthorne, D.M.; Mayo, L.C.; Forster, W.A.; Zabkiewicz, J.A.; Mccue, S.W.; Belward, J.A.; Turner, I.W.; Hanan, J. Towards a model of spray-canopy interactions: Interception, shatter, bounce and retention of droplets on horizontal leaves. Ecol. Model. 2014, 290, 94–101. [Google Scholar] [CrossRef] [Green Version]
- Arritt, R.W.; Clark, C.A.; Goggi, A.S.; Sanchez, H.L.; Westgate, M.E.; Riese, J.M. Lagrangian numerical simulations of canopy air flow effects on maize pollen dispersal. Field Crop. Res. 2007, 102, 151–162. [Google Scholar] [CrossRef]
- Lebeau, F.; Verstraete, A.; Stainier, C.; Destain, M.F. RTDrift: A real time model for estimating spray drift from ground applications. Comput. Electron. Agric. 2011, 77, 161–174. [Google Scholar] [CrossRef]
- Lagzi, I.; Mészáros, R.; Gelybó, G.; Leelőssy, Á. Atmospheric Chemistry; Eötvös Loránd University: Budapest, Hungary, 2013. [Google Scholar]
- Arvidsson, T.; Bergstrom, L.; Kreuger, J. Spray drift as influenced by meteorological and technical factors. Pest Manag. Sci. 2011, 67, 586–598. [Google Scholar] [CrossRef]
- Lazzaro, L.; Otto, S.; Zanin, G. Role of hedgerows in intercepting spray drift: Evaluation and modelling of the effects. Agric. Ecosyst. Environ. 2008, 123, 317–327. [Google Scholar] [CrossRef]
- Smith, D.B.; Bode, L.E.; Gerard, P.D. Predicting ground boom spray drift. Trans. ASAE 2000, 43, 547–553. [Google Scholar] [CrossRef]
- Nuyttens, D.; De Schampheleire, M.; Baetens, K.; Sonck, B. The influence of operator-controlled variables on spray drift from field crop sprayers. Trans. ASABE 2007, 50, 1129–1140. [Google Scholar] [CrossRef]
- Kruckeberg, J.P.; Hanna, M.; Darr, M.; Steward, B. An interactive spray drift simulator. In Proceedings of the American Society of Agricultural and Biological Engineers International Meeting, Pittsburgh, Pennsylvania, 20–23 June 2010; p. 1. [Google Scholar]
- Ellis, M.C.B.; Miller, P.C.H. The Silsoe Spray Drift Model: A model of spray drift for the assessment of non-target exposures to pesticides. Biosyst. Eng. 2010, 107, 169–177. [Google Scholar] [CrossRef]
- Kruckeberg, J.P.; Hanna, H.M.; Steward, B.L.; Darr, M.J. The Relative Accuracy of Driftsim When Used as a Real-Time Spray Drift Predictor. Trans. ASABE 2012, 55, 1159–1165. [Google Scholar] [CrossRef]
- Ganzelmeier, H.; Rautmann, D. Drift, drift reducing sprayers and sprayer testing. Asp. Appl. Biol. 2000, 57, 1–10. [Google Scholar]
- Otto, S.; Loddo, D.; Baldoin, C.; Zanin, G. Spray drift reduction techniques for vineyards in fragmented landscapes. J Environ. Manag. 2015, 162, 290–298. [Google Scholar] [CrossRef]
- Holterman, H.J.; van de Zande, J.C.; Porskamp, H.A.J.; Huijsmans, J.F.M. Modelling spray drift from boom sprayers. Comput. Electron. Agric. 1997, 19, 1–22. [Google Scholar] [CrossRef]
- Briffa, F.E.; Dombrowski, N. Entrainment of air into a liquid spray. AIChE J. 1966, 12, 708–717. [Google Scholar] [CrossRef]
- Delele, M.A.; De Moor, A.; Sonck, B.; Ramon, H.; Nicolai, B.M.; Verboven, P. Modelling and validation of the air flow generated by a cross flow air sprayer as affected by travel speed and fan speed. Biosyst. Eng. 2005, 92, 165–174. [Google Scholar] [CrossRef]
- Abramovich, G.N. The Theory of Turbulent jets; MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Fox, R.; Brazee, R.; Svensson, S.; Reichard, D. Air jet velocities from a cross-flow fan sprayer. Trans. ASAE 1992, 35, 1381–1384. [Google Scholar] [CrossRef]
- Gu, J.; Zhu, H.; Ding, W. Unimpeded Air Velocity Profiles of an Air-Assisted Five-Port Sprayer. Trans. ASABE 2012, 55, 1659–1666. [Google Scholar] [CrossRef]
- Sidahmed, M.M.; Brown, R.B. Simulation of spray dispersal and deposition from a forestry airblast sprayer—Part I: Air jet model. Trans. ASAE 2001, 44, 5–10. [Google Scholar] [CrossRef]
- Zhu, H.; Brazee, R.D.; Derksen, R.C.; Fox, R.D.; Krause, C.R.; Ozkan, H.E.; Losely, K. A specially designed air-assisted sprayer to improve spray penetration and air jet velocity distribution inside dense nursery crops. Trans. ASABE 2006, 49, 1285–1294. [Google Scholar] [CrossRef]
- Friso, D.; Baldoin, C.; Pezzi, F. Mathematical modeling of the dynamics of air jet crossing the canopy of tree crops during pesticide application. Appl. Math. Sci. 2015, 9, 1281–1296. [Google Scholar] [CrossRef]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolai, B.M.; Verboven, P. A new integrated CFD modelling approach towards air-assisted orchard spraying. Part I. Model development and effect of wind speed and direction on sprayer airflow. Comput. Electron. Agric. 2010, 71, 128–136. [Google Scholar] [CrossRef]
- Ashgriz, N. Handbook of Atomization and Sprays: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Sidahmed, M.M.; Brown, R.B.; Darvishvand, M. Drop-size/velocity correlations at formation of sprays from fan nozzles. Trans. ASAE 1999, 42, 1557–1564. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; Lopez-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- Lasheras, J.C.; Villermaux, E.; Hopfinger, E.J. Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 1998, 357, 351–379. [Google Scholar] [CrossRef] [Green Version]
- Reichard, D.; Retzer, H.; Liljedahl, L.; Hall, F. Spray droplet size distributions delivered by air blast orchard sprayers. Trans. ASAE 1977, 20, 232–237. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Atomization and Sprays, Hemisphere Pub. Corp. N. Y. 1989, 1989, 251–261. [Google Scholar]
- Yamada, T. A numerical model study of turbulent airflow in and above a forest canopy. J. Meteorol. Soc. Jpn. Ser. II 1982, 60, 439–454. [Google Scholar] [CrossRef] [Green Version]
- Cionco, R.M. A mathematical model for air flow in a vegetative canopy. J. Appl. Meteorol. 1965, 4, 517–522. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.; Zhu, H.; Ding, W.; Wang, X. Characterization of Air Profiles Impeded by Plant Canopies for a Variable-Rate Air-Assisted Sprayer. Trans. ASABE 2014, 57, 1307–1315. [Google Scholar] [CrossRef]
- Lemon, E.; Ordway, D.; Ritter, A.; Spence, D.; Tan, H.; Ling, S.; Stoller, J. The Energy Balance at the Earth’s Surface; Part II USDA Prod. Rep. No. 72; Government Printing Office: Washington, DC, USA, 1963.
- Wilson, J.D. Numerical studies of flow through a windbreak. J. Wind Eng. Ind. Aerodyn. 1985, 21, 207–221. [Google Scholar] [CrossRef]
- Bartzanas, T.; Boulard, T.; Kittas, C. Effect of vent arrangement on windward ventilation of a tunnel greenhouse. Biosyst. Eng. 2004, 88, 479–490. [Google Scholar] [CrossRef]
- Boulard, T.; Wang, S. Experimental and numerical studies on the heterogeneity of crop transpiration in a plastic tunnel. Comput. Electron. Agric. 2002, 34, 173–190. [Google Scholar] [CrossRef]
- Gromke, C. Modeling vegetation in Wind Engineering wind tunnel studies. In Proceedings of the Seventh International Colloquium on Bluff Body Aerodynamics and Applications, Shanghai, China, 2–6 September 2012; pp. 1421–1428. [Google Scholar]
- Fitzmaurice, L.; Shaw, R.H.; Kyaw, T.P.U.; Patton, E.G. Three-dimensional scalar microfront systems in a large-eddy simulation of vegetation canopy flow. Bound. Layer Meteorol. 2004, 112, 107–127. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Black, T.; Novak, M. E-ε modelling of turbulent air flow downwind of a model forest edge. Bound. Layer Meteorol. 1996, 77, 21–44. [Google Scholar] [CrossRef]
- Cionco, R.M. A wind-profile index for canopy flow. Bound. Layer Meteorol. 1972, 3, 255–263. [Google Scholar] [CrossRef]
- Inoue, E. On the Turbulent Structure of Airflow within. J. Meteorol. Soc. Jpn. Ser. II 1963, 41, 317–326. [Google Scholar] [CrossRef] [Green Version]
- Wilson, J.D. Trajectory models for heavy particles in atmospheric turbulence: Comparison with observations. J. Appl. Meteorol. 2000, 39, 1894–1912. [Google Scholar] [CrossRef]
- Katul, G.; Hsieh, C.-I.; Bowling, D.; Clark, K.; Shurpali, N.; Turnipseed, A.; Albertson, J.; Tu, K.; Hollinger, D.; Evans, B. Spatial variability of turbulent fluxes in the roughness sublayer of an even-aged pine forest. Bound. Layer Meteorol. 1999, 93, 1–28. [Google Scholar] [CrossRef]
- Massman, W.; Weil, J. An analytical one-dimensional second-order closure model of turbulence statistics and the Lagrangian time scale within and above plant canopies of arbitrary structure. Bound. Layer Meteorol. 1999, 91, 81–107. [Google Scholar] [CrossRef]
- Poggi, D.; Porporato, A.; Ridolfi, L.; Albertson, J.; Katul, G. The effect of vegetation density on canopy sub-layer turbulence. Bound. Layer Meteorol. 2004, 111, 565–587. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Meyers, T.P. Turbulence structure in a deciduous forest. Bound. Layer Meteorol. 1988, 43, 345–364. [Google Scholar] [CrossRef]
- Greens, S.; Grace, J.; Hutchings, N. Observations of turbulent air flow in three stands of widely spaced Sitka spruce. Agric. For. Meteorol. 1995, 74, 205–225. [Google Scholar] [CrossRef]
- Nepf, H.; Vivoni, E. Flow structure in depth-limited, vegetated flow (Paper 2000JC900145). J. Geophys. Res. All Ser. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Da Silva, A.; Sinfort, C.; Tinet, C.; Pierrat, D.; Huberson, S. A Lagrangian model for spray behaviour within vine canopies. J. Aerosol Sci. 2006, 37, 658–674. [Google Scholar] [CrossRef] [Green Version]
- Mochida, A.; Tabata, Y.; Iwata, T.; Yoshino, H. Examining tree canopy models for CFD prediction of wind environment at pedestrian level. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1667–1677. [Google Scholar] [CrossRef]
- Sanz, C. A note on k-ε modelling of vegetation canopy air-flows. Bound. Layer Meteorol. 2003, 108, 191–197. [Google Scholar] [CrossRef]
- Cava, D.; Katul, G.G. Spectral short-circuiting and wake production within the canopy trunk space of an alpine hardwood forest. Bound. Layer Meteorol. 2008, 126, 415–431. [Google Scholar] [CrossRef]
- Mercer, G.N.; Sweatman, W.L.; Forster, W.A. A model for spray droplet adhesion, bounce or shatter at a crop leaf surface. In Progress in Industrial Mathematics at ECMI 2008; Springer: Berlin, Germany, 2010; pp. 945–951. [Google Scholar] [CrossRef]
- Zwertvaegher, I.K.; Verhaeghe, M.; Brusselman, E.; Verboven, P.; Lebeau, F.; Massinon, M.; Nicolaï, B.M.; Nuyttens, D. The impact and retention of spray droplets on a horizontal hydrophobic surface. Biosyst. Eng. 2014, 126, 82–91. [Google Scholar] [CrossRef] [Green Version]
- Peters, K.; Eiden, R. Modelling the dry deposition velocity of aerosol particles to a spruce forest. Atmos. Environ. Part A. Gen. Top. 1992, 26, 2555–2564. [Google Scholar] [CrossRef]
- Walklate, P. A simulation study of pesticide drift from an air-assisted orchard sprayer. J. Agric. Eng. Res. 1992, 51, 263–283. [Google Scholar] [CrossRef]
- Mercer, G.N. Modelling to determine the optimal porosity of shelterbelts for the capture of agricultural spray drift. Environ. Model. Softw. 2009, 24, 1349–1352. [Google Scholar] [CrossRef]
- Slinn, W. Predictions for particle deposition to vegetative canopies. Atmos. Environ. (1967) 1982, 16, 1785–1794. [Google Scholar] [CrossRef]
- Attané, P.; Girard, F.; Morin, V. An energy balance approach of the dynamics of drop impact on a solid surface. Phys. Fluids 2007, 19, 012101. [Google Scholar] [CrossRef]
- Mundo, C.; Sommerfeld, M.; Tropea, C. Droplet-Wall Collisions—Experimental Studies of the Deformation and Breakup Process. Int. J. Multiph. Flow 1995, 21, 151–173. [Google Scholar] [CrossRef]
- Yoon, S.S.; DesJardin, P.E.; Presser, C.; Hewson, J.C.; Avedisian, C.T. Numerical modeling and experimental measurements of water spray impact and transport over a cylinder. Int. J. Multiph. Flow 2006, 32, 132–157. [Google Scholar] [CrossRef]
- Løfstrøm, P.; Bruus, M.; Andersen, H.V.; Kjær, C.; Nuyttens, D.; Astrup, P. The OML-SprayDrift model for predicting pesticide drift and deposition from ground boom sprayers. J. Pestic. Sci. 2013, 38, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.W.; Zhao, L.Y.; Zhu, H.P. CFD simulation of airflow inside tree canopies discharged from air-assisted sprayers. Comput. Electron. Agric. 2018, 149, 121–132. [Google Scholar] [CrossRef]
- Hong, S.-W.; Zhao, L.; Zhu, H. CFD simulation of pesticide spray from air-assisted sprayers in an apple orchard: Tree deposition and off-target losses. Atmos. Environ. 2018, 175, 109–119. [Google Scholar] [CrossRef]
- Pontiggia, M.; Derudi, M.; Busini, V.; Rota, R. Hazardous gas dispersion: A CFD model accounting for atmospheric stability classes. J. Hazard. Mater. 2009, 171, 739–747. [Google Scholar] [CrossRef]
- Dyer, A.; Hicks, B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Thompson, N.; Ley, A. Estimating spray drift using a random-walk model of evaporating drops. J. Agric. Eng. Res. 1983, 28, 419–435. [Google Scholar] [CrossRef]
- Vigiak, O.; Sterk, G.; Warren, A.; Hagen, L.J. Spatial modeling of wind speed around windbreaks. Catena 2003, 52, 273–288. [Google Scholar] [CrossRef]
- De Schampheleire, M.; Nuyttens, D.; Dekeyser, D.; Verboven, P.; Spanoghe, P.; Cornelis, W.; Gabriels, D.; Steurbaut, W. Deposition of spray drift behind border structures. Crop Prot. 2009, 28, 1061–1075. [Google Scholar] [CrossRef]
- Davis, B.N.; Brown, M.J.; Frost, A.J.; Yates, T.J.; Plant, R.A. The effects of hedges on spray deposition and on the biological impact of pesticide spray drift. Ecotoxicol. Environ. Saf. 1994, 27, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Cleugh, H.A. Effects of windbreaks on airflow, microclimates and crop yields. Agrofor. Syst. 1998, 41, 55–84. [Google Scholar] [CrossRef]
- Heisler, G.M.; Dewalle, D.R. 2. Effects of windbreak structure on wind flow. Agric. Ecosyst. Environ. 1988, 22, 41–69. [Google Scholar] [CrossRef]
- Lee, J.P.; Lee, S.J. PIV analysis on the shelter effect of a bank of real fir trees. J. Wind Eng. Ind. Aerodyn. 2012, 110, 40–49. [Google Scholar] [CrossRef]
- Rosenfeld, M.; Marom, G.; Bitan, A. Numerical Simulation of the Airflow Across Trees in a Windbreak. Bound. Layer Meteorol. 2010, 135, 89–107. [Google Scholar] [CrossRef]
- Salcedo, R.; Vallet, A.; Granell, R.; Garcera, C.; Molto, E.; Chueca, P. Eulerian-Lagrangian model of the behaviour of droplets produced by an air-assisted sprayer in a citrus orchard. Biosyst. Eng. 2017, 154, 76–91. [Google Scholar] [CrossRef]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolai, B.M.; Verboven, P. A new integrated CFD modelling approach towards air-assisted orchard spraying-Part II: Validation for different sprayer types. Comput. Electron. Agric. 2010, 71, 137–147. [Google Scholar] [CrossRef]
- Senecal, P.K.; Schmidt, D.P.; Nouar, I.; Rutland, C.J.; Reitz, R.D.; Corradini, M.L. Modeling high-speed viscous liquid sheet atomization. Int. J. Multiph. Flow 1999, 25, 1073–1097. [Google Scholar] [CrossRef]
- Tsay, J.; Fox, R.D.; Ozkan, H.E.; Brazee, R.D.; Derksen, R.C. Evaluation of a pneumatic-shielded spraying system by CFD simulation. Trans. ASAE 2002, 45, 47–54. [Google Scholar] [CrossRef]
- Tsay, J.; Ozkan, H.E.; Brazee, R.D.; Fox, R.D. CFD simulation of moving spray shields. Trans. ASAE 2002, 45, 21–26. [Google Scholar] [CrossRef]
- Hong, S.-W.; Zhao, L.; Zhu, H. SAAS, a computer program for estimating pesticide spray efficiency and drift of air-assisted pesticide applications. Comput. Electron. Agric. 2018, 155, 58–68. [Google Scholar] [CrossRef]
- Duga, A.T.; Delele, M.A.; Ruysen, K.; Dekeyser, D.; Nuyttens, D.; Bylemans, D.; Nicolai, B.M.; Verboven, P. Development and validation of a 3D CFD model of drift and its application to air-assisted orchard sprayers. Biosyst. Eng. 2017, 154, 62–75. [Google Scholar] [CrossRef]
- Badules, J.; Vidal, M.; Boné, A.; Llop, J.; Salcedo, R.; Gil, E.; García-Ramos, F.J. Comparative study of CFD models of the air flow produced by an air-assisted sprayer adapted to the crop geometry. Comput. Electron. Agric. 2018, 149, 166–174. [Google Scholar] [CrossRef]
- Dekeyser, D.; Duga, A.T.; Verboven, P.; Endalew, A.M.; Hendrickx, N.; Nuyttens, D. Assessment of orchard sprayers using laboratory experiments and computational fluid dynamics modelling. Biosyst. Eng. 2013, 114, 157–169. [Google Scholar] [CrossRef]
- García-Ramos, F.J.; Malón, H.; Aguirre, A.J.; Boné, A.; Puyuelo, J.; Vidal, M. Validation of a CFD model by using 3D sonic anemometers to analyse the air velocity generated by an air-assisted sprayer equipped with two axial fans. Sensors 2015, 15, 2399–2418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, R.B.; Sidahmed, M.M. Simulation of Spray Dispersal and Deposition from a Forestry Airblast Sprayer—Part II: Droplet Trajectory Model. Trans. ASAE 2001, 44, 11. [Google Scholar] [CrossRef]
- Endalew, A.M.; Hertog, M.; Delele, M.; Baetens, K.; Persoons, T.; Baelmans, M.; Ramon, H.; Nicolaï, B.; Verboven, P. CFD modelling and wind tunnel validation of airflow through plant canopies using 3D canopy architecture. Int. J. Heat Fluid Flow 2009, 30, 356–368. [Google Scholar] [CrossRef]
- Kira, O.; Dubowski, Y.; Linker, R. In-situ open path FTIR measurements of the vertical profile of spray drift from air-assisted sprayers. Biosyst. Eng. 2018, 169, 32–41. [Google Scholar] [CrossRef]
- Musiu, E.M.; Qi, L.; Wu, Y. Evaluation of droplets size distribution and velocity pattern using Computational Fluid Dynamics modelling. Comput. Electron. Agric. 2019, 164, 104886. [Google Scholar] [CrossRef]
- Gosselin, F.P. Mechanics of a plant in fluid flow. J. Exp. Bot. 2019, 70, 3533–3548. [Google Scholar] [CrossRef] [PubMed]
- Duga, A.T.; Defraeye, T.; Nicolai, B.; Verboven, P. Modeling air flow around branches and leaves using fluid-structure interaction simulations. Asp. Appl. Biol. 2014, 122, 315–322. [Google Scholar]
- Delele, M.A.; Nuyttens, D.; Ambaw, A.; Lebeau, F.; Nicolae, B.; Verboven, P. Studying the impact characteristics of spray droplets on plant surfaces using a multiphase CFD model. Int. Adv. Pestic. Appl. 2016, 132, 291–298. [Google Scholar]
- Zhu, L.; Ge, J.-R.; Qi, Y.-Y.; Chen, Q.; Hua, R.-M.; Luo, F.; Chen, P.-R. Droplet impingement behavior analysis on the leaf surface of Shu-ChaZao under different pesticide formulations. Comput. Electron. Agric. 2018, 144, 16–25. [Google Scholar] [CrossRef]
- Jiang, X.; Siamas, G.; Jagus, K.; Karayiannis, T. Physical modelling and advanced simulations of gas–liquid two-phase jet flows in atomization and sprays. Prog. Energy Combust. Sci. 2010, 36, 131–167. [Google Scholar] [CrossRef]
- Buck-Sorlin, G. Process-based Model. In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.-H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013; p. 1755. [Google Scholar] [CrossRef]
- Alix, A.; Knauer, K.; Streloke, M.; Poulsen, V. Development of a harmonized risk mitigation toolbox dedicated to environmental risks of pesticides in farmland in Europe: Outcome of the MAgPIE workshop. Fifth European Workshop on Standardised Procedure for the Inspection of Sprayers in Europe—SPISE 5. Jul. Kühn Arch. 2015, 449, 149–155. [Google Scholar] [CrossRef]
| References | Regression Models | Conditions |
|---|---|---|
| Ganzelmeier and Rautmann (2000) [52] | 15 m, vineyard < 0.4 m | |
| Smith et al. (2000) [47] | 27.5 m, grass area, R2 = 0.83, RMSE = 0.54 | |
| Smith et al. (2000) [47] | ≤ 312 m, no obstruction field, R2 = 0.87, RMSE = 0.53 | |
| Nuyttens et al. (2007) [48] | ≤ 20 m, meadow, R2 = 0.84 | |
| Lazzaro et al. (2008) [46] | 12 m, hedgerow, R2 = 0.98 | |
| Arvidsson et al. (2011) [45] | for total drift for airborne drift for fall-out drift | = 5 m, cereal crops, R2 = 0.87~0.97 |
| Arvidsson et al. (2011) [45] | for total drift for airborne drift for fall-out drift | = 5 m, grazing fields, R2 = 0.84~0.85 |
| Otto et al. (2015) [53] | Tested at 0.2 ≤ ≤ 15 m, vineyard, R2 = 0.97~0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.-w.; Park, J.; Jeong, H.; Lee, S.; Choi, L.; Zhao, L.; Zhu, H. Fluid Dynamic Approaches for Prediction of Spray Drift from Ground Pesticide Applications: A Review. Agronomy 2021, 11, 1182. https://doi.org/10.3390/agronomy11061182
Hong S-w, Park J, Jeong H, Lee S, Choi L, Zhao L, Zhu H. Fluid Dynamic Approaches for Prediction of Spray Drift from Ground Pesticide Applications: A Review. Agronomy. 2021; 11(6):1182. https://doi.org/10.3390/agronomy11061182
Chicago/Turabian StyleHong, Se-woon, Jinseon Park, Hanna Jeong, Seyeon Lee, Lakyeong Choi, Lingying Zhao, and Heping Zhu. 2021. "Fluid Dynamic Approaches for Prediction of Spray Drift from Ground Pesticide Applications: A Review" Agronomy 11, no. 6: 1182. https://doi.org/10.3390/agronomy11061182
APA StyleHong, S.-w., Park, J., Jeong, H., Lee, S., Choi, L., Zhao, L., & Zhu, H. (2021). Fluid Dynamic Approaches for Prediction of Spray Drift from Ground Pesticide Applications: A Review. Agronomy, 11(6), 1182. https://doi.org/10.3390/agronomy11061182







