Climate Change Adaptation Measures in the Irrigation of a Super-Intensive Olive Orchard in the South of Portugal
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil
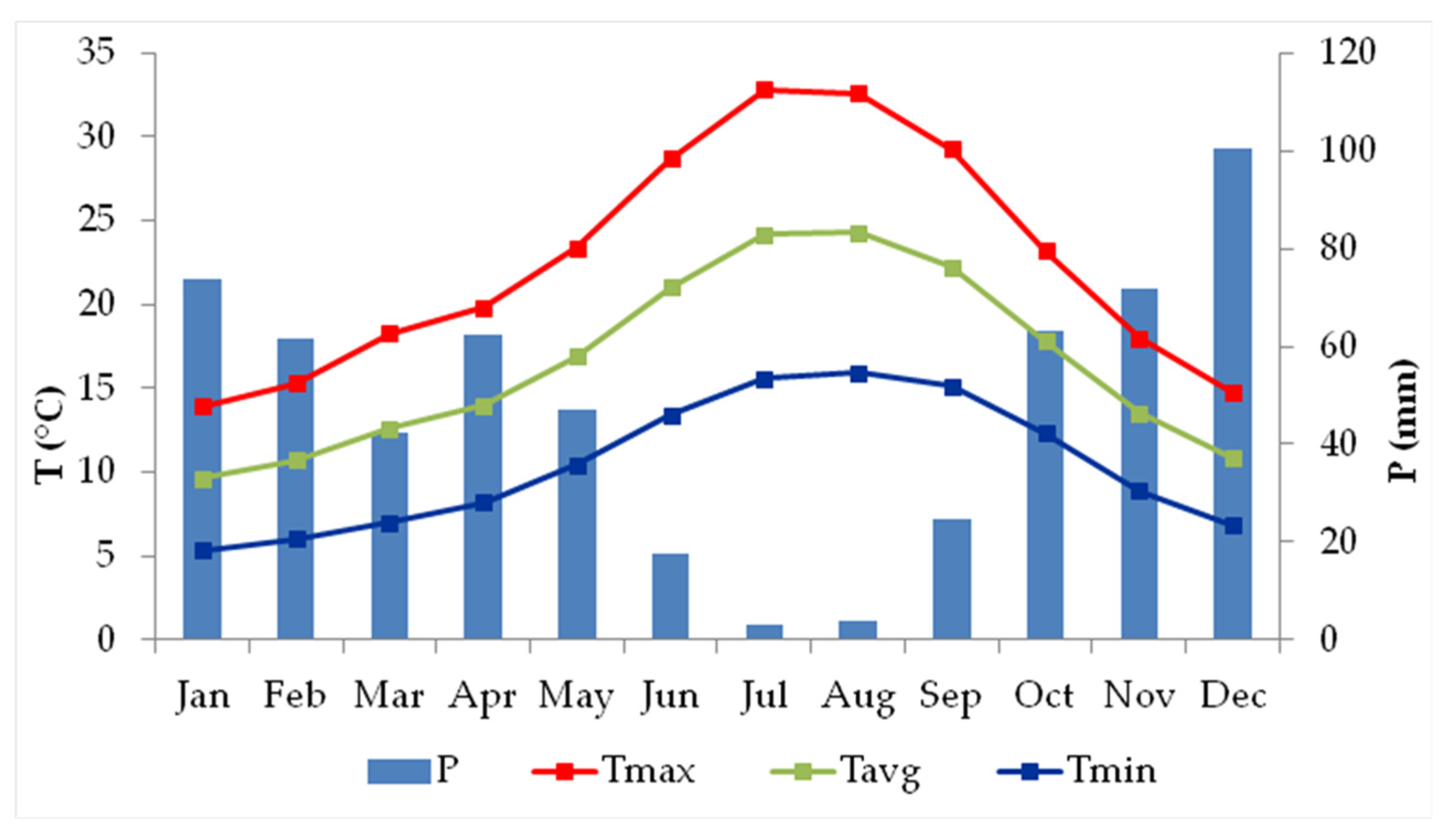
2.3. Climate
Climate Data Sets
2.4. Crop
2.5. Phenology
2.6. Adaptation Measures
2.6.1. Current Irrigation Management (CIM)
2.6.2. Deficit Irrigation Management (DIM)
2.7. Crop Irrigation Requirements Modeling–Climate Change Impacts and Adaptation Measures Evaluation
2.7.1. Model Parameterization
2.7.2. Irrigation Requirements Modeling
3. Discussion and Results
3.1. Climatic Data (Climate Change Scenarios)
3.2. Phenology
3.3. Model Parametrization
3.4. Crop Irrigation Requirements Simulation
3.4.1. Current Irrigation Management (CIM)
3.4.2. Deficit Irrigation Management (DIM)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Kovats, R.S.; Valentini, R.; Bouwer, L.M.; Georgopoulou, E.; Jacob, D.; Martin, E.; Rounsevell, M.; Soussana, J.-F. Europe. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1267–1326. [Google Scholar]
- Miranda, P.M.; Cardoso, R.M.; Soares, P.M.M.; Valente, M.A.; Viterbo, P.A. Mudança Climática. In Cultivar. Cadernos de Análise e Prospective; Gabinete de Planeamento, Políticas e Administração Gera: Lisbon, Portugal, 2018; Volume 12, pp. 29–37. [Google Scholar]
- Pires, V.; Cota, T.M.; Silva, A. Observações Alteradas no Clima Atual e Cenários Climáticos em Portugal Continental-Influência no Setor Agrícola. In Cultivar. Cadernos de Análise e Prospective; Gabinete de Planeamento, Políticas e Administração Gera: Lisbon, Portugal, 2018; Volume 12, pp. 57–67. [Google Scholar]
- Jiménez Cisneros, B.E.; Oki, T.; Arnell, N.W.; Benito, G.; Cogley, J.G.; Döll, P.; Jiang, T.; Mwakalila, S.S. Freshwater Resources. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 229–269. [Google Scholar]
- Mourato, S.; Moreira, M.; Cortereal, J.A.M. Water Resources Impact Assessment Under Climate Change Scenarios in Mediterranean Watersheds. Water Resour. Manag. 2015, 29, 2377–2391. [Google Scholar] [CrossRef]
- Empresa de Desenvolvimento e Infra-Estruturas do Alqueva. Anuário Agrícola de Alqueva 2020. Available online: https://www.edia.pt/wp-content/uploads/2021/01/Anuario_Agricola_Alqueva_2020_ii.pdf (accessed on 21 May 2021).
- Paulo, A.; Pinto, H. Necessidades hídricas do olival no Alentejo e projecções para o período 2071–2100. Rev. Unidade Investig. Inst. Politécnico St. 2014, 4, 148–162. [Google Scholar]
- Rolim, J.; Teixeira, J.L.; Catalão, J.; Shahidian, S. The Impacts of Climate Change on Irrigated Agriculture in Southern Portugal. Irrig. Drain. 2016, 66, 3–18. [Google Scholar] [CrossRef]
- Díaz, J.A.R.; Weatherhead, E.K.; Knox, J.; Camacho, E. Climate change impacts on irrigation water requirements in the Guadalquivir river basin in Spain. Reg. Environ. Chang. 2007, 7, 149–159. [Google Scholar] [CrossRef]
- Tanasijevic, L.; Todorovic, M.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Impacts of climate change on olive crop evapotranspiration and irrigation requirements in the Mediterranean region. Agric. Water Manag. 2014, 144, 54–68. [Google Scholar] [CrossRef]
- Valverde, P.; Serralheiro, R.; Carvalho, M.; Maia, R.; Oliveira, B.; Ramos, V. Climate change impacts on irrigated agriculture in the Guadiana river basin (Portugal). Agric. Water Manag. 2015, 152, 17–30. [Google Scholar] [CrossRef] [Green Version]
- Saadi, S.; Todorovic, M.; Tanasijevic, L.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Climate change and Mediterranean agriculture: Impacts on winter wheat and tomato crop evapotranspiration, irrigation requirements and yield. Agric. Water Manag. 2014, 147, 103–115. [Google Scholar] [CrossRef]
- Lorite, I.; Gabaldón-Leal, C.; Ruiz-Ramos, M.; Belaj, A.; de la Rosa, R.; León, L.; Santos, C. Evaluation of olive response and adaptation strategies to climate change under semi-arid conditions. Agric. Water Manag. 2018, 204, 247–261. [Google Scholar] [CrossRef]
- Fraga, H.; Pinto, J.G.; Santos, J.A. Olive tree irrigation as a climate change adaptation measure in Alentejo, Portugal. Agric. Water Manag. 2020, 237, 106193. [Google Scholar] [CrossRef]
- Soares, D.; Rolim, J.; Fradinho, M.J.; Paço, T.A.D. Climate Change Impacts on Irrigation Requirements of Preserved Forage for Horses under Mediterranean Conditions. Agronomy 2020, 10, 1758. [Google Scholar] [CrossRef]
- Zeleke, K. Simulating Agronomic Adaptation Strategies to Mitigate the Impacts of Climate Change on Wheat Yield in South-Eastern Australia. Agronomy 2021, 11, 337. [Google Scholar] [CrossRef]
- Abreu, J.P.D.M.E. Modelling olive flowering date using chilling for dormancy release and thermal time. Agric. For. Meteorol. 2004, 125, 117–127. [Google Scholar] [CrossRef]
- Teixeira, J.L.; Pereira, L.S. ISAREG an irrigation scheduling model. ICID Bull. 1992, 41, 29–48. [Google Scholar]
- Liu, Y.; Fernando, R.M.; Pereira, L.S. Water Balance Simulation with ISAREG Considering Water Table Interactions. Proc. World Congr. Comput. Agric. Nat. Resour. USA 2013, 857. [Google Scholar] [CrossRef]
- Oweis, T.; Rodrigues, P.N.; Pereira, L.S. Simulation of Supplemental Irrigation Strategies for Wheat in Near East to Cope with Water Scarcity. In Tools for Drought Mitigation in Mediterranean Regions; Rossi, G., Cancelliere, A., Pereira, L.S., Oweis, T., Shatanawi, M., Zairi, A., Eds.; Water Science and Technology Library, Springer: Dordrecht, The Netherlands, 2003; Volume 44, pp. 259–272. [Google Scholar] [CrossRef]
- Al-Zu’Bi, Y.A.; Al-Kharabsheh, A. Multicriteria Analysis For Water Productivity in the Jordan Valley. Water Int. 2003, 28, 501–511. [Google Scholar] [CrossRef]
- Cancela, J.J.; Cuesta, T.S.; Neira, X.; Pereira, L.S. Modelling for Improved Irrigation Water Management in a Temperate Region of Northern Spain. Biosyst. Eng. 2006, 94, 151–163. [Google Scholar] [CrossRef]
- Cholpankulov, E.D.; Inchenkova, O.P.; Paredes, P.; Pereira, L.S. Cotton irrigation scheduling in central Asia: Model calibration and validation with consideration of groundwater contribution. Irrig. Drain. 2008, 57, 516–532. [Google Scholar] [CrossRef] [Green Version]
- Popova, Z.; Pereira, L.S. Modelling for maize irrigation scheduling using long term experimental data from Plovdiv region, Bulgaria. Agric. Water Manag. 2011, 98, 675–683. [Google Scholar] [CrossRef]
- Popova, Z. Impact of climate change on maize yield in South Bulgaria. Bulg. J. Meteorol. Hydrol. 2010, 15, 62–71. [Google Scholar]
- Paço, T.A.; Paredes, P.; Pereira, L.S.; Silvestre, J.; Santos, F.L. Crop Coefficients and Transpiration of a Super Intensive Arbequina Olive Orchard using the Dual Kc Approach and the Kcb Computation with the Fraction of Ground Cover and Height. Water 2019, 11, 383. [Google Scholar] [CrossRef] [Green Version]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2013, 14, 563–578. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Hunsaker, D.; Kimball, B.; Pinter, P.; Wall, G.; Lamorte, R.; Adamsen, F.; Leavitt, S.; Thompson, T.; Matthias, A.; Brooks, T. CO2 enrichment and soil nitrogen effects on wheat evapotranspiration and water use efficiency. Agric. For. Meteorol. 2000, 104, 85–105. [Google Scholar] [CrossRef]
- Martins, J.; Fraga, H.; Fonseca, A.; Santos, J. Climate Projections for Precipitation and Temperature Indicators in the Douro Wine Region: The Importance of Bias Correction. Agronomy 2021, 11, 990. [Google Scholar] [CrossRef]
- European Environment Agency. Climate Change Adaptation in the Agriculture Sector in Europe; EEA Report No 04/2019; Eionet—European Environment Information and Observation Network: Copenhagen, Denmark, 2019; p. 108. [Google Scholar]
- Fraga, H.; Moriondo, M.; Leolini, L.; Santos, J.A. Mediterranean Olive Orchards under Climate Change: A Review of Future Impacts and Adaptation Strategies. Agronomy 2021, 11, 56. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations; International Union of Soil Sciences. World Reference Base for Soil Resources 2014. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps-Update 2015; World Soil Resources Reports No. 106; Food and Agriculture Organization: Rome, Italy, 2015; p. 192. [Google Scholar]
- Cardoso, J.V.J.C. Os Solos de Portugal. Sua Classificação, Caracterização e Génese. Secretaria de Estado da Agricultura; Direcção-Geral dos Serviços Agrícolas: Lisbon, Portugal, 1965; p. 310. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [Green Version]
- International Project Management Association. Climate Normals—1971–2000. Available online: https://www.ipma.pt/en/oclima/normais.clima/1971-2000/#557 (accessed on 12 May 2021).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization Irrigation and Drainage Paper 56; Food and Agriculture Organization: Rome, Italy, 2008; p. 300. [Google Scholar]
- Abu-Hamdeh, N.H.; Al-Widyan, M.I. Effect of axle load, tire inflation pressure, and tillage system on soil physical properties and crop yield of a jordanian soil. Trans. ASAE 2000, 43, 13–21. [Google Scholar] [CrossRef]
- Shahidian, S.; Serralheiro, R.; Teixeira, J.; Serrano, J. Parametric calibration of the Hargreaves-Samani equation for use at new locations. Hydrol. Process. 2013, 27, 605–616. [Google Scholar] [CrossRef]
- Teixeira, J.; Shahidian, S.; Rolim, J. Regional analysis and calibration for the South of Portugal of a simple evapotranspiration model for use in an autonomous landscape irrigation controller. WSEAS Trans. Environ. Dev. 2008, 8, 676–686. [Google Scholar]
- Intergovernmental Panel on Climate Change. Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014; Pachauri, R.K., Meyer, L.A., Eds.; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Instituto Português do Mar e da Atmosfera; Faculdade de Ciências da Universidade de Lisboa. Portal do Clima, Alterações Climáticas em Portugal. Available online: http://portaldoclima.pt/pt/ (accessed on 21 May 2021).
- Graham, L.P.; Andréasson, J.; Carlsson, B. Assessing climate change impacts on hydrology from an ensemble of regional climate models, model scales and linking methods—A case study on the Lule River basin. Clim. Chang. 2007, 81, 293–307. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Van Deursen, W. Estimates of future discharges of the river Rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Räty, O.; Räisänen, J.; Ylhäisi, J.S. Evaluation of delta change and bias correction methods for future daily precipitation: Intermodel cross-validation using ENSEMBLES simulations. Clim. Dyn. 2014, 42, 2287–2303. [Google Scholar] [CrossRef]
- Pastor, M. Riego deficitario del olival: Los programas de recorte de riego en olivar. Agric. Rev. Agropecuária Ganad. 1994, 746, 768–776. [Google Scholar]
- Sanz-Cortes, F.; Martinez-Calvo, J.; Badenes, M.L.; Bleiholder, H.; Hack, H.; Llacer, G.; Meier, U. Phenological growth stages of olive trees (Olea europaea). Ann. Appl. Biol. 2002, 140, 151–157. [Google Scholar] [CrossRef]
- Fernández, J.E.; Perez-Martin, A.; Torres-Ruiz, J.M.; Cuevas, M.V.; Rodriguez-Dominguez, C.M.; Elsayed-Farag, S.; Morales-Sillero, A.; García, J.M.; Hernandez-Santana, V.; Diaz-Espejo, A. A regulated deficit irrigation strategy for hedgerow olive orchards with high plant density. Plant Soil 2013, 372, 279–295. [Google Scholar] [CrossRef] [Green Version]
- Mcmaster, G.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef] [Green Version]
- Fernández, J.-E. Understanding olive adaptation to abiotic stresses as a tool to increase crop performance. Environ. Exp. Bot. 2014, 103, 158–179. [Google Scholar] [CrossRef] [Green Version]
- Kokkotos, E.; Zotos, A.; Patakas, A. Evaluation of Water Stress Coefficient Ks in Different Olive Orchards. Agronomy 2020, 10, 1594. [Google Scholar] [CrossRef]
- Ferreyra, R.; Sellés Van, G.; Sellés, I. Riego Deficitario Controlado en Olivos, 1st ed.; Instituto de Investigaciones Agropecuarias: Santiago, Chile, 2001. [Google Scholar]
- Galán, C.; García-Mozo, H.; Vázquez, L.; Ruiz, L.; De La Guardia, C.D.; Trigo, M.M. Heat requirement for the onset of the Olea europaea L. pollen season in several sites in Andalusia and the effect of the expected future climate change. Int. J. Biometeorol. 2004, 49, 184–188. [Google Scholar] [CrossRef]
- Pérez-López, D.; Ribas, F.; Moriana, A.; Rapoport, H.F.; De Juan, A. Influence of temperature on the growth and development of olive ( Olea europaea L.) trees. J. Hortic. Sci. Biotechnol. 2008, 83, 171–176. [Google Scholar] [CrossRef]
- Avolio, E.; Orlandi, F.; Bellecci, C.; Fornaciari, M.; Federico, S. Assessment of the impact of climate change on the olive flowering in Calabria (southern Italy). Theor. Appl. Clim. 2011, 107, 531–540. [Google Scholar] [CrossRef]
- Garcia-Mozo, H.; Oteros, J.; Galán, C. Phenological changes in olive (Ola europaea L.) reproductive cycle in southern Spain due to climate change. Ann. Agric. Environ. Med. 2015, 22, 421–428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fraga, H.; Pinto, J.G.; Santos, J.A. Climate change projections for chilling and heat forcing conditions in European vineyards and olive orchards: A multi-model assessment. Clim. Chang. 2018, 152, 179–193. [Google Scholar] [CrossRef]
- Pastor, M.; Vega, V.; Hidalgo, J.C. Ensayos en plantaciones de olivar superintensivas e intensivas. Vida Rural 2005, 218, 30–40. [Google Scholar]
- Rosecrance, R.C.; Krueger, W.H.; Milliron, L.; Bloese, J.; Garcia, C.; Mori, B. Moderate regulated deficit irrigation can increase olive oil yields and decrease tree growth in super high density ‘Arbequina’ olive orchards. Sci. Hortic. 2015, 190, 75–82. [Google Scholar] [CrossRef]
- Marra, F.P.; Marino, G.; Marchese, A.; Caruso, T. Effects of different irrigation regimes on a super-high-density olive grove cv. “Arbequina”: Vegetative growth, productivity and polyphenol content of the oil. Irrig. Sci. 2016, 34, 313–325. [Google Scholar] [CrossRef]
- Ahumada-Orellana, L.E.; Ortega-Farías, S.; Searles, P.S. Olive oil quality response to irrigation cut-off strategies in a super-high density orchard. Agric. Water Manag. 2018, 202, 81–88. [Google Scholar] [CrossRef]
- Capra, A.; Scicolone, B. Irrigation Scheduling Optimisation in Olive Groves. J. Exp. Agric. Int. 2018, 28, 1–19. [Google Scholar] [CrossRef]





| Layer | Layer Depth (m) | θFC (cm3 cm−3) | θWP (cm3 cm−3) |
|---|---|---|---|
| Ap | 0.25 | 20.9 | 6.84 |
| B1 | 0.47 | 23.2 | 7.62 |
| B2 | 0.8 | 30.7 | 13.2 |
| C | 1.15 | 26.7 | 11.05 |
| Month | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kc | 0.50 | 0.50 | 0.65 | 0.60 | 0.55 | 0.50 | 0.45 | 0.45 | 0.55 | 0.60 | 0.65 | 0.50 |
| Crop Periods | A–B | B–C | C–D | D–E | E–F | F–G | G–H | H–I |
|---|---|---|---|---|---|---|---|---|
| Irrigation requirements (%) | 100% | 40% | 80% | 40% | 100% | 100% | 40% | |
| Climate Anomalies | |||||
|---|---|---|---|---|---|
| RCP4.5 | RCP8.5 | ||||
| 2011–2040 | 2041–2070 | 2071–2100 | 2011–2040 | 2041–2070 | 2071–2100 |
| T (°C) | |||||
| +0.8 | +1.5 | +1.9 | +1.0 | +2.2 | +3.8 |
| P (mm) | |||||
| −25.4 | −45.1 | −47.2 | −48.7 | −90.7 | −128.3 |
| −4.5% | −7.9% | −8.3% | −8.5% | −15.9% | −22.4% |
| ETo (mm) | |||||
| +36.1 | +71.7 | +83.4 | +47.2 | +98.2 | +171.9 |
| +2.8% | +5.6% | +6.6% | +3.7% | +7.7% | +13.5% |
| Climate Scenarios | Full Flowering |
|---|---|
| Observed in the field (2018) | 28 May |
| Observed in the field (2019) | 10 May |
| Reference scenario (1971–2000) | 23 May |
| RCP4.5 (2011–2040) | 15 May |
| RCP4.5 (2041–2070) | 12 May |
| RCP4.5 (2071–2100) | 7 May |
| RCP8.5 (2011–2040) | 15 May |
| RCP8.5 (2041–2070) | 5 May |
| RCP8.5 (2071–2100) | 24 April |
| Climate Scenarios | Kc adjusted | |||||||
|---|---|---|---|---|---|---|---|---|
| Crop Periods | ||||||||
| A–B | B–C | C–D | D–E | E–F | F–G | G–H | H–I | |
| Ref. (1971–2000) | 0.60 | 0.50 | 0.45 | 0.38 | 0.35 | 0.50 | 0.48 | 0.30 |
| RCP4.5 (2011–2040) | 0.60 | 0.50 | 0.43 | 0.43 | 0.25 | 0.45 | 0.58 | 0.40 |
| RCP4.5 (2041–2070) | 0.60 | 0.55 | 0.45 | 0.35 | 0.23 | 0.43 | 0.53 | 0.35 |
| RCP4.5 (2071–2100) | 0.60 | 0.55 | 0.50 | 0.48 | 0.25 | 0.45 | 0.43 | 0.25 |
| RCP8.5 (2011–2040) | 0.60 | 0.55 | 0.48 | 0.40 | 0.25 | 0.40 | 0.55 | 0.38 |
| RCP8.5 (2041–2070) | 0.60 | 0.55 | 0.48 | 0.45 | 0.28 | 0.48 | 0.50 | 0.33 |
| RCP8.5 (2071–2100) | 0.60 | 0.55 | 0.48 | 0.40 | 0.33 | 0.48 | 0.55 | 0.38 |
| Climate Scenarios | |||||||
|---|---|---|---|---|---|---|---|
| Reference | RCP4.5 | RCP8.5 | |||||
| 1971–2000 | 2011–2040 | 2041–2070 | 2071–2100 | 2011–2040 | 2041–2070 | 2071–2100 | |
| Adaptation Measure—CIM | |||||||
| CIR (mm) | 199.9 | 219.2 | 235.4 | 232.1 | 225.4 | 244.2 | 262.7 |
| ΔCIR (%) | -- | 9.6% | 17.7% | 16.1% | 12.8% | 22.1% | 31.4% |
| Adaptation Measure—DIM | |||||||
| CIR (mm) | 154.9 | 156.8 | 163.6 | 178.9 | 174.1 | 190.9 | 193.2 |
| ΔCIR (%) | −23% | −22% | −18% | −11% | −13% | −5% | −3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Branquinho, S.; Rolim, J.; Teixeira, J.L. Climate Change Adaptation Measures in the Irrigation of a Super-Intensive Olive Orchard in the South of Portugal. Agronomy 2021, 11, 1658. https://doi.org/10.3390/agronomy11081658
Branquinho S, Rolim J, Teixeira JL. Climate Change Adaptation Measures in the Irrigation of a Super-Intensive Olive Orchard in the South of Portugal. Agronomy. 2021; 11(8):1658. https://doi.org/10.3390/agronomy11081658
Chicago/Turabian StyleBranquinho, Sofia, João Rolim, and José Luís Teixeira. 2021. "Climate Change Adaptation Measures in the Irrigation of a Super-Intensive Olive Orchard in the South of Portugal" Agronomy 11, no. 8: 1658. https://doi.org/10.3390/agronomy11081658
APA StyleBranquinho, S., Rolim, J., & Teixeira, J. L. (2021). Climate Change Adaptation Measures in the Irrigation of a Super-Intensive Olive Orchard in the South of Portugal. Agronomy, 11(8), 1658. https://doi.org/10.3390/agronomy11081658








