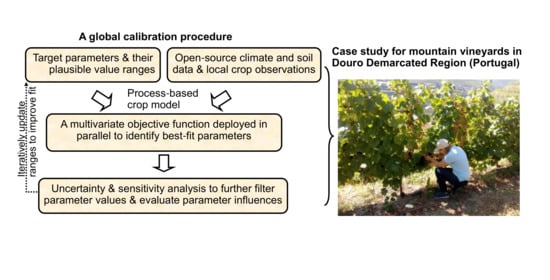
Simultaneous Calibration of Grapevine Phenology and Yield with a Soil–Plant–Atmosphere System Model Using the Frequentist Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Observational Data
2.1.1. Field Measurements on Grapevine
2.1.2. Weather and Soil Inputs
2.2. Brief Description of STICS Grapevine Modules
2.3. Calibration Setup
2.3.1. Identification of the Calibrated Parameters
2.3.2. Establishment of the Unit of Simulation (USM) and Objective Function
2.3.3. Assumption of Error Distributions
2.3.4. Parameter Uncertainty and Sensitivity Analysis
2.4. Evaluations of Calibrated Parameters
2.4.1. Goodness-Of-Fit of the Estimated Parameters
2.4.2. Evaluations Using Additional Published Data
2.5. Data Process and Software Environment
3. Results and Discussion
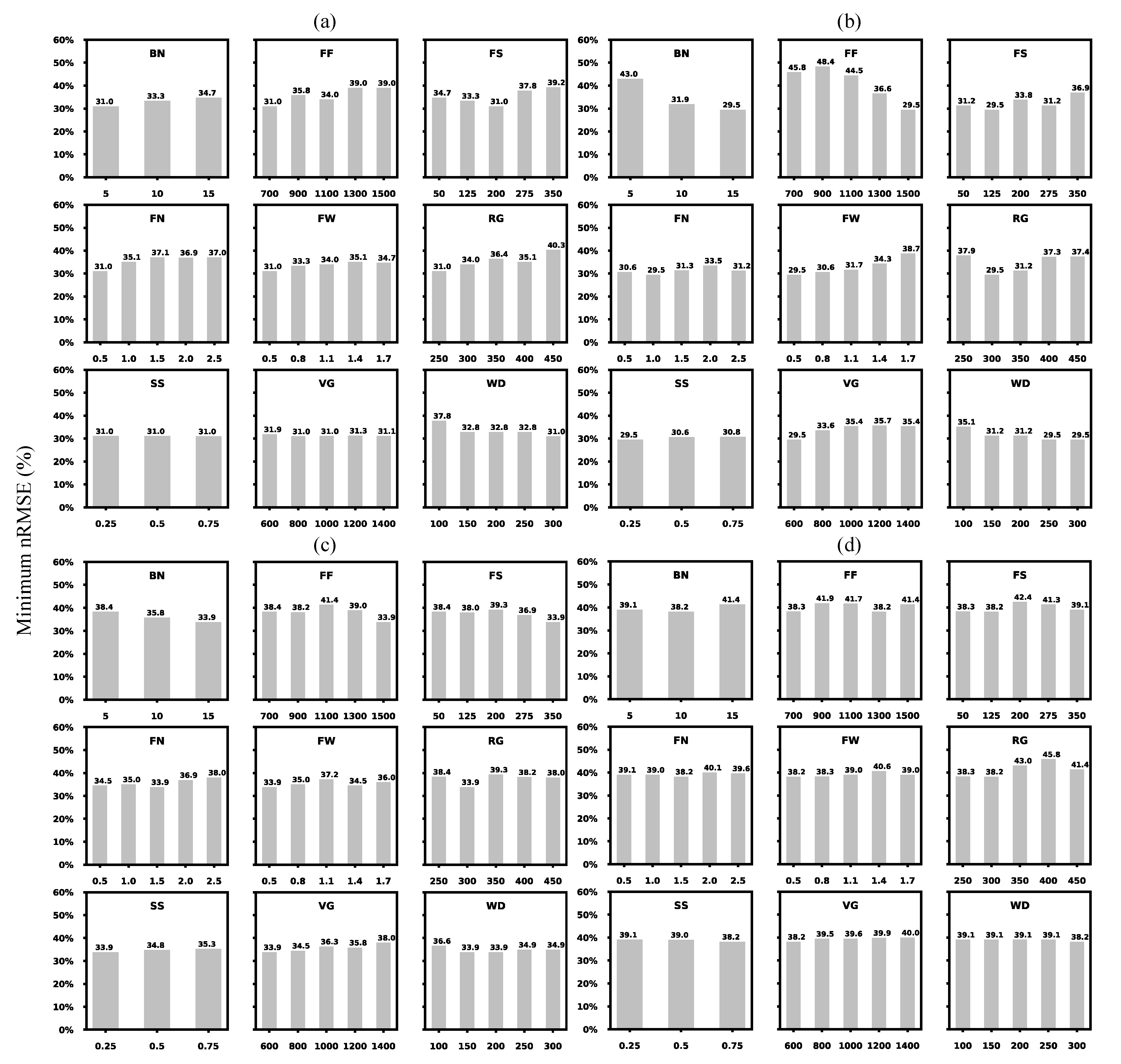
3.1. General Assessment of Testing Parameters
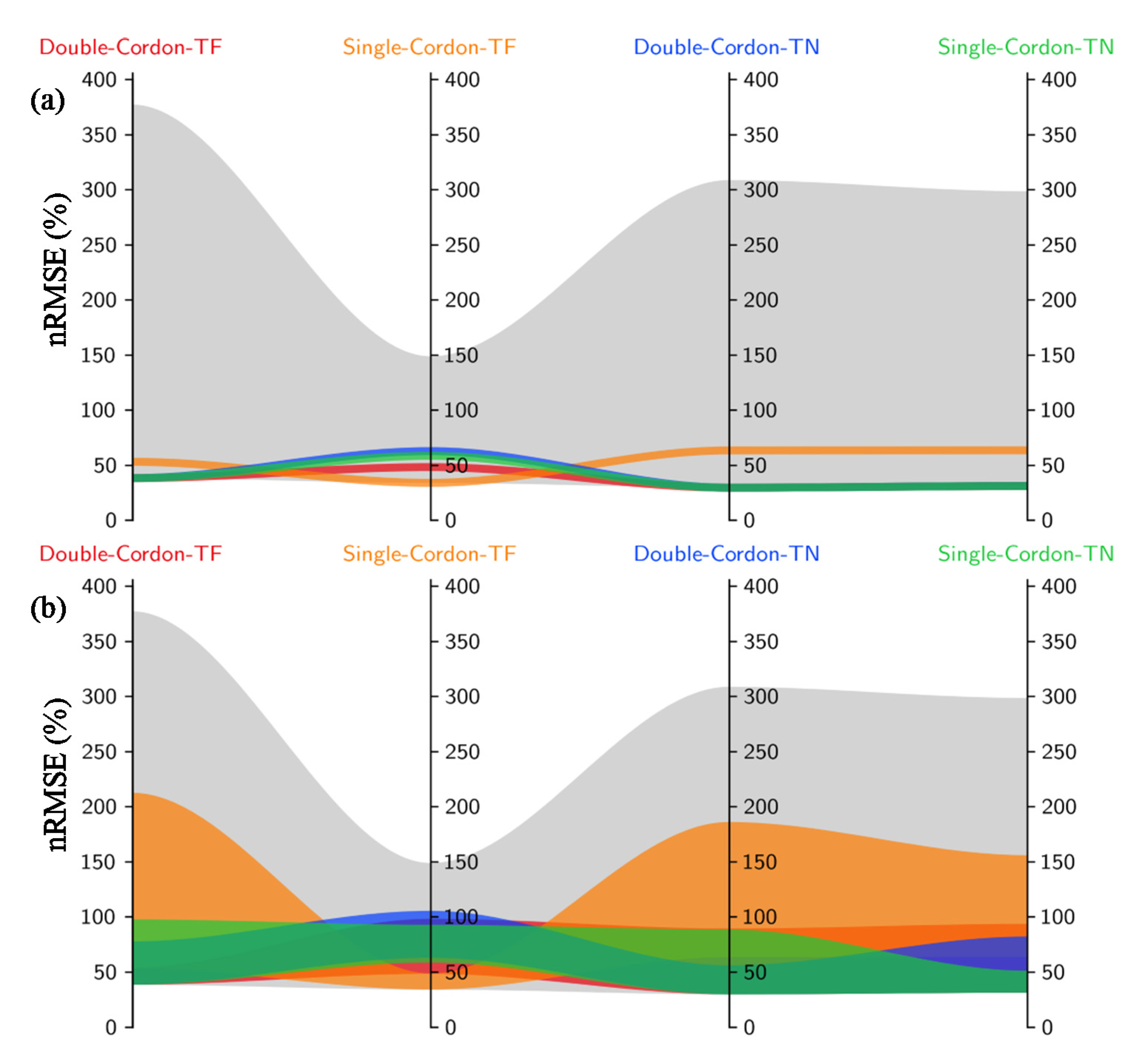
3.1.1. Total Spread of Prediction Uncertainties
3.1.2. Error Dependence and Homoscedasticity Test
3.2. Calibration Results
3.2.1. Calibrated Parameters and Associated Uncertainties
3.2.2. Sensitivity Analysis and Interpretation of Calibrated Parameters
3.2.3. Comparison between Multivariate and Univariate Function
3.3. Variations in the Best-Performing Parameters among Variety–Training Systems
3.4. Evaluations Using Additional Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rötter, R.P.; Hoffmann, M.P.; Koch, M.; Müller, C. Progress in modelling agricultural impacts of and adaptations to climate change. Curr. Opin. Plant Biol. 2018, 45, 255–261. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.; Antle, J.M.; Nelson, G.C.; Porter, C.; Janssen, S.; et al. The Agricultural Model Intercomparison and Improvement Project (AgMIP): Protocols and pilot studies. Agric. For. Meteorol. 2013, 170, 166–182. [Google Scholar] [CrossRef] [Green Version]
- Tao, F.; Palosuo, T.; Rötter, R.P.; Díaz-Ambrona, C.G.H.; Inés Mínguez, M.; Semenov, M.A.; Kersebaum, K.C.; Cammarano, D.; Specka, X.; Nendel, C.; et al. Why do crop models diverge substantially in climate impact projections? A comprehensive analysis based on eight barley crop models. Agric. For. Meteorol. 2020, 281, 107851. [Google Scholar] [CrossRef]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.J.; Rötter, R.P.; Cammarano, D.; et al. Uncertainty in simulating wheat yields under climate change. Nat. Clim. Chang. 2013, 3, 827–832. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Palosuo, T.; Thorburn, P.; Gourdain, E.; Asseng, S.; Basso, B.; Buis, S.; Crout, N.; Dibari, C.; Dumont, B.; et al. How well do crop modeling groups predict wheat phenology, given calibration data from the target population? Eur. J. Agron. 2021, 124, 126195. [Google Scholar] [CrossRef]
- Coucheney, E.; Buis, S.; Launay, M.; Constantin, J.; Mary, B.; García de Cortázar-Atauri, I.; Ripoche, D.; Beaudoin, N.; Ruget, F.; Andrianarisoa, K.S.; et al. Accuracy, robustness and behavior of the STICS soil–crop model for plant, water and nitrogen outputs: Evaluation over a wide range of agro-environmental conditions in France. Environ. Model. Softw. 2015, 64, 177–190. [Google Scholar] [CrossRef]
- Wallach, D.; Palosuo, T.; Thorburn, P.; Hochman, Z.; Gourdain, E.; Andrianasolo, F.; Asseng, S.; Basso, B.; Buis, S.; Crout, N.; et al. The chaos in calibrating crop models. bioRxiv 2020. [Google Scholar] [CrossRef]
- Seidel, S.J.; Palosuo, T.; Thorburn, P.; Wallach, D. Towards improved calibration of crop models—Where are we now and where should we go? Eur. J. Agron. 2018, 94, 25–35. [Google Scholar] [CrossRef]
- Wallach, D.; Thorburn, P.; Asseng, S.; Challinor, A.J.; Ewert, F.; Jones, J.W.; Rotter, R.; Ruane, A. Estimating model predic-tion error: Should you treat predictions as fixed or random? Environ. Model. Softw. 2016, 84, 529–539. [Google Scholar] [CrossRef]
- Wallach, D.; Nissanka, S.P.; Karunaratne, A.S.; Weerakoon, W.M.W.; Thorburn, P.J.; Boote, K.J.; Jones, J.W. Accounting for both parameter and model structure uncertainty in crop model predictions of phenology: A case study on rice. Eur. J. Agron. 2017, 88, 53–62. [Google Scholar] [CrossRef]
- Wallach, D.; Thorburn, P.J. Estimating uncertainty in crop model predictions: Current situation and future prospects. Eur. J. Agron. 2017, 88, A1–A7. [Google Scholar] [CrossRef]
- Bayarri, M.J.; Berger, J.O. The interplay of Bayesian and frequentist analysis. Stat. Sci. 2004, 19, 58–80. [Google Scholar] [CrossRef]
- Wallach, D.; Keussayan, N.; Brun, F.; Lacroix, B.; Bergez, J.-E. Assessing the Uncertainty when Using a Model to Compare Irrigation Strategies. Agron. J. 2012, 104, 1274–1283. [Google Scholar] [CrossRef]
- Liu, L.; Wallach, D.; Li, J.; Liu, B.; Zhang, L.; Tang, L.; Zhang, Y.; Qiu, X.; Cao, W.; Zhu, Y. Uncertainty in wheat phenology simulation induced by cultivar parameterization under climate warming. Eur. J. Agron. 2018, 94, 46–53. [Google Scholar] [CrossRef]
- Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- Brisson, N.; Launay, M.; Mary, B.; Beaudoin, N. Conceptual Basis, Formalisations and Parameterization of the STICS Crop Model; Editions Quae: Versailles, France, 2009; ISBN 2759201694. [Google Scholar]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model stics. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Fraga, H.; García de Cortázar Atauri, I.; Malheiro, A.C.; Santos, J.A. Modelling climate change impacts on viticultural yield, phenology and stress conditions in Europe. Glob. Chang. Biol. 2016, 22, 3774–3788. [Google Scholar] [CrossRef]
- Costa, R.; Fraga, H.; Fonseca, A.; De Cortázar-Atauri, I.G.; Val, M.C.; Carlos, C.; Reis, S.; Santos, J.A. Grapevine phenology of cv. Touriga Franca and Touriga Nacional in the Douro wine region: Modelling and climate change projections. Agronomy 2019, 9, 210. [Google Scholar] [CrossRef] [Green Version]
- Fraga, H.; Costa, R.; Santos, J.A. Multivariate clustering of viticultural terroirs in the Douro winemaking region. Cienc. Tec. Vitivinic. 2017, 32, 142–153. [Google Scholar] [CrossRef] [Green Version]
- Fraga, H.; Costa, R.; Moutinho-Pereira, J.; Correia, C.M.; Dinis, L.T.; Gonçalves, I.; Silvestre, J.; Eiras-Dias, J.; Malheiro, A.C.; Santos, J.A. Modeling phenology, water status, and yield components of three Portuguese grapevines using the STICS crop model. Am. J. Enol. Vitic. 2015, 66, 482–491. [Google Scholar] [CrossRef]
- Santos, J.A.; Ceglar, A.; Toreti, A.; Prodhomme, C. Performance of seasonal forecasts of Douro and Port wine production. Agric. For. Meteorol. 2020, 291, 108095. [Google Scholar] [CrossRef]
- Tosin, R.; Pôças, I.; Cunha, M. Spectral and thermal data as a proxy for leaf protective energy dissipation under kaolin application in grapevine cultivars. Open Agric. 2019, 4, 294–304. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A. Daily prediction of seasonal grapevine production in the Douro wine region based on favourable meteorological conditions. Aust. J. Grape Wine Res. 2017, 23, 296–304. [Google Scholar] [CrossRef]
- Wallach, D.; Buis, S.; Lecharpentier, P.; Bourges, J.; Clastre, P.; Launay, M.; Bergez, J.-E.; Guerif, M.; Soudais, J.; Justes, E. A package of parameter estimation methods and implementation for the STICS crop-soil model. Environ. Model. Softw. 2011, 26, 386–394. [Google Scholar] [CrossRef]
- Reis, S.; Fraga, H.; Carlos, C.; Silvestre, J.; Eiras-Dias, J.; Rodrigues, P.; Santos, J.A. Grapevine phenology in four portuguese wine regions: Modeling and predictions. Appl. Sci. 2020, 10, 3708. [Google Scholar] [CrossRef]
- Malheiro, A.C.; Pires, M.; Conceição, N.; Claro, A.M.; Dinis, L.T.; Moutinho-Pereira, J. Linking sap flow and trunk diameter measurements to assess water dynamics of touriga-nacional grapevines trained in cordon and guyot systems. Agriculture 2020, 10, 315. [Google Scholar] [CrossRef]
- Bates, T.R.; Dunst, R.M.; Joy, P. Seasonal dry matter, starch, and nutrient distribution in “Concord” grapevine roots. HortScience 2002, 37, 313–316. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Fraga, H.; van Ieperen, W.; Santos, J.A. Assessing the impacts of recent-past climatic constraints on potential wheat yield and adaptation options under Mediterranean climate in southern Portugal. Agric. Syst. 2020, 182, 102844. [Google Scholar] [CrossRef]
- Yang, C.; Fraga, H.; van Ieperen, W.; Trindade, H.; Santos, J.A. Effects of climate change and adaptation options on winter wheat yield under rainfed Mediterranean conditions in southern Portugal. Clim. Chang. 2019, 154, 159–178. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Fraga, H.; Ieperen, W.; Van Santos, J.A. Assessment of irrigated maize yield response to climate change scenarios in Portugal. Agric. Water Manag. 2017, 184, 178–190. [Google Scholar] [CrossRef]
- Yang, C.; Fraga, H.; Van Ieperen, W.; Santos, J.A. Modelling climate change impacts on early and late harvest grassland systems in Portugal. Crop. Pasture Sci. 2018, 69, 821–836. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Roma, Italy, 1998; ISBN 9251042195. [Google Scholar]
- LEAF (ex-CEAP). Declives de Portugal Continental. LEAF/ISA/ULisboa. Disponível. 2013. Available online: http://epic-webgis-portugal.isa.utl.pt/ (accessed on 30 June 2020).
- Liu, H.; Pequeno, D.N.L.; Hernández-Ochoa, I.M.; Krupnik, T.J.; Sonder, K.; Xiong, W.; Xu, Y. A consistent calibration across three wheat models to simulate wheat yield and phenology in China. Ecol. Modell. 2020, 430, 109132. [Google Scholar] [CrossRef]
- Garcia de Cortazar Atauri, I. Adaptation du Modèle STICS à la Vigne (Vitis vinifera L.): Utilisation dans le Cadre D’une Étude D’impact du Changement Climatique à L’échelle de la France. Ph.D. Thesis, Montpellier SupAgro, Montpellier, France, 2006. (In French). [Google Scholar]
- García de Cortázar-Atauri, I.; Brisson, N.; Gaudillere, J.P. Performance of several models for predicting budburst date of grapevine (Vitis vinifera L.). Int. J. Biometeorol. 2009, 53, 317–326. [Google Scholar] [CrossRef]
- García de Cortázar-Atauri, I.; Brisson, N.; Ollat, N.; Jacquet, O.; Payan, J.-C. Asynchronous dynamics of grapevine (“Vitis vinifera”) maturation: Experimental study for a modelling approach. OENO One 2009, 43, 83–97. [Google Scholar] [CrossRef]
- Buis, S.; Wallach, D.; Guillaume, S.; Varella, H.; Lecharpentier, P.; Launay, M.; Guérif, M.; Bergez, J.-E.; Justes, E. The STICS Crop Model and Associated Software for Analysis, Parameterization, and Evaluation. Methods Introd. Syst. Model. Agric. Res. 2011, 2, 395–426. [Google Scholar]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. F. Crop. Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Seber, G.A.F. Nonlinear Regression Models. In The Linear Model and Hypothesis: A General Unifying Theory; Springer International Publishing: Cham, Switzerland, 2015; pp. 117–128. ISBN 978-3-319-21930-1. [Google Scholar]
- Sexton, J.; Everingham, Y.L.; Inman-Bamber, G. A global sensitivity analysis of cultivar trait parameters in a sugarcane growth model for contrasting production environments in Queensland, Australia. Eur. J. Agron. 2017, 88, 96–105. [Google Scholar] [CrossRef]
- Kersebaum, K.C.; Boote, K.J.; Jorgenson, J.S.; Nendel, C.; Bindi, M.; Frühauf, C.; Gaiser, T.; Hoogenboom, G.; Kollas, C.; Olesen, J.E.; et al. Analysis and classification of data sets for calibration and validation of agro-ecosystem models. Environ. Model. Softw. 2015, 72, 402–417. [Google Scholar] [CrossRef]
- Roux, S. How sensitive is a vineyard crop model to the uncertainty of its runoff module? Environ. Model. Softw. 2017, 97, 86–92. [Google Scholar] [CrossRef]
- Casadebaig, P.; Debaeke, P.; Wallach, D. A new approach to crop model calibration: Phenotyping plus post-processing. Crop. Sci. 2020, 60, 709–720. [Google Scholar] [CrossRef]
- Valdés-Gómez, H.; Celette, F.; García de Cortázar-Atauri, I.; Jara-Rojas, F.; Ortega-Farías, S.; Gary, C. Modelling soil water content and grapevine growth and development with the stics crop-soil model under two different water management strategies. OENO One 2009, 43, 13–28. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.K.; Afonso, J.; Nogueira, M.; Oliveira, A.A.; Cosme, F.; Falco, V. Silicates of Potassium and Aluminium (Kaolin); Comparative Foliar Mitigation Treatments and Biochemical Insight on Grape Berry Quality in Vitis vinifera L. (cv. Touriga National and Touriga Franca). Biology 2020, 9, 58. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Vineyard Parameters | Plot S | Plot D | Plot O | Plot M | ||
|---|---|---|---|---|---|---|
| Touriga Nacional with a Single Cordon | Touriga Nacional with a Double Cordon | Touriga Franca with a Single Cordon | Touriga Franca with a Double Cordon | |||
| Lat: 41.137° N Lon: −7.262° W | Lat: 41.215° N Lon: −7.538° W | Lat: 41.040° N Lon: −7.037° W | Lat: 41.153° N Lon: −7.623° W | |||
| Target parameters | Flowering day (Julian day) | 132 (6%) | 139 (7%) | 135 (4%) | 140 (9%) | |
| Harvest day (Julian day) | 261 (3%) | 262 (5%) | 261 (6%) | 261 (4%) | ||
| Yield (kg/ha) | 5156 (37%) | 6871 (27%) | 5793 (11%) | 5263 (24%) | ||
| Growth parameters | Individual cluster weight at harvest (kg) | 0.109 (19%) | 0.108 (23%) | 0.180 (22%) | 0.185 (20%) | |
| Cluster number per vine at harvest | 11 (27%) | 19 (14%) | 8 (18%) | 10 (20%) | ||
| Training system parameters | Planting density (vines/ha) | 4132 | 3344 | 4040 | 3030 | |
| Trunk height (m) | 0.6 | 0.6 | 0.6 | 0.6 | ||
| Inter-row distance (m) | 2.2 | 2.2 | 2.2 | 2.2 | ||
| Maximum canopy height (include trunk height) (m) | 1.6 | 1.6 | 1.6 | 1.6 | ||
| Maximum canopy width (m) | 0.5 | 0.6 | 0.5 | 0.6 | ||
| Initial state (assumed at dormancy) | Initial plant carbon (kg/ha) | 3175 | 2801 | 3105 | 2538 | |
| Initial plant nitrogen (kg/ha) | 47.5 | 42.1 | 46.5 | 38.2 | ||
| STICS Codes | Parameter Abbreviations | Description | Units | Min | Max | Interval | |
|---|---|---|---|---|---|---|---|
| Genotype-dependent parameters | stdrpnou | FS | Fruit setting thermal requirement | degree day−1 | 50 | 350 | 75 |
| afruitpot | FN | Potential fruit number formation per degree day−1 per cluster accumulated during fruit setting | / | 0.5 | 2.5 | 0.5 | |
| dureefruit | FF | Fruit filling thermal requirement | degree day−1 | 700 | 1500 | 200 | |
| pgrainmaxi | FW | Genetic potential dry fruit (berry) weight | g | 0.5 | 1.7 | 0.3 | |
| stamflax | VG | Thermal requirement between juvenile onset and veraison onset | degree day−1 | 600 | 1400 | 200 | |
| stlevdrp | RG | Thermal requirement between budbreak onset and reproductive onset | degree day−1 | 250 | 450 | 50 | |
| stdrpdes | WD | Thermal requirement between reproductive onset and fruit water dynamic onset | degree day−1 | 100 | 300 | 50 | |
| Generic or plant-dependent parameters | nboite | BN | Box number or fruit age class | / | 5 | 15 | 5 |
| spfrmin | SS | Source sink ratio threshold that affects fruit setting | / | 0.25 | 0.75 | 0.25 |
| Grapevine Parameter Abbreviation | Touriga Nacional with a Single Cordon | Touriga Nacional with a Double Cordon | Touriga Franca with a Single Cordon | Touriga Franca with a Double Cordon | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| To Minimize | To Minimize | To Minimize | To Minimize | |||||||||||||
| Objective Function | Phenology | Yield | Objective Function | Phenology | Yield | Objective Function | Phenology | Yield | Objective Function | Phenology | Yield | |||||
| FS | 200 | 275 | 50 | 125 | 50 | 125 | 350 | 275 | 125 | 125 | 350 | 50 | ||||
| FN | 0.5 | 2.5 | 2.5 | 1.0 | 0.5 | 1.0 | 1.5 | 2.5 | 2.5 | 1.5 | 2.5 | 1.0 | ||||
| FF | 700 | 700 | 700 | 1500 | 700 | 1500 | 1500 | 700 | 1500 | 1300 | 700 | 1500 | ||||
| FW | 0.5 | 1.1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 1.7 | 1.1 | 0.5 | 1.7 | 1.4 | ||||
| VG | 800, 1000 | 800 | 1000 | 600 | 600, 800 | 600 | 600 | 1000, 1200 | 600 | 600 | 600 | 600 | ||||
| RG | 250 | 300 (F) | 450 (H) | 450 | 300 | 300 (F) | 250 (H) | 450 | 300 | 300 (F) | 450 (H) | 450 | 300 | 300 (F) | 400 (H) | 450 |
| WD | 300 | 100 | 100–300 | 250, 300 | 300 | 150–300 | 150, 200 | 100 | 150–300 | 300 | 100 | 150–300 | ||||
| BN | 5 | 5 | 5 | 15 | 15 | 10 | 15 | 5 | 15 | 10 | 5 | 15 | ||||
| SS | 0.25, 0.5, 0.75 | 0.75 | 0.25 | 0.25 | 0.25, 0.5, 0.75 | 0.25 | 0.25 | 0.75 | 0.25 | 0.75 | 0.75 | 0.5 | ||||
| Goodness-Of-Fit Statistics for the Study Variables | Touriga Nacional with a Single Cordon | Touriga Nacional with a Double Cordon | Touriga Franca with a Single Cordon | Touriga Franca with a Double Cordon | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Objective Function | Univariate Function | Objective Function | Univariate Function | Objective Function | Univariate Function | Objective Function | Univariate Function | ||||||||||
| Flower | Harvest | Yield | Flower | Harvest | Yield | Flower | Harvest | Yield | Flower | Harvest | Yield | ||||||
| Flower Date | MBE | 4 | −3 | −22 | −22 | 1 | 1 | 8 | −18 | 1 | 1 | −16 | −16 | 2 | 2 | −11 | −18 |
| MAE | 4 | 4 | 22 | 22 | 4 | 4 | 8 | 18 | 4 | 4 | 16 | 16 | 4 | 4 | 11 | 18 | |
| RMSE | 6 | 5 | 22 | 22 | 4 | 4 | 10 | 18 | 6 | 6 | 17 | 17 | 4 | 4 | 12 | 18 | |
| nRMSE | 4% | 4% | 16% | 16% | 3% | 3% | 7% | 13% | 5% | 5% | 12% | 12% | 3% | 3% | 8% | 13% | |
| Rsd | 1.5 | 1.5 | 1.3 | 1.3 | 1.2 | 1.2 | 1.3 | 1.1 | 1.7 | 1.7 | 1.6 | 1.6 | 0.9 | 0.9 | 0.9 | 0.9 | |
| Harvest Date | MBE | −2 | 14 | −2 | 5 | −1 | −4 | 1 | −2 | −1 | 21 | 2 | −4 | −2 | 4 | −2 | 2 |
| MAE | 6 | 14 | 3 | 6 | 3 | 5 | 3 | 4 | 10 | 21 | 5 | 9 | 12 | 11 | 3 | 8 | |
| RMSE | 6 | 16 | 4 | 8 | 4 | 6 | 3 | 5 | 10 | 25 | 6 | 11 | 12 | 11 | 4 | 10 | |
| nRMSE | 2% | 6% | 1% | 3% | 1% | 2% | 1% | 2% | 4% | 10% | 2% | 4% | 5% | 4% | 1% | 4% | |
| Rsd | 1.4 | 1.8 | 0.9 | 1.6 | 0.8 | 0.8 | 0.9 | 0.8 | 0.6 | 1.1 | 0.8 | 0.6 | 1.4 | 1.4 | 0.9 | 1.0 | |
| Yield (kg/ha) | MBE | −232 | −8317 | −3865 | 236 | −16 | 4853 | 4533 | 209 | 104 | −4382 | −1301 | −158 | 159 | −9265 | −6612 | 258 |
| MAE | 1168 | 8317 | 3865 | 980 | 1417 | 4853 | 4533 | 1249 | 1294 | 4382 | 2822 | 1117 | 1226 | 9265 | 6612 | 1104 | |
| RMSE | 1255 | 8720 | 4808 | 1060 | 1718 | 5290 | 4941 | 1544 | 1478 | 4984 | 3217 | 1258 | 1611 | 10435 | 8159 | 1315 | |
| nRMSE | 24% | 169% | 93% | 21% | 25% | 77% | 72% | 22% | 26% | 86% | 56% | 22% | 31% | 198% | 155% | 25% | |
| Rsd | 0.7 | 1.8 | 1.9 | 1.1 | 0.7 | 0.3 | 0.3 | 0.7 | 1.8 | 3.8 | 4.5 | 1.5 | 0.7 | 3.8 | 3.7 | 0.6 | |
| Evaluation Statistics of Studied Variables | Touriga Nacional with a Double Cordon | Touriga Franca with a Double Cordon | |
|---|---|---|---|
| Flowering Date | MBE (days) | 10 | 3 |
| MAE (days) | 10 | 3 | |
| RMSE (days) | 11 | 3 | |
| nRMSE (%) | 7% | 2% | |
| Rsd | 1.7 | 1.5 | |
| Harvest Date | MBE (days) | 0 | −15 |
| MAE (days) | 11 | 15 | |
| RMSE (days) | 12 | 17 | |
| nRMSE (%) | 4% | 6% | |
| Rsd | 1.3 | 0.9 | |
| Yield | MBE (kg/ha) | −466 | 619 |
| MAE (kg/ha) | 1196 | 619 | |
| RMSE (kg/ha) | 1208 | 730 | |
| nRMSE (%) | 16% | 11% | |
| Rsd | 1.0 | 0.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Menz, C.; Fraga, H.; Reis, S.; Machado, N.; Malheiro, A.C.; Santos, J.A. Simultaneous Calibration of Grapevine Phenology and Yield with a Soil–Plant–Atmosphere System Model Using the Frequentist Method. Agronomy 2021, 11, 1659. https://doi.org/10.3390/agronomy11081659
Yang C, Menz C, Fraga H, Reis S, Machado N, Malheiro AC, Santos JA. Simultaneous Calibration of Grapevine Phenology and Yield with a Soil–Plant–Atmosphere System Model Using the Frequentist Method. Agronomy. 2021; 11(8):1659. https://doi.org/10.3390/agronomy11081659
Chicago/Turabian StyleYang, Chenyao, Christoph Menz, Helder Fraga, Samuel Reis, Nelson Machado, Aureliano C. Malheiro, and João A. Santos. 2021. "Simultaneous Calibration of Grapevine Phenology and Yield with a Soil–Plant–Atmosphere System Model Using the Frequentist Method" Agronomy 11, no. 8: 1659. https://doi.org/10.3390/agronomy11081659
APA StyleYang, C., Menz, C., Fraga, H., Reis, S., Machado, N., Malheiro, A. C., & Santos, J. A. (2021). Simultaneous Calibration of Grapevine Phenology and Yield with a Soil–Plant–Atmosphere System Model Using the Frequentist Method. Agronomy, 11(8), 1659. https://doi.org/10.3390/agronomy11081659