AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Dataset
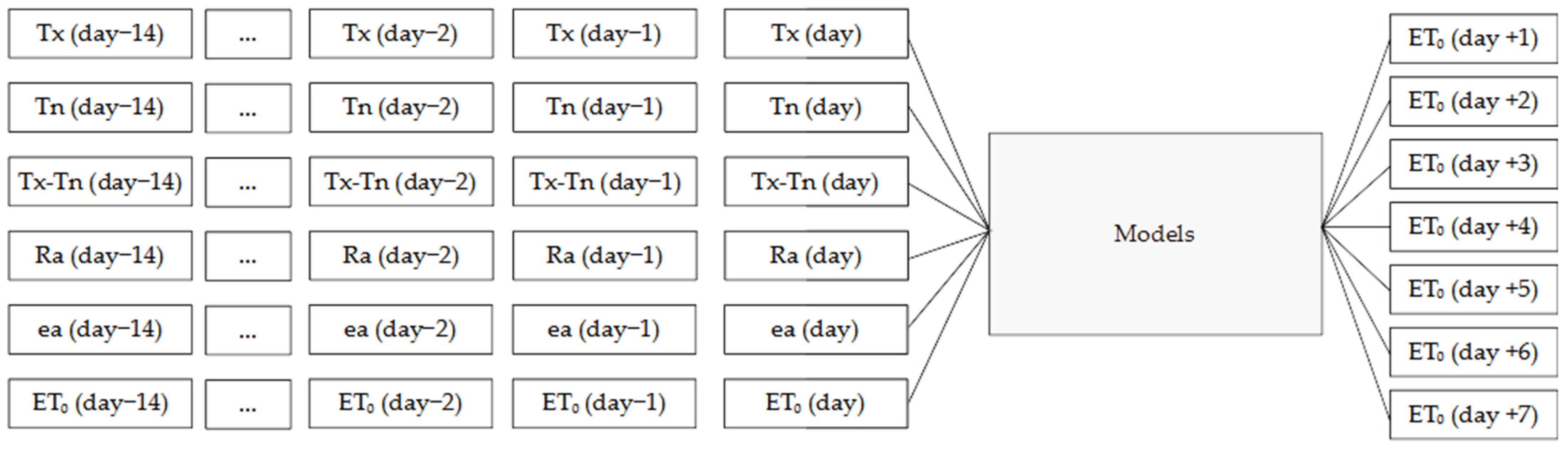
2.2. Preprocessing Methodology
2.3. Reference Evapotranspiration Calculation
2.4. Baselines
2.5. Machine Learning Models
2.5.1. Multilayer Perceptron
2.5.2. Extreme Learning Machine
2.5.3. Support Vector Machine for Regression
2.5.4. Random Forest
2.5.5. Convolutional Neural Network
2.5.6. Long Short-Term Memory
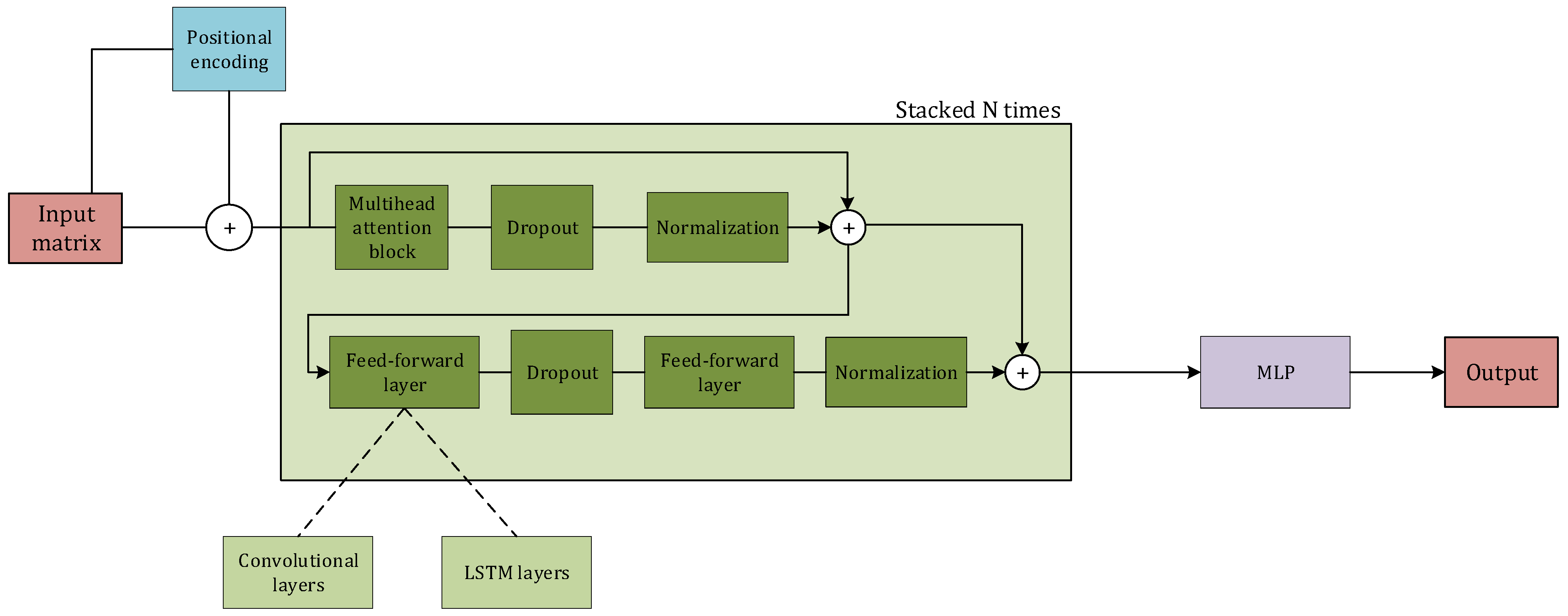
2.5.7. Transformers
2.6. Bayesian Optimization
2.7. Evaluation Metrics
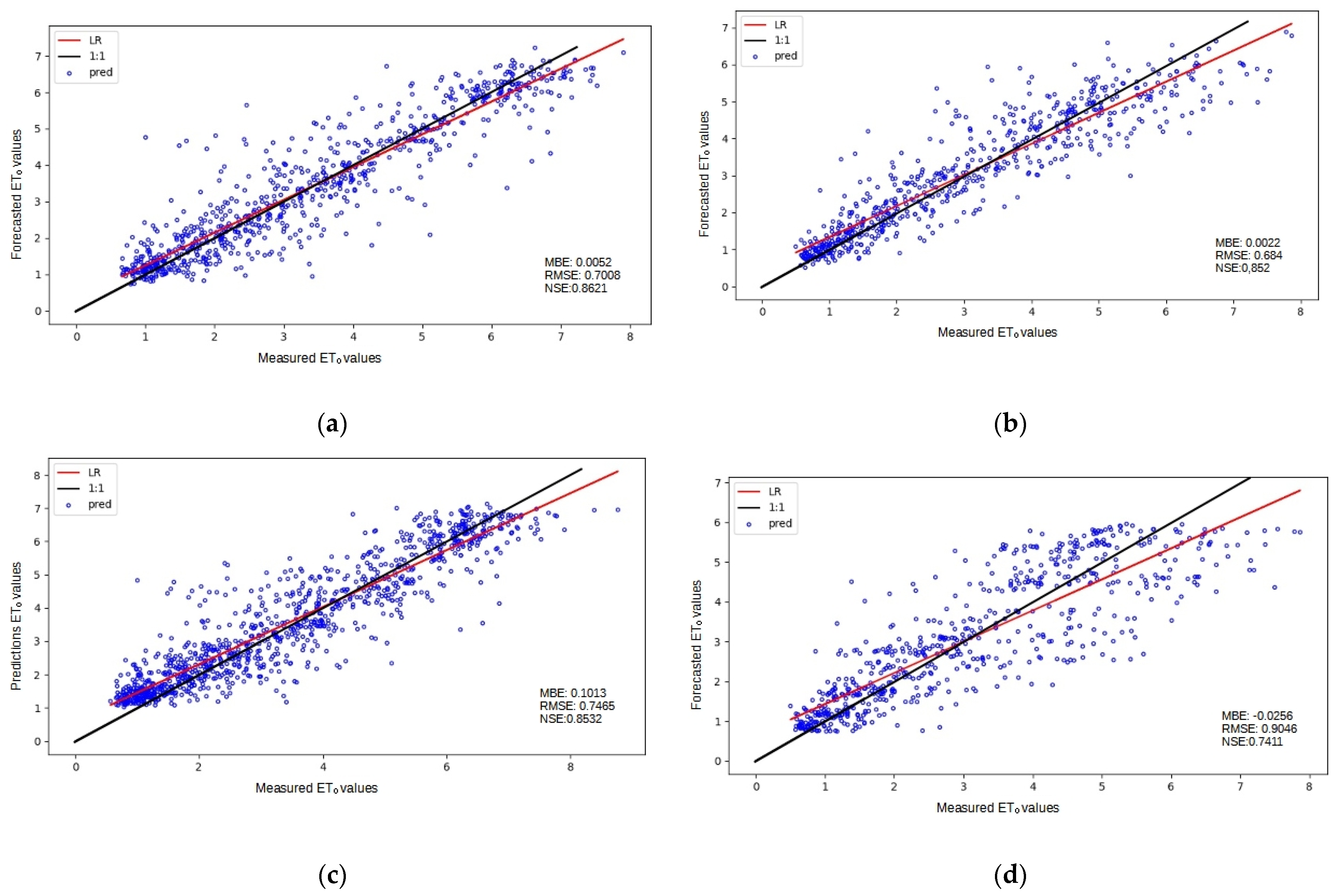
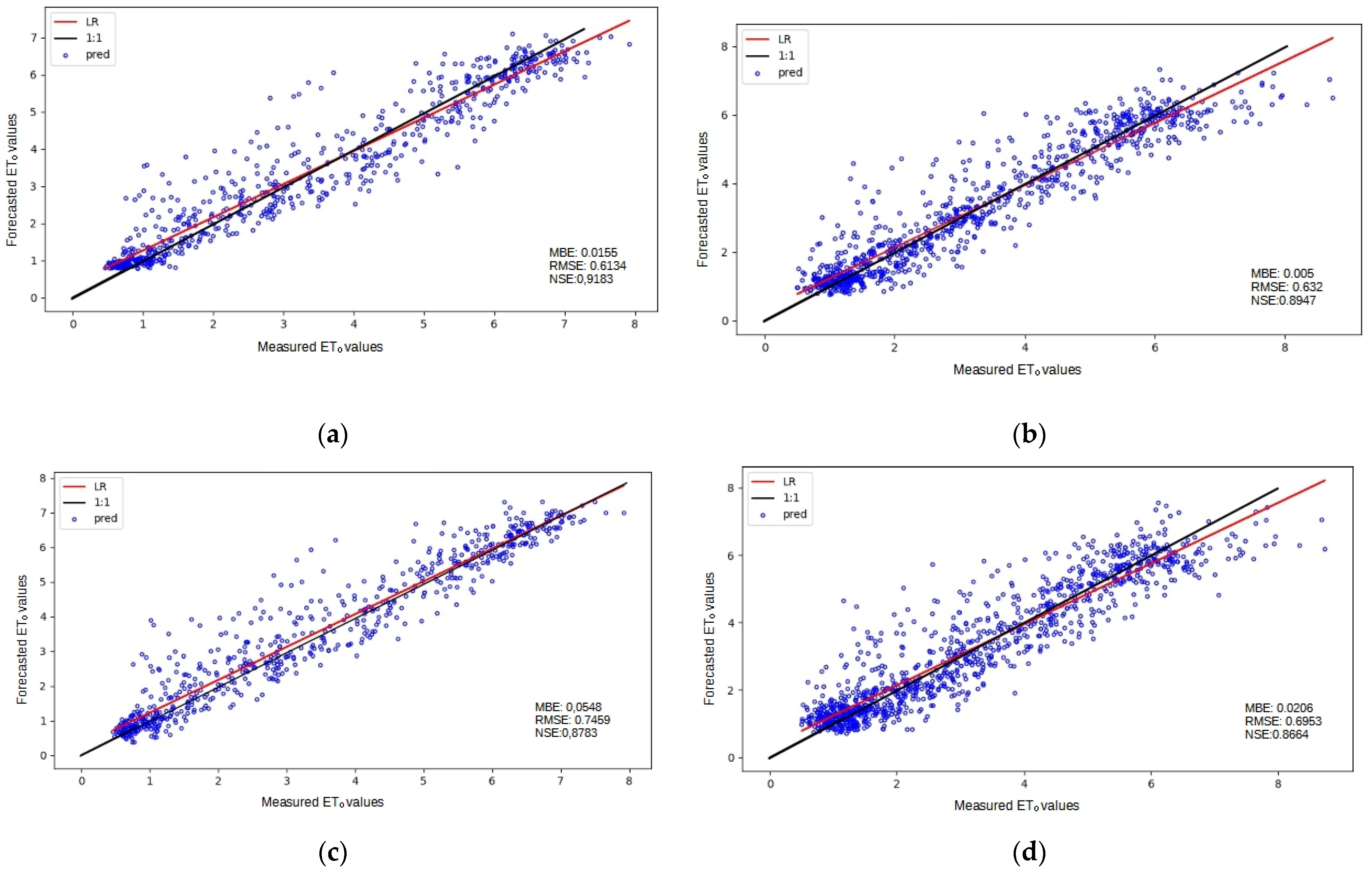
3. Results and Discussion
3.1. Baseline Performance
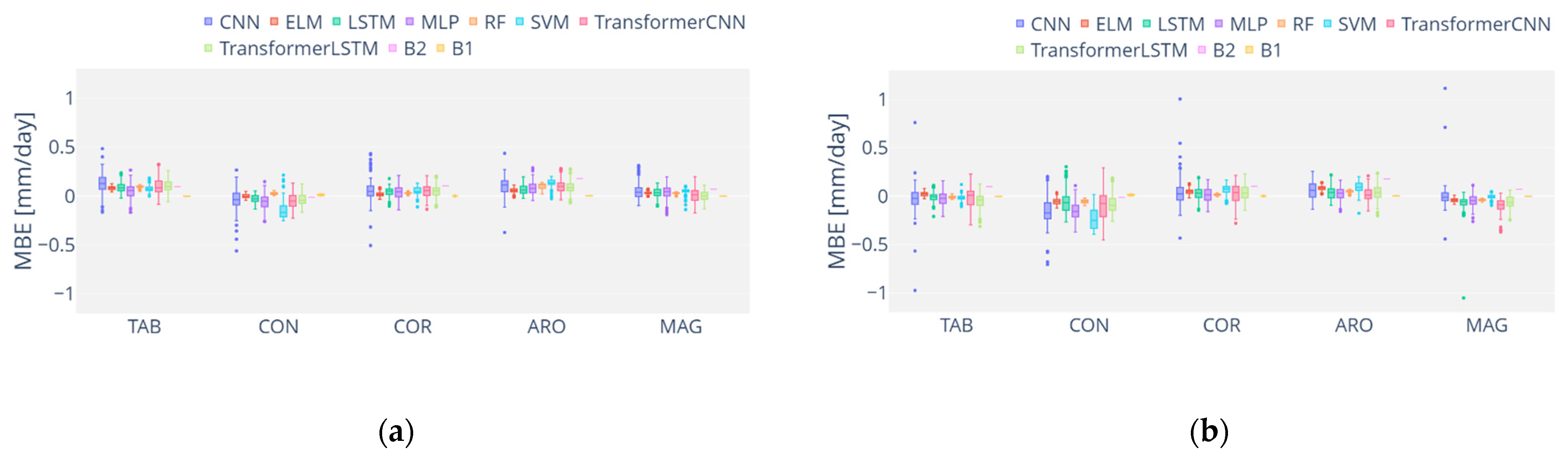
3.2. Analysis of ML Performance
3.3. Assessing the Different Configurations
3.4. Overall Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO. The State of Food Security and Nutrition in the World 2021; FAO: Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage; FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Kwon, H.; Choi, M. Error Assessment of Climate Variables for FAO-56 Reference Evapotranspiration. Meteorol. Atmos. Phys. 2011, 112, 81–90. [Google Scholar] [CrossRef]
- Estévez, J.; García-Marín, A.P.; Morábito, J.A.; Cavagnaro, M. Quality assurance procedures for validating meteorological input variables of reference evapotranspiration in mendoza province (Argentina). Agric. Water Manag. 2016, 172, 96–109. [Google Scholar] [CrossRef]
- Jabloun, M.; Sahli, A. Evaluation of FAO-56 Methodology for Estimating Reference Evapotranspiration Using Limited Climatic Data. Application to Tunisia. Agric. Water Manag. 2008, 95, 707–715. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; Giráldez, J.V. Guidelines on Validation Procedures for Meteorological Data from Automatic Weather Stations. J. Hydrol. 2011, 402, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Estévez, J.; Padilla, F.L.; Gavilán, P. Evaluation and Regional Calibration of Solar Radiation Prediction Models in Southern Spain. J. Irrig. Drain. Eng. 2012, 138, 868–879. [Google Scholar] [CrossRef]
- WMO. Guide to Instruments and Methods of Observations; WMO: Geneva, Switzerland, 2018; Volume 8, ISBN 978-92-63-10008-5. [Google Scholar]
- George, H.H.; Zohrab, A. Samani Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves-Samani and FAO-PM Temperature Methods for a Wide Range of Climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Ravazzani, G.; Corbari, C.; Morella, S.; Gianoli, P.; Mancini, M. Modified Hargreaves-Samani Equation for the Assessment of Reference Evapotranspiration in Alpine River Basins. J. Irrig. Drain. Eng. 2012, 138, 592–599. [Google Scholar] [CrossRef]
- Luo, Y.; Chang, X.; Peng, S.; Khan, S.; Wang, W.; Zheng, Q.; Cai, X. Short-Term Forecasting of Daily Reference Evapotranspiration Using the Hargreaves-Samani Model and Temperature Forecasts. Agric. Water Manag. 2014, 136, 42–51. [Google Scholar] [CrossRef]
- Karimi, S.; Shiri, J.; Marti, P. Supplanting Missing Climatic Inputs in Classical and Random Forest Models for Estimating Reference Evapotranspiration in Humid Coastal Areas of Iran. Comput. Electron. Agric. 2020, 176, 105633. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. New Approach to Estimate Daily Reference Evapotranspiration Based on Hourly Temperature and Relative Humidity Using Machine Learning and Deep Learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Yan, S.; Wu, L.; Fan, J.; Zhang, F.; Zou, Y.; Wu, Y. A Novel Hybrid WOA-XGB Model for Estimating Daily Reference Evapotranspiration Using Local and External Meteorological Data: Applications in Arid and Humid Regions of China. Agric. Water Manag. 2021, 244, 106594. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y.; Huang, G. A Novel Kernel Extreme Learning Machine Model Coupled with K-Means Clustering and Firefly Algorithm for Estimating Monthly Reference Evapotranspiration in Parallel Computation. Agric. Water Manag. 2021, 245, 106624. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abdullahi, J. Multi-Step Ahead Modeling of Reference Evapotranspiration Using a Multi-Model Approach. J. Hydrol. 2020, 581, 124434. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. Multi-Step Ahead Forecasting of Daily Reference Evapotranspiration Using Deep Learning. Comput. Electron. Agric. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 2017, 5999–6009. [Google Scholar]
- Wu, S.; Xiao, X.; Ding, Q.; Zhao, P.; Wei, Y.; Huang, J. Adversarial Sparse Transformer for Time Series Forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17105–17115. [Google Scholar]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case. arXiv 2020, arXiv:2001.08317. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Unep, N.M.; London, D.T. World Atlas of Desertification. Land Degrad. Dev. 1992, 3, 15–45. [Google Scholar]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. New Machine Learning Approaches to Improve Reference Evapotranspiration Estimates Using Intra-Daily Temperature-Based Variables in a Semi-Arid Region of Spain. Agric. Water Manag. 2020, 245, 106558. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. Assessing Neural Network Approaches for Solar Radiation Estimates Using Limited Climatic Data in the Mediterranean Sea. In Proceedings of the 3rd International Electronic Conference on Atmospheric Sciences (ECAS 2020), online, 16–30 November 2020. [Google Scholar]
- Bellido-Jiménez, J.A.; Estévez Gualda, J.; García-Marín, A.P. Assessing New Intra-Daily Temperature-Based Machine Learning Models to Outperform Solar Radiation Predictions in Different Conditions. Appl. Energy 2021, 298, 117211. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; García-Marín, A.P. Spatial Regression Test for Ensuring Temperature Data Quality in Southern Spain. Theor. Appl. Climatol. 2018, 131, 309–318. [Google Scholar] [CrossRef]
- Islam, A.R.M.T.; Shen, S.; Yang, S.; Hu, Z.; Chu, R. Assessing Recent Impacts of Climate Change on Design Water Requirement of Boro Rice Season in Bangladesh. Theor. Appl. Climatol. 2019, 138, 97–113. [Google Scholar] [CrossRef]
- Yi, Z.; Zhao, H.; Jiang, Y. Continuous Daily Evapotranspiration Estimation at the Field-Scale over Heterogeneous Agricultural Areas by Fusing Aster and Modis Data. Remote Sens. 2018, 10, 1694. [Google Scholar] [CrossRef] [Green Version]
- Sattari, M.T.; Apaydin, H.; Band, S.S.; Mosavi, A.; Prasad, R. Comparative Analysis of Kernel-Based versus ANN and Deep Learning Methods in Monthly Reference Evapotranspiration Estimation. Hydrol. Earth Syst. Sci. 2021, 25, 603–618. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Souag-Gamane, D.; Kisi, O. Artificial Intelligence Models versus Empirical Equations for Modeling Monthly Reference Evapotranspiration. Environ. Sci. Pollut. Res. 2020, 27, 30001–30019. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid Particle Swarm Optimization with Extreme Learning Machine for Daily Reference Evapotranspiration Prediction from Limited Climatic Data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Akusok, A.; Björk, K.-M.; Miche, Y.; Lendasse, A. High Performance Extreme Learning Machines: A Complete Toolbox for Big Data Applications. IEEE Access 2015, 3, 1011–1025. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating Daily Reference Evapotranspiration Based on Limited Meteorological Data Using Deep Learning and Classical Machine Learning Methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- de Oliveira, R.G.; Valle Júnior, L.C.G.; da Silva, J.B.; Espíndola, D.A.L.F.; Lopes, R.D.; Nogueira, J.S.; Curado, L.F.A.; Rodrigues, T.R. Temporal Trend Changes in Reference Evapotranspiration Contrasting Different Land Uses in Southern Amazon Basin. Agric. Water Manag. 2021, 250, 106815. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep Solar Radiation Forecasting with Convolutional Neural Network and Long Short-Term Memory Network Algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Kim, S.; Hong, S.; Joh, M.; Song, S.K. DeepRain: ConvLSTM Network for Precipitation Prediction Using Multichannel Radar Data. arXiv 2017, arXiv:1711.02316. [Google Scholar]
- Aloysius, N.; Geetha, M. A Review on Deep Convolutional Neural Networks. In Proceedings of the 2017 IEEE International Conference on Communication and Signal Processing, ICCSP, Chenai, India, 6–8 April 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; Volume 2018, pp. 588–592. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Song, H.; Rajan, D.; Thiagarajan, J.J.; Spanias, A. Attend and Diagnose: Clinical Time Series Analysis Using Attention Models. In Proceedings of the 32th AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-Art Natural Language Processing; Association for Computational Linguistics (ACL): Stroudsburg, PA, USA, 2020; pp. 38–45. [Google Scholar]
- Mohammdi Farsani, R.; Pazouki, E. A Transformer Self-Attention Model for Time Series Forecasting. J. Electr. Comput. Eng. Innov. 2021, 9, 1–10. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Muhammad Adnan, R.; Kuriqi, A. Modelling Reference Evapotranspiration by Combining Neuro-Fuzzy and Evolutionary Strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling Daily Reference Evapotranspiration via a Novel Approach Based on Support Vector Regression Coupled with Whale Optimization Algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Gijsbers, P.; LeDell, E.; Thomas, J.; Poirier, S.; Bischl, B.; Vanschoren, J. An Open Source AutoML Benchmark. arXiv 2019, arXiv:1907.00909. [Google Scholar]
- Kotthoff, L.; Thornton, C.; Hoos, H.; Hutter, F.; Leyton-Brown, K. Auto-WEKA 2.0: Automatic Model Selection and Hyperparameter Optimization in WEKA. J. Mach. Learn. Res. 2017, 18, 826–830. [Google Scholar]
- Jin, H.; Song, Q.; Hu, X. Auto-Keras: An Efficient Neural Architecture Search System. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1946–1956. [Google Scholar]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.T.; Blum, M.; Hutter, F. Auto-Sklearn:: Efficient and Robust Automated Machine Learning. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 2015, pp. 2962–2970. [Google Scholar]
- Hutter, F.; Kotthoff, L.; Vanschoren, J. (Eds.) Automated Machine Learning; The Springer Series on Challenges in Machine Learning; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-030-05317-8. [Google Scholar]
- Borji, A.; Itti, L. Bayesian Optimization Explains Human Active Search. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2013; Volume 26. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- de Oliveira e Lucas, P.; Alves, M.A.; de Lima e Silva, P.C.; Guimarães, F.G. Reference Evapotranspiration Time Series Forecasting with Ensemble of Convolutional Neural Networks. Comput. Electron. Agric. 2020, 177, 105700. [Google Scholar] [CrossRef]
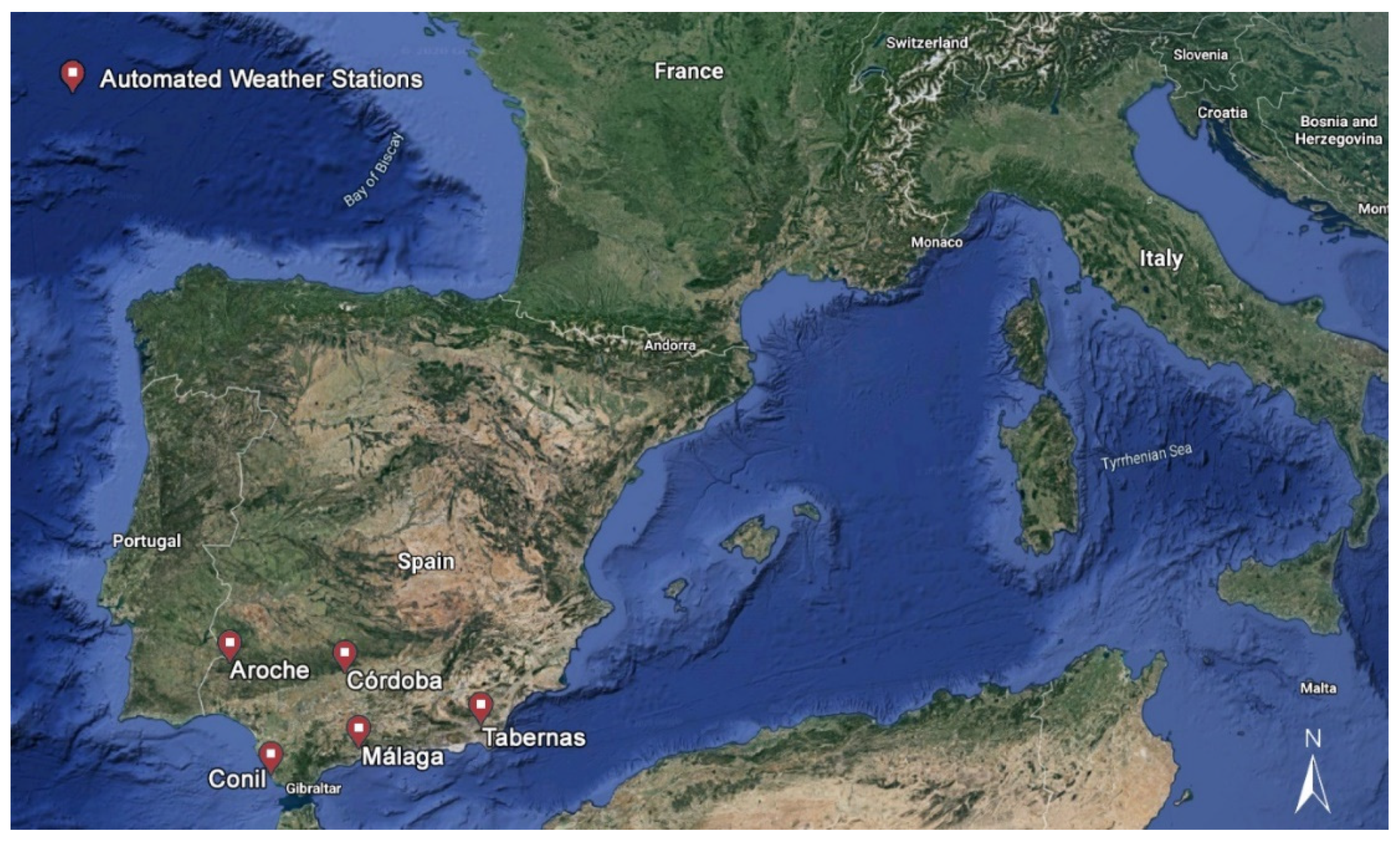












| Site | Lon. (° W) | Lat. (° N) | Alt. (m) | Mean Annual Precipitation (mm) | UNEP Aridity Index | Total Available Days |
|---|---|---|---|---|---|---|
| Aroche (ARO) | 6.94 | 37.95 | 293 | 632 | 0.555 (dry-subhumid) | 6399 |
| Conil de la Frontera (CON) | 6.13 | 36.33 | 22 | 470 | 0.479 (semiarid) | 5868 |
| Córdoba (COR) | 4.80 | 37.85 | 94 | 589 | 0.462 (semiarid) | 6397 |
| Málaga (MAG) | 4.53 | 36.75 | 55 | 434 | 0.366 (semiarid) | 6438 |
| Tabernas (TAB) | 2.30 | 37.09 | 502 | 237 | 0.178 (arid) | 6694 |
| Tx (°C) | Tm (°C) | Tn (°C) | RHx (%) | RHm (%) | RHn (%) | U2 (m/s) | Rs (MJ/m2 day) | ET0 (mm) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| ARO | Min | 2.5 | −0.2 | −8.0 | 32.5 | 17.2 | 5.0 | 0.3 | 1.0 | 0.3 |
| Mean | 23.2 | 16.1 | 8.9 | 89.5 | 65.9 | 39.0 | 1.2 | 17.8 | 3.2 | |
| Max | 44.0 | 34.1 | 24.9 | 100.0 | 100.0 | 100.0 | 5.8 | 34.3 | 8.7 | |
| Std | 8.1 | 6.8 | 5.6 | 11.2 | 17.7 | 19.4 | 0.5 | 8.8 | 2.0 | |
| CON | Min | 6.4 | 0.7 | −5.3 | 39.9 | 24.3 | 6.9 | 0.0 | 0.5 | 0.4 |
| Mean | 23.0 | 17.4 | 12.1 | 89.3 | 72.5 | 50.5 | 1.3 | 18.0 | 3.2 | |
| Max | 41.3 | 31.9 | 26.9 | 100.0 | 99.6 | 97.1 | 7.9 | 31.7 | 9.3 | |
| Std | 5.7 | 5.2 | 5.3 | 9.0 | 12.3 | 14.6 | 1.0 | 7.8 | 1.8 | |
| COR | Min | 3.3 | 0.0 | −8.3 | 38.9 | 21.8 | 4.3 | 0.0 | 0.5 | 0.3 |
| Mean | 24.6 | 17.4 | 11.0 | 86.8 | 64.1 | 37.3 | 1.6 | 17.7 | 3.6 | |
| Max | 45.7 | 34.7 | 27.6 | 100.0 | 100.0 | 100.0 | 7.5 | 33.2 | 9.6 | |
| Std | 8.5 | 7.3 | 6.2 | 12.0 | 18.1 | 19.3 | 0.7 | 8.5 | 2.3 | |
| MAG | Min | 6.2 | 3.3 | −4.2 | 36.0 | 19.4 | 4.6 | 0.0 | 0.3 | 0.4 |
| Mean | 23.9 | 18.2 | 12.6 | 85.1 | 63.4 | 39.1 | 1.3 | 18.2 | 3.4 | |
| Max | 42.7 | 33.7 | 26.8 | 100.0 | 99.7 | 98.3 | 4.6 | 32.4 | 10.3 | |
| Std | 6.3 | 5.8 | 5.5 | 10.5 | 14.2 | 15.1 | 0.5 | 8.2 | 1.9 | |
| TAB | Min | 4.3 | −1.2 | −8.2 | 28.6 | 16.8 | 2.8 | 0.1 | 0.2 | 0.4 |
| Mean | 23.2 | 16.4 | 9.8 | 85.7 | 59.9 | 32.9 | 1.9 | 18.4 | 3.8 | |
| Max | 42.5 | 32.1 | 26.0 | 100.0 | 97.5 | 95.0 | 9.9 | 32.8 | 10.6 | |
| Std | 7.2 | 6.6 | 6.2 | 11.9 | 15.1 | 14.8 | 0.9 | 7.8 | 2.0 |
| Conf. | Tx | Tn | Tx-Tn | Ra | EnergyT | ea | es | VPD | HTx | HTn | HSs-HTx | HSr-HTn | ET0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | X | X | X | X | X | X | |||||||
| II | X | X | X | X | X | X | X | ||||||
| III | X | X | X | X | X | X | X | ||||||
| IV | X | X | X | X | X | X | |||||||
| V | X | X | X | X | X | X | X | ||||||
| VI | X | X | X | X | X | X | X | ||||||
| VII | X | X | X | X | X | X | X | ||||||
| VIII | X | X | X | X | X | X | X | X | |||||
| IX | X | X | X | X | X | X | X | X | |||||
| X | X | X | X | X | X | X | X | ||||||
| XI | X | X | X | X | X | X | X | X | |||||
| XII | X | X | X | X | X | X | X | X | |||||
| XIII | X | X | X | X | X | X | X | X | X | X | X | X | X |
| XIV | X | X | X | X | X | X | X | X | X | ||||
| XV | X | X | X | X | X | X | X | X | X | ||||
| XVI | X | X | X | X | X | X | X | X | |||||
| XVII | X | X | X | X | X | X | X | X | X | ||||
| XVIII | X | X | X | X | X | X | X | X | X | ||||
| XIX | X | X | X | X | X | X | X | X | X | ||||
| XX | X | X | X | X | X | X | X | X | |||||
| XXI | X | X | X | X | X | X | X | ||||||
| XXII | X | X | X | X | X | X | |||||||
| XXIII | X | X | X | X | X | ||||||||
| XXIV | X | X | X | X | X | X | |||||||
| XXV | X | X | X | X | X | X | |||||||
| XXVI | X | X | X | X | X | X | |||||||
| XXVII | X | X | X | X | X | X |
| Location | Baseline | Forecast Horizon | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| COR | B1 | 0.7551 | 0.8733 | 0.9365 | 0.9926 | 1.0172 | 1.0363 | 1.0644 |
| B2 | 0.8374 | 0.8374 | 0.8374 | 0.8374 | 0.8374 | 0.8374 | 0.8374 | |
| MAG | B1 | 0.7665 | 0.9084 | 0.9439 | 0.9632 | 0.9902 | 1.0140 | 1.0188 |
| B2 | 0.8143 | 0.8143 | 0.8143 | 0.8143 | 0.8143 | 0.8143 | 0.8143 | |
| TAB | B1 | 0.8515 | 0.9961 | 1.0451 | 1.0938 | 1.1075 | 1.1568 | 1.1628 |
| B2 | 0.9176 | 0.9176 | 0.9176 | 0.9176 | 0.9176 | 0.9176 | 0.9176 | |
| CON | B1 | 0.7987 | 1.0675 | 1.1950 | 1.2474 | 1.2404 | 1.2444 | 1.2778 |
| B2 | 0.9567 | 0.9567 | 0.9567 | 0.9567 | 0.9567 | 0.9567 | 0.9567 | |
| ARO | B1 | 0.6390 | 0.7882 | 0.8840 | 0.9337 | 0.9820 | 0.9901 | 1.0032 |
| B2 | 0.8027 | 0.8027 | 0.8027 | 0.8027 | 0.8027 | 0.8027 | 0.8027 | |
| Mean | B1 | 0.7622 | 0.9277 | 1.0009 | 1.0461 | 1.0675 | 1.0883 | 1.1054 |
| B2 | 0.8667 | 0.8667 | 0.8667 | 0.8667 | 0.8667 | 0.8667 | 0.8667 | |
| Location | Model | Forecast Horizon | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| COR | B1 | 0.8926 | 0.8564 | 0.8349 | 0.8145 | 0.8052 | 0.7978 | 0.7868 |
| B2 | 0.8680 | 0.8680 | 0.8680 | 0.8680 | 0.8680 | 0.8680 | 0.8680 | |
| MAG | B1 | 0.8376 | 0.7719 | 0.7538 | 0.7436 | 0.7290 | 0.7157 | 0.7129 |
| B2 | 0.8167 | 0.8167 | 0.8167 | 0.8167 | 0.8167 | 0.8167 | 0.8167 | |
| TAB | B1 | 0.8197 | 0.7531 | 0.7283 | 0.7023 | 0.6947 | 0.6671 | 0.6638 |
| B2 | 0.7906 | 0.7906 | 0.7906 | 0.7906 | 0.7906 | 0.7906 | 0.7906 | |
| CON | B1 | 0.8235 | 0.6844 | 0.6042 | 0.5684 | 0.5728 | 0.5695 | 0.5455 |
| B2 | 0.7465 | 0.7465 | 0.7465 | 0.7465 | 0.7465 | 0.7465 | 0.7465 | |
| ARO | B1 | 0.9038 | 0.8537 | 0.8160 | 0.7949 | 0.7732 | 0.7696 | 0.7636 |
| B2 | 0.8481 | 0.8481 | 0.8481 | 0.8481 | 0.8481 | 0.8481 | 0.8481 | |
| Mean | B1 | 0.8554 | 0.7849 | 0.7474 | 0.7247 | 0.7150 | 0.7039 | 0.6945 |
| B2 | 0.8140 | 0.8140 | 0.8140 | 0.8140 | 0.8140 | 0.8140 | 0.8140 | |
| Location | Model | Forecast Horizon | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| COR | B1 | −0.0002 | −0.0001 | −0.0001 | 0.0000 | −0.0002 | −0.0001 | 0.0007 |
| B2 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | |
| MAG | B1 | 0.0000 | 0.0002 | 0.0000 | 0.0000 | −0.0008 | −0.0016 | −0.0015 |
| B2 | 0.0710 | 0.0710 | 0.0710 | 0.0710 | 0.0710 | 0.0710 | 0.0710 | |
| TAB | B1 | 0.0003 | 0.0003 | 0.0000 | −0.0018 | −0.0034 | −0.0041 | −0.0046 |
| B2 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | 0.0972 | |
| CON | B1 | 0.0014 | 0.0047 | 0.0084 | 0.0117 | 0.0157 | 0.0198 | 0.0236 |
| B2 | −0.0113 | −0.0113 | −0.0113 | −0.0113 | −0.0113 | −0.0113 | −0.0113 | |
| ARO | B1 | 0.0006 | 0.0011 | 0.0012 | 0.0021 | 0.0029 | 0.0036 | 0.0052 |
| B2 | 0.1787 | 0.1787 | 0.1787 | 0.1787 | 0.1787 | 0.1787 | 0.1787 | |
| Mean | B1 | 0.0004 | 0.0012 | 0.0019 | 0.0024 | 0.0028 | 0.0035 | 0.0047 |
| B2 | 0.0878 | 0.0878 | 0.0878 | 0.0878 | 0.0878 | 0.0878 | 0.0878 | |
| Station | Model | Lag Days | NSE | RMSE | MBE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | |||
| TAB | CNN | 15 | 0.710 | 0.778 | 0.862 | 0.723 | 0.916 | 1.050 | 0.001 | 0.123 | 0.484 |
| 30 | 0.423 | 0.752 | 0.848 | 0.734 | 0.939 | 1.438 | 0.000 | −0.026 | −0.974 | ||
| ELM | 15 | 0.794 | 0.820 | 0.860 | 0.727 | 0.825 | 0.885 | 0.043 | 0.082 | 0.126 | |
| 30 | 0.778 | 0.807 | 0.853 | 0.722 | 0.830 | 0.892 | −0.000 | 0.021 | 0.079 | ||
| LSTM | 15 | 0.749 | 0.797 | 0.845 | 0.766 | 0.877 | 0.976 | −0.003 | 0.088 | 0.236 | |
| 30 | 0.730 | 0.771 | 0.828 | 0.783 | 0.905 | 0.984 | 0.000 | −0.009 | −0.209 | ||
| MLP | 15 | 0.769 | 0.810 | 0.854 | 0.743 | 0.848 | 0.936 | 0.000 | 0.046 | 0.265 | |
| 30 | 0.715 | 0.781 | 0.841 | 0.750 | 0.883 | 1.012 | −0.000 | −0.029 | −0.210 | ||
| RF | 15 | 0.802 | 0.821 | 0.867 | 0.710 | 0.823 | 0.866 | 0.057 | 0.094 | 0.117 | |
| 30 | 0.799 | 0.819 | 0.859 | 0.706 | 0.805 | 0.850 | 0.000 | −0.011 | −0.033 | ||
| SVM | 15 | 0.779 | 0.817 | 0.869 | 0.704 | 0.831 | 0.915 | 0.000 | 0.074 | 0.183 | |
| 30 | 0.746 | 0.812 | 0.862 | 0.700 | 0.818 | 0.955 | 0.000 | −0.018 | 0.121 | ||
| T_CNN | 15 | 0.742 | 0.789 | 0.840 | 0.779 | 0.893 | 0.989 | 0.000 | 0.100 | 0.324 | |
| 30 | 0.705 | 0.770 | 0.841 | 0.750 | 0.905 | 1.029 | −0.000 | −0.017 | −0.297 | ||
| T_LSTM | 15 | 0.726 | 0.780 | 0.829 | 0.804 | 0.912 | 1.019 | 0.002 | 0.099 | 0.257 | |
| 30 | 0.699 | 0.765 | 0.831 | 0.775 | 0.916 | 1.040 | 0.000 | −0.050 | −0.312 | ||
| CON | CNN | 15 | 0.580 | 0.674 | 0.817 | 0.759 | 1.017 | 1.154 | 0.000 | −0.037 | −0.560 |
| 30 | 0.303 | 0.520 | 0.724 | 0.889 | 1.164 | 1.409 | 0.002 | −0.151 | −0.706 | ||
| ELM | 15 | 0.716 | 0.753 | 0.837 | 0.717 | 0.885 | 0.959 | 0.000 | 0.000 | 0.048 | |
| 30 | 0.635 | 0.697 | 0.779 | 0.796 | 0.927 | 1.021 | −0.002 | −0.057 | −0.122 | ||
| LSTM | 15 | 0.651 | 0.724 | 0.788 | 0.816 | 0.936 | 1.055 | 0.000 | −0.029 | −0.131 | |
| 30 | 0.378 | 0.552 | 0.706 | 0.919 | 1.126 | 1.326 | 0.000 | −0.061 | 0.304 | ||
| MLP | 15 | 0.579 | 0.709 | 0.808 | 0.778 | 0.959 | 1.160 | 0.000 | −0.059 | −0.260 | |
| 30 | 0.368 | 0.573 | 0.738 | 0.866 | 1.099 | 1.338 | 0.003 | −0.153 | −0.371 | ||
| RF | 15 | 0.721 | 0.754 | 0.843 | 0.703 | 0.883 | 0.939 | 0.003 | 0.026 | 0.057 | |
| 30 | 0.667 | 0.704 | 0.799 | 0.759 | 0.915 | 0.967 | −0.020 | −0.054 | −0.099 | ||
| SVM | 15 | 0.640 | 0.752 | 0.851 | 0.684 | 0.885 | 1.065 | 0.000 | −0.146 | −0.250 | |
| 30 | 0.547 | 0.672 | 0.804 | 0.749 | 0.961 | 1.146 | 0.015 | −0.235 | −0.393 | ||
| T_CNN | 15 | 0.561 | 0.679 | 0.800 | 0.794 | 1.008 | 1.184 | 0.000 | −0.047 | −0.225 | |
| 30 | 0.422 | 0.569 | 0.723 | 0.891 | 1.104 | 1.294 | −0.001 | −0.096 | −0.451 | ||
| T_LSTM | 15 | 0.570 | 0.674 | 0.746 | 0.895 | 1.018 | 1.177 | 0.000 | −0.035 | −0.166 | |
| 30 | 0.389 | 0.588 | 0.707 | 0.917 | 1.080 | 1.310 | 0.000 | −0.082 | −0.259 | ||
| COR | CNN | 15 | 0.818 | 0.882 | 0.929 | 0.630 | 0.808 | 1.011 | 0.000 | 0.056 | −0.505 |
| 30 | 0.522 | 0.853 | 0.913 | 0.670 | 0.873 | 1.592 | 0.000 | 0.035 | 1.003 | ||
| ELM | 15 | 0.879 | 0.900 | 0.932 | 0.614 | 0.745 | 0.824 | 0.000 | 0.015 | 0.084 | |
| 30 | 0.848 | 0.874 | 0.909 | 0.686 | 0.813 | 0.896 | −0.001 | 0.046 | 0.128 | ||
| LSTM | 15 | 0.877 | 0.894 | 0.924 | 0.649 | 0.771 | 0.831 | 0.000 | 0.041 | 0.178 | |
| 30 | 0.835 | 0.865 | 0.902 | 0.713 | 0.841 | 0.932 | 0.000 | 0.027 | 0.193 | ||
| MLP | 15 | 0.858 | 0.893 | 0.927 | 0.639 | 0.773 | 0.891 | −0.000 | 0.038 | 0.211 | |
| 30 | 0.801 | 0.858 | 0.908 | 0.690 | 0.860 | 1.029 | −0.001 | 0.011 | 0.172 | ||
| RF | 15 | 0.892 | 0.903 | 0.928 | 0.633 | 0.734 | 0.776 | 0.011 | 0.029 | 0.045 | |
| 30 | 0.870 | 0.883 | 0.912 | 0.674 | 0.783 | 0.826 | 0.000 | 0.015 | 0.033 | ||
| SVM | 15 | 0.869 | 0.900 | 0.934 | 0.605 | 0.744 | 0.855 | −0.000 | 0.053 | 0.130 | |
| 30 | 0.832 | 0.875 | 0.914 | 0.667 | 0.809 | 0.942 | 0.000 | 0.064 | 0.167 | ||
| T_CNN | 15 | 0.857 | 0.885 | 0.906 | 0.725 | 0.802 | 0.896 | 0.003 | 0.052 | 0.207 | |
| 30 | 0.815 | 0.855 | 0.892 | 0.749 | 0.870 | 0.988 | 0.000 | 0.023 | −0.280 | ||
| T_LSTM | 15 | 0.842 | 0.880 | 0.906 | 0.724 | 0.818 | 0.939 | −0.000 | 0.048 | 0.204 | |
| 30 | 0.824 | 0.859 | 0.885 | 0.773 | 0.859 | 0.965 | 0.000 | 0.037 | 0.230 | ||
| ARO | CNN | 15 | 0.799 | 0.851 | 0.913 | 0.624 | 0.816 | 0.951 | 0.000 | 0.106 | 0.436 |
| 30 | 0.737 | 0.840 | 0.916 | 0.620 | 0.851 | 1.097 | 0.001 | 0.056 | 0.256 | ||
| ELM | 15 | 0.850 | 0.874 | 0.917 | 0.609 | 0.751 | 0.823 | −0.001 | 0.056 | 0.113 | |
| 30 | 0.853 | 0.878 | 0.918 | 0.613 | 0.744 | 0.819 | 0.020 | 0.082 | 0.141 | ||
| LSTM | 15 | 0.823 | 0.860 | 0.912 | 0.627 | 0.792 | 0.892 | 0.000 | 0.068 | 0.196 | |
| 30 | 0.798 | 0.850 | 0.908 | 0.647 | 0.827 | 0.960 | −0.002 | 0.038 | 0.220 | ||
| MLP | 15 | 0.803 | 0.861 | 0.911 | 0.632 | 0.789 | 0.943 | −0.001 | 0.079 | 0.288 | |
| 30 | 0.793 | 0.853 | 0.913 | 0.630 | 0.815 | 0.972 | 0.000 | 0.020 | 0.164 | ||
| RF | 15 | 0.860 | 0.877 | 0.914 | 0.620 | 0.742 | 0.794 | 0.022 | 0.098 | 0.139 | |
| 30 | 0.855 | 0.883 | 0.920 | 0.606 | 0.730 | 0.814 | 0.009 | 0.047 | 0.070 | ||
| SVM | 15 | 0.817 | 0.869 | 0.918 | 0.607 | 0.764 | 0.908 | −0.003 | 0.136 | 0.200 | |
| 30 | 0.810 | 0.868 | 0.922 | 0.597 | 0.772 | 0.931 | 0.006 | 0.091 | 0.201 | ||
| T_CNN | 15 | 0.802 | 0.845 | 0.902 | 0.664 | 0.834 | 0.945 | 0.002 | 0.099 | 0.281 | |
| 30 | 0.794 | 0.845 | 0.901 | 0.674 | 0.840 | 0.970 | 0.000 | 0.018 | 0.210 | ||
| T_LSTM | 15 | 0.800 | 0.843 | 0.885 | 0.719 | 0.840 | 0.950 | 0.000 | 0.089 | 0.278 | |
| 30 | 0.780 | 0.838 | 0.882 | 0.736 | 0.859 | 1.001 | 0.000 | 0.042 | 0.238 | ||
| MAG | CNN | 15 | 0.734 | 0.800 | 0.871 | 0.681 | 0.847 | 0.980 | 0.000 | 0.046 | 0.311 |
| 30 | 0.409 | 0.819 | 0.880 | 0.672 | 0.823 | 1.499 | 0.000 | −0.003 | 1.113 | ||
| ELM | 15 | 0.821 | 0.841 | 0.878 | 0.662 | 0.756 | 0.804 | 0.000 | 0.031 | 0.071 | |
| 30 | 0.841 | 0.857 | 0.884 | 0.663 | 0.736 | 0.777 | −0.001 | −0.040 | −0.084 | ||
| LSTM | 15 | 0.810 | 0.830 | 0.862 | 0.705 | 0.782 | 0.828 | 0.000 | 0.036 | 0.132 | |
| 30 | 0.202 | 0.840 | 0.872 | 0.695 | 0.773 | 1.739 | 0.000 | −0.069 | −1.052 | ||
| MLP | 15 | 0.773 | 0.823 | 0.872 | 0.678 | 0.798 | 0.904 | 0.000 | 0.036 | 0.195 | |
| 30 | 0.763 | 0.835 | 0.880 | 0.672 | 0.788 | 0.948 | 0.000 | −0.048 | −0.261 | ||
| RF | 15 | 0.832 | 0.849 | 0.882 | 0.651 | 0.738 | 0.778 | 0.000 | 0.027 | 0.044 | |
| 30 | 0.859 | 0.869 | 0.892 | 0.640 | 0.704 | 0.732 | −0.020 | −0.039 | −0.061 | ||
| SVM | 15 | 0.797 | 0.843 | 0.885 | 0.643 | 0.750 | 0.855 | 0.000 | 0.049 | −0.138 | |
| 30 | 0.814 | 0.858 | 0.894 | 0.631 | 0.731 | 0.839 | 0.000 | −0.006 | −0.094 | ||
| T_CNN | 15 | 0.741 | 0.809 | 0.853 | 0.727 | 0.829 | 0.967 | 0.001 | 0.009 | 0.198 | |
| 30 | 0.773 | 0.825 | 0.864 | 0.716 | 0.812 | 0.928 | 0.002 | −0.097 | −0.371 | ||
| T_LSTM | 15 | 0.768 | 0.801 | 0.835 | 0.771 | 0.846 | 0.916 | 0.000 | 0.001 | −0.130 | |
| 30 | 0.787 | 0.827 | 0.852 | 0.749 | 0.808 | 0.897 | 0.000 | −0.063 | −0.247 | ||
| Conf. | TAB | CON | COR | ARO | MAG | Mean |
|---|---|---|---|---|---|---|
| I | 0.806 (0.704) | 0.886 (0.695) | 0.720 (0.614) | 0.686 (0.605) | 0.724 (0.648) | 0.764 |
| II | 0.801 (0.709) | 0.909 (0.697) | 0.718 (0.618) | 0.703 (0.615) | 0.732 (0.631) | 0.772 |
| III | 0.786 (0.701) | 0.920 (0.694) | 0.710 (0.633) | 0.693 (0.603) | 0.730 (0.643) | 0.767 |
| IV | 0.794 (0.703) | 0.897 (0.694) | 0.724 (0.630) | 0.693 (0.604) | 0.734 (0.646) | 0.768 |
| V | 0.812 (0.706) | 0.914 (0.700) | 0.741 (0.621) | 0.704 (0.598) | 0.732 (0.632) | 0.780 |
| VI | 0.812 (0.709) | 0.870 (0.687) | 0.720 (0.622) | 0.725 (0.602) | 0.743 (0.645) | 0.774 |
| VII | 0.805 (0.703) | 0.902 (0.689) | 0.728 (0.621) | 0.710 (0.601) | 0.733 (0.648) | 0.775 |
| VIII | 0.805 (0.709) | 0.925 (0.693) | 0.737 (0.617) | 0.717 (0.606) | 0.725 (0.642) | 0.781 |
| IX | 0.799 (0.708) | 0.883 (0.694) | 0.735 (0.642) | 0.693 (0.613) | 0.726 (0.639) | 0.767 |
| X | 0.803 (0.704) | 0.897 (0.699) | 0.734 (0.620) | 0.687 (0.613) | 0.730 (0.641) | 0.770 |
| XI | 0.811 (0.709) | 0.931 (0.698) | 0.740 (0.617) | 0.686 (0.597) | 0.702 (0.640) | 0.774 |
| XII | 0.823 (0.712) | 0.926 (0.697) | 0.732 (0.640) | 0.706 (0.605) | 0.722 (0.641) | 0.781 |
| XIII | 0.814 (0.708) | 0.933 (0.691) | 0.734 (0.605) | 0.726 (0.615) | 0.737 (0.642) | 0.788 |
| XIV | 0.809 (0.714) | 0.892 (0.688) | 0.737 (0.643) | 0.721 (0.615) | 0.741 (0.643) | 0.780 |
| XV | 0.811 (0.708) | 0.899 (0.715) | 0.730 (0.614) | 0.698 (0.612) | 0.721 (0.645) | 0.771 |
| XVI | 0.824 (0.709) | 0.904 (0.693) | 0.722 (0.619) | 0.706 (0.599) | 0.736 (0.633) | 0.778 |
| XVII | 0.810 (0.708) | 0.921 (0.691) | 0.753 (0.615) | 0.726 (0.599) | 0.734 (0.633) | 0.788 |
| XVIII | 0.805 (0.707) | 0.904 (0.718) | 0.729 (0.622) | 0.719 (0.606) | 0.735 (0.647) | 0.778 |
| XIX | 0.803 (0.707) | 0.905 (0.688) | 0.736 (0.616) | 0.711 (0.605) | 0.722 (0.633) | 0.775 |
| XX | 0.816 (0.713) | 0.879 (0.695) | 0.733 (0.610) | 0.719 (0.604) | 0.747 (0.642) | 0.778 |
| XXI | 0.801 (0.700) | 0.920 (0.721) | 0.725 (0.623) | 0.696 (0.608) | 0.738 (0.643) | 0.776 |
| XXII | 0.792 (0.709) | 0.893 (0.698) | 0.728 (0.615) | 0.709 (0.609) | 0.722 (0.637) | 0.768 |
| XXIII | 0.803 (0.713) | 0.904 (0.696) | 0.719 (0.627) | 0.705 (0.604) | 0.786 (0.643) | 0.783 |
| XXIV | 0.823 (0.709) | 0.917 (0.695) | 0.741 (0.640) | 0.696 (0.608) | 0.731 (0.635) | 0.781 |
| XXV | 0.821 (0.711) | 0.863 (0.691) | 0.720 (0.618) | 0.714 (0.613) | 0.733 (0.655) | 0.770 |
| XXVI | 0.822 (0.713) | 0.894 (0.684) | 0.736 (0.615) | 0.711 (0.605) | 0.730 (0.647) | 0.778 |
| XXVII | 0.803 (0.710) | 0.917 (0.699) | 0.714 (0.627) | 0.718 (0.612) | 0.734 (0.636) | 0.777 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellido-Jiménez, J.A.; Estévez, J.; Vanschoren, J.; García-Marín, A.P. AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models. Agronomy 2022, 12, 656. https://doi.org/10.3390/agronomy12030656
Bellido-Jiménez JA, Estévez J, Vanschoren J, García-Marín AP. AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models. Agronomy. 2022; 12(3):656. https://doi.org/10.3390/agronomy12030656
Chicago/Turabian StyleBellido-Jiménez, Juan Antonio, Javier Estévez, Joaquin Vanschoren, and Amanda Penélope García-Marín. 2022. "AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models" Agronomy 12, no. 3: 656. https://doi.org/10.3390/agronomy12030656
APA StyleBellido-Jiménez, J. A., Estévez, J., Vanschoren, J., & García-Marín, A. P. (2022). AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models. Agronomy, 12(3), 656. https://doi.org/10.3390/agronomy12030656







