Solar Fertigation: A Sustainable and Smart IoT-Based Irrigation and Fertilization System for Efficient Water and Nutrient Management
Abstract
:1. Introduction
2. The Proposed System: Smart Irrigation System
2.1. Solar Fertigation Irrigation and Fertilization Agronomic Models
2.2. Irrigation Scheduling
2.3. Nutrients
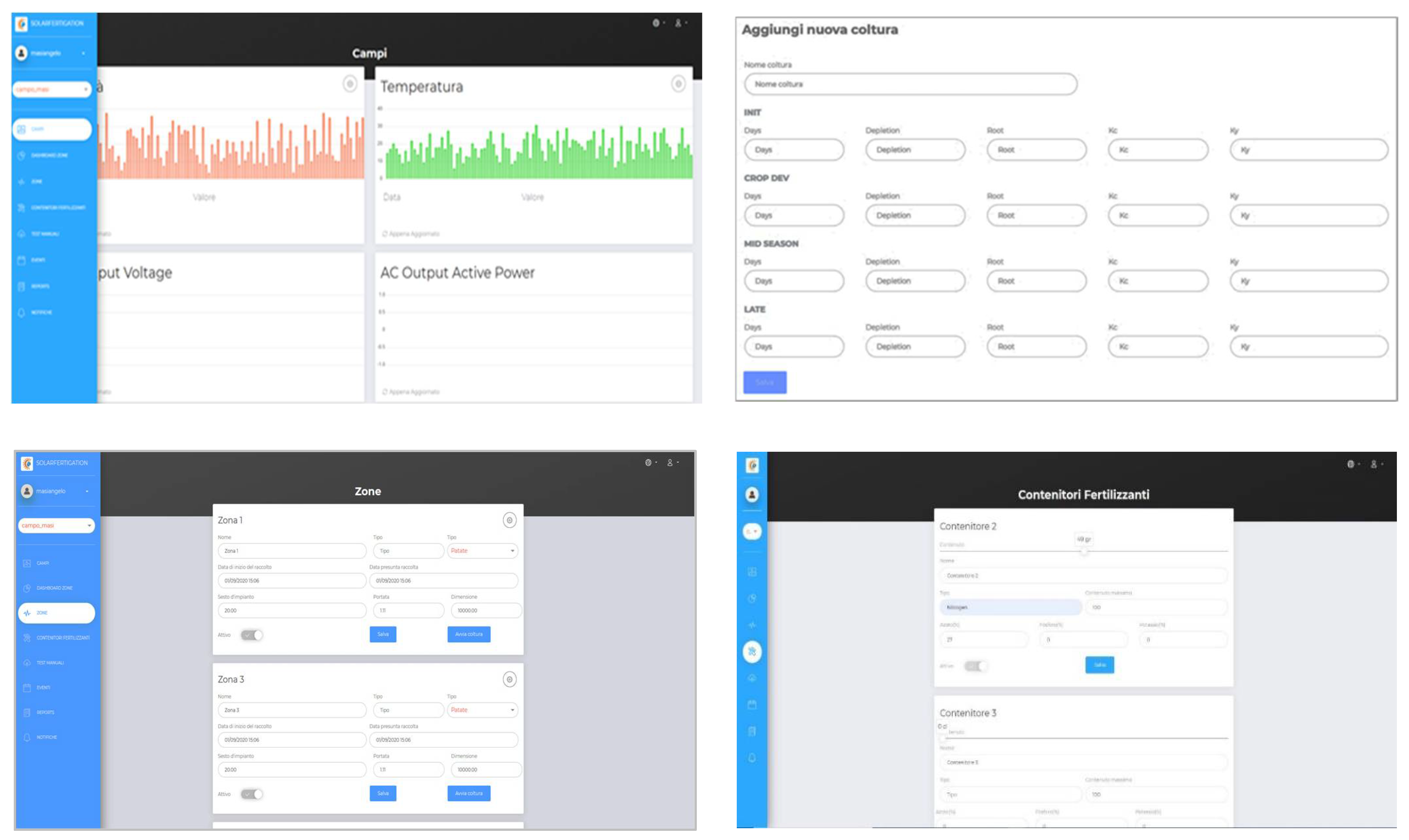
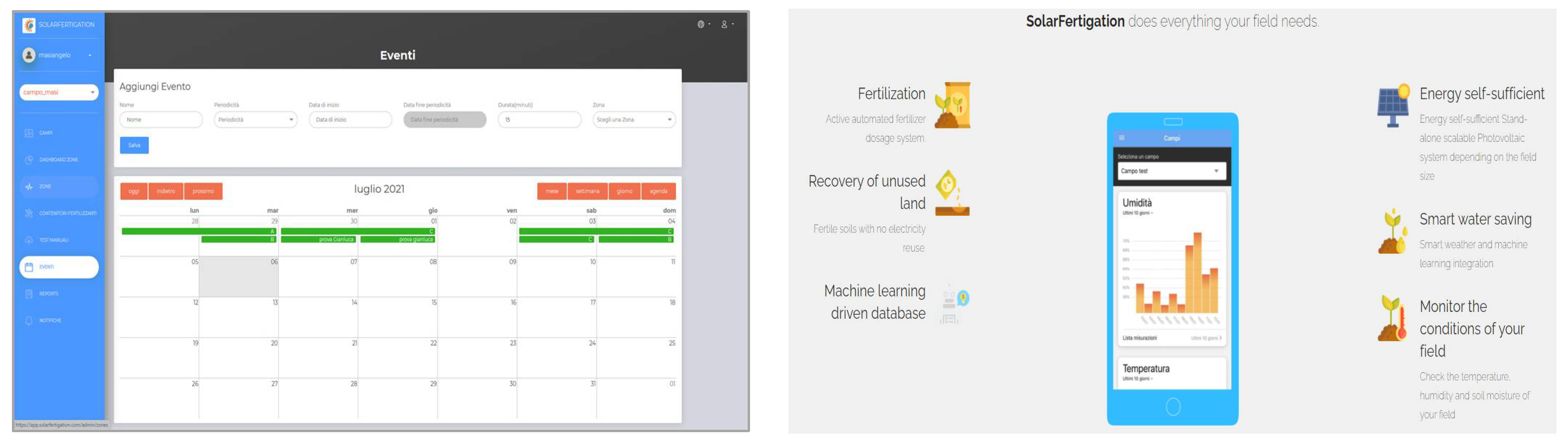
2.4. Real-Time Monitoring and Suggestions
2.4.1. Irrigation Scheduling
Crop Evapotranspiration (ETc)
Rainfall (Effective Rainfall)
Crop Factors
Soil Water Availability
2.4.2. Nutrients
Crop Database
2.4.3. Sensors for Real-Time Soil Moisture and Plant Water Content Monitoring
2.4.4. Web-Based Platform
3. The Proposed System: Experimental Setup for ET Crop Models
3.1. Study Area
3.2. Data Collection
3.3. Temperature-Based Models
3.3.1. Hargreaves–Samani (H–S) Model
3.3.2. Blaney–Criddle (B–C) Model
3.3.3. Thornthwaite Model
3.4. Radiation-Based Models
3.4.1. Priestley–Taylor Model
3.4.2. Makkink Model
3.4.3. Turc Model
3.5. Combination-Based Model
Standard FAO Penman–Monteith (P–M) Model
3.6. Data Analysis
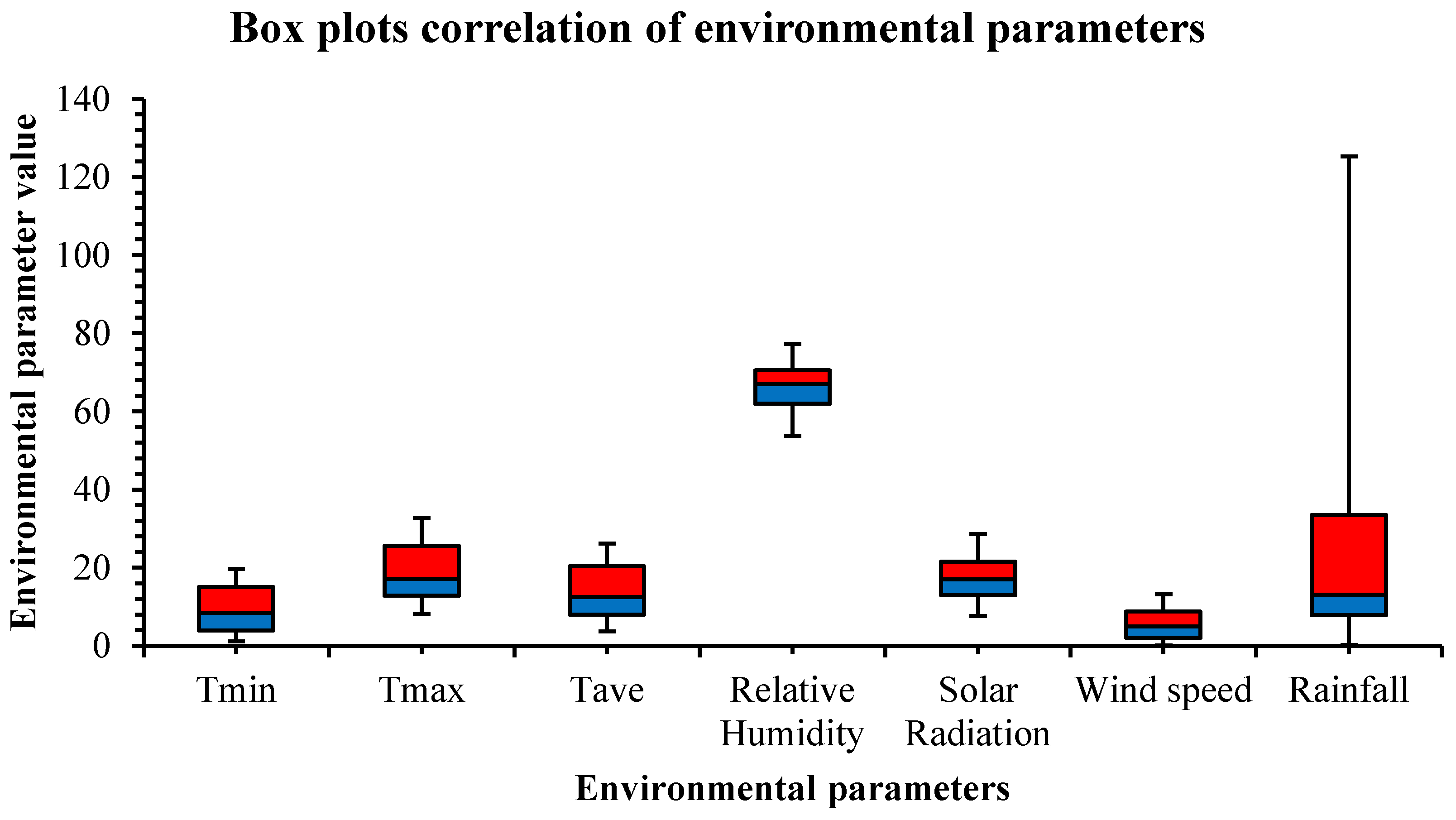
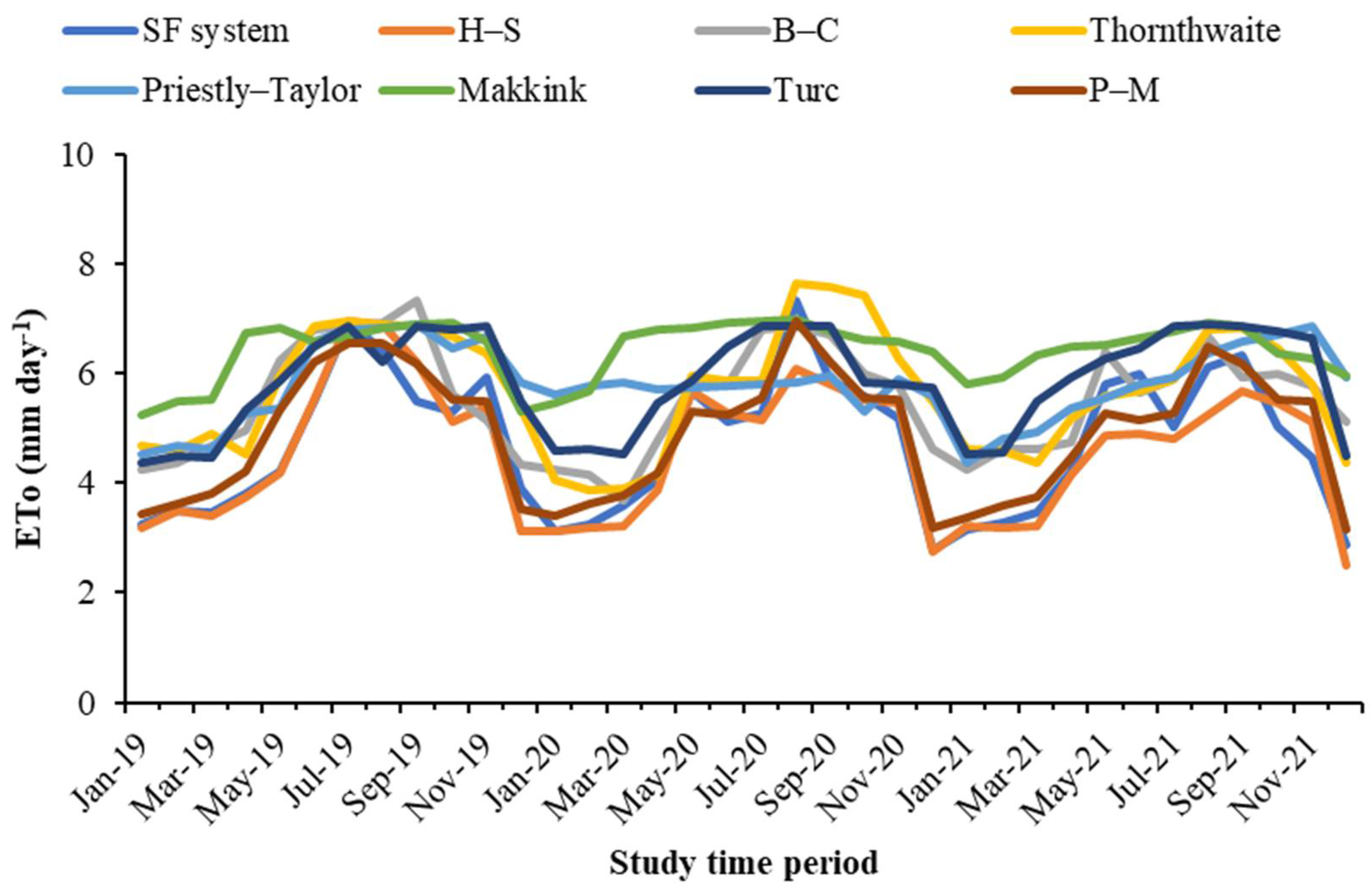
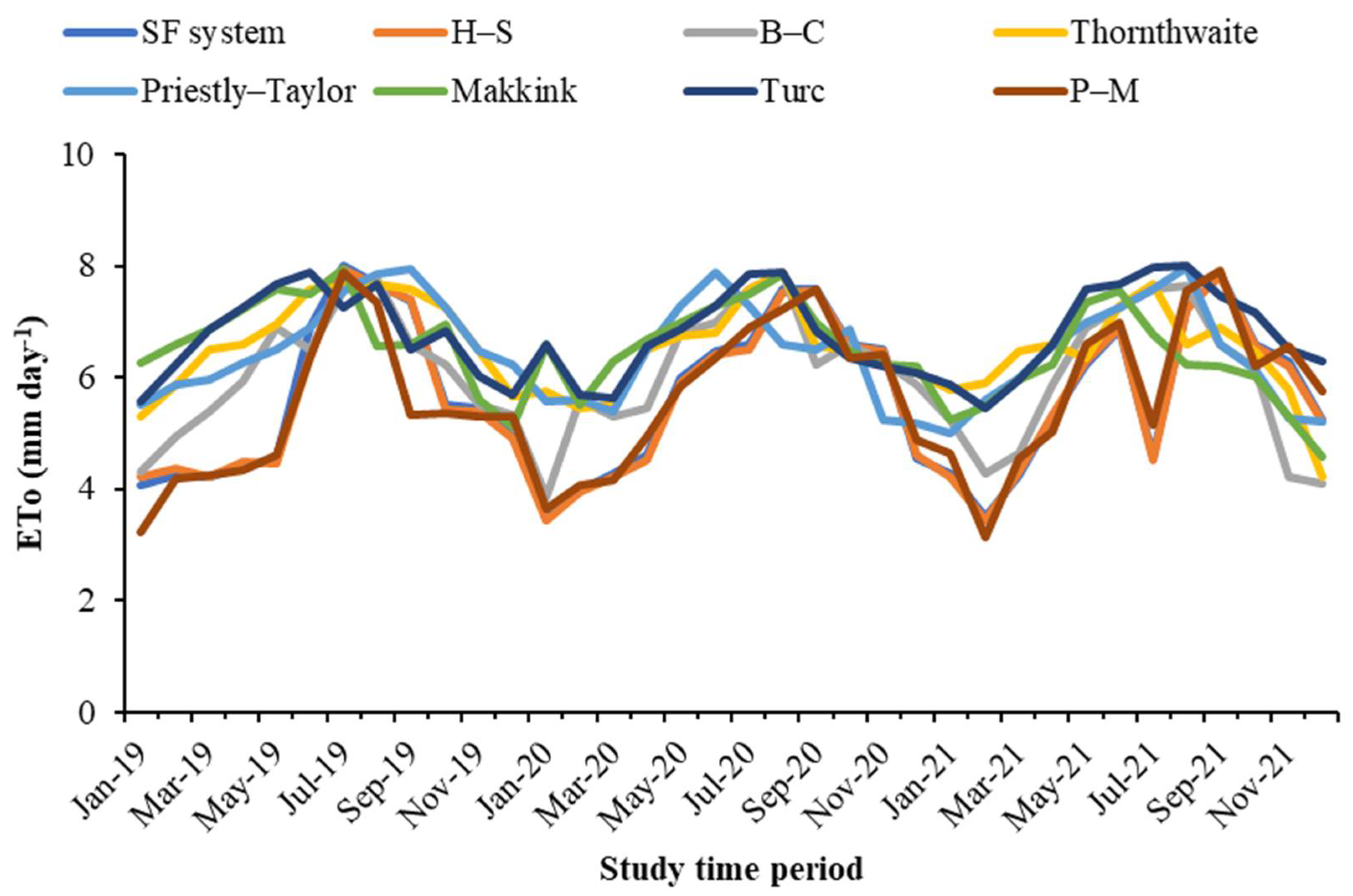
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Months | Minimum Temperature (°C) | Maximum Temperature (°C) | Average Temperature (°C) | Relative Humidity (%) | Solar Radiation (MJ m−2) | Air Speed (km h−1) | Rainfall (mm) |
|---|---|---|---|---|---|---|---|
| 19 January | 0.21 | 4.07 | 2.14 | 72.84 | 10.74 | 1.07 | 80.20 |
| 19 February | 1.70 | 8.57 | 5.13 | 67.08 | 16.00 | 6.23 | 46.33 |
| 19 March | 4.37 | 13.36 | 8.86 | 62.13 | 18.64 | 0.75 | 31.88 |
| 19 April | 6.57 | 14.84 | 10.70 | 61.34 | 26.16 | 1.11 | 65.38 |
| 19 May | 7.85 | 15.39 | 11.62 | 66.13 | 25.68 | 2.93 | 153.45 |
| 19 June | 17.60 | 28.09 | 22.84 | 67.94 | 24.35 | 10.35 | 17.55 |
| 19 July | 18.11 | 28.83 | 23.47 | 60.82 | 16.46 | 9.22 | 31.88 |
| 19 August | 18.55 | 30.59 | 24.57 | 71.73 | 18.73 | 10.40 | 28.53 |
| 19 September | 14.34 | 23.56 | 18.95 | 76.74 | 17.74 | 6.43 | 41.20 |
| 19 October | 11.30 | 20.22 | 15.76 | 56.71 | 19.73 | 2.81 | 40.33 |
| 19 November | 7.62 | 13.50 | 10.56 | 69.78 | 11.15 | 5.27 | 135.18 |
| 19 December | 3.91 | 9.54 | 6.72 | 71.63 | 10.45 | 1.84 | 79.78 |
| 20 January | 2.35 | 9.54 | 5.95 | 73.83 | 11.73 | 2.55 | 3.05 |
| 20 February | 3.31 | 11.85 | 7.58 | 68.07 | 16.99 | 7.71 | 23.38 |
| 20 March | 3.64 | 11.77 | 7.70 | 63.12 | 19.63 | 2.23 | 94.90 |
| 20 April | 6.85 | 15.96 | 11.41 | 62.33 | 27.15 | 2.59 | 29.13 |
| 20 May | 11.23 | 20.55 | 15.89 | 67.12 | 26.67 | 4.41 | 57.03 |
| 20 June | 13.87 | 23.47 | 18.67 | 68.93 | 25.34 | 11.83 | 60.05 |
| 20 July | 17.02 | 27.98 | 22.50 | 61.81 | 17.45 | 10.70 | 37.46 |
| 20 August | 18.38 | 29.60 | 23.99 | 70.67 | 17.67 | 9.83 | 64.20 |
| 20 September | 14.09 | 24.56 | 19.33 | 75.68 | 16.68 | 5.86 | 65.68 |
| 20 October | 9.11 | 17.54 | 13.33 | 55.65 | 18.67 | 2.24 | 31.31 |
| 20 November | 6.63 | 13.72 | 10.17 | 68.72 | 10.09 | 4.70 | 70.93 |
| 20 December | 3.81 | 9.82 | 6.81 | 70.57 | 9.39 | 1.27 | 125.28 |
| 21 January | 1.31 | 6.93 | 4.12 | 70.74 | 8.76 | 1.38 | 113.75 |
| 21 February | 3.86 | 12.12 | 7.99 | 64.98 | 14.02 | 6.54 | 39.78 |
| 21 March | 2.64 | 10.50 | 6.57 | 60.03 | 16.66 | 1.06 | 54.65 |
| 21 April | 5.00 | 13.81 | 9.40 | 59.24 | 24.18 | 1.42 | 27.13 |
| 21 May | 10.84 | 20.55 | 15.69 | 64.03 | 23.70 | 3.24 | 34.83 |
| 21 June | 16.50 | 27.33 | 21.92 | 65.84 | 22.37 | 10.66 | 26.60 |
| 21 July | 18.86 | 29.98 | 24.42 | 58.72 | 14.48 | 9.53 | 28.35 |
| 21 August | 18.19 | 29.71 | 23.95 | 69.62 | 16.75 | 10.71 | 25.28 |
| 21 September | 14.56 | 24.54 | 19.55 | 74.63 | 15.76 | 6.74 | 28.45 |
| 21 October | 8.83 | 15.58 | 12.20 | 54.60 | 17.75 | 3.12 | 9.15 |
| 21 November | 7.95 | 12.49 | 10.22 | 67.67 | 9.17 | 5.58 | 209.98 |
| 21 December | 3.56 | 9.14 | 6.35 | 69.52 | 8.47 | 2.15 | 105.10 |
| Months | Minimum Temperature (°C) | Maximum Temperature (°C) | Average Temperature (°C) | Relative Humidity (%) | Solar Radiation (MJ m−2) | Air Speed (km h−1) | Rainfall (mm) |
|---|---|---|---|---|---|---|---|
| 19 January | 3.09 | 10.09 | 6.59 | 76.31 | 17.43 | 6.48 | 66.83 |
| 19 February | 5.24 | 13.25 | 9.25 | 70.55 | 22.69 | 11.64 | 22.77 |
| 19 March | 7.64 | 16.74 | 12.19 | 65.60 | 25.33 | 6.16 | 22.33 |
| 19 April | 10.23 | 18.73 | 14.48 | 64.81 | 32.85 | 6.52 | 19.40 |
| 19 May | 11.74 | 20.40 | 16.07 | 69.60 | 32.37 | 8.34 | 10.10 |
| 19 June | 19.24 | 31.71 | 25.48 | 71.41 | 31.04 | 15.76 | 8.00 |
| 19 July | 20.46 | 32.81 | 26.64 | 64.29 | 23.15 | 14.63 | 6.50 |
| 19 August | 21.46 | 34.54 | 28.00 | 75.20 | 25.42 | 15.81 | 8.40 |
| 19 September | 18.52 | 28.27 | 23.40 | 80.21 | 24.43 | 11.84 | 21.57 |
| 19 October | 14.10 | 24.27 | 19.19 | 60.18 | 26.42 | 8.22 | 24.33 |
| 19 November | 11.27 | 18.87 | 15.07 | 73.25 | 17.84 | 10.68 | 36.93 |
| 19 December | 7.76 | 14.41 | 11.09 | 75.10 | 17.14 | 7.25 | 52.60 |
| 20 January | 5.16 | 13.71 | 9.43 | 77.45 | 18.57 | 7.62 | 21.97 |
| 20 February | 6.26 | 15.06 | 10.66 | 71.69 | 23.83 | 12.78 | 7.10 |
| 20 March | 6.99 | 15.48 | 11.23 | 66.74 | 26.47 | 7.30 | 7.87 |
| 20 April | 9.25 | 18.28 | 13.77 | 65.95 | 33.99 | 7.66 | 8.83 |
| 20 May | 13.72 | 23.21 | 18.47 | 70.74 | 33.51 | 9.48 | 9.47 |
| 20 June | 16.95 | 26.56 | 21.76 | 72.55 | 32.18 | 16.90 | 12.00 |
| 20 July | 20.37 | 31.18 | 25.78 | 65.43 | 24.29 | 15.77 | 11.47 |
| 20 August | 21.74 | 32.10 | 26.92 | 74.29 | 24.51 | 14.90 | 9.23 |
| 20 September | 18.92 | 28.38 | 23.65 | 79.30 | 23.52 | 10.93 | 18.67 |
| 20 October | 12.42 | 21.63 | 17.03 | 59.27 | 25.51 | 7.31 | 38.53 |
| 20 November | 10.21 | 17.73 | 13.97 | 72.34 | 16.93 | 9.77 | 65.37 |
| 20 December | 7.21 | 14.30 | 10.76 | 74.19 | 16.23 | 6.34 | 81.10 |
| 21 January | 4.73 | 12.03 | 8.38 | 74.83 | 16.07 | 7.41 | 68.77 |
| 21 February | 6.43 | 14.23 | 10.33 | 69.07 | 21.33 | 12.57 | 40.77 |
| 21 March | 5.73 | 14.24 | 9.98 | 64.12 | 23.97 | 7.09 | 31.50 |
| 21 April | 8.23 | 16.45 | 12.34 | 63.33 | 31.49 | 7.45 | 15.83 |
| 21 May | 13.27 | 23.75 | 18.51 | 68.12 | 31.01 | 9.27 | 5.90 |
| 21 June | 18.98 | 29.90 | 24.44 | 69.93 | 29.68 | 16.69 | 4.63 |
| 21 July | 21.86 | 32.63 | 27.25 | 62.81 | 21.79 | 15.56 | 5.77 |
| 21 August | 22.06 | 32.27 | 27.16 | 73.71 | 24.06 | 16.74 | 4.67 |
| 21 September | 17.85 | 27.04 | 22.44 | 78.72 | 23.07 | 12.77 | 32.40 |
| 21 October | 12.88 | 20.38 | 16.63 | 58.69 | 25.06 | 9.15 | 52.87 |
| 21 November | 12.12 | 17.57 | 14.84 | 71.76 | 16.48 | 11.61 | 105.13 |
| 21 December | 8.06 | 14.86 | 11.46 | 73.61 | 15.78 | 8.18 | 96.70 |

References
- Food and Agriculture Organization (FAO) of the United Nations; FAO Land and Water. Crop Information. Available online: https://www.fao.org/land-water/databases-and-software/crop-information/en/ (accessed on 24 March 2022).
- Alvino, A.; Ferreira, M.I.F.R. Refining Irrigation Strategies in Horticultural Production. Horticulturae 2021, 7, 29. [Google Scholar] [CrossRef]
- Chen, J.; Gao, Y.; Qian, H.; Jia, H.; Zhang, Q. Insights into water sustainability from a grey water footprint perspective in an irrigated region of the Yellow River Basin. J. Clean. Prod. 2021, 316, 128329. [Google Scholar] [CrossRef]
- Carriger, S.; Vallée, D. More crop per drop. Rice Today 2007, 6, 10–13. [Google Scholar]
- García, L.; Parra, L.; Jimenez, J.M.; Lloret, J.; Lorenz, P. IoT-Based Smart Irrigation Systems: An Overview on the Recent Trends on Sensors and IoT Systems for Irrigation in Precision Agriculture. Sensors 2020, 20, 1042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adeyemi, O.; Grove, I.; Peets, S.; Norton, T. Advanced monitoring and management systems for improving sustainability in precision irrigation. Sustainability 2017, 9, 353. [Google Scholar] [CrossRef] [Green Version]
- Marino, S.; Cocozza, C.; Tognetti, R.; Alvino, A. Use of proximal sensing and vegetation indexes to detect the inefficient spatial allocation of drip irrigation in a spot area of tomato field crop. Precis. Agric. 2015, 16, 613–629. [Google Scholar] [CrossRef]
- Devanand Kumar, G.; Vidheya Raju, B.; Nandan, D. A review on the smart irrigation system. J. Comput. Theor. Nanosci. 2020, 17, 4239–4243. [Google Scholar] [CrossRef]
- Gu, Z.; Qi, Z.; Burghate, R.; Yuan, S.; Jiao, X.; Xu, J. Irrigation scheduling approaches and applications: A review. J. Irrig. Drain. Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Abioye, E.A.; Abidin, M.S.Z.; Mahmud, M.S.A.; Buyamin, S.; Ishak, M.H.I.; Rahman, M.K.I.A.; Otuoze, A.O.; Onotu, P.; Ramli, M.S.A. A review on monitoring and advanced control strategies for precision irrigation. Comput. Electron. Agric. 2020, 173, 105441. [Google Scholar] [CrossRef]
- Bwambale, E.; Abagale, F.K.; Anornu, G.K. Smart irrigation monitoring and control strategies for improving water use efficiency in precision agriculture: A review. Agric. Water Manag. 2022, 260, 107324. [Google Scholar] [CrossRef]
- Hamami, L.; Nassereddine, B. Application of wireless sensor networks in the field of irrigation: A review. Comput. Electron. Agric. 2020, 179, 105782. [Google Scholar] [CrossRef]
- Li, W.; Awais, M.; Ru, W.; Shi, W.; Ajmal, M.; Uddin, S.; Liu, C. Review of sensor network-based irrigation systems using iot and remote sensing. Adv. Meteorol. 2020, 2020, 8396164. [Google Scholar] [CrossRef]
- Zinkernagel, J.; Maestre-Valero, J.F.; Seresti, S.Y.; Intrigliolo, D.S. New technologies and practical approaches to improve irrigation management of open field vegetable crops. Agric. Water Manag. 2020, 242, 106404. [Google Scholar] [CrossRef]
- Marino, S.; Aria, M.; Basso, B.; Leone, A.P.; Alvino, A. Use of soil and vegetation spectroradiometry to investigate crop water use efficiency of a drip irrigated tomato. Eur. J. Agron. 2014, 59, 67–77. [Google Scholar] [CrossRef]
- Ahmad, U. Evaluating seed rate, cutting and nitrogen level study of yield and yield components of triticale. Pak. J. Biotech. 2017, 14, 193–204. [Google Scholar]
- Ahmad, U.; Begum, U. Enhancing production of Zea mays genotypes by K application in Peshawar, Pakistan. Indian J. Agric. Res. 2017, 51, 257–261. [Google Scholar]
- Delgoda, D.; Saleem, S.K.; Malano, H.; Halgamuge, M.N. Root zone soil moisture prediction models based on system identification: Formulation of the theory and validation using field and AQUACROP data. Agric. Water Manag. 2016, 163, 344–353. [Google Scholar] [CrossRef]
- Prakash, K.J.; Athanasiadis, P.; Gualdi, S.; Trabucco, A.; Mereu, V.; Shelia, V.; Hoogenboom, G. Using daily data from seasonal forecasts in dynamic crop models for yield prediction: A case study for rice in Nepal’s Terai. Agric. For. Meteorol. 2019, 265, 349–358. [Google Scholar]
- Chen, S.; Dou, Z.; Jiang, T.; Li, H.; Ma, H.; Feng, H.; Yu, Q.; He, J. Maize yield forecast with DSSAT-CERES-Maize model driven by historical meteorological data of analogue years by clustering algorithm. Trans. CSAE 2017, 33, 147–155, (In Chinese with English Abstract). [Google Scholar]
- Ferrise, R.; Toscano, P.; Pasqui, M.; Moriondo, M.; Primicerio, J.; Semenov, M.A.; Bindi, M. Monthly-to-seasonal predictions of durum wheat yield over the Mediterranean Basin. Clim. Res. 2015, 65, 7–21. [Google Scholar] [CrossRef] [Green Version]
- White, S.C.; Raine, S.R. A Grower Guide to Plant Based Sensing for Irrigation Scheduling; University of Southern Queensland: Toowoomba, Australia, 2008. [Google Scholar]
- Ahmad, U.; Nasirahmadi, A.; Hensel, O.; Marino, S. Technology and Data Fusion Methods to Enhance Site-Specific Crop Monitoring. Agronomy 2022, 12, 555. [Google Scholar] [CrossRef]
- Visconti, P.; De Fazio, R.; Primiceri, P.; Cafagna, D.; Strazzella, S.; Giannoccaro, N.I. A solar-powered fertigation system based on low-cost wireless sensor network remotely controlled by farmer for irrigation cycles and crops growth optimization. Int. J. Electron. Telecommun. 2020, 66, 59–68. [Google Scholar]
- Valecce, G.; Strazzella, S.; Radesca, A.; Grieco, L.A. Solarfertigation: Internet of Things Architecture for Smart Agriculture. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements–FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization (FAO) of the United Nations: Rome, Italy, 1998; Available online: http://www.fao.org/3/X0490E/x0490e00.htm#Contents (accessed on 5 January 2022).
- Berengena, J.; Gavilán, P. Reference evapotranspiration estimation in a highly advective semiarid environment. J. Irrig. Drain. Eng. ASCE 2005, 131, 147–163. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L.S.; Almorox, J.; Darouich, H. Reference grass evapotranspiration with reduced data sets: Parameterization of the FAO Penman-Monteith temperature approach and the Hargeaves-Samani equation using local climatic variables. Agric. Water Manag. 2020, 240, 106210. [Google Scholar] [CrossRef]
- Moratiel, R.; Bravo, R.; Saa, A.; Tarquis, A.M.; Almorox, J. Estimation of evapotranspiration by the Food and Agricultural Organization of the United Nations (FAO) Penman–Monteith temperature (PMT) and Hargreaves–Samani (HS) models under temporal and spatial criteria—A case study in Duero basin (Spain). Nat. Hazards Earth Syst. Sci. 2020, 20, 859–875. [Google Scholar] [CrossRef] [Green Version]
- del Cerro, R.T.G.; Subathra, M.S.P.; Kumar, N.M.; Verrastro, S.; George, S.T. Modelling the daily reference evapotranspiration in semi-arid region of South India: A case study comparing ANFIS and empirical models. Inf. Process. Agric. 2021, 8, 173–184. [Google Scholar]
- Luo, W.; Chen, M.; Kang, Y.; Li, W.; Li, D.; Cui, Y.; Luo, Y. Analysis of crop water requirements and irrigation demands for rice: Implications for increasing effective rainfall. Agric. Water Manag. 2022, 260, 107285. [Google Scholar] [CrossRef]
- Fadda, L.; ARPAS, IMC. Nota Tecnica 4. Available online: http://www.sar.sardegna.it/pubblicazioni/notetecniche/nota4/pag014.asp (accessed on 24 March 2022).
- Fontanier, C.H.; Aitkenhead-Peterson, J.A.; Wherley, B.G.; White, R.H.; Thomas, J.C. Effective rainfall estimates for St. Augustinegrass lawns under varying irrigation programs. Agron. J. 2021, 113, 3720–3729. [Google Scholar] [CrossRef]
- Bokke, A.S.; Shoro, K.E. Impact of effective rainfall on net irrigation water requirement: The case of Ethiopia. Water Sci. 2020, 34, 155–163. [Google Scholar] [CrossRef]
- Martin, D.L.; Stegman, E.C.; Freres, E. Irrigation scheduling principles. In Management of Farm Irrigation Systems; Hoffman, G.L., Howell, T.A., Solomon, K.H., Eds.; ASAE Monograph: St. Joseph, MI, USA, 1990; pp. 155–372. [Google Scholar]
- Samsuri, S.F.M.; Ahmad, R.; Hussein, M. Development of nutrient solution mixing process on time-based drip fertigation system. In Proceedings of the 2010 IEEE Fourth Asia International Conference on Mathematical/Analytical Modelling and Computer Simulation, Kota Kinabalu, Malaysia, 26–28 May 2010; pp. 615–619. [Google Scholar]
- Kia, P.J.; Far, A.T.; Omid, M.; Alimardani, R.; Naderloo, L. Intelligent control based fuzzy logic for automation of greenhouse irrigation system and evaluation in relation to conventional systems. World Appl. Sci. J. 2009, 6, 16–23. [Google Scholar]
- Bhite, B.R.; Pawar, P.S.; Bulbule, S.V. Standardization of Stage Wise Requirement of Nutrients in Sweet Orange. Trends Biosci. 2017, 10, 5644–5647. [Google Scholar]
- Ben-Gal, A.; Beiersdorf, I.; Yermiyahu, U.; Soda, N.; Presnov, E.; Zipori, I.; Crisostomo, R.R.; Dag, A. Response of young bearing olive trees to irrigation-induced salinity. Irrig. Sci. 2017, 35, 99–109. [Google Scholar] [CrossRef]
- Shen, Y.; Sui, P.; Huang, J.; Wang, D.; Whalen, J.K.; Chen, Y. Global warming potential from maize and maize-soybean as affected by nitrogen fertilizer and cropping practices in the North China Plain. Field Crops Res. 2018, 225, 117–127. [Google Scholar] [CrossRef]
- Jahanzad, E.; Barker, A.V.; Hashemi, M.; Sadeghpour, A.; Eaton, T. Forage Radish and Winter Pea Cover Crops Outperformed Rye in a Potato Cropping System. Agron. J. 2017, 109, 646–653. [Google Scholar] [CrossRef]
- Geisseler, D.; Aegerter, B.J.; Miyao, E.M.; Turini, T.; Cahn, M.D. Nitrogen in soil and subsurface drip-irrigated processing tomato plants (Solanum lycopersicum L.) as affected by fertilization level. Sci. Hortic. 2020, 261, 108999. [Google Scholar] [CrossRef]
- Crops Statistical Year Book of the Food and Agriculture Organization (FAO) of the United Nations. 2001. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 5 January 2022).
- Dey, S.; Amin, E.M.; Karmakar, N.C. Paper Based Chipless RFID Leaf Wetness Detector for Plant Health Monitoring. IEEE Access 2020, 8, 191986–191996. [Google Scholar] [CrossRef]
- Home of the Point Dendrometers, Natkon. Available online: https://natkon.ch/ (accessed on 24 March 2022).
- Marino, S.; Ahmad, U.; Ferreira, M.I.; Alvino, A. Evaluation of the effect of irrigation on biometric growth, physiological response, and essential oil of Mentha spicata (L.). Water 2019, 11, 2264. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Areas from Climatological and Irrigation Data; U.S. Department Agriculture Soil Conservation Service: Washington, DC, USA, 1950; Volume 96, p. 44.
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Priestley, C.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Makkink, G. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Turc, L. Estimation of irrigation water requirements, potential evapotranspiration: A simple climatic formula evolved up to date. Ann. Agron. 1961, 12, 13–49. [Google Scholar]
- Caliandro, A.; Lamaddalena, N.; Stelluti, M.; Steduto, P. Agro-Ecologic characterization of the Puglia region. In ACLA 2 Project; Ideaprint: Bari, Italy, 2005; Volume 2, p. 179. [Google Scholar]
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements; USDA ARS Tech Bull: Washington, DC, USA, 1962. [Google Scholar]
- Chang, X.; Wang, S.; Gao, Z.; Luo, Y.; Chen, H. Forecast of Daily Reference Evapotranspiration Using a Modified Daily Thornthwaite Equation and Temperature Forecasts. Irrig. Drain. 2018, 68, 297–317. [Google Scholar] [CrossRef]
- Arasteh, P.D.; Tajrishy, M. Calibrating Priestley–Taylor model to estimate open water evaporation under regional advection using volume balance method–case study: Chahnimeh reservoir. Iran. J. Appl. Sci. 2008, 8, 4097–4104. [Google Scholar] [CrossRef]
- Liu, X.; Xu, C.; Zhong, X.; Li, Y.; Yuan, X.; Cao, J. Comparison of 16 models for reference crop evapotranspiration against weighing lysimeter measurement. Agr. Water Manag. 2017, 184, 145–155. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; Donnell, J.O.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Oceans 1985, 90, 8995–9005. [Google Scholar] [CrossRef] [Green Version]
- Vishwakarma, D.K.; Pandey, K.; Kaur, A.; Kushwaha, N.L.; Kumar, R.; Ali, R.; Elbeltagi, A.; Kuriqi, A. Methods to estimate evapotranspiration in humid and subtropical climate conditions. Agric. Water Manag. 2022, 261, 107378. [Google Scholar] [CrossRef]
- Thorp, K.R.; Marek, G.W.; DeJonge, K.C.; Evett, S.R. Comparison of evapotranspiration methods in the DSSAT Cropping System Model: II. Algorithm performance. Comput. Electron. Agric. 2020, 177, 105679. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration—A review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Awal, R.; Habibi, H.; Fares, A.; Deb, S. Estimating reference crop evapotranspiration under limited climate data in West Texas. J. Hydrol. 2020, 28, 100677. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Zhang, J.; Du, T.; Tong, L.; Ding, R. Evaluation of six potential evapotranspiration models for estimating crop potential and actual evapotranspiration in arid regions. J. Hydrol. 2016, 543, 450–461. [Google Scholar] [CrossRef]
- Yoder, R.; Odhiambo, L.O.; Wright, W.C. Evaluation of methods for estimating daily reference crop evapotranspiration at a site in the humid southeast United States. Appl. Eng. Agric. 2005, 21, 197–202. [Google Scholar] [CrossRef]
- Cristea, N.C.; Kampf, S.K.; Burges, S.J. Revised coefficients for Priestley-Taylor and Makkink-Hansen equations for estimating daily reference evapotranspiration. J. Hydrol. Eng. 2012, 18, 1289–1300. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.Y.; Singh, V. Evaluation and generalization of radiation-based methods for calculating evaporation. Hydrol. Proc. 2000, 14, 339–349. [Google Scholar] [CrossRef]
- Irmak, A.; Irmak, S. Reference and crop evapotranspiration in South Central Nebraska. II: Measurement and estimation of actual evapotranspiration for corn. J. Irrig. Drain. Eng. 2008, 134, 700–715. [Google Scholar] [CrossRef]
- Xu, J.; Peng, S.; Ding, J.; Wei, Q.; Yu, Y. Evaluation and calibration of simple methods for daily reference evapotranspiration estimation in humid East China. Arch. Agron. Soil Sci. 2013, 59, 845–858. [Google Scholar] [CrossRef]


| Crops/Parameters | p-Factor | Temperature Requirement (°C) | Root Depth (Zr) (m) | Crop Coefficient (kc) | Yield Factor (ky) | Fertilizers (N-P-K) (kg ha−1) | Crop Water Requirement (mm Growing Season−1) | References |
|---|---|---|---|---|---|---|---|---|
| Citrus (Citrus sinensis and Citrus limon | 0.5 | 23–30 | 1.2 | 0.70 | 0.8–1.1 | 100-35-50 | 900–1200 | [38] |
| Olive (Olea europaea) | 0.65 | 15–25 | 6.0 | 0.70 | 0.2 | 200-55-160 | 600–800 | [39] |
| Soybean (Glycine max) | 0.5–0.9 | 18–35 | 1.0 | 1.15 | 0.2–1.0 | 20:40:20 | 450–700 | [40] |
| Potato (Solanum tuberosum) | 0.9 | 18–20 | 1.0 | 0.5 | 0.85 | 34-0-0 | 500–700 | [41] |
| Cabbage (Brassica oleracea var. capitata) | 0.4 | 20–25 | 0.5 | 0.95 | 0.60 | 45:45:45 | 380–500 | [40] |
| Onion (Allium cepa) | 0.3 | 20–30 | 0.6 | 0.75 | 0.3 | 60-25-45 | 350–550 | [39] |
| Pepper (Capsicum annuum) | 0.3 | 18–27 | 0.8 | 0.9 | 1.1 | 5-10-10 | 600–1250 | [42] |
| Tomato (Lycopersicon esculentum) | 0.3 | 18–25 | 1.0 | 0.9 | 0.4 | 200:250:250 | 400–600 | [42] |
| Watermelon (Citrullus lanatus) | 0.4 | 21–29 | 0.8 | 0.75 | 0.3 | 80-25-35 | 600–800 | [1,43] |
| S. No. | Weather Stations | Altitude (m a.s.l.) | Time Period of Tests |
|---|---|---|---|
| Molise Region | |||
| 1. | W1–Campobasso | 700 | 1 January 2019–31 December 2021 |
| 2. | W2–Ferrazzano | 900 | 1 January 2019–31 December 2021 |
| 3. | W3–Oratino | 795 | 1 January 2019–31 December 2021 |
| 4. | W4–Ripalimosani | 640 | 1 January 2019–31 December 2021 |
| Apulia Region | |||
| 5. | W1–Montemesola | 183 | 1 January 2019–31 December 2021 |
| 6. | W2–Castellaneta | 5 | 1 January 2019–31 December 2021 |
| 7. | W3–Marina di Ginosa | 12 | 1 January 2019–31 December 2021 |
| Statistical Attributes/Models | Mean Absolute Error (MAE) | Mean Square Error (MSE) | Root Mean Square Error (RMSE) | Pearson Correlation Coefficient (R) |
|---|---|---|---|---|
| Solar fertigation system | 0.52 | 0.63 | 0.93 | 0.84 |
| H–S | 0.55 | 0.62 | 0.97 | 0.87 |
| B–C | 0.67 | 0.84 | 1.14 | 0.97 |
| Thornthwaite | 0.75 | 0.95 | 1.29 | 1.16 |
| Priestley–Taylor | 0.87 | 1.09 | 1.31 | 1.22 |
| Makkink | 0.95 | 1.36 | 1.74 | 1.65 |
| Turc | 0.83 | 1.17 | 1.45 | 1.57 |
| Statistical Attributes/Models | Mean Absolute Error (MAE) | Mean Square Error (MSE) | Root Mean Square Error (RMSE) | Pearson Correlation Coefficient (R) |
|---|---|---|---|---|
| Solar fertigation system | 0.63 | 0.72 | 0.92 | 0.84 |
| H–S | 0.64 | 0.68 | 0.97 | 0.86 |
| B–C | 0.70 | 0.95 | 1.28 | 0.95 |
| Thornthwaite | 0.86 | 0.99 | 1.37 | 1.28 |
| Priestley–Taylor | 0.92 | 1.18 | 1.46 | 1.32 |
| Makkink | 0.99 | 1.36 | 1.89 | 1.81 |
| Turc | 0.89 | 1.30 | 1.84 | 1.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, U.; Alvino, A.; Marino, S. Solar Fertigation: A Sustainable and Smart IoT-Based Irrigation and Fertilization System for Efficient Water and Nutrient Management. Agronomy 2022, 12, 1012. https://doi.org/10.3390/agronomy12051012
Ahmad U, Alvino A, Marino S. Solar Fertigation: A Sustainable and Smart IoT-Based Irrigation and Fertilization System for Efficient Water and Nutrient Management. Agronomy. 2022; 12(5):1012. https://doi.org/10.3390/agronomy12051012
Chicago/Turabian StyleAhmad, Uzair, Arturo Alvino, and Stefano Marino. 2022. "Solar Fertigation: A Sustainable and Smart IoT-Based Irrigation and Fertilization System for Efficient Water and Nutrient Management" Agronomy 12, no. 5: 1012. https://doi.org/10.3390/agronomy12051012
APA StyleAhmad, U., Alvino, A., & Marino, S. (2022). Solar Fertigation: A Sustainable and Smart IoT-Based Irrigation and Fertilization System for Efficient Water and Nutrient Management. Agronomy, 12(5), 1012. https://doi.org/10.3390/agronomy12051012








