Research and Design of Hybrid Optimized Backpropagation (BP) Neural Network PID Algorithm for Integrated Water and Fertilizer Precision Fertilization Control System for Field Crops

Abstract

China’s field crops such as cotton, wheat, and tomato have been produced on a large scale, but their cultivation process still adopts more traditional manual fertilization methods, which makes the use of chemical fertilizers in China high and causes waste of fertilizer resources and ecological environmental damage. To address the above problems, a hybrid optimization of genetic algorithms and particle swarm optimization (GA–PSO) is used to optimize the initial weights of the backpropagation (BP) neural network, and a hybrid optimization-based BP neural network PID controller is designed to realize the accurate control of fertilizer flow in the integrated water and fertilizer precision fertilization control system for field crops. At the same time, the STM32 microcontroller-based precision fertilizer application control system for integrated water and fertilizer application of large field crops was developed and the performance of the controller was verified experimentally. The results show that the controller has an average maximum overshoot of 5.1% and an average adjustment time of 68.99 s, which is better than the PID and PID control algorithms based on BP neural network (BP–PID) controllers; among them, the hybrid optimization of PID control algorithm based on BP neural network by particle swarm optimization and genetic algorithm(GA–PSO–BP–PID) controller has the best-integrated control performance when the fertilizer application flow rate is 0.6m³/h.

1. Introduction

Water–fertilizer integration is a modern agricultural technology that mixes the right amount of fertilizer with irrigation water and uses an irrigation system to irrigate the mixed water–fertilizer solution directly in the vicinity of the crop roots, thereby saving water resources, reducing fertilizer loss, and improving crop yield and quality [1,2,3]. This technology is widely used in modern agricultural farming because it can supply water and fertilizer to the crop precisely throughout the whole process; thus it can be designed for different growth periods according to water laws and the fertilizer requirements of the crop, regularly quantify water and nutrients, and provide them to the crop in proportion, which reduces labor costs and greatly improves the efficiency of agricultural farming [3,4,5]. This technology is widely used in modern field crop cultivation because it not only greatly reduces the waste of fertilizer caused by rough manual application, but also improves the efficiency of field crop cultivation [6].

Precision fertilization can reduce costs and also improve crop yield and quality, thus increasing agricultural efficiency [7]. However, the regulation process of fertilizer flow in the integrated water and fertilizer control system has the problem of volume delay in the transmission pipeline, which leads to time varying, lagging, and non-linear characteristics of the system, and there are still significant problems in precision and intelligence [8,9,10]. In the face of these problems, the traditional PID control gradually reveals its shortcomings and cannot obtain the expected control effect. Therefore, combining an intelligent optimization algorithm with PID technology to improve the performance of traditional PID systems and effectively solve the problem of precise control in integrated water and fertilizer control systems is of great significance to improve the quality of field crops, increase farmers’ income, and improve economic benefits as well as improve the soil environment and realize the ecologically sustainable development of field crop production [11,12,13].

Section 1 of this paper introduces the advantages and problems of water–fertilizer integration technology; Section 2 introduces the working principle of water–fertilizer integration system for field crops, establishes the mathematical model of precise fertilizer application in water–fertilizer integration systems for field crops, and gradually derives the principle of hybrid optimization algorithm; Section 3 uses Matlab software to establish the PID, BP–PID, and GA–PSO–BP–PID controller simulation models using Matlab software, analyzes the four transient performance indexes of the three control algorithms respectively, and builds a flow regulation test platform to experimentally verify the dynamic performance of the controller; in Section 4, the experimental results are analyzed and summarized; Section 5 summarizes the obtained conclusions.

2. Materials and Methods

2.1. Structural Components of Integrated Water and Fertilizer System for Field Crops

The water–fertilizer integrated system adopts a system of fertilizer and water co-delivery, that is, water and fertilizer are mixed and delivered for irrigation, which can make the fertilizer more evenly distributed in the soil and avoid fertilizer loss and waste caused by uneven fertilization in the traditional fertilizer application method [14,15,16,17]. In practice, since irrigation is a continuous action and the irrigation volume of each irrigation partition is controlled by a wireless electric valve, it is not necessary to think too much about the precision of irrigation in the water–fertilizer integrated precision control system, but the demand for nutrients of different crops has obvious differences, and even for the same crop, its demand for fertilizer is different during different growth periods [18]. Only through precise fertilization can we meet the needs of different crops in different growth periods and thus improve the yield and quality of crops, so the main research of this paper is about precise fertilization in an integrated water and fertilizer system for field crops [19]. The integrated water and fertilizer system for field crops consists of a reservoir, pump, filter, flow meter, fertilizer storage tank, peristaltic pump, control center, wireless electric valve, and drip irrigation belt. The regulating device mainly consists of a pump, peristaltic pump, flow sensor, wireless electric valve, and other devices, and the outlet is connected to the field drip irrigation belt, which constitutes a field crop water and fertilizer control system. As shown in Figure 1, the structure of the integrated water and fertilizer system for field crops is shown.

In particular, there are check valves on the irrigation mains to prevent the backflow of water, and similarly, there are check valves on the liquid fertilizer pipes to prevent the backflow of fertilizer. The fertilizer pump is connected to a flow meter to monitor the flow of supplied liquid fertilizer and calculate the remaining liquid fertilizer storage in the storage tank by collecting the applied fertilizer data. When the wireless electric valve is opened, the integrated water and fertilizer control system for field crops can be irrigated independently. If the peristaltic pump is powered to rotate its internal rotor, the change of roller position will cause the hose to be compressed and rebounded, thus causing the pump to suck in and press out fertilizer, resulting in simultaneous irrigation and fertilization. The control center uses an STM32F103ZET6 microcontroller combined with a hybrid optimization BP neural network PID control algorithm, with the set fertilizer flow rate as the desired value and the actual flow rate collected by the flow meter as the feedback value. When the flow meter detects deviation from the set value, the field crop water and fertilizer integration system changes the frequency of the peristaltic pump inverter to precisely adjust the fertilizer flow rate at the outlet of the peristaltic pump to achieve a more accurate fertilization effect.

In order to effectively solve the problem of accurate fertilization in the integrated system of water and fertilizer for field crops, a mathematical model is needed. Considering the fertilization characteristics of field crops and the complexity of the system, a first-order inertia plus delay link transfer function is used to describe the mathematical model of the system [20].

$$G\left(s\right)=\frac{K{e}^{-\tau s}}{Ts+1}$$

(1)

where K is the gain coefficient, τ is the delay time, and T is the time constant.

The fertilizer flow variation data were obtained by sampling the expected value of fertilizer flow using a 1-s sampling interval and used as input to the open-loop system. The data were fitted in Matlab using a first-order approximation to obtain K = 1, $\tau$ = 11 s, and T = 3.63. These parameters constitute the mathematical model of the integrated precision fertilizer application control system for field crops.

2.2. PID Controller Design Based on Hybrid Optimization BP Neural Network

2.2.1. Conventional PID Controller Design

To implement the hybrid optimization BP neural network-based PID controller design, a conventional PID controller needs to be established first. Conventional PID controller is one of the most widely used strategies in process control, which can solve most of the practical application problems in the field of automatic control, and its controller structure is shown in Figure 2 [21].

The PID controller gives the control quantity u(t) based on the deviation e(t) (i.e., the difference between the set value r(t) and the measured value y(t)) by calculating the deviation and applying it to the controlled object. u(t) is expressed as:

$${u\left(t\right)=K}_p\left[e\left(t\right)+\frac{1}{T_i}{\int }_0^{t}e\left(\tau \right)d\tau +T_d\frac{de\left(t\right)}{dt}\right]$$

(2)

where $K_p$ is the scaling factor. $T_i$ is the integration time constant and $T_d$ is the differential time constant.

Formula (2) is a continuous PID control algorithm expression, but in the actual field crop water integration precision fertilization control system, e(t) needs to be obtained by sampling, so it is necessary to discretize Formula (2). Assuming that the sampling period is T and a total of k samples are performed, it is obtained that:

$${\int }_0^{t}e\left(t\right)dt\approx T\sum _{j=0}^{k}e\left(j\right)$$

(3)

$$\frac{de\left(t\right)}{dt}\approx \frac{e\left(kT\right)-e\left[\left(k-1\right)T\right]}{T}=\frac{e_k-e_{k-1}}{T}$$

(4)

where Formula (3) is the integral part, and Formula (4) is the differential part; brought into Formula (2), the PID control algorithm expression can be obtained:

$$u\left(k\right)=K_p{e}_k+K_i\sum _{j=0}^k{e}_j+K_d\left(e_k-e_{k-1}\right)$$

(5)

where $K_p$ is the proportionality factor, $K_i$ is the integration factor and $K_d$ is the differentiation factor; $K_i$=$K_P\frac{T}{T_i}$, $K_d=K_P\frac{T_d}{T}$.

Conventional PID control is divided into two types: position-based PID control and incremental PID control. Position-based PID control is commonly used for electro-hydraulic servo valves, while the controlled object in the precision fertilizer control system for integrated fertilizer application to field crops is the motor driving the peristaltic pump, which is suitable for incremental PID control, so incremental PID control is selected in this paper. The continuous time t is discretized and k is assumed to be the current sampling moment, which can be obtained recursively according to Formula (5).

$$u\left(k-1\right)=K_p{e}_{k-1}+K_i\sum _{j=0}^{k-1}{e}_j+K_d\left(e_{k-1}-e_{k-2}\right)$$

(6)

Subtracting Formula (5) from Formula (6) yields:

$$∆u\left(k\right)=K_p\left(e_k-e_{k-1}\right)+K_i{e}_k+K_d\left(e_k-{2e}_{k-1}+e_{k-2}\right)$$

(7)

Thus u(k) can be expressed as:

$$u\left(k\right)=u\left(k-1\right)+∆u\left(k\right)$$

(8)

The $K_P$, $T_i$, $T_d$, three parameters of the PID controller are the core part of the design of the integrated water and fertilizer precision fertilizer control system, this paper uses the Cohen-Coon method for the initial adjustment, and the adjustment formula is shown in Formula (9):

$$\left\{\begin{array}{c}{K}_p=\frac{T}{K\tau }\left(\frac{4}{3}+\frac{\tau }{4T}\right)\\ T_i=\tau \left(\frac{32+\frac{6\tau }{T}}{13+\frac{8\tau }{T}}\right)\\ T_d=\tau \left(\frac{4}{11+\frac{2\tau }{T}}\right)\end{array}\right.$$

(9)

The mathematical model of the control object is shown in Formula (1), and the corresponding parameters are brought into the equation to obtain $K_p$ = 0.69, $K_i$ = 0.05, and $K_d$ = 1.78.

PID control in the field of linear system control technology is mature and commonly used, but there are shortcomings. For example, when the controlled object has complex nonlinear characteristics, it is difficult to establish an accurate mathematical model, and due to the uncertainty of the object and the environment, it is often difficult to achieve satisfactory control results.

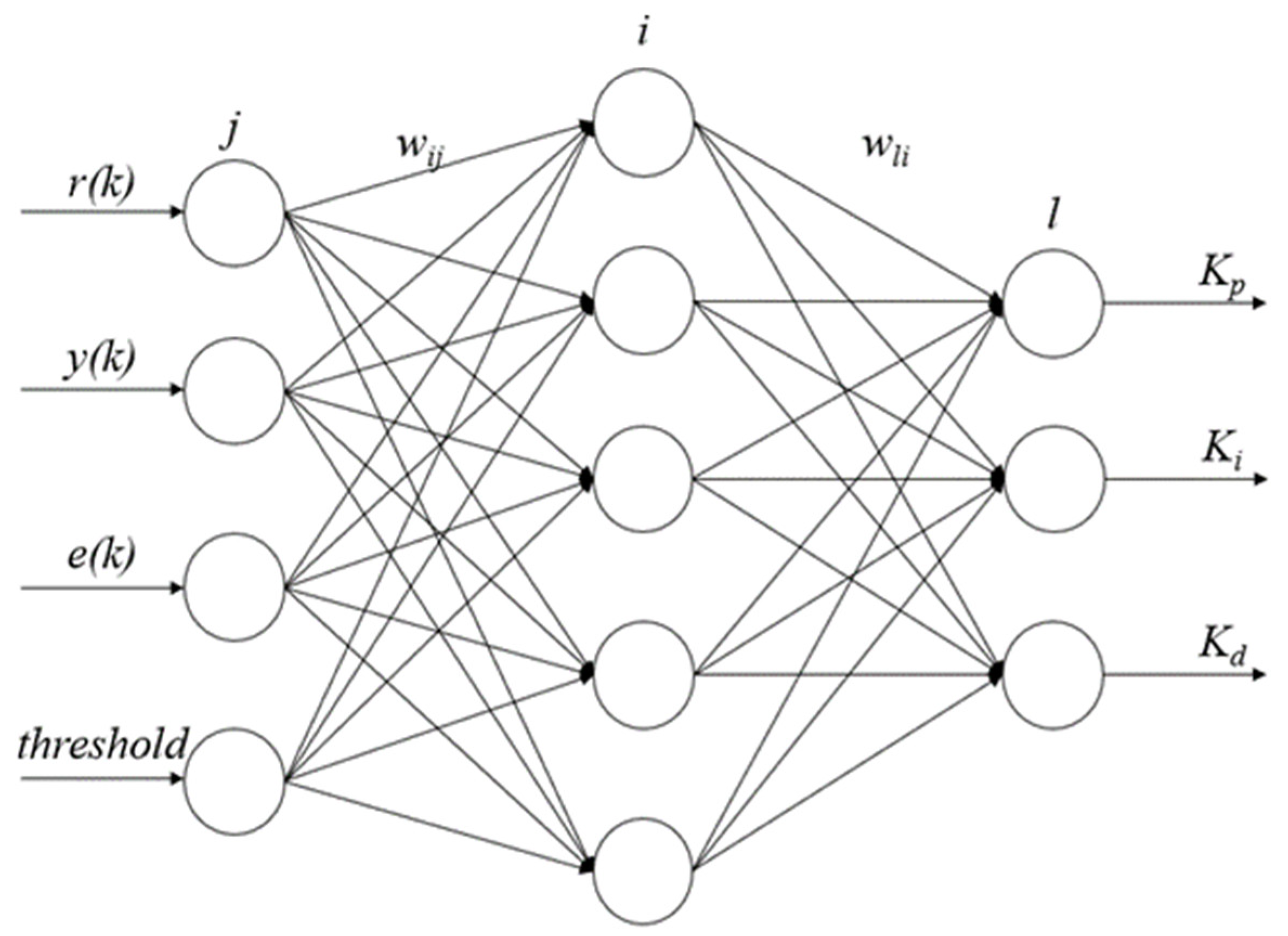
2.2.2. BP Neural Network-Based PID Controller Design

BP neural network-based PID control algorithm (hereinafter referred to as BP–PID) is a control strategy proposed to address the above problem. The nonlinear fitting capability of BP enables it to approximate any nonlinear continuous function with arbitrary accuracy, which gives it the ability to solve complex nonlinear systems and can be used for PID control [22]. Therefore, combining PID control and BP neural networking according to the characteristics of the three parameters of PID control with each other and mutual constraints, and using the mapping ability of BP neural network to nonlinear functions, makes the precision fertilizer application control system for integrated water and fertilizer of field crops adaptive, meaning it can automatically adjust the control parameters, adapt to the changes of the controlled process, improve control performance and reliability, and effectively improve the PID. It can effectively improve the limitations of PID control in complex nonlinear systems. The BP–PID controller structure is shown in Figure 3.

The BP neural network algorithm includes two processes: forward propagation of the sample input signal and backward transmission of the error. In forward propagation, the input sample data is passed to the output node through the implicit layer and then transformed nonlinearly to produce the corresponding output signal, which will enter the backward propagation of the error process if the true result is not consistent with the predicted result. The backpropagation of error is to reverse the output error through the hidden layer to the input layer by layer, assign the error to each layer, and use the error signal received by each layer as the basis for adjusting the weight of each unit. By adjusting the strength and threshold of the coupling between the input nodes and the hidden layer nodes, as well as the hidden layer nodes and the output nodes, the error is allowed to fall down the gradient, and the network parameters corresponding to the minimum error are obtained through repeated training and learning [23]. In this paper, a 4-5-3 style BP neural network structure is used as shown in Figure 4, i.e., 4 input layers, 5 hidden layers, and 3 output layers. The 4 input layers correspond to the desired set value r(k), actual output value y(k), deviation value e(k), and bias term, and 3 output layers correspond to $K_p$, $K_i$ and $K_d$ of PID. j is the number of neurons in the input layer, i is the number of neurons in the hidden layer j is the number of neurons in the input layer, i is the number of neurons in the hidden layer, and l is the number of neurons in the output layer.

The BP neural network input layer output and the implicit layer input and output are:

$$\left\{\begin{array}{c}{O_j}^{\left(1\right)}=x_{\left(j\right)}\left(k\right)\left(j=\mathrm{1,2},\dots ,M\right)\\ {{net}_i}^{\left(2\right)}\left(k\right)={\sum }_{j=1}^M{{\omega }_{ij}}^{\left(2\right)}{O_j}^{\left(1\right)}\left(k\right)\\ O_i^{\left(2\right)}\left(k\right)=f\left({net}_i^{\left(2\right)}\left(k\right)-{\theta }^{\left(2\right)}\right)\left(i=\mathrm{1,2},\dots ,Q\right)\end{array}\right.$$

(10)

where the superscripts (1) and (2) denote the input layer and the hidden layer respectively; M is the number of variables in the input layer of the neural network; ${\theta }^{\left(2\right)}$ is the threshold of the hidden layer; ${{\omega }_{ij}}^{\left(2\right)}$ is the connection weight of the neurons in the input layer and the neurons in the hidden layer; Q is the number of neurons in the hidden layer; f(x) is the activation function of the hidden layer; and its expression is as follows:

$$f\left(x\right)=\tan h\left(x\right)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(11)

The inputs and outputs of the output layer are:

$$\left\{\begin{array}{c}{{net}_l}^{\left(3\right)}\left(k\right)={\sum }_{i=1}^Q{{\omega }_{li}}^{\left(3\right)}{O_i}^{\left(2\right)}\left(k\right)\\ Q_l^{\left(3\right)}\left(k\right)=g\left({net}_l^{\left(3\right)}\left(k\right)-{\beta }^{\left(3\right)}\right)\left(l=\mathrm{1,2},3\right)\end{array}\right.$$

(12)

where the superscript (3) represents the output layer, ${{\omega }_{li}}^{\left(3\right)}$ is the connection weight of the neuron in the hidden layer and the neuron in the output layer, the three outputs of the output layer correspond to the three adjustable parameters $K_p$, $K_i$ and $K_d$ of PID controller, so l = 1, 2, 3; ${\beta }^{\left(3\right)}$ is the output layer threshold; $g\left(x\right)$ is the output layer activation function, $K_d$ cannot be negative, its expression is transformed using the Sigmoid function as follows:

$$g\left(x\right)=\frac{1}{2}\left[1+\tan h\left(x\right)\right]=\frac{e^x}{e^x+e^{-x}}$$

(13)

The above is the forward propagation process, when the difference between the actual output and the desired output value is not 0, the difference in the form of mean square value, as a variable to correct the connection weights, so that the error mean square value approaches 0, that is, the reverse error adjustment process, the error mean square value can be calculated from the performance indicator function, the expression is as follows:

$$E\left(k\right)={\frac{1}{2}\left[r\left(k\right)-y\left(k\right)\right]}^2=\frac{1}{2}{e}^2\left(k\right)$$

(14)

The connection weights ${{\omega }_{il}}^{\left(3\right)}$, ${{\omega }_{li}}^{\left(3\right)}$ are adjusted with E(k) as the variable, and based on the negative gradient rule, the inertia term is adopted and $\alpha$ is added as the inertia factor to increase the convergence speed and reduce the probability of falling into a dead loop [24]. The output layer, implicit layer connection weights are updated as follows:

$$\left\{\begin{array}{c}{\omega }_{li}^{\left(3\right)}\left(k+1\right)=-{\eta }_1\frac{\partial E\left(k\right)}{\partial {\omega }_{li}^{\left(3\right)}}+{\alpha }_1\Delta {\omega }_{li}^{\left(3\right)}\left(k-1\right)+\Delta {\omega }_{li}^{\left(3\right)}\left(k\right)\\ {\omega }_{ij}^{\left(2\right)}\left(k+1\right)=-{\eta }_2\frac{\partial E\left(k\right)}{\partial {\omega }_{ij}^{\left(2\right)}}+{\alpha }_2\Delta {\omega }_{ij}^{\left(2\right)}\left(k-1\right)+{\omega }_{ij}^{\left(2\right)}\left(k\right)\end{array}\right.$$

(15)

where $\alpha$ is the inertia factor; $\eta$ is the learning rate.

Since the partial derivatives in Formula (15) are difficult to calculate directly, the following deformation calculation is done:

$$\left\{\begin{array}{c}\frac{\partial E\left(k\right)}{\partial {\omega }_{li}^{\left(3\right)}}=\frac{\partial E\left(k\right)}{\partial y\left(k\right)}\ast \frac{\partial y\left(k\right)}{\partial ∆u\left(k\right)}\ast \frac{\partial ∆u\left(k\right)}{\partial O_l^{\left(3\right)}\left(k\right)}\ast \frac{\partial O_l^{\left(3\right)}\left(k\right)}{\partial {net}_l^{\left(3\right)}\left(k\right)}\ast \frac{\partial {net}_l^{\left(3\right)}\left(k\right)}{\partial {\omega }_{li}^{\left(3\right)}\left(k\right)}\\ \frac{\partial E\left(k\right)}{\partial {\omega }_{il}^{\left(2\right)}}=\frac{\partial E\left(k\right)}{\partial y\left(k\right)}\ast \frac{\partial y\left(k\right)}{\partial ∆u\left(k\right)}\ast \frac{\partial ∆u\left(k\right)}{\partial O_l^{\left(3\right)}\left(k\right)}\ast \frac{\partial O_l^{\left(3\right)}\left(k\right)}{\partial {net}_l^{\left(3\right)}\left(k\right)}\ast \frac{\partial {net}_i^{\left(3\right)}\left(k\right)}{\partial O_i^{\left(2\right)}\left(k\right)}\ast \frac{\partial O_i^{\left(2\right)}\left(k\right)}{\partial {net}_i\left(k\right)}\ast \frac{\partial {ne{t}_i}^{\left(2\right)}\left(k\right)}{\partial {\omega }_{il}^{\left(2\right)}}\end{array}\right.$$

(16)

After simplification, approximation and other calculations, the updated formula for the output layer and implicit layer connection weights of the traditional BP neural network PID controller is obtained as follows:

$$\left\{\begin{array}{c}{w}_{li}^{\left(3\right)}\left(k+1\right)={\alpha }_1∆w_{li}^{\left(3\right)}\left(k-1\right)+{\eta }_1{\delta }_l^{\left(3\right)}{O}_i^{\left(2\right)}\left(k\right)+w_{li}^{\left(3\right)}\left(k\right)\\ {\delta }_l^{\left(3\right)}=e\left(k\right)sgn\left(\frac{\partial y\left(k\right)}{\partial ∆u\left(k\right)}\right)\frac{\partial ∆u\left(k\right)}{\partial O_l^{\left(3\right)}\left(k\right)}{g}^{\prime }\left[{net}_l^{\left(3\right)}\left(k\right)-{\beta }^{\left(3\right)}\left(k\right)\right]\\ w_{ij}^{\left(2\right)}\left(k+1\right)={\alpha }_2∆w_{ij}^{\left(2\right)}\left(k-1\right)+{\eta }_2{\delta }_i^{\left(2\right)}{O}_j^{\left(1\right)}\left(k\right)-w_{ij}^{\left(2\right)}\left(k\right)\\ {\delta }_i^{\left(2\right)}=f^{\prime }\left[{net}_i^{\left(2\right)}\left(k\right)-{\theta }^{\left(2\right)}\left(k\right)\right]{\displaystyle \sum _{l=1}^3}{\delta }_l^{\left(3\right)}{w}_{li}^{\left(3\right)}\left(k\right)\end{array}\right.$$

(17)

In summary, the control process of the BP–PID control method can be summarized as follows:

(1)

determine the BP neural network structure, and determine the initial values of connection weights and thresholds by the mathematical model of the controlled object, select the appropriate inertia factor $\alpha$ and learning rate $\eta$, and determine the initial values of the proportional, integral and differential coefficients of the PID;

(2)

the flowmeter collects the actual instantaneous flow value of liquid fertilizer at the current moment, inputs the desired instantaneous flow value of liquid fertilizer, and calculates and inputs the metering deviation value of liquid fertilizer;

(3)

according to Formula (8), u(k) is calculated and input to the controlled object to obtain the actual instantaneous flow rate value of liquid fertilizer at the moment k = 1;

(4)

The learning update of the BP neural network part is carried out, and the parameters of the modified PID control are obtained according to Formulas (10)–(17) to realize the adaptive adjustment of the PID parameters.

(5)

When k = k + 1, return to Formula (8).

Through the process of adjusting the weights of the BP learning algorithm, the ideal data of the posting and model are trained, and the adaptive capability of online adjustment of the parameters is used to adjust the parameters of the PID in real time to achieve the optimization of the parameters by constantly adjusting the weights online, so that the control and identification effects can be obtained adaptively, quickly, and accurately.

BP–PID can use its learning ability to adjust the system parameters, but its algorithm for adjusting the weights and thresholds of the network is in the negative gradient direction, which leads to slow convergence of the algorithm in the training process. In the process of network learning training using the gradient descent method, the further ability is needed to make the training results reach the global optimum [25]. To address the defects of the BP neural network such as slow convergence speed and easy falling into local minima, the advantages of the strong global search ability of the genetic algorithm and strong local search ability and fast convergence speed of the particle swarm algorithm are used to optimize the BP neural network weights to obtain a new control method and form a hybrid optimization algorithm to improve the BP neural network.

2.2.3. Design of Hybrid Optimization BP Neural Network-Based PID Controller

The particle swarm optimization algorithm is an optimization algorithm that simulates the phenomenon of biological clusters in nature, which has a fast convergence speed at the early stage of evolution, but a slow convergence speed and low convergence accuracy at the late stage of evolution, and falls easily into the situation of local minima; the genetic algorithm has good parallel computing ability and strong global search ability. Given their complementary advantages, the two algorithms are combined, and the hybrid optimization of genetic algorithms and particle swarm optimization (hereinafter referred to as GA–PSO) algorithm optimizes the connection weights of the BP neural network and applies the optimized optimal weights to the BP neural network. Thereafter, the BP neural network adjusts the weighting coefficients by its self-tuning capability and automatically adjusts the PID control parameters to achieve the goal of optimal control parameters. The hybrid optimization of PID control algorithm based on BP neural network by particle swarm optimization and genetic algorithm (hereinafter referred to as GA–PSO–BP–PID algorithm) is a hybrid algorithm that combines genetic algorithm (GA), particle swarm optimization (PSO), backpropagation (BP), and proportional-integral-derivative (PID) control to optimize a parametric PID controller. The GA–PSO-BP–PID controller structure is shown in Figure 5.

Since most of the GA–PSO improvement algorithms make the algorithm itself complicated, the GA–PSO hybrid optimization algorithm proposed in this paper uses crossover and mutation operations instead of the terms in the standard particle swarm algorithm formulas for particle updates through the crossover and mutation ideas of genetic algorithms. Therefore, it simplifies the algorithm and avoids using the formula to calculate the particle positions, which not only utilizes the characteristics of the particle swarm algorithm to quickly converge to the optimal solution position in the early stage, but also brings into play the global search ability of the genetic algorithm and effectively avoids the premature phenomenon of the population [26].

The velocity and position of any particle in the PSO algorithm is updated during the update process according to the following two Formulas:

$$V_i\left(k+1\right)=\omega V_i\left(k\right)+c_1{r}_1\left[p_i-x_i\left(k\right)\right]+c_2{r}_2\left[p_g-x_i\left(k\right)\right]$$

(18)

$$X_i\left(k+1\right)=X_i\left(k\right)+V_i\left(k+1\right)$$

(19)

where k is the number of iterations; $c_1$, $c_2$ is the acceleration factor; $\omega$ is the inertia coefficient; $r_1$, $r_2$ are random numbers between [0, 1].

From Formulas (18) and (19), the update of the particle expresses as:

$$X_i\left(k+1\right)=X_i\left(k\right)+\omega V_i\left(k\right)+c_1{r}_i\left[p_i-x_i\left(k\right)\right]+c_2{r}_2\left[p_g-x_i\left(k\right)\right]$$

(20)

In Formula (20), the second term $\omega V_i\left(k\right)$ is the inertia originally possessed by the particle, which corresponds to the variational operation in GA for the velocity term at the previous moment; similarly, the first, third, and fourth terms of Formula (20) correspond to the crossover operation in GA for the particle with the individual extremal particle and the global extremal particle.

Therefore, firstly, the second term $\omega V_i\left(k\right)$ in Formula (20) is replaced by the variation operation in GA. Instead of multiplying the velocity term of the particle by the original velocity using the inertia coefficient, the velocity of the particle is updated by the variation operation; then the terms 1, 3 and 4 in Formula (20) are replaced by the crossover operation in GA: the particle is first crossed with its individual extremum and then with the global extremum. Finally, the particle that completes the crossover operation is added with the velocity term corresponding to it to complete the particle update.

In the iterative process, the fitness value of each individual is calculated using the fitness function and is evaluated. The ITAE metric has the advantages of fast, smooth, and low overshoot, and is adopted in most of the literature, so it is introduced into the performance evaluation of the precision fertilizer application control system for field crops in this paper as an important reference index for the controller, and as an important reference index for the GA–PSO hybrid optimization algorithm as an adaptation function. The so-called ITAE criterion, i.e., the time multiplied absolute error integral minimization criterion, can be expressed as:

$$\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{E}={\int }_0^{\infty }t\mid e\left(t\right)\mid \mathrm{d}t$$

(21)

Formula (21) is the mathematical model of the continuous control system, but because the computer uses digital sampling control, the integral part and differential part in Formula (21) cannot be identified. Therefore, it is necessary to discretize the sampling moment points. With T as the period of sampling and k as the serial number of sampling, the discrete formula of the ITAE function is:

$$\mathrm{ITAE}={\sum }_{k=0}^n\mid e\left(kT\right)\mid ·kT·T$$

(22)

where T is the sampling period and k is the sampling moment.

Instead of the gradient descent method of the traditional BP algorithm, the above GA–PSO hybrid optimization algorithm is used for the parameter optimization process of the BP neural network to search for all the weights of the BP neural network and use them as the coded information of the particle swarm individuals. This not only avoids the problem of large computational effort caused by the gradient descent method of derivation but also reduces the risk of falling into local minima. In the optimization process, the memory function of the particle swarm algorithm is used to retain the global optimum, so that each particle quickly approaches the global optimum solution and accelerates the convergence speed. The GA–PSO hybrid optimization algorithm performs an iterative optimization search with ITAE as the objective function and then obtains the optimal weights of the BP algorithm for a given number of iterations.

In summary, the flow of the BP neural network with hybrid optimization of genetic algorithms and particle swarm optimization (hereinafter referred to as GA–PSO-BP) algorithm designed in this paper is shown in Figure 6.

3. Results

3.1. Analysis of Simulation Results

Three different control methods, PID, BP–PID, and GA–PSO–BP–PID, were used in the simulation experiments in Matlab software, the sampling period was set to 1 ms, and the system delay time was 11 s. The three controllers were constructed with the following parameters:

Conventional PID control: According to the parameters obtained in the conventional PID controller design in chapter 3.1 above, $K_p$ = 0.69, $K_i$ = 0.05, $K_d$ = 1.78, and the input step signal is simulated.

BP–PID control: For BP neural network PID, the structure of the neural network is selected as 4-5-3 according to Section 3.2 above, the learning rate $\eta$ is set to 0.28, the inertia factor $\alpha$ is set to 0.04, and the initial value of the weighting coefficient is taken as a random number on the interval [−1.0, 1.0]. Since the adjustable parameters $K_p$, $K_i$, and $K_d$ are taken as non-negative Sigmoid functions, their values are between (0, 1).

GA–PSO–BP–PID control: GA–PSO–BP–PID controller first sets the algorithm parameters, where the BP neural network parameters are set in line with the above PID control for building BP neural networks, the GA–PSO part sets the particle population size to 100, the number of iterations $k$ to 1000, the value of inertia coefficient $\omega$ to 0.6, the acceleration factor $c_1$, $c_2$ is set to 1.85, and the above algorithm parameters are used to initialize the population, find the optimal extrema, and update it for iterative optimization search.

Figure 7 shows the iterative optimization search process for the optimal individual fitness value of the GA–PSO hybrid optimization algorithm and the variation curve of the steady-state performance index ITAE obtained after 1000 iterations.

From Figure 7, it can be seen that after the GA–PSO hybrid optimization algorithm starts, the fitness value ITAE gradually stabilizes and cancan jump out of the local optimal solution as the number of iterations increases. At about 190 iterations, the ITAE metrics stabilized.

To compare more intuitively, the unit step signal is used as the input signal, and four transient performance indicators, namely rise time, peak time, regulation time, and maximum overshoot, are added for comparison, and the simulation time is 100 s. The unit step response comparison simulation results of the three controllers are shown in Figure 8, and the four transient performance indexes are shown in

Table 1. Transient performance index of three controllers.

Controller Type	Rise Time (s)	Peak Time (s)	Regulation Time (s)	Maximum Overshoot
PID	12.42	13.69	25.26	58.61%
BP–PID	27.39	32.96	19.91	1.04%
GA–PSO-BP–PID	11.95	12.50	11.77	3.6%

.

As can be seen from Figure 8, the GA–PSO–BP–PID algorithm is the first to reach the reference curve with the shortest rise time, and the overall response is soon stabilized, although the rise time is not much different compared with the PID algorithm, the PID algorithm produces larger oscillations and overshoot, and the GA–PSO-BP–PID algorithm has an obvious overall advantage in performance. The overall advantage of the GA–PSO–BP–PID algorithm is obvious; the GA–PSO–BP–PID algorithm produces some overshoot compared with the BP–PID algorithm, but the longer rise time, peak time, and regulation time of the BP–PID algorithm make its overall performance decrease and inferior to GA–PSO–BP–PID algorithm.

From the transient performance indexes of the three controllers analyzed in Table 1, all four transient performance indexes of the PID algorithm are inferior to the GA–PSO–BP–PID algorithm, and in terms of overshoot, although the overshoot of the BP–PID algorithm is 1.04%, which is better than that of the GA–PSO-BP–PID algorithm by 3.6%, its rise time and peak time are much longer than that of the GA–PSO–BP–PID. The GA–PSO-BP–PID algorithm can balance the response speed and the stability of the control process, and the overall performance is superior.

3.2. Flow Rate Adjustment Test of Water–fertilizer Integrated Precision Fertilizer Application Control System

3.2.1. Testing Device and System Design

To be able to accurately simulate the operation of the integrated water and fertilizer precision fertilization control system for field crops in the laboratory and to test the control speed and stability of the control algorithm, this paper builds a test platform using the implementation components for integrated water and fertilizer precision fertilization in an actual farm environment, connects the flow meter to the test platform, and interacts with the computer and control system through the RS-485 serial bus to compare test different control strategies. The schematic diagram of the testbed composition is shown in Figure 9.

The flow rate adjustment test platform adopts a STM32F103ZET6 microcontroller as the control element of water and fertilizer integrated precision fertilization control system, and writes the program with the programming software Keil $\mu$Vision4; adopts peristaltic pump as liquid fertilizer conveying device, whose maximum conveying flow rate is 1 m³/h, rated power is 1.5 kW, rated voltage is 380 V; adopts inverter with rated power of 2.2 kW. The output frequency is 0–400 Hz, rated voltage is 380 V; a model LDG-MIK electromagnetic flowmeter with an accuracy of 0.5% is used, as well as a USB3100 model data collector from Altech with total sampling speed of 20 KS/S, 12-bit resolution, single-ended 8-channel analog input, 4-channel programmable I/O, and 1-channel 32-bit counter. The AD cache of 4K points FIFO can meet the real-time acquisition of data required in this test and convert the analog signal to digital for further processing by computer. The flow regulation test platform is shown in Figure 10.

A STM32F103ZET6 microcontroller according to the control amount of targeted control of the system, where the control algorithm uses a hybrid-optimized BP neural network PID control algorithm, electromagnetic flowmeter signal received by the I/O port, calculated by the STM32F103ZET6 microcontroller, and then converted into a variable voltage signal to determine the instantaneous flow rate; the output frequency of the inverter is adjusted accordingly. Eventually, the fertilizer flow rate at the outlet of the mixing tank is changed. During operation, the volume of liquid in the mixing tank is kept at 50 L.

3.2.2. Analysis of Test Results

The fertilizer flow rate of the integrated water and fertilizer precision fertilizer control system for field crops is determined by the fertilizer demand of the field crops planted in the field, and the fertilizer demand varies from field crop to field crop. The flow rate was set to 0.3 m³/h, 0.5 m³/h, and 0.8 m³/h to accommodate the demand for fertilizer flow rate for different crops. The test results of the three controllers are shown in Figure 11, Figure 12 and Figure 13 as well as

Table 2. Transient performance indexes of 0.3 m³/h.

Controller Type	Rise Time (s)	Peak Time (s)	Regulation Time (s)	Maximum Overshoot
PID	20.02	30.64	81.85	77.4%
BP–PID	70.91	106.6	109.2	7.37%
GA–PSO-BP–PID	32.02	74.69	122.3	6.83%

,

Table 3. Transient performance indexes of 0.5 m³/h.

Controller Type	Rise Time (s)	Peak Time (s)	Regulation Time (s)	Maximum Overshoot
PID	20.67	30.2	89.26	50.48%
BP–PID	71.76	105.6	61.83	4.5%
GA–PSO-BP–PID	33.45	51.89	28.65	3.16%

and

Table 4. Transient performance indexes of 0.8 m³/h.

Controller Type	Rise Time (s)	Peak Time (s)	Regulation Time (s)	Maximum Overshoot
PID	20.04	30.92	110.26	75.5%
BP–PID	74.97	106.14	62.91	3.09%
GA–PSO-BP–PID	33.39	53.48	56.02	5.31%

.

4. Discussion

Comprehensive analysis of the results in Figure 11, Figure 12 and Figure 13 and Table 2, Table 3 and Table 4 shows that the performance of the three controllers also changes under different fertilizer application flow rates. Although the maximum overshoot of 3.09% at 0.8 m³/h was lower than that of 5.31% for the BP–PID controller based on hybrid optimization, its rise time, peak time, and regulation time were longer than those of the BP–PID controller based on hybrid optimization, and the maximum overshoot of 3.09% at 0.3 m³/h was lower than that of the PID controller based on hybrid optimization. However, the rise time, peak time, and regulation time are longer than those of the hybrid-optimized BP–PID controller, and all transient performance indexes are inferior to those of the hybrid-optimized BP–PID controller when the fertilizer flow rate is 0.3 m³/h and 0.5 m³/h; the anti-disturbance ability and robustness are poor. Therefore, from the experimental results of three common fertilizer application flow rates, by using the hybrid optimization-based BP neural network PID algorithm to control the precision fertilizer application control system for integrated water and fertilizer application of field crops, the overall performance is better than the control using PID algorithm and the control using BP neural network PID.

To better demonstrate the superiority of the hybrid optimization-based BP neural network PID algorithm studied in this paper for precision fertilizer application control system for field crops, we selected similar literature for comparative analysis, in which Zihao Meng studied the application characteristics of PSO–BP–PID algorithm for precision fertilizer application control system [27]. In the comparative analysis, the GA–PSO–BP–PID algorithm proposed in this paper does better in optimizing the regulation time and maximum overshoot at the same fertilizer application flow rate, but is inferior to the PSO–BP–PID algorithm in optimizing the rise time and peak time. This is because the GA–PSO–BP–PID algorithm is more focused on overall optimization and also higher in accuracy, which allows it to better control the stability and accuracy of the system and thus better optimize the regulation time and maximum overshoot. However, this may also lead to a slightly poorer performance in optimizing rise time and peak time, as these metrics focus more on the dynamic performance of the system, while the GA–PSO–BP–PID algorithm focuses more on the steady-state performance of the system.

In summary, the control method proposed in this paper combines the advantages of hybrid optimization techniques and BP neural networks, which can better cope with the control requirements in practical applications and improve the performance level of the integrated precision fertilizer application control system for field crops with nonlinear time lag characteristics.

5. Conclusions

In this paper, a precision fertilizer application control system for integrated water and fertilizer control of field crops is studied. Firstly, a mathematical model is established for the precision fertilizer application control system of integrated water and fertilizer system of field crops, after which the data of flow rate changes are obtained after sampling and the first-order approximation method is used and fitted to finally derive the transfer function of the system. Since the self-learning of its BP neural network depends on the selection of initial weights, which makes the control effect unsatisfactory, this paper adds a GA–PSO hybrid optimization algorithm based on the PID adaptive control of the BP neural network, which causes the BP neural network self-learning to speed up. The simulation study of the hybrid optimization-based BP neural network PID control algorithm is carried out using MATLAB, and the analysis of the simulation results concludes that its control effect on the precision fertilizer application control system of integrated water and fertilizer for field crops is superior.

To further illustrate the superiority of the control algorithm proposed in this paper, this paper uses the precision fertilizer flow rate adjustment test bench as a platform, which can monitor the fertilizer flow rate in the integrated precision fertilizer control system in real-time, and when the fertilizer pump flow rate is set to 0.3 m³/h, 0.5 m³/h, and 0.8 m³/h, the average maximum overshoot is 5.1% and the average adjustment time is 68.99 s. The peak time and regulation time were the shortest at 0.6 m³/h, 51.89 s, and 28.65 s, respectively, and the maximum overshoot was the smallest at 0.6 m³/h, 3.16%. The results show that the hybrid optimization-based BP neural network PID control algorithm can regulate the integrated fertilizer application flow rate of field crops to the desired value in the shortest time with a small overshoot, while the best effect is achieved at the application flow rate of 0.6 m³/h, which improves the decision level of the controller and achieves good control effect.

The hybrid optimization-based BP neural network PID controller for integrated precision fertilizer application control system for field crops combines the advantages of GA, PSO, BP, and PID control, which can effectively solve the adverse effects of time varying, time lagging, and non-linearity of the model on the controller, and has good dynamic performance and robustness to meet the needs of agricultural production. The integrated water and fertilizer fertilization of field crops can help reduce the pollution of groundwater and surface water by chemical fertilizers and protect the ecological environment of farmland. The research in this paper provides a theoretical basis for precise control to achieve water conservation and weight loss and ecological sustainability of field crop production as well as to enhance the modernization of smart agriculture for field crops, which promotes the formation of a modernized smart agriculture system and improves the technical level of precise fertilizer application control for field crops.