Performance Analysis and Testing of a Multi-Duct Orchard Sprayer

Abstract

A multi-duct orchard sprayer is designed in this paper to address the problem of low droplet coverage during plant protection in walnut orchards in South Xinjiang, China. This spray comprises a base frame, a pesticide tank, an air delivery system, a copying base frame and a drive system. Effects of the sprayer structure on the flow field were simulated using computational fluid dynamics. Operation parameters were optimised using the response surface analysis and validated using a field test. The results demonstrated that five jet tubes in the simulation design could fulfil the design requirements of GB/T 32250.3-2022. The upper, middle and lower droplet coverages were 74.92%, 90.01% and 69.9%, respectively, when the sprayer’s advancing speed, the angle of jet tubes and the nozzle diameter were 0.53 m/s, 70.27° and 0.81 mm, respectively. The machine can effectively enhance the spraying efficiency and droplet coverage of each canopy during plant protection operations in the new walnut orchards of South Xinjiang, China, and provide references for designing and optimising fruit tree spraying machinery.

1. Introduction

In recent years, Xinjiang (government) has promoted scaled and normalised forestry and fruit industry development to encourage sustainable development in South Xinjiang, China. Mechanisation is also realised in the forestry and fruit industries in Xinjiang. Hence, it is crucial to reconstruct existing orchards with short- and high-density plants or create new orchards, refine the planting system of forestry and fruit trees, formulate standards to perfect the orchard construction and reconstruct “automatisation”, and ensure the “entrance of agricultural machine” [1]. Fruit trees under the orchard planting mode in South Xinjiang have strong tree potential, a large canopy and wide line spaces. Many droplets cannot fall on leaves during plant protection based on the sprayer to the arbour and fruit trees, thus resulting in low pesticide utilisation [2]. The spraying effect of sprayers on fruit trees with strong tree potentials and wide line spaces is still unsatisfying under the current planting mode in orchards in South Xinjiang. Hence, a sprayer that can serve for planting modes in orchards in South Xinjiang is needed.

Contemporary sprayers face an issue of low pesticide utilisation during plant protection in orchards in South Xinjiang. To address this problem, many scholars have conducted numerous investigations. At present, the typical air delivery sprayers include axial-flow sprayers [3,4,5], tower-type sprayers [6], cannon-type sprayers [7], tunnel-type sprayers [8,9], electrostatic sprayers [10,11] and air delivery sprayers for various sensors of a unique design or equipment [12,13,14,15]. Cao, 2014, performed a comparative experimental study of the spraying performances of pesticide application machines for orchards in the winter jujube forest. Their results demonstrated that multi-duct pesticide application machines in orchards are superior to other sprayers in terms of droplet distribution uniformity, coverage and drift degree during the copying spray [16]. Chao, 2019, conducted a computational fluid dynamics (CFD) simulation of a multi-channel air-assisted sprayer and investigated the effects of the rotation speed of the draught fan (600–1800 rpm) and distance to the air inlet (0–6.0 m) on the airflow field distribution. An experimental verification revealed that the measured results were consistent with the simulation results in the test range [17]. Ashenafi T. Duga et al., 2015, evaluated outlet airflow distribution in orchards by establishing the air delivery system and the CFD model of fruit trees with different shapes, and verified its accuracy [18]. Hu, 2022, tested the impact of the rotation speed of the draught fan, spraying angle and spraying distance on the spraying performances of the sprayer by using a vertical mode meter and constructed a regression model to optimise the sprayer’s parameters [19]. Based on the above studies, a multi-duct sprayer is highly applicable to the plant protection of arbour and fruit trees. The CFD simulation of airflow field distribution and experimental comparison verification can effectively enhance the production efficiency of machines. However, this method’s applicability to plant protection in orchards in South Xinjiang must be further discussed.

In view of the above problems, this study designed a multi-duct orchard sprayer in combination with the planting methods of orchards in South Xinjiang. The quantity of jet tubes is determined according to CFD simulation results regarding the influence of the sprayer structure on the flow field while applying the Box–Behnken design test. Operation parameters are optimised by response surface analysis (RSA). The coverage effects on the upper, middle and lower canopies of the designed sprayer during the spraying operation were verified via a field test. This study provides a technique for insect control in orchards in South Xinjiang. It has theoretical and practical significance in promoting technological progress in the plant protection of orchards and increasing the income level of farmers.

2. Materials and Methods

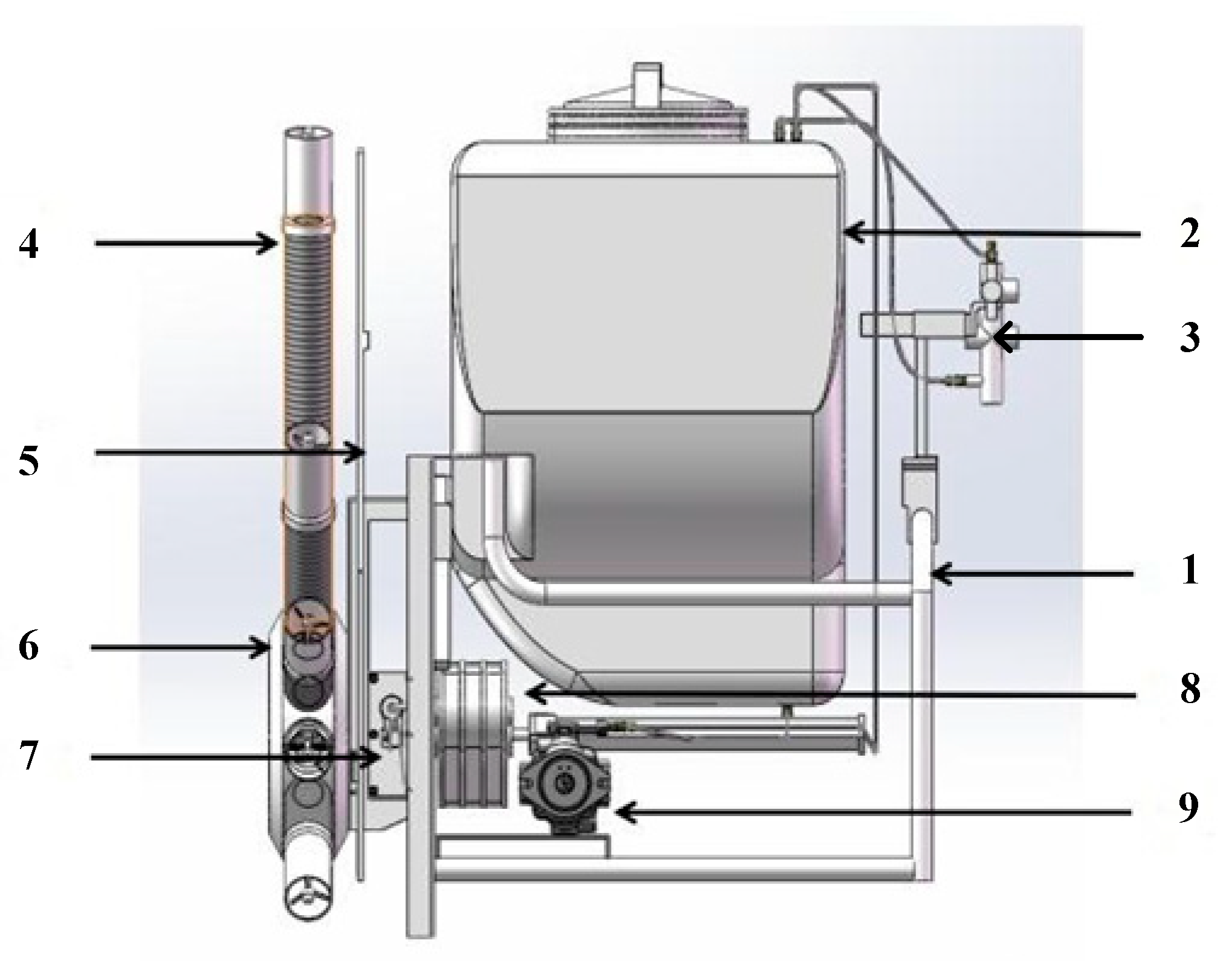
2.1. Overall Structure and Working Principle

The main design objective of the multi-duct orchard sprayer is to adapt to the spraying operation of the new walnut orchards in South Xinjiang and increase the efficiency of the spraying operation and the coverage of droplets in each canopy. Figure 1 depicts the overall structure of a multi-duct orchard sprayer. It primarily comprises a base frame, a pesticide tank, an air delivery system, a copying device, a drive system and a spraying system. The air delivery system includes the centrifugal fan mounted at the rear part of the base frame and several groups of radial flexible wrinkle outlet ducts in a uniform circumferential distribution on the centrifugal draught fan. The air produced by the centrifugal draught fan is distributed into the spraying device using fixed air vents on the centrifugal draught fan and flexible wrinkle outlet ducts. The spraying system includes the pesticide tank on the base frame, the liquid inlet, the piston pump connected with the pesticide tank and the pesticide delivery tube connected to the liquid outlet of the piston pump. Several groups of spray nozzles were set at the corresponding centres of flexible wrinkle outlet ducts, with the nozzles orienting radially outward along the centrifugal draught fan. In the designed sprayer, the copying structure and multiple flexible wrinkle outlet ducts are applied for direct targeted pesticide applications, thus enabling matching of the spraying shape and canopy shape, and effectively increasing pesticide utilisation. It can adapt to different canopy shapes by adjusting the directions of jet tubes. Finally, a multi-duct orchard sprayer can operate continuously, decrease pesticide consumption and enhance the droplet coverage at different canopies through the cooperation of the gearing device, air delivery system and spraying system.

2.2. Numerical Simulation of the Airflow Field out of the CFD Machine

2.2.1. Modelling and Meshing of the Fluid Domain

Figure 2 shows that the influences of the number of jet tubes on the spraying flow field were investigated via CFD simulation. The air delivery system model of the multi-duct orchard sprayer was plotted using SolidWorks 2021. To improve the simulation’s operational efficiency, the model ignored assisting devices in the air delivery system, such as nozzle, fixing, copying and gearing devices [20]. The air delivery system was simplified into two parts: the centrifugal draught fan and flexible wrinkle outlet ducts. This analysis uses ANSYS-Workbench to create model fluid domains and grids. The droplet diffusion space has a length of 6 m, a height of 6 m and a width of 1.5 m. For each model, an unstructured mesh division is used, and the local size adjustment is made to the outlet of the sprayer, modifying the size to 5 mm. The total number of mesh is about 1.5 × 10⁶ triangular mesh elements.

2.2.2. Simulation Test Conditions and Assumptions

To ensure the reliability of the simulation and balance the simulation accuracy and efficiency, the following assumptions were established for the solution conditions based on previous relevant studies: (1) Assuming that the discrete phase (droplets) is relatively thin (i.e., the volume fraction of particles is less than 12%), then the interaction between particles and the volume fraction of particles can be ignored on the continuous phase. (2) Studies have demonstrated that when the tractor’s forward speed is low with small fluctuations (i.e., it is much smaller than the movement speed of fog droplets), the forward speed exerts a little influence on the deposition amount and drift rate of fog droplets [21]. (3) Assuming that droplet distribution follows the Rosin–Rammler distribution, there are only three modes of droplet termination: deposition, drift and evaporation [22].

2.2.3. Parameter Calibration and Simulation Test

Because fog droplets are affected not only by gravity and air resistance but also by the exchange of mass and momentum, the k–$\epsilon$ standard two-equation turbulence model of fluid mechanics is adopted for continuous phase (air) in this simulation. For the discrete phase (droplet), the Lagrange method is used to describe the motion trajectory of the particles, including the density equation, momentum equation and energy equation, and the expression is as follows.

$$\frac{\partial {\alpha }_q}{\partial t}+v_q·\nabla {\alpha }_q=\frac{S_{\alpha q}}{{\rho }_q}$$

(1)

$$\rho ={\alpha }_q{\rho }_q+(1-{\alpha }_q){\rho }_q$$

(2)

$$\frac{\partial }{\partial t}(\rho \overrightarrow{v})+\nabla ·(\rho \overrightarrow{v}\overrightarrow{v})=-\nabla p+\nabla ·[\mu (\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T)]+\rho \overrightarrow{g}+\overrightarrow{F}$$

(3)

$$\frac{\partial }{\partial t}{(}_{\rho }E)+\frac{\partial }{\partial x_i}[u_i{(}_{\rho }E+\rho )]=\frac{\partial }{\partial x_i}[K_{\mathrm{eff}}\frac{\partial T}{\partial x_i}-\sum _{j^{\prime }}{h}_{j^{\prime }}{J}_{j^{\prime }}+u_j({\tau }_{ij}{)}_{\mathrm{eff}}]+S_h$$

(4)

In the equation, ${\alpha }_q$ is the volume ratio of the $q$ phase flow; $S_{\alpha q}$, $S_h$ is a generalised source term; ρ is the average density, kg/m³; ${\rho }_q$ is the $q$ phase density, kg/m³; $\overrightarrow{v}$ is the velocity vector, m/s; μ is the turbulent dynamic viscosity, (N · s)/m²; $\overrightarrow{F}$ is the i velocity component, m/s; $K_{\mathrm{eff}}$ is the effective thermal conductivity coefficient, $K_{\mathrm{eff}}=k+k_t$, $k_t$ is the turbulent thermal conductivity coefficient; and $J_{j^{\prime }}$ is the diffusion flow rate of component j, kg/(m² · s). Other parameters can be referred in the Fluent user manual.

Fluent 2019 R3 was used to conduct the numerical simulation of the three-dimensional model. There was no temperature change during the simulation process. The atmosphere temperature was set at 21 °C and the droplet temperature at 14 °C (the same as that of water), the relative humidity of air was 24% and the viscosity of air was 0.01839 Pa·s. The surface tension $\overrightarrow{F}$ is 0.072 N/m. The fluid flow is treated as a steady state flow to simplify the simulation. Because the Mach number of the model is very small, the airflow is considered incompressible. The exit velocity of the experimental model was set to 10 m/s, the turbulence intensity was set to 5% and the turbulence viscosity ratio was kept at the default 10%. After parameter setting, the k–$\epsilon$ standard two-equation turbulence model is selected to iterate the continuous phase airflow velocity field in each region. The simulation under the same condition is repeated thrice, and the average value is taken as the final simulation result.

2.2.4. Fluent Simulation Results and Analysis

This simulation aims to determine the effects of the number of jet tubes in the multi-duct orchard sprayer on velocity uniformity and spraying width and select the optimal quantity of jet tubes via comparison. Figure 3 illustrates that the spraying shapes of different jet tubes are shown in the upper region, and the spraying flow rates along the side view directions of each jet tube are demonstrated in the lower region. The flow rate has a range of 0~1.5 m/s, and the deeper colour represents the higher flow rate. The spraying shape is oval for two given jet tubes, and the spraying range reaches 1.8 × 0.9 m. For three and four jet tubes, the spraying range of the sprayer is widened significantly, with an uneven spraying distribution. The spraying range reaches 2.11 × 1.5 m under three jet tubes and 2.76 × 1.5 m under four jet tubes. The droplet density in the centre is significantly higher than on the two sides. The spraying ranges under five and six jet tubes are relatively wide, with a uniform spraying coverage. According to measurement, the spraying range is 3.3 × 1.5 m under five jet tubes and 3.4 × 1.5 m under six jet tubes. The spraying distribution under five and six jet tubes conforms to the spraying requirements of GB/T 32250.3-2022 Test of Sprayer in Use of Agricultural and Forest Machines: Part 3: Sprayer for Shrub and Arbor Plants [23]. Moreover, the spraying ranges under five and six jet tubes differ slightly.

In this study, the spraying uniformity was calculated using the velocity uniformity index (λ) based on the area-weighted average velocity and mass-weighted average velocity. The method of velocity uniformity index can analyse all the points in the plane and avoids the effects of the number of sampling points on calculation results, thus, the area-weighted average velocity and mass-weighted average velocity can be calculated automatically by software [24]. Furthermore, this method has obvious advantages in evaluating spraying uniformity. The spraying uniformity was calculated by λ [25]. The higher value of λ indicates a better droplet uniformity, and the maximum value of λ was 1. The calculation formula of λ is expressed as follows:

$$\mathsf{\lambda }=\left(1-\frac{\left|V_a-V_m\right|}{V_m}\right)\times 100\%$$

(5)

$$\left\{\begin{array}{c}{V}_a=\frac{1}{A}{\displaystyle \sum _{j=1}^n}{v}_j\left|A_j\right|\\ V_m=\frac{{\sum }_{j=1}^n{v}_j{\rho }_j\left|v_j·A_j\right|}{{\sum }_{j=1}^n{\rho }_j\left|v_j·A_j\right|}\end{array}\right.$$

(6)

where $V_a$ is the area-weighted average velocity; $V_m$ refers to the mass-weighted average velocity; $A$ is the total surface area; $A_j$ is the area on the jth unit surface; and ${\rho }_j$ is the fluid density on the jth unit surface.

Figure 4 depicts the trend line drawing after data extraction based on the Fluent post-processing function. With the increase in jet tubes, λ increases gradually and tends to be stable after reaching five jet tubes. Combined with Figure 3, the spraying range under six jet tubes is slightly larger than that under five jet tubes. However, following comprehensive calculations, there is only a difference of 0.005 in λ between five and six jet tubes because the spraying flow rate under six jet tubes is less uniform than that under five jet tubes. Because the sprayer’s cost increases by increasing each jet tube, the practicability and the economic efficiency of the sprayer must be considered comprehensively. Hence, five jet tubes were determined in the prototype.

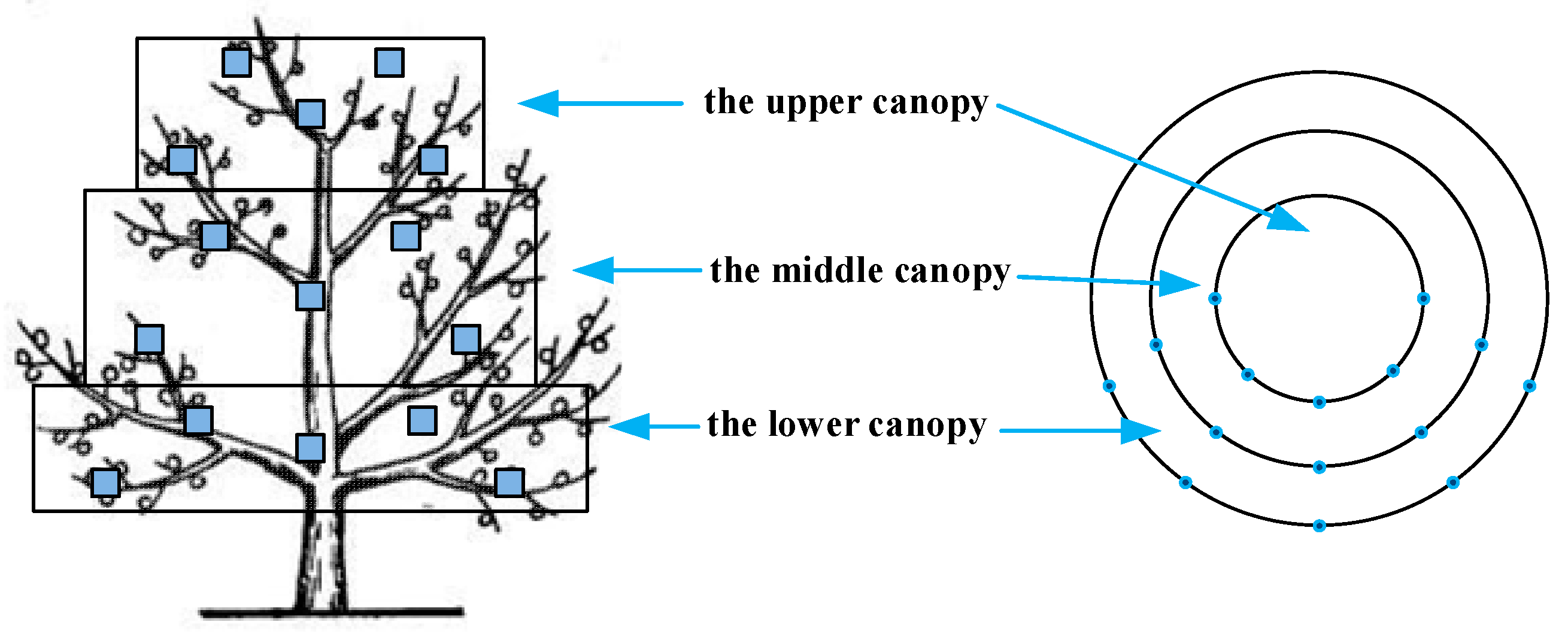
2.3. Spraying Performance Test and Processing Method

In this test, the Dongfeng 354 tractor was used for power supply, and the test was conducted in a conventional management commercial walnut orchard in Twelve Regiments, Alear City, where fruit trees were 7 years old and the line space was 6 × 6 m. Water was used as the experimental medium. Temperature, humidity, wind speed and general conditions of fruit trees were measured before the test. The pesticide application region was determined in the test field, wherein representative plants were chosen randomly. Each fruit tree was set according to the layout of the water-sensitive paper. With respect to the structure of the water-sensitive paper, five positions were selected at each layer of each chosen fruit tree according to directions. A total of 15 points were selected for observation, including the outer cavity, middle cavity and inner cavity according to distance to the tree trunk, the upper layer, middle layer and lower layer according to vertical heights [26,27]. The droplet coverage of each layer was calculated according to the mean of five points (Figure 5).

After finishing the pesticide application, the water-sensitive paper samples were dried in air and then stored in bags, which were then brought to the laboratory. Figure 6 shows that droplets left clear traces on water-sensitive paper. Because diffusion and bleeding may not occur on the water-sensitive paper, droplets remain the size at contact on the water-sensitive paper. Next, a HP Laser NS MFP 1005 w printer was used to scan water-sensitive paper samples, thus obtaining a scanning image in PNG format. The supporting analysis software calculated the coverage area of droplets on water-sensitive paper [28]. During image processing, the part with large-area adhesion of droplets was deleted by selecting feature parameters. Pesticides in this part have not been atomised completely and may drop from leaves if sprayed onto the paper directly. Finally, the droplet coverage was calculated according to the coverage area of droplets [29].

2.4. Box–Behnken Experiment Design

This experiment was conducted in a conventional management commercial walnut orchard in Twelve Regiments, Alear City, on 21 November 2022, where fruit trees were 7 years old and the line space was 6 × 6 m. The air temperature and relative humidity (RH) on the test day were measured as 3 °C and 24%, respectively. There was level 1 northwest wind on the test day. Figure 7 depicts the prototype of the multi-duct orchard sprayer. In the experiment, the Dongfeng 354 tractor was applied for power supply. In this experiment, the Box–Behnken design was used to analyse the effects of three control parameters (advancing speed, angle of jet tubes and the nozzle diameter) on the droplet coverage at different canopies. The level ranges of factors were set as follows: A represents the advancing speed (0.36~1 m/s), B represents the angle of jet tubes (60~80°) and C denotes the nozzle’s diameter (0.6~1 mm).

Table 1. Coding table for experimental factor level.

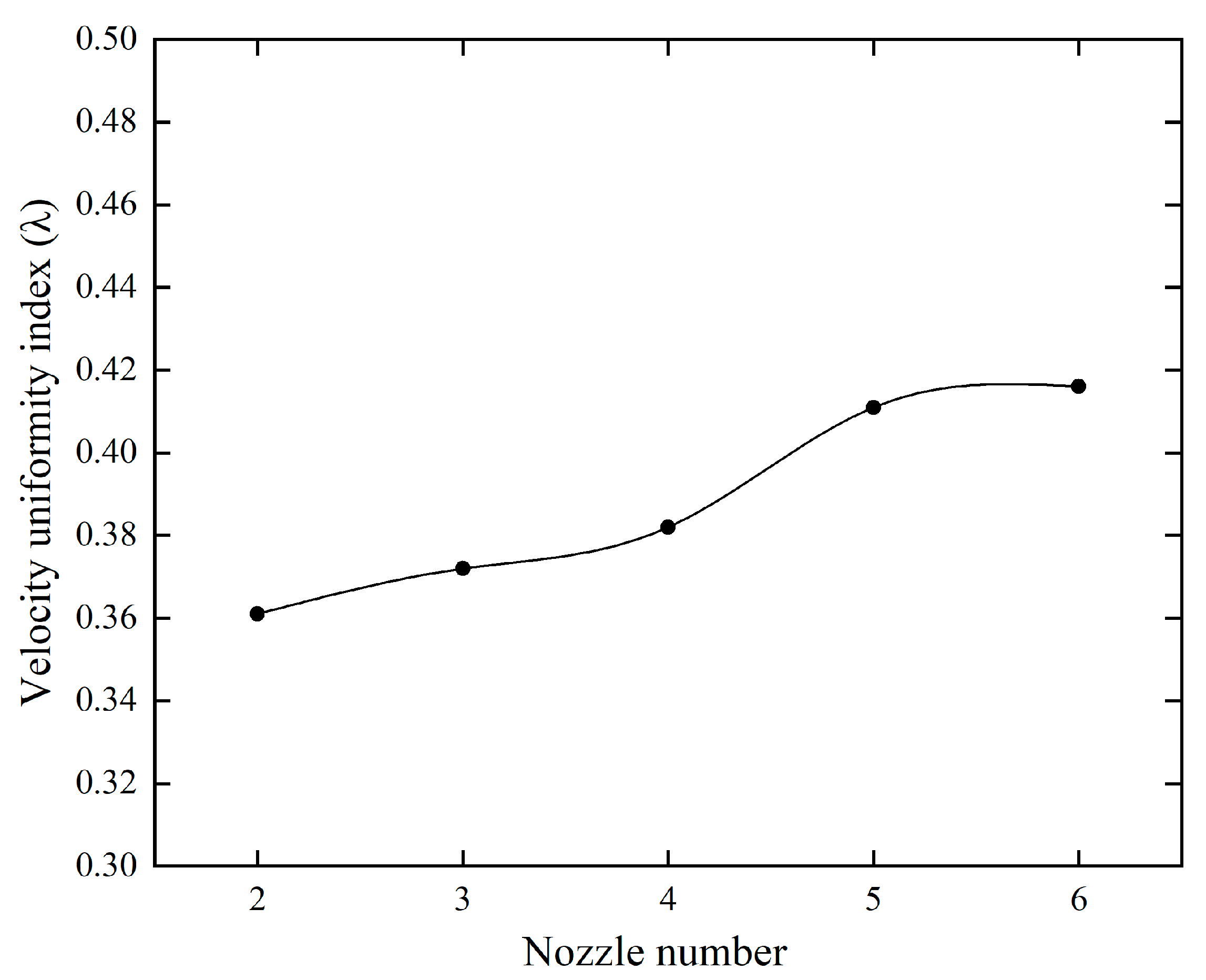
Level	Factor
	A (m/s)	B (°)	C (mm)
−1	0.36	60	0.6
0	0.68	70	0.8
1	1	80	1

presents the level codes of factors. The experiment was repeated thrice, and the droplet coverage at each canopy was calculated as the mean of five points.

3. Results and Analysis

3.1. Experimental Results and Regression Models

After finishing the field test, water-sensitive paper samples with droplet distribution were collected and brought into the laboratory for scanning. The droplet coverage was calculated according to the above method. The test and variance analysis results were obtained, as shown in

Table 2. Test plan and results.

Test Number	A (m/s)	B (°)	C (mm)	The Droplet Coverage of the Upper Canopy (%)	The Droplet Coverage of the Middle Canopy (%)	The Droplet Coverage of the Lower Canopy (%)
1	0.36	80	0.8	75.325	89.426	62.822
2	0.68	70	0.8	70.386	92.554	69.971
3	1	70	1	49.285	65.872	63.288
4	1	80	0.8	73.462	70.812	61.657
5	0.68	80	0.6	73.192	82.084	57.054
6	0.68	70	0.8	72.064	88.955	70.189
7	0.36	70	1	72.826	77.308	68.216
8	0.36	60	0.8	62.95	76.658	73.92
9	0.68	70	0.8	72.547	90.169	69.437
10	1	60	0.8	52.206	70.344	66.126
11	0.36	70	0.6	78.852	71.028	62.27
12	0.68	60	1	47.676	70.843	71.892
13	0.68	60	0.6	56.068	77.624	70.971
14	0.68	80	1	50.265	82.023	66.773
15	1	70	0.6	73.074	73.092	60.68
16	0.68	70	0.8	70.92	88.33	71.596
17	0.68	70	0.8	71.231	90.275	67.937

and

Table 3. Significance and variance analysis.

Source	R1 The Droplet Coverage of the Upper Canopy		R2 The Droplet Coverage of the Middle Canopy		R3 The Droplet Coverage of the Lower Canopy
	F-Value	p-Value	F-Value	p-Value	F-Value	p-Value
Model	90.10	$<$0.0001	20.04	0.0003	27.54	0.0001
A	148.52	$<$0.0001	22.47	0.0021	21.39	0.0024
B	127.98	$<$0.0001	15.92	0.0053	106.93	$<$0.0001
C	230.04	$<$0.0001	1.16	0.3178	32.90	0.0007
AB	0.0017	0.9684	5.78	0.0472	7.85	0.0265
AC	33.49	0.0007	6.96	0.0335	1.99	0.2012
BC	25.18	0.0015	1.72	0.2305	13.82	0.0075
A2	9.13	0.0194	61.56	0.0001	34.30	0.0006
B2	174.58	$<$0.0001	7.72	0.0274	0.3039	0.5986
C2	56.44	0.0001	45.92	0.0003	24.19	0.0017
Lack of Fit	5.11	0.0745	4.49	0.0905	0.5316	0.6846

Extremely significant (p < 0.01), significant (0.01 < p < 0.05) and insignificant (p > 0.05).

, respectively.

The significance level of R₁ (the droplet coverage of the upper canopy) and variance analysis reveal that the model is extremely significant (p < 0.001), and the lack-of-fit term is insignificant (p < 0.0745), indicating that the model is significantly true, without lack-of-fit factors and with a relatively small error. According to the fitting statistics, ${R_1}^2$ = 0.9914 indicates that the model has a very high degree of fitting. A, B, C, AC, BC, B² and C² have extremely significant effects on R₁, whereas A² exert significant effects on R1. The influencing rank of different parameters is C > A > B. The regression equation is expressed as follows:

$$\begin{array}{cc}{R}_1=-594.81343& +5.20955\ast A+15.09612\ast B+344.99122\ast C-65.48047\ast AC-1.81688\ast BC\hfill \\ & +20.82593\ast A^2-0.093264\ast B^2-132.57313\ast C^2\hfill \end{array}$$

(7)

The significance level of R₂ (droplet coverage of the middle canopy) and variance analysis showed that the model is extremely significant (p = 0.0003), and the lack-of-fit term is insignificant (p < 0.0905), indicating that the model is significantly true, without lack-of-fit factors and with a relatively small error. According to fitting statistics, ${R_2}^2$ = 0.9626, suggesting the model has a very high degree of fitting. A², C², A and B have extremely significant effects on R₂, whereas B², AC and AB significantly influence R₂. The influencing rank of different parameters is A > B > C. The regression equation is defined as follows:

$$\begin{array}{cc}{R}_2=-298.69366& +225.97918\ast A+5.19206\ast B-0.960937*AB-52.73437\ast AC-95.53271\ast A^2\hfill \\ & -0.034640\ast B^2-211.22625\ast C^2\hfill \end{array}$$

(8)

The significance level of R₃ (droplet coverage of the lower canopy) and variance analysis demonstrate that the model is extremely significant (p = 0.0001), and the lack-of-fit term is insignificant (p < 0.6846), indicating that the model is significantly accurate, without lack-of-fit factors and with a relatively small error. According to fitting statistics, ${R_3}^2$ = 0.9725 suggests that the model has a very high degree of fitting. B, A², C, C², A and BC have extremely significant influences on R₃, whereas AB exert significant influences on R₃. The influencing rank of different parameters is B > C > A. The regression equation is expressed as follows:

$$\begin{array}{cc}{R}_3=+97.56747& +12.98232\ast A-1.21948\ast B+57.30531*C+0.517891*AB-32.97729\ast A^2\hfill \\ & -70.89063\ast C^2\hfill \end{array}$$

(9)

3.2. Response Surface Analysis

The intuitive analysis of the relationship between test indexes and parameters reveals that the response surface of interaction among parameters was obtained using the Design-Expert 13 software (Figure 8).

Figure 8a shows that a high value of A, R₁ presents a sharp reduction trend with the increase in C. Given a low value of A, R₁ presents a slow reduction trend with a rise in C. When C is high, R₁ depicts a fast reduction trend with an increase in A. When C is low, R₁ decreases slowly and then becomes stable with the rise of A. In Figure 8b, R₁ is negatively related to C for the fixed B. When C is fixed, R₁ increases first and then decreases slowly with the increase in B. In Figure 8c, when A is fixed, R₂ increases gradually with the addition of B. When B is fixed, R₂ increases slowly and decreases continuously with the increase in A. Figure 8d shows that R₂ increases slowly and decreases gradually with the increase in C when A is fixed. When C is fixed, R₂ increases first and then gradually declines with the rise in A. Figure 8e demonstrates that R₃ is negatively related to B when A is fixed. When B is high, R₃ presents an inverted V-shaped variation trend with the increase in A. When B is low, R₃ fluctuates horizontally and then drops quickly with the increase in A. Figure 8f depicts that when B is high, R₃ increases continuously with the increase in C. When B is low, R₃ increases first and then declines slowly with the increase in C. When C is fixed, R₃ drops continuously with the increase in B.

Based on the above analysis, the advancing speed primarily affects the spraying volume per unit displacement. The jet tube’s angle largely influences the height that spraying can reach. The nozzle’s diameter specifically affects the initial velocity when droplets are sprayed.

For the coverage ratio of the upper canopy, the spraying volume per unit displacement is low when the advancing speed is high. The droplet velocity declines accordingly with the increase in the nozzle diameter. Hence, the droplet coverage at the upper canopy drops quickly. The spraying volume per unit displacement is high when the advancing speed is low, so the droplet coverage declines slowly. Similarly, when the nozzle diameter is high, the droplet coverage at the upper canopy decreases quickly with the increase in the advancing speed. When the nozzle’s diameter is low, the droplet coverage at the upper canopy decreases slowly with the increase in the advancing speed. Given the fixed angle of the jet tube, the velocity of the sprayed droplets will decrease with the increase in the nozzle diameter, and the number of droplets reaching the upper canopy may decrease accordingly. Hence, the droplet coverage at the upper canopy declines gradually. For the fixed nozzle diameter, the height that droplets can reach increases with the increase in the angle of jet tubes. However, droplets make a parabolic motion in the air due to gravity. If the distance between the sprayer and the fruit trees is constant, droplets begin to sink before reaching the fruit trees if the angle is excessively large. The droplet coverage increases first and then declines gradually.

When the advancing speed is fixed for the coverage ratio at the middle canopy, the height that droplets can reach increases with the increase in the angle of jet tubes, thus resulting in the rising trend of the droplet coverage. When the angle of the jet tube is fixed, droplets sprayed per unit displacement continue to decrease with the increase in the feed velocity. The sprayed droplets may develop drifts with the increase in velocity, increasing the coverage ratio at the middle canopy. However, the droplet quantity per unit displacement decreases if the velocity is excessively high. As a result, droplet coverage at the middle canopy increases slowly and then decreases continuously. When the advancing speed is fixed, the velocity of the sprayed droplets continues to decrease with the increase in the diameter of droplets. Because droplets make a parabolic motion in the air, the height when droplets reach the fruit tree declines with the velocity reduction. Hence, the droplet coverage at the middle canopy increases slowly and decreases continuously. Similarly, when the nozzle diameter is fixed, the droplet coverage at the upper canopy increases first and then decreases continuously with the increase in the advancing speed. The above test results demonstrate that the reason for the generally high coverage of fog droplets in the middle layer is that the coverage of the five nozzles is large, and the three nozzles in the middle can completely cover the middle layer. As the angle increases, the coverage of fog droplets in the middle layer exhibits a trend of increasing and then decreasing, but generally greater than 70%. Due to the gravity and wind force, a small part of the upper layer of fog droplets is deposited into the middle layer, creating a phenomenon of high coverage of the middle layer of fog droplets.

When the advancing speed is fixed for the droplet coverage at the lower canopy, the height that the sprayed droplets reach the fruit tree increases with the increase in the angle of jet tubes, thereby resulting in a decreasing trend of droplet coverage at the lower canopy. Given a large angle of jet tubes, the sprayed droplets develop drifts with the increase in the advancing speed, and more droplets may fall onto the lower canopy. With the continuous expansion of the advancing speed, the droplet quantity per unit displacement decreases, thus resulting in an inverted V-shaped variation trend of the droplet coverage at the lower canopy. Given a small angle of jet tubes, the height when droplets reach the fruit tree is low, and a lot of droplets reach the lower canopy. Similarly, the droplet quantity per unit displacement decreases with the increase in the advancing speed. As a result, the droplet coverage at the lower canopy fluctuates horizontally and then declines quickly. When the angle of the jet tube is large, the velocity of the sprayed droplets decreases with the increase in the nozzle’s diameter, and the height when droplets reach the fruit tree decreases more and more, finally increasing the droplet coverage at the lower canopy. When the angle of the jet tube is relatively small, the droplet quantity reaching the lower canopy increases with the increase in the nozzle diameter. After an excessive nozzle diameter, some droplets cannot fall onto fruit trees when the velocity and angle are relatively small. Therefore, the droplet coverage at the lower canopy increases first and then decreases. Given the fixed diameter of the nozzle, more droplets fall onto the high canopy with the increase in the angle of jet tubes. Consequently, the droplet coverage at the lower canopy declines gradually.

3.3. Response Surface Optimisation

To achieve the best spraying effect on fruit trees and obtain the favourable combination of test factors and levels, an optimal design of test factors was conducted by using the Design-Expert 13 software. The maximum coverage ratios of the upper, middle and lower canopies were combined to optimise the built test index model. According to the RSA, the optimal spraying effect on fruit trees was achieved when the advancing speed, the angle of jet tubes and the nozzle diameter were 0.53 m/s, 70.27° and 0.81 mm, respectively. Under the optimal parameters, the droplet coverage at the upper, middle and lower canopies was 74.92%, 90.01% and 69.9%, respectively.

3.4. Verification Test

The test was conducted in a commercial walnut orchard in Twelve Regiments, Alear City on 27 November 2022. Under the same test conditions described above, a spraying experiment was performed in the chosen test field at an advancing speed of 0.53 m/s, an angle of jet tubes of 70° and a nozzle diameter of 0.8 mm. After the experiment, the water-sensitive paper samples were dried in the air and brought into the laboratory for data processing.

Table 4. Comparison between response surface optimal value and verification test data.

	The Droplet Coverage of the Upper Canopy	The Droplet Coverage of the Middle Canopy	The Droplet Coverage of the Lower Canopy
Optimal value	74.92%	90.01%	69.9%
Test value	76.59%	87.11%	71.75%
Error	2.23%	3.22%	2.65%

enlists the experimental results.

The optimised spraying performances of the multi-duct orchard sprayer were verified using a field test. According to test results, the error between the response surface optimal value of the coverage ratio of the multi-duct orchard sprayer and the verification test value was lower than 5%. The test fulfils the requirements on the spraying operation of GB/T 17997-2008 Regulation on Field Operation and Spraying Quality Evaluation of Pesticides Sprayer [30].

4. Conclusions

Based on the planting mode and agronomic characteristics of new walnut orchards in South Xinjiang, China, this paper designs and manufactures a multi-duct orchard spray machine that conforms to the planting mode in South Xinjiang. The effects of multi-duct orchard sprayer structures on the flow field were simulated using CFD. The impact of multi-duct orchard sprayers with different quantities of jet tubes on the spraying uniformity and breadth was determined. The optimal quantity of jet tubes was selected through comparison. With careful consideration of the practicability and economic efficiency of the sprayer, the number of jet tubes is finally determined to be five; the five jet tubes meet the design requirements of GB/T 32250.3-2022. After completing the prototype, the droplet coverage of the multi-duct orchard sprayer is tested using the Box–Behnken design. The droplet coverage ratios of upper, middle and lower canopies and the response surfaces of different test factors are established, thus disclosing the relationship between droplet coverage and test factors more intuitively. The RSA results reveal that the optimal spraying effect of fruit trees is achieved when the advancing speed, the angle of the jet tube and the nozzle diameter are 0.53 m/s, 70.27° and 0.81 mm, respectively. Under these optimal conditions, the droplet coverage of the upper, middle and lower canopies is 74.92%, 90.01% and 69.9%, respectively. The study found that the reason for the generally high coverage of fog droplets in the middle layer is that the spraying range of five nozzles can cover the middle layer, and during the spraying operation, due to the action of gravity and wind, a small part of fog droplets in the upper layer are deposited into the middle layer, and eventually form a phenomenon of high coverage of fog droplets in the middle layer. According to the verification test, the optimisation results are consistent with the results. It fulfils the spraying requirements in GB/T 17997-2008 Regulation on Field Operation and Spraying Quality Evaluation of Pesticides Sprayer. The machine is suitable for spraying new walnut orchards in South Xinjiang of China, which can effectively improve the spraying efficiency and the coverage of fog drops in each canopy.