Next Article in Journal
Enhancing Soil Nitrogen Retention Capacity by Biochar Incorporation in the Acidic Soil of Pomelo Orchards: The Crucial Role of pH
Next Article in Special Issue
An In-Depth Presentation of the ‘rhoneycomb’ R Package to Construct and Analyze Field-Experimentation ‘Honeycomb Selection Designs’
Previous Article in Journal
Organic Material Addition Optimizes Soil Structure by Enhancing Copiotrophic Bacterial Abundances of Nitrogen Cycling Microorganisms in Northeast China
Previous Article in Special Issue
Using Block Kriging as a Spatial Smooth Interpolator to Address Missing Values and Reduce Variability in Maize Field Yield Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agronomy
Volume 13
Issue 8
10.3390/agronomy13082109
agronomy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Impact of Data Envelopment Analysis on Effective Management of Inputs: The Case of Farms Located in the Regional Unit of Pieria

by
Asimina Kouriati
1,
Anna Tafidou
2,
Evgenia Lialia
1,
Angelos Prentzas
1,
Christina Moulogianni
1,
Eleni Dimitriadou
1 and
Thomas Bournaris
1,*
1
Department of Agricultural Economics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
2
Department of Mathematics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
*
Author to whom correspondence should be addressed.
Agronomy 2023, 13(8), 2109; https://doi.org/10.3390/agronomy13082109
Submission received: 27 July 2023 / Revised: 9 August 2023 / Accepted: 9 August 2023 / Published: 11 August 2023
(This article belongs to the Special Issue Design and Statistical Analysis in Agricultural, Biological and Environmental Sciences)
Browse Figure
Versions Notes

Abstract

:
Technical efficiency is considered a useful advisory tool for managers whose main goal is to maximize profit and minimize costs. Data envelopment analysis is a widely accepted methodology for technical efficiency estimation in the sector of agriculture. For that reason and with the view to extract useful conclusions regarding farmers’ effective management of inputs, this study aims to present the DEA method through its implementation in a set of farms located in the regional unit of Pieria. To conduct this analysis, relevant data were collected through a survey in which 40 farms participated. The output variable was chosen to be each farm’s total amount of sales, while the inputs were selected in a way to represent the main factors of production, such as (1) land in acres, (2) labor in hours, and (3) variable costs in EUR. The results showed that the examined farms need to reduce the inputs used by 34.6% to operate more efficiently from the point of view of the CRS model. Therefore, farmers should be motivated to reduce the inputs used, something that can be done through the provision of specialized advisory services. This will, of course, be helped by both the local authorities and the policies of the country in which the rational use of inputs seems to be necessary. This study may contribute to the relevant literature, agriculture, and the area since management suggestions are formulated for the farmers of Pieria’s regional unit.

1. Introduction

The general concept of efficiency is taken into account as the comparison between actual and optimal values of a production unit’s inputs and outputs [1,2,3]. Efficiency is generally studied because it is considered a useful advisory tool for managers whose objectives are to maximize profit and minimize costs. If these goals are achieved, positive development may occur at both the microeconomic and macroeconomic levels. The main efficiency types found in the literature are technical efficiency [4,5,6,7,8,9,10], allocative efficiency [11,12], economic efficiency [7,13,14], scale efficiency [15], and eco-efficiency [16,17,18,19]. Other related concepts found in the literature are those of cost [20], revenue [21], and profit efficiencies [22]. The above-mentioned efficiency types are similar to each other and differ in terms of the parameters that are used in order for the efficiency type to be estimated. This is proven by reviewing studies that are discussed in the range of the relevant literature [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].
The efficiency type that is estimated widely in the sector of agriculture is the technical one considered to exist when a farm uses a minimum amount of inputs in order to produce a given level of output, or vice versa, operating to maximize its output using a given level of inputs [1]. Through the above definitions, it is concluded that technical efficiency tries to answer the main question of production theory, such as the effective management of inputs.
It is generally accepted that in Greek agriculture, there is not only an important productivity increase through the intensified use of production factors and the adoption of new technologies but also through the continuous improvement of efficiency levels in the context of agricultural production [23]. Efficiency in agriculture can be characterized differently as a sustainability measure through which the farmer’s behavior can be evaluated in terms of resource utilization and management [24].
Many researchers have identified technical efficiency in order to fulfill the above-mentioned purpose in various Greek areas [4,8,9,10,25] using data envelopment analysis (DEA) which is a widely accepted methodological approach [8]. Considering that a relevant estimation of farms cultivating annual plants located in Pieria (Greece) seems to be missing and having, in parallel, the desire to present how the data envelopment analysis method operates, the present study’s authors were motivated to carry out this analysis which is believed to contribute to both the literature and the area’s agriculture by providing ways of effective management of inputs to the farmers. Therefore, this study tries to answer the following questions:
  • What is the technical efficiency level of farms cultivating annual plants located in the regional unit of Pieria?
  • What are the ways of of effective input management that can be suggested to Pieria’s farmers by interpreting the results of the data envelopment analysis method?
In order to conduct this analysis, relevant data were collected through a survey in which 40 farmers participated. These data were related to technical and economic parameters, while the method used to derive the necessary results was data envelopment analysis (DEA). The interpretation of the results led to the drawing of appropriate conclusions regarding the effective management of inputs by farmers. The rest of this study is structured as follows: (1) At first, related studies are presented (Section 2). (2) Then, the methodology used (DEA), the type of data, and the study area are presented in the materials and methods section (Section 3). (3) The results are presented in the 4th section (Section 4) and are also discussed (Section 5). Lastly, the conclusions of the study, suggestions for further research, and limitations are referred to in the 6th section (Section 6).

2. Literature Review

The estimation of efficiency in the agricultural sector has caught researchers’ attention in the past [26]. This fact created a broad framework of relevant estimations in crop and livestock production farms by using the methods of data envelopment analysis (DEA) [4,5,6,7,8,9,10,25,27,28], stochastic frontier analysis (SFA) [27,29,30], SOFTSCAPES [16], DESIRES [17], and GREENSCOPE [19] through which useful conclusions were extracted. Since the method used to derive the necessary results was decided to be Data Envelopment Analysis (DEA) in the case of this study, the studies that will be presented in the context of the literature review section mainly concern corresponding applications in the farm sector.
Dube and Guveya [5] estimated the technical efficiency of Zimbabwean green tea farms through the use of an input-oriented DEA model, concluding that increasing cultivated acres can contribute to the technical efficiency improvement. In order for the analysis to be carried out, ref. [5] took into account the annual tea production in tones as output while the land in hectares, labor in hours, and fertilizers in kilos were used as the model’s inputs. Later, ref. [7] using DEA estimated the variation in Italian farms’ technical efficiency levels from 2004 to 2014. A comparative analysis between the regions in which the farms are located showed that the Sardinian farms had better technical and scale efficiency than the Sicilian ones.
Bournaris [8] estimated the technical efficiency level of 98 glasshouse farms located in the Peloponnese and Crete (Greece). The assessment was held through an input-oriented DEA model where the turnover of every decision-making unit (€) was taken into account as output. In contrast, acreage (m2), labor (h/year), and various costs (€) were used as inputs. The results showed a mean efficiency score of 0.870 as regards the inputs used [8]. Lastly, ref. [10], using the same method, tried to estimate the technical efficiency of 100 Greek (Kilkis) cereal and legume farms in order to draw useful conclusions about the rational use of resources. Gross profit was used as the output model, and land, labor, and variable costs were used as inputs. Ref. [10] concluded that a reduction in inputs of 48.3% is necessary in order for a farm’s efficiency to be improved.
A general review of related studies could lead to the fact that technical efficiency estimation in farms cultivating annual plants located in Pieria (Northern Greece) lacks literature references. This is something that confirms the above-mentioned literature gap once again, and it is worth also saying that the present review was deemed particularly important as it was the reason that led the authors to fulfill the examined gap through the use of the data envelopment analysis method.
The method’s choice was based on a number of reasons. Firstly, it has been proved that DEA can provide significant findings at the farm level [8]. In addition, DEA is a model that does not impose restrictive conditions on its use as it can produce results on a small sample of decision-making units (DMUs). Additionally, this method enables the use of outputs and inputs expressed in either monetary or physical units because knowledge of their price is not considered necessary [31]. Last but not least, issues about how well an economic unit is performing and how it can be improved can be identified through the implementation of the DEA method. The model used in the context of the present analysis was input-oriented because it is suggested by the relevant literature [5,8]. After all, when a researcher wants to assess the variation between the actual and optimal use of inputs, the DEA model needs to be input-oriented [32].

3. Materials and Methods

As was already mentioned, the analysis concerns a set of farms located in the regional unit of Pieria. These primary data were collected through personal interviews and were related to the economic and technical parameters of the examined farms [33,34]. After the data collection, a necessary technical–economic analysis was held, and finally, an input-oriented DEA model was applied in order to estimate technical efficiency in constant (CRS) and variable returns to scale (VRS).

3.1. Technical Efficiency

The concept of technical efficiency is defined as the ability of an economic unit to use minimum amounts of inputs in order to produce a given level of output [26]. According to that theory, technical efficiency is based on a comparison that presents two ratio forms. That is the minimum actual quantities of inputs required to produce a given quantity of outputs [32,35] or vice versa [7,36]. The measure of technical efficiency by [37] under the assumption of constant returns to scale (CRS) is also defined as a measure of overall technical efficiency which is then divided into pure technical efficiency (PTE) and scale efficiency (SE).
Overall Technical Efficiency = Pure Technical Efficiency × Scale Efficiency
TE (CRS) = TE (VRS) × SE
The measure of pure technical efficiency (PTE) is derived from whether the assumption of constant returns to scale (CRS) is converted to that of variable and is related to the distance between actual data and those represented by the variable returns to scale (VRS) [32]. That is, PTE expresses 100% technical efficiency under the variable returns to scale assumption. If there is a difference between these two measures, then the DMU is not operating at its optimal size and exhibits an inefficient scale [35]. Scale efficiency (SE) refers to a decision-making unit’s ability to operate at the optimal size regarding the use of factors of production. Consequently, scale efficiency measurement provides the possibility of estimating the optimal sizes of a set of decision-making units [38].
SE = TE   ( CRS ) TE   ( VRS )

3.2. Data Envelopment Analysis

The data envelopment analysis model creates a production possibilities frontier, which envelopes a set of data [35] through linear programming. To be more precise, through linear programming, DEA defines a potential production function of sample units. The combinations of outputs and inputs of the DMUs located on the potential function are considered fully technically efficient. The technical efficiency of the remaining DMUs is calculated by their Euclidean distance from the surface of the potential function [35].
Regarding the analysis of CRS and VRS models, ref. [35] considers the existence of K inputs and M outputs for a number of N decision-making units (DMUs) in a data set. Each i unit is represented by the vectors xi (inputs) and yi (outputs), respectively. This assumption results in a K × N matrix of inputs X and an M × N matrix of outputs Y representing the data set of the N decision-making units [10,35].
In the case of this study, the output consists of the gross output, while the land, labor, and variable costs represent each of the factors of production used. The technical efficiency estimation is formulated through the following binary problem (Equation (4)) [35]:
min θ, λ  θ
       Subject to  −y i + Υ λ ≥ 0
               θ xi − Χ λ ≥ 0
          λ ≥ 0
where θ represents the technical efficiency ranging between the values 0 and 1 (0 ≤ θi ≤ 1). If θ = 1 (θ = 100%), a point on the frontier is defined, and a DMU is considered technically efficient. In case that θ corresponds to values smaller than 1 (θ < 1), a point below the frontier is defined, and the unit (i) is considered non-technically efficient. The problem (Equation (1)) is solved N times in order for the efficiency score (θ) for each DMU to be obtained [35]. This linear programming model (Equation (1)) responds to the assumption of input-oriented constant returns to scale (CRS). As mentioned previously, overall technical efficiency (OTE) is divided into pure technical efficiency (PTE) and scale efficiency (SE). Banker [39] modified the linear programming problem (Equation (1)) so as to refer to variable returns to scale [35] as (Equation (5)):
min θ,λ  θi
       Subject to     −yi + Yλ ≥ 0
            θxi − Χλ ≥ 0
              N1′λ = 1
        λ ≥ 0
The main difference between the CRS and VRS models is the convexity constraint “N1′λ = 1” where “N1” represents an N × 1 unit vector [35]. The VRS model presents a more flexible frontier and envelopes data in a stricter way. Therefore, the VRS efficiency is shown to be equal to or greater than that of the CRS model [40]. This is a result of the constraint N1′λ = 1, which modifies the potential frontier into a convex one. Consequently, the point of a non-technical efficient DMU is a convex combination, in contrast to the CRS model, which does not impose convexity constraints [35]. Scale efficiency (SE) is calculated through the equation (Equation (6)):
SEi = θ i CRS θ i VRS
where θiCRS represents the efficiency under the CRS hypothesis and θiVRS under the VRS, respectively. In order for scale efficiency to be more understandable, suppose that there is a difference in the two TE (CRS, VRS) scores for a particular DMU. This indicates that the DMU has scale inefficiency, which can be calculated by extracting the difference between the VRS and CRS TE scores [35]. If a case exists where the scale efficiency is equal to one (100%) [40], then the DMU will operate under constant returns to scale assumption, but if it is smaller than one, may exist increasing (IRS) or decreasing scale returns (DRS) [41]. Regarding these types of returns to scale, the “increasing” one exists in the event that a percentage change in the factors of production causes a larger change in the output. The “decreasing” case exists when a percentage change in the factors of production causes a smaller change in the output [35].

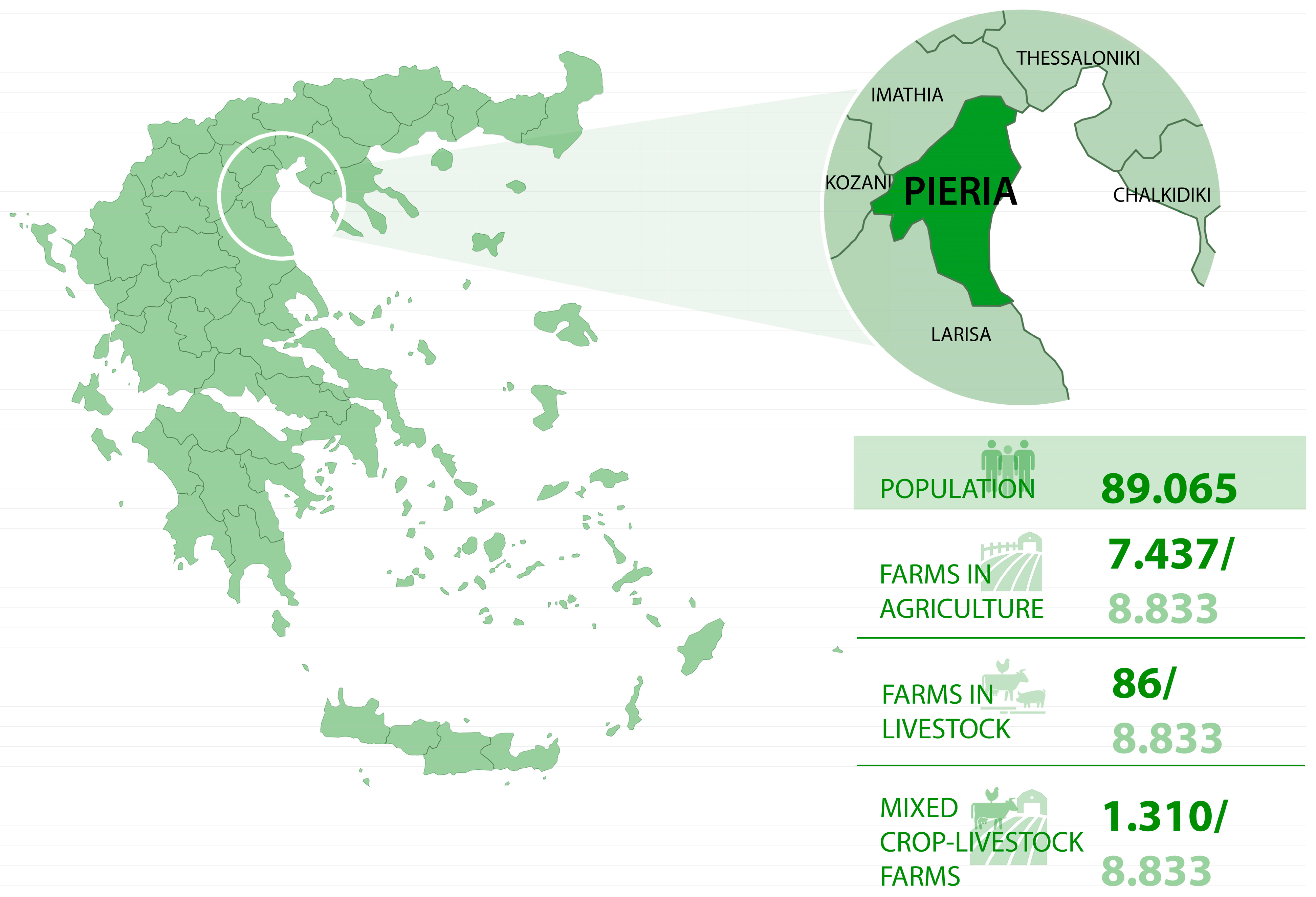
3.3. Study Area

The regional unit of Pieria was selected as the study area [42] not only for the above-mentioned literature gap to be fulfilled but also for the origin of some of this study’s authors who desire to contribute to the area’s agricultural sector (annual crops) through this investigation. Pieria is located in Northern Greece and is oriented towards the historical Mount Olympus (Figure 1). Eighty-nine thousand sixty-five inhabitants [43] live permanently in this regional unit while many of them are engaged in the agricultural sector [44].
According to the Agricultural and Livestock Farm Structure Survey of 2016 [45], the total number of farms was 8833, with an area of 513,606 acres. There are 1310 farms—with an area of 93,841 hectares—active in mixed crop-livestock farming. The farms acting purely in agriculture amount to 7437, while the livestock ones to 86. Purely agricultural activities concern mainly the extensive cultivation of annual (6291 farms) and perennial plants (6219 farms) [45]. In this case, the prevalence of annual crops is noticeable. Livestock refers to cattle breeding, sheep breeding, goat breeding, pig breeding, poultry breeding, rabbit breeding, and beekeeping activities.

3.4. Farms’ Cultivation Type and Data Access

This study focused on farms producing similar products because, in the case of inhomogeneity, the results obtained are considered biased [32]. DEA is responsible for estimating efficiency in a sample of homogeneous units, i.e., performing the same tasks [46]. For that reason, DMUs need to have the same characteristics [47] and similar activities and use a set of similar inputs [39]. It could be concluded that the examined DMUs—or otherwise farms—should operate under the same conditions [47,48].
The fact that the regional unit of Pieria mostly specializes in annual crops [44] helped to fulfill the above condition. However, the exact number of farms cultivating annual plants could not be determined for the 2021′s financial year. Through personal contacts of the authors, 40 farms were found, and their data were taken into account in order for the analysis to be conducted. These farms cultivate annual plants and produce similar products such as maize, oats, “Katerini” tobacco, barley, soft and hard wheat, vetch, and cotton. The collection of these necessary data took place over a period of two months (April 2021–June 2021).

3.5. Data

Necessary technical and economic data were collected in order for the efficiency to be estimated. After the collection, these data were processed for their appropriate use in the implementation of the DEA method from which the results of the analysis were extracted. Each farm’s gross output and input were used as the dependent and independent variables, respectively. Inputs represent the three basic production factors [33,34] and include the land in acres, labor in hours, and—variable—capital in euros (€). The descriptive statistics of the analysis variables are presented below (Table 1).
Gross output was calculated through the multiplication of products’ output and their sales prices [34]. It could otherwise be said that gross output refers to the value of products expressed in money. The land is divided into owned and rented [33,34]. The total cultivated land (owned and rented) was used to investigate the technical efficiency. Labor is divided into family members and paid workers [33,34]. It also includes hours of mechanical labor that employ human resources. The large amount of labor hours shown as maximum values (Table 1) comes as a consequence of the labor-intensive crops of the area. For this investigation, the total number of working hours (Labor) was used since they were calculated cumulatively.
Variable costs are characterized by the cost of raw materials [32], such as seeds, fertilizers, plant protection products, fuel, other costs, and machinery rental costs. The sum of these costs constitutes the –variable- capital [33,34]. Fixed capital was chosen not to be taken into account for the estimation of technical efficiency. This choice was based on the fact that the costs of fixed capital are permanent since they arise from fixed assets. That means that fixed capital items are purchased over a period of time and used in the production process with a long life, while the variable—capital—costs are incurred during a production year [32], such as the 2021 financial year used in the present analysis. For this investigation, the total of variable costs was used since they were calculated cumulatively. Regarding the farms’ profits, gross output (in €) was taken into account.
The possibility of using this set of outputs and inputs in the DEA model is supported by corresponding research applications available in the relevant literature [8,10,49].

4. Results

As the DEA model was input-oriented, there was a desire to study the inputs’ variation between the actual and optimal situation in detail. For the estimation, DEAP version 2.1 of [35] was used. This software is one of the most used to obtain DEA results, as evidenced by literature findings [50]. This model was applied one time—for the data reference period (2021)—and the problem was solved 40 times for each (40) farm(s) participating in the survey. First, the CRS problem was solved to estimate the total technical efficiency (OTE). The VRS problem was then solved to estimate pure technical efficiency (PTE). Lastly, the scale efficiency (SE) was estimated as well. The analysis results are shown in detail in Appendix A, while their descriptive data are presented in Table 2 below.
The average OTE was found to be 0.654. This result indicated that the examined farms would have to reduce their inputs by 34.6% at a given level of output to become more efficient. A percentage of 15.0% of farms are technically fully efficient with current production technology. That means the inputs are used efficiently, and farmers should maintain a constant size. The constant returns to scale (CRS) model is considered appropriate when the farms operate at an optimal size. This may be biased due to imperfect competition and various economic constraints [8]. That was the reason that the BCC model had to be implemented for pure technical efficiency (PTE) to be estimated.
The average PTE was found to be high (0.804). This result means that farms should reduce their inputs by 19.4% at a given level of output. It seems that 15.0% of the examined farms operate at an optimal size since they appear to have a scale efficiency equal to 1 (SE = 1). The opposite occurs when the decision making units (DMUs) use more inputs than they should in relation to their size [32], and it appears that the remaining 85.0% of the examined farms operate under this condition (Table 2). It is worth noting that six (15%) farms (Table 3) present a full technical and scale efficiency. This fact points out that these farms operate under constant returns to scale and have to keep their level of inputs stable in order to continue to be efficient. These farms can be considered operating models for the remaining 34. The 28 (70%) sample’s farms appear to have increasing (IRS) returns to scale, while the other six farms (15%) show a decreasing (DRS) one.
The reorganization of inefficient farms is then presented (Table 4) by presenting the average percentage according to which the farms’ inputs should be reduced. This analysis is considered necessary in order to provide management advice to the farmers of Pieria’s Regional Unit from a holistic point of view.
The first class (0.10–0.59) belongs to the lowest efficiency category. In this case, the “Land” factor is proposed to be reduced by 54.0% and “Labor” by 50.2%. Especially for the factor of production “Capital” (variable costs), the DEA model suggests the biggest change in terms of reduction (63.8%). Reviewing the results of the second (0.6–0.79) and third (0.8–0.99) efficiency classes, a smaller input reduction is proposed -on average- for the farms that participated in this survey..

5. Discussion

The extraction of the results as well as their interpretation shows how functional the data envelopment analysis (DEA) method is, especially in terms of quoting useful conclusions for the farmers’ effective management of inputs. DEA is also considered an easy-to-use method that can be used not only by researchers to fulfill similar research purposes but also by farmers so that they adjust their production process in such a way as to increase their profits without jeopardizing their production performance from the moment which is taken for granted [8]. Finally, the contribution of the method, especially in the context of policy development for farm management, is considered equally remarkable.
To be more specific, the interpretation of the results indicated that the farms’ pure technical efficiency (PTE) exceeds the overall (OTE) for the data reference period (2021). These results are similar to other findings [10,51], proving that the VRS model presents a more flexible frontier than that of CRS [35], with the resulting efficiency being greater [40]. The implementation of the CRS model showed that the examined farms need to reduce their inputs by 34.6% in order to operate more efficiently. Through VRS model implementation, a lower reduction in inputs is suggested (19.4%) as something that must also be taken into account. The findings of the relevant literature on the use of the VRS model and its “flexibility”, especially in the case of the agricultural sector [8], contributed to this conclusion. The highest variations in the aspects of input reduction are reported for farms that belong to the lowest level of efficiency. This fact points out that the proper management of inputs is considered essential [33] as it affects the levels of technical efficiency.
Even though through this analysis, both models (CRS, VRS) were used to better understand the DEA methodology, [8] implemented directly the VRS model because it allows variations in returns to scale. That choice is explained by the fact that in the sector of agriculture, it is not appropriate to hypothesize the elimination of constraints, perfect competition, or easy access to finance [8]. This fact could be taken into account in the case of similar and future research approaches’ conduction.
Another common finding is -that in every relevant research study- technical efficiency (100%) does not fully exist for the total of the examined farms. Many researchers, consequently, suggest a reasonable reduction in inputs for a set of farms in order to operate efficiently [10,52]. It should also be pointed out that the examined farms presented a high level of scale efficiency (SE), which contradicts the results of [10]. This result may indicate that Pieria’s farms may be operating at a better size compared to other Greek regions. Regarding the types of returns to scale, the majority of farms present increasing returns to scale, which indicates that these farms could increase their level of technical efficiency by increasing their size, as also supported by [53].
The literature regarding the largest (declining) change proposed for the “Capital” factor of production points out that better control and more efficient utilization of the cultivation costs is required by the farmers [54]. This goal can be achieved through the institutionalization of state policies such as a reduction in taxes and inputs’ sell prices [10] as well as through the provision of improved advisory services related to agriculture [55]. A reduction in the “Land” factor is also considered necessary since the literature also supports that the extensive land use of farms can reduce their efficiency [56,57,58]. In addition to the land use reduction, the literature presents that proper land management also depends on the farmers’ production plan as mixed production systems, including tree cultivation, are discussed [59]. Last, but not least, it is also seen that the DEA model reveals that the same level of output could be achieved by reducing the labor hours from 22.8% to 62.8%. Similar findings exist in the relevant literature demonstrating the same situation in the Greek agricultural sector [60]. Regarding this issue, other researchers support that the lower the level of technology used, the less invested capital exists, resulting in labor dependence [8,61]. Therefore, the revision of the existing technology could be suggested to the farmers of Pieria.

6. Conclusions

Efficiency is a useful instrument for economics, agriculture, literature, and research. To be more precise, technical efficiency is considered a necessary advisory tool for managers whose objectives are to maximize profit and minimize costs. Data Envelopment Analysis (DEA) is a widely accepted methodology in order to estimate technical efficiency in the agriculture sector. For that reason and with the goal of extracting useful conclusions regarding the farmers’ effective management of inputs, this study aimed to present the DEA method through its implementation in 40 farms located in the regional unit of Pieria. These primary data were collected through personal interviews and were related to the economic and technical parameters of the examined farms. After data collection, a necessary technical-economic analysis was held, and finally, an input-oriented DEA model was applied in order to estimate technical efficiency in constant (CRS) and variable returns to scale (VRS).
Through the interpretation and discussion of the results, it first emerged that the considered farms have the possibility to reduce their inputs. Second, DEA proved to be a functional and easy-to-use method, especially in terms of providing useful conclusions for effective farm management due to the fact that it can be used by both researchers and farmers to fulfill similar research purposes and adjust the productive process in such a way as to increase their profits without jeopardizing the performance from the moment it is taken for granted [8], respectively. The estimation results, in general, showed that the input reduction of Pieria’s farms cultivating annual plants deemed necessary, especially for variable –capital- costs indicating that better control of the cultivating costs is imposed by farmers. Therefore, through the conduction of this study, farmers should be motivated to reduce the inputs used, something that can be achieved through the provision of specialized advisory services. This will, of course, be helped by both the local authorities and the policies of the country in which the rational use of inputs seems to be necessary.
Regarding the originality of this effort, it is worth mentioning that this study is innovative since it refers to the DEA method, a specialized and interesting mathematical tool for estimating and evaluating the technical efficiency of farms in the agricultural sector. It also provides an example application based on original data reporting, not only the results but also a tutorial on the methodology of data collection and analysis. Through this procedure, DEA becomes an operational and easy-to-use method that can be used not only by researchers but also farmers.
This study could initially contribute to the field of agriculture by revealing a method that can help formulate farm management strategies. Secondly, it contributes to the area and society by providing strategic directions to Pieria’s farmers in order to increase their income, reduce their costs, and achieve sustainability. If this goal is achieved, there will be an increase in the regional unit’s economy. Then, it could also contribute at the macro-economic level by strengthening the agricultural sector and its competitiveness. It could also contribute to the literature because such analysis in the context of this historical region is being carried out for the first time.
It is worth mentioning that the present analysis was based on data concerning a small sample of farms. Small data samples may lead to biased and uncertain results, despite the fact that DEA is applicable to small samples [32,62,63,64,65]. Thus, it is deemed necessary to conduct a research approach on a larger sample of farms and then on relevant data covering several years in order to achieve further goals such as the study of technical progress. It could also be suggested to investigate other types of efficiency, such as allocative or eco-efficiency, by using other methodologies, such as stochastic frontier analysis (SFA), Softscapes, Desire and Greenscope. Last, but not least, it is generally believed that this study could certainly provide a background for future research that will be able to develop the present one with more new details about Pieria’s farming sector.

Author Contributions

Methodology, A.K. and A.T.; software, A.K. and A.T.; validation, E.D., C.M. and T.B.; formal analysis, A.K. and A.T.; investigation, A.K.; data curation, A.K. and E.D.; writing—original draft preparation, A.K. and E.L.; writing—review and editing, E.L. and A.P.; supervision, C.M. and T.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not Applicable.

Acknowledgments

We thank the Architect, K. Tafidou, for assistance in editing the map of the regional unit of Pieria (Figure 1).

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Analysis results as extracted from DEAP Version 2.1 package.
Table A1. Analysis results as extracted from DEAP Version 2.1 package.
FirmCrsteVrsteScaleType of Returns to Scale
10.9821.0000.982irs
20.7160.7320.978irs
30.5660.610.927drs
40.2280.4220.54irs
51.0001.0001.000-
60.3871.0000.387irs
70.5980.5980.999-
80.8111.0000.811drs
90.5430.5460.994irs
100.3490.4970.703irs
110.9620.9780.983irs
120.0571.0000.057irs
130.7780.8320.936irs
140.5980.6690.894irs
150.8260.8520.969irs
160.6381.0000.638irs
170.6680.7110.94irs
180.6720.7010.96irs
190.7321.0000.732drs
200.9040.9170.986drs
210.1710.9910.172irs
220.5780.5790.999irs
230.0120.3510.033irs
240.330.7980.414irs
250.9080.9370.969irs
260.8131.0000.813irs
271.0001.0001.000-
281.0001.0001.000-
290.8320.9160.908irs
300.7170.7650.937irs
310.7770.7840.991drs
320.4460.4680.952irs
330.5630.5930.949irs
341.0001.0001.000-
350.5410.6240.867irs
361.0001.0001.000-
370.3090.510.607irs
380.2780.8720.318irs
391.0001.0001.000-
400.8820.8930.988irs
Μean0.6540.8040.808

References

  1. Lovell, C.A.K. Production Frontiers and Productive Efficiency. Meas. Product. Effic. Tech. Appl. 1993, 3, 67. [Google Scholar]
  2. Fried, H.O.; Knox Lovell, C.A.; Schmidt, S.S. The Measurement of Productive Efficiency and Productivity growth; Oxford University Press: Oxford, UK, 2008. [Google Scholar] [CrossRef]
  3. Kaur, S.; Gupta, P.K. Productive Efficiency Mapping of the Indian Banking System Using Data Envelopment Analysis. Procedia Econ. Financ. 2015, 25, 227–238. [Google Scholar] [CrossRef]
  4. Theodoridis, A.; Psychoudakis, A. Efficiency measurement in Greek dairy farms: Stochastic frontier vs. data envelopment analysis. Int. J. Econ. Sci. Appl. Res. 2008, 1, 53–67. [Google Scholar]
  5. Dube, L.; Guveya, E. Technical Efficiency of Smallholder Out-grower Tea (Camellia Sinensis) Farming in Chipinge District of Zimbabwe. Greener J. Agric. Sci. 2014, 4, 368–377. [Google Scholar] [CrossRef] [Green Version]
  6. Ng’ombe, J.; Kalinda, T. A Stochastic Frontier Analysis of Technical Efficiency of Maize Production Under Minimum Tillage in Zambia. Sustain. Agric. Res. 2015, 4, 31. [Google Scholar] [CrossRef] [Green Version]
  7. Galluzzo, N. Technical and economic efficiency in some Italian farms: An analysis in two Italian islands. Agric. Econ. Rev. 2017, 18, 30–39. [Google Scholar]
  8. Bournaris, T.; Vlontzos, G.; Moulogianni, C. Efficiency of vegetables produced in Glasshouses: The Impact of Data Envelopment Analysis (DEA) in land management decision making. Land 2019, 8, 17. [Google Scholar] [CrossRef] [Green Version]
  9. Batzios, A.; Theodoridis, A.; Semos, A.; Bournaris, T. Assessing efficiency of dairy goat farms by performance evaluation and benchmarking. J. Hell. Vet. Med. Soc. 2022, 73, 4389–4398. [Google Scholar] [CrossRef]
  10. Prentzas, A.; Nastis, S.A.; Moulogianni, C.; Kouriati, A. Technical and economic analysis of farms cultivating cereals and legumes: A Greek case study. Int. J. Sustain. Agric. Manag. Inform. 2022, 8, 446. [Google Scholar] [CrossRef]
  11. Vidoli, F.; Fusco, E. Level of services, spatial dependence and allocative efficiency in local governments. Local Gov. Stud. 2018, 44, 848–873. [Google Scholar] [CrossRef]
  12. Hadian, E.; Shabani, Z.D.; Farmanbar, F. Impact of energy carriers’ price distortions on energy allocative efficiency: The case study of Iranian provinces. Environ. Sci. Pollut. Res. 2022, 29, 88725–88736. [Google Scholar] [CrossRef]
  13. Chebil, A.; Frija, A.; Thabet, C. Economic efficiency measures and its determinants for irrigated wheat farms in Tunisia: A DEA approach. New Medit 2015, 14, 32–38. [Google Scholar]
  14. Vidal-Tomás, D.; Ibáñez, A.M.; Farinós, J.E. The effect of the launch of bitcoin futures on the cryptocurrency market: An economic efficiency approach. Mathematics 2021, 9, 413. [Google Scholar] [CrossRef]
  15. Fumbwe, F.; Lihawa, R.; Andrew, F.; Kinyanjui, G.; Mkuna, E. Examination on level of scale efficiency in public hospitals in Tanzania. Cost Eff. Resour. Alloc. 2021, 19, 1–10. [Google Scholar] [CrossRef]
  16. Mangili, P.V.; Santos, L.S.; Prata, D.M. A Systematic Methodology for Comparing the Sustainability of Process Systems Based on Weighted Performance Indicators. Comput. Chem. Eng. 2019, 130, 106558. [Google Scholar]
  17. Azapagic, A.; Stamford, L.; Youds, L.; Barteczko-Hibbert, C. Towards Sustainable Production and Consumption: A Novel DEcision-Support Framework IntegRating Economic, Environmental and Social Sustainability (DESIRES). Comput. Chem. Eng. 2016, 91, 93–103. [Google Scholar]
  18. Mangili, P.V.; Prata, D.M. Preliminary design of sustainable industrial process alternatives based on eco-efficiency approaches: The maleic anhydride case study. Chem. Eng. Sci. 2020, 212, 115313. [Google Scholar] [CrossRef]
  19. Ruiz-Mercado, G.J.; Smith, R.L.; Gonzalez, M.A. Gonzalez. Sustainability Indicators for Chemical Processes: II. Data Needs. Ind. Eng. Chem. Res. 2012, 51, 2329–2353. [Google Scholar]
  20. Hyvärinen, H.; Skyttä, A.; Jernberg, S.; Meissner, K.; Kuosa, H.; Uusitalo, L. Cost-efficiency assessments of marine monitoring methods lack rigor—A systematic mapping of literature and an end-user view on optimal cost-efficiency analysis. Environ. Monit. Assess. 2021, 193, 1–13. [Google Scholar] [CrossRef]
  21. Nguyen, M.A.T.; Yu, M.M.; Lirn, T.C. Revenue efficiency and its drivers in the cruise industry. Marit. Policy Manag. 2022, 49, 1010–1026. [Google Scholar] [CrossRef]
  22. Pilar, P.G.; Marta, A.P.; Antonio, A. Profit efficiency and its determinants in small and medium-sized enterprises in Spain. BRQ Bus. Res. Q. 2018, 21, 238–250. [Google Scholar] [CrossRef]
  23. Rezitis, A.; Mygdakos, E.; Zaverda, Μ. Study of the Effect of the “THEOFRASTOS” System on the Technical Efficiency of Greenhouse Crops: A Comparative Analysis. Hellenic Statistical Institute. In Proceedings of the 17th Panhellenic Statistics Conference (2004), Lefkada, Greece, 17–19 June 2004; pp. 375–382. (In Greek). [Google Scholar]
  24. Galanopoulos, Κ.; Kamenidou, Ε.; Tziakas, Β.; Mitsopoulos, A. Technological progress in agricultural production: Analysis of Improvement Plans in Central Macedonia. In Proceedings of the 8th Panhellenic Agricultural Economy Conference, Thessaloniki, Greece, 25–27 November 2004. (In Greek). [Google Scholar]
  25. Tsiouni, M.; Gourdouvelis, D.; Aggelopoulos, S.; Vrontis, D.; Galati, A. Measuring Technical Efficiency of Greek Red Suckler Cow Breed’s Farms in Central Macedonia Region Using a Data Envelopment Analysis Model. J. Int. Bus. Entrep. Dev. 2022, 14, 329–348. [Google Scholar]
  26. Manos, B.; Psychoudakis, A. Investigation of the relative efficiency of dairy farms using data envelopment analysis. Q. J. Int. Agric. 1997, 36, 188–197. [Google Scholar]
  27. Sultana, S.; Hossain, M.M.; Haque, M.N. Estimating the potato farming efficiency: A comparative study between stochastic frontier analysis and data envelopment analysis. PLoS ONE 2023, 18, e0284391. [Google Scholar] [CrossRef]
  28. De Koeijer, T.J.; Wossink, G.A.A.; Struik, P.C.; Renkema, J.A. Measuring agricultural sustainability in terms of efficiency: The case of Dutch sugar beet growers. J. Environ. Manag. 2002, 66, 9–17. [Google Scholar]
  29. Aigner, D.; Lovell, C.A.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
  30. Jote, A.; Feleke, S.; Tufa, A.; Manyoung, V.; Lemma, T. Assessing the Efficiency of Sweet Potato Producers in the Southern Region of Ethiopia. Exp. Agric. 2018, 54, 491–506. [Google Scholar] [CrossRef] [Green Version]
  31. Callens, I.; Tyteca, D. Towards indicators of sustainable development for firms: A productive efficiency perspective. Ecol. Econ. 1999, 28, 41–53. [Google Scholar] [CrossRef]
  32. Coelli, T.J.; Prasada Rao, D.S.; O’Donnell, C.J.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
  33. Kitsopanidis, G.; Kamenidis, C. Agricultural Economics, 3rd ed.; ZHTH: Thessaloniki, Greece, 2003. (In Greek) [Google Scholar]
  34. Kouriati, A.; Dimitriadou, E.; Bournaris, T. Farm accounting for farm decision making: A case study in Greece. Int. J. Sustain. Agric. Manag. Inform. 2021, 7, 77. [Google Scholar] [CrossRef]
  35. Coelli, T. A Guide to DEAP Version 2.1: A Data Envelopment Analysis (Computer) Program. CEPA Working Paper 96/08 ABSTRACT. 1996. Available online: https://www.owlnet.rice.edu/~econ380/DEAP.PDF (accessed on 22 March 2023).
  36. Bojnec, Š.; Latruffe, L. Measures of farm business efficiency. Ind. Manag. Data Syst. 2008, 108, 258–270. [Google Scholar]
  37. Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. Ser. A Gen. 1957, 120, 253–290. [Google Scholar] [CrossRef]
  38. Kumar, S.; Gulati, R. An Examination of Technical, Pure Technical, and Scale Efficiencies in Indian Public Sector Banks using Data Envelopment Analysis. Eurasian J. Bus. Econ. 2008, 1, 33–69. [Google Scholar]
  39. Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
  40. Sharma, K.R.; Leung, P.S.; Zaleski, H.M. Technical, allocative and economic efficiencies in swine production in Hawaii: A comparison of parametric and nonparametric approaches. Agric. Econ. 1999, 20, 23–35. [Google Scholar] [CrossRef]
  41. Rodrigues, A.; Silveira Gontijo, T.; De Muylder, C. Measuring the technical and scale efficiency of Rio de Janeiro samba schools: A DEA approach Mensuração da eficiência técnica e de escala das escolas de samba do Rio de Janeiro: Uma abordagem DEA. Exacta 2019, 17, 201. [Google Scholar] [CrossRef]
  42. Regional unit of Pieria. 2022. Available online: https://pieria.pkm.gov.gr/ (accessed on 24 December 2022).
  43. Hellenic Statistical Authority. Demographic Characteristics/2011. Available online: https://www.statistics.gr/el/statistics/-/publication/SAM03/ (accessed on 8 August 2023).
  44. Hellenic Statistical Authority. Economic Characteristics/2011. Available online: https://www.statistics.gr/el/statistics/-/publication/SAM04/ (accessed on 5 March 2023).
  45. Hellenic Statistical Authority. Farms and Lands/2016. Available online: https://www.statistics.gr/el/statistics/-/publication/SPG32/ (accessed on 5 March 2023).
  46. Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef] [Green Version]
  47. Haas, D.A.; Murphy, F.H. Compensating for non-homogeneity in decision-making units in data envelopment analysis. Eur. J. Oper. Res. 2003, 144, 530–544. [Google Scholar] [CrossRef]
  48. Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
  49. Theodoridis, A.; Batzios, C.; Ragkos, A.; Angelidis, P. Technical efficiency measurement of mussel aquaculture in Greece. Aquac. Int. 2017, 25, 1025–1037. [Google Scholar] [CrossRef]
  50. Kyrgiakos, L.S.; Kleftodimos, G.; Vlontzos, G.; Pardalos, P.M. A systematic literature review of data envelopment analysis implementation in agriculture under the prism of sustainability. Oper. Res. Int. J. 2023, 23, 7. [Google Scholar] [CrossRef]
  51. Candemir, M.; Koyubenbe, N. Efficiency analysis of dairy farms in the province of Izmir (Turkey): Data envelopment analysis (DEA). J. Appl. Anim. Res. 2006, 29, 61–64. [Google Scholar] [CrossRef]
  52. Mukhtar, U.; Mohamed, Z.; Shamsuddin, M.N.; Sharifuddin, J.; Iliyasu, A. Application of data envelopment analysis for technical efficiency of smallholder pearl millet farmers in Kano state, Nigeria. Bulg. J. Agric. Sci. 2018, 24, 213–222. [Google Scholar]
  53. Vlontzos, G. Measuring Efficiency of the Greek Flourmill Firms Using Data Envelopment Analysis. Int. J. Sustain. Agric. Manag. Inform. 2015, 1, 61. [Google Scholar]
  54. Iráizoz, B.; Rapún, M.; Zabaleta, I. Assessing the Technical Efficiency of Horticultural Production in Navarra, Spain. Agric. Syst. 2003, 78, 387–403. [Google Scholar]
  55. Świtłyk, M.; Sompolska-Rzechuła, A.; Kurdyś-Kujawska, A. Measurement and Evaluation of the Efficiency and Total Productivity of Dairy Farms in Poland. Agronomy 2021, 11, 2095. [Google Scholar] [CrossRef]
  56. Wang, L.; Chang, W. Total Factor Productivity and Its Differences of Family Farms in China. J. South China Agric. Univ. 2017, 6, 20–31. [Google Scholar]
  57. Guo, X.; Gong, G. Can Adoption of New Technologies Raise Economic Efficiency of Family Farms? From the Perspective of Realization of New Technological Demand. J. Huazhong Agric. Univ. 2021, 1, 33–42, discussion 174–175. [Google Scholar]
  58. Chen, Z.; Meng, Q.; Yan, K.; Xu, R. The Analysis of Family Farm Efficiency and Its Influencing Factors: Evidence from Rural China. Land 2022, 11, 487. [Google Scholar] [CrossRef]
  59. Bai, W.; Sun, Z.; Zheng, J.; Du, G.; Feng, L.; Cai, Q.; Yang, N.; Feng, C.; Zhang, Z.; Evers, J.B.; et al. Mixing Trees and Crops Increases Land and Water Use Efficiencies in a Semi-Arid Area. Agric. Water Manag. 2016, 178, 281–290. [Google Scholar]
  60. Papadopoulou, A.; Ragkos, A.; Theodoridis, A.; Skordos, D.; Parissi, Z.; Abraham, E. Evaluation of the Contribution of Pastures on the Economic Sustainability of Small Ruminant Farms in a Typical Greek Area. Agronomy 2021, 11, 63. [Google Scholar] [CrossRef]
  61. Gollin, D.; Parente, S.L.; Rogerson, R. Farm work, home work and international productivity differences. Rev. Econ. Dyn. 2004, 7, 827–850. [Google Scholar]
  62. Assaf, A.; Knežević, C.L. The performance of the Slovenian hotel industry: Evaluation post-privatisation. Int. J. Tour. Res. 2010, 12, 462–471. [Google Scholar]
  63. Cheng, H.; Lu, Y.C.; Chung, J.T. Improved slack-based context-dependent DEA—A study of international tourist hotels in Taiwan. Expert Syst. Appl. 2010, 37, 6452–6458. [Google Scholar]
  64. Gaviglio, A.; Filippini, R.; Madau, F.A.; Marescotti, M.E.; Demartini, E. Technical efficiency and productivity of farms: A periurban case study analysis. Agric. Econ. 2021, 9, 11. [Google Scholar] [CrossRef]
  65. Poldrugovac, K.; Tekavcic, M.; Jankovic, S. Efficiency in the Hotel Industry: An Empirical Examination of the Most Influential Factors. Econ. Res.-Ekon. Istraz. 2016, 29, 583–597. [Google Scholar]
Agronomy 13 02109 g001
Figure 1. Regional Unit of Pieria. Source: Edited figure from Google Maps.
Figure 1. Regional Unit of Pieria. Source: Edited figure from Google Maps.
Agronomy 13 02109 g001
Table 1. Descriptive statistics of variables used in the data envelopment analysis method.
Table 1. Descriptive statistics of variables used in the data envelopment analysis method.
Descriptive MeasuresGross Output (€)Land (acres)Labor (h) Variable Costs (€)
Average13,348.8351.293940.858961.03
Min180.005.70250.00900.00
Max34,260.00467.008560.0064,464.00
St. Dev9073.7580.192141.8311,790.67
Table 2. Descriptive statistics of Data Envelopment Analysis results.
Table 2. Descriptive statistics of Data Envelopment Analysis results.
ModelCRSVRSSE
Average0.6540.8040.808
Min0.0120.3510.033
Max1.0001.0001.000
St. dev361474361
Number of efficient farms6136
Percentage (%) of efficient farms15.0032.5015.00
Table 3. Economic characteristics of Technical Efficient Farms.
Table 3. Economic characteristics of Technical Efficient Farms.
FarmsGross Output (€)Land (acres)Labor (h) Variable Capital (€)
528,700.00467.002100.0024,174.00
2717,325.0017.008500.009000.00
289750.0013.003100.002450.00
3422,360.0043.003000.002990.00
3634,260.0027.005080.0038,660.00
3922,800.0025.004100.007300.00
Table 4. The actual and optimal situation of the inefficient farms (on average).
Table 4. The actual and optimal situation of the inefficient farms (on average).
Efficiency Class0.1–0.5990.6–0.7990.8–0.999
ActualOptimalVar. (%)ActualOptimalVar. (%)ActualOptimalVar. (%)
Land
(acres)		80.640.2−54.0%39.127.7−27.7%19.716.49−15.2%
Labor (hours)3817.51937.6−50.2%4057.92792.9−29.4%4013.72879.8−22.8%
Variable Capital (€)14,631.53089.9−63.8%7609.55398.3−30.6%4078.52520.0−21.2%
Gross Output (€)12,580.912,580.90.0%13,249.913,249.90.0%10,467.210,467.20.00%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kouriati, A.; Tafidou, A.; Lialia, E.; Prentzas, A.; Moulogianni, C.; Dimitriadou, E.; Bournaris, T. The Impact of Data Envelopment Analysis on Effective Management of Inputs: The Case of Farms Located in the Regional Unit of Pieria. Agronomy 2023, 13, 2109. https://doi.org/10.3390/agronomy13082109

AMA Style

Kouriati A, Tafidou A, Lialia E, Prentzas A, Moulogianni C, Dimitriadou E, Bournaris T. The Impact of Data Envelopment Analysis on Effective Management of Inputs: The Case of Farms Located in the Regional Unit of Pieria. Agronomy. 2023; 13(8):2109. https://doi.org/10.3390/agronomy13082109

Chicago/Turabian Style

Kouriati, Asimina, Anna Tafidou, Evgenia Lialia, Angelos Prentzas, Christina Moulogianni, Eleni Dimitriadou, and Thomas Bournaris. 2023. "The Impact of Data Envelopment Analysis on Effective Management of Inputs: The Case of Farms Located in the Regional Unit of Pieria" Agronomy 13, no. 8: 2109. https://doi.org/10.3390/agronomy13082109

APA Style

Kouriati, A., Tafidou, A., Lialia, E., Prentzas, A., Moulogianni, C., Dimitriadou, E., & Bournaris, T. (2023). The Impact of Data Envelopment Analysis on Effective Management of Inputs: The Case of Farms Located in the Regional Unit of Pieria. Agronomy, 13(8), 2109. https://doi.org/10.3390/agronomy13082109

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop