Using Block Kriging as a Spatial Smooth Interpolator to Address Missing Values and Reduce Variability in Maize Field Yield Data
Abstract
1. Introduction
- Do the harvested maize plants grown in the border (margin) rows significantly affect data variability and the mean values of plants grown in the central rows of the experimental field plots?
- Should Block Kriging be preferred over the most used statistical log10 transformation method to reduce data variability and estimate missing values in crop data without changing the means?
2. Materials and Methods
2.1. Site Description and Sampling
2.2. Theoretical Background
2.2.1. The Use of Log Transformation in Achieving Normality and Reducing Variability in Data
2.2.2. Using Kriging Interpolation to Estimate Missing Data and Reduce Outliers
2.3. Data Analysis
3. Results
3.1. Descriptive Statistics of the Original, Log10-Trarnsformed, and Interpolated Kriging Maize Fresh Weight Data
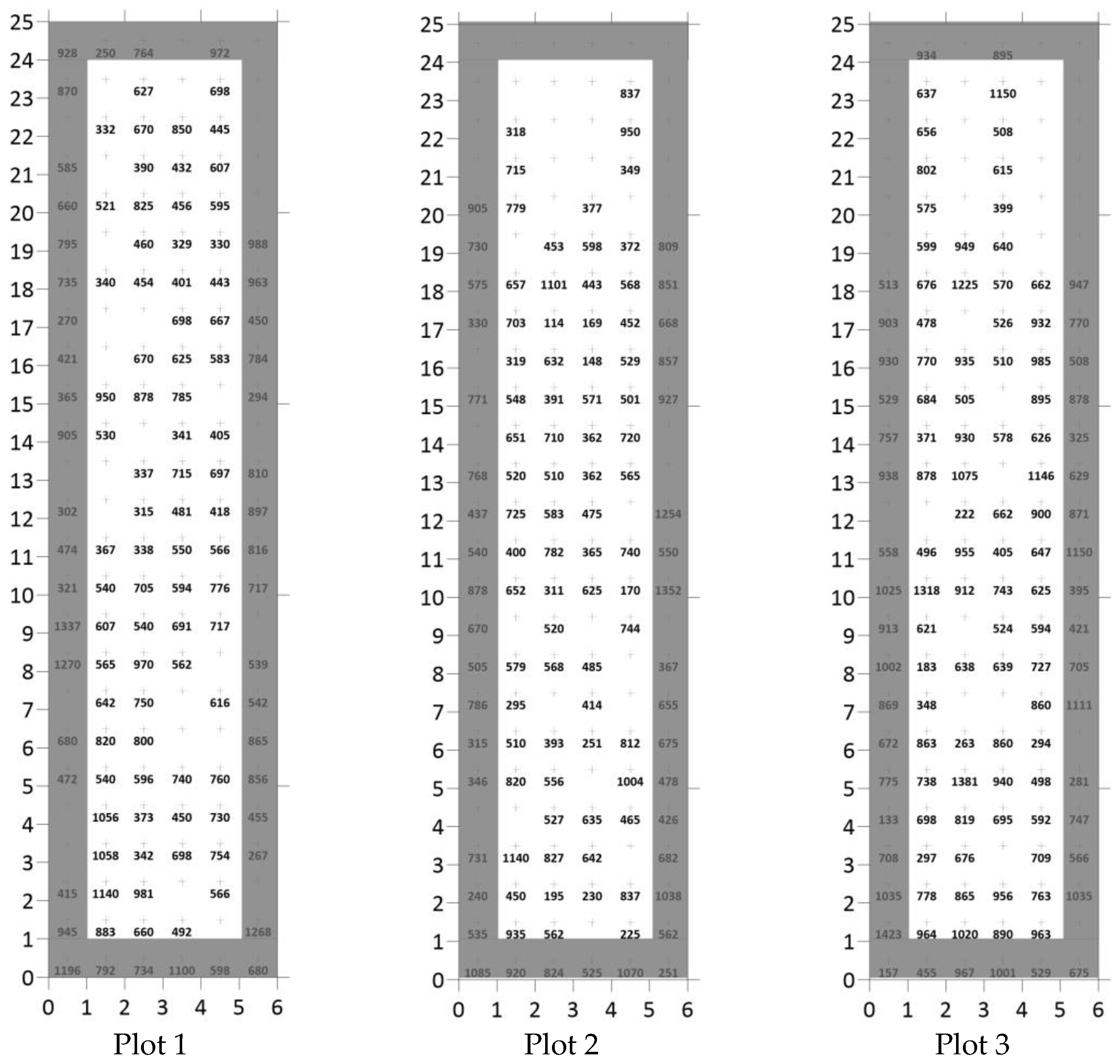
3.2. Box Plots of the Original and Interpolated Kriging Maize Fresh Weight Data
3.3. Diagrammatic Presentation of the Original, Point, and Block Kriging Data
3.4. Contour Maps of the Point and Block Interpolation Grids
3.5. Fitted Variogram Variables for Point and Block Kriging
4. Discussion
5. Conclusions
- Log10-transformation was found appropriate at the analysis stage of maize crop yield data as provides a notable reduction in data variability (CV values), but it failed to estimate means leading to non-existent economic loss for the producers.
- The Block Kriging interpolation method was found to adequately replace the commonly used the statistical method of log10 transformation so far as it managed to reduce data variability without altering the means, leading to more precise estimates of crop yield. A summary of the highlighted advantages of Block Kriging interpolation versus log10 transformation showed that this method can successfully (a) estimate and fill in missing values, (b) smooth unrepresentative or extreme values (usually present in agricultural data), (c) adjust the estimated values to account for the spatial correlation of experimental units with respect to the measured characteristics, (d) reduce the data variability without altering the estimated mean values of the measured characteristics, and (e) improve the overall quality of the data.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nogueira Martins, R.; Ferreira Lima Dos Santos, F.; de Moura Araújo, G.; de Arruda Viana, L.; Fim Rosas, J.T. Accuracy Assessments of Stochastic and Deterministic Interpolation Methods in Estimating Soil Attributes Spatial Variability. Commun. Soil Sci. Plant Anal. 2019, 50, 2570–2578. [Google Scholar] [CrossRef]
- Piepho, H.P. Data Transformation in Statistical Analysis of Field Trials with Changing Treatment Variance. Agron. J. 2009, 101, 865–869. [Google Scholar] [CrossRef]
- Kosmowski, F.; Chamberlin, J.; Ayalew, H.; Sida, T.; Abay, K.; Craufurd, P. How Accurate Are Yield Estimates from Crop Cuts? Evidence from Smallholder Maize Farms in Ethiopia. Food Policy 2021, 102, 102122. [Google Scholar] [CrossRef] [PubMed]
- Lobell, D.B.; Azzari, G.; Burke, M.; Gourlay, S.; Jin, Z.; Kilic, T.; Murray, S. Eyes in the Sky, Boots on the Ground: Assessing Satellite- and Ground-Based Approaches to Crop Yield Measurement and Analysis. Am. J. Agric. Econ. 2020, 102, 202–219. [Google Scholar] [CrossRef]
- Norman, J.M.; Becker, F. Terminology in Thermal Infrared Remote Sensing of Natural Surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- Wahab, I. In-Season Plot Area Loss and Implications for Yield Estimation in Smallholder Rainfed Farming Systems at the Village Level in Sub-Saharan Africa. GeoJournal 2020, 85, 1553–1572. [Google Scholar] [CrossRef]
- Abay, K.A.; Abate, G.T.; Barrett, C.B.; Bernard, T. Correlated Non-Classical Measurement Errors, ‘Second Best’ Policy Inference, and the Inverse Size-Productivity Relationship in Agriculture. J. Dev. Econ. 2019, 139, 171–184. [Google Scholar] [CrossRef]
- Poate, D. A Review of Methods for Measuring Crop Production from Smallholder Producers. Exp. Agric. 1988, 24, 1–14. [Google Scholar] [CrossRef]
- Ndakidemi, B.J.; Mbega, E.R.; Ndakidemi, P.A.; Belmain, S.R.; Arnold, S.E.J.; Woolley, V.C.; Stevenson, P.C. Field Margin Plants Support Natural Enemies in Sub-Saharan Africa Smallholder Common Bean Farming Systems. Plants 2022, 11, 898. [Google Scholar] [CrossRef]
- Marshall, E.J.P.; Moonen, A.C. Field Margins in Northern Europe: Their Functions and Interactions with Agriculture. Agric. Ecosyst. Environ. 2002, 89, 5–21. [Google Scholar] [CrossRef]
- Mante, J.; Gerowitt, B. Learning from Farmers’ Needs: Identifying Obstacles to the Successful Implementation of Field Margin Measures in Intensive Arable Regions. Landsc. Urban Plan. 2009, 93, 229–237. [Google Scholar] [CrossRef]
- Feng, C.; Wang, H.; Lu, N.; Chen, T.; He, H.; Lu, Y.; Tu, X.M. Log-Transformation and Its Implications for Data Analysis. Shanghai Arch. Psychiatry 2014, 26, 105–109. [Google Scholar] [CrossRef]
- Cressie, N. Block Kriging for Lognormal Spatial Processes. Math. Geol. 2006, 38, 413–443. [Google Scholar] [CrossRef]
- Taleb, I.; Serhani, M.A.; Bouhaddioui, C.; Dssouli, R. Big Data Quality Framework: A Holistic Approach to Continuous Quality Management. J. Big Data 2021, 8, 76. [Google Scholar] [CrossRef]
- Desiere, S.; Jolliffe, D. Land Productivity and Plot Size: Is Measurement Error Driving the Inverse Relationship? J. Dev. Econ. 2018, 130, 84–98. [Google Scholar] [CrossRef]
- Kim, T.; Ko, W.; Kim, J. Analysis and Impact Evaluation of Missing Data Imputation in Day-Ahead PV Generation Forecasting. Appl. Sci. 2019, 9, 204. [Google Scholar] [CrossRef]
- Piepho, H.P.; Möhring, J.; Williams, E.R. Why Randomize Agricultural Experiments? J. Agron. Crop Sci. 2013, 199, 374–383. [Google Scholar] [CrossRef]
- Fermont Volcafe, A.; Benson, T. Estimating Yield of Food Crops Grown by Smallholder Farmers: A Review in the Uganda Context Evolution of Farming Systems in Africa View Project; International Food Policy Research Institute: Washington, DC, USA, 2011. [Google Scholar]
- Hancock, G.R. The Impact of Different Gridding Methods on Catchment Geomorphology and Soil Erosion over Long Timescales Using a Landscape Evolution Model. Earth Surf. Process Landf. 2006, 31, 1035–1050. [Google Scholar] [CrossRef]
- Tziachris, P.; Metaxa, E.; Papadopoulos, F.; Papadopoulou, M. Spatial Modelling and Prediction Assessment of Soil Iron Using Kriging Interpolation with PH as Auxiliary Information. ISPRS Int. J. Geoinf. 2017, 6, 283. [Google Scholar] [CrossRef]
- Ismail, H.Y.; Fayyad, S.; Ahmad, M.N.; Leahy, J.J.; Naushad, M.; Walker, G.M.; Albadarin, A.B.; Kwapinski, W. Modelling of Yields in Torrefaction of Olive Stones Using Artificial Intelligence Coupled with Kriging Interpolation. J. Clean. Prod. 2021, 326, 129020. [Google Scholar] [CrossRef]
- Wiens, D.P.; Zhou, J. Robust Estimators and Designs for Field Experiments. J. Stat. Plan. Inference 2008, 138, 93–104. [Google Scholar] [CrossRef]
- Cho, J.B.; Guinness, J.; Kharel, T.P.; Sunoj, S.; Kharel, D.; Oware, E.K.; van Aardt, J.; Ketterings, Q.M. Spatial Estimation Methods for Mapping Corn Silage and Grain Yield Monitor Data. Precis. Agric. 2021, 22, 1501–1520. [Google Scholar] [CrossRef]
- Bowman, D.T. Crop Ecology, Production, & Management: Plot Configuration in Corn Yield Trials. Crop Sci. 1989, 29, 1202–1206. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Castrignanò, A.; Cucci, G.; Lacolla, G.; Lucà, F. Geostatistical Modelling of Within-Field Soil and Yield Variability for Management Zones Delineation: A Case Study in a Durum Wheat Field. Precis. Agric. 2017, 18, 37–58. [Google Scholar] [CrossRef]
- Maldaner, L.F.; Molin, J.P. Data Processing within Rows for Sugarcane Yield Mapping. Sci. Agric. 2020, 77, e20180391. [Google Scholar] [CrossRef]
- Betzek, N.M.; de Souza, E.G.; Bazzi, C.L.; Schenatto, K.; Gavioli, A.; Magalhães, P.S.G. Computational Routines for the Automatic Selection of the Best Parameters Used by Interpolation Methods to Create Thematic Maps. Comput. Electron. Agric. 2019, 157, 49–62. [Google Scholar] [CrossRef]
- McKinion, J.M.; Willers, J.L.; Jenkins, J.N. Spatial Analyses to Evaluate Multi-Crop Yield Stability for a Field. Comput. Electron. Agric. 2010, 70, 187–198. [Google Scholar] [CrossRef]
- Allakonon, M.G.B.; Zakari, S.; Tovihoudji, P.G.; Fatondji, A.S.; Akponikpè, P.B.I. Grain Yield, Actual Evapotranspiration and Water Productivity Responses of Maize Crop to Deficit Irrigation: A Global Meta-Analysis. Agric. Water Manag. 2022, 270, 107746. [Google Scholar] [CrossRef]
- Yan, P.; Lin, K.; Wang, Y.; Zheng, Y.; Gao, X.; Tu, X.; Bai, C. Spatial Interpolation of Red Bed Soil Moisture in Nanxiong Basin, South China. J. Contam. Hydrol. 2021, 242, 103860. [Google Scholar] [CrossRef]
- Řezník, T.; Pavelka, T.; Herman, L.; Leitgeb, Š.; Lukas, V.; Širůček, P. Deployment and Verifications of the Spatial Filtering of Data Measured by Field Harvesters and Methods of Their Interpolation: Czech Cereal Fields between 2014 and 2018. Sensors 2019, 19, 4879. [Google Scholar] [CrossRef] [PubMed]
- Koutsos, T.M.; Menexes, G.C.; Eleftherohorinos, I.G. The Use of Spatial Interpolation to Improve the Quality of Corn Silage Data in Case of Presence of Extreme or Missing Values. ISPRS Int. J. Geoinf. 2022, 11, 153. [Google Scholar] [CrossRef]
- Zimmerman, D.L.; Zimmerman, M.B. A Comparison of Spatial Semivariogram Estimators and Corresponding Ordinary Kriging Predictors. Technometrics 1991, 33, 77–91. [Google Scholar] [CrossRef]





| Plot | Data Used | n | Min | Max | Mean | CV (%) + | SD ++ | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | All harvested | 119 | 250 | 1337 | 649 | 36.9 | 239.5 | 57,351.3 | 0.5 | 0.0 |
| No margin | 75 | 315 | 1140 | 611 | 32.2 | 196.5 | 38,629.2 | 0.5 | −0.2 | |
| 2 | All harvested | 111 | 114 | 1352 | 598 | 41.6 | 248.7 | 61,830.4 | 0.5 | 0.1 |
| No margin | 72 | 114 | 1140 | 548 | 41.0 | 224.8 | 50,536.6 | 0.3 | 0.0 | |
| 3 | All harvested | 116 | 133 | 1352 | 730 | 35.6 | 259.8 | 67,495.7 | 0.0 | −0.1 |
| No margin | 75 | 183 | 1381 | 720 | 34.5 | 248.3 | 61,664.5 | 0.2 | 0.1 |
| Plot | Data Used | n | Min | Max | Mean * | CV (%) + | SD ++ | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | All harvested | 119 | 2.4 | 3.1 | 605 | 6.0 | 0.2 | 0.028 | −0.3 | −0.6 |
| No margin | 75 | 2.5 | 3.1 | 580 | 5.2 | 0.1 | 0.020 | −0.2 | −0.7 | |
| 2 | All harvested | 111 | 2.1 | 3.1 | 542 | 7.5 | 0.2 | 0.042 | −0.8 | 0.8 |
| No margin | 72 | 2.1 | 3.1 | 496 | 7.7 | 0.2 | 0.043 | −0.9 | 0.9 | |
| 3 | All harvested | 116 | 2.1 | 3.2 | 674 | 6.7 | 0.2 | 0.036 | −1.3 | 2.3 |
| No margin | 75 | 2.3 | 3.1 | 673 | 6.1 | 0.2 | 0.030 | −1.0 | 1.4 |
| Plot | Kriging Type | Data Used | n | Min | Max | Mean | CV (%) + | SD ++ | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Point Kriging | All harvested | 150 | 250 | 1337 | 646 | 33.4 | 215.5 | 46,447.5 | 0.6 | 0.6 |
| No margin | 92 | 315 | 1140 | 611 | 29.5 | 180.3 | 32,518.2 | 0.5 | 0.3 | ||
| 2 | Point Kriging | All harvested | 150 | 114 | 1352 | 600 | 35.8 | 214.6 | 46,047.3 | 0.5 | 1.1 |
| No margin | 92 | 114 | 1140 | 558 | 35.9 | 200.4 | 40,160.6 | 0.2 | 0.6 | ||
| 3 | Point Kriging | All harvested | 150 | 133 | 1423 | 728 | 31.4 | 228.8 | 52,332.0 | 0.1 | 0.8 |
| No margin | 92 | 183 | 1381 | 720 | 31.2 | 224.5 | 50,418.2 | 0.2 | 0.8 |
| Plot | Kriging Type | Data Used | n | Min | Max | Mean | CV (%) + | SD ++ | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Block Kriging | All harvested | 150 | 404 | 1033 | 646 | 19.9 | 128.3 | 16,468.4 | 0.5 | 0.4 |
| No margin | 92 | 404 | 948 | 621 | 18.0 | 112.0 | 12,545.9 | 0.3 | 0.2 | ||
| 2 | Block Kriging | All harvested | 150 | 323 | 950 | 600 | 18.1 | 108.6 | 11,799.2 | 0.4 | 0.7 |
| No margin | 92 | 323 | 849 | 571 | 17.3 | 99.0 | 9804.2 | 0.2 | 0.4 | ||
| 3 | Block Kriging | All harvested | 150 | 452 | 1036 | 728 | 14.5 | 105.3 | 11,085.3 | 0.1 | 0.4 |
| No margin | 92 | 495 | 1015 | 723 | 14.3 | 103.3 | 10,662.48 | 0.4 | 0.3 |
| Kriging Type | Plot | n | Variogram | Nugget | Sill | Range | R2 | RSS | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Point Kriging | 1 | 150 | Exponential | 0 | 53,470 | 0.96 | 0.99 | 9.5 × 10−12 | 2.5 × 10−7 |
| Block Kriging | 1 | 150 | Exponential | 0 | 53,510 | 0.97 | 0.93 | 14.5 × 105 | 98.5 |
| Point Kriging | 2 | 150 | Exponential | 0 | 60,600 | 0.70 | 0.99 | 6.3 × 10−12 | 2.04 × 10−7 |
| Block Kriging | 2 | 150 | Exponential | 0 | 60,270 | 0.72 | 0.94 | 1.9 × 105 | 113.5 |
| Point Kriging | 3 | 150 | Exponential | 0 | 68,000 | 0.53 | 0.99 | 8.2 × 10−12 | 2.34 × 10−7 |
| Block Kriging | 3 | 150 | Exponential | 0 | 68,000 | 0.62 | 0.96 | 24.7 × 105 | 128.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsos, T.M.; Menexes, G.C.; Eleftherohorinos, I.G.; Alexandridis, T.K. Using Block Kriging as a Spatial Smooth Interpolator to Address Missing Values and Reduce Variability in Maize Field Yield Data. Agronomy 2023, 13, 1685. https://doi.org/10.3390/agronomy13071685
Koutsos TM, Menexes GC, Eleftherohorinos IG, Alexandridis TK. Using Block Kriging as a Spatial Smooth Interpolator to Address Missing Values and Reduce Variability in Maize Field Yield Data. Agronomy. 2023; 13(7):1685. https://doi.org/10.3390/agronomy13071685
Chicago/Turabian StyleKoutsos, Thomas M., Georgios C. Menexes, Ilias G. Eleftherohorinos, and Thomas K. Alexandridis. 2023. "Using Block Kriging as a Spatial Smooth Interpolator to Address Missing Values and Reduce Variability in Maize Field Yield Data" Agronomy 13, no. 7: 1685. https://doi.org/10.3390/agronomy13071685
APA StyleKoutsos, T. M., Menexes, G. C., Eleftherohorinos, I. G., & Alexandridis, T. K. (2023). Using Block Kriging as a Spatial Smooth Interpolator to Address Missing Values and Reduce Variability in Maize Field Yield Data. Agronomy, 13(7), 1685. https://doi.org/10.3390/agronomy13071685







