Evaluation of the Potential of Using Machine Learning and the Savitzky–Golay Filter to Estimate the Daily Soil Temperature in Gully Regions of the Chinese Loess Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Analysis and Processing
2.3. Methods
2.3.1. Principles of RF
2.3.2. Principles of MLP
2.3.3. Principles of LSTM
2.3.4. Schematic Workflow of Deep Soil Temperature Prediction
2.3.5. Evaluation Metrics
3. Results
3.1. Input Combination of Shallow Soil Temperature
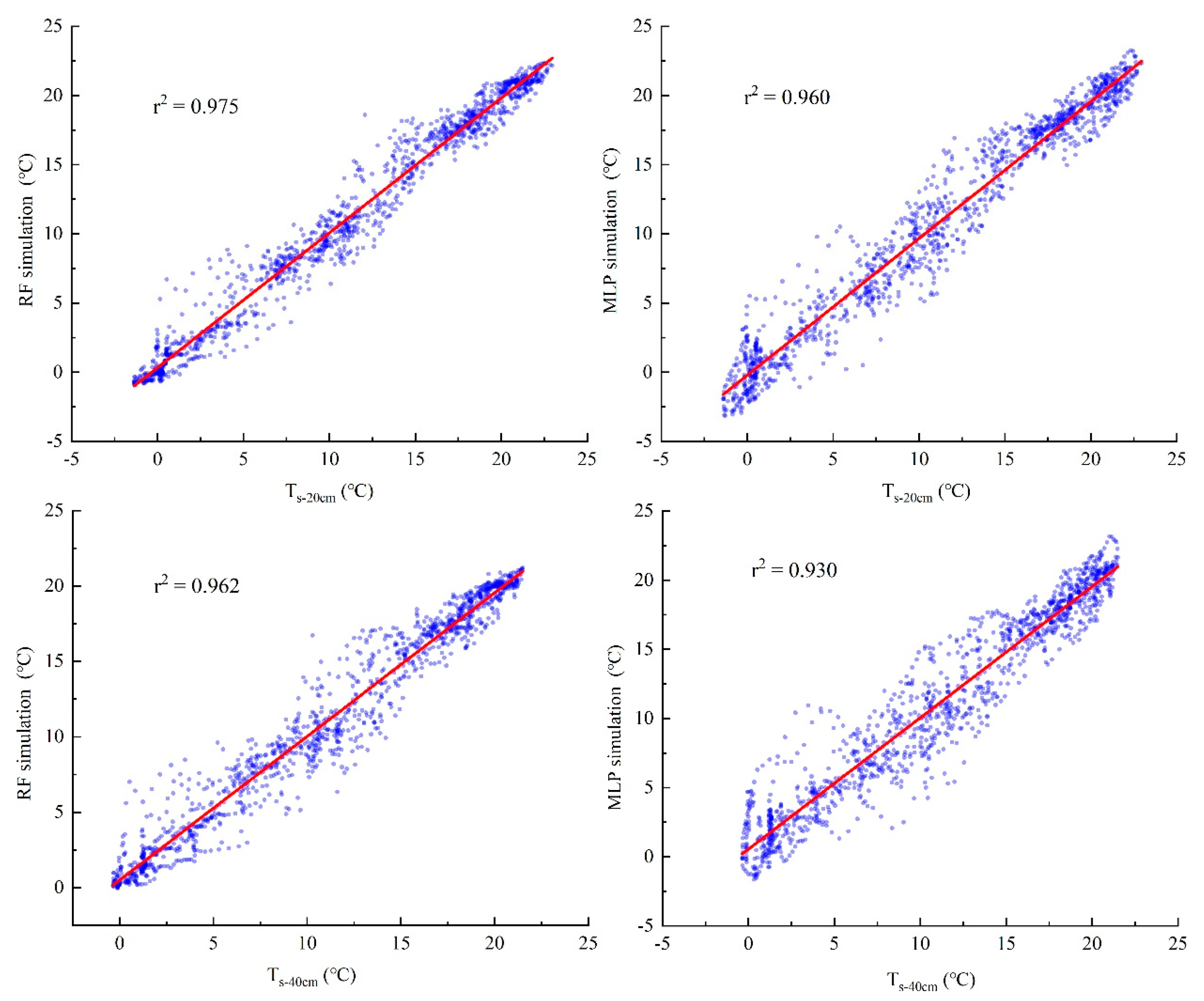
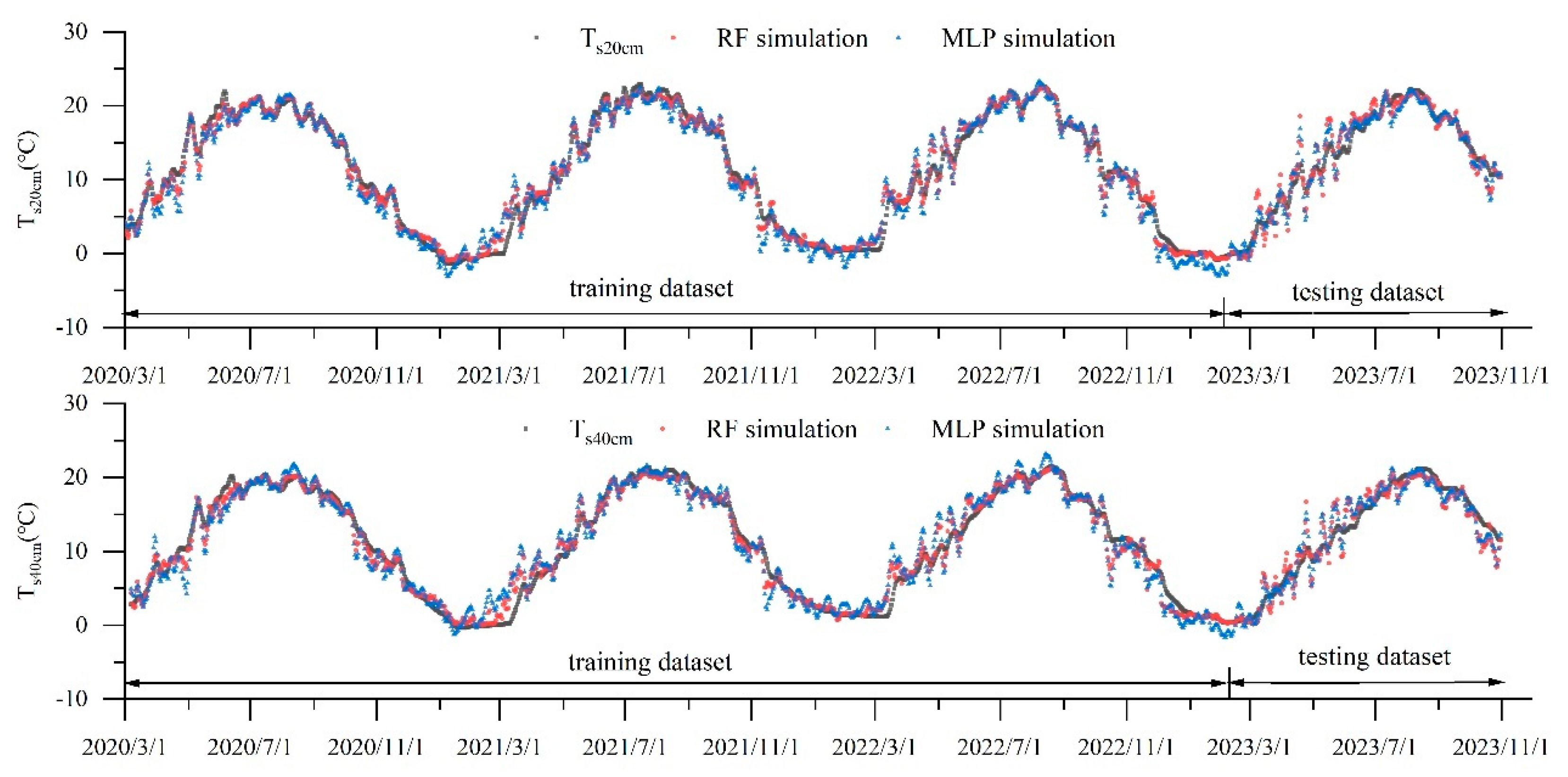
3.2. Evaluation of the Results of Different Combinations of Input
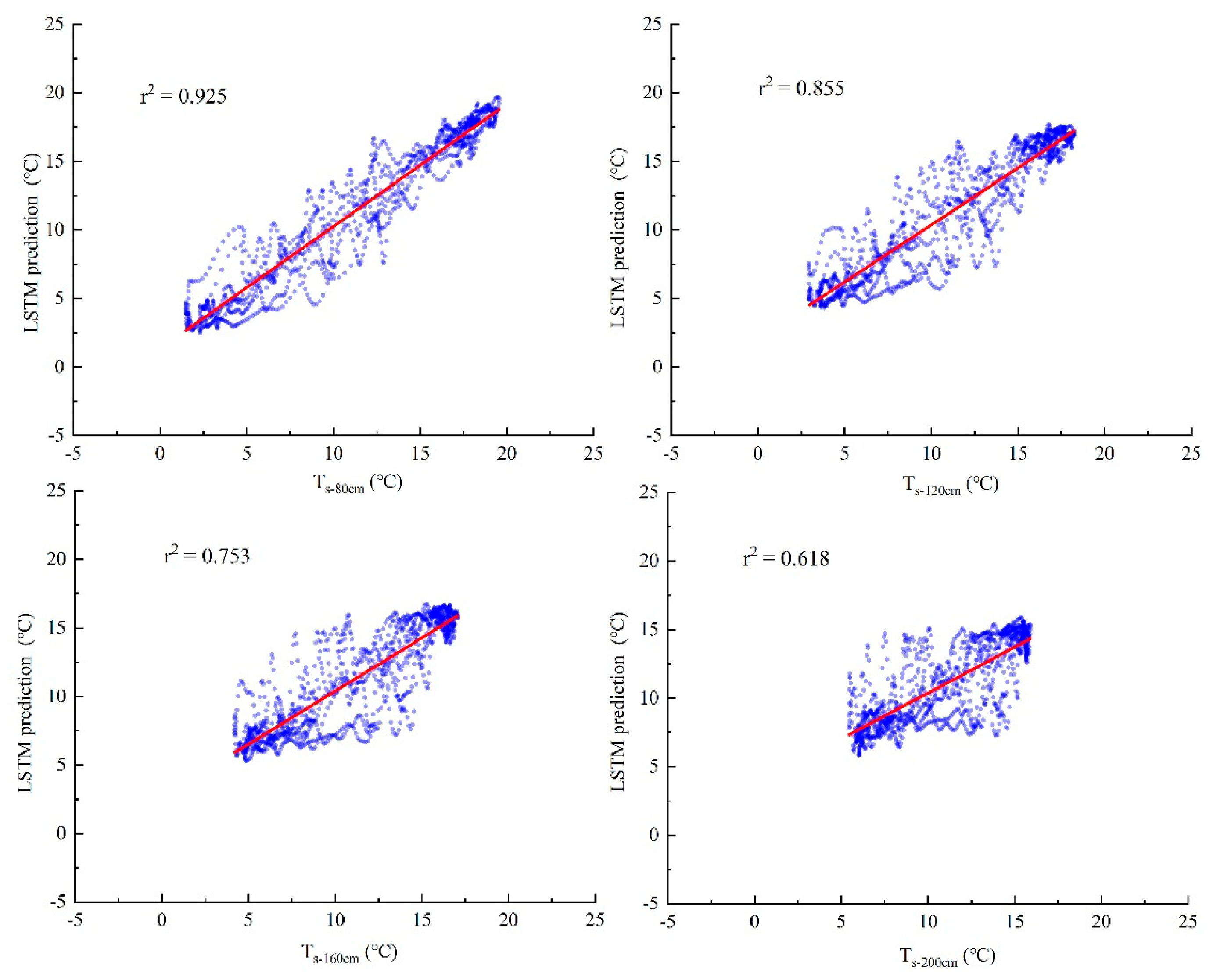
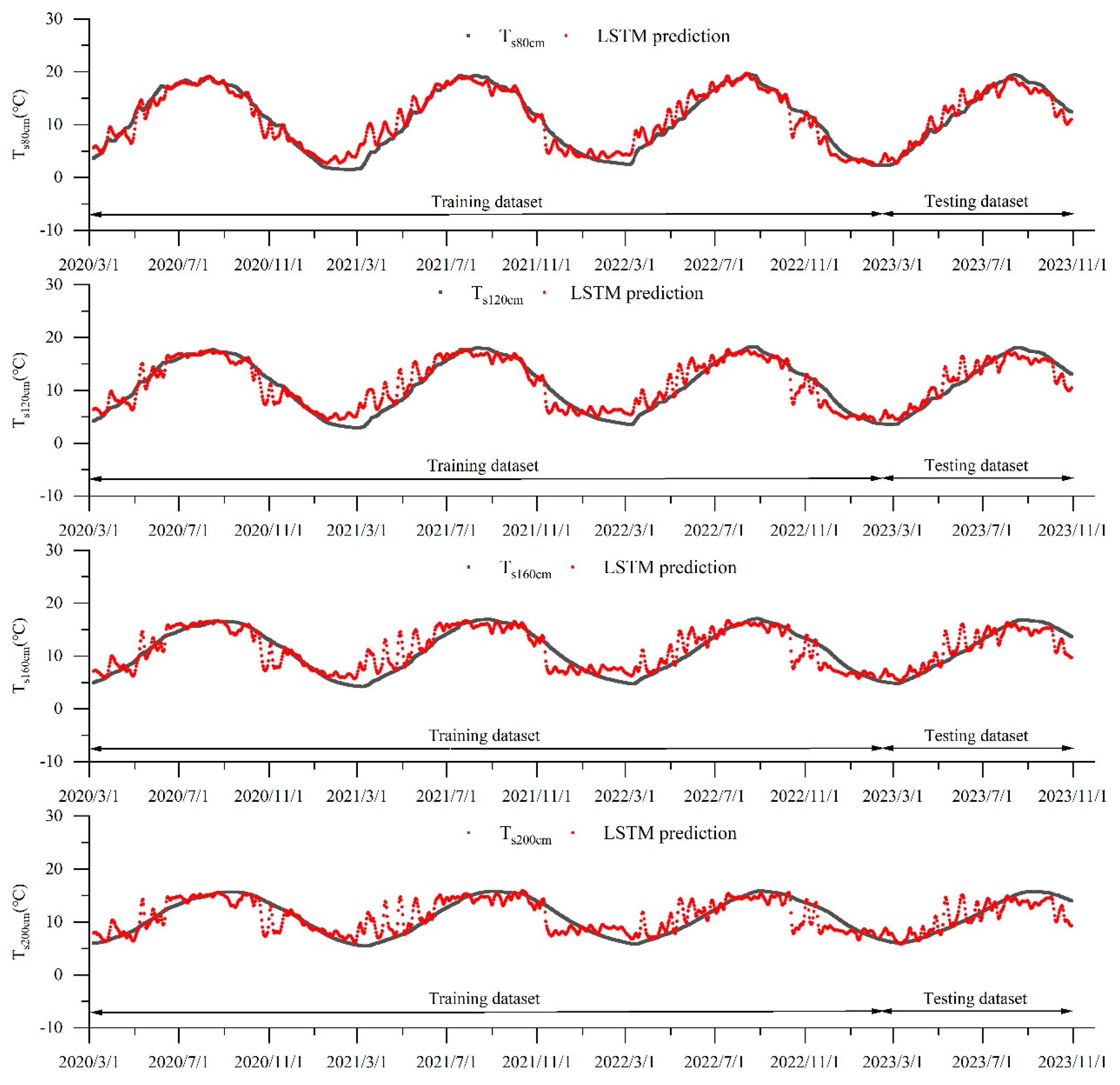
3.3. Evaluating the Performance of LSTM Prediction of Deep Soil Temperature
3.4. Impact of Sliding Panes on Prediction Accuracy
3.5. Effect of Savitzky–Golay Filter on Prediction Accuracy
4. Discussion
5. Conclusions
- (1)
- For different combinations of input variables, the inclusion of relevant environmental factors can improve the model’s performance. When the daily temperature of the air is at a height of 2 m (Tair), daily water vapor pressure data (Pw), net radiation (Rn), and soil moisture data (VWC20cm) were jointly used as inputs for all the simulations at 20 cm and 40 cm depths, the results of RF and MLP were the best. Both RF and MLP can simulate shallow soil temperature well, but the performance of MLP is better than that of RF.
- (2)
- It is feasible to use LSTM to predict the deep soil temperature with the simulated shallow soil temperature and the measured air temperature as input.
- (3)
- The accuracy of soil temperature prediction is different at different depths. With the increase in soil depth, the accuracy of soil temperature prediction decreases. The simulation accuracy of shallow soil temperature directly affects the prediction accuracy of deep soil temperature. In addition, the size of the sliding pane of the LSTM model also affects the prediction accuracy.
- (4)
- The SG filter is more suitable for data preprocessing, and its ability to post-process prediction results is very limited.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Veldhuizen, L.J.; Giller, K.E.; Oosterveer, P.; Brouwer, I.D.; Janssen, S.; van Zanten, H.H.; Slingerland, M.A. The Missing Middle: Connected action on agriculture and nutrition across global, national and local levels to achieve Sustainable Development Goal 2. Glob. Food Secur. 2020, 24, 100336. [Google Scholar] [CrossRef]
- Linghu, L.; Sun, P.; Zhang, M.; Wu, Y. Data-Driven Projections Demonstrate Non-Farming Use of Cropland in Non-Major Grain-Producing Areas: A Case Study of Shaanxi Province, China. Agronomy 2023, 13, 2060. [Google Scholar] [CrossRef]
- Furtak, K.; Gawryjołek, K.; Marzec-Grządziel, A.; Niedźwiecki, J. The Influence of Human Agricultural Activities on the Quality of Selected Fluvisols from the Vistula River Valley, Poland—Preliminary Research. Agronomy 2024, 14, 480. [Google Scholar] [CrossRef]
- Zeynoddin, M.; Ebtehaj, I.; Bonakdari, H. Development of a linear based stochastic model for daily soil temperature prediction: One step forward to sustainable agriculture. Comput. Electron. Agric. 2020, 176, 105636. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Flerchinger, G.N.; Murdock, M.D.; Hanson, C.L.; Van Vactor, S. Long-Term Soil Temperature Database, Reynolds Creek Experimental Watershed, Idaho, United States. Water Resour. Res. 2001, 37, 2843–2846. [Google Scholar] [CrossRef]
- Kramer, P.J. Effects of Soil Temperature on the Absorption of Water by Plants. Science 1934, 79, 371–372. [Google Scholar] [CrossRef] [PubMed]
- Alizamir, M.; Kisi, O.; Ahmed, A.N.; Mert, C.; Fai, C.M.; Kim, S.; Kim, N.W.; El-Shafie, A.; Lin, L. Advanced machine learning model for better prediction accuracy of soil temperature at different depths. PLoS ONE 2020, 15, e231055. [Google Scholar] [CrossRef] [PubMed]
- Ganeshi, N.G.; Mujumdar, M.; Takaya, Y.; Goswami, M.M.; Singh, B.B.; Krishnan, R.; Terao, T. Soil moisture revamps the temperature extremes in a warming climate over India. npj Clim. Atmos. Sci. 2023, 6, 12. [Google Scholar] [CrossRef]
- Onwuka, B.; Mang, B. Effects of soil temperature on some soil properties and plant growth. Adv. Plants Agric. Res. 2018, 8, 34–37. [Google Scholar] [CrossRef]
- Yin, X.; Arp, P.A. Predicting forest soil temperatures from monthly air temperature and precipitation records. Can. J. Forest Res. 1993, 23, 2521–2536. [Google Scholar] [CrossRef]
- Zhao, H.; Sassenrath, G.F.; Kirkham, M.B.; Wan, N.; Lin, X. Daily soil temperature modeling improved by integrating observed snow cover and estimated soil moisture in the USA Great Plains. Hydrol. Earth Syst. Sci. 2021, 25, 4357–4372. [Google Scholar] [CrossRef]
- Mihalakakou, G. On estimating soil surface temperature profiles. Energy Build. 2002, 34, 251–259. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Li, Q.; Xing, Z.; Bourque, P.A.; Meng, F.R. A new soil-temperature module for SWAT application in regions with seasonal snow cover. J. Hydrol. 2016, 538, 863–877. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A.B. Machine learning and soil sciences: A review aided by machine learning tools. Soil 2020, 6, 35–52. [Google Scholar] [CrossRef]
- Recknagel, F.; French, M.; Harkonen, P.; Yabunaka, K. Artificial neural network approach for modelling and prediction of algal blooms. Ecol. Model. 1997, 96, 11–28. [Google Scholar] [CrossRef]
- Lin, X.; Duan, X.; Jacobs, C.; Ullmann, J.; Chan, C.; Chen, S.; Cheng, S.; Zhao, W.; Poduri, A.; Wang, X.; et al. High-throughput brain activity mapping and machine learning as a foundation for systems neuropharmacology. Nat. Commun. 2018, 9, 5142. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, C.; Rouet-Leduc, B.; Johnson, P.A.; Ren, C.X.; Rivière, J.; Bolton, D.C.; Marone, C. Similarity of fast and slow earthquakes illuminated by machine learning. Nat. Geosci. 2019, 12, 69–74. [Google Scholar] [CrossRef]
- Fang, K.; Kifer, D.; Lawson, K.; Shen, C. Evaluating the potential and challenges of an uncertainty quantification method for long short-term memory models for soil moisture predictions. Water Resour. Res. 2020, 56, e2020WR028095. [Google Scholar] [CrossRef]
- Cui, Q.; Ammar, M.E.; Iravani, M.; Kariyeva, J.; Faramarzi, M. Regional wetland water storage changes: The influence of future climate on geographically isolated wetlands. Ecol. Indic. 2021, 120, 106941. [Google Scholar] [CrossRef]
- Zhong, L.; Lei, H.; Gao, B. Developing a Physics-Informed Deep Learning Model to Simulate Runoff Response to Climate Change in Alpine Catchments. Water Resour. Res. 2023, 59, e2022WR034118. [Google Scholar] [CrossRef]
- Nabavi-Pelesaraei, A.; Shaker-Koohi, S.; Dehpour, M.B. Modeling and optimization of energy inputs and greenhouse gas emissions for eggplant production using artificial neural network and multi-objective genetic algorithm. Int. J. Adv. Biol. Biomed. Res. 2013, 4, 170–183. [Google Scholar]
- Sándor, R.; Barcza, Z.; Acutis, M.; Doro, L.; Hidy, D.; Chy, M.K.; Minet, J.; Lellei-Kovács, E.; Ma, S.; Perego, A. Multi-model simulation of soil temperature, soil water content and biomass in Euro-Mediterranean grasslands: Uncertainties and ensemble performance. Eur. J. Agron. 2017, 88, 22–40. [Google Scholar] [CrossRef]
- Samadianfard, S.; Ghorbani, M.A.; Mohammadi, B. Forecasting soil temperature at multiple-depth with a hybrid artificial neural network model coupled-hybrid firefly optimizer algorithm. Inf. Process. Agric. 2018, 5, 465–476. [Google Scholar] [CrossRef]
- Li, Q.; Hao, H.; Zhao, Y.; Geng, Q.; Liu, G.; Zhang, Y.; Yu, F. GANs-LSTM Model for Soil Temperature Estimation from Meteorological: A New Approach. IEEE Access 2020, 8, 59427–59443. [Google Scholar] [CrossRef]
- Nahvi, B.; Habibi, J.; Mohammadi, K.; Shamshirband, S.; Al Razgan, O.S. Using self-adaptive evolutionary algorithm to improve the performance of an extreme learning machine for estimating soil temperature. Comput. Electron. Agric. 2016, 124, 150–160. [Google Scholar] [CrossRef]
- Bayatvarkeshi, M.; Bhagat, S.K.; Mohammadi, K.; Kisi, O.; Farahani, M.; Hasani, A.; Deo, R.; Yaseen, Z.M. Modeling soil temperature using air temperature features in diverse climatic conditions with complementary machine learning models. Comput. Electron. Agric. 2021, 185, 106158. [Google Scholar] [CrossRef]
- Tsai, Y.Z.; Hsu, K.S.; Wu, H.Y.; Lin, S.I.; Yu, H.L.; Huang, K.T.; Hu, M.C.; Hsu, S.Y. Application of random forest and ICON models combined with weather forecasts to predict soil temperature and water content in a greenhouse. Water 2020, 12, 1176. [Google Scholar] [CrossRef]
- Recknagel, F. Applications of machine learning to ecological modelling. Ecol. Model. 2001, 146, 303–310. [Google Scholar] [CrossRef]
- Massoud, E.C.; Hoffman, F.; Shi, Z.; Tang, J.; Alhajjar, E.; Barnes, M.; Braghiere, R.K.; Cardon, Z.; Collier, N.; Crompton, O.; et al. Perspectives on Artificial Intelligence for Predictions in Ecohydrology. Artif. Intell. Earth Syst. 2023, 2, e230005. [Google Scholar] [CrossRef]
- Chan, W.S.; Recknagel, F.; Cao, H.; Park, H. Elucidation and short-term forecasting of microcystin concentrations in Lake Suwa (Japan) by means of artificial neural networks and evolutionary algorithms. Water Res. 2007, 41, 2247–2255. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Ren, X. Modeling Hourly Soil Temperature Using Deep BiLSTM Neural Network. Algorithms 2020, 13, 173. [Google Scholar] [CrossRef]
- Tsai, W.P.; Feng, D.; Pan, M.; Beck, H.; Lawson, K.; Yang, Y.; Liu, J.; Shen, C. From calibration to parameter learning: Harnessing the scaling effects of big data in geoscientific modeling. Nat. Commun. 2020, 12, 5988. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Wang, X.; Liang, B. Forecasting greenhouse air and soil temperatures: A multi-step time series approach employing attention-based LSTM network. Comput. Electron. Agric. 2024, 217, 108602. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Barzegar, R.; Aalami, M.T.; Heddam, S.; Omidvar, E.; Keesstra, S.D.; López-Vicente, M. Multi-step ahead soil temperature forecasting at different depths based on meteorological data: Integrating resampling algorithms and machine learning models. Pedosphere 2023, 33, 479–495. [Google Scholar] [CrossRef]
- Taki, M.; Abdanan Mehdizadeh, S.; Rohani, A.; Rahnama, M.; Rahmati-Joneidabad, M. Applied machine learning in greenhouse simulation; new application and analysis. Inf. Process. Agric. 2018, 5, 253–268. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, D.; Liu, H.; Lei, H.; Guo, F.; Xie, S.; Meng, X.; Huang, Q. Energy flux observation in a shrub ecosystem of a gully region of the Chinese Loess Plateau. Ecohydrol. Hydrobiol. 2022, 22, 323–336. [Google Scholar] [CrossRef]
- Guo, F.; Liu, D.; Mo, S.; Huang, Q.; Ma, L.; Xie, S.; Deng, W.; Ming, G.; Fan, J. Estimation of daily evapotranspiration in gully area scrub ecosystems on Loess Plateau of China based on multisource observation data. Ecol. Indic. 2023, 154, 110671. [Google Scholar] [CrossRef]
- Trok, J.T.; Davenport, F.V.; Barnes, E.A.; Diffenbaugh, N.S. Using Machine Learning with Partial Dependence Analysis to Investigate Coupling Between Soil Moisture and Near-Surface Temperature. J. Geophys. Res. Atmos. 2023, 128, e2022JD038365. [Google Scholar] [CrossRef]
- Sahoo, M. Winter soil temperature and its effect on soil nitrate Status: A Support Vector Regression-based approach on the projected impacts. Catena 2022, 211, 105958. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Isles, P.D.F. A random forest approach to improve estimates of tributary nutrient loading. Water Res. 2024, 248, 120876. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2017, 40, 2681–2693. [Google Scholar] [CrossRef]
- Mohanty, M.D.; Mohanty, M.N. Chapter 5—Verbal sentiment analysis and detection using recurrent neural network. In Advanced Data Mining Tools and Methods for Social Computing; De, S., Dey, S., Bhattacharyya, S., Bhatia, S., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 85–106. [Google Scholar]
- Abirami, S.; Chitra, P. Chapter Fourteen—Energy-efficient edge based real-time healthcare support system. In Advances in Computers; Raj, P., Evangeline, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 117, pp. 339–368. [Google Scholar]
- Abinaya, S.; Devi, M.K.K. Chapter 12—Enhancing crop productivity through autoencoder-based disease detection and context-aware remedy recommendation system. In Application of Machine Learning in Agriculture; Khan, M.A., Khan, R., Ansari, M.A., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 239–262. [Google Scholar]
- Rahmani, F.; Shen, C.; Oliver, S.; Lawson, K.; Appling, A. Deep learning approaches for improving prediction of daily stream temperature in data-scarce, unmonitored, and dammed basins. Hydrol. Process. 2021, 35, e14400. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Q.; Wu, Y.; Chen, M.; Yin, H.; Zhao, J. Edible Mushroom Greenhouse Environment Prediction Model Based on Attention CNN-LSTM. Agronomy 2024, 14, 473. [Google Scholar] [CrossRef]
- Di, Y.; Gao, M.; Feng, F.; Li, Q.; Zhang, H. A New Framework for Winter Wheat Yield Prediction Integrating Deep Learning and Bayesian Optimization. Agronomy 2022, 12, 3194. [Google Scholar] [CrossRef]
- Bai, Y.; Scott, T.A.; Min, Q. Climate change implications of soil temperature in the Mojave Desert, USA. Front. Earth Sci. 2014, 8, 302–308. [Google Scholar] [CrossRef]
- Miralles, D.G.; Van, D.B.M.J.; Teuling, A.J.; De Jeu, R.A.M. Soil moisture-temperature coupling: A multiscale observational analysis. Geophys. Res. Lett. 2012, 39, 6. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, J.; Lei, Q.; Liang, X.; Lindsey, S.; Luo, J.; Zhu, A.; Bao, W.; Liu, H. Empirical estimation of soil temperature and its controlling factors in Australia: Implication for interaction between geographic setting and air temperature. Catena 2022, 208, 105696. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, P.; Lu, Y.; Ma, M.; Dong, G.; Tang, J. Convection-permitting regional climate simulation on soil moisture-heatwaves relationship over eastern China. Atmos. Res. 2024, 301, 107285. [Google Scholar] [CrossRef]
- Amato, M.T.; Giménez, D. Predicting monthly near-surface soil temperature from air temperature and the leaf area index. Agric. Forest Meteorol. 2024, 345, 109838. [Google Scholar] [CrossRef]
- Citakoglu, H. Comparison of artificial intelligence techniques for prediction of soil temperatures in Turkey. Theor. Appl. Climatol. 2017, 130, 545–556. [Google Scholar] [CrossRef]
- Gao, S.; Wu, Q.; Zhang, Z.; Jiang, G. Simulating active layer temperature based on weather factors on the Qinghai–Tibetan Plateau using ANN and wavelet-ANN models. Cold Reg. Sci. Technol. 2020, 177, 103118. [Google Scholar] [CrossRef]
- Gao, B.; Coon, E.T.; Thornton, P.E.; Lu, D. Improving the estimation of atmospheric water vapor pressure using interpretable long short-term memory networks. Agric. Forest Meteorol. 2024, 347, 109907. [Google Scholar] [CrossRef]
- Bonachela, S.; Fernández, M.D.; Hernández, J.; López, J.C. Adaptation of standardised (FAO and ASCE) procedures of estimating net longwave and shortwave radiation to Mediterranean greenhouse crops. Biosyst. Eng. 2023, 231, 104–116. [Google Scholar] [CrossRef]
- He, Z.; Wang, J.; Jiang, M.; Hu, L.; Zou, Q. Random Subsequence Forests. Inf. Sci. 2024, 667, 120478. [Google Scholar] [CrossRef]
- Jiao, Y.; Chen, C.; Li, G.; Fu, H.; Mi, X. Research on the variation patterns and predictive models of soil temperature in a solar greenhouse. Sol. Energy 2024, 270, 112267. [Google Scholar] [CrossRef]

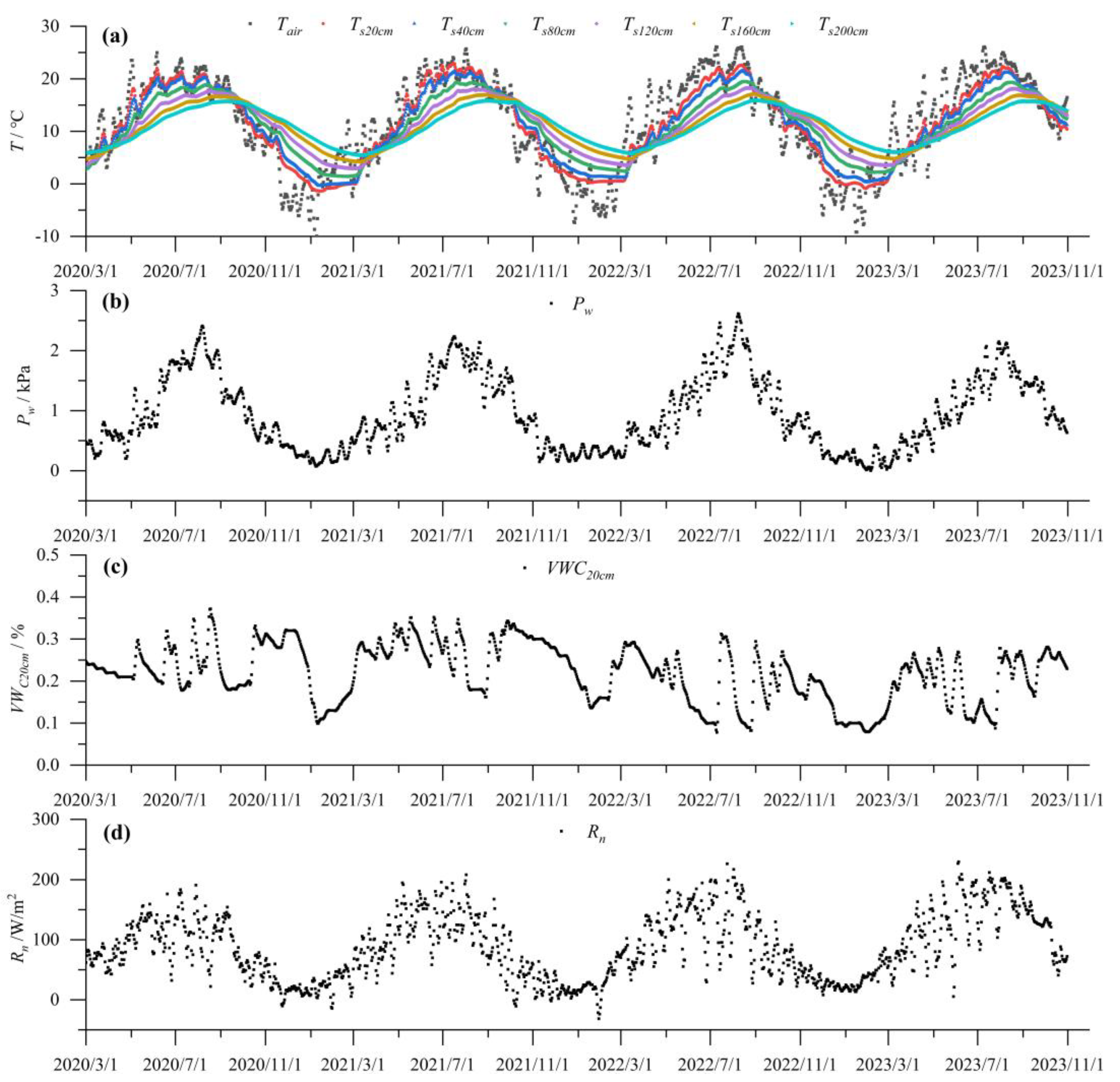
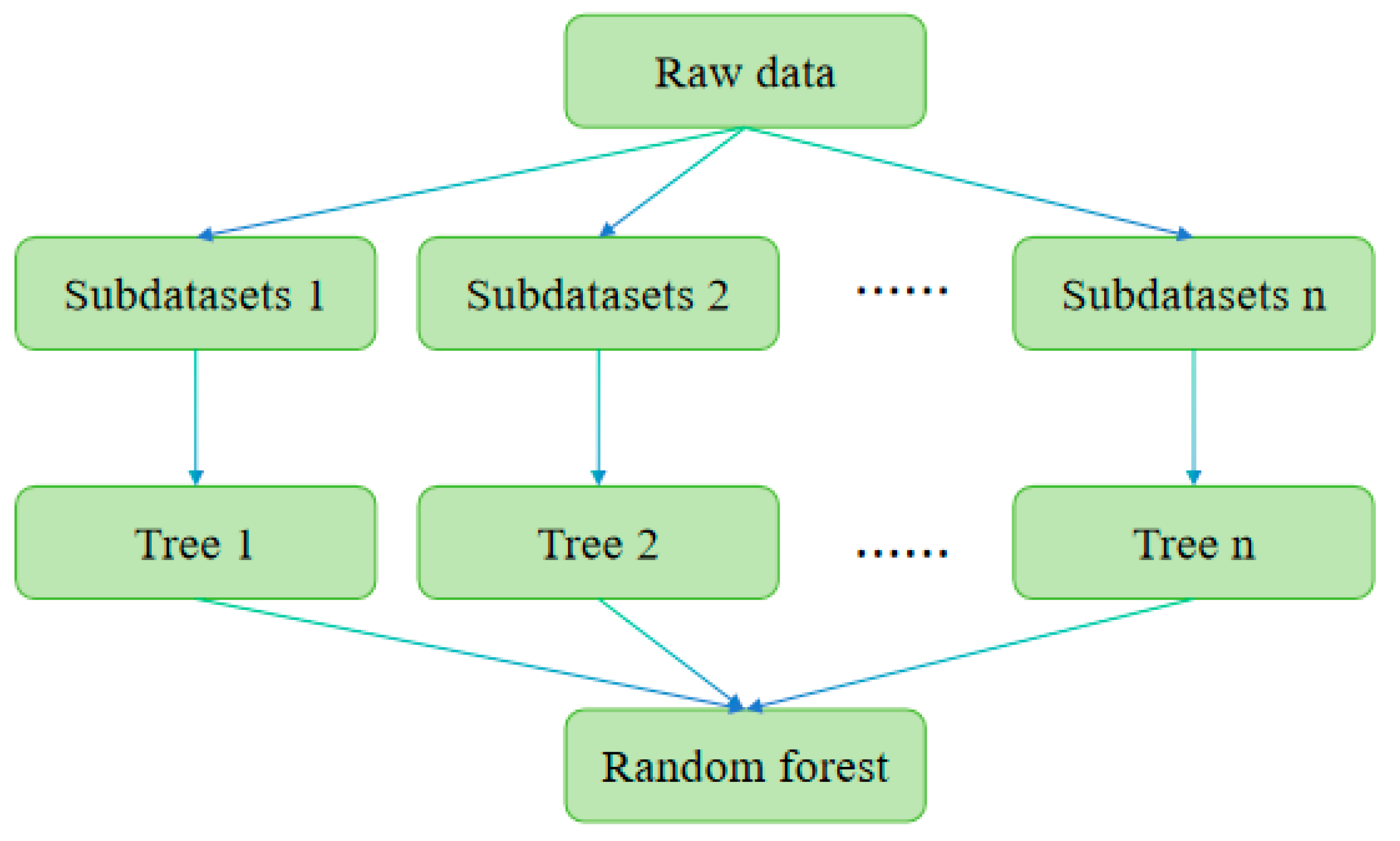
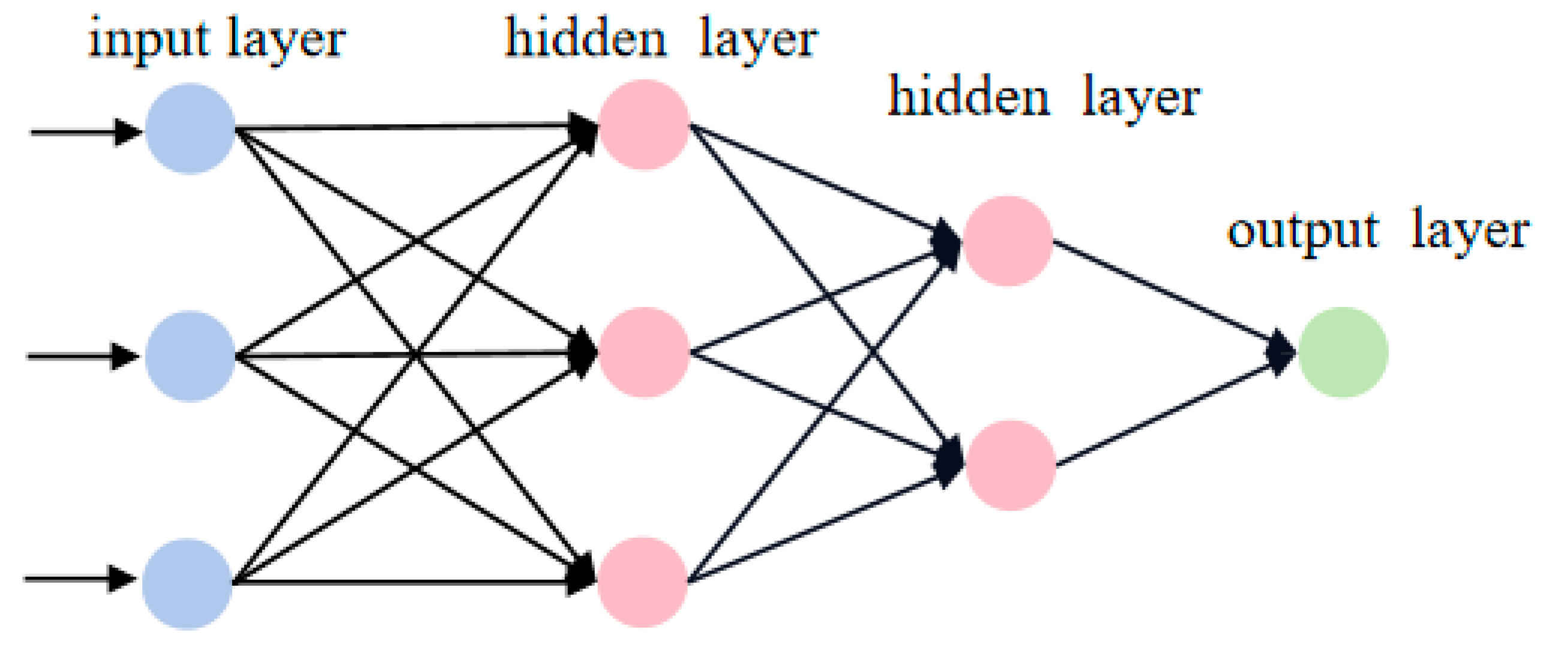

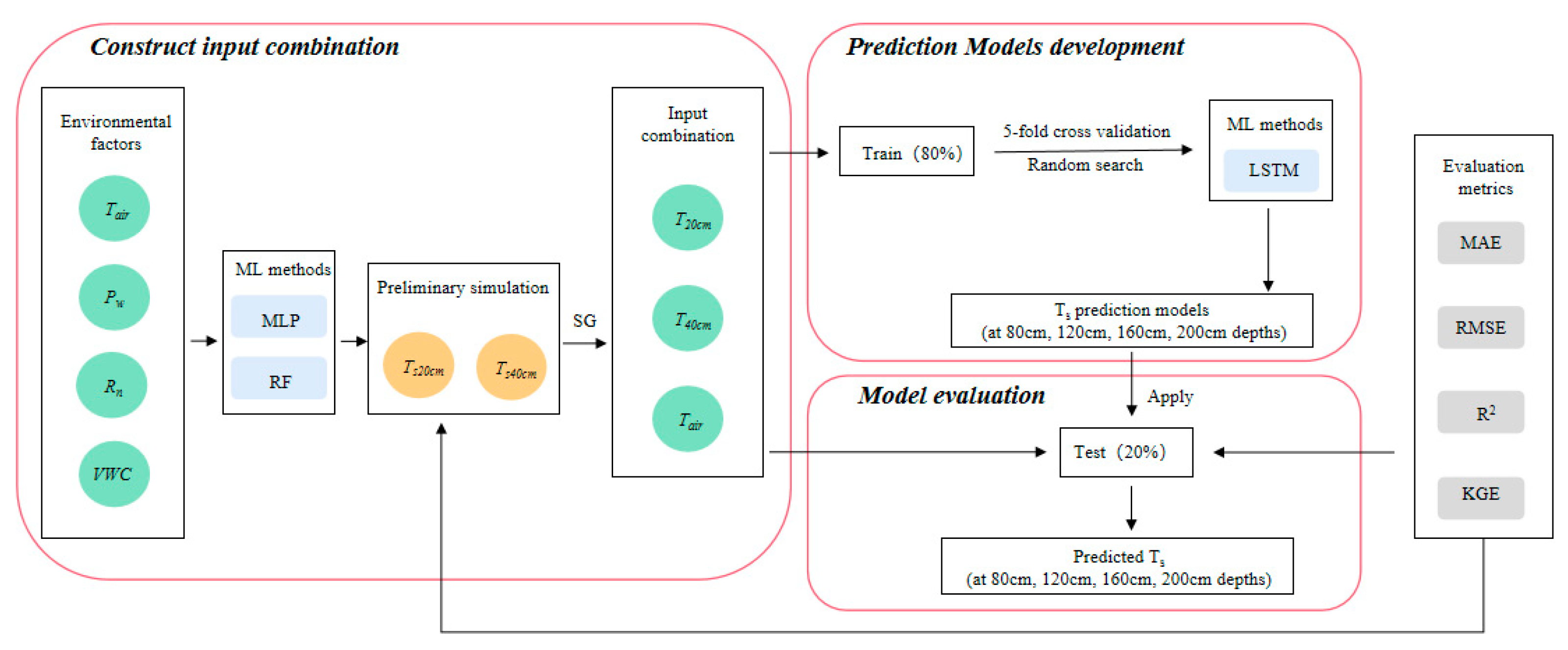
| Statistics | Ts20cm | Ts40cm | Ts80cm | Ts120cm | Ts160cm | Ts200cm |
|---|---|---|---|---|---|---|
| Tair | 0.92 | 0.89 | 0.81 | 0.73 | 0.63 | 0.48 |
| Pw | 0.91 | 0.91 | 0.89 | 0.84 | 0.77 | 0.66 |
| VWC20cm | 0.14 | 0.16 | 0.17 | 0.18 | 0.18 | 0.16 |
| Rn | 0.74 | 0.69 | 0.60 | 0.50 | 0.38 | 0.24 |
| Ts20cm | 1.00 | 0.99 | 0.95 | 0.89 | 0.79 | 0.66 |
| Ts40cm | 0.99 | 1.00 | 0.98 | 0.93 | 0.85 | 0.74 |
| Ts80cm | 0.95 | 0.98 | 1.00 | 0.99 | 0.94 | 0.85 |
| Ts120cm | 0.89 | 0.93 | 0.99 | 1.00 | 0.98 | 0.93 |
| Ts160cm | 0.79 | 0.85 | 0.94 | 0.98 | 1.00 | 0.98 |
| Ts200cm | 0.66 | 0.74 | 0.85 | 0.93 | 0.98 | 1.00 |
| Data | xmean | xmax | xmin | xstd | Cv | CS | Ck |
|---|---|---|---|---|---|---|---|
| Tair (°C) | 11.66 | 26.07 | −11.44 | 8.64 | 0.74 | −0.37 | −0.90 |
| Pw (kPa) | 0.95 | 2.62 | 0.00 | 0.62 | 0.65 | 0.50 | −0.83 |
| Rn (W/m2) | 87.68 | 229.85 | −31.50 | 54.80 | 0.63 | 0.30 | −0.89 |
| VWC20cm (%) | 0.22 | 0.37 | 0.08 | 0.07 | 0.31 | −0.26 | −0.84 |
| Ts20cm (°C) | 11.27 | 22.96 | −1.38 | 7.56 | 0.67 | −0.17 | −1.34 |
| Ts40cm (°C) | 11.23 | 21.50 | −0.36 | 6.93 | 0.62 | −0.18 | −1.36 |
| Ts80cm (°C) | 11.14 | 19.56 | 1.49 | 5.80 | 0.52 | −0.16 | −1.40 |
| Ts120cm (°C) | 11.09 | 18.24 | 2.95 | 4.96 | 0.45 | −0.14 | −1.43 |
| Ts160cm (°C) | 11.10 | 17.09 | 4.21 | 4.18 | 0.38 | −0.11 | −1.46 |
| Ts200cm (°C) | 11.04 | 15.90 | 5.45 | 3.46 | 0.31 | −0.07 | −1.48 |
| Combination No. | Input Variables |
|---|---|
| 1 | Tair |
| 2 | Tair-Pw |
| 3 | Tair-Pw-Rn |
| 4 | Tair-Pw-Rn-VWC20cm |
| Model | Depths | Input | Training Dataset | Testing Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | KGE | MAE (°C) | RMSE (°C) | R2 | KGE | |||
| RF | 20 cm | 1 | 1.924 | 2.565 | 0.889 | 0.918 | 2.125 | 2.924 | 0.804 | 0.867 |
| 2 | 1.266 | 1.693 | 0.952 | 0.947 | 1.309 | 1.725 | 0.932 | 0.958 | ||
| 3 | 1.109 | 1.484 | 0.963 | 0.952 | 1.173 | 1.497 | 0.949 | 0.925 | ||
| 4 | 0.771 | 1.088 | 0.980 | 0.972 | 1.161 | 1.538 | 0.946 | 0.963 | ||
| 40 cm | 1 | 2.131 | 2.823 | 0.839 | 0.877 | 2.415 | 3.151 | 0.750 | 0.804 | |
| 2 | 1.437 | 1.935 | 0.924 | 0.927 | 1.491 | 1.879 | 0.911 | 0.915 | ||
| 3 | 1.280 | 1.719 | 0.940 | 0.929 | 1.434 | 1.782 | 0.920 | 0.892 | ||
| 4 | 0.857 | 1.236 | 0.969 | 0.962 | 1.379 | 1.769 | 0.921 | 0.958 | ||
| MLP | 20 cm | 1 | 2.111 | 2.731 | 0.874 | 0.916 | 2.104 | 2.783 | 0.823 | 0.876 |
| 2 | 1.339 | 1.796 | 0.946 | 0.967 | 1.203 | 1.551 | 0.945 | 0.955 | ||
| 3 | 1.319 | 1.778 | 0.947 | 0.938 | 1.118 | 1.436 | 0.953 | 0.958 | ||
| 4 | 1.241 | 1.614 | 0.956 | 0.935 | 1.041 | 1.404 | 0.955 | 0.973 | ||
| 40 cm | 1 | 2.323 | 3.032 | 0.814 | 0.896 | 2.375 | 3.113 | 0.756 | 0.834 | |
| 2 | 1.523 | 2.064 | 0.914 | 0.880 | 1.389 | 1.803 | 0.918 | 0.891 | ||
| 3 | 1.476 | 1.997 | 0.919 | 0.952 | 1.296 | 1.652 | 0.931 | 0.959 | ||
| 4 | 1.384 | 1.879 | 0.929 | 0.960 | 1.278 | 1.639 | 0.932 | 0.966 | ||
| Depths | Training Dataset | Testing Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | KGE | MAE (°C) | RMSE (°C) | R2 | KGE | |
| 80 cm | 1.192 | 1.637 | 0.921 | 0.910 | 1.158 | 1.449 | 0.928 | 0.885 |
| 120 cm | 1.418 | 1.913 | 0.848 | 0.869 | 1.436 | 1.773 | 0.868 | 0.815 |
| 160 cm | 1.538 | 2.098 | 0.741 | 0.827 | 1.554 | 1.971 | 0.787 | 0.775 |
| 200 cm | 1.561 | 2.155 | 0.600 | 0.740 | 1.610 | 2.088 | 0.665 | 0.708 |
| Depths | Training Dataset | Testing Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | KGE | MAE (°C) | RMSE (°C) | R2 | KGE | |
| 80 cm | 1.144 | 1.619 | 0.923 | 0.901 | 1.249 | 1.647 | 0.908 | 0.949 |
| 120 cm | 1.146 | 1.663 | 0.886 | 0.927 | 1.586 | 2.042 | 0.825 | 0.888 |
| 160 cm | 1.243 | 1.769 | 0.816 | 0.869 | 1.786 | 2.330 | 0.703 | 0.779 |
| 200 cm | 1.158 | 1.763 | 0.732 | 0.821 | 1.666 | 2.339 | 0.579 | 0.741 |
| Models | Different Size of the Sliding Pane |
|---|---|
| LSTM3 | 3 |
| LSTM7 | 7 |
| LSTM10 | 10 |
| LSTM14 | 14 |
| LSTM21 | 21 |
| Model | Depths | Training Dataset | Testing Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | KGE | MAE (°C) | RMSE (°C) | R2 | KGE | ||
| LSTM3 | 80 cm | 1.383 | 1.900 | 0.894 | 0.923 | 1.371 | 1.732 | 0.901 | 0.881 |
| 120 cm | 1.589 | 2.173 | 0.805 | 0.866 | 1.599 | 2.013 | 0.835 | 0.808 | |
| 160 cm | 1.711 | 2.327 | 0.683 | 0.808 | 1.740 | 2.203 | 0.738 | 0.751 | |
| 200 cm | 1.768 | 2.314 | 0.541 | 0.697 | 1.842 | 2.292 | 0.598 | 0.653 | |
| LSTM7 | 80 cm | 1.192 | 1.637 | 0.921 | 0.910 | 1.158 | 1.449 | 0.928 | 0.885 |
| 120 cm | 1.418 | 1.913 | 0.848 | 0.869 | 1.436 | 1.773 | 0.868 | 0.815 | |
| 160 cm | 1.538 | 2.098 | 0.741 | 0.827 | 1.554 | 1.971 | 0.787 | 0.775 | |
| 200 cm | 1.561 | 2.155 | 0.600 | 0.740 | 1.610 | 2.088 | 0.665 | 0.708 | |
| LSTM10 | 80 cm | 1.040 | 1.448 | 0.938 | 0.951 | 0.926 | 1.215 | 0.948 | 0.935 |
| 120 cm | 1.233 | 1.720 | 0.877 | 0.917 | 1.161 | 1.525 | 0.900 | 0.889 | |
| 160 cm | 1.387 | 1.933 | 0.780 | 0.879 | 1.310 | 1.800 | 0.820 | 0.839 | |
| 200 cm | 1.421 | 1.997 | 0.655 | 0.794 | 1.385 | 1.937 | 0.709 | 0.772 | |
| LSTM14 | 80 cm | 0.957 | 1.289 | 0.951 | 0.975 | 0.829 | 1.051 | 0.960 | 0.971 |
| 120 cm | 1.132 | 1.531 | 0.902 | 0.949 | 0.991 | 1.269 | 0.929 | 0.914 | |
| 160 cm | 1.262 | 1.754 | 0.818 | 0.902 | 1.166 | 1.510 | 0.870 | 0.848 | |
| 200 cm | 1.255 | 1.699 | 0.774 | 0.776 | 1.280 | 1.825 | 0.711 | 0.836 | |
| LSTM21 | 80 cm | 0.724 | 0.979 | 0.972 | 0.977 | 0.679 | 0.833 | 0.972 | 0.981 |
| 120 cm | 0.752 | 1.052 | 0.954 | 0.967 | 0.797 | 1.007 | 0.952 | 0.957 | |
| 160 cm | 0.802 | 1.171 | 0.918 | 0.950 | 0.850 | 1.135 | 0.923 | 0.949 | |
| 200 cm | 0.795 | 1.238 | 0.866 | 0.909 | 0.842 | 1.221 | 0.880 | 0.895 | |
| Model | Depths | Training Dataset | Testing Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | R2 | KGE | MAE (°C) | RMSE (°C) | R2 | KGE | ||
| LSTM7 | 80 cm | 1.192 | 1.637 | 0.921 | 0.910 | 1.158 | 1.449 | 0.928 | 0.885 |
| 120 cm | 1.418 | 1.913 | 0.848 | 0.869 | 1.436 | 1.773 | 0.868 | 0.815 | |
| 160 cm | 1.538 | 2.098 | 0.741 | 0.827 | 1.554 | 1.971 | 0.787 | 0.775 | |
| 200 cm | 1.561 | 2.155 | 0.600 | 0.740 | 1.610 | 2.088 | 0.665 | 0.708 | |
| LSTM7-SG | 80 cm | 1.186 | 1.626 | 0.922 | 0.909 | 1.152 | 1.435 | 0.930 | 0.885 |
| 120 cm | 1.409 | 1.896 | 0.851 | 0.869 | 1.430 | 1.755 | 0.871 | 0.814 | |
| 160 cm | 1.526 | 2.076 | 0.747 | 0.827 | 1.543 | 1.948 | 0.792 | 0.774 | |
| 200 cm | 1.548 | 2.128 | 0.610 | 0.742 | 1.598 | 2.061 | 0.673 | 0.707 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, W.; Liu, D.; Guo, F.; Zhang, L.; Ma, L.; Huang, Q.; Li, Q.; Ming, G.; Meng, X. Evaluation of the Potential of Using Machine Learning and the Savitzky–Golay Filter to Estimate the Daily Soil Temperature in Gully Regions of the Chinese Loess Plateau. Agronomy 2024, 14, 703. https://doi.org/10.3390/agronomy14040703
Deng W, Liu D, Guo F, Zhang L, Ma L, Huang Q, Li Q, Ming G, Meng X. Evaluation of the Potential of Using Machine Learning and the Savitzky–Golay Filter to Estimate the Daily Soil Temperature in Gully Regions of the Chinese Loess Plateau. Agronomy. 2024; 14(4):703. https://doi.org/10.3390/agronomy14040703
Chicago/Turabian StyleDeng, Wei, Dengfeng Liu, Fengnian Guo, Lianpeng Zhang, Lan Ma, Qiang Huang, Qiang Li, Guanghui Ming, and Xianmeng Meng. 2024. "Evaluation of the Potential of Using Machine Learning and the Savitzky–Golay Filter to Estimate the Daily Soil Temperature in Gully Regions of the Chinese Loess Plateau" Agronomy 14, no. 4: 703. https://doi.org/10.3390/agronomy14040703
APA StyleDeng, W., Liu, D., Guo, F., Zhang, L., Ma, L., Huang, Q., Li, Q., Ming, G., & Meng, X. (2024). Evaluation of the Potential of Using Machine Learning and the Savitzky–Golay Filter to Estimate the Daily Soil Temperature in Gully Regions of the Chinese Loess Plateau. Agronomy, 14(4), 703. https://doi.org/10.3390/agronomy14040703







