Leveraging Hyperspectral Images for Accurate Insect Classification with a Novel Two-Branch Self-Correlation Approach
Abstract
:1. Introduction
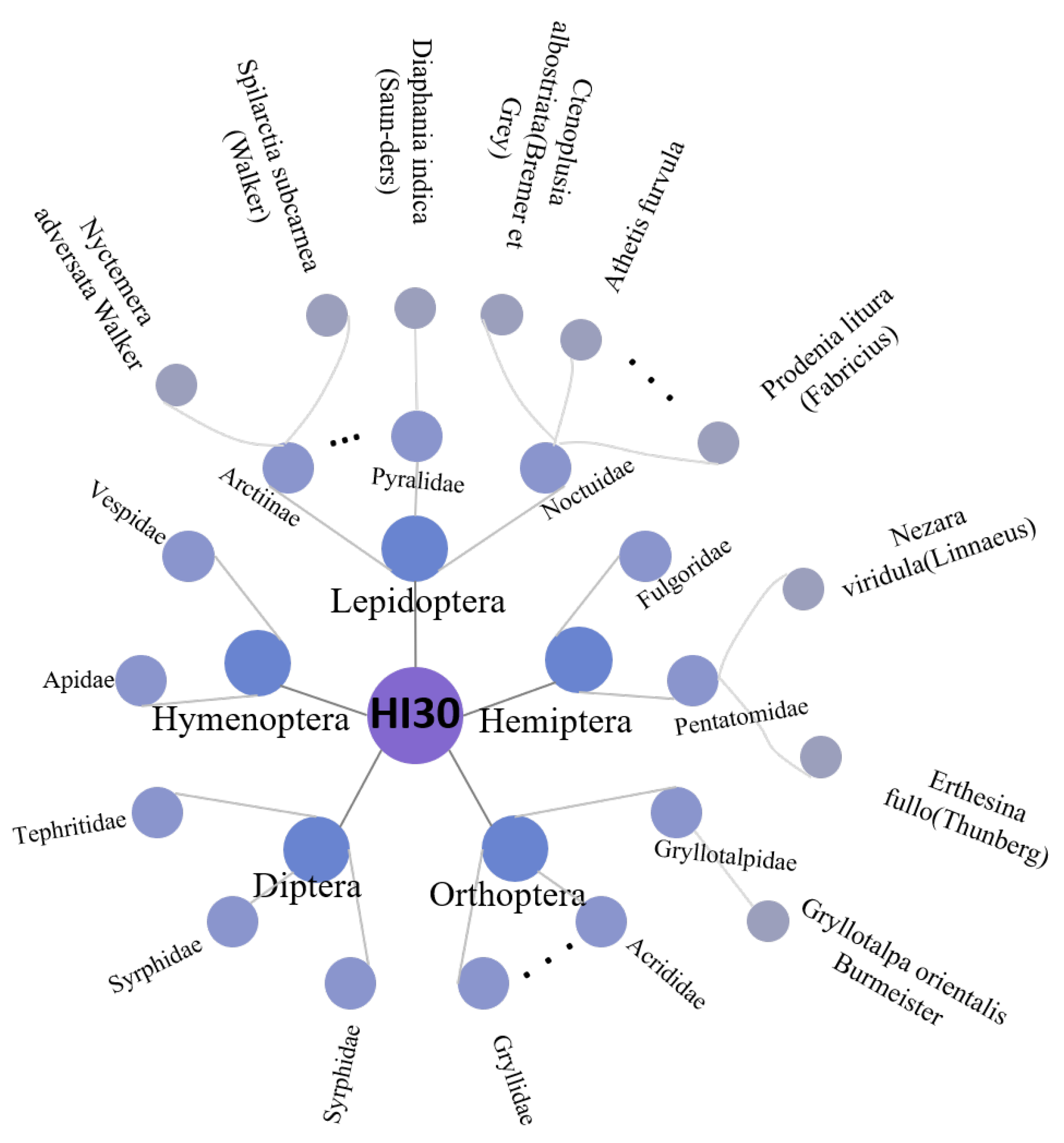
- A new benchmark hyperspectral dataset for the classification of insect species is established, captured via a line-scanning hyperspectral camera, consisting of 2115 samples across 30 insect species. This dataset is publicly available to the community at: https://github.com/Huwz95/HI30-dataset (accessed on 12 April 2024). To the best of our knowledge, this is the first work to use hyperspectral images for insect classification.
- This paper develops a novel algorithm, TBSCN, which merges PCA dimensionality reduction with correlation processing, tailored for efficient classification of insect hyperspectral images. By combining spectral and spatial information, this method significantly enhances classification accuracy while maintaining processing speed.
- A thorough evaluation is provided, comparing original and PCA-compressed hyperspectral data, as well as raw hyperspectral versus derived RGB data. This comparative analysis underscores the effects of hyperspectral data on classification efficiency and potential, offering crucial insights for the advancement of future algorithms and their applications.
2. Materials and Methods
2.1. Dataset
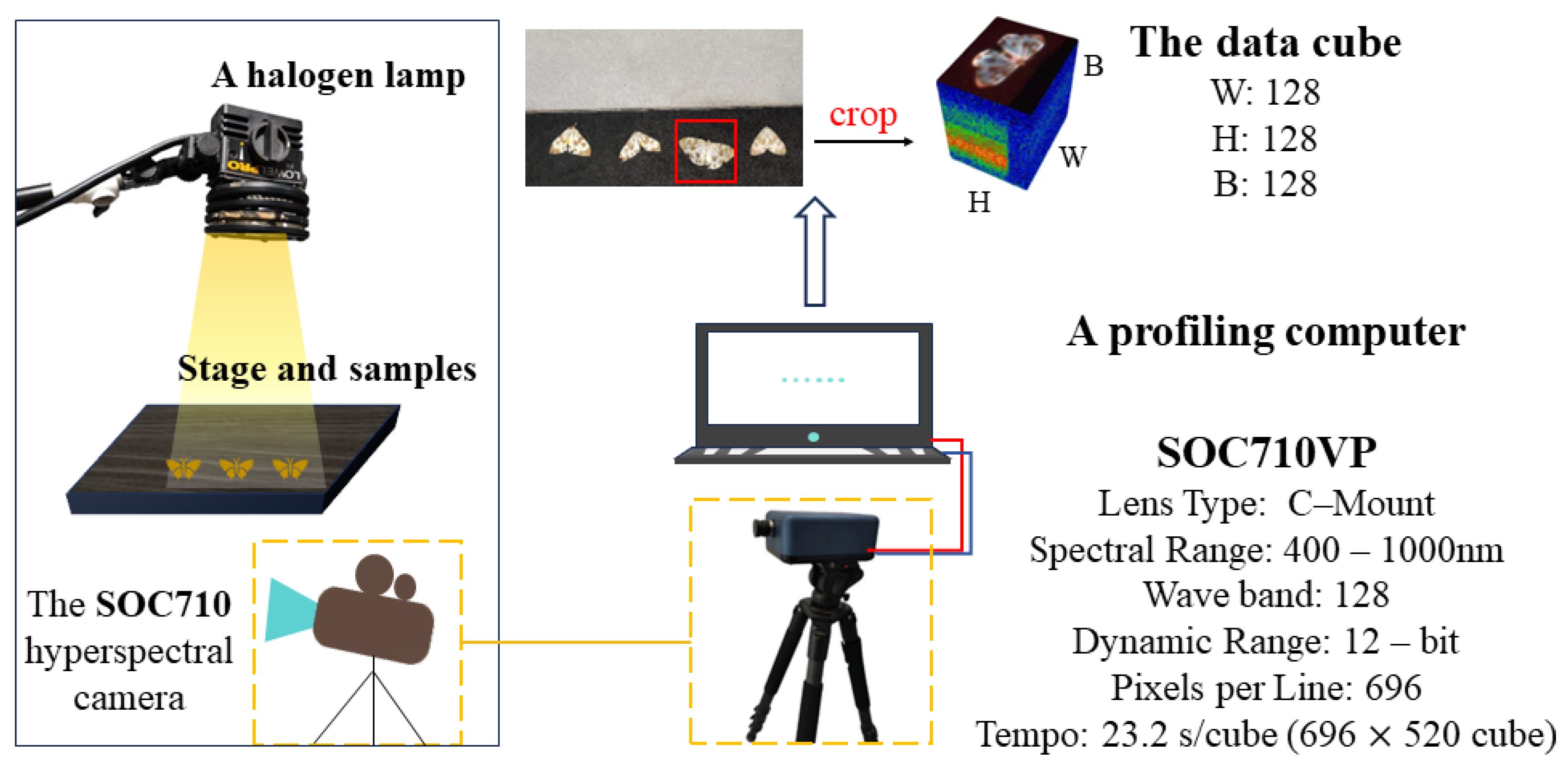
2.1.1. Data Collection
2.1.2. Dataset Construction and Labeling
2.2. Methods
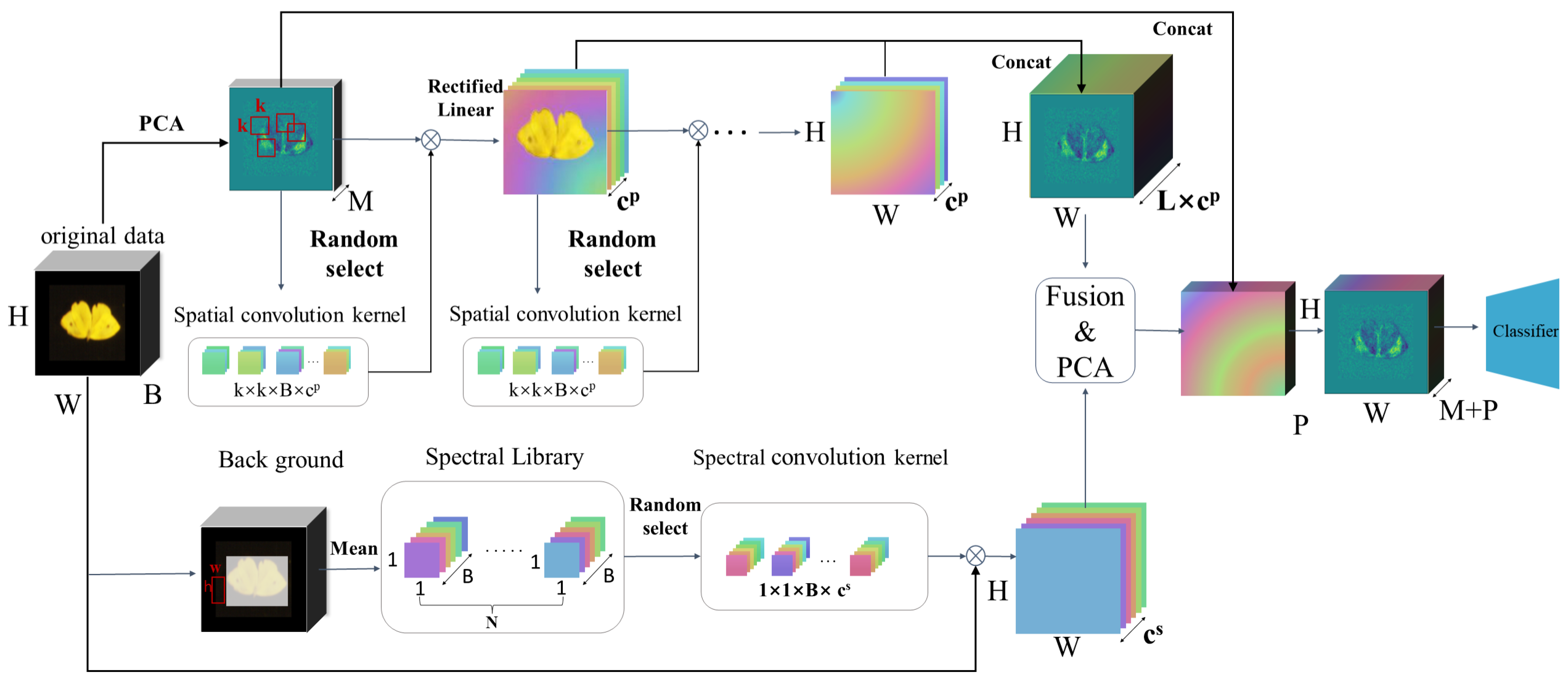
2.2.1. Framework
2.2.2. PCA
2.2.3. Random Spectrum Correlation
2.2.4. Random Patch Correlation
2.2.5. The Classifier
3. Results
3.1. Experimental Setup and Evaluation Metrics
3.2. Results and Analysis
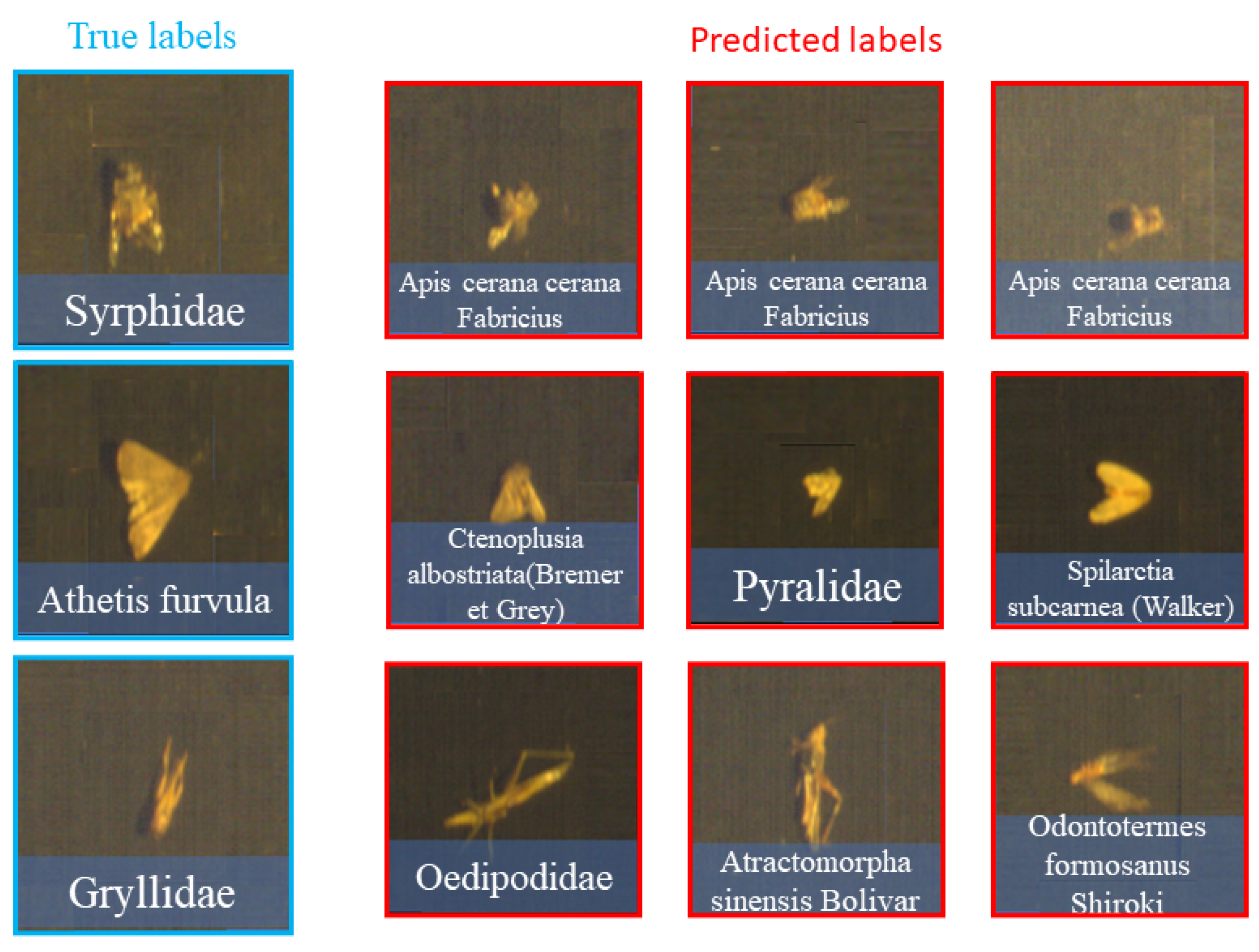
3.3. Further Analysis
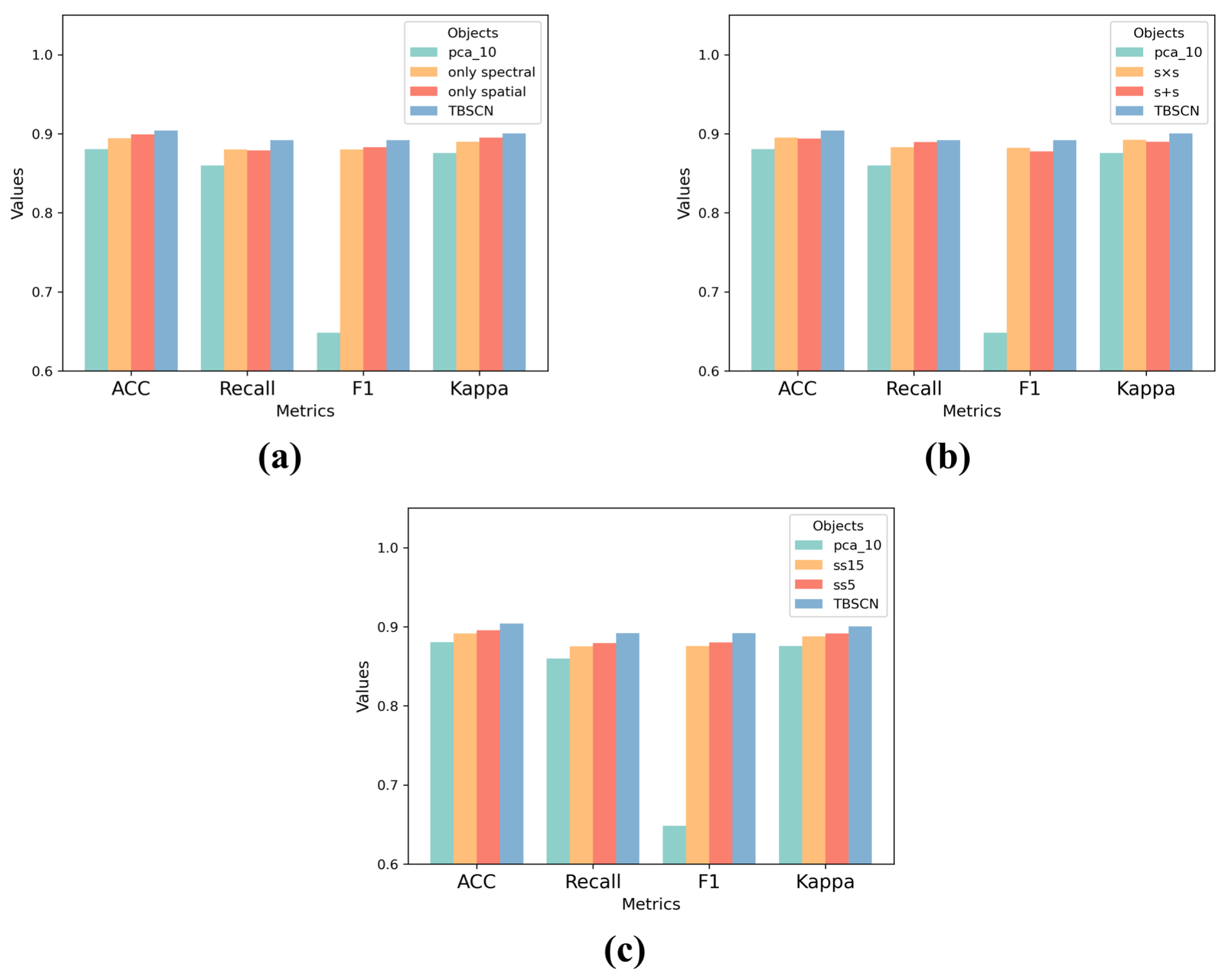
3.3.1. Ablation Study on Random Correlation Section
3.3.2. Ablation on Fusion Way
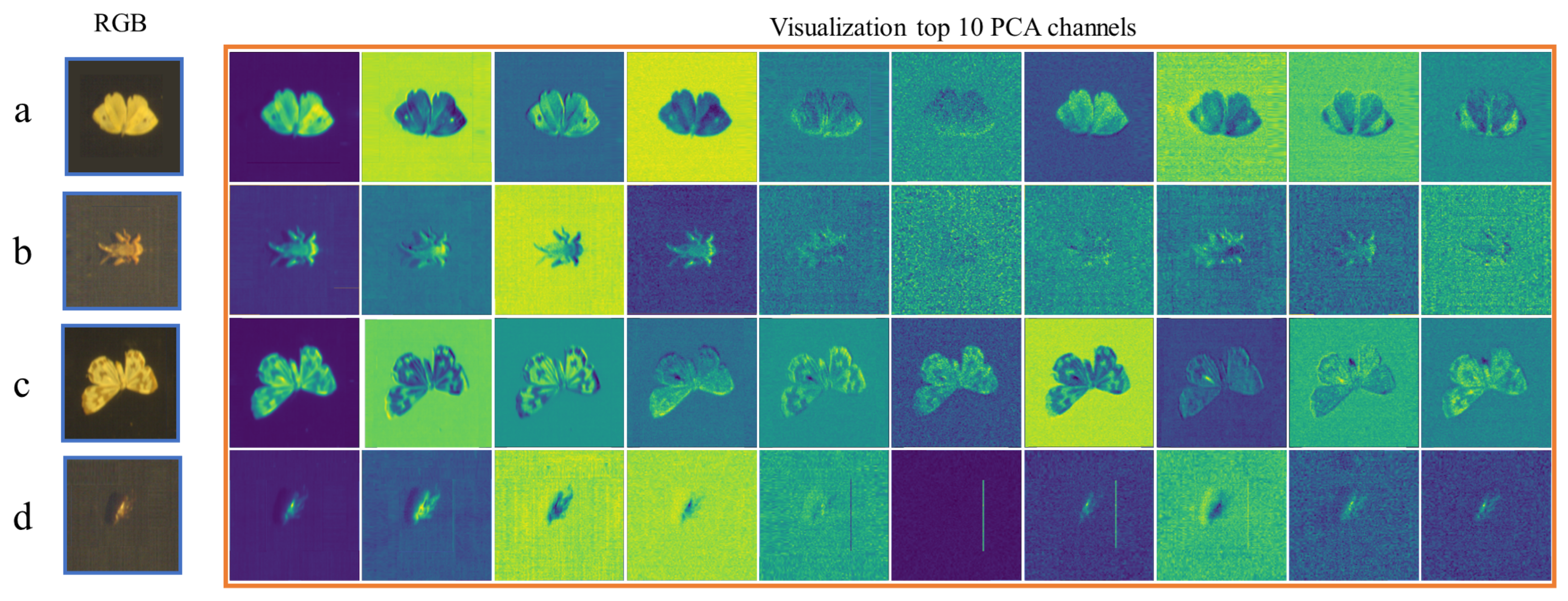
3.3.3. Ablation Study on Input Channel
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Order | Genus | Species | Amount | |
|---|---|---|---|---|
| HI30 | Hemiptera | Pentatomidae | Nezara viridula (Linnaeus) | 139 |
| Erthesina fullo (Thunberg) | 63 | |||
| Fulgoridae | Lycorma delicatula | 50 | ||
| Lepidoptera | Arctiinae | Nyctemera adversata Walker | 112 | |
| Spilarctia subcarnea (Walker) | 60 | |||
| Gelechiidae | Sweetpotato leaf folder | 46 | ||
| Pyralidae | Diaphania indica (Saun-ders) | 84 | ||
| – | 100 | |||
| Noctuidae | Ctenoplusia albostriata (Bremer et Grey) | 55 | ||
| Athetis furvula | 55 | |||
| Prodenia litura (Fabricius) | 83 | |||
| – | 127 | |||
| Hesperiidae | Parnara guttata (Bremer et Grey) | 53 | ||
| Lycaenidae | Deudorix dpijarbas Moore | 48 | ||
| Pieridae | Pieris rapae | 56 | ||
| Nymphalidae | Polygonia c-album (Linnaeus) | 60 | ||
| Coleoptera | Scarabaeoidea | Melolontha | 56 | |
| Diptera | Tephritidae | – | 35 | |
| Syrphidae | – | 119 | ||
| Calliphoridae | – | 66 | ||
| Hymenoptera | Vespidae | – | 48 | |
| Apidae | Apis cerana cerana Fabricius | 132 | ||
| Dermaptera | Forficulidae | – | 74 | |
| Odonata | Platycnemididae | – | 56 | |
| Gomphidae | – | 48 | ||
| Orthoptera | Gryllidae | – | 65 | |
| Oedipodidae | – | 60 | ||
| Gryllotalpidae | Gryllotalpa orientalis Burmeister | 45 | ||
| Acrididae | Atractomorpha sinensis Bolivar | 48 | ||
| Isoptera Brullé | Termitidae | Odontotermes formosanus Shiroki | 72 |
References
- Stork, N.E.; McBroom, J.; Gely, C.; Hamilton, A.J. New approaches narrow global species estimates for beetles, insects, and terrestrial arthropods. Proc. Natl. Acad. Sci. USA 2015, 112, 7519–7523. [Google Scholar] [CrossRef] [PubMed]
- Majeed, W.; Khawaja, M.; Rana, N.; de Azevedo Koch, E.B.; Naseem, R.; Nargis, S. Evaluation of insect diversity and prospects for pest management in agriculture. Int. J. Trop. Insect Sci. 2022, 42, 2249–2258. [Google Scholar] [CrossRef]
- Wen, C.; Guyer, D. Image-based orchard insect automated identification and classification method. Comput. Electron. Agric. 2012, 89, 110–115. [Google Scholar] [CrossRef]
- Zhang, T.; Long, C.F.; Deng, Y.J.; Wang, W.Y.; Tan, S.Q.; Li, H.C. Low-rank preserving embedding regression for robust image feature extraction. IET Comput. Vis. 2023, 18, 124–140. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y.; Han, Z.; Yu, R. Research on insect pest image detection and recognition based on bio-inspired methods. Biosyst. Eng. 2018, 169, 139–148. [Google Scholar] [CrossRef]
- Alfarisy, A.A.; Chen, Q.; Guo, M. Deep Learning Based Classification for Paddy Pests & Diseases Recognition. In Proceedings of the 2018 International Conference on Mathematics and Artificial Intelligence, ICMAI ‘18, New York, NY, USA, 9–15 July 2018; pp. 21–25. [Google Scholar] [CrossRef]
- Wu, X.; Zhan, C.; Lai, Y.K.; Cheng, M.M.; Yang, J. IP102: A Large-Scale Benchmark Dataset for Insect Pest Recognition. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8779–8788. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Dang, L.M.; Sadeghi-Niaraki, A.; Moon, H. Crop pest recognition in natural scenes using convolutional neural networks. Comput. Electron. Agric. 2020, 169, 105174. [Google Scholar] [CrossRef]
- Abeywardhana, D.L.; Dangalle, C.D.; Nugaliyadde, A.; Mallawarachchi, Y. An ultra-specific image dataset for automated insect identification. Multimed. Tools Appl. 2022, 81, 3223–3251. [Google Scholar] [CrossRef]
- Hansen, O.L.; Svenning, J.C.; Olsen, K.; Dupont, S.; Garner, B.H.; Iosifidis, A.; Price, B.W.; Høye, T.T. Species-level image classification with convolutional neural network enables insect identification from habitus images. Ecol. Evol. 2020, 10, 737–747. [Google Scholar] [CrossRef] [PubMed]
- Kusrini, K.; Suputa, S.; Setyanto, A.; Agastya, I.M.A.; Priantoro, H.; Chandramouli, K.; Izquierdo, E. Data augmentation for automated pest classification in Mango farms. Comput. Electron. Agric. 2020, 179, 105842. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Feng, H.; Ren, L.; Du, X.; Wu, J. Common pests image recognition based on deep convolutional neural network. Comput. Electron. Agric. 2020, 179, 105834. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C.; Feng, Y.; Li, D. Pests Identification of IP102 by YOLOv5 Embedded with the Novel Lightweight Module. Agronomy 2023, 13, 1583. [Google Scholar] [CrossRef]
- Li, W.; Zhu, T.; Li, X.; Dong, J.; Liu, J. Recommending advanced deep learning models for efficient insect pest detection. Agriculture 2022, 12, 1065. [Google Scholar] [CrossRef]
- De Backer, S.; Kempeneers, P.; Debruyn, W.; Scheunders, P. A band selection technique for spectral classification. IEEE Geosci. Remote Sens. Lett. 2005, 2, 319–323. [Google Scholar] [CrossRef]
- Kuo, B.C.; Li, C.H.; Yang, J.M. Kernel nonparametric weighted feature extraction for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1139–1155. [Google Scholar]
- Huang, X.; Liu, X.; Zhang, L. A Multichannel Gray Level Co-Occurrence Matrix for Multi/Hyperspectral Image Texture Representation. Remote Sens. 2014, 6, 8424–8445. [Google Scholar] [CrossRef]
- Shen, L.; Jia, S. Three-dimensional Gabor wavelets for pixel-based hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 5039–5046. [Google Scholar] [CrossRef]
- Deng, Y.J.; Li, H.C.; Tan, S.Q.; Hou, J.; Du, Q.; Plaza, A. t-Linear Tensor Subspace Learning for Robust Feature Extraction of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5501015. [Google Scholar] [CrossRef]
- Deng, Y.J.; Yang, M.L.; Li, H.C.; Long, C.F.; Fang, K.; Du, Q. Feature Dimensionality Reduction with L 2, p-Norm-Based Robust Embedding Regression for Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5509314. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM-and MRF-based method for accurate classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Huang, K.; Li, S.; Kang, X.; Fang, L. Spectral–spatial hyperspectral image classification based on KNN. Sens. Imaging 2016, 17, 1. [Google Scholar] [CrossRef]
- Xia, J.; Ghamisi, P.; Yokoya, N.; Iwasaki, A. Random forest ensembles and extended multiextinction profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 202–216. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. A subspace-based multinomial logistic regression for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2105–2109. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Ge, Z.; Cao, G.; Li, X.; Fu, P. Hyperspectral Image Classification Method Based on 2D–3D CNN and Multibranch Feature Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5776–5788. [Google Scholar] [CrossRef]
- Wu, H.; Li, D.; Wang, Y.; Li, X.; Kong, F.; Wang, Q. Hyperspectral Image Classification Based on Two-Branch Spectral–Spatial-Feature Attention Network. Remote Sens. 2021, 13, 4262. [Google Scholar] [CrossRef]
- Jin, H.; Peng, J.; Bi, R.; Tian, H.; Zhu, H.; Ding, H. Comparing Laboratory and Satellite Hyperspectral Predictions of Soil Organic Carbon in Farmland. Agronomy 2024, 14, 175. [Google Scholar] [CrossRef]
- Carrino, T.A.; Crósta, A.P.; Toledo, C.L.B.; Silva, A.M. Hyperspectral remote sensing applied to mineral exploration in southern Peru: A multiple data integration approach in the Chapi Chiara gold prospect. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 287–300. [Google Scholar] [CrossRef]
- Shao, Y.; Ji, S.; Xuan, G.; Ren, Y.; Feng, W.; Jia, H.; Wang, Q.; He, S. Detection and Analysis of Chili Pepper Root Rot by Hyperspectral Imaging Technology. Agronomy 2024, 14, 226. [Google Scholar] [CrossRef]
- Long, C.F.; Wen, Z.D.; Deng, Y.J.; Hu, T.; Liu, J.L.; Zhu, X.H. Locality Preserved Selective Projection Learning for Rice Variety Identification Based on Leaf Hyperspectral Characteristics. Agronomy 2023, 13, 2401. [Google Scholar] [CrossRef]
- Xiao, Z.; Yin, K.; Geng, L.; Wu, J.; Zhang, F.; Liu, Y. Pest identification via hyperspectral image and deep learning. Signal Image Video Process. 2022, 16, 873–880. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, T.; Fu, Y. A large-scale hyperspectral dataset for flower classification. Knowl.-Based Syst. 2022, 236, 107647. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, F.; Zhang, L. Hyperspectral image classification via a random patches network. ISPRS J. Photogramm. Remote Sens. 2018, 142, 344–357. [Google Scholar] [CrossRef]
- Cheng, C.; Li, H.; Peng, J.; Cui, W.; Zhang, L. Hyperspectral image classification via spectral-spatial random patches network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4753–4764. [Google Scholar] [CrossRef]
- Shenming, Q.; Xiang, L.; Zhihua, G. A new hyperspectral image classification method based on spatial-spectral features. Sci. Rep. 2022, 12, 1541. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Zapryanov, G.; Ivanova, D.; Nikolova, I. Automatic White Balance Algorithms forDigital StillCameras—A Comparative Study. Inf. Technol. Control. 2012. Available online: http://acad.bg/rismim/itc/sub/archiv/Paper3_1_2012.pdf (accessed on 8 March 2024).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Magnusson, M.; Sigurdsson, J.; Armansson, S.E.; Ulfarsson, M.O.; Deborah, H.; Sveinsson, J.R. Creating RGB images from hyperspectral images using a color matching function. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2045–2048. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]




| Classifiers | RGB | Original | PCA_3 | PCA_10 | TBSCN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc. (%) | Acc. (%) | Acc. (%) | Acc. (%) | Acc. (%) | |||||||
| DL | RN18 | 58.40 | 56.69 | 88.25 | 87.78 | 78.63 | 77.76 | 87.93 | 87.44 | 89.72 | 89.30 |
| RN34 | 59.87 | 58.21 | 84.99 | 84.38 | 80.27 | 79.45 | 88.09 | 87.60 | 89.23 | 88.79 | |
| MobileV2 | 64.44 | 62.97 | 84.50 | 83.88 | 81.07 | 80.31 | 84.50 | 83.87 | 88.74 | 88.29 | |
| Dense121 | 71.77 | 70.62 | 90.05 | 89.64 | 87.28 | 87.60 | 91.68 | 91.34 | 93.96 | 93.72 | |
| DL + SVM | RN18 + SVM | 58.70 | 56.73 | 89.23 | 88.79 | 89.56 | 89.13 | 90.54 | 90.15 | 89.39 | 88.97 |
| RN34 + SVM | 56.42 | 55.36 | 85.97 | 85.40 | 87.44 | 86.92 | 87.92 | 87.44 | 91.57 | 91.18 | |
| Mobile + SVM | 63.49 | 61.56 | 84.99 | 84.38 | 82.38 | 81.66 | 86.30 | 85.74 | 89.23 | 88.80 | |
| Dense + SVM | 71.17 | 70.49 | 91.19 | 90.83 | 87.60 | 87.10 | 92.50 | 92.19 | 92.49 | 92.19 | |
| HandScraft + SVM | Gabor + SVM | 43.28 | 43.28 | __ | __ | 52.37 | 52.37 | __ | __ | __ | __ |
| SIFT + SVM | 28.06 | 24.77 | __ | __ | 29.36 | 26.40 | __ | __ | __ | __ | |
| Histogram + SVM | 58.78 | 56.14 | __ | __ | 71.45 | 70.30 | __ | __ | __ | __ | |
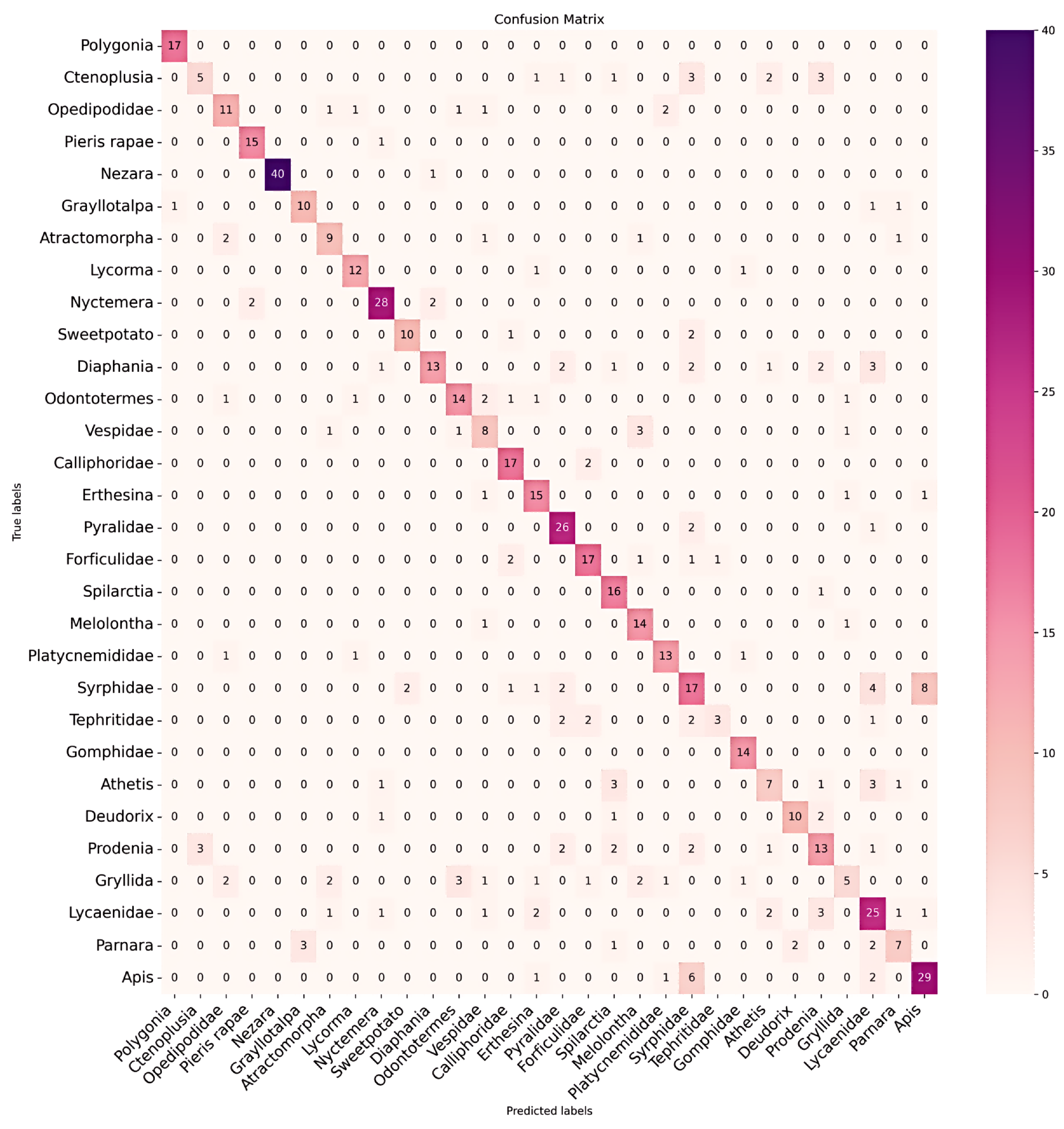
| Species | RGB Data | Hyperspectral Data | |||||
|---|---|---|---|---|---|---|---|
| (%) | Acc. (%) | Recall | |||||
| Polygonia | 100 | 1.00 | 0.97 | 100 | 1.00 | 1.00 | |
| Ctenoplusia | 31 | 0.31 | 0.42 | 62 | 0.62 | 0.77 | |
| Oedipodidae | 64 | 0.65 | 0.65 | 82 | 0.82 | 0.82 | |
| Pieris | 93 | 0.94 | 0.91 | 87 | 0.88 | 0.88 | |
| Nezara | 97 | 0.98 | 0.99 | 100 | 1.00 | 1.00 | |
| Gryllotalpa | 76 | 0.77 | 0.77 | 69 | 0.69 | 0.78 | |
| Atractomorpha | 64 | 0.64 | 0.64 | 71 | 0.71 | 0.74 | |
| Lycorma | 85 | 0.86 | 0.83 | 100 | 1.00 | 1.00 | |
| Nyctemera | 87 | 0.88 | 0.86 | 93 | 0.94 | 0.94 | |
| Sweetpotato | 76 | 0.77 | 0.80 | 100 | 1.00 | 1.00 | |
| Diaphania | 52 | 0.52 | 0.63 | 96 | 0.96 | 0.98 | |
| Odontotermes | 66 | 0.67 | 0.70 | 95 | 0.95 | 0.93 | |
| Vespidae | 57 | 0.57 | 0.53 | 64 | 0.64 | 0.72 | |
| Calliphoridae | 89 | 0.89 | 0.83 | 100 | 1.00 | 0.95 | |
| Erthesina | 83 | 0.83 | 0.73 | 100 | 1.00 | 1.00 | |
| Pyralidae | 89 | 0.90 | 0.81 | 89 | 0.90 | 0.93 | |
| Forficulidae | 77 | 0.77 | 0.77 | 86 | 0.86 | 0.90 | |
| Spilarctia | 94 | 0.94 | 0.76 | 100 | 1.00 | 0.94 | |
| Melolontha | 87 | 0.88 | 0.76 | 100 | 1.00 | 1.00 | |
| Platycnemididae | 81 | 0.81 | 0.79 | 93 | 0.94 | 0.91 | |
| Syrphidae | 48 | 0.49 | 0.47 | 100 | 1.00 | 1.00 | |
| Tephritidae | 30 | 0.30 | 0.43 | 70 | 0.70 | 0.78 | |
| Gomphidae | 100 | 1.00 | 0.90 | 100 | 1.00 | 0.93 | |
| Athetis | 43 | 0.44 | 0.48 | 100 | 1.00 | 0.94 | |
| Deudorix | 71 | 0.71 | 0.77 | 92 | 0.93 | 0.96 | |
| Prodenia | 54 | 0.54 | 0.53 | 91 | 0.92 | 0.83 | |
| Gryllidae | 26 | 0.26 | 0.36 | 78 | 0.79 | 0.79 | |
| Lycaenidae | 67 | 0.68 | 0.63 | 97 | 0.97 | 0.96 | |
| Parnara | 46 | 0.47 | 0.54 | 93 | 0.93 | 0.82 | |
| Apis | 74 | 0.74 | 0.74 | 100 | 1.00 | 0.99 | |
| RGB | Original | PCA_3 | PCA_10 | ||
|---|---|---|---|---|---|
| RN18 | . (%) | 70.63 | 84.34 | 80.91 | 87.27 |
| 69.42 | 83.71 | 80.13 | 86.75 | ||
| Recall | 69.06 | 83.08 | 78.84 | 85.74 | |
| F1 | 68.82 | 82.70 | 79.04 | 85.72 | |
| RN34 | . (%) | 70.96 | 82.87 | 81.40 | 86.62 |
| 69.77 | 82.18 | 80.62 | 86.08 | ||
| Recall | 69.87 | 82.23 | 79.49 | 85.16 | |
| F1 | 69.70 | 81.73 | 79.78 | 85.18 | |
| MobileV2 | . (%) | 79.61 | 85.97 | 82.22 | 87.27 |
| 78.78 | 85.40 | 81.49 | 86.75 | ||
| Recall | 77.52 | 84.69 | 80.33 | 85.88 | |
| F1 | 77.76 | 84.64 | 80.64 | 86.37 | |
| Dense | . (%) | 81.73 | 90.53 | 89.23 | 91.68 |
| 80.98 | 90.15 | 88.79 | 91.34 | ||
| Recall | 80.83 | 88.68 | 87.98 | 90.68 | |
| F1 | 81.32 | 88.87 | 88.20 | 90.85 |
| Classifiers | RGB | Original | PCA_3 | PCA_10 | TBSCN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DL | RN18 | 55.67 | 55.25 | 86.15 | 85.59 | 77.08 | 78.00 | 86.00 | 86.00 | 88.26 | 88.24 |
| RN34 | 58.41 | 59.05 | 86.27 | 82.74 | 78.00 | 78.20 | 86.34 | 86.31 | 87.6 | 87.76 | |
| MobileV2 | 63.41 | 63.80 | 83.82 | 83.55 | 80.15 | 79.96 | 81.74 | 82.12 | 87.79 | 87.76 | |
| Dense121 | 70.66 | 70.01 | 88.61 | 88.47 | 86.84 | 86.72 | 89.89 | 90.13 | 93.12 | 92.91 | |
| DL + SVM | RN18 + SVM | 55.93 | 55.72 | 87.09 | 87.23 | 88.48 | 89.13 | 88.57 | 88.53 | 87.97 | 87.92 |
| RN34 + SVM | 56.75 | 57.73 | 84.28 | 84.35 | 86.33 | 86.68 | 86.59 | 86.35 | 90.74 | 90.60 | |
| Mobile + SVM | 61.32 | 60.86 | 84.03 | 84.17 | 80.43 | 80.96 | 85.12 | 85.08 | 88.14 | 88.06 | |
| Dense + SVM | 70.86 | 69.44 | 89.27 | 89.38 | 86.02 | 85.99 | 91.22 | 91.23 | 91.25 | 91.96 | |
| HandScraft + SVM | Gabor + SVM | 40.43 | 43.28 | __ | __ | 50.17 | 52.37 | __ | __ | __ | __ |
| SIFT + SVM | 24.70 | 23.88 | __ | __ | 28.51 | 28.40 | __ | __ | __ | __ | |
| Histogram + SVM | 55.68 | 54.51 | __ | __ | 70.14 | 69.72 | __ | __ | __ | __ | |
| RN18 | RN34 | MobileV2 | Dense | RN18 + SVM | RN34 + SVM | MobileV2 + SVM | Dense + SVM | ||
|---|---|---|---|---|---|---|---|---|---|
| PCA_10 | Acc. (%) | 87.93 | 88.09 | 84.50 | 91.68 | 90.54 | 87.92 | 86.30 | 92.50 |
| 86.00 | 86.34 | 81.74 | 89.89 | 88.57 | 86.59 | 85.12 | 91.22 | ||
| 86.00 | 86.31 | 82.12 | 90.13 | 88.53 | 86.35 | 85.08 | 91.23 | ||
| 87.44 | 87.06 | 83.87 | 91.34 | 90.15 | 87.44 | 85.74 | 92.19 | ||
| only spatial | Acc. (%) | 89.55 | 90.05 | 87.27 | 92.82 | 91.68 | 91.03 | 90.05 | 93.64 |
| 87.43 | 88.30 | 84.89 | 90.89 | 90.38 | 89.59 | 89.05 | 92.32 | ||
| 87.97 | 88.50 | 85.60 | 91.13 | 90.23 | 89.57 | 88.92 | 92.29 | ||
| 89.13 | 89.64 | 86.75 | 92.53 | 91.34 | 90.66 | 89.65 | 93.38 | ||
| only spectral | Acc. (%) | 88.42 | 88.90 | 87.11 | 93.31 | 91.57 | 89.72 | 89.56 | 93.96 |
| 86.20 | 87.08 | 86.40 | 92.32 | 90.19 | 88.50 | 88.22 | 92.97 | ||
| 86.00 | 87.20 | 86.31 | 92.50 | 90.00 | 88.51 | 88.39 | 92.68 | ||
| 87.95 | 88.45 | 86.59 | 93.04 | 91.17 | 89.30 | 89.13 | 93.72 | ||
| TBSCN | Acc. (%) | 89.72 | 89.23 | 88.74 | 93.96 | 89.39 | 91.57 | 89.23 | 92.49 |
| 88.26 | 87.60 | 87.79 | 93.12 | 87.97 | 90.74 | 88.14 | 91.25 | ||
| 88.24 | 87.76 | 87.76 | 92.91 | 87.92 | 90.60 | 88.06 | 90.96 | ||
| 89.30 | 88.79 | 88.29 | 93.72 | 88.97 | 91.18 | 88.80 | 92.19 |
| RN18 | RN34 | MobileV2 | Dense | RN18 + SVM | RN34 + SVM | MobileV2 + SVM | Dense + SVM | ||
|---|---|---|---|---|---|---|---|---|---|
| s + s | Acc | 88.41 | 90.86 | 86.62 | 91.68 | 91.35 | 91.03 | 88.58 | 92.98 |
| 86.99 | 89.42 | 89.44 | 90.00 | 89.87 | 89.42 | 87.12 | 92.27 | ||
| 86.70 | 89.44 | 84.81 | 90.14 | 89.88 | 89.56 | 87.05 | 92.07 | ||
| 87.95 | 90.49 | 86.08 | 91.34 | 91.00 | 90.66 | 88.12 | 92.70 | ||
| s × s | Acc | 90.21 | 87.76 | 86.95 | 93.15 | 91.19 | 87.93 | 88.74 | 91.68 |
| 89.10 | 86.04 | 85.74 | 92.32 | 90.06 | 85.71 | 87.48 | 90.37 | ||
| 88.90 | 86.17 | 85.70 | 92.14 | 89.99 | 85.99 | 87.57 | 90.13 | ||
| 89.82 | 87.77 | 86.42 | 92.87 | 90.83 | 87.43 | 88.29 | 91.34 | ||
| ss_15 | Acc | 88.79 | 87.93 | 86.79 | 92.99 | 91.35 | 89.56 | 87.60 | 93.15 |
| 87.10 | 86.24 | 85.00 | 91.83 | 89.50 | 88.93 | 85.96 | 92.16 | ||
| 87.29 | 86.32 | 84.80 | 91.88 | 89.66 | 88.54 | 85.87 | 92.05 | ||
| 88.80 | 87.44 | 86.25 | 92.70 | 91.00 | 89.14 | 87.10 | 92.87 | ||
| ss_5 | Acc | 87.77 | 88.74 | 88.91 | 92.82 | 90.86 | 89.72 | 88.91 | 93.31 |
| 85.56 | 87.24 | 87.27 | 91.67 | 89.26 | 88.12 | 87.77 | 92.44 | ||
| 86.09 | 87.14 | 87.14 | 91.71 | 89.28 | 87.87 | 87.55 | 92.39 | ||
| 87.26 | 88.29 | 88.46 | 92.53 | 90.49 | 89.30 | 88.46 | 93.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, S.; Hu, S.; He, S.; Zhu, L.; Qian, Y.; Deng, Y. Leveraging Hyperspectral Images for Accurate Insect Classification with a Novel Two-Branch Self-Correlation Approach. Agronomy 2024, 14, 863. https://doi.org/10.3390/agronomy14040863
Tan S, Hu S, He S, Zhu L, Qian Y, Deng Y. Leveraging Hyperspectral Images for Accurate Insect Classification with a Novel Two-Branch Self-Correlation Approach. Agronomy. 2024; 14(4):863. https://doi.org/10.3390/agronomy14040863
Chicago/Turabian StyleTan, Siqiao, Shuzhen Hu, Shaofang He, Lei Zhu, Yanlin Qian, and Yangjun Deng. 2024. "Leveraging Hyperspectral Images for Accurate Insect Classification with a Novel Two-Branch Self-Correlation Approach" Agronomy 14, no. 4: 863. https://doi.org/10.3390/agronomy14040863
APA StyleTan, S., Hu, S., He, S., Zhu, L., Qian, Y., & Deng, Y. (2024). Leveraging Hyperspectral Images for Accurate Insect Classification with a Novel Two-Branch Self-Correlation Approach. Agronomy, 14(4), 863. https://doi.org/10.3390/agronomy14040863






