Transformation of Discarded Pumpkin into High-Value Powder: A Drying Process Model for Functional Food Ingredients
Abstract
:1. Introduction
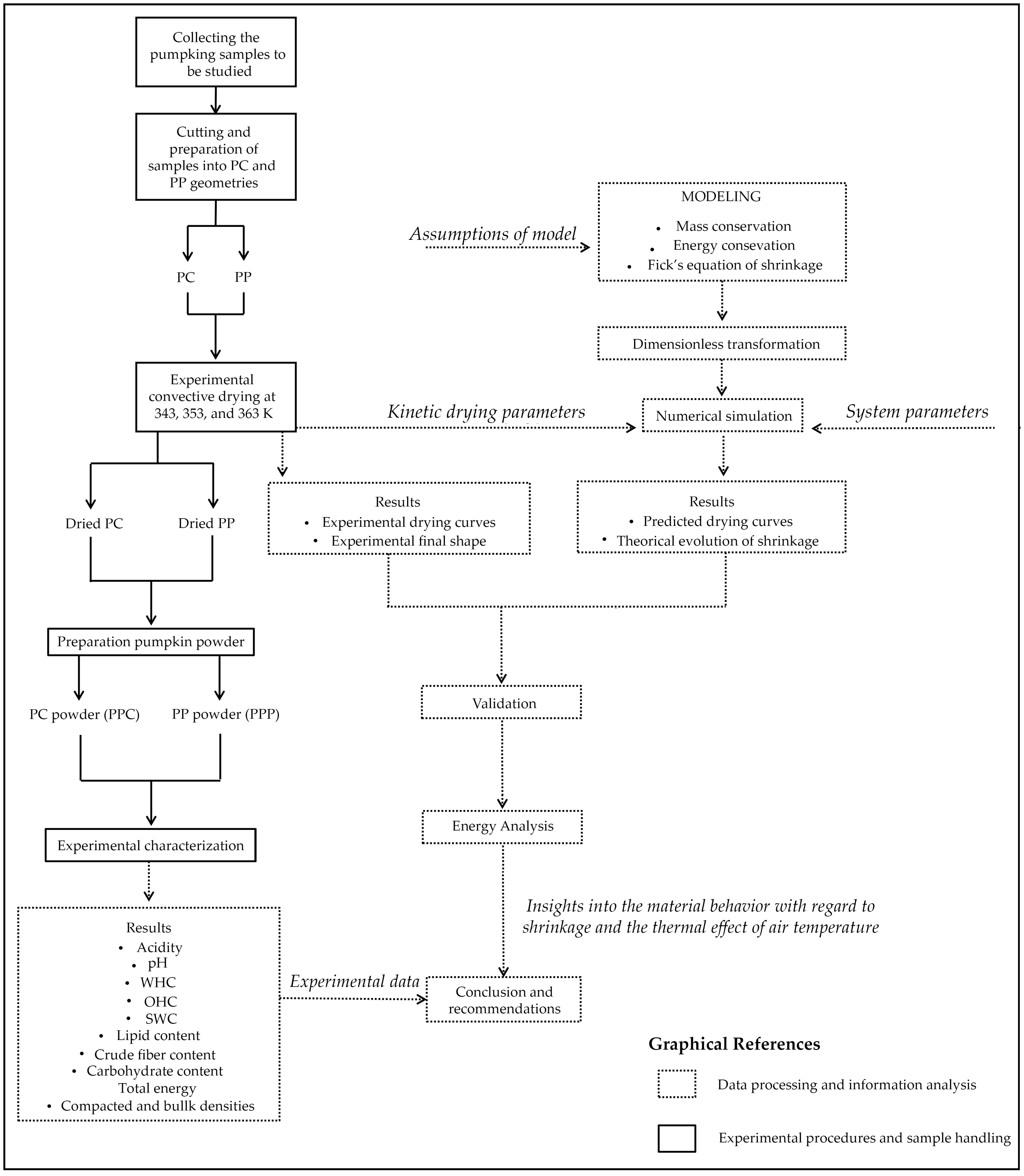
2. Materials and Methods
2.1. Sample Preparation
2.2. Drying Procedure
2.3. Determination of Kinetic Parameters
2.4. Mathematical Model
2.5. Numerical Simulation in COMSOL Multiphysics: Equations, Method, and Parameters
- Zero-flux boundary condition is represented by the following equation:
- b.
- The flux/source boundary condition in COMSOL is represented by the following equation:
2.6. Numerical Solution Methodology and Parameters
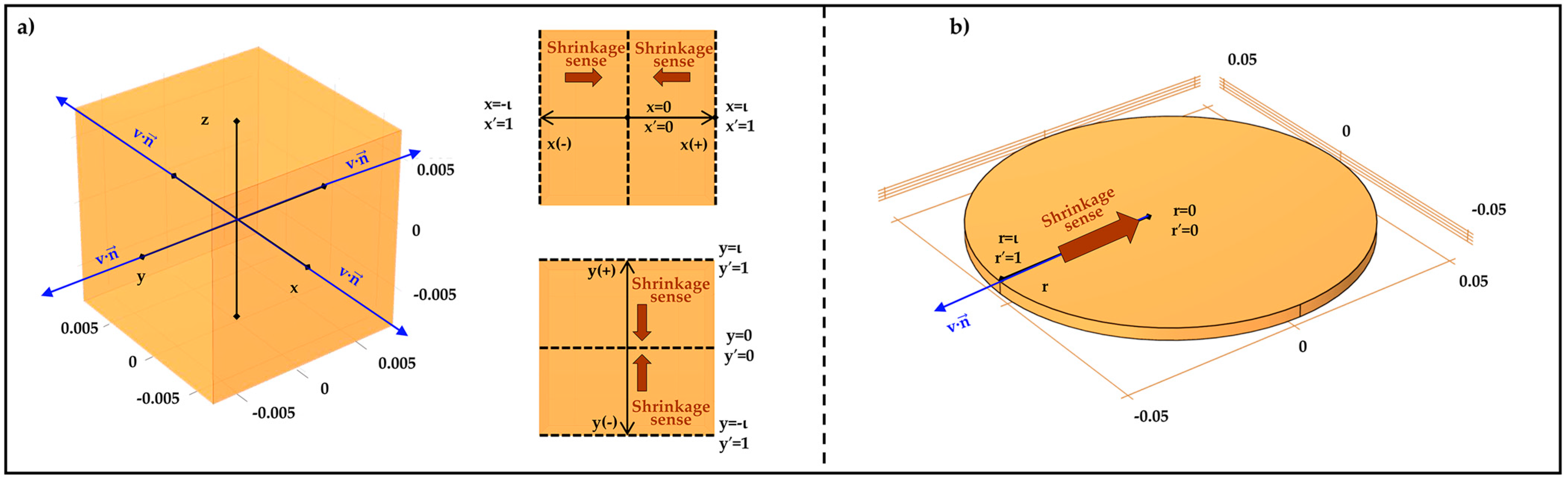
2.7. Graphical Representation of the Sample Shrinkage
2.8. Preparation and Characterization of Pumpkin Powder
2.9. Energy Analysis
2.10. Emissions of CO2
2.11. Statistical Analysis
3. Results and Discussion
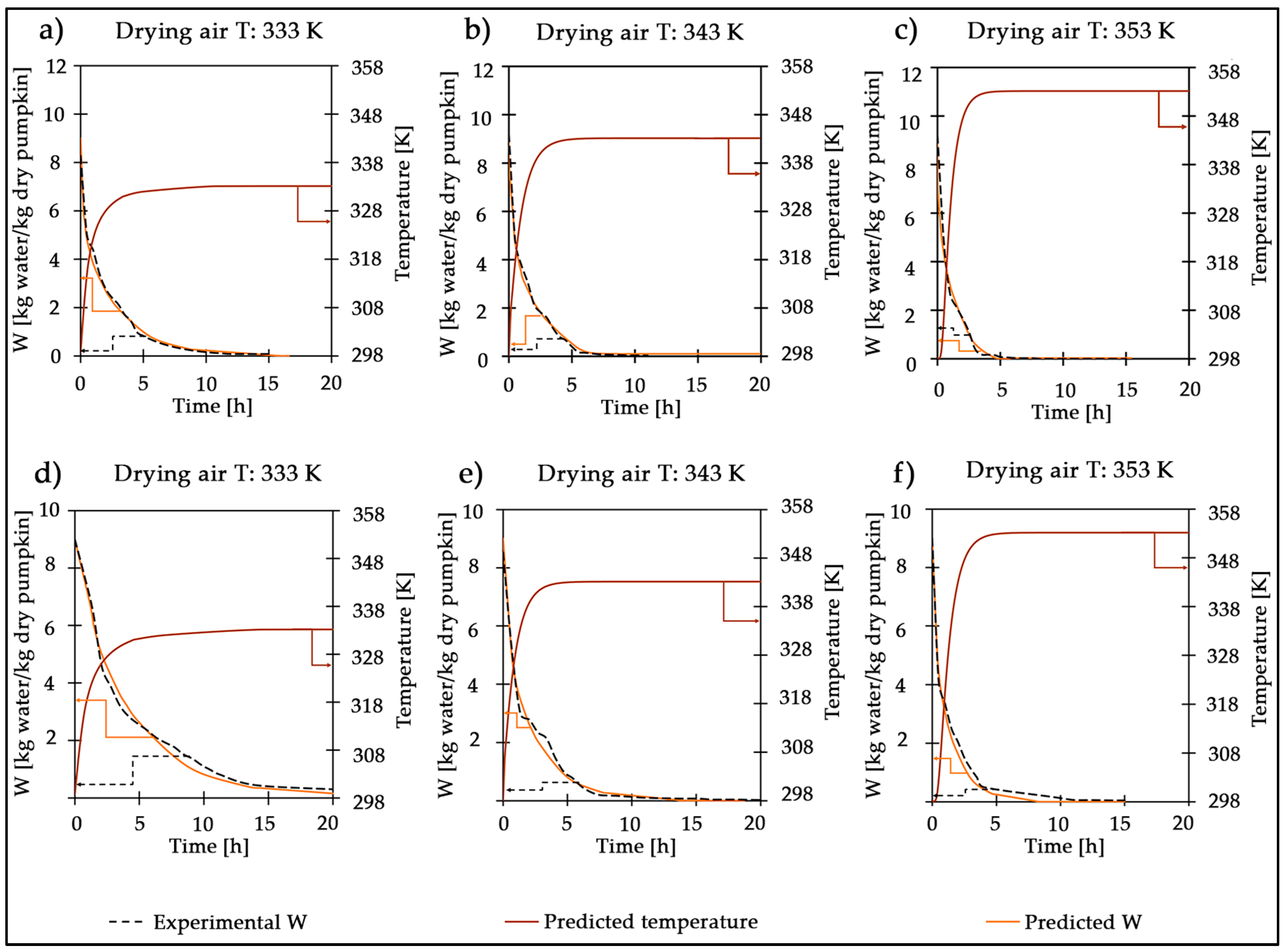
3.1. Mathematical Model: Drying Curves for PC and CC Geometries
3.2. Graphical Representation of the Sample Shrinkage
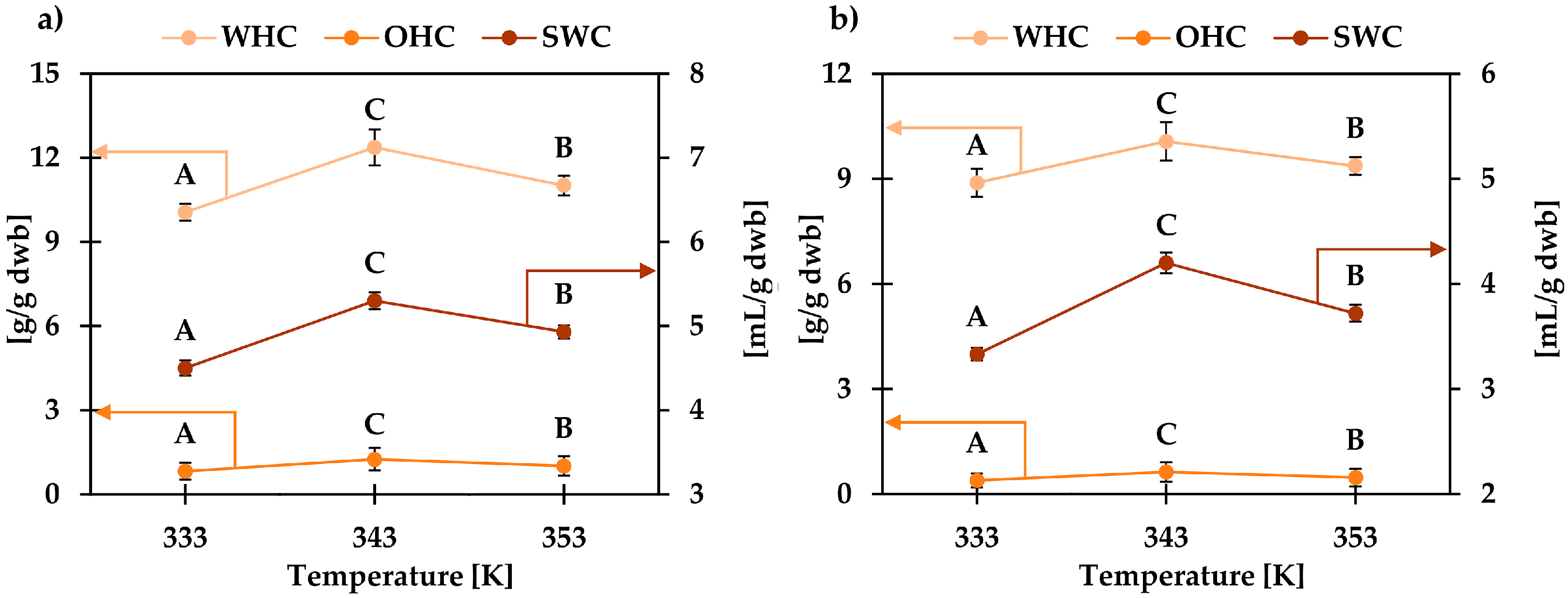
3.3. Obtaining Dried Pumpkin Powder and Corresponding Characterization
3.4. SEC and CO2 Emissions
3.5. Innovative Contributions and Originality of This Research
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| dwb | Dry weight basis |
| OHC | Oil holding capacity |
| PC | Pumpkin cubes |
| PPC | Pumpkin powders from cubes |
| PP | Pumpkin puree |
| PPP | Pumpkin powders from puree |
| RMSE | Squared root squared errors |
| SSE | Sum of squared errors |
| SWC | Swelling capacity |
| WHC | Water holding capacity |
Nomenclature
| Symbols | |
| Surface vector (m2) | |
| BiT | Thermal Biot number (dimensionless) |
| Bm | Mass Biot number (dimensionless) |
| Ca | Concentration of water vapor in the air (kg/m3) |
| Cp | Solid (pumpkin) specific heat (kJ/(kg K)) |
| Cs | Concentration of water vapor at the surface of the sample (kg/m3) |
| D0 | Arrhenius pre-exponential factor (m2/s) |
| Deff | Effective diffusion coefficient (m2/s) |
| Ea | Activation energy (kJ/mol) |
| G | Lag factor (dimensionless) |
| g | Heat input rate (flux/source boundary condition) (dimensionless) |
| hm | Convective mass transfer coefficient (m/s) |
| hc | Heat transfer coefficient (W/m2 K) |
| Gradient term of flux/source boundary condition (dimensionless) | |
| k | Thermal conductivity (W/m K) |
| L | Length change with respect to time (m) |
| Le | Lewis number (dimensionless) |
| MR | Moisture ratio, dimensionless |
| Unit vector normal to the transfer area (dimensionless) | |
| Nu | Nusselt dimensionless number (dimensionless) |
| Saturated water vapor pressure (dimensionless) | |
| Pr | Prandtl dimensionless number (dimensionless) |
| q | Coefficient of a Robin boundary condition of COMSOL (dimensionless) |
| r | R-coordinate (m) |
| R | Universal gas constant (kJ/mol K) |
| Re | Reynolds number (dimensionless) |
| Sdr | Drying rate constant (1/s) |
| S | Shrinkage ratio (dimensionless) |
| Sc | Schmidt dimensionless number (dimensionless) |
| Sh | Sherwood dimensionless number (dimensionless) |
| t | Time (s) |
| T | Surface temperature (K) |
| U | Term of the dependent variable of boundary condition (the units of U in the boundary condition depend on the considered variable) |
| V | Velocity module (m/s) |
| Vs | Volume of the food sample (m3) |
| x | X coordinate (m) |
| y | Y coordinate (m) |
| z | Z coordinate (m) |
| W | Specific moisture content (kg water/kg dry matter) |
| Water vaporization latent heat of (kJ/kg) | |
| Greek letters | |
| Thermal diffusivity of the material (m2/s) | |
| Pumpkin sample thickness length (m) | |
| Solid (pumpkin) density on a dry basis (kg/m3) | |
| Water density (kg/m3) | |
| χ2 | Chi-squared (dimensionless) |
| τ | Fourier number (dimensionless time), (dimensionless) |
| Superscripts and subscripts | |
| ′ | Prime symbol indicates the dimensionless version of the variable or parameter |
| 0 | Initial condition |
| a | Relative to the air |
| e | Equilibrium condition |
| r | Relative to the r coordinate direction |
| sat | Relative to the saturated vapor |
| x | Relative to the x coordinate direction |
| y | Relative to the y coordinate direction |
| z | Relative to the z coordinate direction |
Appendix A
Appendix A.1. Fick’s Equation of Shrinkage
- The equations representing the transport mechanisms had domains in the x and y variables for PC (2D) and in the r variable for PP (1D-axisymmetric).
- Shrinkage occurs on the x and y axes for PC, and the r axis for PP.
- The moisture content is homogeneously distributed throughout the volume of the cube or area of puree and slices, respectively, at the initial time.
- The effective diffusion coefficient is a function of two variables, namely moisture content and temperature.
- Shrinkage occurs at the interface between the solid and air.
- Water transport occurs only by diffusive phenomena.
- Air flux is uniform throughout the convective dryer and drying occurs at isothermal conditions.
- To model the deformation of PC, the lengths of the x and y axes, which form the structure, were shortened in length ι (see Figure 2a). Thus, the cube walls attached to these axes contract causing the volume reduction.
- Similarly, for PP samples, the radius to be shortening was considered (see Figure 2b). Although the PP samples do not symmetrically contract (because the tissue structures were broken and decreased in size) were modeled considering the equivalent transfer area calculated from r.
Appendix A.2. Dimensionless Transformation of Equation
Appendix A.2.1. Mass Conservation
- For 2D (PC geometry):
Appendix A.2.2. Energy Conservation
Appendix A.2.3. Fick’s Equation of Shrinkage
Appendix A.2.4. General Formulation for Modeling in COMSOL
References
- Enneb, S.; Drine, S.; Bagues, M.; Triki, T.; Boussora, F.; Guasmi, F.; Nagaz, K.; Ferchichi, A. Phytochemical Profiles and Nutritional Composition of Squash (Cucurbita moschata D.) from Tunisia. S. Afr. J. Bot. 2020, 130, 165–171. [Google Scholar] [CrossRef]
- Bemfeito, C.M.; Carneiro, J.d.D.S.; Carvalho, E.E.N.; Coli, P.C.; Pereira, R.C.; Vilas Boas, E.V.d.B. Nutritional and Functional Potential of Pumpkin (Cucurbita moschata) Pulp and Pequi (Caryocar brasiliense Camb.) Peel Flours. J. Food Sci. Technol. 2020, 57, 3920–3925. [Google Scholar] [CrossRef]
- Sathiya Mala, K.; Aathira, P.; Anjali, E.K.; Srinivasulu, K.; Sulochanamma, G. Effect of Pumpkin Powder Incorporation on the Physico-Chemical, Sensory and Nutritional Characteristics of Wheat Flour Muffins. Int. Food Res. J. 2018, 25, 1081–1087. [Google Scholar]
- Melese, A.D.; Keyata, E.O. Effects of Blending Ratios and Baking Temperature on Physicochemical Properties and Sensory Acceptability of Biscuits Prepared from Pumpkin, Common Bean, and Wheat Composite Flour. Heliyon 2022, 8, e10848. [Google Scholar] [CrossRef]
- Gul, K.; Tak, A.; Singh, A.K.; Singh, P.; Yousuf, B.; Wani, A.A. Chemistry, Encapsulation, and Health Benefits of β-Carotene—A Review. Cogent Food Agric. 2015, 1, 1018696. [Google Scholar] [CrossRef]
- Nasrollahzadeh, A.; Mokhtari, S.; Khomeiri, M.; Saris, P.E.J. Antifungal Preservation of Food by Lactic Acid Bacteria. Foods 2022, 11, 395. [Google Scholar] [CrossRef]
- Zalazar-Garcia, D.; Román, M.C.; Fernandez, A.; Asensio, D.; Zhang, X.; Fabani, M.P.; Rodriguez, R.; Mazza, G. Exergy, Energy, and Sustainability Assessments Applied to RSM Optimization of Integrated Convective Air-Drying with Pretreatments to Improve the Nutritional Quality of Pumpkin Seeds. Sustain. Energy Technol. Assess. 2022, 49, 101763. [Google Scholar] [CrossRef]
- Riveros-Gomez, M.; Baldán, Y.; Román, M.C.; Fabani, M.P.; Mazza, G.; Rodríguez, R. Drying and Rehydration Kinetics of Peeled and Unpeeled Green Apple Slices (Granny Smith Cv). J. Environ. Sci. Health Part B 2022, 57, 835–847. [Google Scholar] [CrossRef]
- Sandoval-Torres, S.; Tovilla-Morales, A.S.; Hernández-Bautista, E. Dimensionless Modeling for Convective Drying of Tuberous Crop (Solanum tuberosum) by Considering Shrinkage. J. Food Eng. 2017, 214, 147–157. [Google Scholar] [CrossRef]
- Ferreira, M.S.L.; Santos, M.C.P.; Moro, T.M.A.; Basto, G.J.; Andrade, R.M.S.; Gonçalves, É.C.B.A. Formulation and Characterization of Functional Foods Based on Fruit and Vegetable Residue Flour. J. Food Sci. Technol. 2015, 52, 822–830. [Google Scholar] [CrossRef] [PubMed]
- Mitiku, D.H.; Bereka, T.Y. Effects of Pumpkin (Cucurbita moschata)/Soybean (Glycine max) Flour Blends on Functional, Physic-Chemical Properties and Sensory Attributes of Breads Produced from Whole Wheat (Triticum aestivum L.). Carpathian J. Food Sci. Technol. 2021, 13, 134–144. [Google Scholar]
- Román, M.C.; Mut, I.; Echegaray, M.; Fabani, M.P.; Mazza, G.; Rodríguez, R. Pumpkin Peel Dehydration Using a Fluidized Bed Contactor: A Technical and Environmental Study. Biomass Convers. Biorefinery 2024. [Google Scholar] [CrossRef]
- Rahman, M.M.; Joardder, M.U.H.; Khan, M.I.H.; Pham, N.D.; Karim, M.A. Multi-Scale Model of Food Drying: Current Status and Challenges. Crit. Rev. Food Sci. Nutr. 2018, 58, 858–876. [Google Scholar] [CrossRef]
- Buvaneswaran, M.; Natarajan, V.; Sunil, C.K.; Rawson, A. Effect of Pretreatments and Drying on Shrinkage and Rehydration Kinetics of Ginger (Zingiber officinale). J. Food Process Eng. 2022, 45, e13972. [Google Scholar] [CrossRef]
- Srikiatden, J.; Roberts, J.S. Predicting Moisture Profiles in Potato and Carrot during Convective Hot Air Drying Using Isothermally Measured Effective Diffusivity. J. Food Eng. 2008, 84, 516–525. [Google Scholar] [CrossRef]
- Zheng, Z.; Wei, S.; Xie, W.; Ren, L.; Fan, B.; Fu, H.; Yang, D. Determination and Comparison of Effective Moisture Diffusivity of Carrot (Core and Cortex) during Hot Air Drying. J. Food Process Eng. 2022, 46, e14236. [Google Scholar] [CrossRef]
- Singh, P.; Talukdar, P. Determination of Shrinkage Characteristics of Cylindrical Potato during Convective Drying Using Novel Image Processing Technique. Heat Mass Transf. Stoffuebertragung 2020, 56, 1223–1235. [Google Scholar] [CrossRef]
- Dadmohammadi, Y.; Datta, A.K. Food as Porous Media: A Review of the Dynamics of Porous Properties during Processing. Food Rev. Int. 2022, 38, 953–985. [Google Scholar] [CrossRef]
- Marques, B.; Perré, P.; Casalinho, J.; Tadini, C.C.; Plana-Fattori, A.; Almeida, G. Evidence of Iso-Volume Deformation during Convective Drying of Yacón: An Extended van Meel Model Adapted to Large Volume Reduction. J. Food Eng. 2023, 341, 111311. [Google Scholar] [CrossRef]
- Maskan, M. Drying, Shrinkage and Rehydration Characteristics of Kiwifruits during Hot Air and Microwave Drying. J. Food Eng. 2001, 48, 177–182. [Google Scholar] [CrossRef]
- Seremet, L.; Botez, E.; Nistor, O.V.; Andronoiu, D.G.; Mocanu, G.D. Effect of Different Drying Methods on Moisture Ratio and Rehydration of Pumpkin Slices. Food Chem. 2016, 195, 104–109. [Google Scholar] [CrossRef] [PubMed]
- Chikpah, S.K.; Korese, J.K.; Sturm, B.; Hensel, O. Colour Change Kinetics of Pumpkin (Cucurbita moschata) Slices during Convective Air Drying and Bioactive Compounds of the Dried Products. J. Agric. Food Res. 2022, 10, 100409. [Google Scholar] [CrossRef]
- Chandramohan, V.P. Convective Drying of Food Materials: An Overview with Fundamental Aspect, Recent Developments, and Summary. Heat Transf.-Asian Res. 2020, 49, 1281–1313. [Google Scholar] [CrossRef]
- Katekawa, M.E.; Silva, M.A. A Review of Drying Models Including Shrinkage Effects. Dry. Technol. 2006, 24, 5–20. [Google Scholar] [CrossRef]
- Agrawal, S.G.; Methekar, R.N. Mathematical Model for Heat and Mass Transfer during Convective Drying of Pumpkin. Food Bioprod. Process. 2017, 101, 68–73. [Google Scholar] [CrossRef]
- Jin, X.; van der Sman, R.G.M.; van Boxtel, A.J.B. Evaluation of the Free Volume Theory to Predict Moisture Transport and Quality Changes During Broccoli Drying. Dry. Technol. 2011, 29, 1963–1971. [Google Scholar] [CrossRef]
- Nan, H.; Huang, R.; Zhang, X.; Wang, C. How Does Ball-Milling Elevate Biochar as a Value-Added Peroxydisulfate Activator for Antibiotics Removal? Ind. Crops Prod. 2024, 214, 118569. [Google Scholar] [CrossRef]
- Zalazar-Garcia, D.; Fernandez, A.; Rodriguez-Ortiz, L.; Rodriguez, R.; Mazza, G. Sustainable Slow-Pyrolysis Simulation of 12 Lignocellulosic Bio-Wastes: CO2 Emission, Energy, and Water Consumption. IOP Conf. Ser. Earth Environ. Sci. 2022, 952, 012008. [Google Scholar] [CrossRef]
- Fernandez, A.; Zalazar-García, D.; Lorenzo-Doncel, C.; Yepes Maya, D.M.; Silva Lora, E.E.; Rodriguez, R.; Mazza, G. Kinetic Modeling of Co-Pyrogasification in Municipal Solid Waste (MSW) Management: Towards Sustainable Resource Recovery and Energy Generation. Sustainability 2024, 16, 4056. [Google Scholar] [CrossRef]
- Garau, M.C.; Simal, S.; Femenia, A.; Rosselló, C. Drying of Orange Skin: Drying Kinetics Modelling and Functional Properties. J. Food Eng. 2006, 75, 288–295. [Google Scholar] [CrossRef]
- Panyawong, S.; Devahastin, S. Determination of Deformation of a Food Product Undergoing Different Drying Methods and Conditions via Evolution of a Shape Factor. J. Food Eng. 2007, 78, 151–161. [Google Scholar] [CrossRef]
- De Michelis, A.; Márquez, C.A.; Mabellini, A.; Ohaco, E.; Giner, S.A. Effect of Structural Modifications on the Drying Kinetics of Foods: Changes in Volume, Surface Area and Product Shape. Int. J. Food Stud. 2013, 2, 188–211. [Google Scholar] [CrossRef]
- Márquez, C.A.; de Michelis, A. Comparison of Drying Kinetics for Small Fruits with and without Particle Shrinkage Considerations. Food Bioprocess Technol. 2011, 4, 1212–1218. [Google Scholar] [CrossRef]
- Pineda-Vargas, A.J.; Mejía-Doria, C.M.; Duque-Cifuentes, A.L. Evaluation of the Drying Effect on Some Properties of Chayote Flour Sechium edule (Jacq.) Sw. DYNA 2020, 87, 191–195. [Google Scholar] [CrossRef]
- Fabani, M.P.; Román, M.C.; Rodriguez, R.; Mazza, G. Minimization of the Adverse Environmental Effects of Discarded Onions by Avoiding Disposal through Dehydration and Food-Use. J. Environ. Manag. 2020, 271, 110947. [Google Scholar] [CrossRef] [PubMed]
- FAO. Codex Alimentarius Codex Standard for Wheat Flour. In International Food Standards; FAO: Rome, Italy, 1985; p. 152. [Google Scholar]
- Roman, M.C.; Fabani, M.P.; Luna, L.C.; Feresin, G.E.; Mazza, G.; Rodriguez, R. Convective Drying of Yellow Discarded Onion (Angaco INTA): Modelling of Moisture Loss Kinetics and Effect on Phenolic Compounds. Inf. Process. Agric. 2020, 7, 333–341. [Google Scholar] [CrossRef]
- AOAC. Official Method of Analysis: Association of Analytical Chemists; AOAC INTERNATIONAL, Ed.; AOAC: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Dincer, I.; Dost, S. An Analytical Model for Moisture Diffusion in Solid Objects during Drying. Dry. Technol. 1995, 13, 425–435. [Google Scholar] [CrossRef]
- Dincer, I.; Dost, S. A Modelling Study for Moisture Diffusivities and Moisture Transfer Coefficients in Drying of Solid Objects. Int. J. Energy Res. 1996, 20, 531–539. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Janius, R.B.; Nawi, N.; Abdan, K. Modelling Effective Moisture Diffusivity of Pumpkin (Cucurbita moschata) Slices under Convective Hot Air Drying Condition. Int. J. Food Eng. 2016, 12, 481–489. [Google Scholar] [CrossRef]
- Brodkey, R.S.; Hershey, H.C. Transport Phenomena: A Unified Approach; McGraw-Hill Series in Marketing; McGraw-Hill: New York, NY, USA, 1988; ISBN 9780070079632. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: London, UK, 1975. [Google Scholar]
- Dwivedi, P.N.; Upadhyay, S.N. Particle-Fluid Mass Transfer in Fixed and Fluidized Beds. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 157–165. [Google Scholar] [CrossRef]
- Marques, B.C.; Plana-Fattori, A.; Flick, D.; Tadini, C.C. Convective Drying of Yacón (Smallanthus sonchifolius) Slices: A Simple Physical Model Including Shrinkage. LWT 2022, 159, 113151. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Comsol Multiphysics Reference Manual: Version 5.6. Manual; 2014; Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 26 June 2024).
- Afaghi, N.; Motlagh, A.M.; Seiedlou, S.S.; Hasanpour, A. Simulation Shrinkage and Stress Generated during Convective Drying of Carrot Slices. Int. J. Adv. Biol. Biomed. Res. 2013, 1, 1660–1668. [Google Scholar]
- Turner, I.W. A Two-Dimensional Orthotropic Model for Simulating Wood Drying Processes. Appl. Math. Model. 1996, 20, 60–81. [Google Scholar] [CrossRef]
- Wang, N.; Brennan, J.G. A Mathematical Model of Simultaneous Heat and Moisture Transfer during Drying of Potato. J. Food Eng. 1995, 24, 47–60. [Google Scholar] [CrossRef]
- Sweat, V.E.; Lafayette, W. Experimental values of thermal conductivity of selected fruits and vegetables. J. Food Sci. 1974, 39, 1080–1083. [Google Scholar] [CrossRef]
- Rao, M.A.; Rizvi, S.S.; Datta, A.K.; Ahmed. Engineering Properties of Foods; Springer: Singapore, 2014. [Google Scholar]
- Mayor, L.; Moreira, R.; Sereno, A.M. Shrinkage, Density, Porosity and Shape Changes during Dehydration of Pumpkin (Cucurbita pepo L.) Fruits. J. Food Eng. 2011, 103, 29–37. [Google Scholar] [CrossRef]
- Yang, H.; Sakai, N.; Watanabe, M. Drying Model with Non-Isotropic Shrinkage Deformation Undergoing Simultaneous Heat and Mass Transfer. Dry. Technol. 2001, 19, 1441–1460. [Google Scholar] [CrossRef]
- Capossio, J.P.; Fabani, M.P.; Román, M.C.; Zhang, X.; Baeyens, J.; Rodriguez, R.; Mazza, G. Zero-Waste Watermelon Production through Nontraditional Rind Flour: Multiobjective Optimization of the Fabrication Process. Processes 2022, 10, 1984. [Google Scholar] [CrossRef]
- Robertson, J.A.; de Monredon, F.D.; Dysseler, P.; Guillon, F.; Amado, R.; Thibault, J.-F. Hydration Properties of Dietary Fibre and Resistant Starch: A European Collaborative Study. LWT—Food Sci. Technol. 2000, 33, 72–79. [Google Scholar] [CrossRef]
- ASTM. Annual Book of ASTM Standards; American Society for Testing and Materials Staff: West Conshohocken, PA, USA, 1985; ISBN 9780803106628. [Google Scholar]
- Campuzano, A.; Rosell, C.M.; Cornejo, F. Physicochemical and Nutritional Characteristics of Banana Flour during Ripening. Food Chem. 2018, 256, 11–17. [Google Scholar] [CrossRef]
- Baldán, Y.; Riveros, M.; Fabani, M.P.; Rodriguez, R. Grape Pomace Powder Valorization: A Novel Ingredient to Improve the Nutritional Quality of Gluten-Free Muffins. Biomass Convers. Biorefinery 2021, 13, 9997–10009. [Google Scholar] [CrossRef]
- Yusof, Y.A.; Mohd Salleh, F.S.; Chin, N.L.; Talib, R.A. The Drying and Tabletting of Pitaya Powder. J. Food Process Eng. 2012, 35, 763–771. [Google Scholar] [CrossRef]
- Kaveh, M.; Amiri Chayjan, R. Modeling Thin-Layer Drying of Turnip Slices Under Semi-Industrial Continuous Band Dryer. J. Food Process. Preserv. 2017, 41, e12778. [Google Scholar] [CrossRef]
- Climate Transparency Comparing G20 Climate Action and Responses to the COVID-19 Crisis. 2020, pp. 1–20. Available online: https://www.climate-transparency.org/wp-content/uploads/2020/11/Climate-Transparency-Report-2020.pdf (accessed on 26 June 2024).
- Vega-Gálvez, A.; Di Scala, K.; Rodríguez, K.; Lemus-Mondaca, R.; Miranda, M.; López, J.; Perez-Won, M. Effect of Air-Drying Temperature on Physico-Chemical Properties, Antioxidant Capacity, Colour and Total Phenolic Content of Red Pepper (Capsicum annuum, L. Var. Hungarian). Food Chem. 2009, 117, 647–653. [Google Scholar] [CrossRef]
- Balzarini, M.F.; Reinheimer, M.A.; Ciappini, M.C.; Scenna, N.J. Mathematical Model, Validation and Analysis of the Drying Treatment on Quality Attributes of Chicory Root Cubes Considering Variable Properties and Shrinkage. Food Bioprod. Process. 2018, 111, 114–128. [Google Scholar] [CrossRef]
- Yuan, Y.; Tan, L.; Xu, Y.; Yuan, Y.; Dong, J. Numerical and Experimental Study on Drying Shrinkage-Deformation of Apple Slices during Process of Heat-Mass Transfer. Int. J. Therm. Sci. 2019, 136, 539–548. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, J.; Liao, X.; Chen, F.; Zhao, G.; Wu, J.; Hu, X. Mathematical Modeling on Hot Air Drying of Thin Layer Apple Pomace. Food Res. Int. 2007, 40, 39–46. [Google Scholar] [CrossRef]
- Das Purkayastha, M.; Nath, A.; Deka, B.C.; Mahanta, C.L. Thin Layer Drying of Tomato Slices. J. Food Sci. Technol. 2013, 50, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Cano-Chauca, M.; Ramos, A.M.; Stringheta, P.; Pereira, J.A.M. Drying Curves and Water Activity Evaluation of Dried Banana. In Proceedings of the Drying 2004—Proceedings of the 14th International Drying Symposium (IDS 2004), São Paulo, Brazil, 22–25 August 2004; Volume C, pp. 2013–2020. [Google Scholar]
- Mutuli, G.P.; Gitau, A.N.; Mbuge, D.O. Convective Drying Modeling Approaches: A Review for Herbs, Vegetables, and Fruits. J. Biosyst. Eng. 2020, 45, 197–212. [Google Scholar] [CrossRef]
- Aguilera, J.M.; Stanley, D.W. Microstructural Principles of Food Processing and Engineering; Springer Science & Business Media: Berlin, Germany, 1999; ISBN 0834212560. [Google Scholar]
- Zzaman, W.; Biswas, R.; Hossain, M.A. Application of Immersion Pre-Treatments and Drying Temperatures to Improve the Comprehensive Quality of Pineapple (Ananas comosus) Slices. Heliyon 2021, 7, e05882. [Google Scholar] [CrossRef]
- Rodríguez, Ó.; Gomes, W.; Rodrigues, S.; Fernandes, F.A.N. Effect of Acoustically Assisted Treatments on Vitamins, Antioxidant Activity, Organic Acids and Drying Kinetics of Pineapple. Ultrason. Sonochem. 2017, 35, 92–102. [Google Scholar] [CrossRef] [PubMed]
- Garau, M.C.; Simal, S.; Rosselló, C.; Femenia, A. Effect of Air-Drying Temperature on Physico-Chemical Properties of Dietary Fibre and Antioxidant Capacity of Orange (Citrus aurantium v. Canoneta) by-Products. Food Chem. 2007, 104, 1014–1024. [Google Scholar] [CrossRef]
- Salehi, F.; Hosseini Ghaboos, S.H. Modeling of Peach Drying Process Using Infrared Dryer by Genetic Algorithm Method. J. Food Technol. Nutr. 2019, 16, 17–26. [Google Scholar]
- Brandão, S.C.R.; da Silva, E.M.; de Arruda, G.M.P.; de Souza Netto, J.M.; de Medeiros, R.A.B.; Honorato, F.A.; Azoubel, P.M. Ethanol Pretreatment and Infrared Drying of Melon: Kinetics, Quality Parameters, and NIR Spectra. J. Food Process Eng. 2023, 46, e14269. [Google Scholar] [CrossRef]
- Wang, W.; Yan, Z.; Yao, H.; Li, P.; Peng, W.; Su, W.; Wang, Y. Extraction and Purification of Pedunculoside from the Dried Barks of Ilex Rotunda Using Crystallization Combined with Polyamide Column Chromatography. Sep. Sci. Technol. 2021, 56, 1710–1720. [Google Scholar] [CrossRef]
- Praznik, W.; Loeppert, R.; Viernstein, H.; Haslberger, A.G.; Unger, F.M. Dietary Fiber and Prebiotics BT. In Polysaccharides: Bioactivity and Biotechnology; Ramawat, K.G., Mérillon, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 891–925. ISBN 978-3-319-16298-0. [Google Scholar]
- Guiné, R.P.F.; Henrriques, F.; João Barroca, M. Mass Transfer Coefficients for the Drying of Pumpkin (Cucurbita moschata) and Dried Product Quality. Food Bioprocess Technol. 2012, 5, 176–183. [Google Scholar] [CrossRef]
- Lewin, M.; Basch, A. Structure, Pyrolysis, and Flammability of Cellulose. Flame-Retard. Polym. Mater. 1978, 2, 1–41. [Google Scholar] [CrossRef]
- López Mejía, N.; Morales Posada, N.B.; Lobatón García, H.F. Convective Drying Kinetics of Squash Epicarp of Cucurbita maxima and Its Uses in Developing Gluten-Free Bread. Rev. Mutis 2022, 12, 1–17. [Google Scholar] [CrossRef]
- Benítez, V.; Cantera, S.; Aguilera, Y.; Mollá, E.; Esteban, R.M.; Díaz, M.F.; Martín-Cabrejas, M.A. Impact of Germination on Starch, Dietary Fiber and Physicochemical Properties in Non-Conventional Legumes. Food Res. Int. 2013, 50, 64–69. [Google Scholar] [CrossRef]
- Chinma, C.E.; Lata, L.J.; Chukwu, T.M.; Azeez, S.O.; Ogunsina, B.S.; Ohuoba, E.U.; Yakubu, C.M. Effect of Germination Time on the Proximate Composition and Functional Properties of Moringa Seed Flour. Afr. J. Agric. Technol. Environ. 2017, 6, 117–133. [Google Scholar]
- Miquilena, E.; Higuera, A.M.; Rodríguez, B. Evaluation of Functional Properties of Four Flours from Edible Legume Seeds Cultivated in Venezuela. Rev. Fac. Agron. 2016, 33, 58–75. [Google Scholar]

| Mass Conservation | |
|---|---|
| Applied to the PC geometry: | |
| Equation of mass balance for 2D (PC geometry) | (3) |
| (4) | |
| (5) | |
| Applied to the PP geometry: | |
| (6) | |
| (7) | |
| (8) | |
| Energy conservation | |
| Applied to the PC geometry: | |
| Equation of energy balance for 2D (PC geometry) | (9) |
| Applied to the PP geometry: | |
| (10) | |
| Initial conditions | |
| (11) | |
| Symmetry considerations Applied to the PC geometry: | |
| (12) | |
| (13) | |
| Applied to the PP geometry: | |
| (14) | |
| (15) | |
| Domain | Mathematical Dimensionless Expression | Unknowns | |
|---|---|---|---|
| Mass conservation | PC geometry | (18) | W′ |
| PP geometry: | |||
| Energy conservation | PC geometry | (19) | T′ |
| PP geometry: | |||
| Fick’s equation of shrinkage | For PC geometry: | (20) | S′ |
| For PP geometry: | |||
| Flux Constraint | Mathematical Dimensionless Expression | Independent Variable Value for Specified Boundary Condition | |
|---|---|---|---|
| Zero-flux mass | (21) | ||
| For PP geometry: | |||
| Flux/source mass | For PC geometry: | (22) | |
| For PP geometry: | |||
| Zero-flux energy | (23) | ||
| For PP geometry: | |||
| Flux/source Energy | (24) | ||
| For PP geometry: | |||
| Parameter | Expression | Reference | |
|---|---|---|---|
| Arrhenius pre-exponential factor (m2/s) | Calculated for temperature range (333–353 K) | ||
| PC geometry | Calculated from experimental data | ||
| PP geometry | Calculated from experimental data | ||
| (kJ/mol) | Calculated for temperature range (333–353 K) | ||
| PC geometry | Calculated from experimental data | ||
| PP geometry | Calculated from experimental data | ||
| Mass Biot number, dimensionless | (25) | [8] | |
| Thermal Biot number, dimensionless | [9] | ||
| Latent heat of vaporization (kJ/kg) | (26) | [15] | |
| Heat transfer coefficient (W/m2K) estimated between (48.8–59.3) | (27) | [47] | |
| Mass transfer coefficient (m/s) Analogy dimensionless number (forced convection flux and flat plate with laminar flux) estimated between (0.11–0.124) | (28) | [25] | |
| Saturated water vapor pressure (Pa) | (29) | [48] | |
| Water vapor concentration at the surface of the sample (kg/m3) | (30) | [49] | |
| Thermal conductivity (W/(m K)) | (31) | [50] | |
| Specific heat Cp (J/(kg K)) | (32) | [51] | |
| Solid density on a dry basis (kg/m3) | (33) | [52] | |
| Density liquid water (kg/m3) | 1000 kg/m3 | [53] | |
| Initial moisture content of PC sample (kg water/kg dry matter) | 8.27 (333 K), 9.20 (343 K) and 9.20 (353 K) | Experimentally determined | |
| Initial moisture content of the PP sample (kg water/kg dry matter) | 9.00 (333 K), 8.52 (343 K) and 9.00 (353 K) | Experimentally determined | |
| Chemical Property | 343 K | 353 K |
|---|---|---|
| Moisture content [%] | 5.0 ± 0.6 a | 5.4 ± 0.5 a |
| Ash content [g/100 g dwb] | 8.26 ± 0.15 a | 8.01 ± 0.08 a |
| Lipids [g/100 g dwb] | 0.47 ± 0.02 b | 0.33 ± 0.01 a |
| Protein [g/100 g dwb] | 10.35 ± 0.30 a | 10.87 ± 0.72 a |
| Crude fibers [g/100 g dwb] | 7.01 ± 0.08 a | 13.58 ± 0.42 b |
| Total carbohydrates [g/100 g dwb] | 76.0 ± 0.2 a | 75.4 ± 0.8 a |
| Total energy [kcal/100 g dwb] | 349 ± 2 a | 348 ± 3 a |
| 333 K | 343 K | 353 K | |
|---|---|---|---|
| SEC [kW/kg] | 3911.44 | 3592.85 | 3502.97 |
| CO2 emissions [kg CO2/kW] | 1401.47 | 1287.32 | 1255.11 |
| Aspect | In this Study | Similarities and Differences | Referenced Studies |
|---|---|---|---|
| Impact of temperature | Higher temperatures accelerate the drying rate, leading to greater moisture removal and shorter drying times | Similar observation | Balzarini et al. [63]; Yuan et al. [64]; Wang et al. [65]; Das Purkayastha et al. [66] |
| Falling rate period | No constant rate phase was identified in the drying process; the entire drying process was in the falling rate period | Similar observation | Cano-Chauca et al. [67]; Das Purkayastha et al. [66] |
| Geometry and surface area | Differences between PC and PP geometries; smaller surface area in PP reduces the moisture transfer rate | No study emphasized the difference in geometry and moisture transfer rate | - |
| Shrinkage effects | Significant shrinkage and crack formation in PP affect the area of mass and heat transfer | Drying quality was mentioned but not delved into the effects of shrinkage and cracking | Balzarini et al. [63] |
| Particle-level modeling | Incorporates shrinkage effects and captures complex phenomena, surpassing limitations of empirical models | There was a focus on linear and empirical contraction models, but they did not fully capture complex phenomena | Garau et al. [30]; Panyawong and Devahastin [31] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mut, I.; Zalazar-García, D.; Román, M.C.; Baldán, Y.; Fernandez, A.; Fabani, M.P.; Blasetti, A.P.; Mazza, G.; Rodriguez, R. Transformation of Discarded Pumpkin into High-Value Powder: A Drying Process Model for Functional Food Ingredients. Agronomy 2024, 14, 1424. https://doi.org/10.3390/agronomy14071424
Mut I, Zalazar-García D, Román MC, Baldán Y, Fernandez A, Fabani MP, Blasetti AP, Mazza G, Rodriguez R. Transformation of Discarded Pumpkin into High-Value Powder: A Drying Process Model for Functional Food Ingredients. Agronomy. 2024; 14(7):1424. https://doi.org/10.3390/agronomy14071424
Chicago/Turabian StyleMut, Iside, Daniela Zalazar-García, María Celia Román, Yanina Baldán, Anabel Fernandez, María Paula Fabani, Alberto P. Blasetti, Germán Mazza, and Rosa Rodriguez. 2024. "Transformation of Discarded Pumpkin into High-Value Powder: A Drying Process Model for Functional Food Ingredients" Agronomy 14, no. 7: 1424. https://doi.org/10.3390/agronomy14071424
APA StyleMut, I., Zalazar-García, D., Román, M. C., Baldán, Y., Fernandez, A., Fabani, M. P., Blasetti, A. P., Mazza, G., & Rodriguez, R. (2024). Transformation of Discarded Pumpkin into High-Value Powder: A Drying Process Model for Functional Food Ingredients. Agronomy, 14(7), 1424. https://doi.org/10.3390/agronomy14071424












