Design and Test of the Outside-Filling Chinese Chive Adjustable-Capacity Precision Seed-Metering Device

Abstract

In order to innovate the planting mode and improve the quality of Chinese chive, we designed an outside-filling Chinese chive adjustable-capacity precision seed-metering device with an adjustable number of sown seeds. The diameter, number of shaped holes, and seed slot parameters of the seeding plate were designed based on the physical characteristics and agronomic planting requirements of the Haoji Chinese chive. A simulation of the seed-metering device’s seeding process was carried out using EDEM software. To carry out the quadratic general rotary combination design experiment, use seed slot diameter and seed slot depth as test factors, longitudinal concentration and transverse concentration as evaluation indexes, and carry out the bench validation test and comparison test under the optimal parameter combination. In the simulation test, the factors affecting the longitudinal concentration in order of priority were seed slot depth and seed slot diameter, and the factors affecting the transverse concentration in order of priority were seed slot diameter and seed slot depth. The optimal parameters were seed slot diameter of 3.075 mm, seed slot depth of 3.323 mm, longitudinal concentration of 0.563, and transverse concentration of 0.634. In the bench test, the relative error of longitudinal concentration was 3.20%, the relative error of transverse concentration was 2.47%, and the number of seeds sown per hole was linearly correlated with the length of the seed slot. The results of the bench test and simulation test are close to each other, which proves that the outside-filling Chinese chive adjustable-capacity precision seed-metering device has a better sowing effect, and the number of sowing grains can be adjusted.

1. Introduction

Chinese chive is a perennial root vegetable native to China. It has a long history of cultivation. The masses especially like it because of its high nutritional value and uniquely pungent flavour. It is also one of the most widely cultivated vegetables in China, with young leaves and tender flower stems, flowers, and young seeds for food [1,2]. In recent years, anti-seasonal Chinese chive planting has been increasing. However, the level of mechanization of Chinese chive in China is still low, the coverage of machinery application is not high enough, and many growers still use much manual labour in the production process. The labour force accounts for a large number of high production costs, and production efficiency is low, which seriously restricts vegetable farmers’ enthusiasm for planting vegetables. Chinese chive planting methods include direct seeding and seedling transplanting; mechanized Chinese chive planting is recommended using mechanical direct seeding. Direct seeding saves cost and increases income; high productivity and good quality can significantly improve economic and social benefits, but the sparse density is not uniform, there are differences in growth, and it is difficult to unify management, all of which affects the quality of Chinese chives [3,4]. The existing precision seed-metering devices are mainly divided into two categories: air-suction type and mechanical, according to different working principles. The air-suction seed-metering device has the characteristics of high sowing precision and strong adaptability to the shape and size of the seed. It adapts to the high-speed operation of large-scale seeding machines [5,6,7]. The mechanical seed-metering device, through the optimization of the design of the seed-taking parts, single- or multi-seed seed-taking, achieves the effect of precision sowing operations because of its reliable operation, simple structure, low cost, and other advantages, are in line with the needs of small-scale farmers in China and widely used in the current stage of agricultural production process [8,9]. Domestic scholars have done different research on precision hole-sowing seed-metering devices. Li et al. [10] designed a group air suction- type celery seed-metering device that breaks through the difficulty of air-suction seeder precision sowing, realizes celery precision hole sowing, and meets the agronomic requirements of celery with multiple seeds in one hole. Liu et al. [11] designed a duckbill millet seed-metering device, which realizes precise seeding per hole according to the physical characteristics of grain and combines with agronomic requirements. This device solves the serious problem of reseeding the existing grain seed-metering device. Li et al. [12] designed a seed ladle tongue-type flax precision burrow planter, combined with the agronomic requirements of film-covered planting in the Gansu region, to solve the traditional flax seed-metering device’s waste of seed, inaccurate number of holes, and uneven sowing problems. Ding et al. [13] designed a Cyperus esculentus cell-wheel seed-metering device with low-position seeding and cavitation function in response to the problem of irregular seed shape and dispersion of seed casting in hole sowing to reduce the seed- casting height and improve the effect of hole sowing. The above seed-metering devices can realize precision seeding, but their research focuses on precision hole sowing. For sowing, the number of adjustable aspects of the seed has seen much research; at this stage, for Chinese chive, seed-metering device research is also minimal. The most notable thing about manual planting of Chinese chive is that it consumes a lot of time and labour costs, and it is difficult to precisely control the number of seeds sown based on experience alone. This not only affects the seedling rate and growth quality of Chinese chive but may also result in the wastage of seeds, increase the cost of planting, and ultimately have a negative impact on farmers’ economic benefits. To effectively solve these problems, designing a mechanical Chinese chive seed-metering device with a simple structure and low cost is especially necessary. In this paper, based on the Chinese chive agronomic requirements and Chinese chive physical parameters, it is proposed to design an outside-filling Chinese chive adjustable-capacity precision seed-metering device with mechanical structure and determine the structural parameters of the seeder through theoretical analysis and simulation analysis. 3D printing technology is used to make a unique seed dispenser for a bench test, and image recognition technology is utilized to capture the horizontal and vertical coordinates of Chinese chive in the bench test to verify the simulation results, so as to reach the expected goal of precision hole sowing.

2. Materials and Methods

2.1. Structural Components

The outside-filling Chinese chive adjustable-capacity precision seed-metering device consists of a shell, barrier, seed-clearing brush, seeding plate, adjustment plate, limit screw, hexagonal shaft, seed-guide axis and so on, as shown in Figure 1. The seed box consists of the upper part of the shell, the barrier, and the seeding plate. The seed-clearing brush is fixed outside on the right side of the seed box. The adjustment plate is inserted and fitted with the seeding plate to form an adjustable seed groove, which is secured by a limit screw. Change the length of the seed slot to accommodate different seed quantity adjustments, thereby increasing or decreasing its volume.

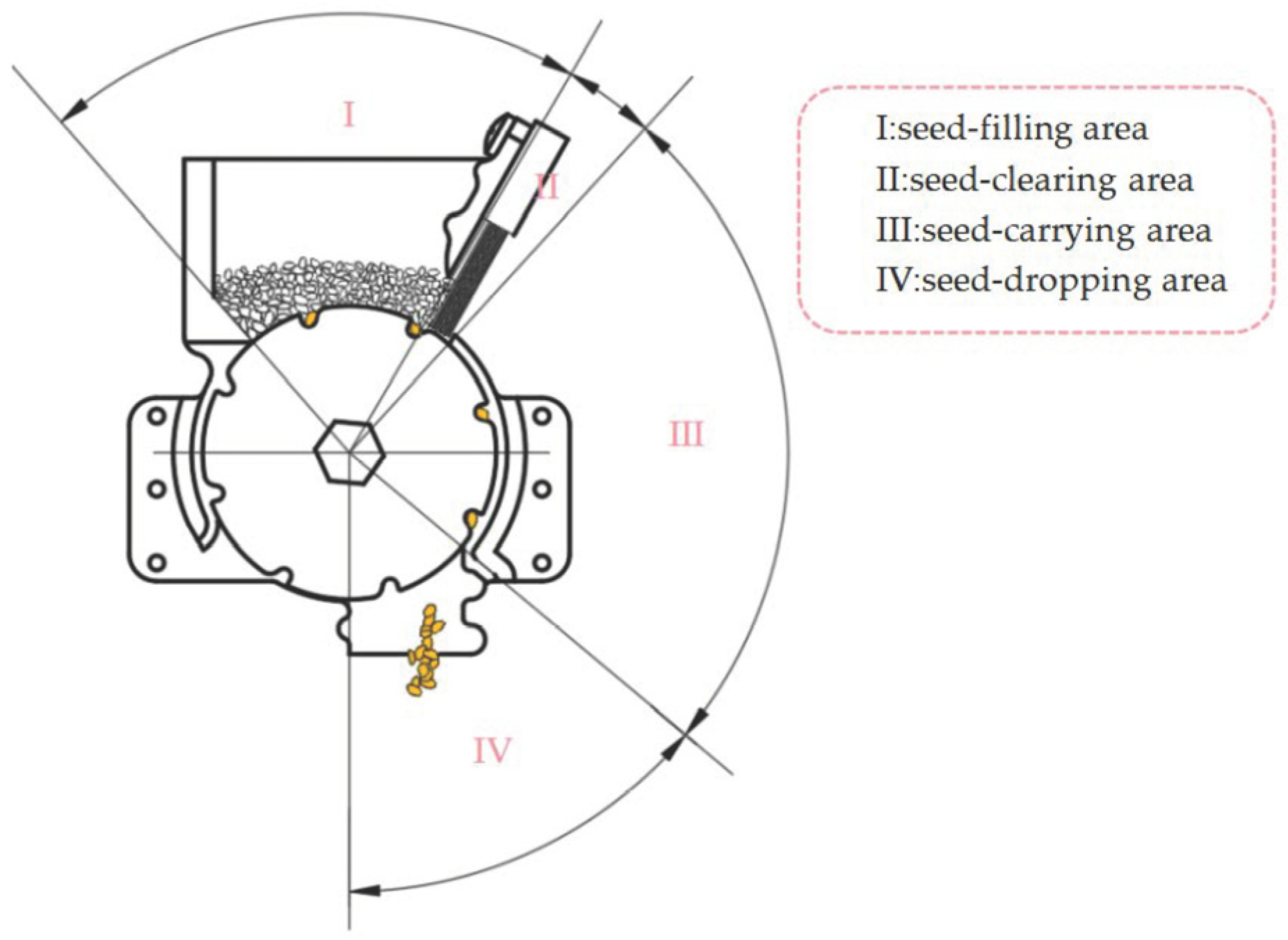
2.2. Work Principle

Adjustment plate and seeding plate is inserted with the formation of seed slot before work according to different seed varieties and the number of seeds-per-hole sowing requirements. Adjust the length of the seed slot and tighten the limit screws to fix the length of the seed slot. The seeding plate’s working process is divided into four stages: filling, clearing, carrying, and dropping. When the Chinese chive seed is placed into the seed box, the motor is inserted into the hexagonal shaft core to drive the row of seeding plate rotation in the clockwise direction. Seeds in the seed-filling area move through the row of seeding plate perturbation so that the seed group is in a discrete state and is more conducive to the filling of seeds [14]. Seeds in the seed box, in their gravity, friction, and the surrounding seed extrusion under the combined effect, fall into the seed-filling slot with the seeding plate rotation into the seed-cleaning area. The excess seed is scraped off under the action of the seed-clearing brush and enters the seed-carrying area with the seed-filling groove [15]. When the seeding plate is rotated to the upper end of the seed-guide axis, the seed enters the seed-dropping area under gravity and centrifugal force and falls into the seed furrow through the seed-guide axis (Figure 2).

2.3. Agronomic Requirements for Growing Chinese Chive

Chinese chive is usually used in spring and fall planting, with sowing from March to May and transplanting from September to October. The sowing row spacing is 30 cm, and the plant spacing is 20 cm and about 15 grains per hole. Compared with direct sowing, hole sowing can better control the number and location of seeds, making the spacing between plants more uniform and facilitating growth and harvesting [16]. Planting agronomic requirements provide the basis for the structural design of the seed-metering device [17].

2.4. Basic Parameters Chinese Chive

The physical parameters of the seed are essential in the design of seed-metering devices [18]. In this paper, the seed-metering device is designed based on the parameters of the Haoji Chinese chive, and 200 grains were randomly selected as the test object. The maximum values of triaxial dimensions of length, width, and thickness of seeds were measured as 3.95, 3.09, and 1.61 mm, respectively; the minimum values of triaxial dimensions of length, width, and thickness were calculated as 2.95, 1.94, and 0.63 mm, respectively; the mean values of triaxial dimensions of length, width, and thickness were measured as 3.39, 2.64, and 1.24 mm, respectively; and the average mass of 1000 kernels was 3.26 g. The density of seeds was 1.129 g/cm³.

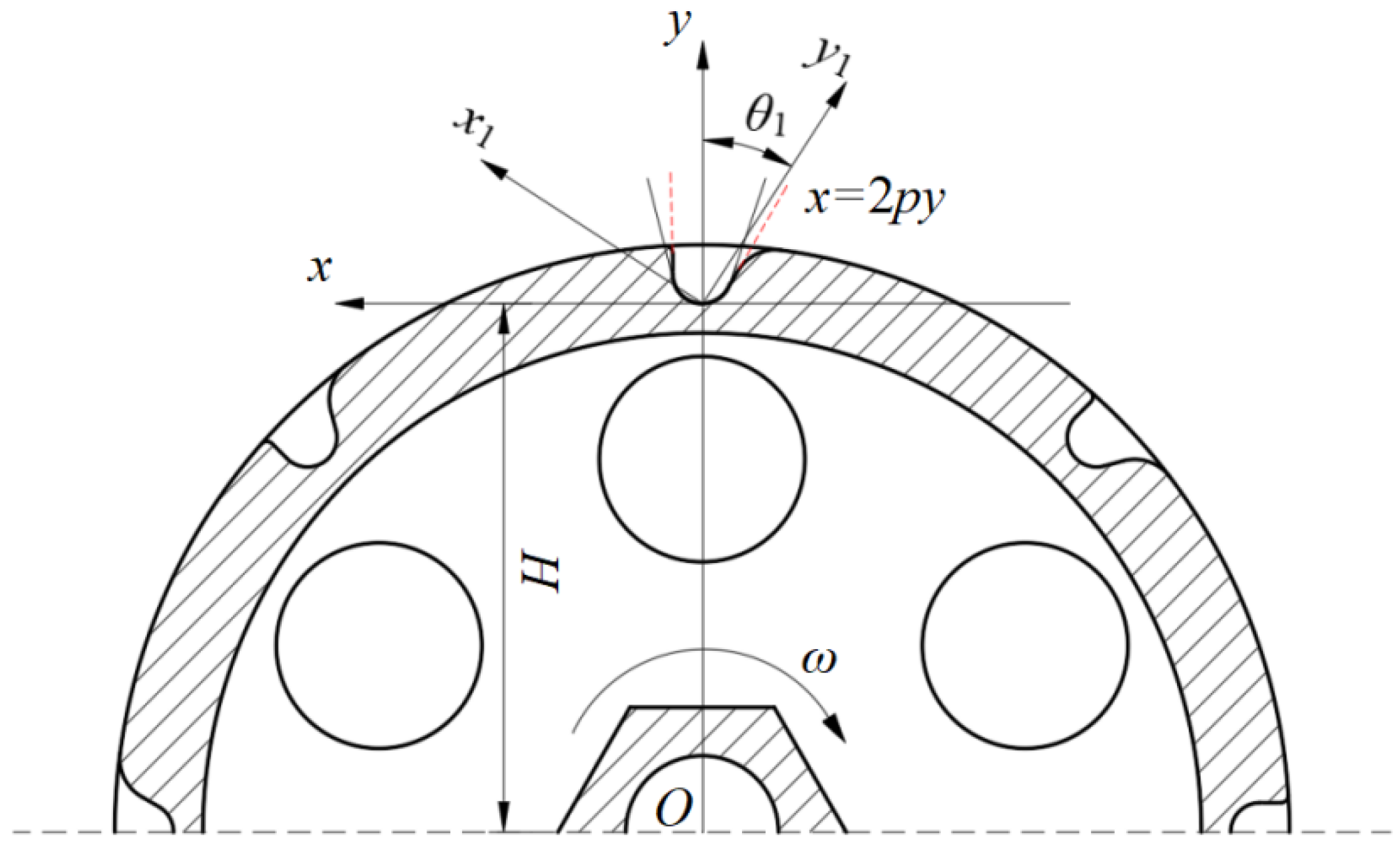
2.5. Design of Seeding Plate Diameter and Shaped Hole

Seeding plate diameter is a significant factor affecting sowing, which determines the number of seed slots, the seeding plate’s wheel linear speed, and other parameters of the critical basis [19]. The relationship between the diameter of the seeding plate and the seed filling time is as follows [20]:

$$\left\{\begin{array}{l}t=l/v\\ l=\theta \left(R-C\right)\\ v=2\mathsf{\pi }n\left(R-C\right)\end{array}\right.$$

(1)

where t is the seed-filling time, in s; l is the arc length of the seeding-filling area, mm; v is the line speed of the seeding plate, m/s; θ is the radius of the seed-filling area, rad; R is the radius of the seeding plate, mm; C is the depth of the seed slot, mm; n is the rotational speed of the seeding plate, r/min.

Collating Equation (1) yields Equation (2) as follows:

$$t={\displaystyle \frac{\theta }{2\mathsf{\pi }n}}$$

(2)

From Equation (2), the seed-filling time T has nothing to do with the diameter of the seeding plate. The diameter of the seed plate should not be too small, as excessive curvature is not conducive to seed filling into the holes and may result in missed sowing. Referring to the agricultural machinery design manual, the vertical seed tray diameter is generally 80~200 mm. Considering that the structural design of the machine needs to be miniaturized, choose 80 mm as the diameter of the seeding plate.

Under the condition that the diameter of the seeding plate and the operating speed of the seeder are specific, increasing the number of seed slots in the seeding plate reduces the seeding plate’s linear speed and improves the seed-filling performance. When the number of seed slots is too large, the angle between the centres of two adjacent seed slots decreases, and the span decreases, which is not conducive to seed filling. The number of seed slots is limited by the diameter of the seeding plate and the hole spacing; the following formula calculates the number of seed slots:

$$Z={\displaystyle \frac{\mathsf{\pi }d{v}_m}{sv}}={\displaystyle \frac{60\mathsf{\pi }d{v}_m}{s\mathsf{\pi }nd(1-\delta )}}={\displaystyle \frac{60v_m}{sn(1-\delta )}}$$

(3)

where Z is the number of seed slots; v_m is the forward speed of the planter, m/s; v is the linear speed of the seeding plate, m/s; n is the rotational speed of the seeding plate, r/min; s is the spacing of the seeding holes, m; δ is the slip rate of the ground wheel, in %.

From Equation (3), the number of seed slots is directly proportional to the forward speed of the planter. Combined with the above Chinese chive planting agronomic requirements, with spacing of the seeding holes s for 20 cm, v_m takes 0.5 m/s, n generally takes 15~40 r/min, and δ takes 0.05. To get the number of seed tray seed slots in the row of seed tray between 4 and 10, the seed slot row by the row of seeding plate‘s diameter, seed slot spacing, and the limitations of the size of the seed slots, a comprehensive consideration of the design of this row of seed slots for the number of 8 is important.

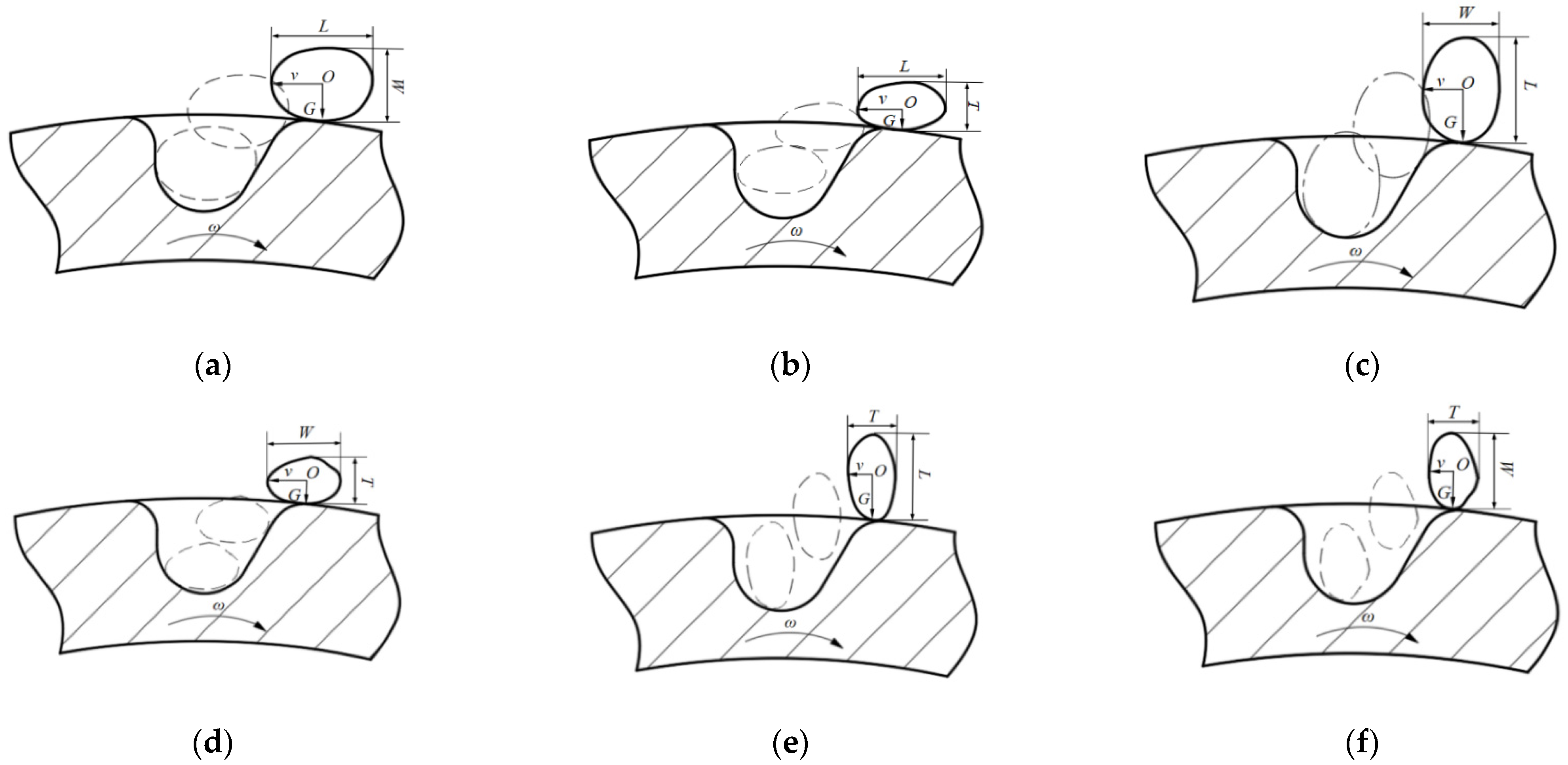
2.6. Design of Seed Slot

The cross-section of the seed slot is designed with an inclined hole structure with rounded corners, which can increase the seed-filling time and improve the seed-filling effect [21,22,23]. Its design is based on the parabola x² = 2py. The slope of each point changes continuously and uniformly and in the lowest point of the slope of 0, not only to ensure that smooth transportation of the seed in the filling and dropping process, but also to ensure the stability of the seed in the seed slot inside. Therefore, based on the principle of the parabola to design a radial cross-section for the inclined parabolic structure of the seed slot, as shown in Figure 3, the parabolic axis of symmetry and the apex of the y-axis and the origin O, respectively, to establish a right-angled coordinate system, (0, −H) is the center of the seeding plate.

The relationship between the coordinates of the parabola and the origin before and after the parabola is tilted should satisfy Equation (4):

$$\left\{\begin{array}{l}{x}^2=2py\\ R^2=x^2+{\left(y+H\right)}^2\\ x=-x_1\cos {\theta }_1-y_1\sin {\theta }_1\\ y=y_1\cos {\theta }_1-x_1\sin {\theta }_1\end{array}\right.$$

(4)

where x and y are the unrotated parabola and circle intersection coordinates, mm; x₁ and y₁ are the parabola rotation and circle intersection coordinates, mm; p is the parabola focal distance, mm; L is the parabola apex to the center of the circle, mm; R is the radius of the seeding plate, mm; H is the parabola apex to the center of the seeding plate, mm; C is the depth of the seed slot, mm; and θ₁ is the parabolic tilt angle, (°).

The distance between the regulating disk and the seeding plate can be adjusted to form the seed slot. The material characteristics of Chinese chives are the basis for the design of the seed slot. There are various situations when the seed is filled into the seed slot. The probability of filling the seed slot with different attitudes is inversely proportional to the cross-sectional area of the seed at the edge of the seeding plate as well as to the height of the centre of mass, so that k is the value of the attitude, k_i is the simplified attitude coefficient, and p_i is the probability of the attitude, which is calculated by the following formula:

$$S={\displaystyle \frac{\mathsf{\pi }{a}_1{a}_2}{4}}$$

(5)

$$k={\displaystyle \frac{1}{S{a_2}^2}}={\displaystyle \frac{4}{\mathsf{\pi }{a}_1{a_2}^2}}$$

(6)

$$k_i={\displaystyle \frac{1}{a_1{a_2}^2}}$$

(7)

$$p_i={\displaystyle \frac{k_i}{k_t}}$$

(8)

where, a₁ is the length of the seed cross-section, mm²; a₂ is the width of the seed cross-section, mm²; S is the area of the seed cross-section, mm²; k is the attitude value; k_i is the attitude coefficient of the seed at the i-th state; p_i is the probability of the seed’s attitude at the i-th state; and k_t is the sum of the three attitude values.

The specific state diagrams of seeds horizontally filling the typed hole with six different attitudes are shown in Figure 4; based on the cross-sectional correspondence, the three-axis dimensions of the seeds are sequentially brought into Equation (6) to obtain the attitude value of each state. The sum of the attitude values, k_t, is calculated as Equation (9):

$$\left\{\begin{array}{l}{k}_a=1/L{W}^2, k_b=1/L{T}^2, k_c=1/W{L}^2\\ k_d=1/W{T}^2, k_e=1/T{L}^2, k_f=1/T{W}^2\end{array}\right.$$

(9)

$$k_t=k_a+k_b+k_c+k_d+k_e+k_f$$

(10)

The probabilities of the corresponding six postures follow Equation (8):

$$\left\{\begin{array}{l}{p}_a=k_a/k_t, p_b=k_b/k_t, p_c=k_c/k_t\\ p_d=k_d/k_t, p_e=k_e/k_t, p_f=k_f/k_t\end{array}\right.$$

(11)

The specific dimensional parameters of the seeds are known from the above. Based on the six states in Figure 4, the probabilities of the six postures are calculated by taking the three-axis dimensions of the seeds in order according to the cross-sectional correspondences and bringing the average values of the seed lengths, widths, and thicknesses into Equation (11). Since one attitude of the seed corresponds to one state of seed filling during the horizontal filling of the seed slot, the attitude probability is equal to the state probability at this point.

After calculation, the six gesture probabilities were obtained as d, b, f, e, a, and c in descending order, corresponding to 0.361, 0.283, 0.170, 0.104, 0.063, and 0.019. Among them, the d attitude has the highest probability, followed by the b attitude. The attitude of Chinese chive filling provides the basis for regulating the length of the seed slot, and the structural parameters of the seed filling tank should satisfy Equation (12):

$$\left\{\begin{array}{l}5L\le A\le 15T\\ W\le B\le L_{\max }\\ 3T_{\min }\le C\le L_{\max }\end{array}\right.$$

(12)

where A is the seed slot length, mm; B is the seed slot diameter, mm; C is the line seed slot depth, mm; L_max is the maximum value of seed length, mm; and T_min is the minimum value of seed thickness, mm.

The seed-metering device is processed using 3D printing technology. To facilitate the processing of the seed slot, the bottom is designed as a circle, and the left side is tangent to the vertical line; to increase the seed’s mobility and prevent seed damage, the seed slot is set up on both sides of the chamfered corner of the structure, as shown in Figure 5. Ideally, the seed lies flat in the seed slot in the d position or is filled into the seed slot side by side in the b position, so the distance between the adjustment plate and the seeding plate is minimal. It is necessary to satisfy the need to fill the seed slot with 15 seeds side by side in a d state and ensure that the seeds can be accommodated in a b state along the long axis in accordance with the arrangement of 5 seeds per layer in 3 layers inside the seed slot. The diameter of the seed slot should be greater than the average value of the broad axis of the seed, and less than or equal to the maximum value of the long axis; the depth of the seed groove should be greater than the average value of the thickness of the Chinese chive seed 3 grains, and less than or equal to the maximum value of the long axis of the seed. This ensures that the 3 seeds overlap and lie flat inside the seed slot and that the slot’s diameter and depth can accommodate the maximum value of the seed’s long axis. Combined with the physical parameters of the seeds and sowing requirements, the pre-test seed slot length A was designed to be 17~18.5 mm, the seed groove diameter B to be 2.7~3.3 mm, the depth of the seed groove C to be 2.9~3.9 mm, and the chamfering corners r¹ and r² to have a radius of 1.5 mm.

3. Results

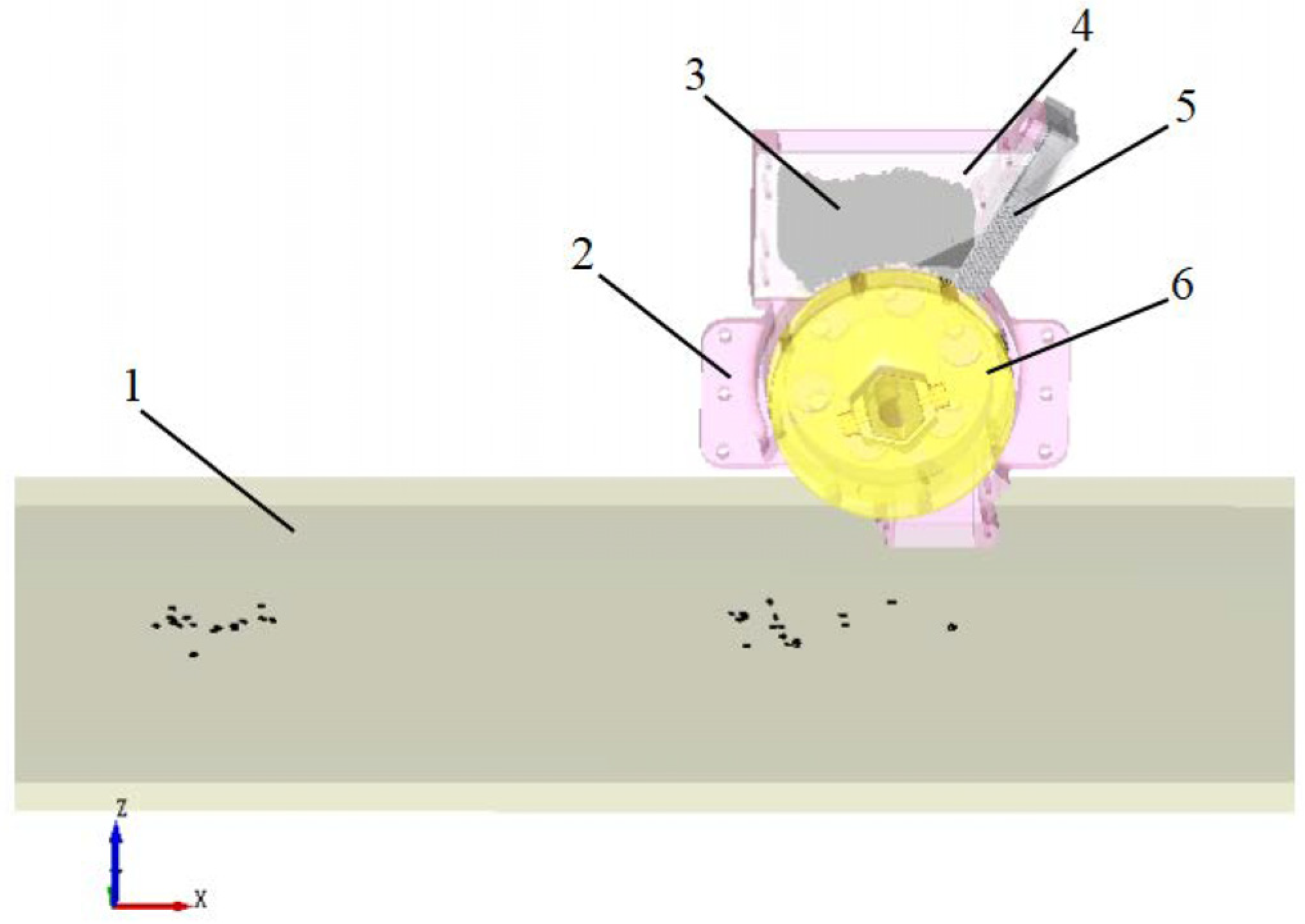
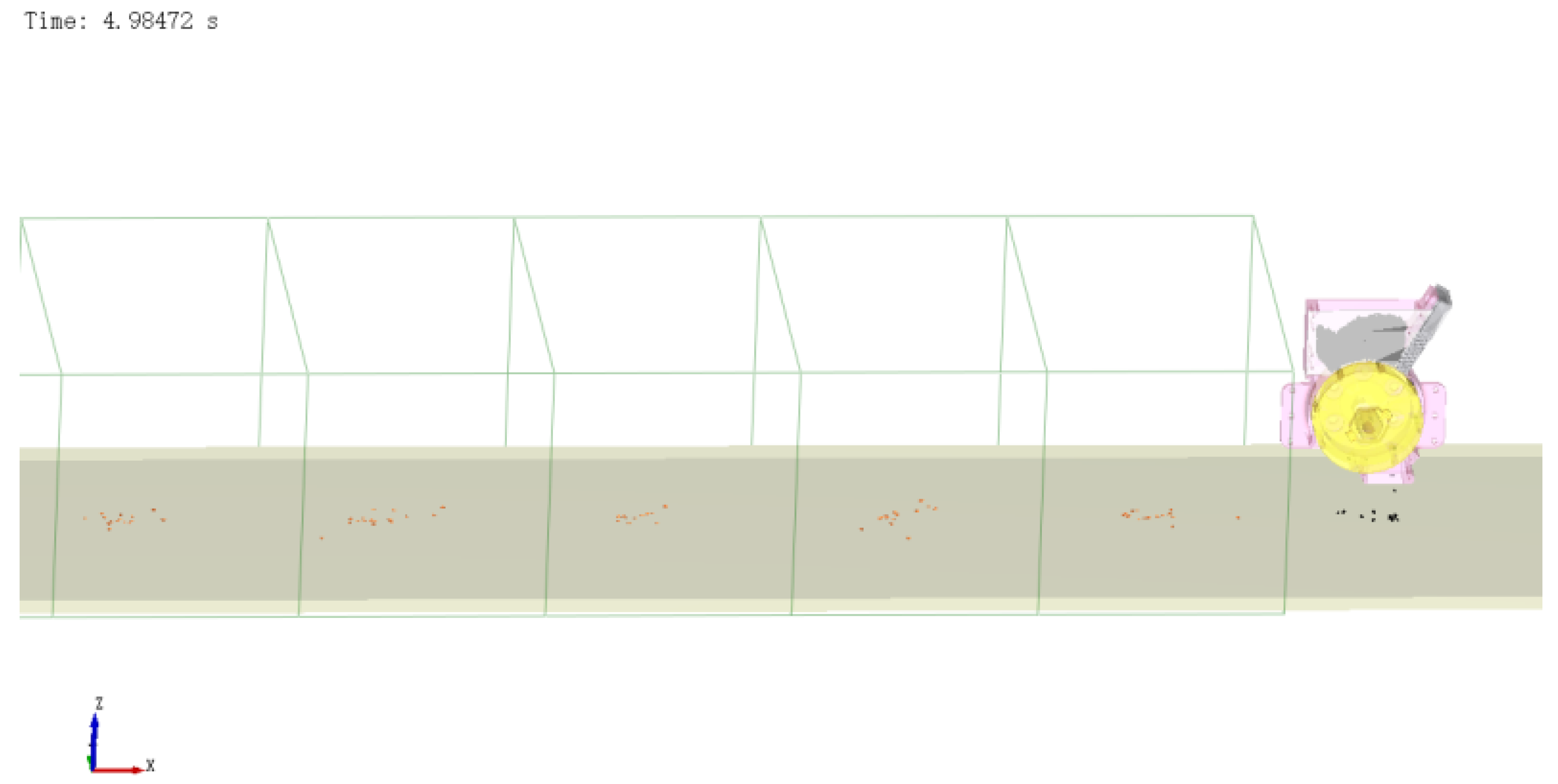
3.1. EDEM Discrete Element Simulation Test

The Chinese chive was used as the modeling object, based on the mean values of the three-axis dimensions of the seeds measured above, and exported as an STL format file. EDEM2022 software created the model using the fast fill function to get the seed particle model [24,25]. The Chinese chive’s actual image and simulation model are shown in Figure 5.

SolidWorks2022 software was used to establish a three-dimensional model of the seed-metering device, which was then imported into EDEM2022 software in STL format. The structure is simplified to reduce the simulation time [26]. By combining the seeding plate and adjustment plate into a whole, the simplified simulation model mainly consists of ground, shell, barrier, seed-clearing brush, seeding plate, etc., as shown in Figure 6. Set the seed particle generation method to dynamic and generate 250 seeds. Where the particle size is set to be normally distributed, the number of seed slots, eight, is brought into Equation (3) above to find the rotational speed of the seed-metering device, which is 19.74 r/min. Thus, the simulation is set to rotate the seeding plate at 20 rpm. Wait until the seed-metering devices have stabilized and start timing. The total simulation time is 5 s.

There is no adhesion on the seed surface, and the Hertz–Mindlin (no slip) model was chosen for the contact between seeds, between seeds and seed-metering device, and between seeds and seed-clearing brush, which is accurate and efficient in the calculation of forces [27,28]. The basic physical parameters of the seeds and the coefficients of static friction, rolling friction, and static friction coefficients between the seeds were obtained according to the relevant studies [29]. The purpose of this simulation test is to count the coordinates of seed falling after sowing to prevent the seed particles from bouncing in contact with the ground (which would affect the test results); the coefficient of static friction, and the coefficient of restitution between the seed and the ground were set to 0.05 and 0.01, respectively. Other simulation parameters were determined by parameter calibration [30], as shown in

Table 1. Simulation parameter.

Parameter	Value
Density of Chinese chive seeds/kg·m−3	1274
Shear modulus of Chinese chive seeds/Pa	1.36 × 107
Poisson’s ratio of Chinese chive seeds	0.26
Density of PLA plastics/kg·m−3	1290
Shear modulus of PLA plastics/Pa	1.04 × 107
Poisson’s ratio of PLA plastics	0.30
Density of seed-clearing brush/kg·m−3	1150
Shear modulus of seed-clearing brush/Pa	1.1 × 108
Poisson’s ratio of seed-clearing brush	0.4
Density of ground plastics/kg·m−3	1400
Shear modulus of ground/Pa	1.06 × 106
Poisson’s ratio of ground	0.37
Coefficient of restitution between seeds and seeds	0.16
Coefficient of static friction between seeds and seeds	0.87
Coefficient of rolling friction between seeds and seeds	0.08
Coefficient of restitution between seeds and PLA plastics	0.29
Coefficient of static friction between seeds and PLA plastics	0.56
Coefficient of rolling friction between seeds and PLA plastics	0.04
Coefficient of restitution between seeds and seed-clearing brush	0.40
Coefficient of static friction between seeds and seed-clearing brush	0.40
Coefficient of rolling friction between seeds and seed-clearing brush	0.01
Coefficient of restitution between seeds and seed-clearing brush	0.01
Coefficient of static friction between seeds and seed-clearing brush	0.05
Coefficient of rolling friction between seeds and seed-clearing brush	0.5

.

3.2. Sowing Performance Evaluation

In this paper, we mainly study the seed slot structure’s influence on the seed-metering device’s seeding performance and take the seeding longitudinal offset coefficient of dissimilarity and transverse offset coefficient of dissimilarity as the evaluation indexes of the seeding performance. If the coefficient of variation is too large, the seeding performance is poor, and conversely, the smaller the value, the denser the seed dispersal, and the better the seeding. To calculate the seeding longitudinal offset coefficient of dissimilarity and transverse offset coefficient of dissimilarity, 10 monitoring zones were established at the end of the simulation, as shown in Figure 7, using the Grid Bin Group module of the EDEM software’s post-processing. Then, the longitudinal and transverse coordinates of the seeds in each hole in the monitoring area were counted, the data were exported, and the coefficient of variation of the offset scale was calculated according to the formula.

The longitudinal offset mean value $\overline{Y}$_ij and the transverse offset mean value $\overline{X}$_ij during the simulation are as follows:

$$\left\{\begin{array}{l}{Y}_C={\displaystyle \frac{{\displaystyle \sum _{j=1}^{m_t}{Y}_{ij}}}{m_t}}\\ {\overline{Y}}_{ij}={\displaystyle \frac{{\displaystyle \sum _{j=1}^{m_t}\left|Y_{ij}-Y_C\right|}}{m_t}}\\ X_C={\displaystyle \frac{{\displaystyle \sum _{j=1}^{m_t}{X}_{ij}}}{m_t}}\\ {\overline{X}}_{ij}={\displaystyle \frac{{\displaystyle \sum _{j=1}^{m_t}\left|X_{ij}-X_C\right|}}{m_t}}\end{array}\right.$$

(13)

where Y_C is the center position of the i-th hole along the longitudinal direction, mm; Y_ij is the vertical axis of the j-th seed in the i-th hole, mm; m_t is the total number of seeds in the i-th hole, mm; $\overline{Y}$_ij is the mean vertical axis offset of the seed, mm; X_C is the center position of the i-th hole along the transverse direction, (mm); X_ij is the horizontal axis of the j-th seed in the i-th hole, mm; and $\overline{X}$_ij is the mean vertical axis offset of the seed, mm.

The equations for the standard deviation of the longitudinal scale offset σ_Y, and the standard deviation of the transverse scale offset σ_X in the monitoring area during the simulation are as follows:

$$\left\{\begin{array}{l}{\sigma }_1={\displaystyle \frac{{\overline{Y}}_{ij}}{{\sigma }_Y}}\\ {\sigma }_2={\displaystyle \frac{{\overline{X}}_{ij}}{{\sigma }_X}}\end{array}\right.$$

(14)

where σ₁ is the vertical concentration of seeds and σ₂ is the horizontal concentration of seeds.

3.3. Single-Factor Experiment

The length of the seed slot changes the size and shape of the seed-holding space, which in turn shadows the homogenization of the seed drop during the sowing process. According to the Chinese chive agronomic planting requirements, about 15 seeds were sown in each hole to ensure that the number of seeds sown in each hole was close to 15 and to further determine the length of the seed slot for this simulation test. From the above-mentioned scenario based on the Haoqi Chinese chive seeds, the pre-tested seed tray was designed with a seed slot length A of 17~18.5 mm, and the seed slot diameter B and depth C were both set at 3 mm. In this single-factor experiment to compare the coefficient of variation of sowing accuracy, the length of the seed slot was selected to be 17.0 mm, 17.3 mm, 17.6 mm, 17.9 mm, 18.2 mm, and 18.5 mm. The rotational speed of the seed-metering device was set to 20 rpm, the forward speed to 0.5 m/s, and the simulation time to be 5 s. The seed slot diameter and seed slot depth of the six groups were uniformly taken as 3 mm according to the mean value of the long axis of the seeds. To calculate the seeding accuracy, the number of seeds per hole was counted at the end of the simulation, and the standard deviation of the number of seeds σ_k and the seeding accuracy σ3 were calculated as follows:

$${\sigma }_k=\sqrt{{\displaystyle \frac{1}{m_s-1}}{\displaystyle \sum _{i=1}^{m_s}{\left(k_i-\overline{k}\right)}^2}}$$

(15)

$${\sigma }_3={\displaystyle \frac{\overline{k}}{{\sigma }_k}}$$

(16)

where σ_k is the standard deviation of the number of grains sown; m_s is the total number of holes sown; k_i is the number of seeds sown in the i-th hole; $\overline{k}$ is the average seeding value per hole and is taken as 15; and σ₃ is the seeding accuracy.

The smaller value of seeding accuracy indicates that the number of sown grains is closer to 15 grains. Figure 8 shows the trend of different seed slot lengths and seeding accuracy. As the length of the seed slot increases, the value of seeding accuracy decreases and then increases. When the length of the seed slot is 17.9 mm, the number of seeds sown is closest to the agronomic planting requirements of Chinese chive, so the length of the seed slot in the subsequent test is set to 17.9 mm.

3.4. Response Surface Test

3.4.1. Experimental Design

A quadratic general rotary combination design experiment was selected to analyze the effect of seed slot diameter and seed slot depth length on the number of seeds sown [31]. Using seed longitudinal and transverse concentrations as evaluation indexes, the range of seed slot diameter was selected as 2.7~3.3 mm, and the range of seed slot depth as 1.9~3.9 mm. The coding table of test factors is shown in

Table 2. Coding of test factors.

Coding	Factors
	Diameter of Seed Slot (mm)	Depth of Seed Slot (mm)
1.414	3.30	3.90
1	3.21	3.61
0	3.00	2.90
−1	2.79	2.19
−1.414	2.70	1.90

.

3.4.2. Experimental Results and Analysis of Variance

Apply Design-Expert 13 software to regression analysis of the test results to determine the change rule of seed vertical concentration and horizontal concentration under the two test factors, where X₁ and X₂ are the factor coding values. The test results are shown in

Table 3. Test results.

Test Number	Factors		Vertical Concentration	Horizontal Concentration
	X1	X2
1	−1	−1	0.746	0.915
2	1	−1	0.685	0.898
3	−1	1	0.667	0.843
4	1	1	0.561	0.632
5	−1.414	0	0.697	0.768
6	1.414	0	0.684	0.749
7	0	−1.414	0.725	0.937
8	0	1.414	0.591	0.722
9	0	0	0.566	0.664
10	0	0	0.574	0.676
11	0	0	0.569	0.652
12	0	0	0.614	0.701
13	0	0	0.582	0.628

.

For the ANOVA of the longitudinal concentration model as shown in

Table 4. Analysis of variance.

Source of Variance	Vertical Concentration					Horizontal Concentration
	Sum of Squares	Degrees of Freedom	The Mean Square	F-Value	p-Value	Sum of Squares	Degrees of Freedom	The Mean Square	F-Value	p-Value
Model	0.0492	5	0.0098	15.41	0.0012 **	0.1377	5	0.0275	59.46	0.0005 **
X1	0.0043	1	0.0043	6.72	0.0358 *	0.0081	1	0.0081	95.24	0.0462 *
X2	0.0193	1	0.0193	30.14	0.0009 **	0.0515	1	0.0515	0.0768	0.0005 **
X1X2	0.0005	1	0.0005	0.7924	0.4029	0.0094	1	0.0094	4.39	0.0353 *
X12	0.0191	1	0.0191	29.87	0.0009 **	0.0204	1	0.0204	17.08	0.0064 **
X22	0.0091	1	0.0091	14.21	0.0070 **	0.0559	1	0.0559	192.11	0.0004 **
Residual	0.0045	7	0.0006			0.0097	7	0.0014
Lack of fit	0.003	3	0.001	2.62	0.1875	0.0068	3	0.0023	3.06	0.1543
Error	0.0015	5	0.0004			0.0030	4	0.0007
Cor total	0.0537	12				0.1474	12

Note: p < 0.01 (highly significant, **); p < 0.05 (significant, *).

, the significance test of the model F = 15.41, p < 0.01, and the result of the test of the misfit term is non-significant (p > 0.05), which indicates that the regression model is well fitted within the range of the test. From the model of vertical concentration, it can be seen that the effect of X₁ on the equation is significant (p < 0.05), and the effect of X₂, X₁², and X₂² on the equation is highly significant (p < 0.01), and the regression equation of vertical concentration is obtained as follows:

$${\sigma }_1=11.54-6.88X_1-0.26X_2-0.08X_1{X}_2+1.63{X_1}^2+0.07{X_2}^2$$

(17)

For the ANOVA of the horizontal concentration model as shown in Table 4, the significance test of the model F = 59.46, p < 0.01, and the test of the misfit term was non-significant (p > 0.05), indicating that the regression model was well fitted within the test range. From the model of horizontal concentration, it can be seen that the effect of X₁, X₁², and X₂² on the equation is highly significant (p < 0.01), and the regression equation of horizontal concentration is obtained as follows:

$${\sigma }_2=0.66-0.03X_1-0.08X_2-0.05X_1{X}_2+0.05{X_1}^2+0.09{X_2}^2$$

(18)

3.4.3. Response Surface Analysis

The effect of seed slot diameter and depth on the longitudinal and transverse concentrations is shown in Figure 9. From Figure 9a, it can be seen that the longitudinal concentration σ₁ tends to decrease and then increase as the diameter of the seed slot decreases. The longitudinal concentration σ₁ tends to decrease as the depth of the seed slot increases. From the response surface plot in Figure 9b, it can be seen that the lateral concentration σ₂ tends to decrease and then increase with the increase of both seed slot diameter and seed slot depth.

3.4.4. Simulation Parameter Optimization

The smaller the vertical concentration, the more concentrated the seeds are in the longitudinal direction. The smaller the lateral concentration, the more laterally concentrated the seed is and the better the seeding. To obtain the optimal structural parameters of the seed slot, the parameters of the seed slot diameter and depth were optimized to minimize the coefficient of variation, and then the optimization module of the Design-Expert 13 software was used to solve the constrained objective optimization. Finally, the longitudinal concentration σ₁ of 0.563 and the transverse concentration σ₂ of 0.634 were obtained for a seed slot diameter of 3.075 mm and a seed slot depth of 3.323 mm.

3.5. Bench and Field Tests

3.5.1. Test Condition

The test site is the Intelligent Agricultural Machinery and Equipment Engineering Laboratory of Harbin Cambridge University in August 2024. To verify the simulation test optimization results, according to the optimization of the best results, to determine the seed slot diameter of 3.075 mm and the depth of the seed slot of 3.323 mm, we selected Hao Ji Chinese chive seeds, using 3D printing technology to process the seed discharger prototype and build the test stand, through the controller to adjust the motor speed to drive the seed discharge disk rotation, as shown in Figure 10. To facilitate the observation of the sowing effect after the test and prevent seed bouncing from affecting its accuracy, the test stand’s conveyor belt is equipped with a homemade sand spreader, which is operated simultaneously with the conveyor belt. The relevant parameters of the bench test were consistent with the simulation parameters, three groups of repetitive tests were conducted, and the test results were counted by taking pictures with a camera at the end of the test.

3.5.2. Verification Test

The OpenMV is fixed above the conveyor belt by means of a riser at a certain distance from it under uniform indoor lighting. Together with an aberration correction algorithm, the system captures the seed image after the target seed is transferred to the acquisition area through the conveyor belt [32,33,34]. The captured image in RGB565 coding format is converted to a grayscale map, binarized by selecting an appropriate threshold value, and the target seed color is set to black. Use the find_blobs( ) function to find all blobs (connected pixel regions that pass the threshold test) within the ROI and obtain the center pixel coordinates of each blob. Number the blobs in the image from top to bottom and multiply the center pixel coordinates of the target seed by a pre-measured conversion factor to obtain the coordinate values of the seed (using the upper left corner of the image as the origin, building horizontal coordinates to the right and vertical coordinates down) and output them to the serial terminal [35] (Figure 11).

The relative error δ between the simulation and bench test results is calculated as follows [36]:

$$\delta ={\displaystyle \frac{|\epsilon -{\epsilon }^{\prime }|}{{\epsilon }^{\prime }}}$$

(19)

where δ is the relative error; ε is the simulation test value; and ε′ is the measured value.

As can be seen from

Table 5. Test bench verification results.

Number	Vertical Concentration	Horizontal Concentration	Relative Error in Vertical Concentration (%)	Relative Error in Horizontal Concentration (%)
1	0.584	0.655	3.73	3.31
2	0.552	0.623	1.95	1.73
3	0.541	0.649	3.91	2.37
Average	0.559	0.642	3.20	2.47

, under the action of the optimal parameters, the average value of the longitudinal concentration of the bench test results is 0.559, the average value of the transverse concentration is 0.642, the average value of the relative error of the longitudinal concentration is 3.20%, and the average value of the relative error of the transverse concentration is 2.47%.

3.5.3. Seed Slot Volume-Adjustment Tests and Field Trials

In this paper, for the physical parameters of Haoji Chinese chive seeds, taking about 15 seeds as the research premise, it was determined that when the seed slot diameter was 2.972 mm, and the seed slot depth was 3.051 mm, the sowing simulation test and the bench test had the best concentration effect. Based on this, the length of the seed slot is adjusted, and the number of seeds sown in different slot lengths is counted using field tests to realize the precise sowing of various seeds (Figure 12). A single-factor experiment method was used. The test factor was the length of the seed slot taken as 6, 9, 12, 15, and 18 mm, a total of five levels; the test index was the number of seeds sown, and the average of the five holes sown in each seed slot length was counted. Origin2021 was applied to fit the test results. The mean value of the number of seeds sown per hole increased with the increase of the length of the seed slot, and the results of the fitted curve showed that the number of seeds sown per hole and the length of the seed slot were linearly correlated with each other. The equation of the fitted curve was y = 0.7667x + 1.08, R² = 0.995.

4. Discussion

Li et al. [12] designed a seed ladle tongue-type flax precision burrow planter, which was optimized to meet the unique agronomic requirements of film-covered planting in Gansu, China. The need was to solve the traditional seeding machine in the hu ma sowing operations; due to the limitations of technical means, a large number of seeds in the sowing process is wasted, the number of holes complicates the achievement of precise control standards, resulting of uneven distribution of plants in the field after the seedling distribution; sowing uniformity cannot effectively safeguard the problem. Ding et al. [13] designed a Cyperus esculentus cell-wheel seed-metering device with low-position seeding and cavitation function in response to the thorny problem of irregular seed shape and seed dispersion in hole-collecting seed casting. It solves the problem of seed dispersal due to the irregular shape of the seed and the inability to accurately control the drop point and distribution of the seed when the seed is dropped, resulting in the seed being dispersed at too high a height and failing to gather in the predetermined holes efficiently. Adopting the unique design concepts of an eyelet seed discharge wheel and low-level hole collection, it effectively reduces the seeding height and thus improves the hole-sowing effect. However, the focus of the two teams was on precision hole sowing of seeds, and not much research was done on the number of seeds sown.

At this stage of the Chinese chive planting process, the traditional artificial planting method is still widely used by many farmers. This approach has a number of disadvantages, the most prominent of which is that it takes a lot of time and labor costs; based on experience, it is difficult to accurately control the number of seeds sown, which not only affects the rate of emergence and quality of growth, but also may lead to waste of seeds, increasing the cost of planting, and ultimately have a negative impact on the economic benefits of farmers. In order to effectively solve these problems, the design of a simple structure and low-cost mechanical seed-metering device is essential; this seed dispenser can be well suited to the planting of small-scale farmers in China’s planting practices and needs. During the actual sowing operation, farmers can easily adjust the length of the seed slot according to the different seeding number requirements, so as to achieve the desired goal of precision hole sowing. Not only can this significantly improve the efficiency and accuracy of Chinse chive sowing, but this can also reduce the waste of seeds; for small farmers, Chises chive planting operations have brought significant convenience and benefits, providing a strong impetus to small farmers toward the refinement and efficiency of Chinese chive planting. The seed-metering device can sow Chinese chives and other vegetable seeds with similar seeds—for example, spinach, radish, cabbage, etc. However, because the shape of the seed slot is designed according to the size of the Chinse chive, there is still a certain lack of adaptability to other vegetable varieties. This planting pattern of precision hole sowing and the structural design of adjustable-sowing quantity is significant to Chinese chive cultivation in China and foreign countries.

5. Conclusions

(1)

The seed-metering device was designed and trial-produced to realize Chinese chive precision hole sowing and improve the concentration of Chinese chive hole sowing. The overall structure and working principle of the seed-metering device are described, the material characteristics of Chinese chive seeds are measured, the probability of seed filling is analyzed, and the diameter of the seeding plate and the seed slot are designed to realize the precise adjustment of the number of seeds.

(2)

By constructing an EDEM discrete-element simulation model of Chinese chive seeds and seed displacer, a single-factor experiment was first used to determine the best seeding effect when the seed slot length was 17.9 mm. A quadratic general rotary combination design experiment was also designed to obtain regression equations for vertical concentration and horizontal concentration. The analysis of variance showed that the factors affecting vertical concentration were seed slot depth and seed slot diameter, in that order of priority, and the factors affecting horizontal concentration were seed slot diameter and seed slot depth, in that order of priority. The smaller the coefficient of variation, the more concentrated the hole sowing. The optimal combination of parameters was obtained using the minimum longitudinal and transverse concentrations as the optimization objectives. The longitudinal concentration was 0.563, the transverse concentration was 0.634 when the seed slot diameter was 3.075 mm, and the seed slot depth was 3.323 mm.

(3)

The simulation test optimization results for the optimal parameter combinations were experimentally verified. The results of the bench test show that the longitudinal concentration is 0.559, the transverse concentration is 0.642, the relative error of the longitudinal concentration is 3.20%, and the relative error of the transverse concentration is 2.47%, which is close to the results of the bench test and the simulation test. A seed slot adjustment test was also designed to count the number of seeds sown in five horizontal lengths of seed slots. The number of seeds planted per hole and the length of the seed slots were linearly correlated. It shows that the outside-filling Chinese chive adjustable-capacity precision seed-metering device can meet the challenge of having different grain numbers in sowing by adjusting the length of the seed slot, improving sowing centralization.