Modeling Whole-Plant Carbon Stock in Olea europaea L. Plantations Using Logarithmic Nonlinear Seemingly Unrelated Regression
Abstract
:1. Introduction
2. Data and Methods
2.1. Overview of the Study Area
2.2. Data and Preprocessing
2.2.1. CS of Samples
2.2.2. Correlation Analysis
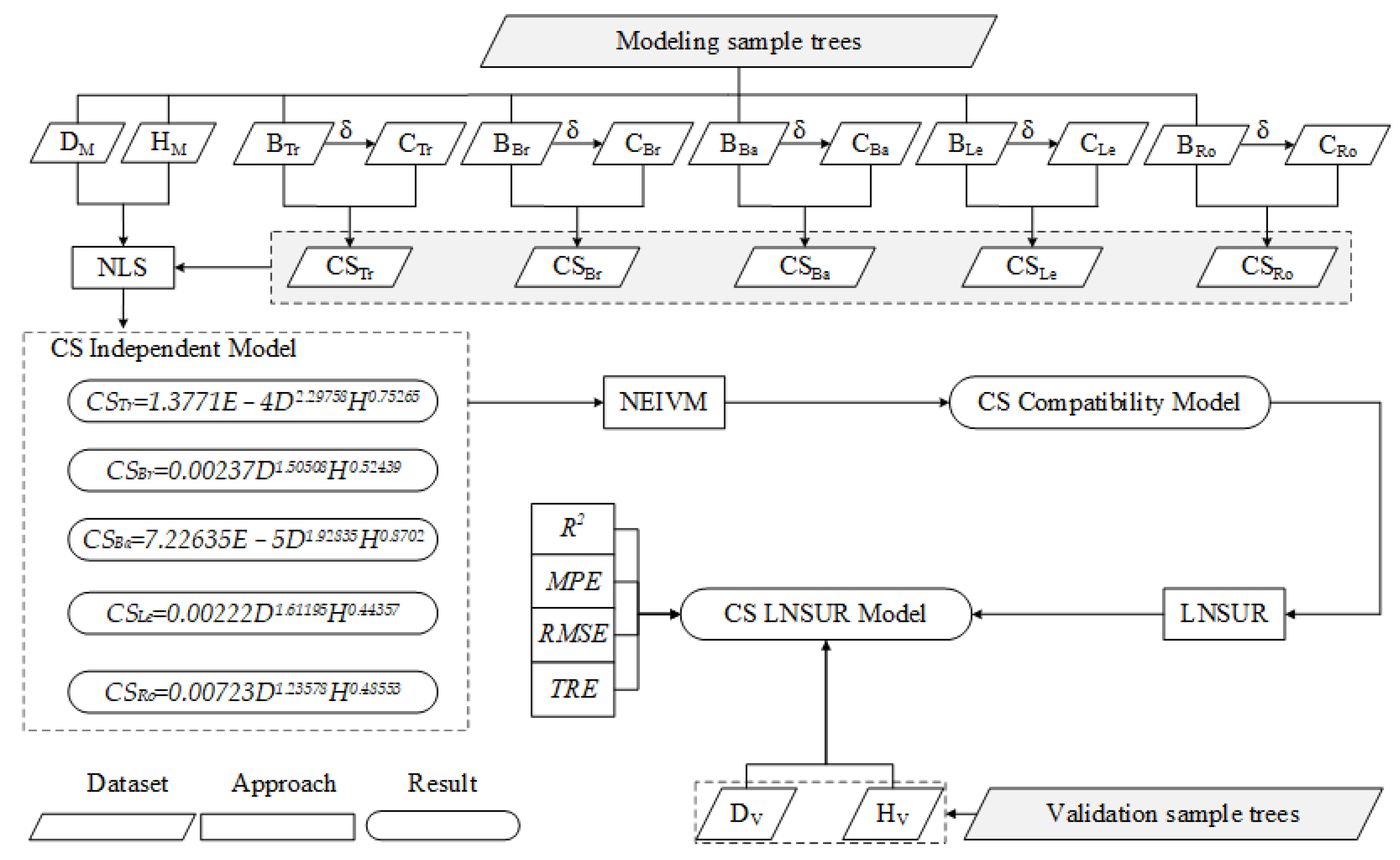
2.3. Construction of Olea europaea L. CS Model
2.3.1. CS Independent Model
2.3.2. CS Compatibility Model
- (1)
- Unitary compatibility model
- (2)
- Binary compatibility model
2.3.3. LNSUR Model
2.4. Model Accuracy Assessment
3. Results
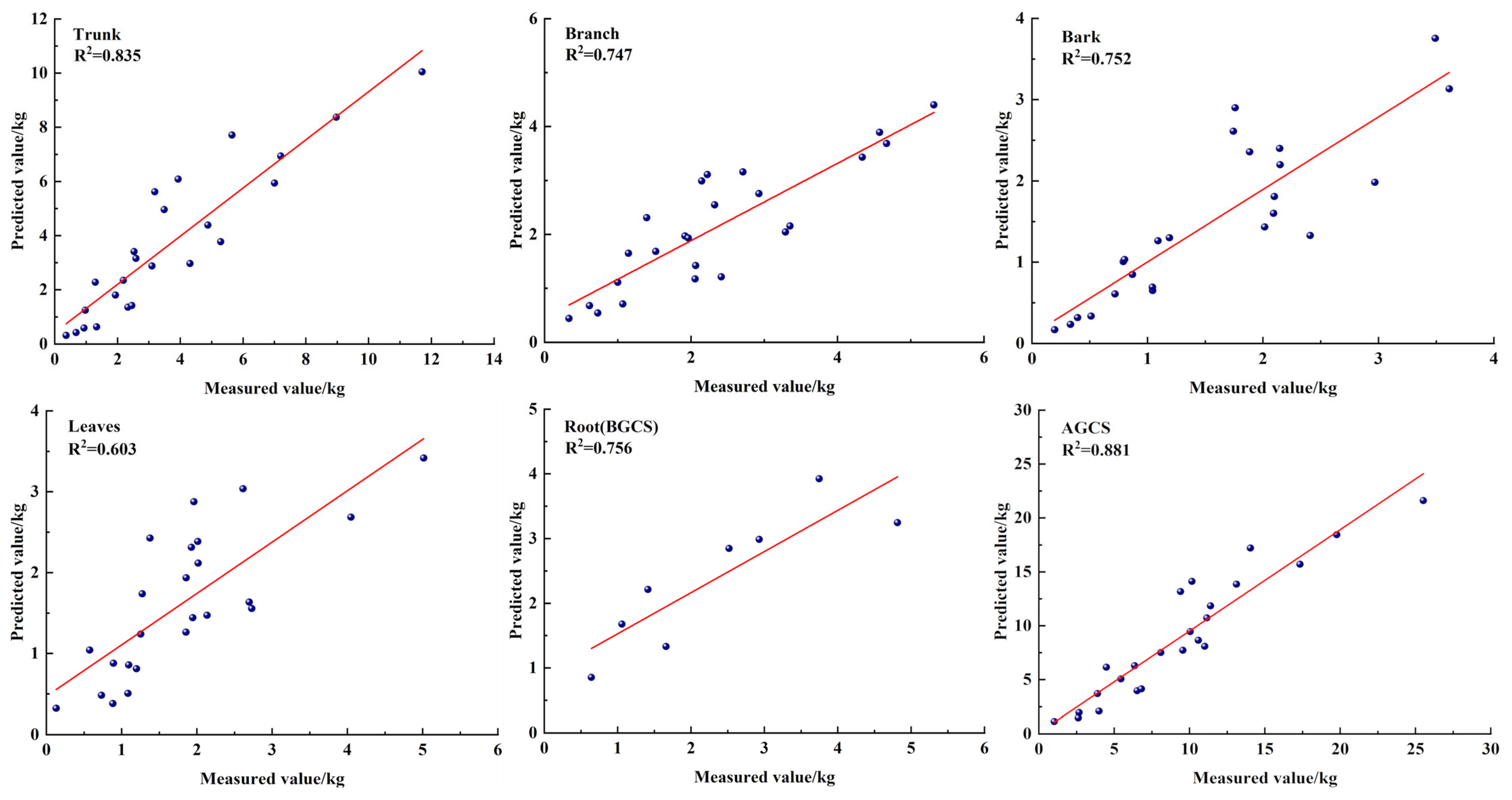
3.1. Optimal CS Independent Model
3.2. CS Compatibility Model for Each Organ
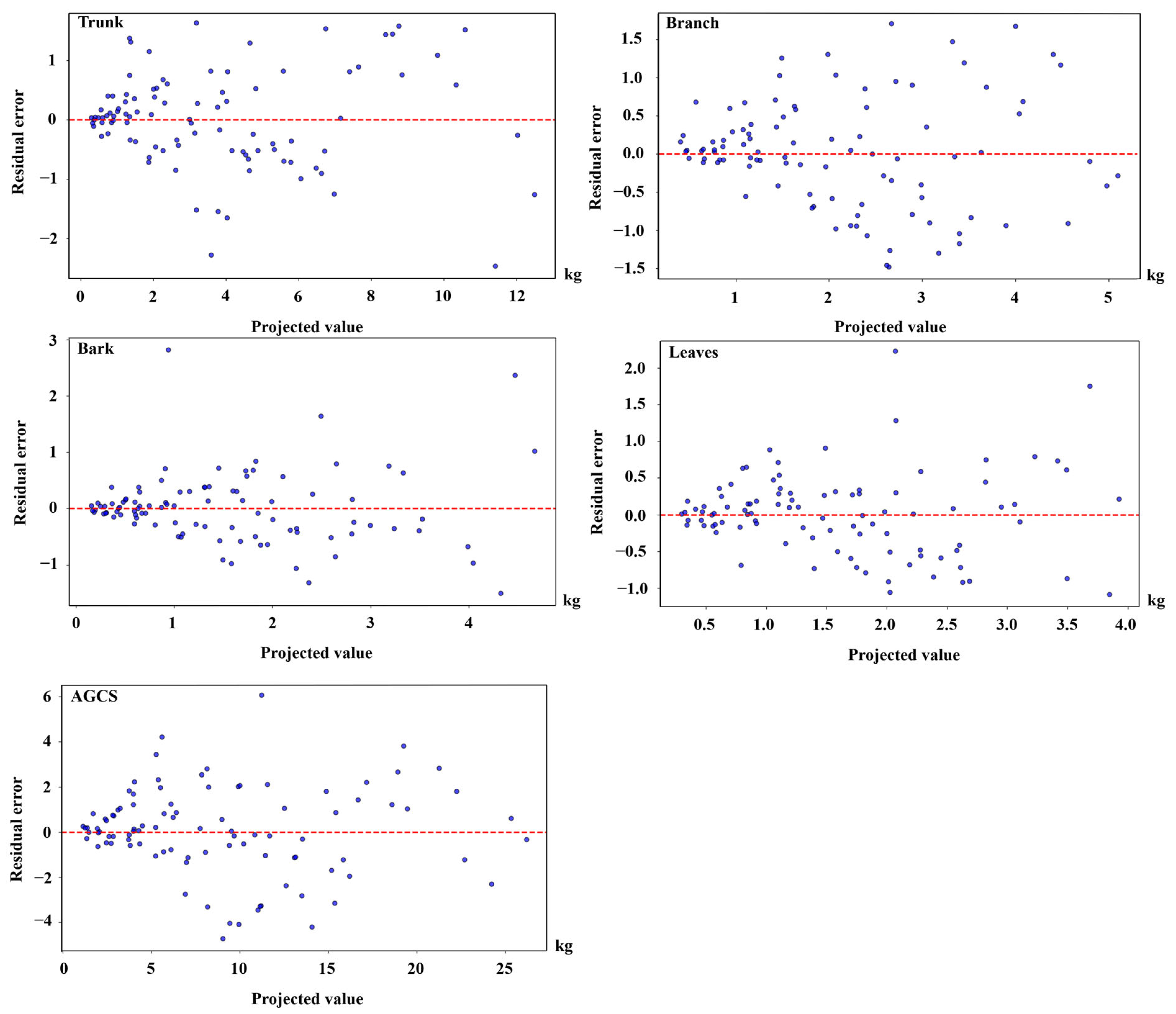
3.3. CS LNSUR Model
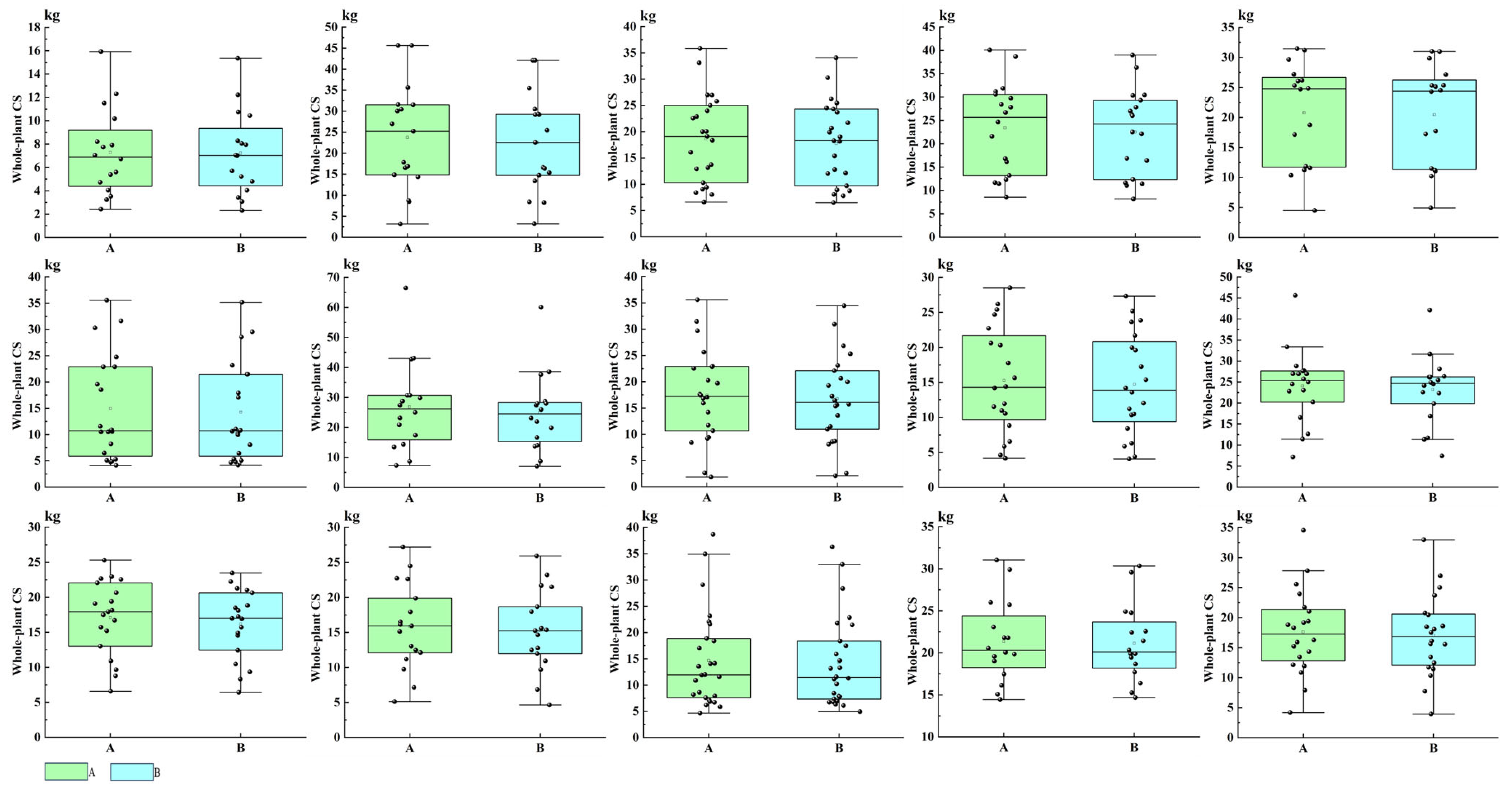
3.4. Estimation of Whole-Plant CS in Olea europaea L. from Validation Sample Trees
4. Discussion
4.1. The First Attempt to Construct a CS Independent Model of Olea europaea L.
4.2. Construction of the Compatibility Model Using the CS Independent Model
4.3. Advantages of the LNSUR Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mansour, H.M.M.; Zeitoun, A.A.; Abd-Rabou, H.S.; El Enshasy, H.A.; Dailin, D.J.; Zeitoun, M.A.A.; El-Sohaimy, S.A. Antioxidant and Anti-Diabetic Properties of Olive (Olea europaea) Leaf Extracts: In Vitro and In Vivo Evaluation. Antioxidants 2023, 12, 1275. [Google Scholar] [CrossRef] [PubMed]
- Bouarroudj, K.; Tamendjari, A.; Larbat, R. Quality, Composition and Antioxidant Activity of Algerian Wild Olive (Olea europaea L. subsp. Oleaster) Oil. Ind. Crops Prod. 2016, 83, 484–491. [Google Scholar] [CrossRef]
- Mirón, I.J.; Linares, C.; Díaz, J. The Influence of Climate Change on Food Production and Food Safety. Environ. Res. 2023, 216, 114674. [Google Scholar] [CrossRef]
- Ito, A.; Nishina, K.; Noda, H.M. Impacts of Future Climate Change on the Carbon Budget of Northern High-Latitude Terrestrial Ecosystems: An Analysis Using ISI-MIP Data. Polar Sci. 2016, 10, 346–355. [Google Scholar] [CrossRef]
- Wu, G.; Huang, G.; Lin, S.; Huang, Z.; Cheng, H.; Su, Y. Changes in Soil Organic Carbon Stocks and Its Physical Fractions along an Elevation in a Subtropical Mountain Forest. J. Environ. Manag. 2024, 351, 119823. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Guo, Y.; Chen, Z.; Luo, X.; Wang, P.; Shi, M.; Wang, X. A New Method for Estimating Forest Stand Carbon Stock: Segmentation and Modeling Based on Forest Aboveground Imagery. Ecol. Indic. 2024, 167, 112697. [Google Scholar] [CrossRef]
- Lei, L.; Chai, G.; Wang, Y.; Jia, X.; Yin, T.; Zhang, X. Estimating Individual Tree Above-Ground Biomass of Chinese Fir Plantation: Exploring the Combination of Multi-Dimensional Features from UAV Oblique Photos. Remote Sens. 2022, 14, 504. [Google Scholar] [CrossRef]
- Lv, Z.; Duan, A. Biomass and Carbon Storage Model of Cunninghamia Lanceolata in Different Production Areas. Sci. Silvae Sin. 2024, 60, 1–11. [Google Scholar]
- Chen, X.; Xie, D.; Zhang, Z.; Sharma, R.P.; Chen, Q.; Liu, Q.; Fu, L. Compatible Biomass Model with Measurement Error Using Airborne LiDAR Data. Remote Sens. 2023, 15, 3546. [Google Scholar] [CrossRef]
- Qin, L.; Meng, S.; Zhou, G.; Liu, Q.; Xu, Z. Uncertainties in above Ground Tree Biomass Estimation. J. For. Res. 2021, 32, 1989–2000. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Z.; Zhang, D.; Huang, X. Biomass Allometric Models for Larix Rupprechtii Based on Kosak’s Taper Curve Equations and Nonlinear Seemingly Unrelated Regression. Front. Plant Sci. 2023, 13, 1056837. [Google Scholar] [CrossRef] [PubMed]
- Sandoval, S.; Montes, C.R.; Olmedo, G.F.; Acuña, E.; Mena-Quijada, P. Modelling Above-Ground Biomass of Pinus Radiata Trees with Explicit Multivariate Uncertainty. For. Int. J. For. Res. 2022, 95, 380–390. [Google Scholar]
- Xiong, N.; Qiao, Y.; Ren, H.; Zhang, L.; Chen, R.; Wang, J. Comparison of Parameter Estimation Methods Based on Two Additive Biomass Models with Small Samples. Forests 2023, 14, 1655. [Google Scholar] [CrossRef]
- Parresol, B.R. Additivity of Nonlinear Biomass Equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, C.; Mu, L.; Zhao, Z.; Ma, H. Robinia Pseudoacacia Biomass Model in Coastal Area of Qinhuangdao City. J. Northwest For. Univ. 2024, 1–10. [Google Scholar]
- Zeng, W.; Tang, S. Using Measurement Error Modeling Method to Establish Compatible Single-Tree Biomass Equations System. For. Res. 2010, 23, 797–803. [Google Scholar]
- Cao, L.; Li, H. Comparison of Two Compatible Biomass Models: A Case Study from Three Broadleaved Tree Species in Guangdong. Chin. J. Ecol. 2019, 38, 1916–1925. [Google Scholar]
- Zhao, D.; Westfall, J.; Coulston, J.W.; Lynch, T.B.; Bullock, B.P.; Montes, C.R. Additive Biomass Equations for Slash Pine Trees: Comparing Three Modeling Approaches. Can. J. For. Res. 2019, 49, 27–40. [Google Scholar] [CrossRef]
- Cao, Q.V. A Unified System for Tree- and Stand-Level Predictions. For. Ecol. Manag. 2021, 481, 118713. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing Additive Systems of Biomass Equations for Nine Hardwood Species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Fu, L.; Lei, Y.; Wang, G.; Bi, H.; Tang, S.; Song, X. Comparison of Seemingly Unrelated Regressions with Error-in-Variable Models for Developing a System of Nonlinear Additive Biomass Equations. Trees 2016, 30, 839–857. [Google Scholar] [CrossRef]
- Ning, D.; Lu, B.; Du, C.; Li, Y.; Liao, Y.; Zhang, Y. Division of Suitable Cultivation Areas for Olive in Yunnan Province. China For. Sci. Technol. 2008, 5, 39–41. [Google Scholar]
- LY/T 2259-2014; Technical Regulation on Sample Collections for Biomass Modeling. National Forestry and Grassland Administration: Beijing, China, 2014.
- Xu, H.; Wang, Z.; Li, Y.; He, J.; Wu, X. Dynamic Growth Models for Caragana korshinskii Shrub Biomass in China. J. Environ. Manag. 2020, 269, 110675. [Google Scholar] [CrossRef]
- Zhu, B.; Yuan, J. Pressure Transfer Modeling for an Urban Water Supply System Based on Pearson Correlation Analysis. J. Hydroinform. 2014, 17, 90–98. [Google Scholar] [CrossRef]
- Månsson, R.; Tsapogas, P.; Åkerlund, M.; Lagergren, A.; Gisler, R.; Sigvardsson, M. Pearson Correlation Analysis of Microarray Data Allows for the Identification of Genetic Targets for Early B-Cell Factor * [Boxs]. J. Biol. Chem. 2004, 279, 17905–17913. [Google Scholar] [CrossRef]
- Blujdea, V.N.B.; Pilli, R.; Dutca, I.; Ciuvat, L.; Abrudan, I.V. Allometric Biomass Equations for Young Broadleaved Trees in Plantations in Romania. For. Ecol. Manag. 2012, 264, 172–184. [Google Scholar] [CrossRef]
- Wang, W.; Wang, B.; Zhang, X.; Zhang, Q.; Hao, S. Biomass Estimation Models of Natural Betula Platyphylla Forests in Daxing’anling, Inner Mongolia. J. Northwest For. Univ. 2023, 38, 180–188. [Google Scholar]
- Zeng, W.; Xia, Z.; Zhu, S.; Luo, H. Compatible Tree Volume and Above-Ground Biomass Equations for Chinese Fir Plantations in Guizhou. J. Beijing For. Univ. 2011, 33, 1–6. [Google Scholar]
- Tang, S.; Li, Y.; Wang, Y. Simultaneous Equations, Error-in-Variable Models, and Model Integration in Systems Ecology. Ecol. Model. 2001, 142, 285–294. [Google Scholar] [CrossRef]
- Trautenmüller, J.W.; Péllico Netto, S.; Balbinot, R.; Watzlawick, L.F.; Dalla Corte, A.P.; Sanquetta, C.R.; Behling, A. Regression Estimators for Aboveground Biomass and Its Constituent Parts of Trees in Native Southern Brazilian Forests. Ecol. Indic. 2021, 130, 108025. [Google Scholar] [CrossRef]
- Zhou, Z.; Fu, L.; Zhou, C.; Sharma, R.P.; Zhang, H. Simultaneous Compatible System of Models of Height, Crown Length, and Height to Crown Base for Natural Secondary Forests of Northeast China. Forests 2022, 13, 148. [Google Scholar] [CrossRef]
- Wang, J.H.; Li, F.R.; Dong, L.H. Additive Aboveground Biomass Equations Based on Different Predictors for Natural Tilia Linn. Ying Yong Sheng Tai Xue Bao 2018, 29, 3685–3695. [Google Scholar] [PubMed]
- Dong, L.; Zhang, L.; Li, F. A Compatible System of Biomass Equations for Three Conifer Species in Northeast, China. For. Ecol. Manag. 2014, 329, 306–317. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L.; Shi, J. Effect of Competition on the Prediction Accuracy of Individual Tree Biomass Model for Natural Larix Gmelinii Forests. Chin. J. Appl. Ecol. 2024, 35, 1474–1482. [Google Scholar]
- Xia, Z.; Jia, B.; Wang, X.; Liu, J. Shrub Biomass Models of Castanopsis Kawakamii Natural Forest. J. Northwest For. Univ. 2024, 39, 30–38. [Google Scholar]
- Qin, J.; Li, Y.; Ma, J.; Lan, C.; Li, H.; Tang, S.; Li, M. Biomass Model Construction and Distribution Pattern of Pinus Massoniana Plantations under Different Climatic Conditions in Guangxi. Guangxi Sci. 2020, 27, 165–174. [Google Scholar]
- Liu, C.; Luo, D. Model Construction and Optimization of Abies Fabri Scrub Biomass in the Sedera Mountains. J. Green Sci. Technol. 2024, 26, 44–50. [Google Scholar]
- Li, F.; Feng, Y.; Zhao, Y.; Zhu, J.; Wei, X.; Liang, W. Construction and Comparison of Artificial Robinia Pseudoacacia Biomass Model in Caijiachuan Watershed. J. For. Environ. 2024, 44, 62–70. [Google Scholar]
- Sileshi, G.W. A Critical Review of Forest Biomass Estimation Models, Common Mistakes and Corrective Measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Z.; Zhang, Y.; Liu, H.; Gu, G.; Peng, X.; Wu, J.; Ye, Z.; Zhang, S.; Shang, S. Construction of Compatible Individual Tree Biomass Model of Myrica Rubra Plantation. J. Zhejiang A&F Univ. 2022, 39, 272–279. [Google Scholar]
- Cao, L.; Li, H. Establishment and Analysis of Compatible Biomass Model for Cinnamomum Camphora in Guangdong Province. J. For. Environ. 2018, 38, 458–465. [Google Scholar]
- Zheng, X.; Yi, L.; Li, Q.; Bao, A.; Wang, Z.; Xu, W. Developing Biomass Estimation Models of Young Trees in Typical Plantation on the Qinghai-Tibet Plateau, China. Chin. J. Appl. Ecol. 2022, 33, 2923–2935. [Google Scholar]
- Mao, C.; Yi, L.; Xu, W.; Dai, L.; Bao, A.; Wang, Z.; Zheng, X. Study on Biomass Models of Artificial Young Forest in the Northwestern Alpine Region of China. Forests 2022, 13, 1828. [Google Scholar] [CrossRef]
- António, N.; Tomé, M.; Tomé, J.; Soares, P.; Fontes, L. Effect of Tree, Stand, and Site Variables on the Allometry of Eucalyptus Globulus Tree Biomass. Can. J. For. Res. 2007, 37, 895–906. [Google Scholar] [CrossRef]
- Meng, S.; Liu, Q.; Zhou, G.; Jia, Q.; Zhuang, H.; Zhou, H. Aboveground Tree Additive Biomass Equations for Two Dominant Deciduous Tree Species in Daxing’anling, Northernmost China. J. For. Res. 2017, 22, 233–240. [Google Scholar] [CrossRef]
- Kaushal, R.; Islam, S.; Tewari, S.; Tomar, J.M.S.; Thapliyal, S.; Madhu, M.; Trinh, T.L.; Singh, T.; Singh, A.; Durai, J. An Allometric Model-Based Approach for Estimating Biomass in Seven Indian Bamboo Species in Western Himalayan Foothills, India. Sci. Rep. 2022, 12, 7527. [Google Scholar] [CrossRef]
- Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree Height and Tropical Forest Biomass Estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree Allometry and Improved Estimation of Carbon Stocks and Balance in Tropical Forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D.; Liu, G.; Yang, C.; Teskey, R.O. Additive Tree Biomass Equations for Betula Platyphylla Suk. Plantations in Northeast China. Ann. For. Sci. 2018, 75, 60. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A. Dynamic of forest biomass carbon pools in China and their significance. Acta Bot. Sin. 2001, 43, 967–973. [Google Scholar]
- Vonderach, C.; Kändler, G.; Dormann, C.F. Consistent Set of Additive Biomass Functions for Eight Tree Species in Germany Fit by Nonlinear Seemingly Unrelated Regression. Ann. For. Sci. 2018, 75, 49. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive Biomass Equations for Native Eucalypt Forest Trees of Temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Cai, H.; Lu, F.; Xu, Z.; Pan, H.; Meng, X.; Zeng, W. Research and Development of Compatible and Additive Individual Tree Biomass Model Systems for Eucalyptus. For. Resour. Manag. 2023, 01, 87–93. [Google Scholar]
- Laskar, S.Y.; Sileshi, G.W.; Nath, A.J.; Das, A.K. Allometric Models for above and Below-Ground Biomass of Wild Musa Stands in Tropical Semi Evergreen Forests. Glob. Ecol. Conserv. 2020, 24, 01208. [Google Scholar] [CrossRef]
- De La Casa, J.A.; Bueno, J.S.; Castro, E. Recycling of Residues from the Olive Cultivation and Olive Oil Production Process for Manufacturing of Ceramic Materials. A Comprehensive Review. J. Clean. Prod. 2021, 296, 126436. [Google Scholar] [CrossRef]
- Wang, R.; Zheng, J.; Huang, Y.; Jiang, D. Research Advances on Breeding and Cultivation Techniques of Olive. Biot. Resour. 2024, 46, 103–111. [Google Scholar]
- Lantero, E.; Matallanas, B.; Callejas, C. Current Status of the Main Olive Pests: Useful Integrated Pest Management Strategies and Genetic Tools. Appl. Sci. 2023, 13, 12078. [Google Scholar] [CrossRef]
- Ali, A.O.; Awla, H.K.; Rashid, T.S. Investigating the in Vivo Biocontrol and Growth-Promoting Efficacy of Bacillus sp. and Pseudomonas fluorescens against Olive Knot Disease. Microb. Pathog. 2024, 191, 106645. [Google Scholar] [CrossRef]
- Montilon, V.; Potere, O.; Susca, L.; Bottalico, G. Phytosanitary Rules for the Movement of Olive (Olea europaea L.) Propagation Material into the European Union (EU). Plants 2023, 12, 699. [Google Scholar] [CrossRef] [PubMed]
- Pennisi, R.; Ben Amor, I.; Gargouri, B.; Attia, H.; Zaabi, R.; Chira, A.B.; Saoudi, M.; Piperno, A.; Trischitta, P.; Tamburello, M.P.; et al. Analysis of Antioxidant and Antiviral Effects of Olive (Olea europaea L.) Leaf Extracts and Pure Compound Using Cancer Cell Model. Biomolecules 2023, 13, 238. [Google Scholar] [CrossRef] [PubMed]
- Bencresciuto, G.F.; Mandalà, C.; Migliori, C.A.; Cortellino, G.; Vanoli, M.; Bardi, L. Assessment of Starters of Lactic Acid Bacteria and Killer Yeasts: Selected Strains in Lab-Scale Fermentations of Table Olives (Olea europaea L.) Cv. Leccino. Fermentation 2023, 9, 182. [Google Scholar] [CrossRef]



| D (cm) | Trunk CS (kg) | Branch CS (kg) | Bark CS (kg) | Leaf CS (kg) | Root CS (kg) | AGCS (kg) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | |
| 6 | 0.640 | 0.309 | 0.712 | 0.226 | 0.318 | 0.159 | 0.503 | 0.251 | 0.929 | 0.436 | 2.174 | 0.813 |
| 8 | 1.643 | 0.604 | 1.396 | 0.482 | 0.744 | 0.293 | 0.972 | 0.399 | 1.676 | 0.501 | 4.756 | 1.502 |
| 10 | 2.497 | 0.929 | 1.745 | 0.489 | 1.172 | 0.740 | 1.424 | 0.361 | 2.363 | 0.858 | 6.838 | 1.833 |
| 12 | 3.390 | 1.183 | 2.172 | 0.832 | 1.591 | 0.607 | 1.679 | 0.565 | 2.386 | 0.690 | 8.832 | 2.571 |
| 14 | 4.846 | 1.020 | 2.651 | 0.978 | 1.965 | 0.560 | 2.051 | 0.780 | 3.859 | 1.193 | 11.513 | 2.470 |
| 16 | 9.166 | 2.032 | 4.312 | 1.060 | 3.377 | 1.206 | 3.236 | 1.060 | 3.990 | 1.098 | 20.091 | 4.081 |
| Factor | Trunk CS | Branch CS | Bark CS | Leaf CS | Root CS | AGCS |
|---|---|---|---|---|---|---|
| D | 0.901 ** | 0.831 ** | 0.822 ** | 0.818 ** | 0.826 ** | 0.910 ** |
| H | 0.721 ** | 0.651 ** | 0.680 ** | 0.626 ** | 0.631 ** | 0.724 ** |
| DH | 0.931 ** | 0.835 ** | 0.852 ** | 0.816 ** | 0.823 ** | 0.930 ** |
| D2H | 0.955 ** | 0.850 ** | 0.864 ** | 0.831 ** | 0.825 ** | 0.950 ** |
| Organ | CS Model | Fitting Formula | R2 | MPE | RMSE | TRE |
|---|---|---|---|---|---|---|
| Trunk | C = aDb | C = 0.00496D2.65726 | 0.905 | 26.532 | 0.945 | 0.914 |
| C = a(DH)b | C = 4.26305E − 6(DH)1.62211 | 0.895 | 23.738 | 0.996 | −0.826 | |
| C = a(D2H)b | C = 4.03036E − 5(D2H)1.04609 | 0.927 | 20.713 | 0.827 | −0.013 | |
| C = aDbHc | C = 1.3771E − 4D2.29758H0.75265 | 0.931 | 21.524 | 0.804 | 0.427 | |
| Branch | C = aDb | C = 0.02896D1.75331 | 0.709 | 29.981 | 0.730 | 0.919 |
| C = a(DH)b | C = 1.98879E − 4(DH)1.10686 | 0.703 | 27.785 | 0.738 | 0.096 | |
| C = a(D2H)b | C = 0.00109(D2H)0.69899 | 0.724 | 27.418 | 0.711 | 0.469 | |
| C = aDbHc | C = 0.00237D1.50508H0.52439 | 0.726 | 27.769 | 0.709 | 0.629 | |
| Bark | C = aDb | C = 0.00462D2.33944 | 0.715 | 35.324 | 0.667 | 1.334 |
| C = a(DH)b | C = 6.44296E − 6(DH)1.46964 | 0.731 | 33.358 | 0.648 | −0.127 | |
| C = a(D2H)b | C = 5.37873E − 5(D2H)0.94012 | 0.748 | 31.815 | 0.627 | 0.695 | |
| C = aDbHc | C = 7.22635E − 5D1.92835H0.8702 | 0.749 | 31.932 | 0.627 | 0.806 | |
| Leaves | C = aDb | C = 0.01883D1.81405 | 0.715 | 35.849 | 0.569 | 0.642 |
| C = a(DH)b | C = 1.11394E − 4(DH)1.14226 | 0.696 | 35.672 | 0.587 | −0.031 | |
| C = a(D2H)b | C = 6.39547E − 4(D2H)0.72241 | 0.722 | 34.255 | 0.562 | 0.290 | |
| C = aDbHc | C = 0.00222D1.61195H0.44357 | 0.726 | 34.344 | 0.557 | 0.492 | |
| Root (BGCS) | C = aDb | C = 0.07892D1.42825 | 0.671 | 27.897 | 0.766 | 0.042 |
| C = a(DH)b | C = 8.99959E − 4(DH)0.95572 | 0.669 | 30.014 | 0.768 | −0.366 | |
| C = a(D2H)b | C = 0.00444(D2H)0.59079 | 0.685 | 28.380 | 0.748 | −0.106 | |
| C = aDbHc | C = 0.00723D1.23578H0.48553 | 0.686 | 28.103 | 0.747 | −0.053 | |
| AGCS | C = aDb | C = 0.03465D2.24598 | 0.884 | 21.499 | 2.175 | 1.182 |
| C = a(DH)b | C = 7.1117E − 5(DH)1.39622 | 0.878 | 20.770 | 2.235 | −0.120 | |
| C = a(D2H)b | C = 5.42937E − 4(D2H)0.89188 | 0.906 | 18.957 | 1.957 | 0.514 | |
| C = aDbHc | C = 0.0014D1.92876H0.67174 | 0.909 | 19.164 | 1.929 | 0.793 |
| Organ | CS Model | Fitting Formula | R2 | MPE | RMSE | TRE |
|---|---|---|---|---|---|---|
| Trunk | C = aDbHc | C = 1.3771E − 4D2.29758H0.75265 | 0.832 | 30.333 | 1.153 | −0.434 |
| Branch | C = aDbHc | C = 0.00237D1.50508H0.52439 | 0.721 | 25.923 | 0.716 | 9.886 |
| Bark | C = aDbHc | C = 7.22635E − 5D1.92835H0.8702 | 0.722 | 24.456 | 0.508 | 3.856 |
| Leaves | C = aDbHc | C = 0.00222D1.61195H0.44357 | 0.570 | 37.124 | 0.713 | 11.507 |
| Root | C = aDbHc | C = 0.00723D1.23578H0.48553 | 0.736 | 27.563 | 0.735 | −1.588 |
| AGCS | C = aDbHc | C = 0.0014D1.92876H0.67174 | 0.871 | 20.018 | 2.073 | 5.074 |
| Model Type | Univariate | Binary | |
|---|---|---|---|
| Parameters | |||
| a | 0.0346691 | 0.0014155 | |
| b | 2.2457308 | 1.9287284 | |
| c | 0.6698741 | ||
| r1 | 5.1440537 | 22.2450445 | |
| r2 | 0.9246553 | 0.5577064 | |
| r3 | 3.3038916 | 20.4319071 | |
| k1 | −0.8565350 | −0.7296256 | |
| k2 | −0.3149435 | −0.3426050 | |
| k3 | −0.7913422 | −0.6298362 | |
| f1 | −0.2985259 | ||
| f2 | 0.0956456 | ||
| f3 | −0.3730051 | ||
| Model Type | Organ | Testing Indicators | |||
|---|---|---|---|---|---|
| R2 | MPE | RMSE | TRE | ||
| Univariate | Trunk | 0.905 | −6.135 | 0.943 | 0.187 |
| Branch | 0.706 | −6.697 | 0.729 | 0.265 | |
| Bark | 0.714 | −13.064 | 0.665 | 0.289 | |
| Leaves | 0.713 | −13.371 | 0.568 | 0.259 | |
| AGCS | 0.884 | −3.004 | 2.164 | 0.172 | |
| Binary | Trunk | 0.931 | −4.438 | 0.800 | 0.162 |
| Branch | 0.724 | −6.437 | 0.707 | 0.254 | |
| Bark | 0.747 | −10.554 | 0.625 | 0.276 | |
| Leaves | 0.725 | −13.543 | 0.556 | 0.251 | |
| AGCS | 0.909 | −2.195 | 1.918 | 0.159 | |
| Variable | Organ | a | b | R2 | MPE | RMSE | TRE |
|---|---|---|---|---|---|---|---|
| D | Trunk | −4.9551 | 2.4977 | 0.873 | −26.185 | 0.335 | 28.930 |
| Branch | −3.2209 | 1.6165 | 0.733 | −24.640 | 0.329 | 41.542 | |
| Bark | −5.0375 | 2.1723 | 0.801 | 672.234 | 0.380 | 836.374 | |
| Leaves | −3.9243 | 1.7870 | 0.693 | −74.706 | 0.418 | 120.344 | |
| Root | −2.8500 | 1.5258 | 0.766 | 8.334 | 0.307 | 36.141 | |
| AGCS | −2.8883 | 2.0493 | 0.866 | −37.829 | 0.283 | 11.423 | |
| D2H | Trunk | −10.0297 | 1.0343 | 0.910 | −9.773 | 0.281 | 23.750 |
| Branch | −6.5314 | 0.6719 | 0.770 | 74.271 | 0.318 | 46.524 | |
| Bark | −9.4859 | 0.9029 | 0.841 | 362.885 | 0.339 | 751.624 | |
| Leaves | −7.5306 | 0.7377 | 0.718 | −70.617 | 0.400 | 114.479 | |
| Root | −6.2625 | 0.6629 | 0.787 | 2.701 | 0.293 | 35.303 | |
| AGCS | −7.0525 | 0.8487 | 0.903 | −18.167 | 0.241 | 9.867 |
| Index | T | p | Index | T | p | ||
|---|---|---|---|---|---|---|---|
| SN | SN | ||||||
| 1 | −0.800 | 0.436 | 9 | 5.114 | 0.000 * | ||
| 2 | 4.793 | 0.083 | 10 | 2.024 | 0.052 | ||
| 3 | 5.648 | 0.000 * | 11 | 2.367 | 0.099 | ||
| 4 | 3.614 | 0.006 | 12 | 3.752 | 0.002 | ||
| 5 | 1.615 | 0.127 | 13 | 1.743 | 0.094 | ||
| 6 | 3.871 | 0.000 * | 14 | −0.206 | 0.839 | ||
| 7 | 3.864 | 0.007 | 15 | 1.803 | 0.087 | ||
| 8 | 4.413 | 0.000 * | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Kou, W.; Lu, N.; Yang, Y.; Duan, C.; Yang, Z.; Song, Y.; Gao, J.; Zhuang, W. Modeling Whole-Plant Carbon Stock in Olea europaea L. Plantations Using Logarithmic Nonlinear Seemingly Unrelated Regression. Agronomy 2025, 15, 917. https://doi.org/10.3390/agronomy15040917
He Y, Kou W, Lu N, Yang Y, Duan C, Yang Z, Song Y, Gao J, Zhuang W. Modeling Whole-Plant Carbon Stock in Olea europaea L. Plantations Using Logarithmic Nonlinear Seemingly Unrelated Regression. Agronomy. 2025; 15(4):917. https://doi.org/10.3390/agronomy15040917
Chicago/Turabian StyleHe, Yungang, Weili Kou, Ning Lu, Yi Yang, Chunqin Duan, Ziyi Yang, Yongjun Song, Jiayue Gao, and Weiyu Zhuang. 2025. "Modeling Whole-Plant Carbon Stock in Olea europaea L. Plantations Using Logarithmic Nonlinear Seemingly Unrelated Regression" Agronomy 15, no. 4: 917. https://doi.org/10.3390/agronomy15040917
APA StyleHe, Y., Kou, W., Lu, N., Yang, Y., Duan, C., Yang, Z., Song, Y., Gao, J., & Zhuang, W. (2025). Modeling Whole-Plant Carbon Stock in Olea europaea L. Plantations Using Logarithmic Nonlinear Seemingly Unrelated Regression. Agronomy, 15(4), 917. https://doi.org/10.3390/agronomy15040917







