Design and Testing of Film Picking–Unloading Device of Tillage Residual Film Recycling Machine Based on DEM Parameter Calibration
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of the Air Suction Tillage Layer Residual Film Recycling Machine
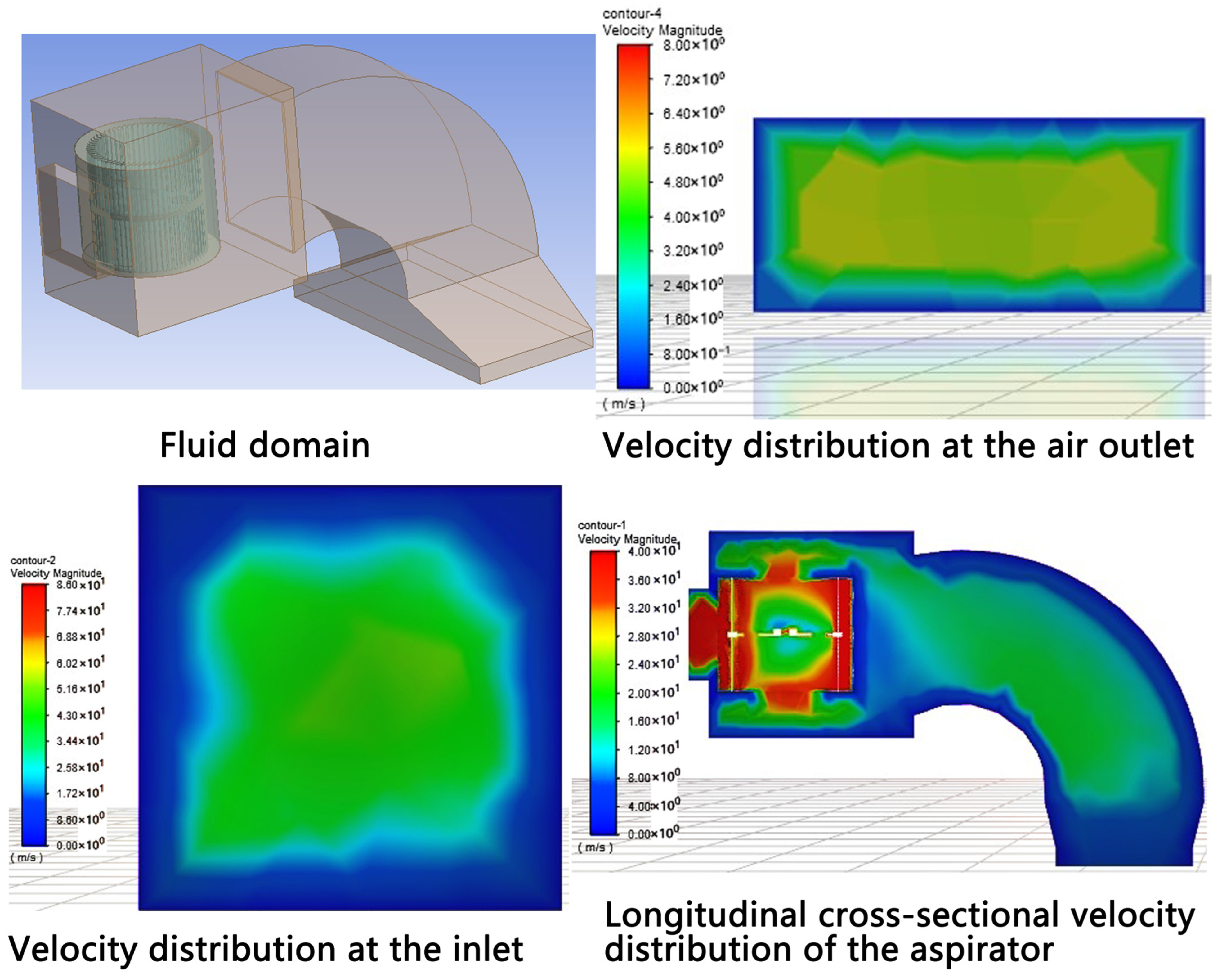
2.2. Analysis of Flow Velocity Distribution Inside the Suction Device
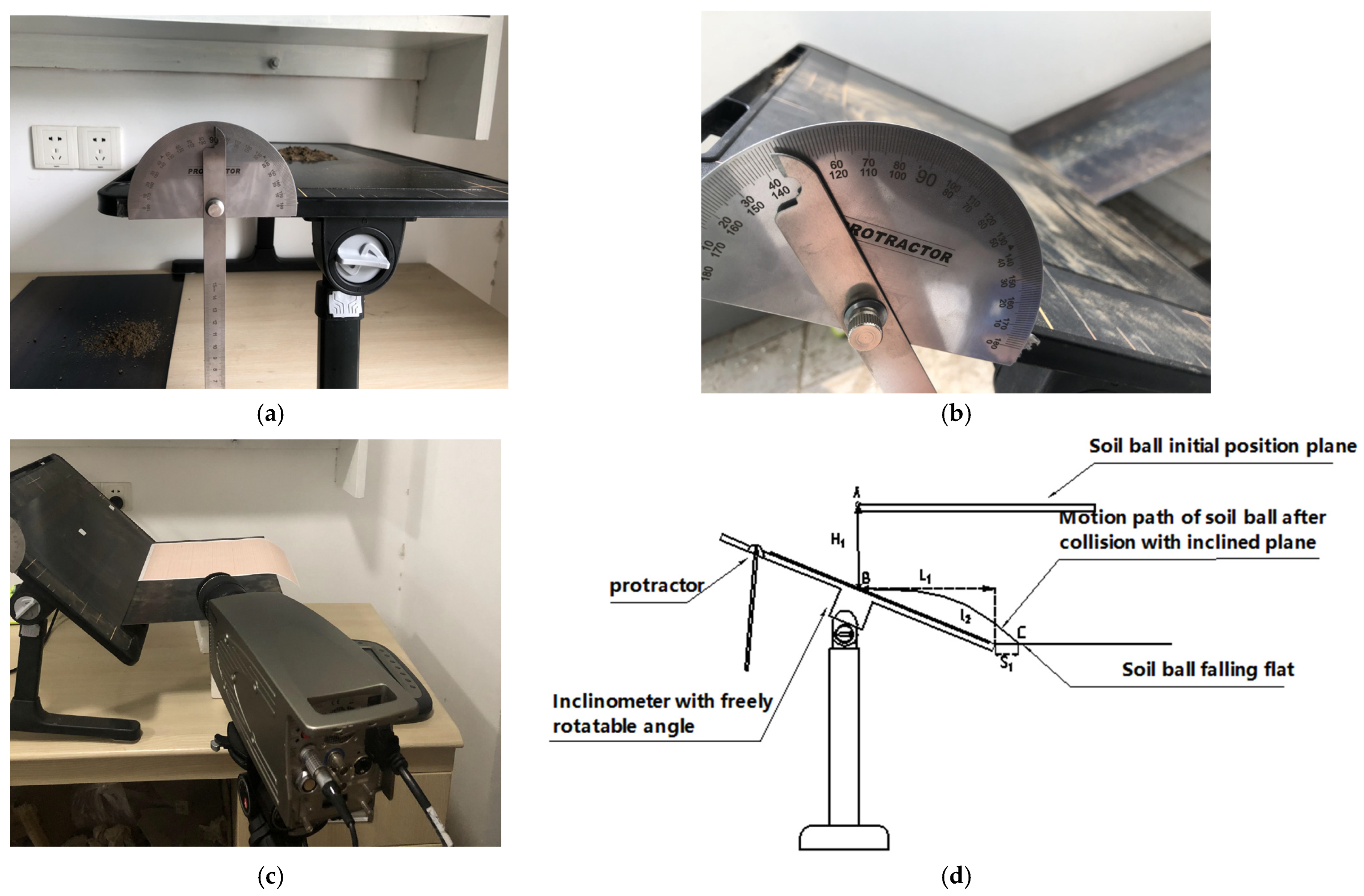
2.3. Measurement and Calibration of Intrinsic Parameters of the Residual Film and Soil
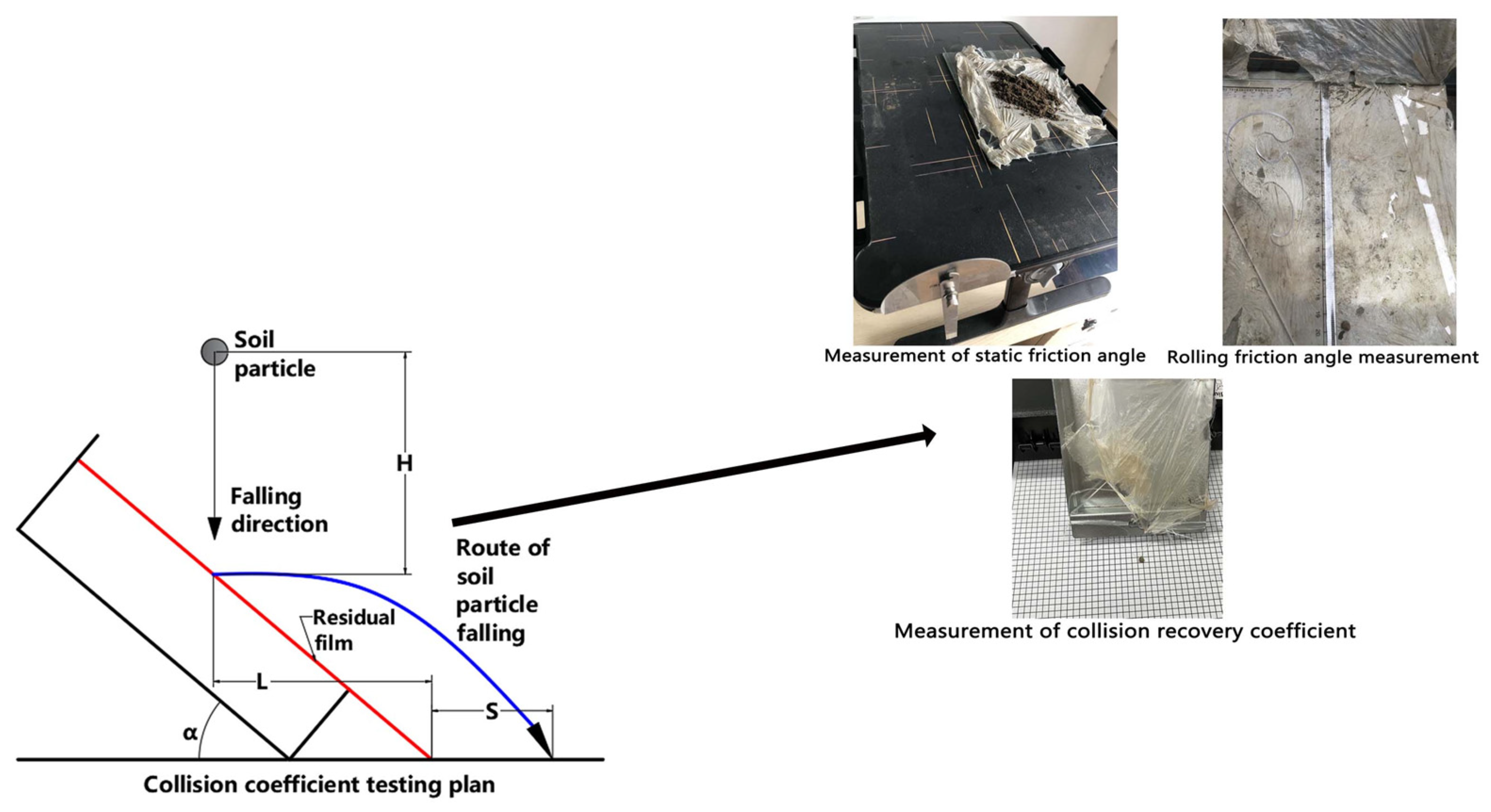
2.4. Contact Parameters
2.4.1. Contact Parameters of Soil–Elastic Tooth (65 Mn)
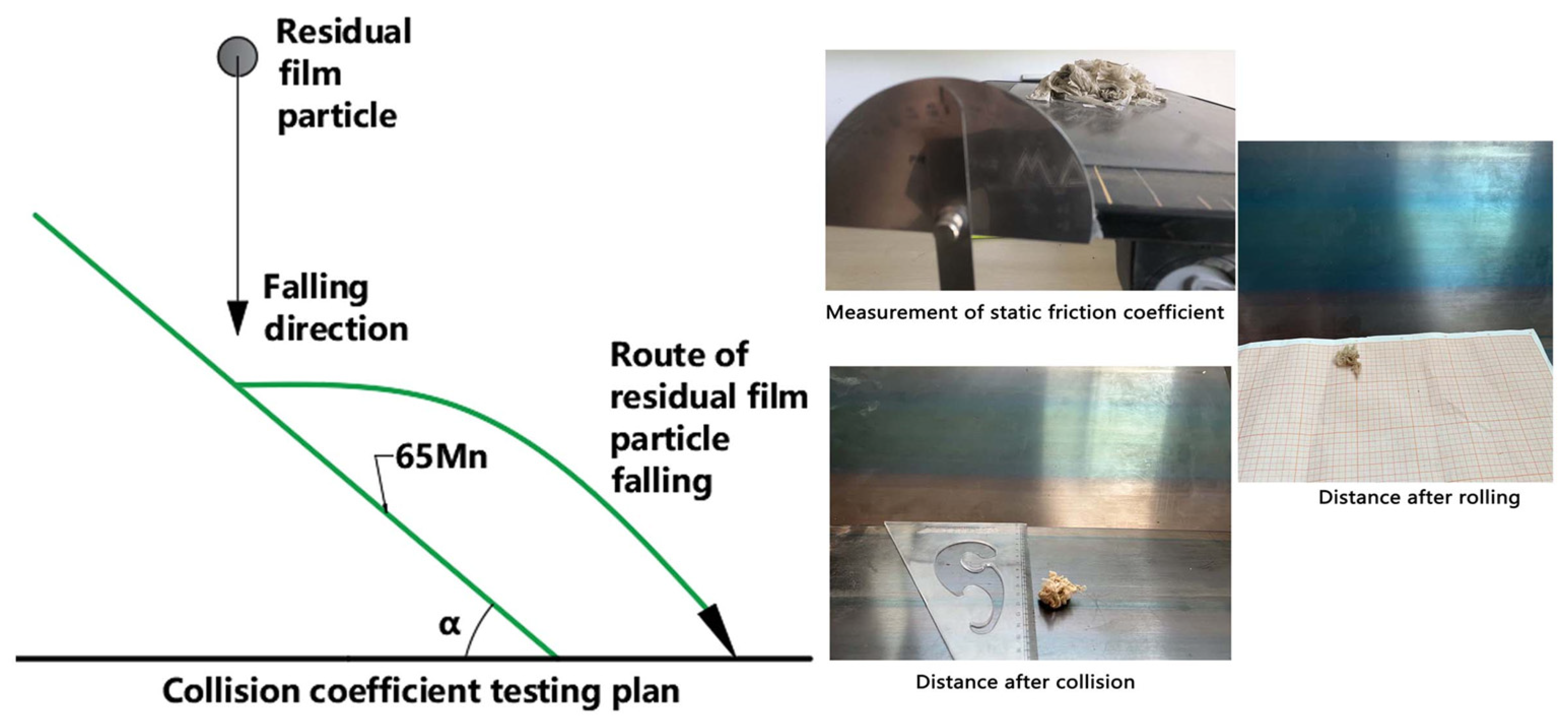
2.4.2. Contact Parameters of Soil–Residual Film
- (1)
- Static friction coefficient of soil–residual film
- (2)
- Dynamic friction coefficient of soil–residual film
2.4.3. Contact Parameters of Residual Film–Elastic Tooth
3. Results
3.1. Residual Film—Residual Film Contact Parameters
3.2. Soil–Soil Contact Parameters
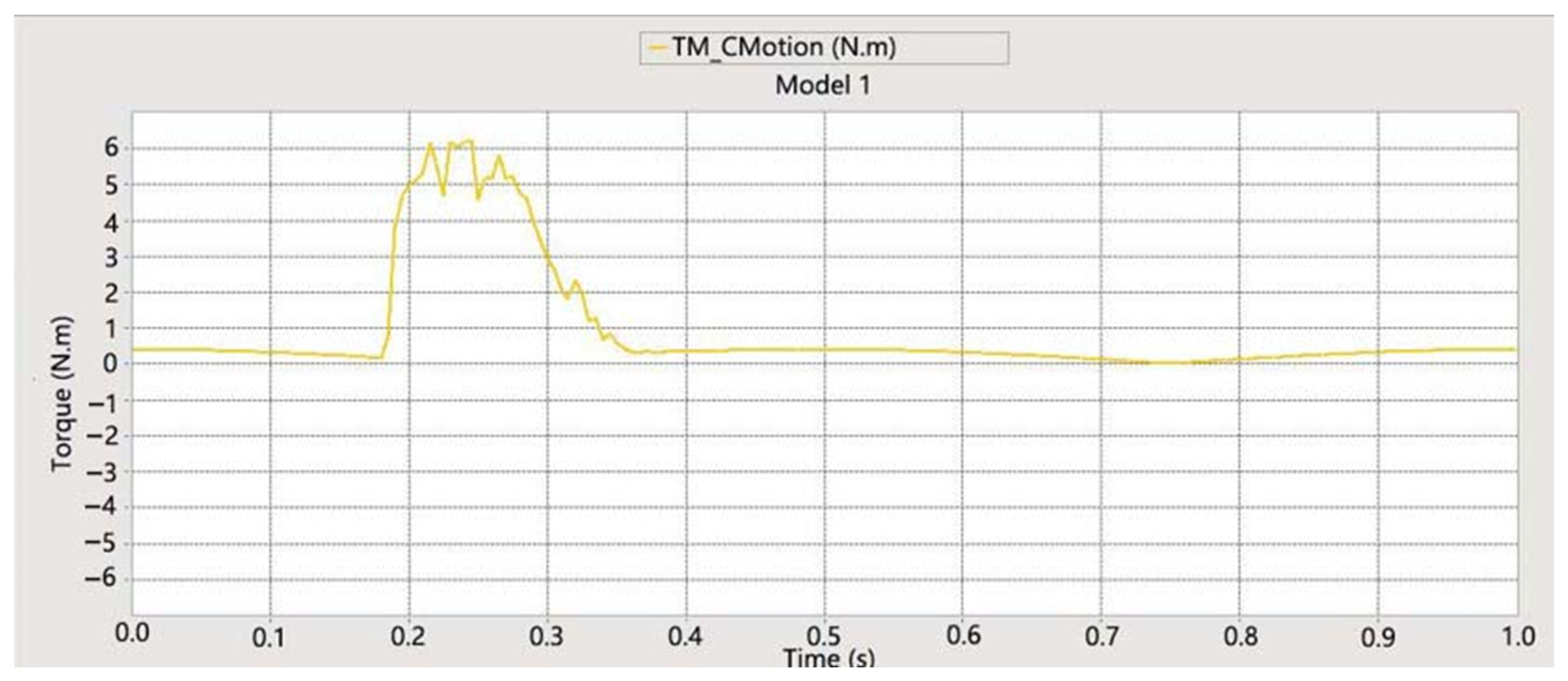
3.3. Analysis of the Torque Experienced During Film Picking with Elastic Teeth Based on DEM–MBD Coupling Simulation
3.4. Analysis of the Peeling Characteristics and Mechanical Properties of Residual Film–Soil Based on DEM Simulation
3.5. Field Film Harvesting Experiment Based on the Collaborative Operation of Membrane Picking Device and Air Suction Device
4. Discussion
5. Conclusions
- (1)
- This paper calibrates the parameters for the elastic tooth–soil–residual film system. Intrinsic soil parameters, including Poisson’s ratio, density, shear modulus, stacking angle, and particle size distribution, were determined through experimental methods and a literature review. Contact parameters, such as the static friction coefficient, rolling friction coefficient, and collision recovery coefficient for soil–steel interactions, were measured using the slip method, inclined method, and inclined collision method. The soil–soil contact parameters—static friction coefficient, rolling friction coefficient, and collision recovery coefficient—were more difficult to obtain experimentally, so they were determined via virtual parameter calibration. The calibrated values for the soil–soil contact parameters were 0.74, 0.22, and 0.52, respectively, with a stacking angle error of 2.7% compared to experimental results. The residual film–residual film rolling friction coefficient and collision recovery coefficient were calibrated at 0.4 and 0.57, respectively, with a stacking angle error of 1.6%, which is within the acceptable range.
- (2)
- A DEM–MBD coupling simulation model of the elastic tooth–soil–residual film system was established to predict the force required to extract residual film from soil and the residual film recovery rate. Comparative analysis of simulation and experimental results for both force and recovery rate revealed an 8.1% error in the force measurement (simulation: 0.34 N, experiment: 0.37 N) and a 2% error in the recovery rate (simulation: 90%, experiment: 92%). This study provides valuable insights for the microscopic analysis of soil-touching components, soil–plant root interactions, and the optimization of agricultural machinery performance. This study can also provide a reference for the design of similar residual film recycling equipment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, R.; Zhu, Z.; Peng, C.; Bian, Z.; Yang, X.; Wang, H.; Wang, X.-X. Mulch film to plastic debris: A survey of agricultural soils of Hebei Province, North China. Sci. Total Environ. 2024, 918, 170509. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Fang, W.; Han, D.; Chen, X. Review of the research on soil disturbance by tools. Appl. Sci. 2023, 13, 338. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, S.D.; Baek, S.M.; Baek, S.Y.; Jeon, H.H.; Lee, J.H.; Siddique, A.A.; Kim, Y.J.; Kim, W.S.; Sim, T.; et al. Development of DEM-MBD coupling model for draft force prediction of agricultural tractor with plowing depth. Comput. Electron. Agric. 2022, 202, 107405. [Google Scholar] [CrossRef]
- Tamas, K.; Bernon, L. Role of particle shape and plant roots in the discrete element model of soil-sweep interaction. Biosyst. Eng. 2021, 211, 77–96. [Google Scholar] [CrossRef]
- Du, J.; Heng, Y.; Zheng, K.; Luo, C.; Zhu, Y.; Zhang, J.; Xia, J. Investigation of the burial and mixing performance of a rotary tiller using discrete element method. Soil Tillage Res. 2022, 220, 105349. [Google Scholar] [CrossRef]
- Li, C.; Yin, H.; Wu, C.; Zhang, Y.; Zhang, J.; Wu, Z.; Wang, W.; Jia, D.; Guan, S.; Ren, R. Calibration of the discrete element method and modeling of shortening experiments. Front. Earth Sci. 2021, 9, 636512. [Google Scholar] [CrossRef]
- Syed, Z.; Tekeste, M.; White, D. A coupled sliding and rolling friction model for DEM calibration. J. Terramechanics 2017, 72, 9–20. [Google Scholar] [CrossRef]
- Qu, T.; Feng, Y.; Zhao, T.; Wang, M. A hybrid calibration approach to Hertz-type contact parameters for discrete element models. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1281–1300. [Google Scholar] [CrossRef]
- Liang, Z.; Huang, Y.; Li, D.; Wada, M.E. Parameter determination of a viscoelastic-plastic contact model for potatoes during transient collisions. Biosyst. Eng. 2023, 234, 156–171. [Google Scholar] [CrossRef]
- Du, C.; Han, D.; Song, Z.; Chen, Y.; Chen, X.; Wang, X. Calibration of contact parameters for complex shaped fruits based on discrete element method: The case of pod pepper (Capsicum annuum). Biosyst. Eng. 2023, 226, 43–54. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, B.; Mao, H.; Liu, Y. Calibration and measurement of micrometre-scale pollen particles for discrete element method parameters based on the Johnson-Kendal-Roberts model. Biosyst. Eng. 2024, 237, 83–91. [Google Scholar] [CrossRef]
- Cheng, J.; Zheng, K.; Xia, J.; Liu, G.; Jiang, L.; Li, D. Analysis of adhesion between wet clay soil and rotary tillage part in paddy field based on discrete element method. Processes 2021, 9, 845. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, B.; Ding, L.; Li, L.; Chen, X.; Li, J. Soil particle modeling and parameter calibration for use with discrete element method. Trans. ASABE 2021, 64, 2011–2023. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, H.; Xu, L.; Song, S.; Zhang, C.; Yu, Q. Parameter calibration of coconut bran substrate simulation model based on discrete element and response surface methodology. Powder Technol. 2022, 395, 183–194. [Google Scholar] [CrossRef]
- Dai, Z.; Wu, M.; Fang, Z.; Qu, Y. Calibration and verification test of lily bulb simulation parameters based on discrete element method. Appl. Sci. 2021, 11, 10749. [Google Scholar] [CrossRef]
- Yuan, H.; Liang, S.; Wang, J.; Lu, Y. Numerical Simulation and Analysis of Vibrating Rice Filling Based on EDEM Software. Agriculture 2022, 12, 2013. [Google Scholar] [CrossRef]
- Fang, W.; Wang, X.; Han, D.; Chen, X. Review of Material Parameter Calibration Method. Agriculture 2022, 12, 706. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Li, X.; Xue, Z.; Jin, M.; Deng, B. Near-Infrared-Based Measurement Method of Mass Flow Rate in Grain Vibration Feeding System. Agriculture 2024, 14, 1476. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, Z.; Li, Y.; Song, Z.; Yu, J.; Li, Y.; Xu, L. Study of the grain particle-conveying performance of a bionic non-smooth-structure screw conveyor. Biosyst. Eng. 2024, 238, 94–104. [Google Scholar] [CrossRef]
- Mudarisov, S.; Farkhutdinov, I.; Khamaletdinov, R.; Khasanov, E.; Mukhametdinov, A. Evaluation of the significance of the contact model particle parameters in the modelling of wet soils by the discrete element method. Soil Tillage Res. 2022, 215, 105228. [Google Scholar] [CrossRef]
- Wang, X.; Li, J. Simulation of triaxial response of granular materials by modified DEM. Sci. China-Phys. Mech. Astron. 2014, 57, 2297–2308. [Google Scholar] [CrossRef]
- Schramm, M.W.; Tekeste, M.Z.; Steward, B.L. Simulation of uniaxial compression for flexible fibers of wheat straw using the discrete element method. Trans. ASABE 2021, 64, 2025–2034. [Google Scholar] [CrossRef]
- Xia, R.; Li, B.; Wang, X.; Li, T.; Yang, Z. Measurement and calibration of the discrete element parameters of wet bulk coal. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]
- Mak, J.; Chen, Y.; Sadek, M.A. Determining parameters of a discrete element model for soil-tool interaction. Soil Tillage Res. 2012, 118, 117–122. [Google Scholar] [CrossRef]
- Wang, X.; Gao, P.; Yue, B.; Shen, H.; Fu, Z.; Zheng, Z.; Huang, Y. Optimization of installation parameters of subsoiler’ wing using the discrete element method. Comput. Electron. Agric. 2019, 162, 523–530. [Google Scholar] [CrossRef]
- Kim, Y.S.; Siddique, M.A.A.; Kim, W.S.; Kim, Y.J.; Lee, S.D.; Lee, D.K.; Hwang, S.J.; Nam, J.S.; Park, S.U.; Lim, R.G. DEM simulation for draft force prediction of moldboard plow according to the tillage depth in cohesive soil. Comput. Electron. Agric. 2021, 189, 106368. [Google Scholar] [CrossRef]
- Kesner, A.; Choteborsky, R.; Linda, M.; Hromasova, M.; Katinas, E.; Sutanto, H. Stress distribution on a soil tillage machine frame segment with a chisel shank simulated using discrete element and finite element methods and validate by experiment. Biosyst. Eng. 2021, 209, 125–138. [Google Scholar] [CrossRef]
- Zhang, L.; Zhai, Y.; Wu, C.; Huang, S.; Zhang, Z. Modeling the interaction between a new four-bar subsoiling mechanism and red soil using the improved differential evolution algorithm and DEM. Comput. Electron. Agric. 2023, 208, 107783. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Q.; Muhammad, S.M.; Ji, C.; Zhao, Z. Design and experiment of bionic mole’s toe arrangement serrated blade for soil-rototilling and straw-shattering. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 43–50. [Google Scholar] [CrossRef]
- Hu, G.; Quan, L.; Zou, Y.; Shen, H. Establishment and simulation test of membrane-soil separation model for mechanical recycling of agricultural residual film. J. Hunan Agric. Univ. 2021, 47. [Google Scholar] [CrossRef]
- Fang, W.; Wang, X.; Han, D.; Zang, N.; Xue, G.; Israel, E.O. Parameter Optimization and Disturbance Analysis of the Film Picking Device of the Chain-Type Plough Layer Residual Film Recovery Machine Based on DEM-MBD Coupling. Comput. Electron. Agric. 2024, 222, 109041. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, J.; Sun, K.; Wang, Y.; Liang, L.; Sun, Y.; Zhou, L.; Yu, Y. A discrete element method model and experimental verification for wheat root systems. Biosyst. Eng. 2024, 244, 146–165. [Google Scholar] [CrossRef]
- Yang, Q.; Shi, L.; Shi, A.; He, M.; Zhao, X.; Zhang, L.; Addy, M. Determination of key soil characteristic parameters using angle of repose and direct shear stress test. Int. J. Agric. Biol. Eng. 2023, 16, 143–150. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, M.; Liu, Y.; Gao, K.; Su, B.; Qi, Y. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, H.; Liu, J.; Yang, S.X. Control method of seedbed compactness based on fragment soil compaction dynamic characteristics. Soil Tillage Res. 2020, 198, 104551. [Google Scholar] [CrossRef]
- Pasthy, L.; Farkasm, Z.J.; Haba, T.; Tamas, K. Development of a multi-way coupled discrete-finite element method simulation procedure for modelling soil-passive vibration tool interaction. Comput. Electron. Agric. 2024, 216, 108459. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, F.; Dong, J.; Chen, X.; Liu, Y.; Mi, G.; Wang, T.; Jia, X.; Huang, Y.; Wang, X. Calibration of Discrete Element Parameters of Maize Root and Its Mixture with Soil. Processes 2022, 10, 2433. [Google Scholar] [CrossRef]
- Walunj, A.; Chen, Y.; Tian, Y.; Zeng, Z. Modeling Soil-Plant-Machine Dynamics Using Discrete Element Method: A Review. Agronomy 2023, 13, 1260. [Google Scholar] [CrossRef]



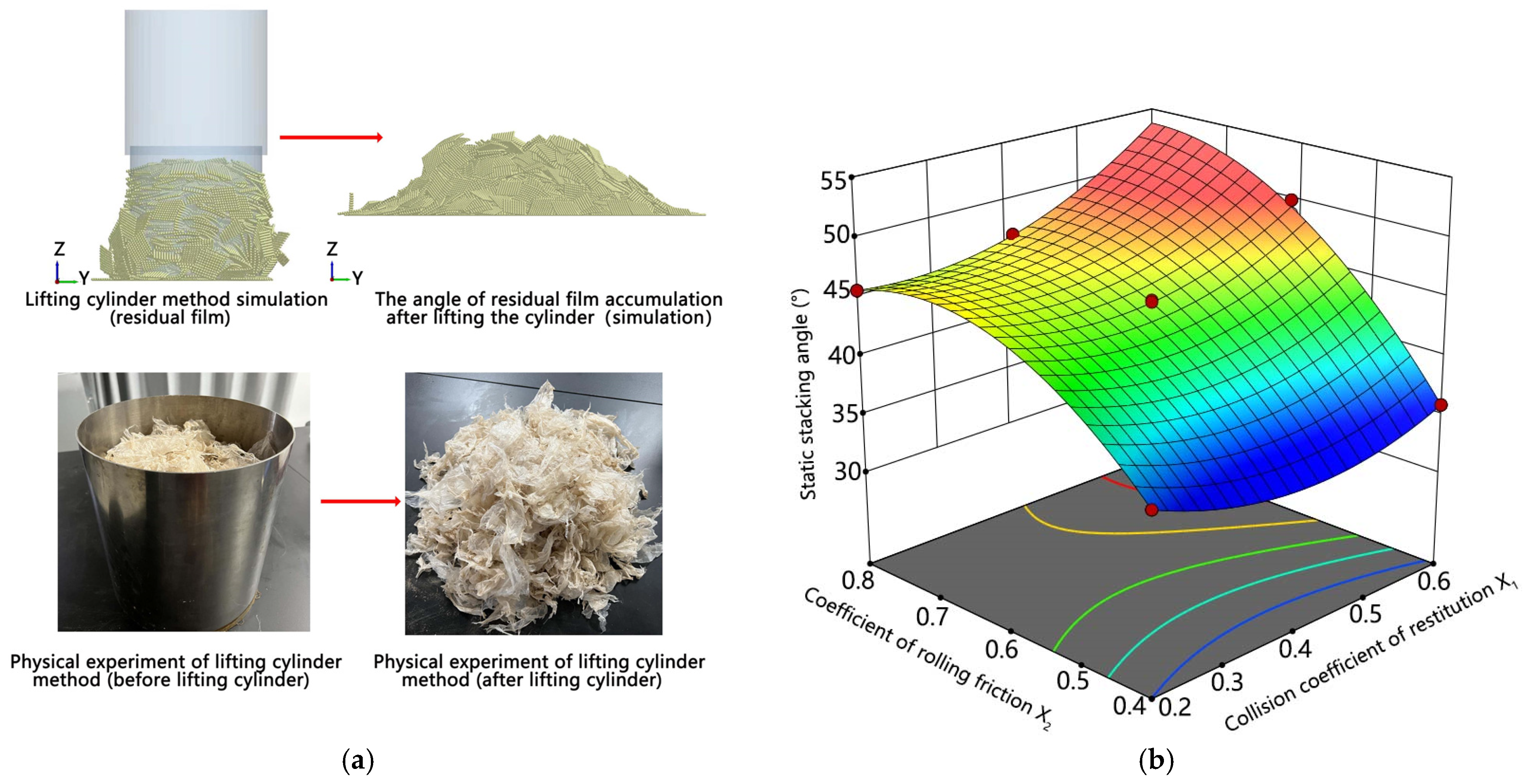



| Coefficient of Recovery Restitution | Coefficient of Rolling Friction |
|---|---|
| 0.2 | 0.4 |
| 0.4 | 0.6 |
| 0.6 | 0.8 |
| No. | Collision Coefficient of Restitution X1 | Coefficient of Rolling Friction X2 | Static Stacking Angle Y1/° |
|---|---|---|---|
| 1 | 0.2 | 0.4 | 36.81 |
| 2 | 0.2 | 0.8 | 45.65 |
| 3 | 0.4 | 0.8 | 46.71 |
| 4 | 0.4 | 0.6 | 44.68 |
| 5 | 0.4 | 0.8 | 46.88 |
| 6 | 0.4 | 0.6 | 44.49 |
| 7 | 0.4 | 0.6 | 44.53 |
| 8 | 0.4 | 0.6 | 44.85 |
| 9 | 0.6 | 0.4 | 35.88 |
| 10 | 0.6 | 0.6 | 48.73 |
| 11 | 0.6 | 0.6 | 49.90 |
| Source | Static Stacking Angle Y1/° | |||
|---|---|---|---|---|
| Sum of Squares | Degree of Freedom | F | Significant Level | |
| Model | 191.73 | 5 | 40.55 | <0.0001 ** |
| A | 10.44 | 1 | 29.57 | 0.0004 * |
| B | 45.64 | 1 | 155.90 | <0.0001 ** |
| AB | 10.73 | 1 | 108.66 | 0.0004 ** |
| 15.05 | 1 | 24.07 | 0.0002 | |
| 36.67 | 1 | <0.0001 ** | ||
| Pure Error | 0.7792 | 5 | ||
| Cor Total | 192.51 | 10 | ||
| Levels | Collision Recovery Coefficient | Coefficient of Static Friction | Coefficient of Rolling Friction |
|---|---|---|---|
| −1 | 0.40 | 0.70 | 0.20 |
| 0 | 0.50 | 0.75 | 0.26 |
| 1 | 0.60 | 0.80 | 0.32 |
| Run | A-Collision Recovery Coefficient | B-Coefficient of Static Friction | C-Coefficient of Rolling Friction | -Static Stacking Angle/° |
|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 43.13 |
| 2 | 1 | −1 | 0 | 42.42 |
| 3 | −1 | 1 | 0 | 41.84 |
| 4 | 1 | 1 | 0 | 39.98 |
| 5 | −1 | 0 | −1 | 38.55 |
| 6 | 1 | 0 | −1 | 41.13 |
| 7 | −1 | 0 | 1 | 43.71 |
| 8 | 1 | 0 | 1 | 44.57 |
| 9 | 0 | −1 | −1 | 43.85 |
| 10 | 0 | 1 | −1 | 38.12 |
| 11 | 0 | −1 | 1 | 40.27 |
| 12 | 0 | 1 | 1 | 42.71 |
| 13 | 0 | 0 | 0 | 44.71 |
| 14 | 0 | 0 | 0 | 44.71 |
| 15 | 0 | 0 | 0 | 44.71 |
| 16 | 0 | 0 | 0 | 44.71 |
| 17 | 0 | 0 | 0 | 44.71 |
| Source | Static Stacking Angle Y1/° | |||
|---|---|---|---|---|
| Sum of Squares | Degree of Freedom | F | Significant Level | |
| Model | 62.39 | 9 | 51.31 | <0.0001 ** |
| A | 3.29 | 1 | 24.35 | 0.0017 * |
| B | 45.03 | 1 | 333.29 | <0.0001 ** |
| C | 7.24 | 1 | 53.58 | 0.0002 * |
| AB | 1.16 | 1 | 8.55 | 0.0222 |
| AC | 0.1296 | 1 | 0.9592 | 0.3600 |
| BC | 0.3422 | 1 | 2.53 | 0.1555 |
| A2 | 4.51 | 1 | 33.42 | 0.0007 |
| B2 | 0.3492 | 1 | 2.58 | 0.1519 |
| C2 | 0.0831 | 1 | 0.6152 | 0.4586 |
| Residual | 0.9457 | 7 | ||
| Lack of Fit | 0.5502 | 3 | 1.85 | 0.2779 |
| Pure Error | 0.3955 | 4 | ||
| Cor Total | 63.34 | 16 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.; Wang, X.; Han, D.; Enema Ohiemi, I. Design and Testing of Film Picking–Unloading Device of Tillage Residual Film Recycling Machine Based on DEM Parameter Calibration. Agronomy 2025, 15, 955. https://doi.org/10.3390/agronomy15040955
Fang W, Wang X, Han D, Enema Ohiemi I. Design and Testing of Film Picking–Unloading Device of Tillage Residual Film Recycling Machine Based on DEM Parameter Calibration. Agronomy. 2025; 15(4):955. https://doi.org/10.3390/agronomy15040955
Chicago/Turabian StyleFang, Weiquan, Xinzhong Wang, Dianlei Han, and Israel Enema Ohiemi. 2025. "Design and Testing of Film Picking–Unloading Device of Tillage Residual Film Recycling Machine Based on DEM Parameter Calibration" Agronomy 15, no. 4: 955. https://doi.org/10.3390/agronomy15040955
APA StyleFang, W., Wang, X., Han, D., & Enema Ohiemi, I. (2025). Design and Testing of Film Picking–Unloading Device of Tillage Residual Film Recycling Machine Based on DEM Parameter Calibration. Agronomy, 15(4), 955. https://doi.org/10.3390/agronomy15040955






