Impact of β-Amyloids Induced Disruption of Ca2+ Homeostasis in a Simple Model of Neuronal Activity
Abstract
:1. Introduction
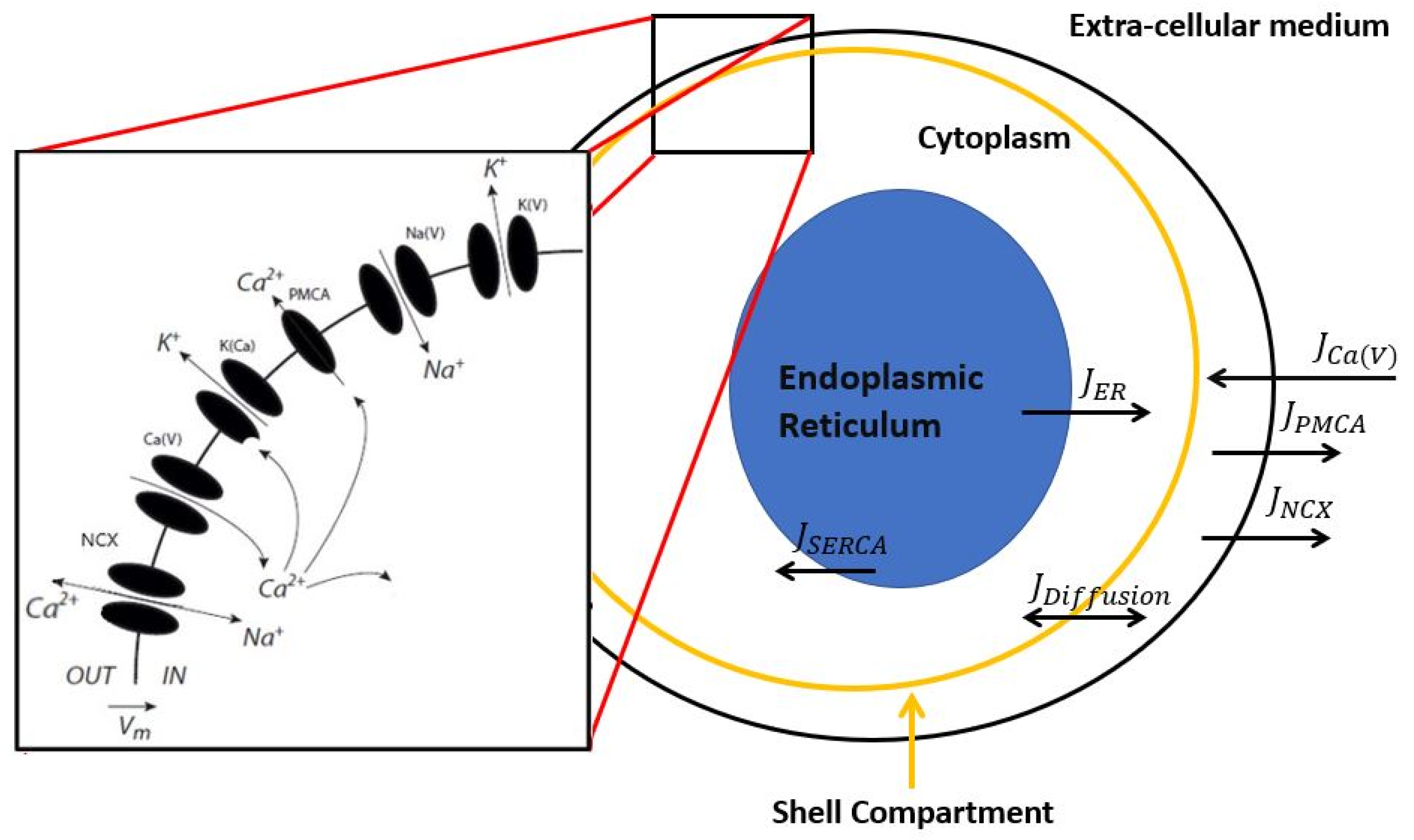
2. Description of the Model
3. Results
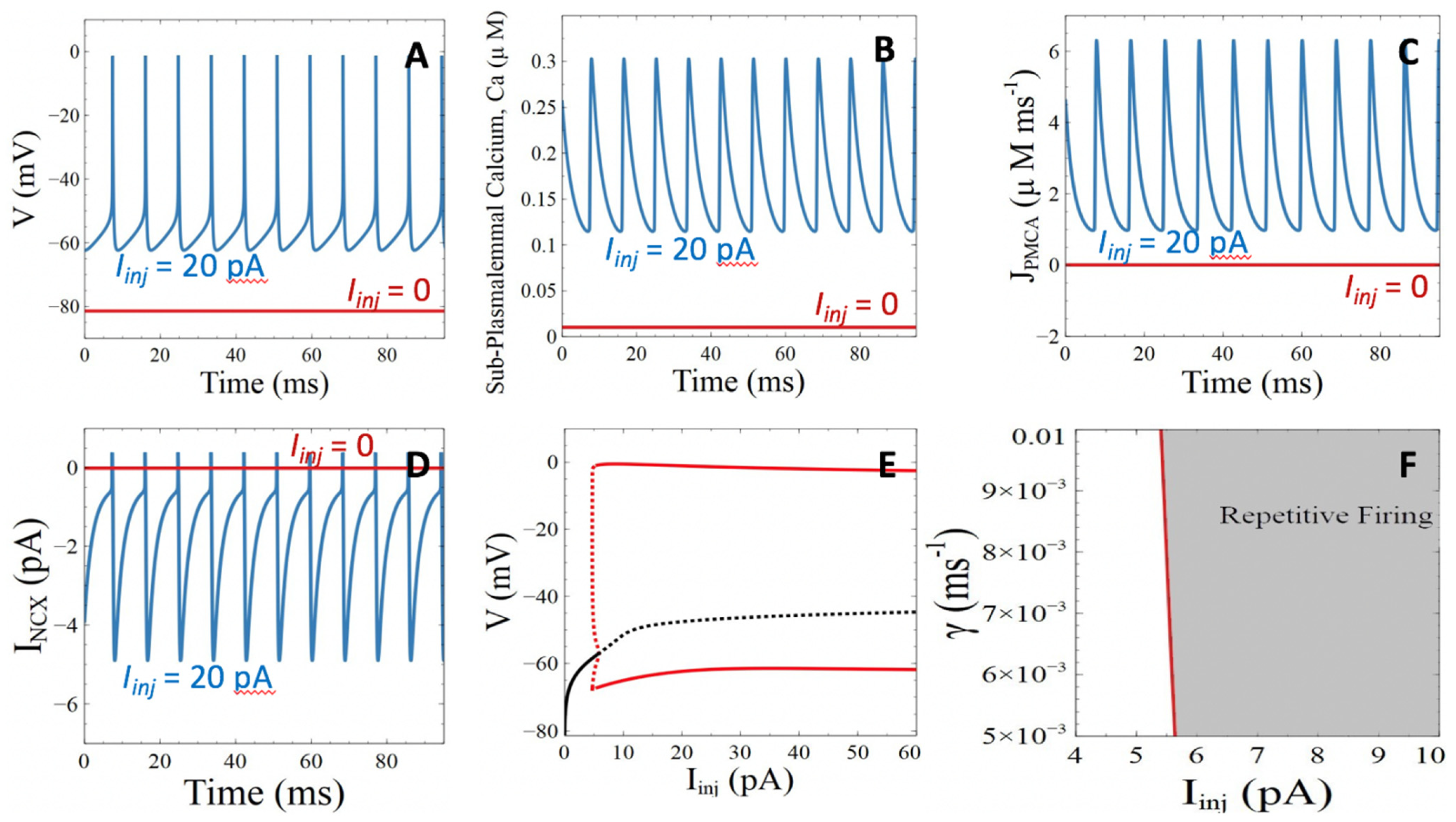
3.1. Model Behavior in the Absence of Aβ Peptides
3.2. Aβ Peptides Induced Changes in the Rates of Ca2+ Pumps and Pores
3.2.1. Ca2+ ATPases
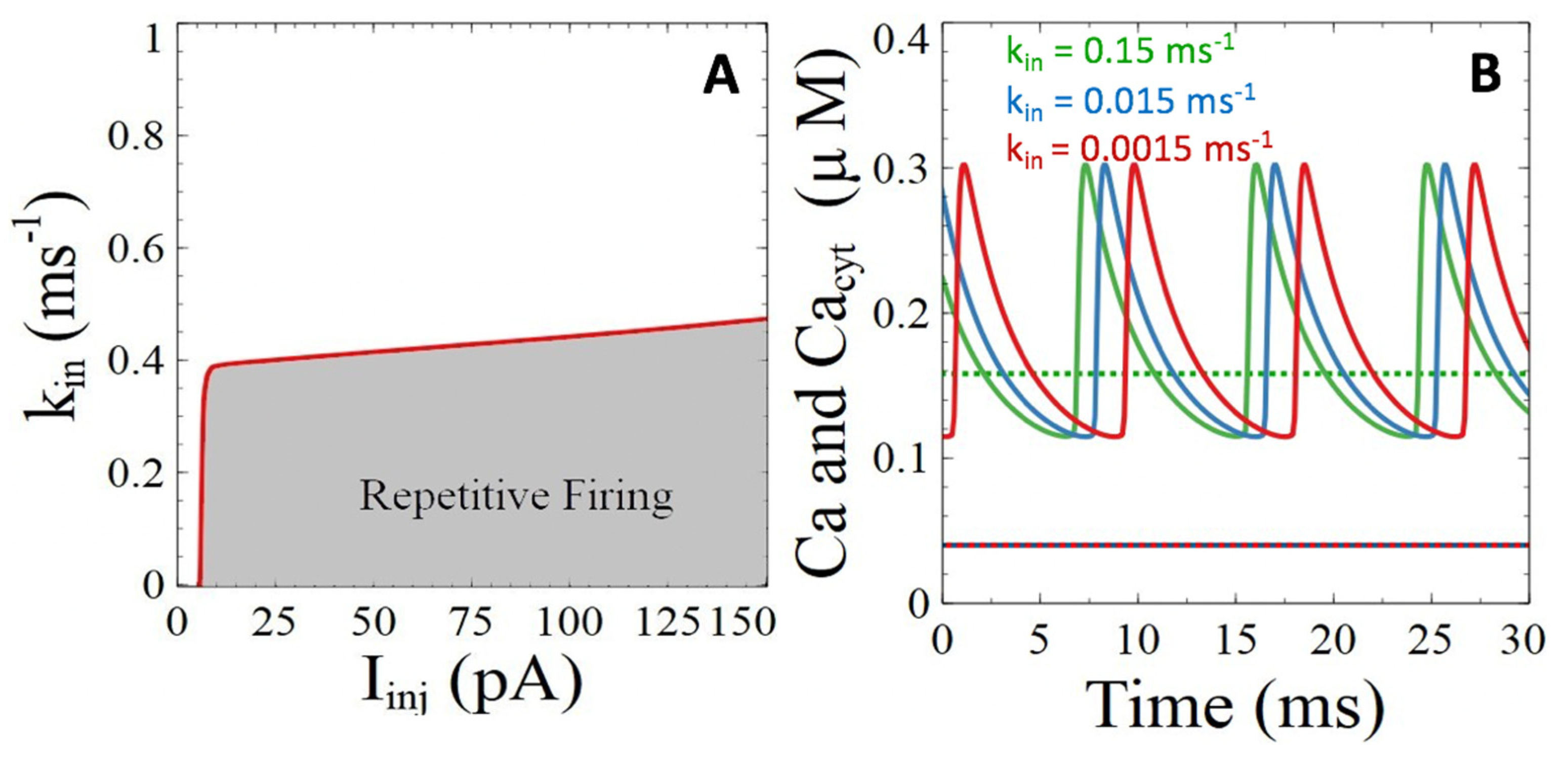
3.2.2. Ryanodine Receptor- and IP3 Receptor-Mediated Basal Release of ER Ca2+
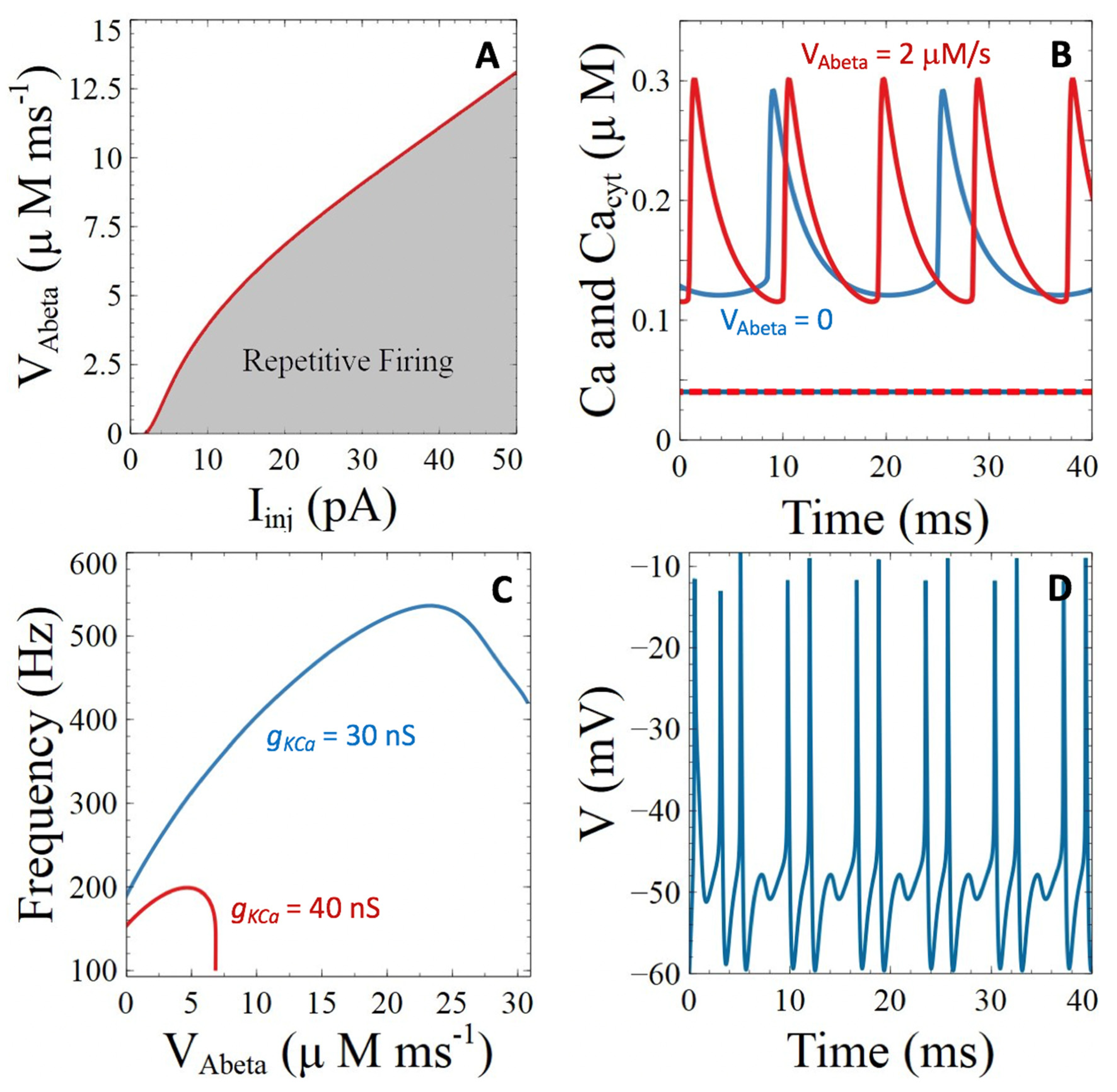
3.2.3. Pores of β-Amyloids in the Plasma Membrane
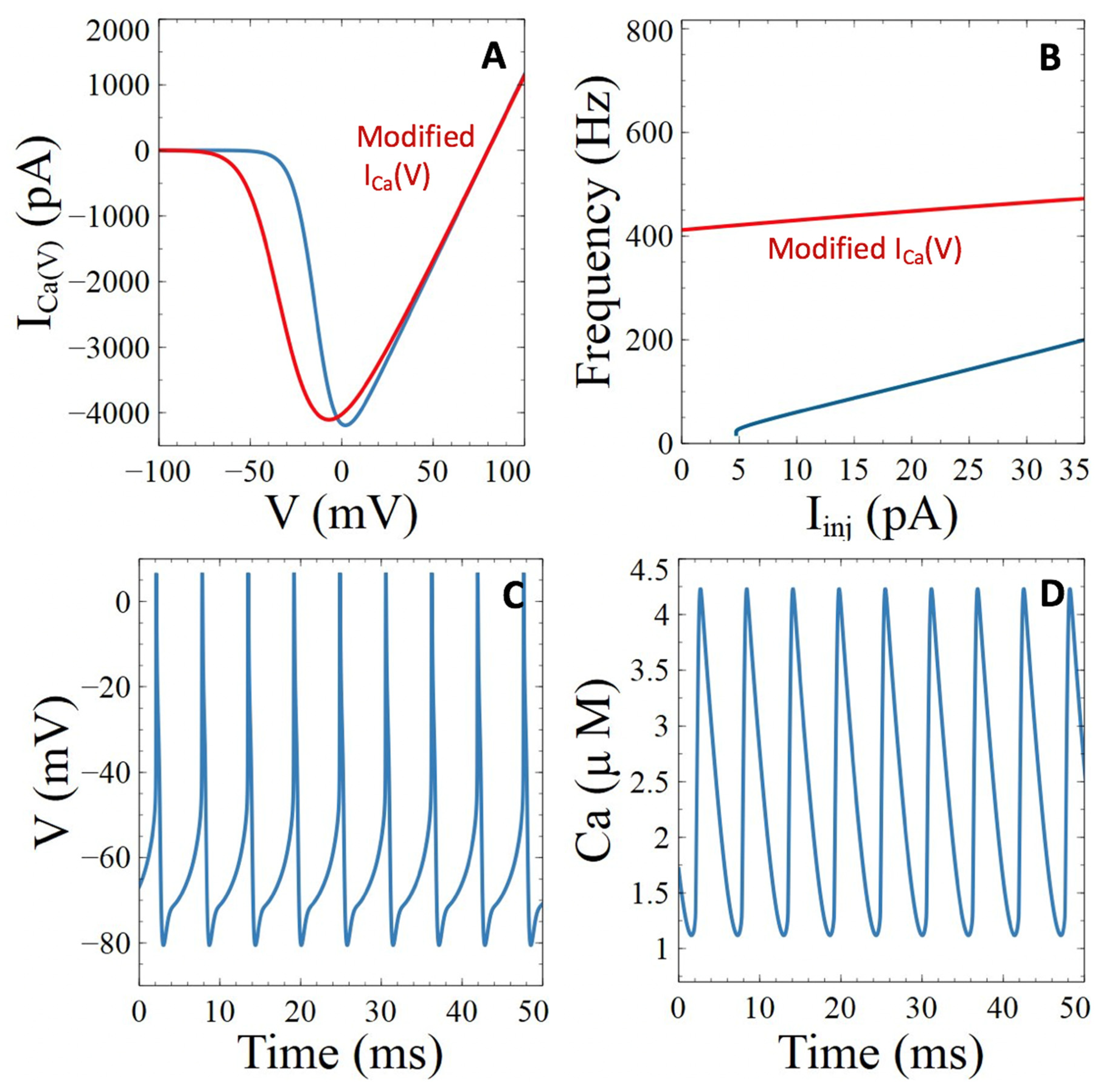
3.3. Aβ Peptides Induced Changes in Voltage-Sensitive Ca2+ Currents
3.3.1. Voltage-Gated Ca2+ Channels
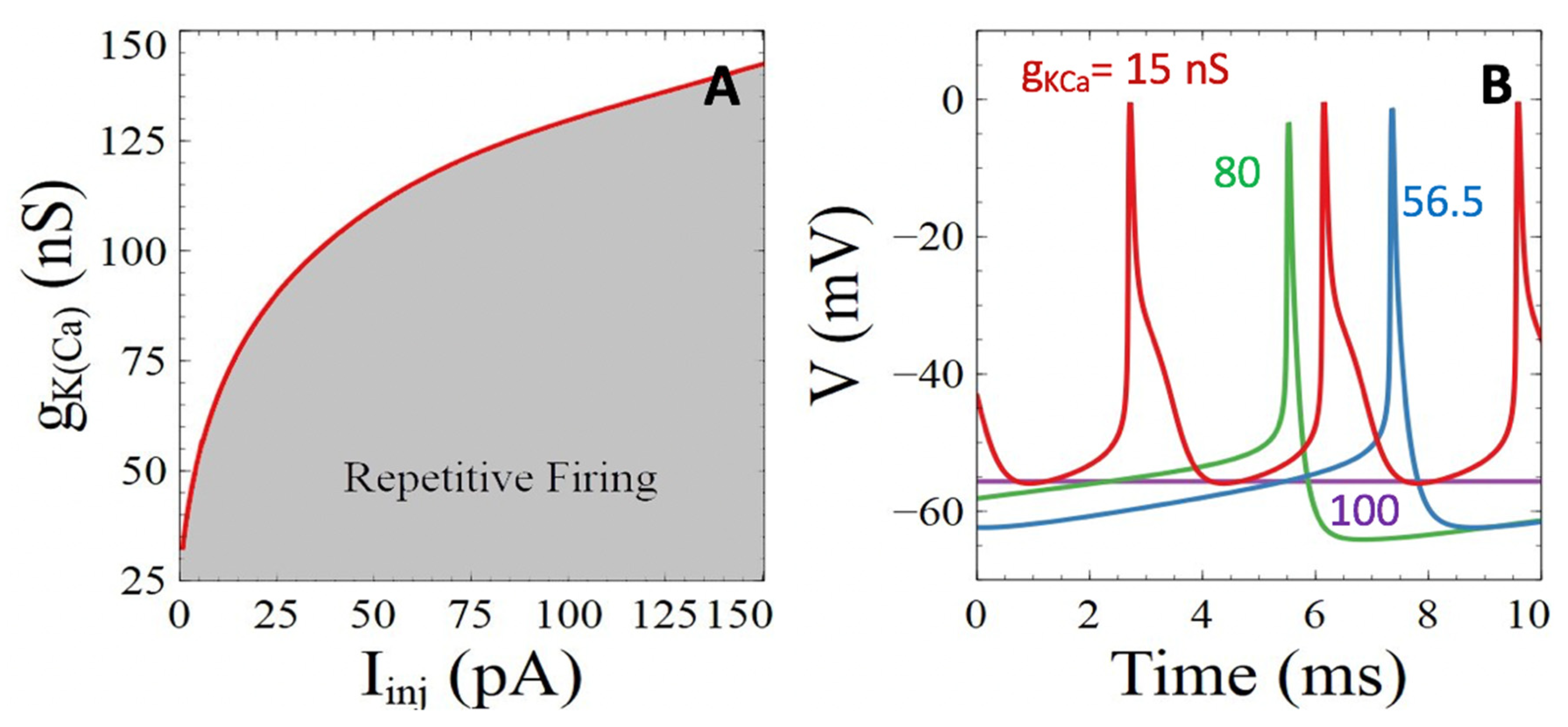
3.3.2. Ca2+-Sensitive Potassium Channels
4. Discussion
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berridge, M.J.; Bootman, M.D.; Lipp, P. Calcium—A life and death signal. Nature 1998, 395, 645–648. [Google Scholar] [CrossRef] [PubMed]
- Gall, D.; Roussel, C.; Susa, I.; D’Angelo, E.; Rossi, P.; Bearzatto, B. Altered neuronal excitability in cerebellar granule cells of mice lacking calretinin. J. Neurosci. 2003, 23, 9320–9327. [Google Scholar] [CrossRef] [Green Version]
- Alzheimer’s Association Calcium Hypothesis Workgroup. Calcium hypothesis of Alzheimer’s disease and brain aging: A framework for integrating new evidence into a comprehensive theory of pathogenesis. Alzheimer’s Dement. 2017, 13, 178–182. [Google Scholar] [CrossRef]
- Berridge, M.J. Calcium hypothesis of Alzheimer’s disease. Pflug. Arch. 2010, 459, 441–449. [Google Scholar] [CrossRef]
- LaFerla, F. Calcium dyshomeostasis and intracellular signalling in Alzheimer’s disease. Nat. Rev. Neurosci. 2012, 3, 862–872. [Google Scholar] [CrossRef]
- McDaid, J.; Mustaly-Kalimi, S.; Stutzmann, G. Ca2+ dyshomeostasis disrupts neuronal and synaptic function in Alzheimer’s disease. Cells 2020, 9, 2655. [Google Scholar] [CrossRef] [PubMed]
- Schrank, S.; Barrington, N.; Stutzmann, G. Calcium-handling defects and neurodegenerative disease. Cold Spring Harb. Perspect. Biol. 2020, 21, a035212. [Google Scholar] [CrossRef] [PubMed]
- De Caluwé, J.; Dupont, G. The progression towards Alzheimer’s disease described as a bistable switch arising from the positive loop between amyloids and Ca2+. J. Theor. Biol. 2013, 331, 12–18. [Google Scholar] [CrossRef]
- Busche, M.A.; Eichhoff, G.; Adelsberger, H.; Abramowski, D.; Wiederhold, K.H.; Haass, C.; Staufenbiel, M.; Konnerth, A.; Garaschuk, O. Clusters of hyperactive neurons near amyloid plaques in a mouse model of Alzheimer’s disease. Science 2002, 321, 1686–1689. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, B.; Thomas, V.; Ingram, V. Mechanism of membrane depolarization caused by the Alzheimer Aβ1-42 peptide. Biochem. Biophys. Res. Commun. 2002, 293, 1197–1203. [Google Scholar] [CrossRef]
- Sosulina, L.; Mittag, M.; Geis, H.-R.; Hoffman, K.; Klyubin, I.; Qi, Y.; Steffen, J.; Friedrichs, D.; Henneberg, N.; Fuhrman, F.; et al. Hippocampal hyperactivity in a rat model of Alzheimer’s disease. J. Neurochem. 2021, 157, 2128–2144. [Google Scholar] [CrossRef] [PubMed]
- Tamagnini, F.; Scullion, S.; Brown, J.; Randall, A. Intrinsic excitability changes induced by acute treatment of hippocampal CA1 pyramidal neurons with exogenous amyloid βpeptide. Hippocampus 2015, 25, 786–797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Latulippe, J.; Lotito, D.; Murby, D. A mathematical model for the effects of amyloid beta on intracellular calcium. PLoS ONE 2018, 13, e0202503. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Goa, H.; Zaikin, A.; Chen, S. Unraveling Aβ-mediated multi-pathway calcium dynamics in astrocytes: Implications for Alzheimer’s disease treatment from simulations. Front. Physiol. 2021, 12, 767892. [Google Scholar] [CrossRef] [PubMed]
- Felix-Martinez, G.; Godinez-Fernandez, J. Mathematical models of electrical activity of the pancreatic beta-cell: A physiological review. Islets 2014, 6, e949195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gall, D.; Gromada, J.; Susa, I.; Rorsman, P.; Herchuelz, A.; Bokvist, K. Significance of Na/Ca exchange for Ca2+ buffering and electrical activity in mouse pancreatic β-cells. Biophys. J. 1999, 79, 2018–2028. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, P.; Li, Y.X. An integrated model of electrical spiking, bursting, and calcium oscillations in GnRH neurons. Biophys. J. 2009, 96, 4514–4524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wada, K.; Sakaguchi, Y. Repetitive firing in a model motoneuron: Inhibitory effect of a Ca2+-activated potassium conductance on the slope of the frequency-current relationship. Neurosci. Res. 2007, 57, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Dupont, G.; Falcke, M.; Kirk, V.; Sneyd, J. Models of Calcium Signalling; Springer: New York, NY, USA, 2016. [Google Scholar]
- Rasmusson, R.; Clark, J.; Giles, W.; Robinson, K.; Clark, R.; Shibata, E.; Campbell, D. A mathematical model of electrophysiological activiy in a bulfrog atrial cell. Am. J. Physiol. 1990, 259, H370–H389. [Google Scholar]
- Good, T.; Murphy, R. Effect of β-amyloid block of the fast-inactivating K+ channel on intracellular Ca2+ and excitability in a modeled neuron. Proc. Natl. Acad. Sci. USA 1996, 93, 15130–15135. [Google Scholar] [CrossRef] [Green Version]
- Gall, D.; Dupont, G. Tonic activation of extrasynaptic NMD—A receptors decreases intrinsic excitability and promotes bistability in a model of neuronal activity. Int. J. Mol. Sci. 2019, 21, 206. [Google Scholar] [CrossRef] [Green Version]
- Talantova, M.; Sanz-Blasco, S.; Zhang, X.; Xia, P.; Akhtar, M.; Okamoto, S.; Dziewczapolski, G.; Nakamura, T.; Cao, G.; Pratt, A.; et al. Ab induces astrocytic glutamate release, extrasynaptic NMDA receptor activation, and synaptic loss. Proc. Natl. Acad. Sci. USA 2013, 110, E2518–E2527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zott, B.; Simon, M.; Hong, W.; Unger, F.; Chen-Engerer, H.-J.; Frosch, M.; Sakmann, B.; Walsh, D.; Konnerth, A. A vicious cycle of β-amyloid-dependent neuronal hyperactivation. Science 2019, 365, 559–565. [Google Scholar] [CrossRef]
- Kim, S.; Rhim, H. Effects of amyloid peptides on voltage-gated L-type CaV1.2 and Cav1.3 Ca2+ channels. Mol. Cells 2011, 32, 289–294. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Kang, H.; Li, Y.; Shui, Y.; Yamamoto, R.; Sugai, T.; Kato, N. Cognitive recovery by chronic activation of the large-conductance calcium-activated potassium channel in a mouse model of Alzheimer’s disease. Neuropharmacolgy 2015, 92, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Demuro, A.; Mina, E.; Kayed, R.; Milton, S.; Parker, I.; Glabe, C. Calcium dysregulation and membrane disruption as ubiquitous neurotoxic mechanism of soluble amyloid oligomers. J. Biol. Chem. 2005, 280, 17294–17300. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ullah, G.; Demuro, A.; Parker, I.; Pearson, J. Analyzing and modeling the kinetics of amyloid beta pores associated with Alzheimer’s disease pathology. PLoS ONE 2015, 10, e0137357. [Google Scholar] [CrossRef] [PubMed]
- Roussel, C.; Erneux, T.; Schiffmann, S.; Gall, D. Modulation of neuronal excitability by intracellular calcium buffering: From spiking to bursting. Cell Calcium 2016, 39, 455–466. [Google Scholar] [CrossRef] [PubMed]
- Bicca, M.; Figueiredo, C.; Piermartiri, T.; Meotti, F.; Bouzon, Z.; Tasca, C.; Medeiros, R.; Calixto, J. The selective and competitive N-methyl-D-aspartate receptor antagonist, (-)-6-phosphonomethyl-deca-hydroisoquinoline-”-carboxylic acid, prevents synaptic toxicity induced by amyloid-β in mice. Neuroscience 2011, 192, 631–641. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R.C. The plasma membrane Ca2+ ATPase (PMCA) of neurones is electroneutral and exchanges 2H+ for each Ca2+ or Ba2+ ion extruded. J. Physiol. 2009, 587, 315–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allbritton, N.; Meyer, T.; Stryer, L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science 1992, 258, 1812–1815. [Google Scholar] [CrossRef] [PubMed]
- Berridge, M.J. Calcium oscillations. J. Biol. Chem. 1990, 265, 9583–9586. [Google Scholar] [CrossRef]
- Sun, C.H.; Wacquier, B.; Aguilar, D.; Carayol, N.; Denis, K.; Boucherie, S. The Shigella type III effector IpgD recodes Ca2+ signals during invasion of epithelia cells. EMBO J. 2017, 36, 2567–2580. [Google Scholar] [CrossRef] [PubMed]
- Toglia, P.; Cheung, K.; Mak, D.; Ullah, G. Impaired mitochondrial function due to familial Alzheimer’s disease-causing presenilins mutants via Ca2+ disruptions. Cell Calcium 2016, 59, 240–250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chatton, J.Y.; Liu, H.; Stucki, J.W. Simultaneous measurements of Ca2+ in the intracellular stores and the cytosol of hepatocytes during hormone induced Ca2+ oscillations. FEBS Lett. 1995, 368, 165–168. [Google Scholar] [CrossRef] [Green Version]
- Ermentrout, B. Simulating, Analyzing and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Duman, J.; Chen, L.; Hille, B. Calcium transport mechanisms of PC12 cells. J. Gen. Physiol. 2008, 131, 307–323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berrocal, M.; Marcos, D.; Sepulveda, M.; Perez, M.; Avila, J.; Mata, A. Altered Ca2+ dependence of synaptosomal plasma membrane Ca2+-ATPase in human brain affected by Alzheimer’s disease. FASEB J. 2009, 23, 1826–1834. [Google Scholar] [CrossRef]
- Chami, M.; Checler, F. Alteration of the endoplasmic reticulum (ER) calcium signaling molecular components in Alzheimer’s disease. Cells 2020, 9, 2577. [Google Scholar] [CrossRef] [PubMed]
- Demuro, A.; Parker, I. Cytotoxicity of intracellular Aβ42 amyloid oligomers involves Ca2+ release from the endoplasmic reticulum by stimulated production of inositol trisphosphate. J. Neurosci. 2013, 33, 3824–3833. [Google Scholar] [CrossRef] [Green Version]
- Wacquier, B.; Combettes, L.; Dupont, G. Dual dynamics of mitochondrial permeability transition pore opening. Sci. Rep. 2020, 10, 3924. [Google Scholar] [CrossRef] [Green Version]
- Ueda, K.; Shinohara, S.; Yagami, T.; Asakura, K.; Kawasaki, K. Amyloid beta protein potentiates Ca2+ influx through L-type voltage-sensitive Ca2+ channels: A possible involvement of free radicals. J. Neurochem. 1997, 68, 265–271. [Google Scholar]
- Willis, M.; Kaufmann, W.; Wietzorrek, G.; Hutter-Paier, B.; Moosmang, S.; Humpel, C. L-type calcium channel CaV 1.2 in transgenic mice overexpressing human AbetaPP751 with the London (V717l) and Swedish (K670M/N671L) mutations. J. Alzheimers Dis. 2010, 20, 1167–1180. [Google Scholar]
- Ishii, M.; Hiller, A.; Pham, L.; McGuire, M.J.; Iadecola, C.; Wang, G. Amyloid-beta modulates low-threshold activated voltage-gated L-Type calcium channels of arcuate neuropeptide Y neurons leading to calcium dysregulation and hypothalamic dysfunction. J. Neurosci. 2019, 39, 8816–8825. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; Ueta, Y.; Wang, L.; Yamamoto, R.; Inoue, N.; Inokuchi, K. Suppression of a neocortical potassium channel activity by intracellular amyloid-beta and its rescue with Homer1a. J. Neurosci. 2011, 31, 11100–11109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamamoto, K.; Yamamoto, R.; Kato, N. Amyloid β and amyloid precursor protein synergistically suppress large-conductance calcium-activated potassium channel in cortical neurons. Front. Aging Neurosci. 2021, 13, 660319. [Google Scholar] [CrossRef]
- Yao, J.; Sun, B.; Institoris, A.; Zhan, X.; Guo, W. Limiting RYR2 open time prevents Alzheimer’s disease-related neuronal hyperactivity and memory loss but not β-amyloid accumulation. Cell Rep. 2020, 32, 108169. [Google Scholar] [CrossRef] [PubMed]
- Chakroborty, S.; Hill, E.; Christian, D.; Helfrich, R.; Riley, S. Reduced presynaptic vesicle stores mediate cellular and network plasticity defects in an early-stage mouse model of Alzheimer’s disease. Mol. Neurodegener. 2019, 14, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gavello, D.; Calorio, C.; Franchino, C.; Cesano, F.; Carabelli, V.; Carbone, E.; Marcantoni, A. Early alterations of hippocampal neuronal firing induced by Abeta42. Cereb. Cortex 2018, 28, 433–446. [Google Scholar] [CrossRef]
- Kaczorowski, C.; Sametsky, E.; Shah, S.; Vassar, R.; Disterhoft, J.F. Mechanisms underlying basal and learning-related intrinsic excitability in a mouse model of Alzheimer’s disease. Neurobiol. Aging 2011, 32, 1452–1465. [Google Scholar] [CrossRef] [Green Version]
- Briggs, C.; Chakroborty, S.; Stutzmann, G.E. Emerging pathways driving early synaptic pathology in Alzheimer’s disease. Biochem. Biophys. Res. Commun. 2017, 483, 988–997. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Parameter Name | Parameter Meaning | Value |
|---|---|---|
| Membrane capacity | 3.14 pF | |
| Volume of the shell | ||
| F | Faraday constant | |
| f | Calcium buffering capacity of the cytoplasm | 0.01 |
| Injected Current | [0.150] pA | |
| release from the ER | ||
| concentration | ||
| γ | Shell-Cytoplasm Diffusion Coefficient | |
| ions | 55 mV | |
| ions | −90 mV | |
| ions | 80 mV | |
| Equilibrium Potential for the NCX channel | −20 mV | |
| channel | 172 nS | |
| channel | 28 nS | |
| channel | 58 nS | |
| channel | 56.5 nS | |
| Half saturation constant of the NCX channel | ||
| Half saturation constant of the PMCA | ||
| Half saturation constant of the SERCA | ||
| Maximal velocity of the PMCA | ||
| Maximal velocity of the SERCA | ||
| release through pores of Aβ peptides | ||
| entry through the pores of Aβ peptides | −30 mV | |
| entry through the pores of Aβ peptides | 23 mV |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prista von Bonhorst, F.; Gall, D.; Dupont, G. Impact of β-Amyloids Induced Disruption of Ca2+ Homeostasis in a Simple Model of Neuronal Activity. Cells 2022, 11, 615. https://doi.org/10.3390/cells11040615
Prista von Bonhorst F, Gall D, Dupont G. Impact of β-Amyloids Induced Disruption of Ca2+ Homeostasis in a Simple Model of Neuronal Activity. Cells. 2022; 11(4):615. https://doi.org/10.3390/cells11040615
Chicago/Turabian StylePrista von Bonhorst, Francisco, David Gall, and Geneviève Dupont. 2022. "Impact of β-Amyloids Induced Disruption of Ca2+ Homeostasis in a Simple Model of Neuronal Activity" Cells 11, no. 4: 615. https://doi.org/10.3390/cells11040615
APA StylePrista von Bonhorst, F., Gall, D., & Dupont, G. (2022). Impact of β-Amyloids Induced Disruption of Ca2+ Homeostasis in a Simple Model of Neuronal Activity. Cells, 11(4), 615. https://doi.org/10.3390/cells11040615







