Integrating Bioinformatics and Machine Learning for Genomic Prediction in Chickens
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Quality Control and Imputation
2.3. Genome-Wide Association Study (GWAS)
2.4. Functional Annotation
2.5. Feature Engineering
2.6. Model Building
3. Results
3.1. Phenotype Statistics and Genome-Wide Association Study (GWAS)
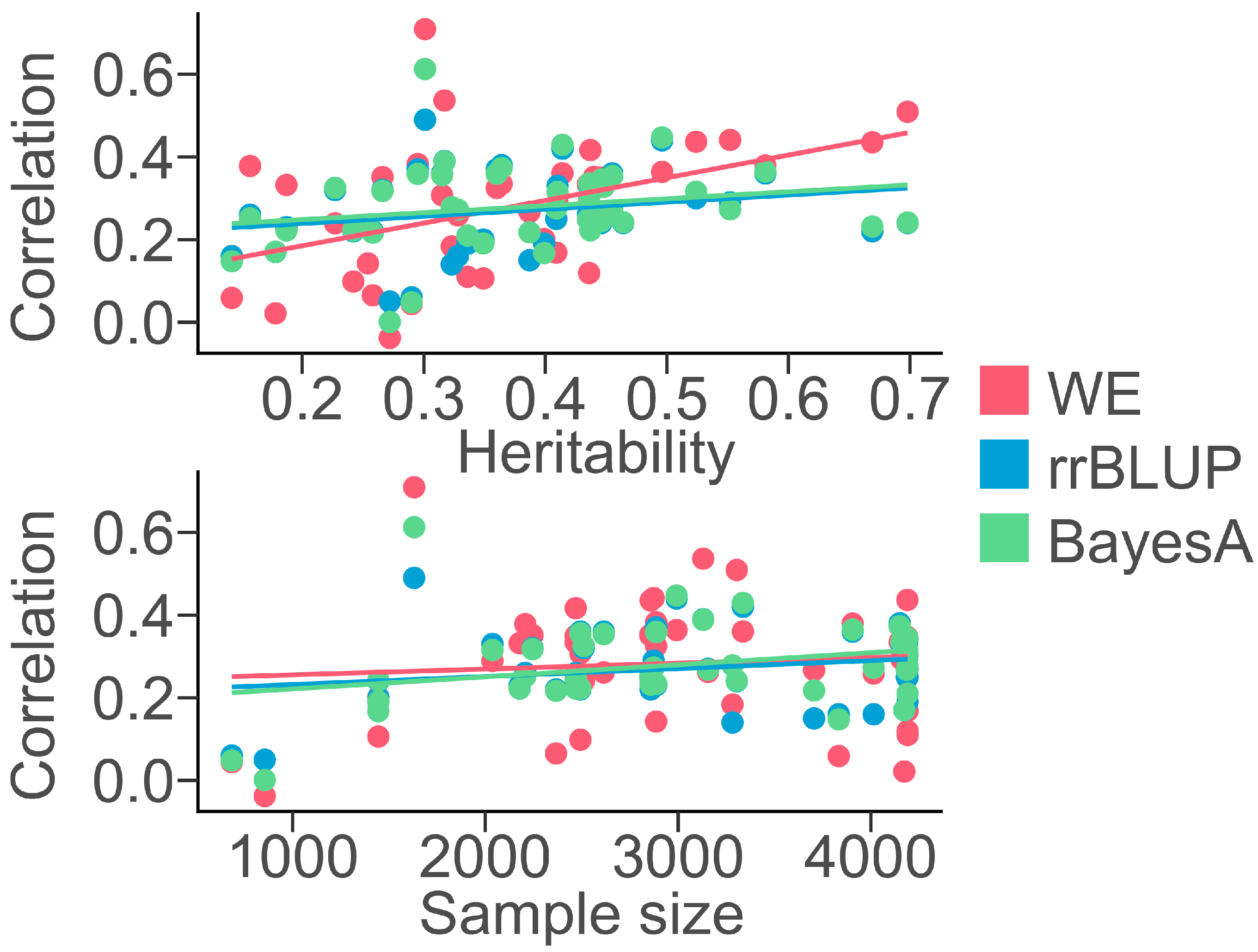
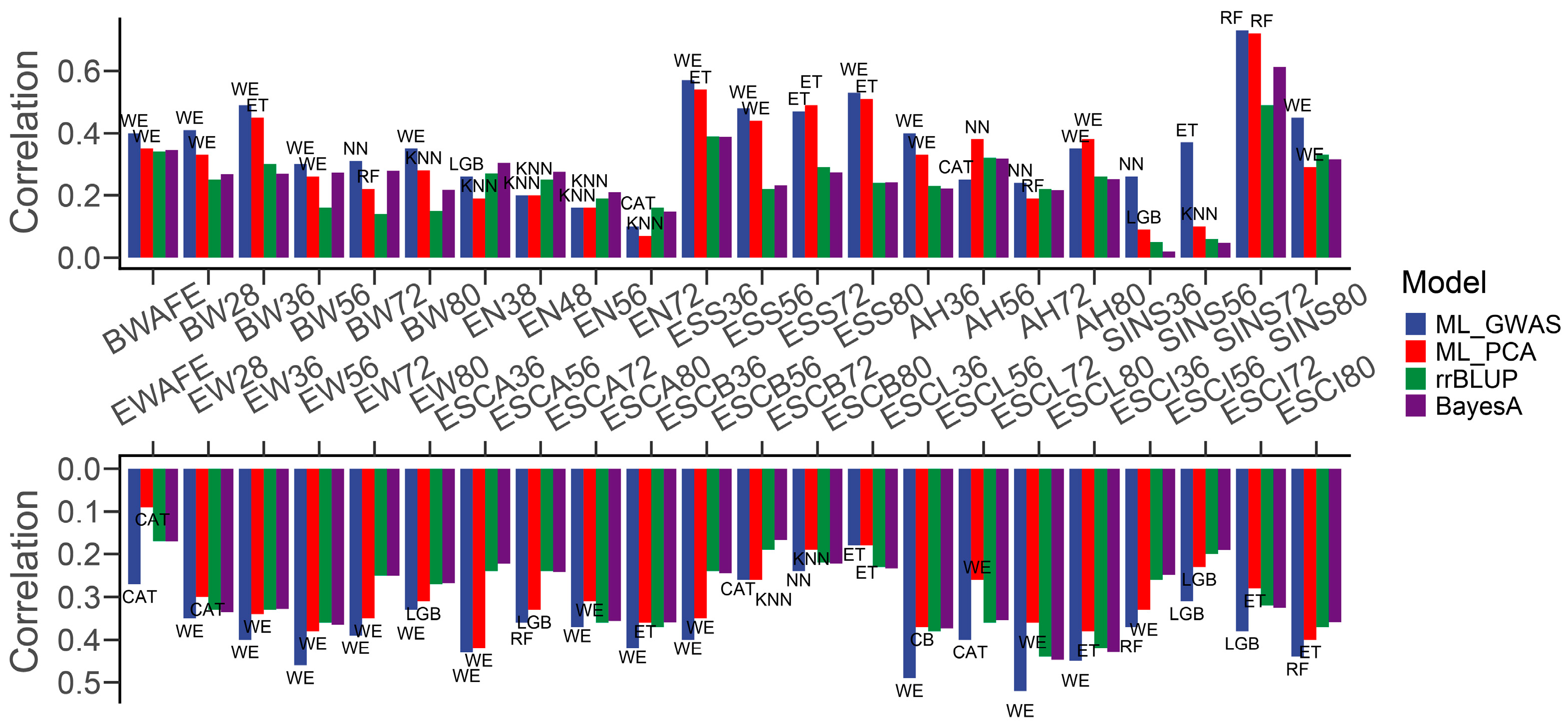
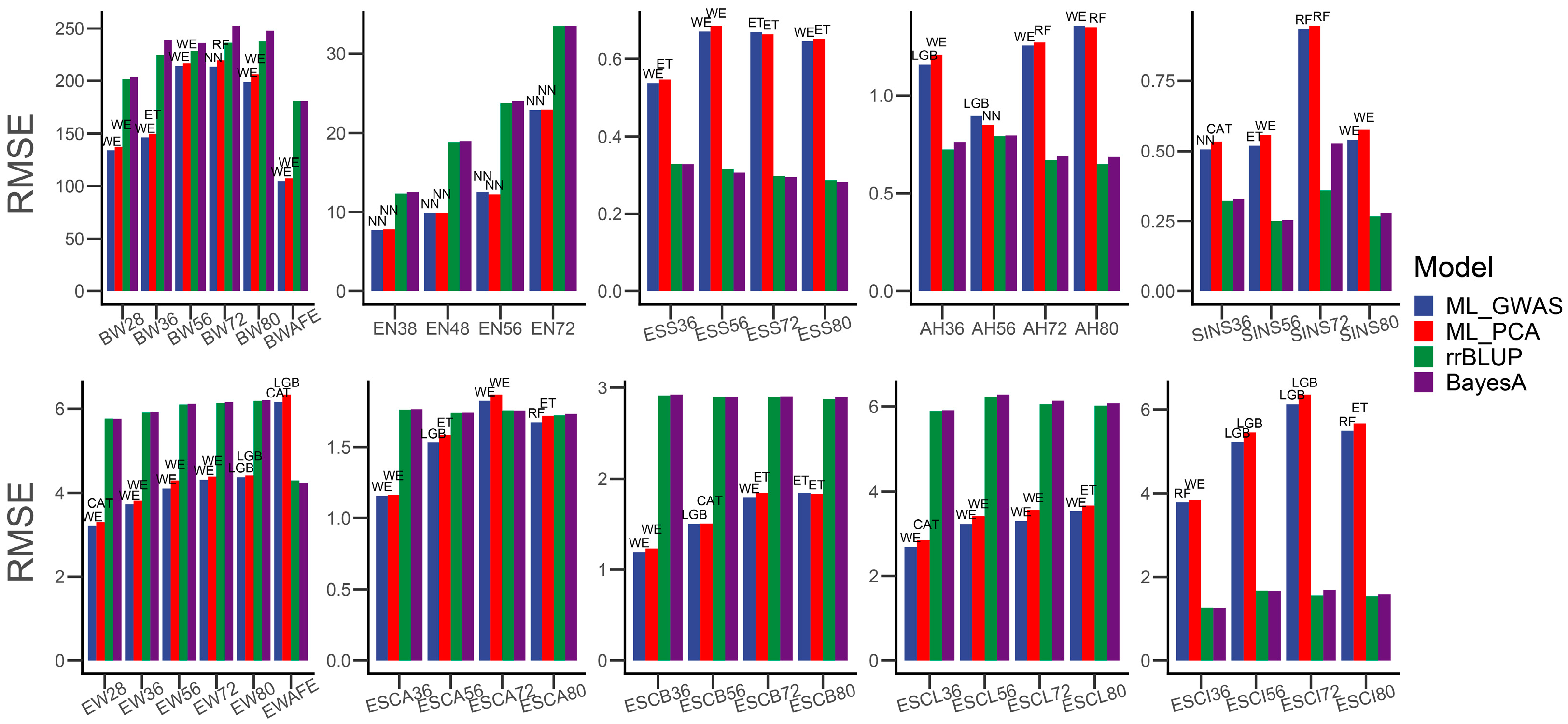
3.2. Machine Learning Methods for Chicken Genomic Prediction
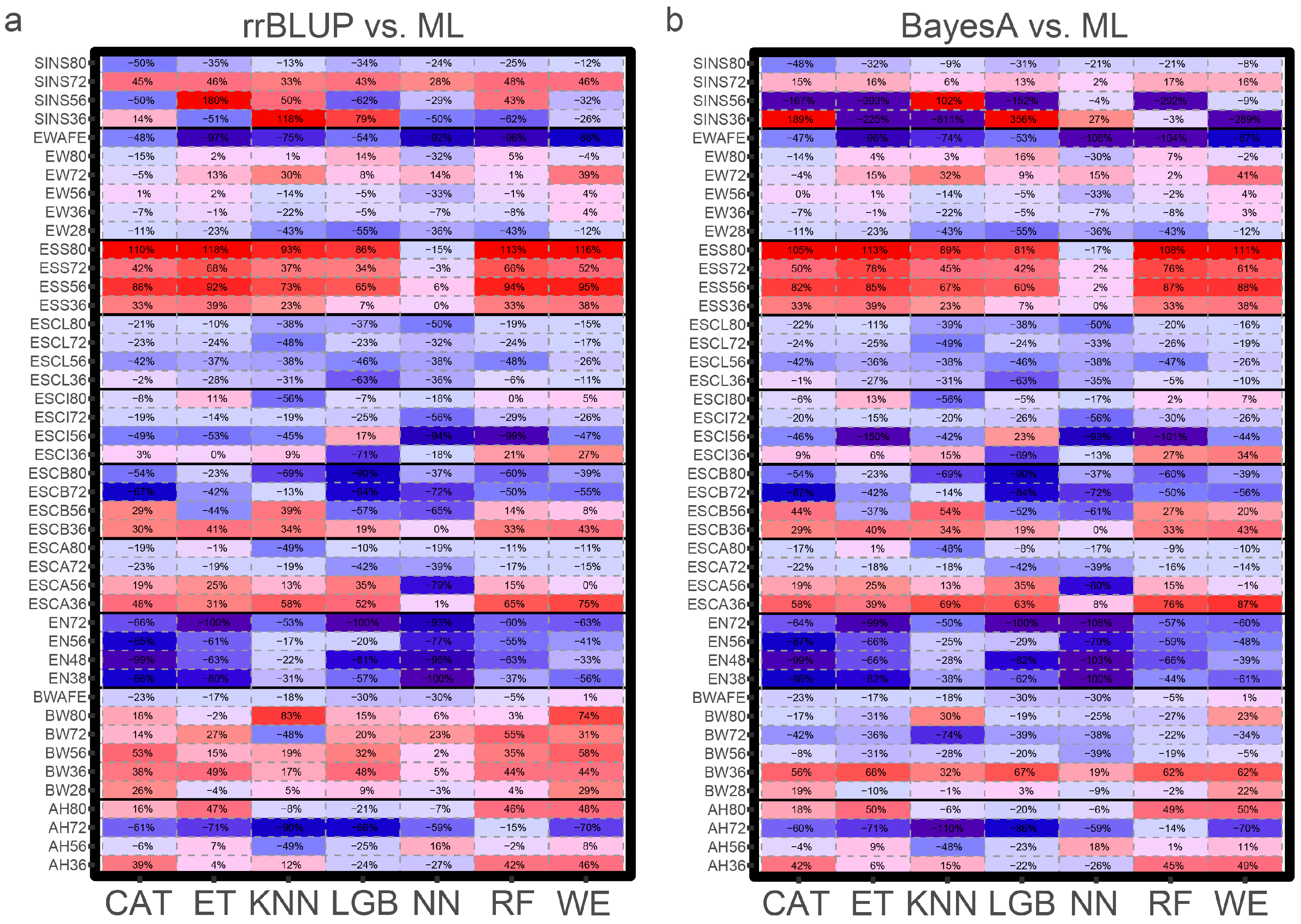
3.3. Comparison of Different Feature Engineering Methods
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Gianola, D. Priors in whole-genome regression: The bayesian alphabet returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef]
- Xavier, A.; Muir, W.M.; Rainey, K.M. bWGR: Bayesian Whole-Genome Regression. Bioinformatics 2019, 36, 1957–1959. [Google Scholar] [CrossRef]
- Christensen, O.F.; Lund, M.S. Genomic prediction when some animals are not genotyped. Genet. Sel. Evol. 2010, 42, 2. [Google Scholar] [CrossRef]
- Esposito, S.; Ruggieri, V.; Tripodi, P. Editorial: Machine Learning for Big Data Analysis: Applications in Plant Breeding and Genomics. Front. Genet. 2022, 13, 916462. [Google Scholar] [CrossRef]
- Long, N.; Gianola, D.; Rosa, G.J.; Weigel, K.A. Application of support vector regression to genome-assisted prediction of quantitative traits. Theor. Appl. Genet. 2011, 123, 1065–1074. [Google Scholar] [CrossRef] [PubMed]
- Naderi, S.; Yin, T.; Konig, S. Random forest estimation of genomic breeding values for disease susceptibility over different disease incidences and genomic architectures in simulated cow calibration groups. J. Dairy Sci. 2016, 99, 7261–7273. [Google Scholar] [CrossRef]
- Lourenço, M.; Ogutu, O.; Rodrigues, A.P.; Posekany, A.; Piepho, H.-P. Genomic prediction using machine learning: A comparison of the performance of regularized regression, ensemble, instance-based and deep learning methods on synthetic and empirical data. BMC Genom. 2024, 25, 152. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-López, O.A.; Pérez-Rodríguez, P.; Barrón-López, J.A.; Martini, J.W.R.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A review of deep learning applications for genomic selection. BMC Genom. 2021, 22, 19. [Google Scholar] [CrossRef]
- Wang, X.; Shi, S.; Wang, G.; Luo, W.; Wei, X.; Qiu, A.; Luo, F.; Ding, X. Using machine learning to improve the accuracy of genomic prediction of reproduction traits in pigs. J. Anim. Sci. Biotechnol. 2022, 13, 60. [Google Scholar] [CrossRef]
- Mota, L.F.M.; Arikawa, L.M.; Santos, S.W.B.; Fernandes Junior, G.A.; Alves, A.A.C.; Rosa, G.J.M.; Mercadante, M.E.Z.; Cyrillo, J.N.S.G.; Carvalheiro, R.; Albuquerque, L.G. Benchmarking machine learning and parametric methods for genomic prediction of feed efficiency-related traits in Nellore cattle. Sci. Rep. 2024, 14, 6404. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, H.; Zhou, X.; Yuan, X.; Zhao, S.; Li, X.; Liu, X. KAML: Improving genomic prediction accuracy of complex traits using machine learning determined parameters. Genome Biol. 2020, 21, 146. [Google Scholar] [CrossRef] [PubMed]
- Abdollahi-Arpanahi, R.; Morota, G.; Valente, B.D.; Kranis, A.; Rosa, G.J.; Gianola, D. Assessment of bagging GBLUP for whole-genome prediction of broiler chicken traits. J. Anim. Breed. Genet. 2015, 132, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Enciso, M.; Zingaretti, L.M. A Guide for Using Deep Learning for Complex Trait Genomic Prediction. Genes 2019, 10, 553. [Google Scholar] [CrossRef] [PubMed]
- Vellido, A.; Martín-Guerrero, J.D.; Lisboa, P.J.G. (Eds.) Making machine learning models interpretable. In Proceedings of the European Symposium on Artificial Neural Networks (ESANN 2012), Bruges, Belgium, 25–27 April 2012. [Google Scholar]
- Stańczyk, U.; Jain, L.C. (Eds.) Feature Selection for Data and Pattern Recognition. In Feature Selection for Data and Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2015; Volume 584, p. 355. [Google Scholar]
- Liu, Z.; Sun, C.; Yan, Y.; Li, G.; Li, X.C.; Wu, G.; Yang, N. Design and evaluation of a custom 50K Infinium SNP array for egg-type chickens. Poult. Sci. 2021, 100, 101044. [Google Scholar] [CrossRef] [PubMed]
- Kent, W.J.; Sugnet, C.W.; Furey, T.S.; Roskin, K.M.; Pringle, T.H.; Zahler, A.M.; Haussler, D. The human genome browser at UCSC. Genome Res. 2002, 12, 996–1006. [Google Scholar] [CrossRef] [PubMed]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.W.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef] [PubMed]
- Browning, B.L.; Tian, X.; Zhou, Y.; Browning, S.R. Fast two-stage phasing of large-scale sequence data. Am. J. Hum. Genet. 2021, 108, 1880–1890. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lee, S.H.; Goddard, M.E.; Visscher, P.M. GCTA: A tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011, 88, 76–82. [Google Scholar] [CrossRef]
- Gao, X. Multiple testing corrections for imputed SNPs. Genet. Epidemiol. 2011, 35, 154–158. [Google Scholar] [CrossRef]
- Reimand, J.; Arak, T.; Vilo, J. g:Profiler—A web server for functional interpretation of gene lists (2011 update). Nucleic Acids Res. 2011, 39, W307–W315. [Google Scholar] [CrossRef] [PubMed]
- Erickson, N.; Mueller, J.; Shirkov, A.; Zhang, H.; Larroy, P.; Li, M.; Smola, A. AutoGluon-Tabular: Robust and Accurate AutoML for Structured Data. arXiv 2020, arXiv:2003.06505b. [Google Scholar]
- Endelman, J.B. Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef]
- Pérez, P.; de los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Karacaören, B. An evaluation of machine learning for genomic prediction of hairy syndrome in dairy cattle. Anim. Sci. Pap. Rep. 2022, 40, 45–58. [Google Scholar]
- Grinberg, N.F.; Orhobor, O.I.; King, R.D. An evaluation of machine-learning for predicting phenotype: Studies in yeast, rice, and wheat. Mach. Learn. 2020, 109, 251–277. [Google Scholar] [CrossRef] [PubMed]
- Silveira, L.; Lima, L.; Nascimento, M.; Nascimento, A.C.; Silva, F. Regression trees in genomic selection for carcass traits in pigs. Genet. Mol. Res. 2020, 19, 1–11. [Google Scholar]
- Chen, X.; Li, X.; Zhong, C.; Jiang, X.; Wu, G.; Li, G.; Yan, Y.; Yang, N.; Sun, C. Genetic patterns and genome-wide association analysis of eggshell quality traits of egg-type chicken across an extended laying period. Poult. Sci. 2024, 103, 103458. [Google Scholar] [CrossRef]
- Liao, R.; Zhang, X.; Chen, Q.; Wang, Z.; Wang, Q.; Yang, C.; Pan, Y. Genome-wide association study reveals novel variants for growth and egg traits in Dongxiang blue-shelled and White Leghorn chickens. Anim. Genet. 2016, 47, 588–596. [Google Scholar] [CrossRef]
- Sreenivas, D.; Prakash, M.G.; Mahender, M.; Chatterjee, R. Genetic analysis of egg quality traits in White Leghorn chicken. Vet. World 2013, 6, 263–266. [Google Scholar] [CrossRef]
- Blanco, A.E.; Icken, W.; Ould-Ali, D.; Cavero, D.; Schmutz, M. Genetic parameters of egg quality traits on different pedigree layers with special focus on dynamic stiffness. Poult. Sci. 2014, 93, 2457–2463. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Liu, L.; He, Y.; Dou, T.; Jia, J.; Ge, C. Endocrine and genetic factors affecting egg laying performance in chickens: A review. Br. Poult. Sci. 2020, 61, 538–549. [Google Scholar] [CrossRef] [PubMed]
- Mueller, S.; Kreuzer, M.; Siegrist, M.; Mannale, K.; Messikommer, R.E.; Gangnat, I.D.M. Carcass and meat quality of dual-purpose chickens (Lohmann Dual, Belgian Malines, Schweizerhuhn) in comparison to broiler and layer chicken types. Poult. Sci. 2018, 97, 3325–3336. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Sun, C.; Yan, Y.; Li, G.; Wu, G.; Liu, A.; Yang, N. Genome-Wide Association Analysis of Age-Dependent Egg Weights in Chickens. Front. Genet. 2018, 9, 128. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Duan, Z.; Sun, C.; Zheng, J.; Xu, G.; Yang, N. Genetic variations for the eggshell crystal structure revealed by genome-wide association study in chickens. BMC Genom. 2021, 22, 786. [Google Scholar] [CrossRef] [PubMed]
- Nayeri, S.; Sargolzaei, M.; Tulpan, D. A review of traditional and machine learning methods applied to animal breeding. Anim. Health Res. Rev. 2019, 20, 31–46. [Google Scholar] [CrossRef] [PubMed]
- González-Recio, O.; Rosa, G.J.M.; Gianola, D. Machine learning methods and predictive ability metrics for genome-wide prediction of complex traits. Livest. Sci. 2014, 166, 217–231. [Google Scholar] [CrossRef]
- Morota, G.; Abdollahi-Arpanahi, R.; Kranis, A.; Gianola, D. Genome-enabled prediction of quantitative traits in chickens using genomic annotation. BMC Genom. 2014, 15, 109. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Nie, C.; Zhang, J.; Li, X.; Zhu, T.; Guan, Z.; Qu, L. Identification of candidate genomic regions for chicken egg number traits based on genome-wide association study. BMC Genom. 2021, 22, 610. [Google Scholar] [CrossRef]
- Abdollahi-Arpanahi, R.; Gianola, D.; Peñagaricano, F. Deep learning versus parametric and ensemble methods for genomic prediction of complex phenotypes. Genet. Sel. Evol. 2020, 52, 12. [Google Scholar] [CrossRef]
- Ogutu, J.O.; Piepho, H.P.; Schulz-Streeck, T. A comparison of random forests, boosting and support vector machines for genomic selection. BMC Proc. 2011, 5 (Suppl. S3), S11. [Google Scholar] [CrossRef]
- Ghafouri-Kesbi, F.; Rahimi-Mianji, G.; Honarvar, M.; Nejati-Javaremi, A. Predictive ability of Random Forests, Boosting, Support Vector Machines and Genomic Best Linear Unbiased Prediction in different scenarios of genomic evaluation. Anim. Prod. Sci. 2016, 57, 229–236. [Google Scholar] [CrossRef]
- He, J.; Ding, L.X.; Jiang, L.; Ma, L. Kernel ridge regression classification. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN) 2014, Beijing, China, 6–11 July 2014; pp. 2263–2267. [Google Scholar]
- Tusell, L.; Pérez-Rodríguez, P.; Forni, S.; Wu, X.L.; Gianola, D. Genome-enabled methods for predicting litter size in pigs: A comparison. Animal 2013, 7, 1739–1749. [Google Scholar] [CrossRef]
- Meuwissen, T.; Hayes, B.; Goddard, M. Accelerating improvement of livestock with genomic selection. Annu. Rev. Anim. Biosci. 2013, 1, 221–237. [Google Scholar] [CrossRef]
- An, B.; Liang, M.; Chang, T.; Duan, X.; Du, L.; Xu, L.; Gao, H. KCRR: A nonlinear machine learning with a modified genomic similarity matrix improved the genomic prediction efficiency. Brief. Bioinform. 2021, 22, bbab132. [Google Scholar] [CrossRef]
- Wilkinson, M.J.; Yamashita, R.; James, M.E.; Bally, I.S.E.; Dillon, N.L.; Ali, A.; Hardner, C.M.; Ortiz-Barrientos, D. The influence of genetic structure on phenotypic diversity in the Australian mango (Mangifera indica) gene pool. Sci. Rep. 2022, 12, 20614. [Google Scholar] [CrossRef]
- Lu, C.; Zaucha, J.; Gam, R.; Fang, H.; Ben, S.; Oates, M.E.; Bernabe-Rubio, M.; Williams, J.; Zelenka, N.; Pandurangan, A.P.; et al. Hypothesis-free phenotype prediction within a genetics-first framework. Nat. Commun. 2023, 14, 919. [Google Scholar] [CrossRef]
- Azodi, C.B.; Bolger, E.; McCarren, A.; Roantree, M.; de Los Campos, G.; Shiu, S.H. Benchmarking Parametric and Machine Learning Models for Genomic Prediction of Complex Traits. G3 2019, 9, 3691–3702. [Google Scholar] [CrossRef]
- Wang, K.; Yang, B.; Li, Q.; Liu, S. Systematic Evaluation of Genomic Prediction Algorithms for Genomic Prediction and Breeding of Aquatic Animals. Genes 2022, 13, 2247. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Wang, L.; Liu, J.; Deng, T.; Yan, H.; Zhang, L.; Liu, X.; Gao, H.; Hou, X.; Wang, L.; et al. Estimation of inbreeding and identification of regions under heavy selection based on runs of homozygosity in a Large White pig population. J. Anim. Sci. Biotechnol. 2020, 11, 46. [Google Scholar] [CrossRef] [PubMed]
- Peripolli, E.; Munari, D.P.; Silva, M.; Lima, A.L.F.; Irgang, R.; Baldi, F. Runs of homozygosity: Current knowledge and applications in livestock. Anim. Genet. 2017, 48, 255–271. [Google Scholar] [CrossRef]

| Model | Parameter Name | Parameter |
|---|---|---|
| AutoGluon | eval_metric | root_mean_squared_error |
| pearsonr | ||
| presets | best_quality | |
| num-bag-folds | 10 | |
| CatBoost (CAT) | iterations | 500 |
| learning_rate | 0.009 | |
| depth | 6 | |
| random_strength | 1.0 | |
| max_leaves | 31 | |
| rsm | 1.0 | |
| sampling_frequency | PerTreeLevel | |
| bagging_temperature | 1.0 | |
| grow_policy | SymmetricTree | |
| Extra Tree (ET) | n_estimators | 500 |
| max_depth | None | |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| max_features | 1 | |
| K-Nearest Neighbors (KNNs) | K | 50 |
| LightGBM (LGB) | num_boost_round | 100 |
| learning_rate | 0.1 | |
| num_leaves | 64 | |
| feature_fraction | 0.9 | |
| bagging_fraction | 0.9 | |
| max_depth | 6 | |
| min_data_in_leaf | 3 | |
| boosting | gbdt | |
| NNFastAi (NN) | y_scaler | - |
| clipping | - | |
| layers | 32 | |
| emb_drop | 0.1 | |
| ps | 0.1 | |
| bs | 256 | |
| epochs | 150 | |
| Random Forest (RF) | n_estimators | 500 |
| min_samples_split | 2 | |
| min_samples_leaf | 1 | |
| max_features | 1 | |
| max_depth | None |
| Traits | N | Mean | SD | CV (%) | Min | Max | h2 |
|---|---|---|---|---|---|---|---|
| AH36 | 2178 | 6.87 | 1.27 | 18.54% | 2.1 | 10.8 | 0.187 |
| AH56 | 2245 | 7.10 | 1.05 | 14.77% | 2.2 | 11 | 0.266 |
| AH72 | 2367 | 6.02 | 1.29 | 21.37% | 2.2 | 11.1 | 0.258 |
| AH80 | 2207 | 5.85 | 1.47 | 25.17% | 1 | 13.5 | 0.157 |
| BW28 | 4186 | 1968 | 147.02 | 7.47% | 1125 | 2649 | 0.442 |
| BW36 | 4189 | 2043 | 171.40 | 8.39% | 1575 | 2638 | 0.524 |
| BW56 | 4014 | 2146 | 222.51 | 10.37% | 1299 | 3119 | 0.328 |
| BW72 | 3282 | 2178 | 224.35 | 10.30% | 1271 | 2874 | 0.323 |
| BW80 | 3705 | 2215 | 228.53 | 10.32% | 1033 | 3088 | 0.387 |
| BWAFE | 4189 | 1782 | 113.12 | 6.35% | 1030 | 2265 | 0.446 |
| EN38 | 4190 | 123.3 | 7.70 | 6.24% | 100 | 146 | 0.436 |
| EN48 | 4190 | 188.2 | 9.51 | 5.06% | 131 | 217 | 0.409 |
| EN56 | 4190 | 238.1 | 12.97 | 5.45% | 146 | 270 | 0.336 |
| EN72 | 3833 | 339 | 22.63 | 6.67% | 190 | 379 | 0.142 |
| ESCA36 | 2469 | 17.42 | 1.35 | 7.76% | 12.61 | 21.5 | 0.437 |
| ESCA56 | 1445 | 16.94 | 1.72 | 10.17% | 2.17 | 23.5 | 0.464 |
| ESCA72 | 2493 | 17.02 | 2.05 | 12.04% | 2.51 | 22.18 | 0.315 |
| ESCA80 | 2886 | 16.54 | 1.89 | 11.44% | 5.29 | 21.79 | 0.360 |
| ESCB36 | 2469 | 28.79 | 1.40 | 4.85% | 19.99 | 32.81 | 0.446 |
| ESCB56 | 1445 | 28.68 | 1.69 | 5.88% | 12.39 | 32.75 | 0.399 |
| ESCB72 | 2493 | 28.74 | 1.97 | 6.86% | 10.01 | 33.83 | 0.242 |
| ESCB80 | 2886 | 28.12 | 1.86 | 6.63% | 15.01 | 32.19 | 0.254 |
| ESCI36 | 2469 | 12.86 | 4.39 | 34.13% | −0.43 | 28.46 | 0.435 |
| ESCI56 | 1445 | 16.71 | 5.51 | 32.95% | 1.75 | 63.83 | 0.349 |
| ESCI72 | 2510 | 15.47 | 6.87 | 44.44% | 1.24 | 70.19 | 0.227 |
| ESCI80 | 2886 | 16.05 | 6.47 | 40.32% | −0.57 | 55.31 | 0.295 |
| ESCL36 | 4149 | 59.15 | 3.02 | 5.11% | 47.39 | 73 | 0.364 |
| ESCL56 | 2614 | 62.42 | 3.43 | 5.50% | 50.97 | 78.7 | 0.455 |
| ESCL72 | 2992 | 61.72 | 3.67 | 5.95% | 51.57 | 82.71 | 0.496 |
| ESCL80 | 3336 | 60.87 | 3.83 | 6.29% | 49.13 | 85.12 | 0.414 |
| ESS36 | 3130 | 3.151 | 0.70 | 22.14% | 1.049 | 5.401 | 0.317 |
| ESS56 | 2858 | 3.203 | 0.74 | 23.04% | 0.89 | 5.456 | 0.669 |
| ESS72 | 2873 | 3.017 | 0.75 | 24.91% | 0.803 | 5.224 | 0.552 |
| ESS80 | 3304 | 2.752 | 0.71 | 25.69% | 0.515 | 5.182 | 0.698 |
| EW28 | 4158 | 56.97 | 3.51 | 6.16% | 40 | 89.7 | 0.436 |
| EW36 | 4172 | 58.41 | 3.77 | 6.45% | 40 | 75 | 0.448 |
| EW56 | 3905 | 60.44 | 4.47 | 7.39% | 35 | 80.6 | 0.581 |
| EW72 | 2855 | 61.51 | 4.69 | 7.62% | 35 | 84.7 | 0.440 |
| EW80 | 3155 | 61.86 | 4.75 | 7.68% | 35 | 81.5 | 0.455 |
| EWAFE | 4173 | 43.06 | 5.88 | 13.65% | 18.9 | 88 | 0.178 |
| SINS36 | 856 | 3.167 | 0.59 | 18.60% | 1.87 | 5.6 | 0.272 |
| SINS56 | 685 | 2.45 | 0.48 | 19.69% | 1.4 | 4.8 | 0.290 |
| SINS72 | 1631 | 3.545 | 1.47 | 41.34% | 1.3 | 11 | 0.301 |
| SINS80 | 2037 | 2.494 | 0.57 | 22.84% | 1.15 | 4.93 | 0.410 |
| Traits | Source | Term Name | Term ID | p Value |
|---|---|---|---|---|
| AH | GO:MF | molecular function | GO:0003674 | 9.62 × 10−13 |
| GO:MF | heparin binding | GO:0008201 | 1.42 × 10−2 | |
| GO:BP | biological process | GO:0008150 | 6.33 × 10−11 | |
| GO:CC | cellular anatomical entity | GO:0110165 | 9.98 × 10−15 | |
| BW | GO:MF | molecular function | GO:0003674 | 7.48 × 10−29 |
| GO:MF | RNA polymerase II transcription regulatory region sequence-specific DNA binding | GO:0000977 | 1.15 × 10−2 | |
| GO:BP | biological process | GO:0008150 | 1.09 × 10−20 | |
| GO:BP | cell–cell junction organization | GO:0045216 | 5.50 × 10−5 | |
| GO:BP | inorganic cation transmembrane transport | GO:0098662 | 5.78 × 10−3 | |
| GO:BP | regulation of receptor-mediated endocytosis | GO:0048259 | 4.96 × 10−2 | |
| GO:CC | cellular component | GO:0005575 | 3.08 × 10−22 | |
| EN | GO:MF | molecular function | GO:0003674 | 9.64 × 10−9 |
| GO:BP | cellular process | GO:0009987 | 8.63 × 10−10 | |
| GO:BP | cellular response to salt | GO:1902075 | 3.00 × 10−2 | |
| GO:CC | cellular anatomical entity | GO:0110165 | 2.66 × 10−8 | |
| GO:CC | MOZ/MORF histone acetyltransferase complex | GO:0070776 | 1.12 × 10−2 | |
| ESC | GO:MF | molecular function | GO:0003674 | 2.24 × 10−64 |
| GO:MF | monoatomic cation channel activity | GO:0005261 | 8.11 × 10−3 | |
| GO:MF | adenylate cyclase regulator activity | GO:0010854 | 1.17 × 10−2 | |
| GO:MF | tubulin binding | GO:0015631 | 2.41 × 10−2 | |
| GO:MF | metal ion transmembrane transporter activity | GO:0046873 | 2.80 × 10−2 | |
| GO:BP | biological process | GO:0008150 | 3.04 × 10−58 | |
| GO:BP | inorganic ion homeostasis | GO:0098771 | 2.09 × 10−3 | |
| GO:BP | negative regulation of cytoskeleton organization | GO:0051494 | 8.00 × 10−3 | |
| GO:CC | cellular anatomical entity | GO:0110165 | 4.66 × 10−47 | |
| ESS | GO:MF | binding | GO:0005488 | 1.94 × 10−11 |
| GO:MF | voltage-gated calcium channel activity involved in cardiac muscle cell action potential | GO:0086007 | 2.98 × 10−5 | |
| GO:MF | sequence-specific double-stranded DNA binding | GO:1990837 | 2.75 × 10−3 | |
| GO:MF | histone reader activity | GO:0140566 | 2.76 × 10−2 | |
| GO:BP | biological process | GO:0008150 | 1.11 × 10−12 | |
| GO:BP | myeloid cell differentiation | GO:0030099 | 1.23 × 10−3 | |
| GO:BP | membrane depolarization during cardiac muscle cell action potential | GO:0086012 | 2.49 × 10−3 | |
| GO:BP | cell–cell signaling involved in cardiac conduction | GO:0086019 | 1.98 × 10−2 | |
| GO:CC | cellular anatomical entity | GO:0110165 | 8.57 × 10−17 | |
| GO:CC | clathrin-coated pit | GO:0005905 | 3.80 × 10−2 | |
| GO:CC | monoatomic ion channel complex | GO:0034702 | 4.13 × 10−2 | |
| EW | GO:MF | binding | GO:0005488 | 2.73 × 10−30 |
| GO:MF | transcription coactivator activity | GO:0003713 | 1.68 × 10−4 | |
| GO:MF | frizzled binding | GO:0005109 | 1.94 × 10−2 | |
| GO:BP | biological process | GO:0008150 | 9.56 × 10−31 | |
| GO:BP | response to oxygen-containing compound | GO:1901700 | 5.21 × 10−3 | |
| GO:BP | peptidyl–threonine modification | GO:0018210 | 4.36 × 10−2 | |
| GO:BP | cellular response to insulin stimulus | GO:0032869 | 4.43 × 10−2 | |
| GO:CC | cellular anatomical entity | GO:0110165 | 1.23 × 10−38 | |
| SINS | GO:MF | molecular function | GO:0003674 | 1.19 × 10−16 |
| GO:MF | dipeptidyl–peptidase activity | GO:0008239 | 1.86 × 10−2 | |
| GO:BP | biological process | GO:0008150 | 2.87 × 10−15 | |
| GO:BP | intracellular signal transduction | GO:0035556 | 8.65 × 10−3 | |
| GO:BP | gene expression | GO:0010467 | 1.18 × 10−2 | |
| GO:CC | cellular component | GO:0005575 | 6.02 × 10−12 | |
| GO:CC | lamellipodium membrane | GO:0031258 | 3.73 × 10−2 |
| Traits | CAT | ET | KNN | LGB | NN | RF | WE | rrBLUP | BayesA |
|---|---|---|---|---|---|---|---|---|---|
| AH36 | 0.32 (1.21) | 0.24 (1.24) | 0.25 (1.31) | 0.17 (1.21) | 0.17 (1.27) | 0.32 (1.21) | 0.33 (1.21) | 0.23 (0.73) | 0.22 (0.76) |
| AH56 | 0.3 (0.87) | 0.35 (0.86) | 0.16 (0.98) | 0.24 (0.87) | 0.38 (0.85) | 0.32 (0.87) | 0.35 (0.86) | 0.32 (0.79) | 0.32 (0.8) |
| AH72 | 0.09 (1.29) | 0.06 (1.29) | −0.02 (1.46) | 0.03 (1.29) | 0.09 (1.28) | 0.19 (1.27) | 0.07 (1.28) | 0.22 (0.67) | 0.22 (0.69) |
| AH80 | 0.30 (1.39) | 0.38 (1.36) | 0.24 (1.49) | 0.2 (1.38) | 0.24 (1.42) | 0.37 (1.35) | 0.38 (1.36) | 0.26 (0.65) | 0.25 (0.69) |
| BW28 | 0.32 (138.03) | 0.24 (141.35) | 0.27 (147.12) | 0.27 (141.21) | 0.24 (141.33) | 0.26 (140.55) | 0.33 (137.41) | 0.25 (201.87) | 0.27 (203.69) |
| BW36 | 0.42 (151.99) | 0.45 (149.78) | 0.36 (164.36) | 0.45 (149.95) | 0.32 (156.9) | 0.44 (150.77) | 0.44 (152.23) | 0.3 (224.72) | 0.27 (238.91) |
| BW56 | 0.25 (216.9) | 0.19 (220.08) | 0.19 (233.42) | 0.22 (218.92) | 0.17 (224.95) | 0.22 (218.65) | 0.26 (216.58) | 0.16 (228.27) | 0.27 (236.08) |
| BW72 | 0.16 (221.8) | 0.18 (221.41) | 0.07 (246.96) | 0.17 (221.5) | 0.17 (221.56) | 0.22 (219.31) | 0.18 (220.76) | 0.14 (236.28) | 0.28 (252.72) |
| BW80 | 0.18 (210.63) | 0.15 (211.38) | 0.28 (217.12) | 0.18 (213.07) | 0.16 (211.72) | 0.16 (211.3) | 0.27 (205.85) | 0.15 (237.68) | 0.22 (247.77) |
| BWAFE | 0.26 (109.82) | 0.29 (109.71) | 0.28 (112.45) | 0.24 (109.34) | 0.24 (110.89) | 0.33 (108.35) | 0.35 (107.11) | 0.34 (180.89) | 0.34 (180.55) |
| EN38 | 0.04 (8.15) | 0.05 (8.43) | 0.19 (9.09) | 0.12 (8.39) | 0 (7.8) | 0.17 (7.98) | 0.12 (7.98) | 0.27 (12.31) | 0.3 (12.51) |
| EN48 | 0 (10.32) | 0.09 (10.32) | 0.2 (10.92) | 0.05 (10.56) | −0.01 (9.86) | 0.09 (10.31) | 0.17 (9.96) | 0.25 (18.8) | 0.28 (18.99) |
| EN56 | 0.03 (12.64) | 0.07 (12.89) | 0.16 (14.77) | 0.15 (13.53) | 0.04 (12.22) | 0.09 (13.18) | 0.11 (12.28) | 0.19 (23.75) | 0.21 (23.99) |
| EN72 | 0.05 (23.63) | 0 (24.64) | 0.07 (28.15) | 0 (24.59) | −0.01 (22.95) | 0.06 (23.55) | 0.06 (22.96) | 0.16 (33.51) | 0.15 (33.57) |
| ESCA36 | 0.35 (1.19) | 0.31 (1.23) | 0.38 (1.2) | 0.36 (1.18) | 0.24 (1.24) | 0.39 (1.17) | 0.42 (1.17) | 0.24 (1.76) | 0.22 (1.77) |
| ESCA56 | 0.29 (1.59) | 0.3 (1.58) | 0.27 (1.67) | 0.33 (1.59) | 0.05 (1.66) | 0.28 (1.61) | 0.24 (1.62) | 0.24 (1.74) | 0.24 (1.74) |
| ESCA72 | 0.28 (1.88) | 0.29 (1.88) | 0.29 (1.97) | 0.21 (1.88) | 0.22 (1.96) | 0.3 (1.87) | 0.31 (1.87) | 0.36 (1.76) | 0.36 (1.76) |
| ESCA80 | 0.3 (1.75) | 0.36 (1.72) | 0.19 (1.91) | 0.33 (1.73) | 0.3 (1.76) | 0.33 (1.74) | 0.32 (1.75) | 0.37 (1.72) | 0.36 (1.73) |
| ESCB36 | 0.32 (1.24) | 0.34 (1.23) | 0.33 (1.3) | 0.29 (1.25) | 0.24 (1.27) | 0.33 (1.24) | 0.35 (1.23) | 0.24 (2.91) | 0.24 (2.92) |
| ESCB56 | 0.24 (1.51) | 0.11 (1.56) | 0.26 (1.56) | 0.08 (1.53) | 0.07 (1.56) | 0.21 (1.56) | 0.2 (1.52) | 0.19 (2.89) | 0.17 (2.9) |
| ESCB72 | 0.03 (1.85) | 0.13 (1.85) | 0.19 (1.94) | 0.04 (1.85) | 0.06 (1.94) | 0.11 (1.87) | 0.1 (1.88) | 0.22 (2.9) | 0.22 (2.9) |
| ESCB80 | 0.11 (1.85) | 0.18 (1.83) | 0.07 (1.98) | 0.02 (1.86) | 0.15 (1.87) | 0.09 (1.87) | 0.14 (1.85) | 0.23 (2.87) | 0.23 (2.89) |
| ESCI36 | 0.27 (3.91) | 0.26 (3.95) | 0.29 (4.03) | 0.08 (3.91) | 0.22 (3.91) | 0.32 (3.89) | 0.33 (3.85) | 0.26 (1.27) | 0.25 (1.27) |
| ESCI56 | 0.1 (5.45) | −0.09 (5.64) | 0.11 (5.81) | 0.23 (5.45) | 0.01 (5.73) | 0 (5.59) | 0.11 (5.64) | 0.2 (1.67) | 0.19 (1.66) |
| ESCI72 | 0.26 (6.4) | 0.28 (6.37) | 0.26 (6.73) | 0.24 (6.35) | 0.14 (6.68) | 0.23 (6.51) | 0.24 (6.42) | 0.32 (1.56) | 0.33 (1.69) |
| ESCI80 | 0.34 (5.75) | 0.4 (5.67) | 0.16 (6.41) | 0.34 (5.76) | 0.3 (5.82) | 0.37 (5.7) | 0.38 (5.73) | 0.37 (1.53) | 0.36 (1.59) |
| ESCL36 | 0.37 (2.84) | 0.27 (2.93) | 0.26 (3.07) | 0.14 (2.85) | 0.24 (2.93) | 0.35 (2.86) | 0.33 (2.86) | 0.38 (5.89) | 0.37 (5.91) |
| ESCL56 | 0.2 (3.46) | 0.23 (3.45) | 0.22 (3.6) | 0.19 (3.48) | 0.22 (3.51) | 0.19 (3.47) | 0.26 (3.4) | 0.36 (6.23) | 0.35 (6.28) |
| ESCL72 | 0.34 (3.59) | 0.33 (3.58) | 0.23 (3.86) | 0.34 (3.58) | 0.3 (3.64) | 0.33 (3.58) | 0.36 (3.55) | 0.44 (6.06) | 0.45 (6.13) |
| ESCL80 | 0.34 (3.69) | 0.38 (3.66) | 0.26 (3.98) | 0.27 (3.71) | 0.21 (3.88) | 0.34 (3.69) | 0.36 (3.66) | 0.42 (6.02) | 0.43 (6.08) |
| ESS36 | 0.52 (0.56) | 0.54 (0.55) | 0.48 (0.59) | 0.42 (0.56) | 0.39 (0.6) | 0.52 (0.56) | 0.54 (0.55) | 0.39 (0.33) | 0.39 (0.33) |
| ESS56 | 0.42 (0.7) | 0.43 (0.69) | 0.39 (0.72) | 0.37 (0.69) | 0.24 (0.77) | 0.43 (0.69) | 0.44 (0.69) | 0.22 (0.32) | 0.23 (0.31) |
| ESS72 | 0.41 (0.69) | 0.49 (0.66) | 0.4 (0.71) | 0.39 (0.67) | 0.28 (0.73) | 0.48 (0.67) | 0.44 (0.68) | 0.29 (0.3) | 0.27 (0.29) |
| ESS80 | 0.49 (0.67) | 0.51 (0.65) | 0.45 (0.68) | 0.44 (0.65) | 0.2 (0.76) | 0.5 (0.66) | 0.51 (0.65) | 0.24 (0.29) | 0.24 (0.28) |
| EW28 | 0.3 (3.3) | 0.26 (3.32) | 0.19 (3.57) | 0.15 (3.3) | 0.21 (3.39) | 0.19 (3.43) | 0.29 (3.3) | 0.33 (5.76) | 0.34 (5.76) |
| EW36 | 0.3 (3.84) | 0.32 (3.84) | 0.25 (4.07) | 0.31 (3.83) | 0.3 (3.95) | 0.3 (3.85) | 0.34 (3.82) | 0.33 (5.91) | 0.33 (5.93) |
| EW56 | 0.37 (4.31) | 0.37 (4.3) | 0.31 (4.57) | 0.35 (4.34) | 0.24 (4.48) | 0.36 (4.32) | 0.38 (4.3) | 0.36 (6.1) | 0.36 (6.12) |
| EW72 | 0.24 (4.53) | 0.29 (4.47) | 0.33 (4.61) | 0.27 (4.46) | 0.29 (4.47) | 0.25 (4.51) | 0.35 (4.39) | 0.25 (6.14) | 0.25 (6.16) |
| EW80 | 0.23 (4.56) | 0.28 (4.49) | 0.27 (4.79) | 0.31 (4.42) | 0.19 (4.64) | 0.29 (4.48) | 0.26 (4.51) | 0.27 (6.19) | 0.27 (6.21) |
| EWAFE | 0.09 (6.36) | 0.01 (6.43) | 0.04 (6.9) | 0.08 (6.34) | −0.01 (6.42) | −0.01 (6.56) | 0.02 (6.38) | 0.17 (4.3) | 0.17 (4.25) |
| SINS36 | 0.06 (0.53) | −0.03 (0.55) | −0.14 (0.63) | 0.09 (0.53) | 0.03 (0.54) | 0.02 (0.55) | −0.04 (0.55) | 0.05 (0.32) | 0.02 (0.33) |
| SINS56 | −0.03 (0.57) | −0.14 (0.57) | 0.1 (0.59) | −0.02 (0.56) | 0.05 (0.57) | −0.09 (0.58) | 0.04 (0.56) | 0.06 (0.25) | 0.05 (0.25) |
| SINS72 | 0.71 (0.96) | 0.71 (0.96) | 0.65 (1.07) | 0.69 (0.98) | 0.62 (1.06) | 0.72 (0.95) | 0.71 (0.95) | 0.49 (0.36) | 0.61 (0.53) |
| SINS80 | 0.16 (0.59) | 0.21 (0.59) | 0.29 (0.61) | 0.22 (0.58) | 0.25 (0.59) | 0.25 (0.58) | 0.29 (0.58) | 0.33 (0.27) | 0.32 (0.28) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, X.; Wang, Q.; Yang, N.; Sun, C. Integrating Bioinformatics and Machine Learning for Genomic Prediction in Chickens. Genes 2024, 15, 690. https://doi.org/10.3390/genes15060690
Li X, Chen X, Wang Q, Yang N, Sun C. Integrating Bioinformatics and Machine Learning for Genomic Prediction in Chickens. Genes. 2024; 15(6):690. https://doi.org/10.3390/genes15060690
Chicago/Turabian StyleLi, Xiaochang, Xiaoman Chen, Qiulian Wang, Ning Yang, and Congjiao Sun. 2024. "Integrating Bioinformatics and Machine Learning for Genomic Prediction in Chickens" Genes 15, no. 6: 690. https://doi.org/10.3390/genes15060690
APA StyleLi, X., Chen, X., Wang, Q., Yang, N., & Sun, C. (2024). Integrating Bioinformatics and Machine Learning for Genomic Prediction in Chickens. Genes, 15(6), 690. https://doi.org/10.3390/genes15060690




