Effect of Bulk Composition on the Heterogeneous Oxidation of Semi-Solid Atmospheric Aerosols
Abstract
:1. Introduction
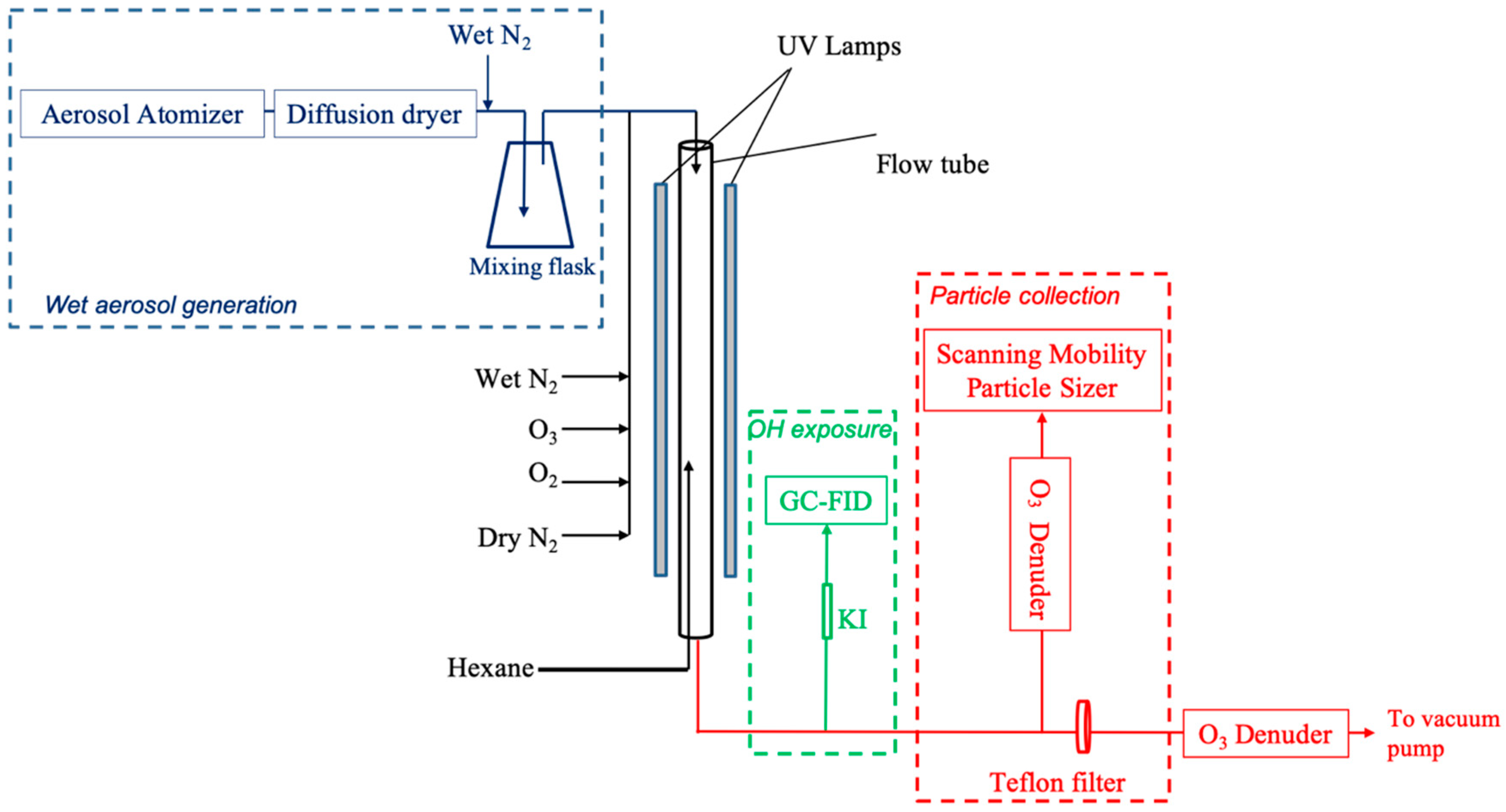
2. Experiments
3. Modeling of the Particle Composition
4. Results and Discussion
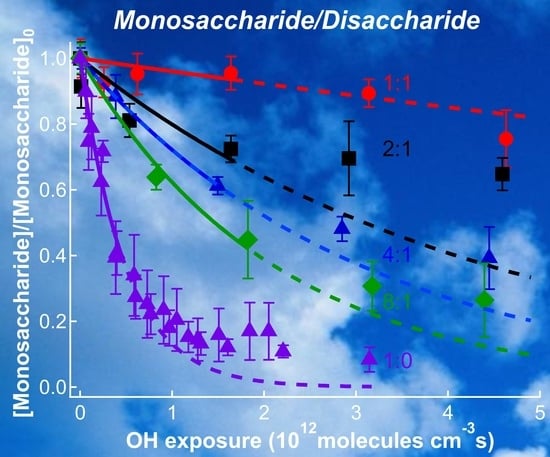
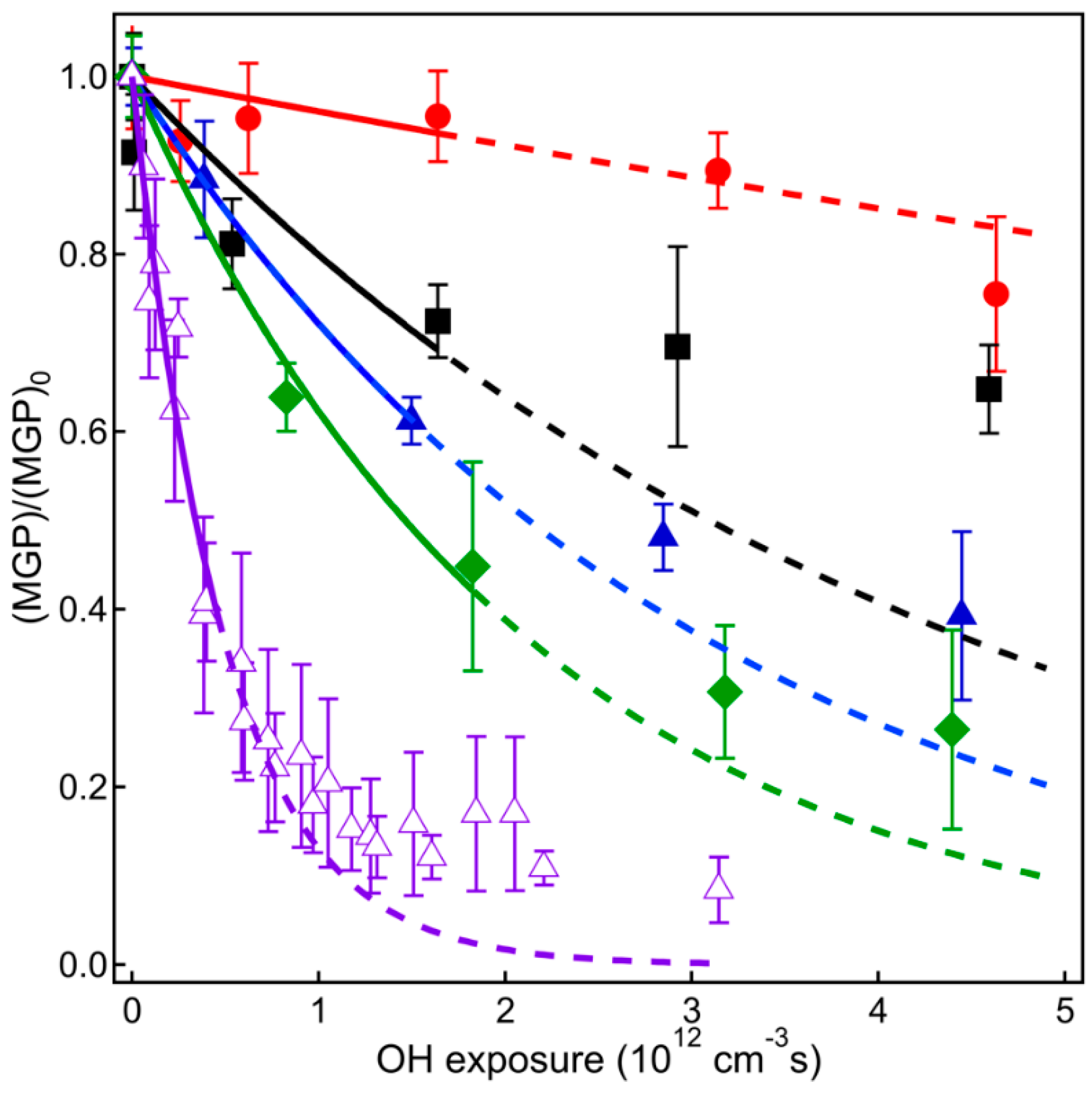
4.1. VUV-AMS Analysis
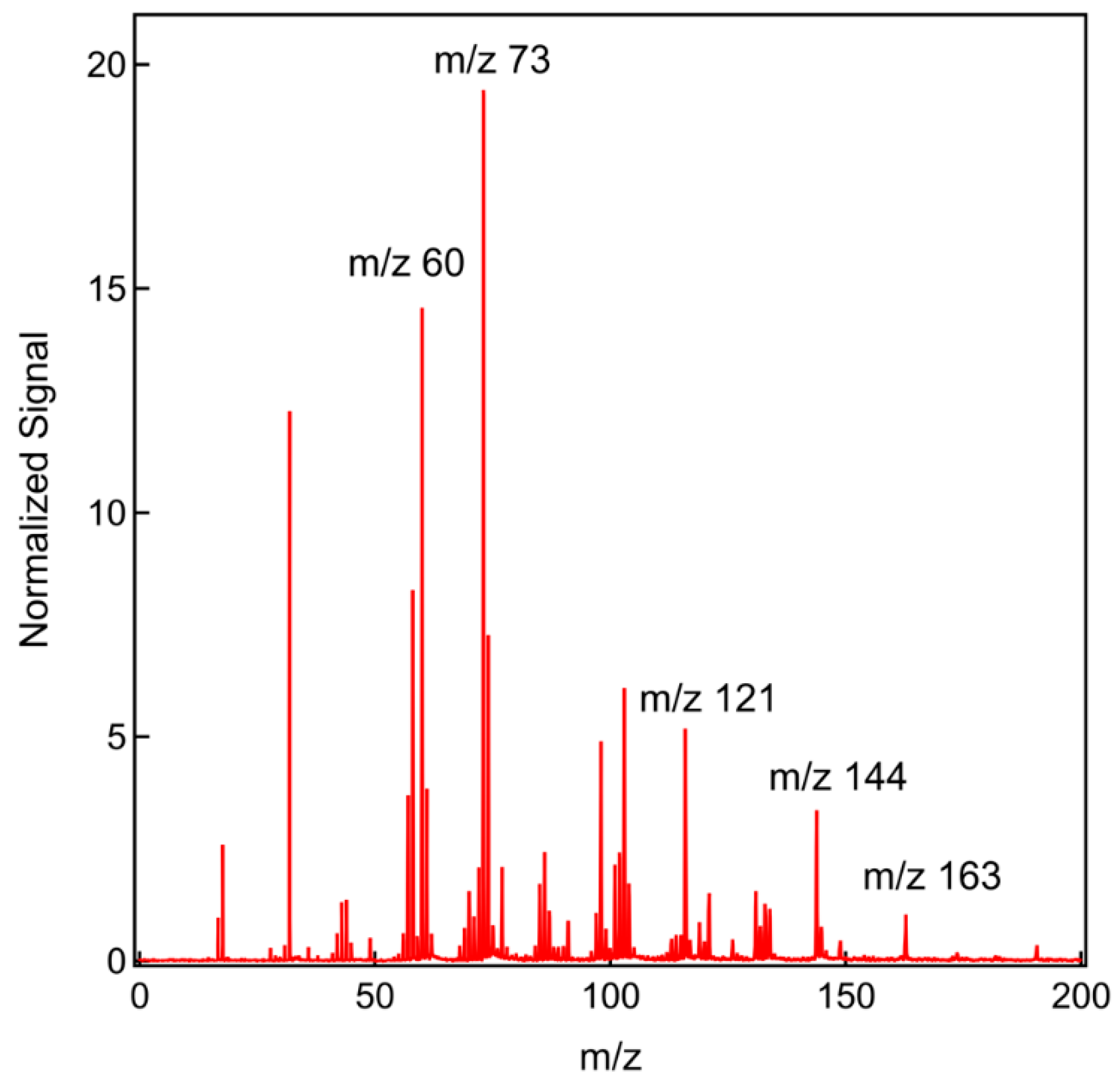
4.2. GC-MS Analysis
5. Relevance for Atmospheric Chemistry
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shiraiwa, M.; Li, Y.; Tsimpidi, A.P.; Karydis, V.A.; Berkemeier, T.; Pandis, S.N.; Lelieveld, J.; Koop, T.; Pöschl, U. Global distribution of particle phase state in atmospheric secondary organic aerosols. Nat. Commun. 2017, 8, 15002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baustian, K.J.; Wise, M.E.; Jensen, E.J.; Schill, G.P.; Freedman, M.A.; Tolbert, M.A. State transformations and ice nucleation in amorphous (semi-)solid organic aerosol. Atmos. Chem. Phys. 2013, 13, 5615–5628. [Google Scholar] [CrossRef] [Green Version]
- Kalberer, M.; Paulsen, D.; Sax, M.; Steinbacher, M.; Dommen, J.; Prevot, A.S.H.; Fisseha, R.; Weingartner, E.; Frankevich, V.; Zenobi, R.; et al. Identification of Polymers as Major Components of Atmospheric Organic Aerosols. Science 2004, 303, 1659–1662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russell, L.M.; Bahadur, R.; Ziemann, P.J. Identifying organic aerosol sources by comparing functional group composition in chamber and atmospheric particles. Proc. Nati. Acad. Sci. USA 2011, 108, 3516–3521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Virtanen, A.; Joutsensaari, J.; Koop, T.; Kannosto, J.; Yli-Pirilä, P.; Leskinen, J.; Mäkelä, J.M.; Holopainen, J.K.; Pöschl, U.; Kulmala, M.; et al. An amorphous solid state of biogenic secondary organic aerosol particles. Nature 2010, 467, 824–827. [Google Scholar] [CrossRef] [PubMed]
- Saukko, E.; Lambe, A.; Massoli, P.; Koop, T.P.; Wright, J.R.; Croasdale, D.; Pedernera, D.B.; Onasch, T.; Laaksonen, A.; Davidovits, P.; et al. Humidity-dependent phase state of SOA particles from biogenic and anthropogenic precursors. Atmos. Chem. Phys. 2012, 12, 4447–4476. [Google Scholar] [CrossRef]
- Hand, J.L.; Malm, W.C.; Laskin, A.; Day, D.; Lee, T.; Wang, C.; Carrico, C.; Carrillo, J.; Cowin, J.P.; Collett, J., Jr.; et al. Optical, physical, and chemical properties of tar balls observed during the Yosemite Aerosol Characterization Study. J. Geophys. Res. 2005, 110, D21210. [Google Scholar] [CrossRef]
- Pósfai, M.; Gelencsér, A.; Simonics, R.; Arató, K.; Li, J.; Hobbs, P.V.; Buseck, P.R. Atmospheric tar balls: Particles from biomass and biofuel burning. J. Geophys. Res. 2004, 109, D06213. [Google Scholar] [CrossRef] [Green Version]
- Reid, J.P.; Bertram, A.K.; Topping, D.O.; Laskin, A.; Martin, S.T.; Petters, M.D.; Pope, F.D.; Rovelli, G. The viscosity of atmospherically relevant organic particles. Nat. Commun. 2018, 9, 956. [Google Scholar] [CrossRef] [Green Version]
- Mikhailov, E.; Vlasenko, S.; Martin, S.T.; Koop, T.; Pöschl, U. Amorphous and crystalline aerosol particles interacting with water vapor: Conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations. Atmos. Chem. Phys. 2009, 9, 9491–9522. [Google Scholar] [CrossRef] [Green Version]
- Browne, E.C.; Zhang, X.L.; Franklin, J.P.; Ridley, K.J.; Kirchstetter, T.W.; Wilson, K.R.; Cappa, C.D.; Kroll, J.H. Effect of heterogeneous oxidative aging on light absorption by biomass burning organic aerosol. Aerosol Sci. Technol. 2019, 53, 663–674. [Google Scholar] [CrossRef]
- Shi, X.J.; Zhang, W.T.; Liu, J.J. Comparison of Anthropogenic Aerosol Climate Effects among Three Climate Models with Reduced Complexity. Atmosphere 2019, 10, 456. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.Y.; Bae, S.Y.; Park, R.S.; Han, J.Y. Aerosol Indirect Effects on the Predicted Precipitation in a Global Weather Forecasting Model. Atmosphere 2019, 10, 392. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.F.; Li, Y.J.; Wang, Y.; Bateman, A.P.; Zhang, Y.; Gong, Z.H.; Bertram, A.K.; Martin, S.T. Highly Viscous States Affect the Browning of Atmospheric Organic Particulate Matter. ACS Cent. Sci. 2018, 4, 207–215. [Google Scholar] [CrossRef] [Green Version]
- Shiraiwa, M.; Ammann, M.; Koop, T.; Pöschl, U. Gas uptake and chemical aging of semisolid organic aerosol particles. Proc. Nati. Acad. Sci. USA 2011, 108, 11003–11008. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Tinsley, M.R.; Goulay, F. Effect of Relative Humidity on the OH-Initiated Heterogeneous Oxidation of Monosaccharide Nanoparticles. J. Phys. Chem. A 2015, 119, 11182–11190. [Google Scholar] [CrossRef]
- Laskin, A.; Gilles, M.K.; Knopf, D.A.; Wang, B.; China, S. Progress in the Analysis of Complex Atmospheric Particles. Annu. Rev. Anal. Chem. 2016, 9, 117–143. [Google Scholar] [CrossRef] [Green Version]
- Slade, J.H.; Knopf, D.A. Multiphase OH oxidation kinetics of organic aerosol: The role of particle phase state and relative humidity. Geophys. Res. Lett. 2014, 41, 5297–5306. [Google Scholar] [CrossRef]
- Davies, J.F.; Wilson, K.R. Nanoscale interfacial gradients formed by the reactive uptake of OH radicals onto viscous aerosol surfaces. Chem. Sci. 2015, 6, 7020–7027. [Google Scholar] [CrossRef] [Green Version]
- Steimer, S.S.; Berkemeier, T.; Gilgen, A.; Krieger, U.K.; Peter, T.; Shiraiwa, M.; Ammann, M. Shikimic acid ozonolysis kinetics of the transition from liquid aqueous solution to highly viscous glass. Phys. Chem. Chem. Phys. 2015, 17, 31101–31109. [Google Scholar] [CrossRef] [Green Version]
- Chim, M.M.; Chow, C.Y.; Davies, J.F.; Chan, M.N. Effects of Relative Humidity and Particle Phase Water on the Heterogeneous OH Oxidation of 2-Methylglutaric Acid Aqueous Droplets. J. Phys. Chem. A 2017, 121, 1666–1674. [Google Scholar] [CrossRef]
- Marshall, F.H.; Miles, R.E.H.; Song, Y.-C.; Ohm, P.B.; Power, R.M.; Reid, J.P.; Dutcher, C.S. Diffusion and reactivity in ultraviscous aerosol and the correlation with particle viscosity. Chem. Sci. 2016, 7, 1298–1308. [Google Scholar] [CrossRef] [Green Version]
- Katrib, Y.; Biskos, G.; Buseck, P.R.; Davidovits, P.; Jayne, J.T.; Mochida, M.; Wise, M.E.; Worsnop, D.R.; Martin, S.T. Ozonolysis of Mixed Oleic-Acid/Stearic-Acid Particles: Reaction Kinetics and Chemical Morphology. J. Phys. Chem. A 2005, 109, 10910–10919. [Google Scholar] [CrossRef] [PubMed]
- Hearn, J.D.; Smith, G.D. Ozonolysis of Mixed Oleic Acid/n-Docosane Particles: The Roles of Phase, Morphology, and Metastable States. J. Phys. Chem. A 2007, 111, 11059–11065. [Google Scholar] [CrossRef] [PubMed]
- Mendez, M.; Visez, N.; Gosselin, S.; Crenn, V.; Riffault, V.; Petitprez, D. Reactive and Nonreactive Ozone Uptake during Aging of Oleic Acid Particles. J. Phys. Chem. A 2014, 118, 9471–9481. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yao, L.; Zheng, J.; Wang, X.; Chen, J.; Yang, X.; Worsnop, D.R.; Donahue, N.M.; Wang, L. Reactions of Atmospheric Particulate Stabilized Criegee Intermediates Lead to High-Molecular-Weight Aerosol Components. Environ. Sci. Technol. 2016, 50, 5702–5710. [Google Scholar] [CrossRef]
- Jacobs, M.I.; Xu, B.; Kostko, O.; Wiegel, A.A.; Houle, F.A.; Ahmed, M.; Wilson, K.R. Using Nanoparticle X-ray Spectroscopy to Probe the Formation of Reactive Chemical Gradients in Diffusion-Limited Aerosols. J. Phys. Chem. A 2019, 123, 6034–6044. [Google Scholar] [CrossRef] [Green Version]
- Wiegel, A.A.; Liu, M.J.; Hinsberg, W.D.; Wilson, K.R.; Houle, F.A. Diffusive confinement of free radical intermediates in the OH radical oxidation of semisolid aerosols. Phys. Chem. Chem. Phys. 2017, 19, 6814–6830. [Google Scholar] [CrossRef] [Green Version]
- Wiegel, A.A.; Wilson, K.R.; Hinsberg, W.D.; Houle, F.A. Stochastic methods for aerosol chemistry: A compact molecular description of functionalization and fragmentation in the heterogeneous oxidation of squalane aerosol by OH radicals. Phys. Chem. Chem. Phys. 2015, 17, 4398–4411. [Google Scholar] [CrossRef] [Green Version]
- Power, R.M.; Simpson, S.H.; Reid, J.P.; Hudson, A.J. The transition from liquid to solid-like behaviour in ultrahigh viscosity aerosol particles. Chem. Sci. 2013, 4, 2597–2604. [Google Scholar] [CrossRef]
- Price, H.C.; Murray, B.J.; Mattsson, J.; O’Sullivan, D.; Wilson, T.W.; Baustian, K.J.; Benning, L.G. Quantifying water diffusion in high-viscosity and glassy aqueous solutions using a Raman isotope tracer method. Atmosph. Chem. Phys. 2014, 14, 3817–3830. [Google Scholar] [CrossRef] [Green Version]
- Eyoy, E.; Maclean, A.M.; Royelli, G.; Li, Y.; Tsimpidi, A.P.; Karydis, V.A.; Kamal, S.; Lelieveld, J.; Shiraiwa, M.; Reid, J.P.; et al. Predictions of diffusion rates of large organic molecules in secondary organic aerosols using the Stokes-Einstein and fractional Stokes-Einstein relations. Atmos. Chem. Phys. 2019, 19, 10073–10085. [Google Scholar] [CrossRef] [Green Version]
- Price, H.C.; Mattsson, J.; Murray, B.J. Sucrose diffusion in aqueous solution. Phys. Chem. Chem. Phys. 2016, 18, 19207–19216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Meara, S.; Topping, D.O.; Zaveri, R.A.; McFiggans, G. An efficient approach for treating composition-dependent diffusion within organic particles. Atmos. Chem. Phys. 2017, 17, 10477–10494. [Google Scholar] [CrossRef] [Green Version]
- Fowler, K.; Connolly, P.J.; Topping, D.O.; O’Meara, S. Maxwell-Stefan diffusion: A framework for predicting condensed phase diffusion and phase separation in atmospheric aerosol. Atmos. Chem. Phys. 2018, 18, 1629–1642. [Google Scholar] [CrossRef] [Green Version]
- Burkholder, J.B.; Abbate, J.P.D.; Barnes, I.; Roberts, J.M.; Melamed, M.L.; Ammann, M.; Bertram, A.K.; Cappa, C.D.; Carlton, A.G.; Carpenter, L.J.; et al. The Essential Role for Laboratory Studies in Atmospheric Chemistry. Environ. Sci. Technol. 2017, 51, 2519–2528. [Google Scholar] [CrossRef] [Green Version]
- Houle, F.A.; Hinsberg, W.D.; Wilson, K.R. Oxidation of a model alkane aerosol by OH radical: The emergent nature of reactive uptake. Phys. Chem. Chem. Phys. 2015, 17, 4412–4423. [Google Scholar] [CrossRef] [Green Version]
- Nah, T.; Kessler, S.H.; Daumit, K.E.; Kroll, J.H.; Leone, S.R.; Wilson, K.R. Influence of Molecular Structure and Chemical Functionality on the Heterogeneous OH-Initiated Oxidation of Unsaturated Organic Particles. J. Phys. Chem. A 2014, 118, 4106–4119. [Google Scholar] [CrossRef] [Green Version]
- Kolesar, K.R.; Buffaloe, G.; Wilson, K.R.; Cappa, C.D. OH-Initiated Heterogeneous Oxidation of Internally-Mixed Squalane and Secondary Organic Aerosol. Environ. Sci. Technol. 2014, 48, 3196–3202. [Google Scholar] [CrossRef] [Green Version]
- Arangio, A.M.; Slade, J.H.; Berkemeier, T.; Poeschl, U.; Knopf, D.A.; Shiraiwa, M. Multiphase Chemical Kinetics of OH Radical Uptake by Molecular Organic Markers of Biomass Burning Aerosols: Humidity and Temperature Dependence, Surface Reaction, and Bulk Diffusion. J. Phys. Chem. A 2015, 119, 4533–4544. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.W.; Rickards, A.M.J.; Walker, J.S.; Knox, K.J.; Miles, R.E.H.; Reid, J.P.; Signorell, R. Timescales of water transport in viscous aerosol: Measurements on sub-micron particles and dependence on conditioning history. Phys. Chem. Chem. Phys. 2014, 16, 9819–9830. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.Y.; Liu, Y.C.; Ma, J.Z.; Ma, Q.X.; He, H. Degradation kinetics of levoglucosan initiated by hydroxyl radical under different environmental conditions. Atmos. Environ. 2014, 91, 32–39. [Google Scholar] [CrossRef]
- Tong, H.-J.; Reid, J.P.; Bones, D.L.; Luo, B.P.; Krieger, U.K. Measurements of the timescales for the mass transfer of water in glassy aerosol at low relative humidity and ambient temperature. Atmos. Chem. Phys. 2011, 11, 4739–4754. [Google Scholar] [CrossRef] [Green Version]
- Zobrist, B.; Soonsin, V.; Luo, B.P.; Krieger, U.K.; Marcolli, C.; Peter, T.; Koop, T. Ultra-slow water diffusion in aqueous sucrose glasses. Phys. Chem. Chem. Phys. 2011, 13, 3514–3526. [Google Scholar] [CrossRef] [PubMed]
- Houle, F.A.; Wiegel, A.A.; Wilson, K.R. Predicting Aerosol Reactivity Across Scales: From the Laboratory to the Atmosphere. Environ. Sci. Technol. 2018, 52, 13774–13781. [Google Scholar] [CrossRef]
- Fan, H.; Wenyika Masaya, T.; Goulay, F. Effect of surface–bulk partitioning on the heterogeneous oxidation of aqueous saccharide aerosols. Phys. Chem. Chem. Phys. 2019, 21, 2992–3001. [Google Scholar] [CrossRef]
- Song, Y.C.; Haddrell, A.E.; Bzdek, B.R.; Reid, J.P.; Bannan, T.; Topping, D.O.; Percival, C.; Cai, C. Measurements and Predictions of Binary Component Aerosol Particle Viscosity. J. Phys. Chem. A 2016, 120, 8123–8137. [Google Scholar] [CrossRef] [Green Version]
- Mysak, E.R.; Wilson, K.R.; Jimenez-Cruz, M.; Ahmed, M.; Baer, T. Synchrotron radiation based aerosol time-of-flight mass spectrometry for organic constituents. Anal. Chem. 2005, 77, 5953–5960. [Google Scholar] [CrossRef]
- Smith, J.D.; Kroll, J.H.; Cappa, C.D.; Che, D.L.; Liu, C.L.; Ahmed, M.; Leone, S.R.; Worsnop, D.R.; Wilson, K.R. The heterogeneous reaction of hydroxyl radicals with sub-micron squalane particles: A model system for understanding the oxidative aging of ambient aerosols. Atmos. Chem. Phys. 2009, 9, 3209–3222. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, R. Kinetics of the gas-phase reactions of OH radicals with alkanes and cycloalkanes. Atmosph. Chem. Phys. 2003, 3, 2233–2307. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, R. Kinetics and mechanistics of the gas-phase reactions of the hydroxyl radical with organic-compounds under atmospheric conditions. Chem. Rev. 1986, 86, 69–201. [Google Scholar] [CrossRef]
- Hearn, J.D.; Smith, G.D. A mixed-phase relative rates technique for measuring aerosol reaction kinetics. Geophys. Res. Lett. 2006, 33, L17805. [Google Scholar] [CrossRef]
- Vieceli, J.R.M.; Potter, N.; Dang, L.X.; Garrett, B.C.; Tobias, D.J. Molecular Dynamics Simulations of Atmospheric Oxidants at the Air−Water Interface: Solvation and Accommodation of OH and O3. J. Phys. Chem. B 2005, 15876–15892. [Google Scholar] [CrossRef] [PubMed]
- Bucknall, T.; Edwards, H.E.; Kemsley, K.G.; Moore, J.S.; Phillips, G.O. The formation of malonaldehyde in irradiated carbohydrates. Carbohydr. Res. 1978, 62, 49–59. [Google Scholar] [CrossRef]
- Zakatova, N.V.; Minkhadzhiddinova, D.P.; Sharpatyi, V.A. Role of OH-radicals in the radiolytic decomposition of carbohydrates and polysaccharides. Russ. Chem. Bull. 1969. [Google Scholar] [CrossRef]
- Davies, J.F.; Wilson, K.R. Raman Spectroscopy of Isotopic Water Diffusion in Ultraviscous, Glassy, and Gel States in Aerosol by Use of Optical Tweezers. Anal. Chem. 2016, 88, 2361–2366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vignes, A. Diffusion in Binary Solutions. Variation of Diffusion Coefficient with Composition. Ind. Eng. Chem. Fundam. 1966, 5, 189–199. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 64th ed.; CRC Press: Boca Raton, FL, USA, 1983. [Google Scholar]
- Mai, H.; Shiraiwa, M.; Flagan, R.C.; Seinfeld, J.H. Under What Conditions Can Equilibrium Gas–Particle Partitioning Be Expected to Hold in the Atmosphere? Environ. Sci. Technol. 2015, 49, 11485–11491. [Google Scholar] [CrossRef] [Green Version]
- Yli-Juuti, T.; Pajunoja, A.; Tikkanen, O.P.; Buchholz, A.; Faiola, C.; Vaisanen, O.; Hao, L.Q.; Kari, E.; Perakyla, O.; Garmash, O.; et al. Factors controlling the evaporation of secondary organic aerosol from alpha-pinene ozonolysis. Geophys. Res. Lett. 2017, 44, 2562–2570. [Google Scholar] [CrossRef]

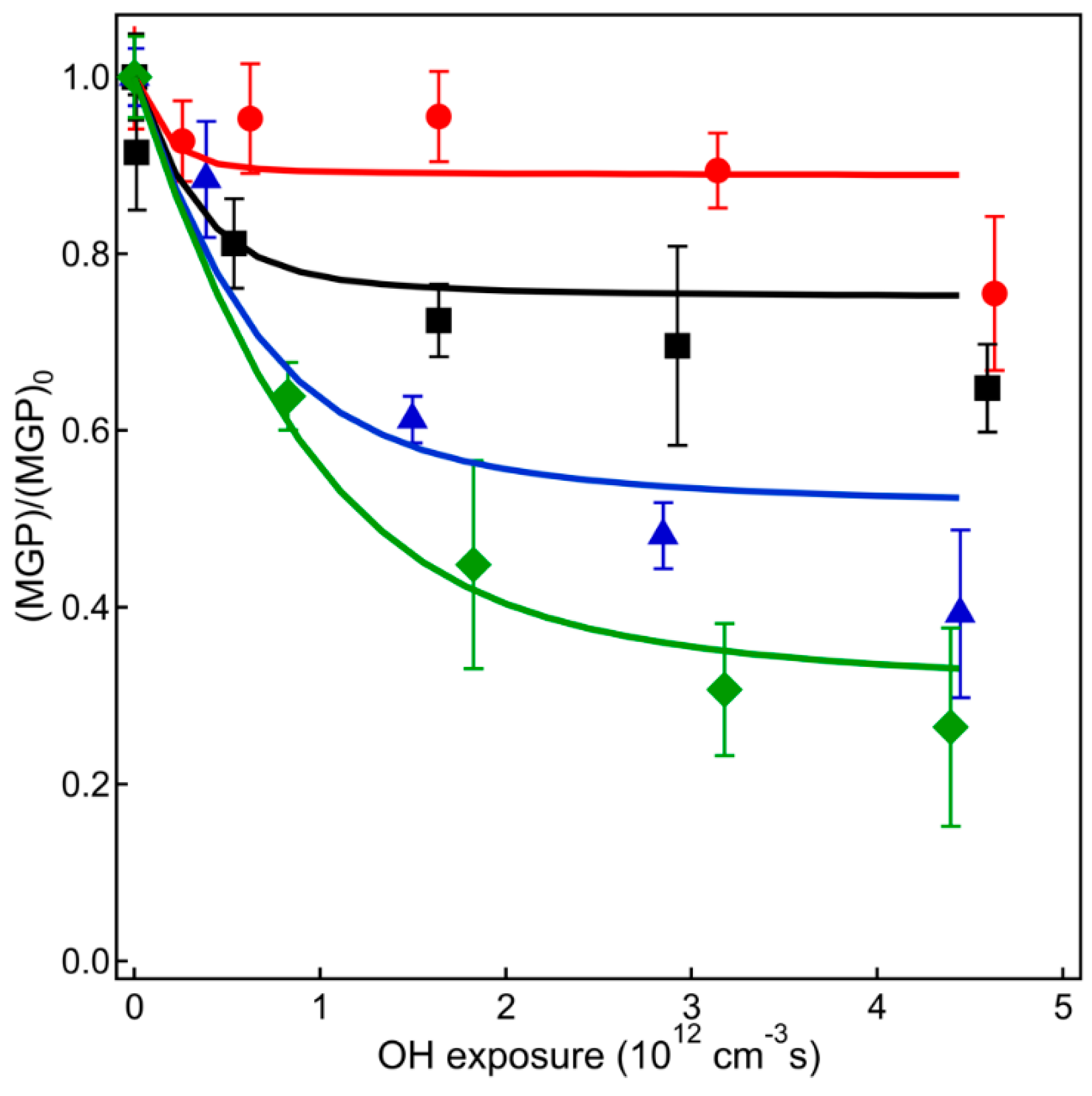

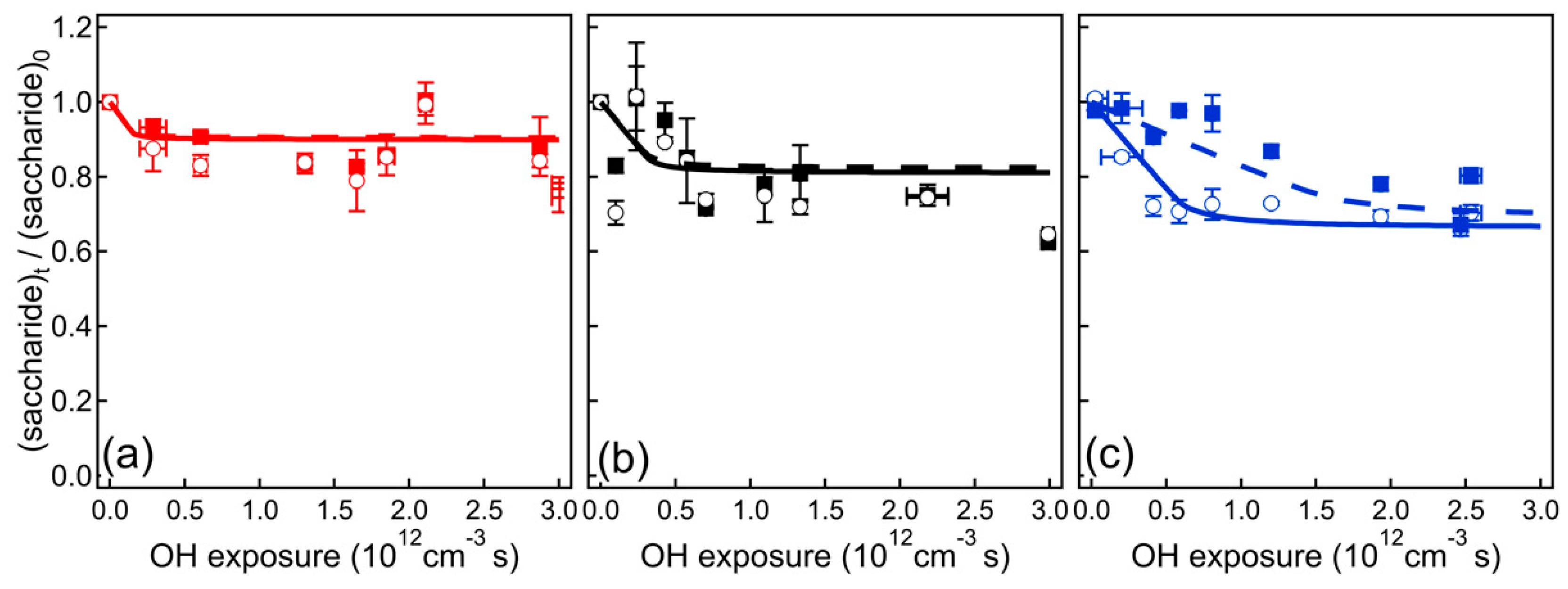
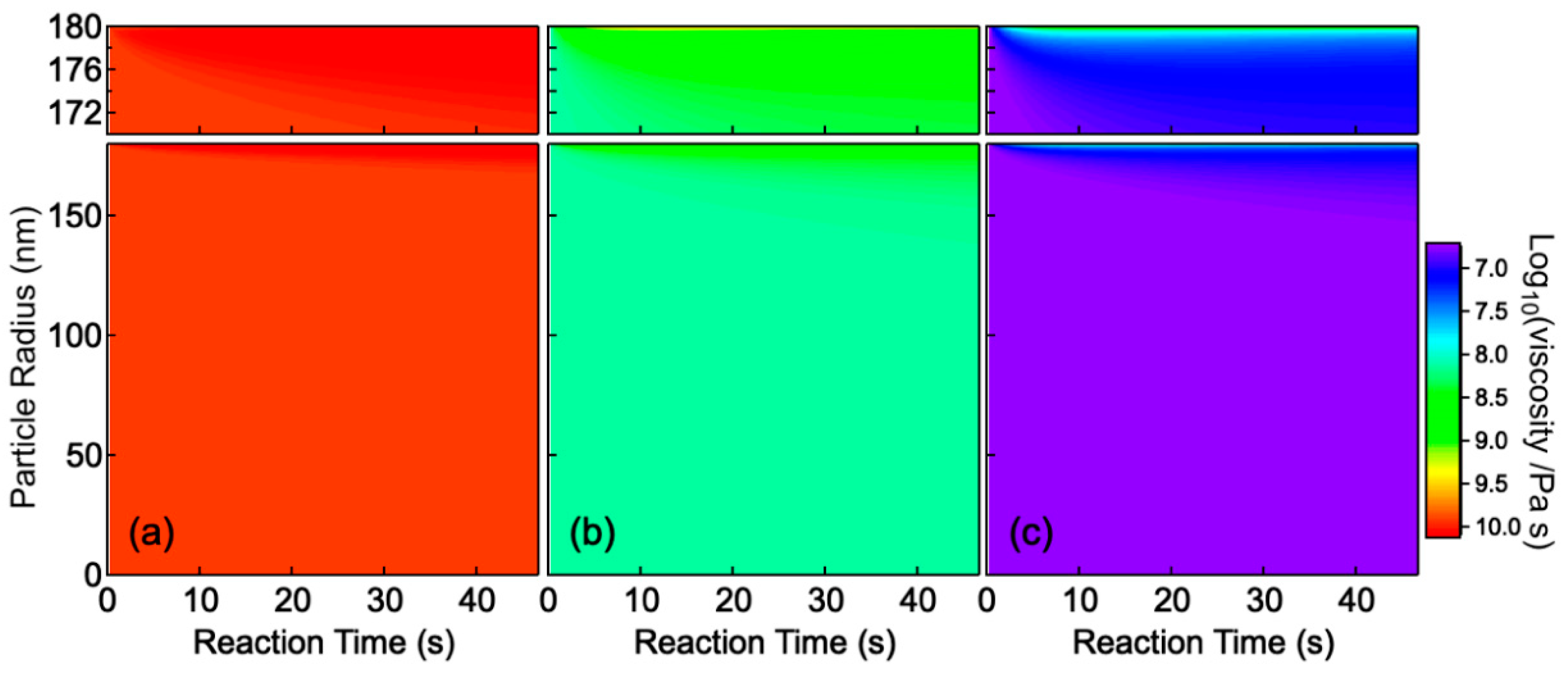
| Parameter | Value | Description |
|---|---|---|
| RH | 30% | Relative humidity |
| (OH) | 1.35 × 1011 cm−3 (VUV-AMS) 8.70 × 1010 cm−3 (GC-MS) | OH average experimental number density 1 |
| 100 nm (VUV-AMS) 180 nm (GC-MS) | Particle radius | |
| 10 s−1 | Pseudo first-order adsorption rate for OH [28] | |
| 2.86 × 1010 s−1 | OH desorption rate coefficient [53] | |
| 5.31 × 10−12 cm3 s−1 | OH + MGP rate coefficient in aqueous solutions [55] | |
| 5.15 × 10−12 cm3 s−1 | OH + lactose rate coefficient in aqueous solutions [54] | |
| 1 × 109 cm2 s−1 | OH diffusion coefficient [56] | |
| 6.0 × 10−13 cm2 s−1 | MGP diffusion coefficient at RH = 30% (35 times the value obtained based on the S–E: logη = 5.554 [47]) 2 | |
| 1.5 × 10−17 cm2 s−1 | Lactose diffusion coefficient at RH = 30% (from S–E equation: logη = 8.526 [47]) 2 |
| Molar Ratio (MGP:lactose) | Rate Constant kMGP ± 2σ (cm3 s−1) | Uptake Coefficient (γMGP ± 2σ) |
|---|---|---|
| 1:1 | 4.02 ± 4.78 × 10−14 | 0.05 ± 0.06 |
| 2:1 | 2.24 ± 1.10 × 10−13 | 0.27 ± 0.15 |
| 4:1 | 3.26 ± 0.04 × 10−13 | 0.38 ± 0.01 |
| 8:1 | 4.73 ± 0.68 × 10−13 | 0.53 ± 0.10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Goulay, F. Effect of Bulk Composition on the Heterogeneous Oxidation of Semi-Solid Atmospheric Aerosols. Atmosphere 2019, 10, 791. https://doi.org/10.3390/atmos10120791
Fan H, Goulay F. Effect of Bulk Composition on the Heterogeneous Oxidation of Semi-Solid Atmospheric Aerosols. Atmosphere. 2019; 10(12):791. https://doi.org/10.3390/atmos10120791
Chicago/Turabian StyleFan, Hanyu, and Fabien Goulay. 2019. "Effect of Bulk Composition on the Heterogeneous Oxidation of Semi-Solid Atmospheric Aerosols" Atmosphere 10, no. 12: 791. https://doi.org/10.3390/atmos10120791
APA StyleFan, H., & Goulay, F. (2019). Effect of Bulk Composition on the Heterogeneous Oxidation of Semi-Solid Atmospheric Aerosols. Atmosphere, 10(12), 791. https://doi.org/10.3390/atmos10120791