Towards Hyper-Dimensional Variography Using the Product-Sum Covariance Model
Abstract
:1. Introduction
2. Theory
2.1. Original Product-Sum Model and Modeling Procedure
2.2. Modeling of the Hyper-Dimensional Variogram Based on the Product-Sum Model
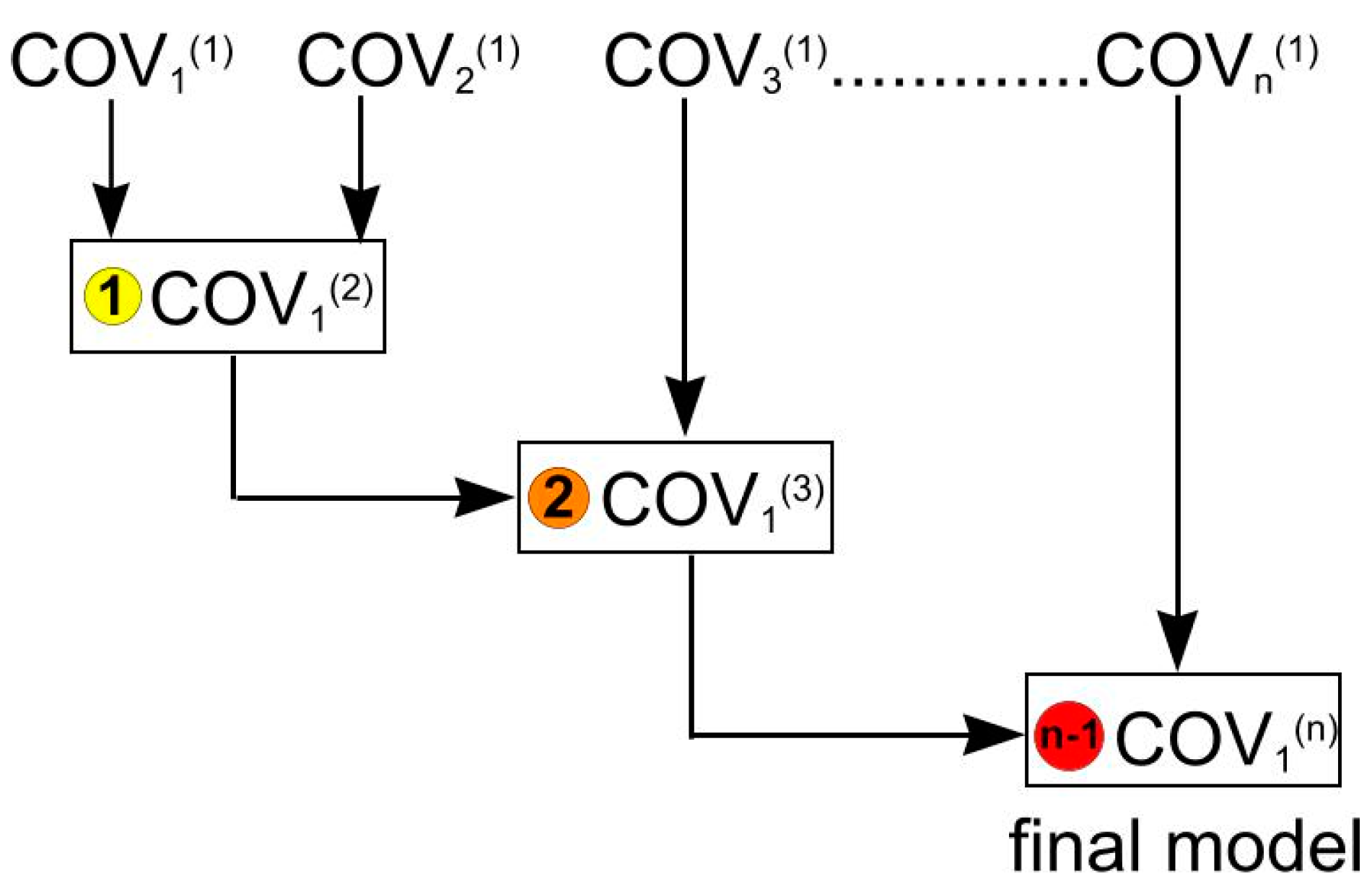
2.2.1. Sequential Hierarchical Modeling
… + a1a5Ch(hh)(1)Cv(hv)(1) + a2a5Ch(hh)(1) + a3a5Cv(hv)(1) + a6Ct(ht)(1)
2.2.2. Modeling “All at Once”
3. Application
4. Conclusions
5. Software and/or Data Availability Section
Author Contributions
Funding
Conflicts of Interest
References
- Chilès, J.-P.; Delfiner, P. Kriging. In Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Stein, M. Statistical methods for regular monitoring data. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 667–687. [Google Scholar] [CrossRef]
- Montero, J.M.; Fernández-Avilés, G.; Mateu, J. Spatial and Spatio-Temporal Geostatistical Modeling and Kriging; Wiley: Chichester, UK, 2015. [Google Scholar]
- Tadić, J.M.; Ilić, V.; Biraud, S. Examination of geostatistical and machine-learning techniques as interpolators in anisotropic atmospheric environments. Atmos. Environ. 2015, 111, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Hammerling, D.M.; Michalak, A.M.; O’Dell, C.; Kawa, S.R. Global CO2 distributions over land from the Greenhouse Gases Observing Satellite (GOSAT). Geophys. Res. Lett. 2012, 39, L08804. [Google Scholar] [CrossRef]
- Tadić, J.M.; Qiu, X.; Yadav, V.; Michalak, A.M. Mapping of satellite Earth observations using moving window block kriging. Geosci. Model Dev. 2015, 8, 1–9. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C. Statistics for Spatio-Temporal Data; Wiley: Hoboken, NJ, USA, 2011; 588p. [Google Scholar]
- Gneiting, T.; Genton, M.G.; Guttorp, P. Geostatistical space-time models, stationarity, separability and full symmetry. In Statistics of Spatio-Temporal Systems; Finkenstaedt, B., Held, L., Isham, V., Eds.; Monographs in Statistics and Applied Probability; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2007; pp. 151–175. [Google Scholar]
- Kyriakidis, P.C.; Journel, A.G. Geostatistical space–time models: A review. Math. Geol. 1999, 31, 651–684. [Google Scholar] [CrossRef]
- Snepvangers, J.J.J.C.; Heuvelink, G.B.M.; Huisman, J.A. Soil water content interpolation using spatio-temporal kriging with external drift. Geoderma 2003, 112, 253–271. [Google Scholar] [CrossRef]
- Stein, M. Space–Time Covariance Functions; Technical Rep. 4; Center for Integrating Statistical and Environ Science, University of Chicago: Chicago, IL, USA, 2004. [Google Scholar] [Green Version]
- Horrell, M.T.; Stein, M.L. Half-spectral space–time covariance models. Spat. Stat. 2017, 19, 90–100. [Google Scholar] [CrossRef]
- Rodrigues, A.; Diggle, P. A class of convolution-based models for spatio-temporal processes with non-separable covariance structure. Scand. J. Stat. 2010, 37, 553–567. [Google Scholar] [CrossRef]
- Zastavnyi, V.; Porcu, E. Characterization theorems for the gneiting class of space-time covariances. Bernoulli 2011, 17, 456–465. [Google Scholar] [CrossRef]
- De Iaco, S.; Myers, D.; Posa, D. On strict positive definiteness of product and product-sum covariance models. J. Stat. Plan. Inference 2011, 141, 1132–1140. [Google Scholar] [CrossRef]
- De Iaco, S.; Posa, D. Predicting Spatio-Temporal Random Fields: Some Computational Aspects. Comput. Geosci. 2012, 41, 12–24. [Google Scholar] [CrossRef]
- De Iaco, S.; Posa, D. Positive and Negative Non-Separability for Space-Time Covariance Models. J. Stat. Plan. Inference 2013, 143, 378–391. [Google Scholar] [CrossRef]
- De Iaco, S.; Posa, D.; Myers, D.E. Characteristics of Some Classes of Space-Time Co-variance Functions. J. Stat. Plan. Inference 2013, 143, 2002–2015. [Google Scholar] [CrossRef]
- De Iaco, S.; Palma, M.; Posa, D. A General Procedure for Selecting a Class of Fully Symmetric Space-Time Covariance Functions. Environmetrics 2016, 112, 212–224. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Pebesma, E.; Gräler, B. Space-Time Geostatistics published in Encyclopedia of GIS; Springer International Publishing: Cham, Switzerland, 2017; pp. 1919–1926. [Google Scholar] [CrossRef]
- De Iaco, S.; Posa, D. Strict positive definiteness in geostatistics. Stoch. Environ. Res. Risk Assess. 2018, 32, 577–590. [Google Scholar] [CrossRef]
- De Iaco, S.; Myers, D.; Posa, D. Space-time analysis using a general product–sum model. Stat. Probab. Lett. 2001, 52, 21–28. [Google Scholar] [CrossRef]
- Tadić, J.M.; Michalak, A.M.; Iraci, L.; Ilić, V.; Biraud, S.C.; Feldman, D.R.; Built, T.; Johnson, M.S.; Loewenstein, M.; Jeong, S.; et al. Elliptic Cylinder Airborne Sampling and Geostatistical Mass Balance Approach for Quantifying Local Greenhouse Gas Emissions. Environ. Sci. Technol. 2017, 51, 10012–10021. [Google Scholar] [CrossRef]
- Brock, F.V.; Crawford, K.C.; Elliott, R.L.; Cuperus, G.W.; Stadler, S.J.; Johnson, H.W.; Eilts, M.D. The Oklahoma Mesonet—A technical overview. J. Atmos. Ocean. Technol. 1995, 12, 5–19. [Google Scholar] [CrossRef]
- McPherson, R.A.; Fiebrich, C.A.; Crawford, K.C.; Kilby, J.R.; Grimsley, D.L.; Martinez, J.E.; Basara, J.B.; Illston, B.G.; Morris, D.A.; Kloesel, K.A.; et al. Statewide monitoring of the mesoscale environment: A technical update on the Oklahoma Mesonet. J. Atmos. Oceanic Technol. 2007, 24, 301–321. [Google Scholar] [CrossRef]
- Tadić, J.M.; Qiu, X.; Miller, S.; Michalak, A.M. Spatio-temporal approach to moving window block kriging of satellite data V1.0. Geosci. Model Dev. 2017, 10, 709–720. [Google Scholar] [CrossRef]
- Christakos, G. On the problem of permissible covariance and variogram models. Water Resour. Res. 1984, 20, 251–265; [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Luo, X. Spatiotemporal modeling: Covariances and ordinary kriging systems. In Quantitative Geology and Geostatistics, Geostatistics for the Next Century; Dimitrakopoulos, R., Ed.; Springer: Dordrecht, The Netherlands, 1994; pp. 88–93. [Google Scholar]
- Rouhani, S.; Hall, T.J. Space-Time Kriging of Groundwater Data. In Geostatistics; Armstrong, M., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989; Volume 2, pp. 639–651. [Google Scholar]
- De Cesare, L.; Myers, D.E.; Posa, D. Spatio-temporal modelling of SO2 in Milan district. In Geostatistics Wollongong; Baafi, E.Y., Schofield, N.A., Eds.; Kluwer Academic Publishing: Dordrecht, The Netherlands, 1996; pp. 1031–1042. [Google Scholar]
- Cressie, N.; Huang, H.C. Classes of nonseperable, spatio-temporal stationary covariance functions. J. Am. Stat. Assoc. 1999, 94, 1–53. [Google Scholar] [CrossRef]
- Guo, L.; Lei, L.; Zeng, Z. Spatiotemporal correlation analysis of satellite-observed CO2: Case studies in China and USA. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Zeng, Z.; Lei, L.; Guo, L.; Zhang, L.; Zhang, B. Incorporating temporal variability to improve geostatistical analysis of satellite-observed CO2 in China. Chin. Sci. Bull. 2013, 58, 1948–1954. [Google Scholar] [CrossRef]
- Zeng, Z.-C.; Lei, L.; Strong, K.; Jones, D.B.A.; Guo, L.; Liu, M.; Deng, F.; Deutscher, N.M.; Dubey, M.K.; Griffith, D.W.T.; et al. Global land mapping of satellite-observed CO2 total columns using spatio-temporal geostatistics. Int. J. Digit. Earth 2017, 10, 426–456. [Google Scholar] [CrossRef] [Green Version]
- De Cesare, L.; Myers, D.; Posa, D. Estimating and modeling space–time correlation structures. Stat. Prob. Lett. 2001, 51, 9–14. [Google Scholar] [CrossRef]
- De Cesare, L.; Myers, D.E.; Posa, D. Product–sum covariance for space–time modeling: An environmental application. Environmetrics 2001, 12, 11–23. [Google Scholar] [CrossRef]
- Salmon, M.M. Introduction to Logic and Critical Thinking, 6th ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Million, E. The Hadamard Product. 2007. Available online: http://buzzard.ups.edu/courses/2007spring/projects/million-paper.pdf (accessed on 9 January 2019).
- Mathias, R. Matrix completions, norms and Hadamard products. Proc. Am. Math. Soc. 1993, 117, 905–918. [Google Scholar]
- Baldocchi, D. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef] [Green Version]
- Vilà-Guerau de Arellano, J.; Ouwersloot, H.G.; Baldocchi, D.; Jacobs, C.M.J. Shallow cumulus rooted in photosynthesis. Geophys. Res. Lett. 2014, 41, 1796–1802. [Google Scholar] [CrossRef]
- Lambers, H.; Stuart Chapin, F.S.; Pons, T.L. Photosynthesis. In Plant Physiological Ecology; Springer: New York, NY, USA, 2008; pp. 11–99. [Google Scholar]
- Williams, I.N.; Riley, W.J.; Kueppers, L.M.; Biraud, S.C.; Torn, M.S. Separating the effects of phenology and diffuse radiation on gross primary productivity in winter wheat. J. Geophys. Res. Biogeosci. 2016, 121, 1903–1915. [Google Scholar] [CrossRef]
- Haas, T.C. Lognormal and moving window methods of estimating acid deposition. J. Am. Stat. Assoc. 1990, 85, 950–963. [Google Scholar] [CrossRef]
- Bagley, J.E.; Kueppers, L.M.; Billesbach, D.P.; Williams, I.N.; Biraud, S.C.; Torn, M.S. The influence of land cover on surface energy partitioning and evaporative fraction regimes in the U.S. Southern Great Plains. J. Geophys. Res. Atmos. 2017, 122, 5793–5807. [Google Scholar] [CrossRef]
- Romanowicz, R.; Young, P.; Brown, P.; Diggle, P. A recursive estimation approach to the spatio-temporal analysis and modelling of air quality data. Environ. Model. Softw. 2006, 21, 759–769. [Google Scholar] [CrossRef]
- Tadić, J. Hyperdimensional Variography Code. Available online: https://www.researchgate.net/publication/313387764_Hyperdimensional_Variography_Code (accessed on 10 January 2019).
- Creative Commons. Available online: https://creativecommons.org/licenses/ (accessed on 10 January 2019).

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadić, J.M.; Williams, I.N.; Tadić, V.M.; Biraud, S.C. Towards Hyper-Dimensional Variography Using the Product-Sum Covariance Model. Atmosphere 2019, 10, 148. https://doi.org/10.3390/atmos10030148
Tadić JM, Williams IN, Tadić VM, Biraud SC. Towards Hyper-Dimensional Variography Using the Product-Sum Covariance Model. Atmosphere. 2019; 10(3):148. https://doi.org/10.3390/atmos10030148
Chicago/Turabian StyleTadić, Jovan M., Ian N. Williams, Vojin M. Tadić, and Sébastien C. Biraud. 2019. "Towards Hyper-Dimensional Variography Using the Product-Sum Covariance Model" Atmosphere 10, no. 3: 148. https://doi.org/10.3390/atmos10030148
APA StyleTadić, J. M., Williams, I. N., Tadić, V. M., & Biraud, S. C. (2019). Towards Hyper-Dimensional Variography Using the Product-Sum Covariance Model. Atmosphere, 10(3), 148. https://doi.org/10.3390/atmos10030148




