Winter Weather Regimes in Southeastern China and its Intraseasonal Variations
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Clustering Method
The k-means Clustering Technique
Classifiability Index
2.2.2. Attribution of Intraseasonal Precipitation Differences
2.2.3. Calculation of the Teleconnection Patterns
3. Results
3.1. WTs
3.1.1. Determine the Optimal Number of Clusters
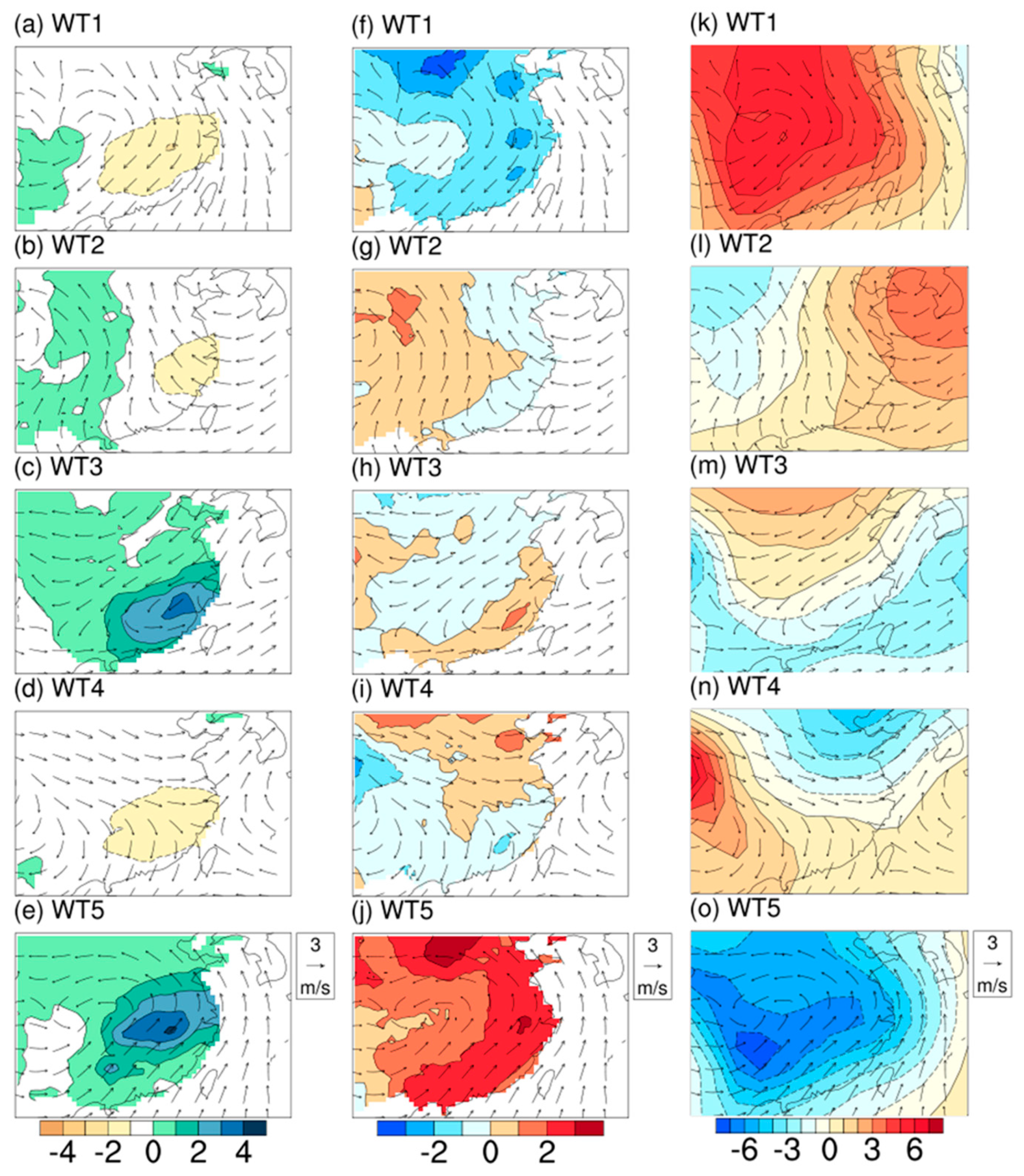
3.1.2. Occurrence Frequency and Spatial Distribution Characteristics of WTs
3.2. Progression and Persistence of WTs
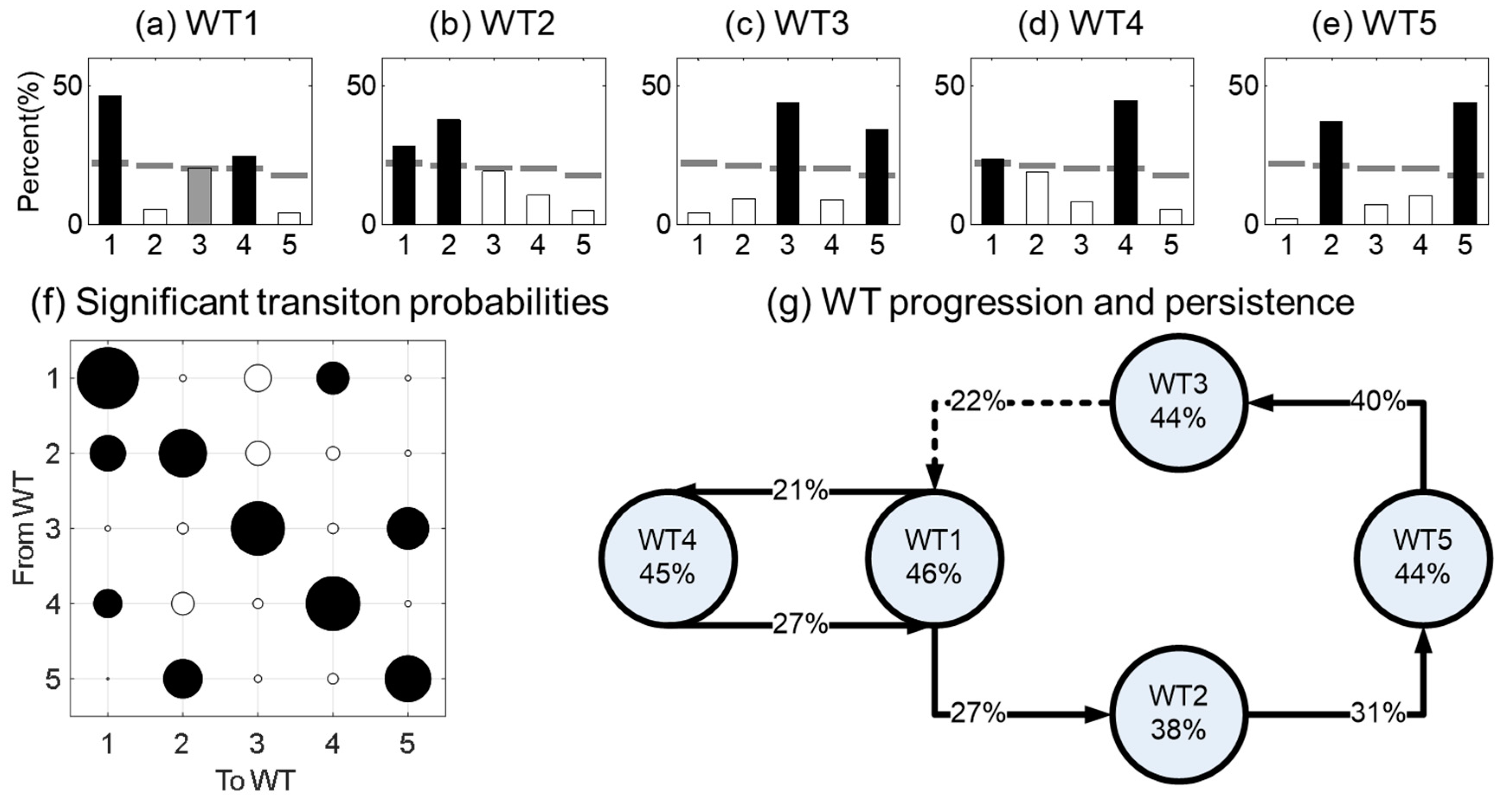
3.2.1. WT Persistence
3.2.2. WT Progression
3.3. Relationships between WTs and Precipitation
3.3.1. Characteristics of Precipitation and Extreme Precipitation
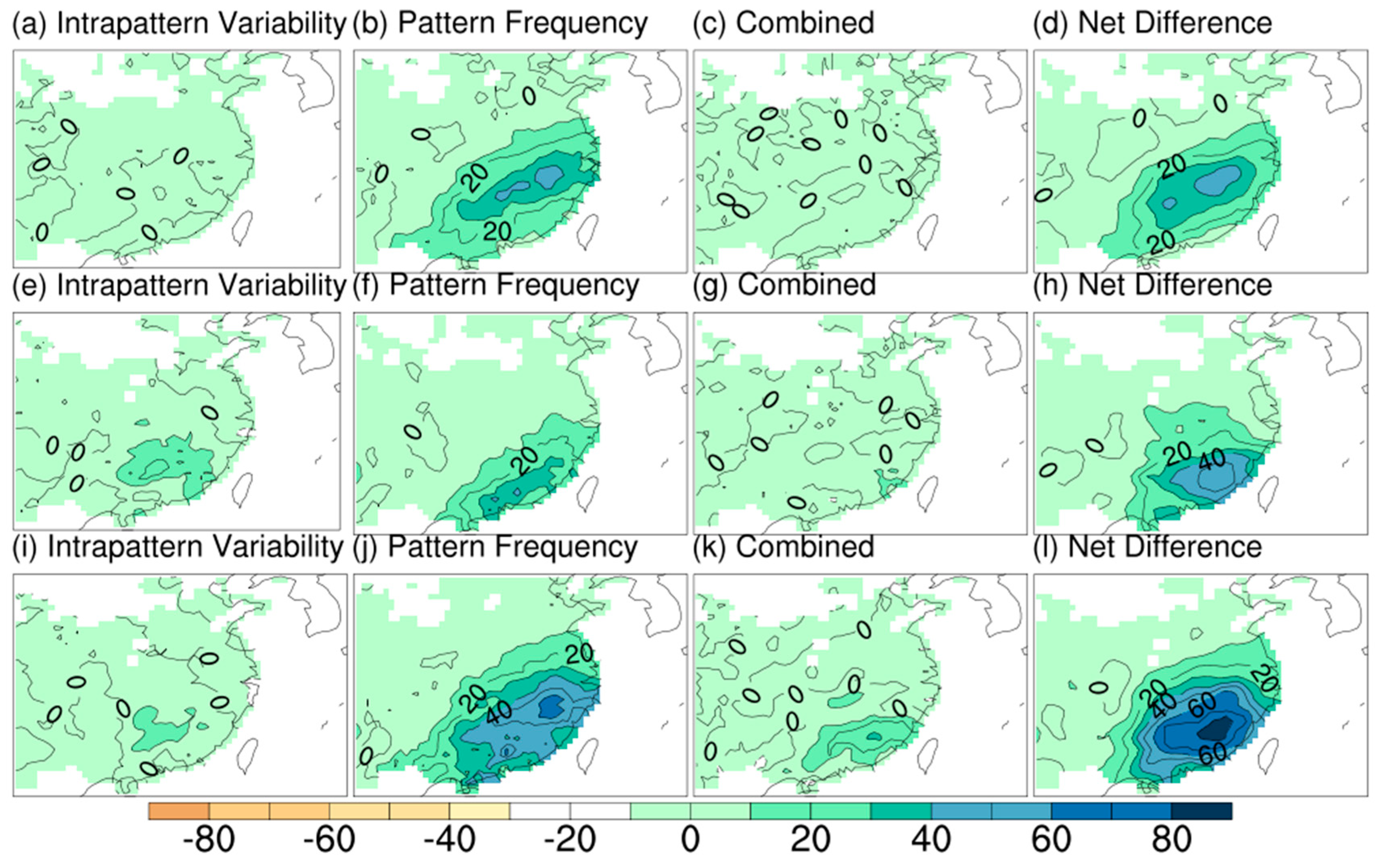
3.3.2. Attribution of Intraseasonal Precipitation Differences
3.4. Relationships between WTs and Teleconnections
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Cao, G.; Zhang, Q.; Sun, J.; Wang, Z.; Zhang, Y.; Zhao, S.; Chen, X.; Chen, Y. Analysis of the severe cold Surge, ice-snow and frozen disasters in South China during January 2008: I. Climatic features and its impacts. Meteorol. Mon. 2008, 34, 95–100. (In Chinese) [Google Scholar]
- Gao, H.; Chen, L.; Jia, X.; Ke, Z.; Han, R.; Zhang, P.; Wang, Q.; Sun, C.; Zhu, Y.; Li, W.; et al. Analysis of the severe cold surge, ice-snow and frozen disasters in south China during January 2008: II. Possible climatic causes. Meteorol. Mon. 2008, 34, 101–106. (In Chinese) [Google Scholar]
- Roller, C.D.; Qian, J.; Agel, L.; Barlow, M.; Moron, V. Winter weather regimes in the Northeast United States. J. Clim. 2016, 29, 2963–2980. [Google Scholar] [CrossRef]
- Gerlitz, L.; Steirou, E.; Schneider, C.; Moron, V.; Vorogushyn, S.; Merz, B. Variability of the cold season climate in Central Asia-Part I: Weather types and their tropical and extratropical drivers. J. Clim. 2018, 31, 7185–7207. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Comput. Soc. 1979, 1, 224–227. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Diaz, H. Global climatic anomalies associated with extremes in the Southern Oscillation. J. Clim. 1989, 2, 1069–1090. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Observations of the 40–50-Day Tropical Oscillation—A Review. Mon. Weather Rev. 1994, 122, 814–837. [Google Scholar] [CrossRef] [Green Version]
- Schuenemann, K.C.; Cassano, J.J. Changes in synoptic weather patterns and Greenland precipitation in the 20th and 21st centuries: 1. Evaluation of late 20th century simulations from IPCC models. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Chen, D.; Ou, T.; Gong, L.; Xu, C.; Li, W.; Ho, C.H.; Qian, W. Spatial interpolation of daily precipitation in China: 1951–2005. Adv. Atmos. Sci. 2010, 27, 1221–1232. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Wheeler, M.C.; Hendon, H.H. An all-season real-time multivariate MJO Index: Development of an index for monitoring and prediction. Mon. Weather Rev. 2004, 132, 1917–1932. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, X.; Shen, Y.; Xu, C.; Shi, Y.; Giorgi, F. A Daily Temperature Dataset over China and Its Application in Validating a RCM Simulation. Adv. Atmos. Sci. 2009, 26, 763–772. [Google Scholar] [CrossRef]
- Diday, E.; Simon, J.C. Clustering analysis. In Digital Pattern Recognition; Springer: Berlin, Germany, 1976; pp. 47–94. [Google Scholar]
- Ghil, M.; Robertson, A.W. “Waves” vs. “particles” in the atmosphere’s phase space: A pathway to long-range forecasting? Proc. Natl. Acad. Sci. USA 2002, 99, 2493–2500. [Google Scholar] [CrossRef]
- Straus, D.M.; Corti, S.; Molteni, F. Circulation Regimes: Chaotic Variability versus SST-Forced Predictability. J. Clim. 2007, 20, 2251–2272. [Google Scholar] [CrossRef]
- Moron, V.; Robertson, A.W.; Qian, J. Local versus regional-scale characteristics of monsoon onset and post-onset rainfall over Indonesia. Clim. Dyn. 2010, 34, 281–299. [Google Scholar] [CrossRef]
- Qian, J.H.; Robertson, A.W.; Moron, V. Interactions among ENSO, the Monsoon, and Diurnal Cycle in Rainfall Variability over Java, Indonesia. J. Atmos. Sci. 2010, 67, 3509–3524. [Google Scholar] [CrossRef]
- Conway, D.; Jones, P.D. The use of weather types and air flow indices for GCM downscaling. J. Hydrol. 1998, 212, 348–361. [Google Scholar] [CrossRef]
- Moron, V.; Robertson, A.W.; Ward, M.N.; Ndiaye, O. Weather Types and Rainfall over Senegal. Part I: Observational Analysis. J. Clim. 2008, 21, 266–287. [Google Scholar] [CrossRef]
- Demuzere, M.; Werner, M.; van Lipzig, N.P.M.; Roeckner, E. An analysis of present and future ECHAM5 pressure fields using a classification of circulation patterns. Int. J. Climatol. 2009, 29, 1796–1810. [Google Scholar] [CrossRef] [Green Version]
- Riddle, E.E.; Stoner, M.B.; Johnson, N.C.L.; Heureux, M.L.; Collins, D.C.; Feldstein, S.B. The impact of the MJO on clusters of wintertime circulation anomalies over the North American region. Clim. Dyn. 2012, 40, 1749–1766. [Google Scholar] [CrossRef] [Green Version]
- Perez, J.; Menendez, M.; Mendez, F.J.; Losada, I.J. Evaluating the performance of CMIP3 and CMIP5 global climate models over the north-east Atlantic region. Clim. Dyn. 2014, 43, 2663–2680. [Google Scholar] [CrossRef]
- Michelangeli, P.A.; Vautard, R.; Legras, B. Weather regimes: Recurrence and quasi stationarity. J. Atmos. Sci. 1995, 52, 1237–1256. [Google Scholar] [CrossRef]
- Coleman, J.S.M.; Rogers, J.C. A Synoptic Climatology of the Central United States and Associations with Pacific Teleconnection Pattern Frequency. J. Clim. 2007, 20, 3485–3497. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, D.; Hu, M.; Guo, D.; He, X.; Lei, Y. Anomalous Winter Temperature and Precipitation Events in Southern China. J. Geogr. Sci. 2009, 19, 471–488. [Google Scholar] [CrossRef]
- Jia, X.; Chen, L.; Ren, F.; Li, C. Impacts of the MJO on winter rainfall and circulation in China. Adv. Atmos. Sci. 2011, 28, 521–533. [Google Scholar] [CrossRef]





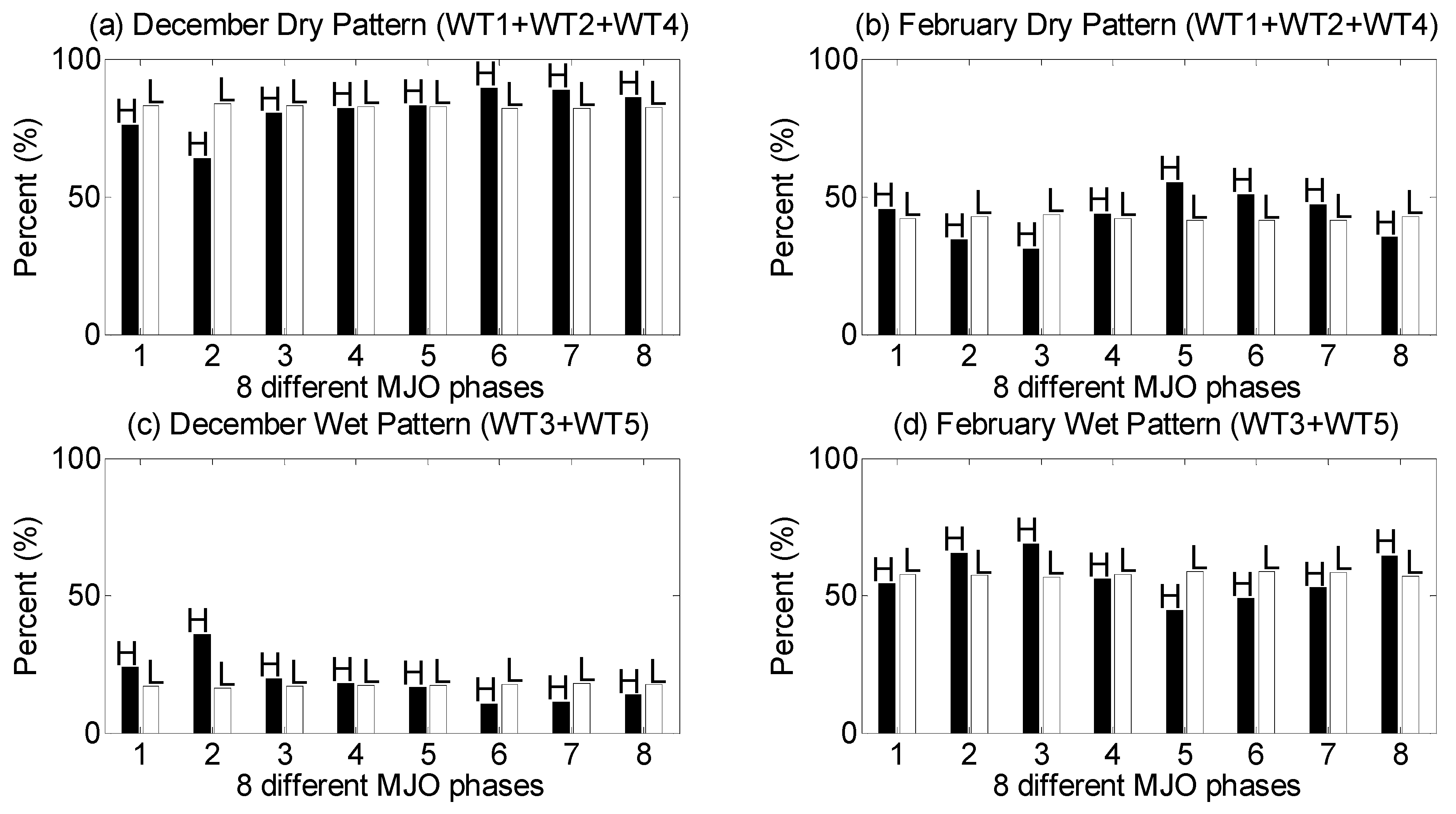
| Category | EA | PNA | WA | WP | EU | ENSO | Frequency | Precipitation |
|---|---|---|---|---|---|---|---|---|
| Dec_ Dry (WT1 + WT2 + WT4) | + | + | + | − | + | − | ↑ | ↓ |
| Feb_ Dry (WT1 + WT2 + WT4) | + | − | − | − | + | − | ↓ | ↓ |
| Dec_ Wet (WT3 + WT5) | − | − | − | + | − | + | ↓ | ↑ |
| Feb_ Wet (WT3 + WT5) | − | + | + | + | − | + | ↑ | ↑ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Jin, S.; Sun, X.; Wang, F. Winter Weather Regimes in Southeastern China and its Intraseasonal Variations. Atmosphere 2019, 10, 271. https://doi.org/10.3390/atmos10050271
Wang Y, Jin S, Sun X, Wang F. Winter Weather Regimes in Southeastern China and its Intraseasonal Variations. Atmosphere. 2019; 10(5):271. https://doi.org/10.3390/atmos10050271
Chicago/Turabian StyleWang, Yongdi, Shuanggen Jin, Xinyu Sun, and Fei Wang. 2019. "Winter Weather Regimes in Southeastern China and its Intraseasonal Variations" Atmosphere 10, no. 5: 271. https://doi.org/10.3390/atmos10050271
APA StyleWang, Y., Jin, S., Sun, X., & Wang, F. (2019). Winter Weather Regimes in Southeastern China and its Intraseasonal Variations. Atmosphere, 10(5), 271. https://doi.org/10.3390/atmos10050271






