1. Introduction
Evaluation of reference evapotranspiration (ETo) plays an important and undeniable role in irrigation scheduling, drought analysis, climate change studies, water level balance, agricultural and forest meteorology, long-term decision-making in food and water security policies, and optimum allocation of water resources [
1,
2,
3]. Although several methods have been developed to predict ETo throughout the world, there is a limited number of models to estimate ETo where meteorological data is restricted or insufficient [
1,
2].
A solution to deal with this limitation is to use data-driven machine learning techniques, particularly genetic approaches, including genetic algorithm (GA) and gene expression programming (GEP). One advantage of the GEP to estimate ETo was that, unlike the artificial neural networks (ANN) method, the GEP generated an explicit model structure that can be easily comprehended and adopted [
3].
The GA and GEP methods have been developed in various aspects of water resources such as streamflow forecasting [
4], rainfall–runoff modeling [
5,
6,
7,
8], modeling transport streams with suspended sediment [
9], predicting velocity in compound channels [
10], characterizing risks in water supply systems [
11], and modeling evaporation [
12].
Although the GEP has been developed in water resources studies, the application of this technique for ETo modeling is limited. Some of the successful applications of the GEP to estimate ETo can be listed as follows.
Parasuraman et al. [
3] modeled ETo using only ground temperature and net radiation. Irmak and Kamble [
13] investigated evapotranspiration data assimilation with the GA and soil, water, atmosphere, and plant (SWAP) model for on-demand irrigation. The data assimilation methodology obtained from the present research can be considered a practical tool at the field scale for scheduling the irrigation estimated by remote sensing-based evapotranspiration. The results showed that the GA was effectively able to determine the terms included in the fitness function, and parameters were predicted reasonably, especially if only four variables were included. Traore and Guven [
14] developed regional-specific numerical models of ETo using the GEP in Sahel. Statistically, the GEP was an effectual modeling tool for the successful computation of ETo under the study area. The results indicated that, using the GEP model, it would be possible to formulate an accurate and applicable numerical equation for each region by irrigation systems for the manual computation of ETo under the study area, where sufficient meteorological variable is often missing. Shiri [
15] claimed that GEP outperforms empirical model to calculate ETo in hyper arid regions over Iran. Traore et al. [
16] found that GEP is a robust tool to model ETo in in Jiangsu province, China. Mattar [
17] demonstrated that GEP is a more accurate method than empirical equations to estimate ETo in Egypt.
Machine learning methods are needed in data sparse regions because Penman–Monteith equation requires a lot of data input, and many places do not have such data. Therefore, achieving similar results with fewer input data is desirable.
In addition, some studies reported greater accuracy of the GA/GEP rather than the ANN [
18,
19,
20,
21], Support Vector Regression (SVR) [
20,
22], Adaptive Neuro-Fuzzy Inference System (ANFIS) [
1,
2,
23], and empirical models [
2,
24].
According to the literature review there are some investigations for which the superiority of the GA and GEP over other techniques such as the ANN, LP, ANFIS, and regression models have been reported. However, genetic approaches have not been simultaneously assessed under various climates. In addition, in most of previous studies, these methods were employed with many input data to estimate ETo. In different parts of the world, there is insufficient meteorological data due to the lack of synoptic stations or other limitations. Therefore, the current research seeks to evaluate ETo in four different climates in Iran to recognize the parameters with the most significant roles in ETo.
2. Materials and Methods
2.1. Designing Structure of Genetic Algorithm (GA) for the Current Research
In most of the previous investigations [
1,
2], a power function is presented as the optimal model to estimate ETo after modifying or calibrating the empirical models. Therefore, in the present research, various functions of the mean temperature (Tmean), maximum temperature (Tmax), minimum temperature (Tmin), relative humidity (RH), wind speed (WS), and sunshine (n) were defined and then combined by using summation and multiplying functions. The goal is to minimize the difference between the current functions with the FAO-Penman–Monteith (FPM) (
Table 1).
In the next step, a GA program was coded in MATLAB environment using the values shown in
Table 2.
2.2. Parameters of Gene Expression Programming (GEP) Employed in the Current Research by Using GeneXpro Tools Version 5.0
Table 3 shows the values of each option employed to design the GEP structures by using GeneXpro Tools version 5.0.
As shown in
Table 3, the population size of 500 is the same as most previous research.
However, different functions are employed to enhance the results and to reduce the uncertainty in the research, and the number of replication is increased (almost 217). As a result, the elapsed time to run the GEP can be prolonged. In addition, the ranking method showed better performance compared to Roulet’s function (a fitness evaluation function).
2.3. Materials
The monthly averages of meteorological data were collocated from the Islamic Republic of Iran Meteorological Organization (IRIMO). These data contain mean, minimum, and maximum daily air temperature (°C), saturated vapor pressure deficit (kPa), mean and minimum relative humidity (%), wind speed (m s
−1) and direction, rainfall (mm month
−1), cloudy days, and sunshine (hr month
−1).
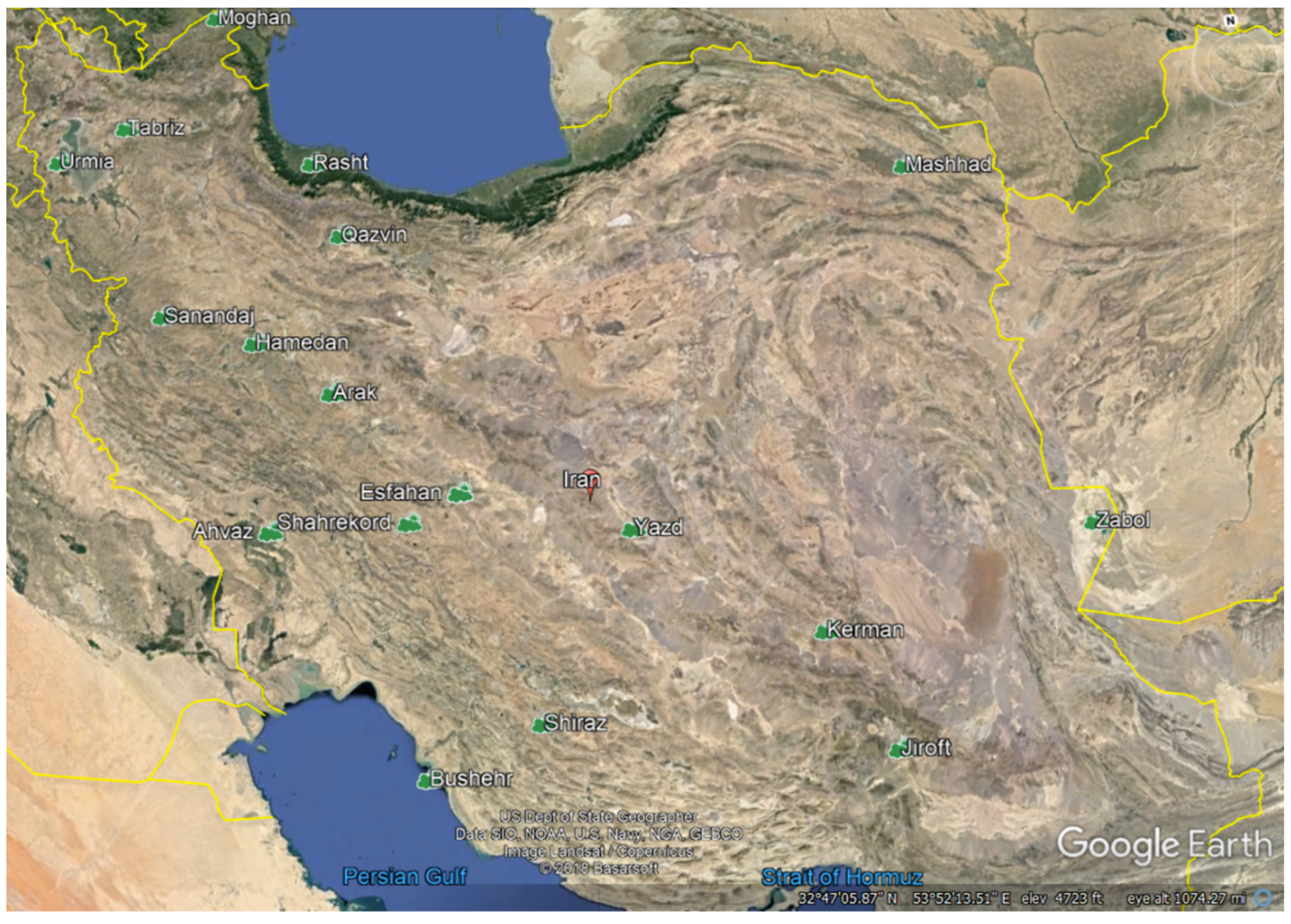
Table 4 shows the position of all 18 synoptic stations and their climates. It should be noted that Iran is in an arid and semiarid zone in Persian Gulf region, and the major part of Iran has the same climate mentioned in
Table 4.
Figure 1 shows location of the weather station in Iran.
Among all stations, there is 50-year period information for 16 regions. The accuracy of the Food and Agricultural Organization of the United Nations (FAO)−Penman−Monteith (FPM) is confirmed for these regions by using lysimeter measurements and with respect to the previous investigations [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34]. In addition, there are 27-year and 21-year period datasets for Moghan and Jiroft, respectively, which due to the availability of lysimeter data, confirms the accuracy of the FPM for these two regions; they were also added to other 16 regions (with 50–year data).
The authors have used the last five years as the testing period and the rest of the data as training period.
Table 5 shows the selected models with their references and parameters.
Among the numerous empirical methods to estimate ETo, nine models were selected that had the best performance under different climates on the basis of previous investigations [
1,
46,
47,
48,
49,
50], and the results were compared with the FPM.
ETo is the reference crop evapotranspiration (mm/day), Rn is the net radiation (MJ/m2/day), G is the soil heat flux (MJ/m2/day), γ is the psychrometric constant (kPa/°C), es is the saturation vapor pressure (kPa), ea is the actual vapor pressure (kPa), Δ is the slope of the saturation vapor pressure–temperature curve (kPa/°C), T is the average daily air temperature (°C), u is the mean daily wind speed at 2 m (m/s), H is the elevation (m), φ is the latitude (rad), Tmin is the minimum air temperature (°C), Tmax is the maximum air temperature (°C), RH is the average relative humidity (%), n is the actual duration of sunshine (hr), Rs is the solar radiation (MJ/m2/day), Ra is the extraterrestrial radiation (MJ/m2/day), λ is the latent heat of vaporization (MJ/kg), and CT, I, KT, a, b, P, at, and Tx are empirical coefficients
Genetic algorithm (GA), genetic programming (GP), and gene expression programming (GEP) are different kinds of data-driven machine learning techniques to find an optimum solution for complex problems by artificial intelligence (AI). In a cell, the expression of the genetic information is an intricate procedure involving more than one hundred molecules. Two of the major players are DNA and proteins. DNA is the carrier of the genetic information and the proteins read and express the genetic information. GA employed biological evolution theory for computer applications (i.e., AI). In fact, GA is an oversimplification of biological evolution [
51]. GP, introduced by [
52,
53], solves the problem of fixed length solutions (as stated for GA) by creating nonlinear entities. Each entity (parse tree) has a distinguished shape and size. GEP is the reliable modification of GP and GA, combining both the methodology of simple, linear chromosomes with fixed length (GA) and branched structures of various sizes and shapes (GP). GEP applies the same type of diagram representation of GP, however the entities (expression trees) evolved by GEP are the expression of a linear genome. The GEP is a constructive approach because the search operators of the GEP may constantly generate valid structures and are highly suited to genetic diversity. The GEP surpasses the old GP system for more than 100 times. In this study, the GA was employed to understand which parameters are more influential on the estimation accuracy of ETo. In addition, the GEP was used to model ETo considering the obtained results by the GA to achieve the maximum accuracy compared with the empirical methods. Therefore, a hybrid data-driven machine learning technique (considering both GA and GEP) was applied to model ETo in various climates.
To evaluate the accuracy of the models two indices were used as follows
where,
Xi and
Yi are the
ith observed and estimated values, respectively;
and
are the mean of
Xi and
Yi; and
N is the total numbers of data.
3. Results
3.1. Performance of Genetic Algorithm (GA) for Different Parameters
Table 6 shows that although GA8 (combination of all parameters) was obtained with the highest accuracy (RMSE = 0.3030 mm day
−1) in Iran (average), it requires four parameters: Tmean, RH, WS, and n. On the other hand, GA5 is also obtained, which is approximately equal to GA8 (RMSE = 0.3263 mm day
−1) with less input data (only Tmean and WS). Meanwhile, GA5 estimated ETo throughout Iran with more accuracy than GA2, GA3, and GA4. This means that the WS was introduced as the most important factor (after Tmean) to control the dynamics of ETo process throughout Iran.
Table 6 reveals that a function of the Tmean and WS may predict ETo with acceptable accuracy. Therefore, this result is the basis for the development of the genetic models using the GEP. However, the Tmean is the first parameter to be measured in each station or region. Hence, the Tmean is considered as the input parameter in the entire GEP models in this study.
3.2. Performance of Gene Expression Programming (GEP) for Mean Temperature (Tmean) as Input Data
In the first step of the GEP—ETo—was estimated in all 18 stations using only the Tmean and then compared with the FPM (
Table 7).
According to
Table 7, the best performance of the GEP belongs to Rasht (RMSE = 0.1100 mm day
−1), while, the worst accuracy was reported for Zabol (RMSE = 0.8229 mm day
−1). In 56% of regions the GEP was obtained with a RMSE < 0.3000 mm day
−1. Furthermore, the natural logarithm (ln) function was employed more than sinus, cosines, and particularly exponential functions in the GEP structures. It means that we can expect to have logarithmic relationship between ETo and Tmean more than other kinds of functions. Moreover, plus and minus functions were used more than multiplication and specially division.
3.3. Performance of Gene Expression Programming (GEP) for Mean Temperature (Tmean), Minimum Temperature (Tmin), and Maximum Temperature (Tmax) as Input Data
In the second step of the GEP, ETo was estimated in all 18 stations using the Tmean, Tmin, and Tmax was then compared with the FPM.
The results reveal that the best performance of the GEP belongs to Rasht (RMSE = 0.0884 mm day−1), while the worst accuracy was reported for Zabol (RMSE = 0.8020 mm day−1). In 61% of regions the GEP was obtained with a RMSE < 0.3000 mm day−1. Furthermore, sine and cosine functions were employed more than the natural logarithm (ln) and particularly exponential functions in the GEP structures. It means that we can expect to have periodic relationship between ETo and temperature more than other kinds of functions. Moreover, plus and minus functions were used more frequent than multiplication sign and particularly division sign. In all regions, the accuracy was improved compared to the GEP models based on the Tmean only.
3.4. Performance of Gene Expression Programming (GEP) for Mean Temperature (Tmean) and Wind Speed (WS) as Input Data
With respect to
Table 6, WS was introduced as the most important factor to control the variations of ETo. Thus, in the third step of GEP, ETo was estimated in all 18 stations using the Tmean, and WS was then compared with the FPM (
Table 8).
Table 8 represents that the best performance of the GEP belongs to Shahrekord (RMSE = 0.0650 mm day
−1), while the worst accuracy was reported for Kerman (RMSE = 0.4177 mm day
−1). In 83% of regions the GEP resulted with a RMSE < 0.2000 mm day
−1. Furthermore, the natural logarithm (ln) function was employed more than sinus, cosines, and particularly exponential functions in the GEP structures. Moreover, plus and minus functions were used more than multiplication sign and specially division. In all regions (with the exception of Rasht), the accuracy was improved compared to the GEP models based on the Tmean, Tmin, and Tmax. Therefore, for Rasht, wind speed is not required. It may correspond to minimum diurnal temperature rate (DTR) in very humid regions compared to other climates (role of relative humidity and saturated vapor pressure). However, wind speed-based GEP models predicted ETo in arid, semiarid, and Mediterranean climates more accurate than the other models.
It should be noted that the arctan has not acceptable accuracy compared to other functions. In addition, the results represent that ln and exp functions have a better performance than sine and cosine functions. Therefore, in future investigations, we can more focus on other functions than arctan. In addition, we can expect to have logarithmic relationship between ETo and temperature/wind speed more than other kinds of functions.
The obtained results are comparable and sometimes better than those reported by Wang et al. [
54]. They resulted RMSE between 0.222 to 0.555 mm day
−1. In addition, Mehdizadeh [
55] reported RMSE for GEP models from 0.46 to 2.08 mm day
−1.
3.5. Performance of Gene Expression Programming (GEP) for Mean Temperature (Tmean), Wind Speed (WS), and Relative Humidity (RH) as Input Data
The results of the GA revealed that use of the RH and n do not increase accuracy of the GEP significantly (
Table 6). This is also confirmed by the GEP.
According to the results, the best performance of the GEP was for Esfahan (RMSE = 0.0730 mm day−1), while the worst accuracy was reported for Kerman (RMSE = 0.4252 mm day−1). In 89% of regions the GEP resulted with a RMSE < 0.2000 mm day−1. Furthermore, sinus and cosines functions were employed more than the natural logarithm (ln) and particularly exponential functions in the GEP structures. Moreover, plus and minus functions were used more than multiplication sign and specially division.
A comparison of
Table 8 indicates that adding the RH as input parameter not only did not increase the GEP’s accuracy, but also led to the reduction in the accuracy relevant to 56% of the regions. In addition, the improvements are inconsiderable. It should be noted that the best structures of the GEP are not a function of the RH in 44% of the regions (Arak, Bushehr, Mashhad, Moghan, Qazvin, Sanandaj, Shahrekord, Shiraz, Tabriz, and Yazd). It is an important result and confirms that the Tmean and WS have more value to be used as input variable for the GEP compared to the RH.
3.6. Accuracy of Empirical Models Against Gene Expression Programming (GEP)
Figure 2 and
Figure 3 show that the best empirical models with respect to the smallest RMSE values for estimating ETo on a monthly scale lack a good performance at annual scale and this is alarming considering the importance of the agricultural water management to deal with water crisis in the world. However, the GEP may predict ETo in the most regions of Iran with considerable accuracy.
In arid regions (
Figure 2), the best accuracy belongs to Esfahan (R
2 = 0.9217) and the worst accuracy belongs to Kerman (R
2 = 0.3636), due to poor performance of the GEP for peak events in this region. In the semiarid regions (
Figure 3), the best accuracy belongs to Shahrekord (R
2 = 0.9403) and the worst accuracy belongs to Hamedan (R
2 = 0.8049).
The obtained results are comparable and sometimes better than those reported by Wang et al. [
54]. They resulted R
2 between 0.639 to 0.944. In addition, Mehdizadeh [
55] reported R
2 for GEP models from 0.084 to 0.969.
4. Discussion
The current research shows that the GEP is a robust tool to model ETo in semiarid and Mediterranean climates (R2 > 0.80). However, the use of the GEP should be recommended cautiously in Rasht, Bushehr, and Kerman (R2 < 0.50) due to its poor performance in extreme events of these areas. To enhance the accuracy of the GEP in extreme values, use of hybrid methods (coupling GEP with ANN, fuzzy logic, honey bee algorithm, etc.) can be recommended.
The results of this study has a potential to be compared with real data. However, reference evapotranspiration (ETo) refers to maximum evapotranspiration in the best growing conditions of a crop without any limitation (drought and salinity stresses). However, plant requirements evapotranspiration (actual evapotranspiration) refers to actual conditions of a crop in the field considering all limitations. Therefore, it is not acceptable to compare these to variables. To this end, a crop coefficient (Kc) must be considered to characterize actual evapotranspiration (ETa); Eta = Kc × ETo.
Considering complex processes of evapotranspiration, there are many difficulties to measure this parameter. Some of the methods for this end are lysimeter, remote sensing, eddy covariance, and Bowen ratio. Allen et al. [
35] determined an accurate model (FPM) which has the highest adaptability with lysimeter measurements in all over the world. Therefore, in this study, such as most of previous investigations [
13,
18,
19,
20], the authors compared the outputs of the GEP with the FPM and the results (
Figure 1 and
Figure 2) appear that the accuracy of the GEP has been improved compared to empirical models.
It should be noted that we cannot see similar results for the stations. In fact, all the results are completely independent of each other. This is in line with previous investigations [
1,
2].
It is notable that, in future research, the findings obtained from the GEP models in comparison to what is noted in the biological literature as affecting this process, should be checked to achieve a reliable result to recommend the GEP for other regions and research.
The GEP has worse performance over extreme conditions. The reason is related to the structure of GEP models. In this study, the authors focused on the models in which we need one or two weather parameters (mean temperature and mean wind speed) to estimate ETo. However, in extreme conditions, sometimes other variables, like maximum and minimum temperatures, maximum wind speed, rainfall, minimum humidity, solar radiation, and vapor pressure deficit, are also important. Therefore, if we are looking to increase the accuracy of GEP model we should consider more variables. However, in many regions we have no access to all of weather parameters to apply them to support GEP models to estimate ETo.
The next step of this study is to train the GA/GEP using ETo calculated at one site with all the meteorological variables available. Then, use the resulting functions to estimate ETo at a site where there are insufficient meteorological variables. Indeed, if we do have enough meteorological information to calculate ETo, we can then train the GA/GEP on fewer input variables.
5. Conclusions
In this study, the capability of both GA and GEP was assessed using 50-year time series data under 18 regions in Iran with arid, semiarid, very humid, and Mediterranean climates. The GA suggested that use of a double-parameter basis including the Tmean and WS may predict ETo with good accuracy in arid, semiarid, and Mediterranean regions. However, in very humid regions, temperature-based models (Tmean, Tmax, and Tmin) are better alternatives to reduce uncertainty. Finally, the GEP is recommended to evaluate the annual dynamics of ETo process in arid, semiarid, and Mediterranean climates with reliable accuracy under conditions where meteorological information is limited. In this study, we represented the best structures of GEP models. In future research, when a researcher or expert is going to use an accurate model based on this study, s/he may employ the best structures of GEP whose have been considered for his/her climate region.