Next Article in Journal
Sources of Particulate Matter in the Hunter Valley, New South Wales, Australia
Next Article in Special Issue
Southern Hemisphere Sensitivity to ENSO Patterns and Intensities: Impacts over Subtropical South America
Previous Article in Journal
Estimating Ensemble Flood Forecasts’ Uncertainty: A Novel “Peak-Box” Approach for Detecting Multiple Peak-Flow Events
Previous Article in Special Issue
Tropical Atlantic Variability: Observations and Modeling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 11
Issue 1
10.3390/atmos11010003
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analyzing the Influence of the North Atlantic Ocean Variability on the Atlantic Meridional Mode on Decadal Time Scales

by
Sandro F. Veiga
1,*,
Emanuel Giarolla
2,
Paulo Nobre
3 and
Carlos A. Nobre
4
1
Earth System Science Center-CCST, National Institute for Space Research (INPE), 12227-010 São José dos Campos, Brazil
2
Center for Weather Forecasting and Climate Studies-CPTEC, National Institute for Space Research (INPE), 12227-010 São José dos Campos, Brazil
3
Center for Weather Forecasting and Climate Studies-CPTEC, National Institute for Space Research (INPE), 12630-000 Cachoeira Paulista, Brazil
4
Institute for Advanced Studies (IEA), University of São Paulo (USP), 05508-050 São Paulo, Brazil
*
Author to whom correspondence should be addressed.
Atmosphere 2020, 11(1), 3; https://doi.org/10.3390/atmos11010003
Submission received: 16 August 2019 / Revised: 30 September 2019 / Accepted: 2 October 2019 / Published: 18 December 2019
(This article belongs to the Special Issue Tropical Atlantic Variability)
Browse Figures
Versions Notes

Abstract

:
Important features of the Atlantic meridional mode (AMM) are not fully understood. We still do not know what determines its dominant decadal variability or the complex physical processes that sustain it. Using reanalysis datasets, we investigated the influence of the North Atlantic Ocean variability on the dominant decadal periodicity that characterizes the AMM. Statistical analyses demonstrated that the correlation between the sea surface temperature decadal variability in the Atlantic Ocean and the AMM time series characterizes the Atlantic multidecadal oscillation (AMO). This corroborates previous studies that demonstrated that the AMO precedes the AMM. A causal inference with a newly developed rigorous and quantitative causality analysis indicates that the AMO causes the AMM. To further understand the influence of the subsurface ocean on the AMM, the relationship between the ocean heat content (0–300 m) decadal variability and AMM was analyzed. The results show that although there is a significant zero-lag correlation between the ocean heat content in some regions of the North Atlantic (south of Greenland and in the eastern part of the North Atlantic) and the AMM, their cause-effect relationship on decadal time scales is unlikely. By correlating the AMO with the ocean heat content (0–300 m) decadal variability, the former precedes the latter; however, the causality analysis shows that the ocean heat content variability drives the AMO, corroborating several studies that point out the dominant role of the ocean heat transport convergence on AMO.

1. Introduction

The last four decades of climate research have revealed the influence of the ocean-atmosphere coupled system variability within the tropical Atlantic basin on the observed climate conditions in the adjacent continental regions [1,2,3,4,5,6]. Recent studies have also shown that atmospheric perturbations generated in this region by the ocean-atmosphere coupled variability act as forcing conditions on the El Niño–Southern oscillation (ENSO) [7,8,9,10], Pacific meridional mode [11], North Atlantic oscillation (NAO) [10,12], and Indian monsoon [13,14]. Therefore, a more accurate understanding of the tropical Atlantic variability could improve climate prediction over the adjacent regions, benefiting their populations, and, from a broader perspective, deepen our understanding of the interactions between the tropical Atlantic variability and diverse large-scale phenomena.
Tropical Atlantic ocean-atmosphere coupled variability is characterized by the Atlantic zonal mode (AZM) [15] and the Atlantic meridional mode (AMM) [4,16]. The former presents an interannual periodicity and impacts the precipitation regime in the West African region [15,16,17], whereas the latter presents interannual and decadal periodicities that impact the precipitation regimes in northeastern Brazil [1,4,18] and West Africa [2,3]. The AMM manifests as an interhemispheric sea surface temperature anomaly (SSTA) gradient that is coupled to anomalous cross-equatorial low-level winds that modulate the intertropical convergence zone (ITCZ) towards the positive lobe of the SSTA gradient [4,16,19,20,21]. The physical mechanism that initiates and sustains the AMM is known as wind-evaporation-SST positive feedback (WES feedback) [19,20,22], a thermodynamic coupling between the low-level wind speed, the sea surface evaporation induced by the wind stress, and the SSTA. Several studies have shown that external forcing excites the AMM. The ENSO impacts the tropical North Atlantic (TNA) SSTAs by inducing anomalous surface latent heat flux, particularly via the Pacific–North America teleconnection pattern [4,23], as well as via changes in the Walker and Hadley tropical circulation cells [24,25]. These TNA SSTAs can propagate equatorward via the WES feedback, potentially generating an AMM in the tropical Atlantic [26,27,28,29]. The ENSO influence dominates on interannual time scales [30,31,32,33]. During similar physical processes, the NAO can excite the AMM via its southern lobe (the Azores high) [16,31,34,35,36]. Although the AMM is characterized by interannual and decadal time scale periodicities, the decadal periodicity, with a spectral peak at ~11–13 years, is the dominant temporal pattern [37,38]. Despite significant advances in our understanding of the AMM features, the basis for its dominant decadal variability remains to be explained [39].
The multidecadal variability of the SSTAs in the North Atlantic, known as the Atlantic multidecadal oscillation (AMO), is also statistically linked to the AMM on decadal time scales. Based on a lead–lag correlation analysis of their low-pass filtered time series, Vimont and Kossin [40] found that the AMO is maximally correlated with the AMM when the former leads by roughly a year, suggesting that the AMO can excite the AMM on decadal time scales. A lead–lag relationship between the Atlantic high-latitude SSTAs and the AMM has also been highlighted [41,42], although Vimont [42] points out that the mechanism underlying this link is unclear. Since a lead–lag statistical relationship is not solid proof of causality between two phenomena, we can propose hypotheses based on two scenarios: that the AMO induces mechanisms that modulate the AMM on decadal time scales or that a third variability excites both the AMO and AMM on decadal time scales. The ocean dynamics in the North Atlantic exhibit a complex behavior that is most strongly influenced by the dominant imprint of the different components of the Atlantic Meridional Overturning Circulation (AMOC), as the thermohaline circulation (THC) and wind-driven circulations, which includes the subtropical, subpolar gyres and Ekman transport [43]. The upper limb of the AMOC is responsible for the poleward heat transport in the Atlantic Ocean that impacts the SSTAs variability in the North Atlantic [44], manifested as the AMO [45,46] and the ocean heat content variability in the upper layers on decadal to multidecadal time scales [47,48,49]. In this paper, the relationship between the SSTAs over the Atlantic Ocean and the AMM on decadal time scales is investigated using the traditional lead–lag correlation analysis and a newly developed causality analysis that is capable of inferring the causal relationship between two time series in a rigorous and quantitative sense [50,51]. Next, the same methodologies are used to analyze the relationships between the AMM and the ocean heat content in the upper 300 m (OHC300) and the SSTAs and OHC300 on decadal time scales to investigate whether the OHC300 variability over the North Atlantic modulates both phenomena or not.

2. Data and Methodology

2.1. Data

For these analyses, the SST data are taken from the extended reconstructed sea surface temperature version 4 (ERSSTv4) [52], which has a 2° × 2° horizontal global resolution covering 1854 to the present. The wind components at 10 m are taken from the 20th century reanalysis dataset version 2 (20CRv2) [53], which has a global horizontal resolution of 2° × 2° covering 1871 to 2012. The OHC300 has been obtained from the Centro Euro–Mediterraneo sui cambiamenti climatici (CMCC) historical pcean reanalysis (CHOR_RL) [54], which covers the period 1900–2010. Since the original OHC300 dataset is not in a regular grid resolution, the data has been interpolated into a 1° × 1° grid resolution. The CHOR_RL reanalysis assimilates vertical profile data by being nudged to monthly Hadley Centre global sea ice coverage and SST (HadISST) reconstructed fields, while the atmospheric forcings are from the 20CRv2 reanalysis [54].

2.2. Methodology

In all of the analyses, we used a detrended monthly anomalies dataset covering the period 1900–2010. The anomalies were obtained by removing the annual cycle via subtraction of the climatological monthly means from the respective individual months. The detrended datasets were obtained by removing the linear trend based on a least-squares regression. To compute the AMM, we followed the methodology proposed by Chiang and Vimont [16] and Amaya et al. [55]. The AMM was obtained by performing a maximum covariance analysis (MCA) [56] using the SST and 10-m wind components over the tropical Atlantic region (30° S–30° N). The MCA consisted of applying singular value decomposition on the cross-covariance matrix between anomalies in the SST and 10-m wind components, which yielded a two time series (known as expansion coefficients) (Figure 1b) related to the SST (AMM-SST) and 10-m wind components (AMM-Wind). We obtained the regression map by projecting the original SST and 10-m wind anomaly components at each grid point onto the AMM-SST expansion coefficient (Figure 1a), which in this case represents the leading zero-lag coupled variability between SST and 10-m wind. Figure 1c shows the predominant decadal timescale variability (11–13 years) of the AMM determined via a power spectral analysis of the AMM-SST time series; a similar result was observed using AMM-Wind time series (not shown). Detailed discussions of the features that characterize the AMM are presented in Chiang and Vimont [16] and Amaya et al. [55]. Although the datasets and period analyzed differ from those used in these references, the results are similar, with a correlation of 0.90 between the AMM-SST computed here and that computed by Chiang and Vimont [16] over the period 1948–2010. Before applying the MCA, the datasets were processed in several ways. First, the 10-m wind components were interpolated into SST grid resolution, and the SST and 10-m wind components were smoothed via a three-month running mean at each grid point. Second, the linear ENSO influence was removed by removing the cold tongue index (CTI; SSTAs averaged over the Pacific regions from 6° S–6° N to 180°–90° W) at each grid point based on a least-squares regression. Finally, each field was normalized to its corresponding long-term standard deviation at each grid point.
Since we are interested in understanding the decadal variability relationship between the AMM and other variables, all of the analyses are performed using low-pass filtered datasets. Following Zhang et al. [57] and Vimont [58], to filter the high-frequencies, 25- and 37-month running means were successively applied to the AMM-SST expansion coefficient and to each grid point of the OHC300 and SST fields. Figure 1 of Vimont [58] shows the filter amplitude response function of such a low-pass filter. Throughout this paper, the AMM-SST expansion coefficient was used to characterize the AMM temporal variability.
The analyses performed in this paper are mainly based on the statistical relationship between the variabilities reflected by correlation spatial patterns and time series lead–lag correlations. Since these methods do not prove causality between the analyzed variabilities, a more rigorous method has been applied to reinforce the conclusions. In a newly developed method, the causality analysis between two time series is measured as the rate of information flowing from one time series to the other computed via the following equation:
T 2 → 1 = C 11 C 12 C 2 , d 1 − C 12 2 C 1 , d 1 C 11 2 C 22 − C 11 C 12 2 ,
in which C i j ( i , j = 1 , 2 ) is the sample covariance between two time series ( X i and X j ) and C i d j is the sample covariance between X i and X ˙ j = X j , n + 1 − X j , n ∆ t , with ∆ t being the time step size. The units are natural unit of information (nats) per unit time. Ideally, if | T 2 → 1 | ≠ 0 , then X 2 is causal to X 1 , otherwise it is noncausal. In practice, statistical significance must be tested. To assess whether the results are different from zero, significance test were carried out at the 95% confidence level. Equation (1) is the maximum likelihood estimator of a rigorously derived physical formula from first principles. A negative value of T 2 → 1 means that X 2 makes X 1 more uncertain, while a negative value means that X 2 makes X 1 more stable. A detailed description of the method and its theoretical basis can be found in Liang [50,51]. As example of climate variability application, Liang [50] tested the Equation (1) to analyze the causality relationship between the El Niño/La Niña and the Indian ocean dipole (IOD) over the period 1958–2010. The results showed that the flow of information from El Niño to IOD was T N i n o → I O D = − 6 × 10 − 3 nats/month, while the flow of information from IOD to El Niño was T I O D → N i n o = 13 × 10 − 3 nats/month. This means that both phenomena are mutually causal, in which El Niño tends to stabilize IOD and IOD tends to make El Niño more uncertain. Stips et al. [59] used this technique to investigate the relationship between the global CO2 radiative forcing and the global mean surface temperature anomalies (GMTA) over the period 1850–2005. The authors show that T C O 2 → G M T A = 0.316 ± 0.108 nats/year, while T C O 2 → G M T A = 0.003 ± 0.003 nats/year. Here, the values 0.108 and 0.003 represent the confidence interval significant at the 95% level. Therefore, based on this new technique, such one-way causality between the CO2 and GMTA adds more evidence supporting anthropogenic climate change in the last decades. This technique has been used to study climatological change patterns over Southeast Asia [60,61].
Two-tailed Student’s t-tests with an effective number of degrees of freedom Neff given by the approximation:
1 N e f f ( j ) ≈ 1 N + 2 N ∑ j = 1 N N − j N ϱ x x ( j ) ϱ y y ( j ) ,
in which N is the sample size and ϱ x x ( j ) and ϱ y y ( j ) are the autocorrelations of two sampled time series X and Y at time lag j were used to assess the statistical significance of correlations between two autocorrelated time series, as are present in the low-pass filtered datasets [62,63,64]. Correlation coefficients were considered significant at the 95% confidence level.

3. Results and Discussion

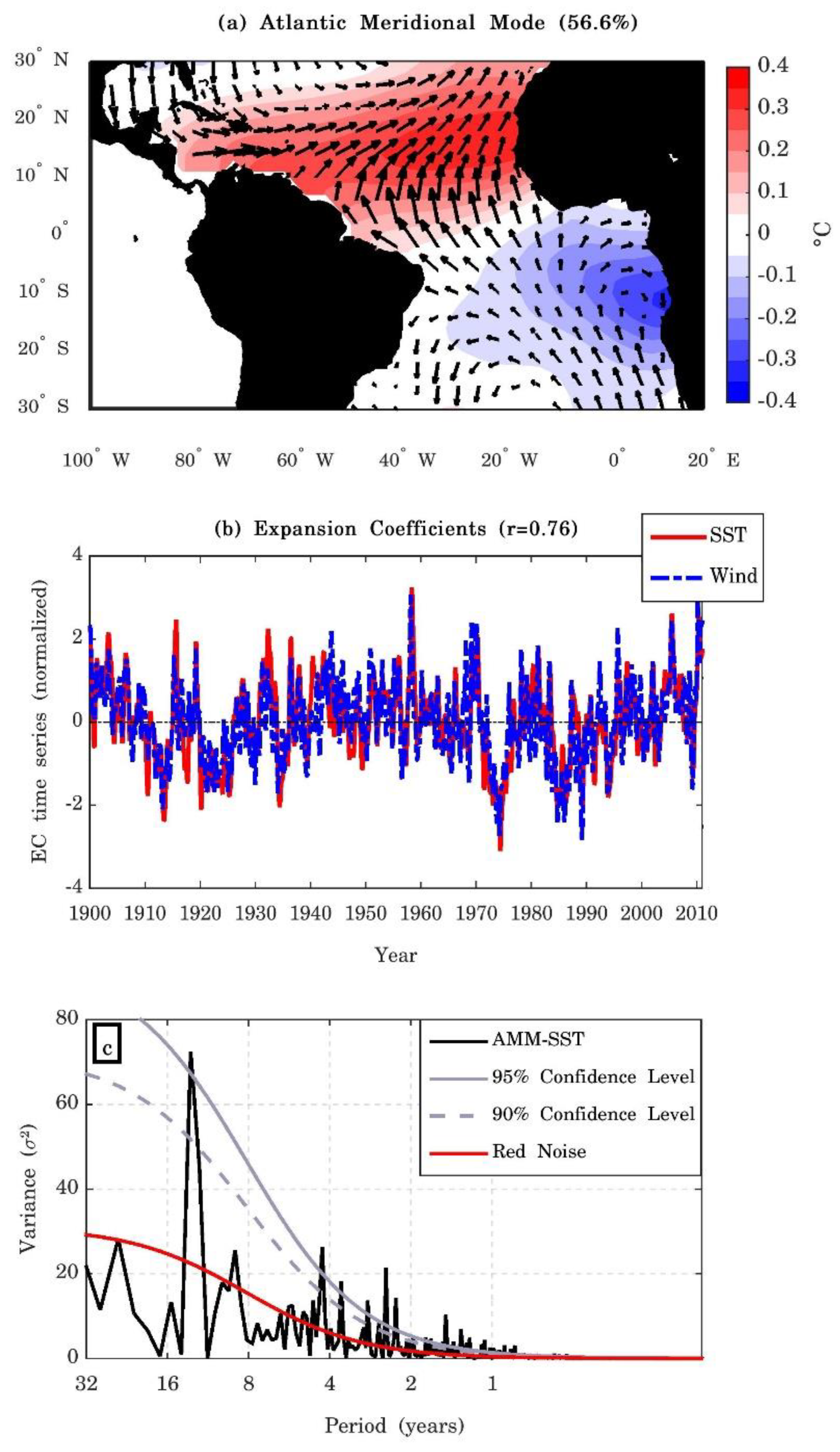
3.1. Relationship between the AMM and SSTAs

Vimont and Kossin [40] found a strong correlation between the AMM and AMO for the period 1950–2005, with a maximum of ~0.82 when the AMO led the AMM by one year (using low pass-filtered yearly data). Here, by analyzing the correlation between the AMM-SST and the SSTA variability at each grid point over the Atlantic basin, we identified a significant positive spatial correlation pattern in the south of Greenland where the AMO peaks (black box, Figure 2a). Since the SSTAs over the south of Greenland resembles an AMO-like variability, as defined by Goldenberg et al. [65], we will use the term AMO for simplicity.
Moreover, when taking the entire Atlantic basin into consideration, the pattern resembles the pan-Atlantic pattern [34], with significant positive correlations in the tropical North Atlantic (TNA), significant negative correlations in the center of the tropical South Atlantic (TSA), and significant positive correlations in the western part of the subtropical South Atlantic. Nevertheless, it should be noted that the significant correlations in the TNA and TSA are expected since the AMM-SST index was taken from this region. To analyze the relationship between the AMM and the SSTAs over the south of Greenland, an index was defined based on the spatially averaged SSTAs for the region to the south of Greenland (10°–50° W; 50°–65° N; black box). The unfiltered and low-pass filtered time series of the AMM-SST and AMO are shown in Figure 2b. The relationship reported by Vimont and Kossin [40] is corroborated by the lead–lag correlation between the AMM-SST and AMO on a decadal time scale, in which the AMO leads by two to three months with clear persistence (Figure 2c). Nevertheless, a maximum correlation of only 0.55 was observed for the period 1900–2010, while the correlation for the period 1950–2010 increased to 0.77.
The difference between the correlations of the two periods is likely related to the lack of quality of the dataset prior 1950. For instance, the reconstruction of the monthly ERSSTv4 SST is based on measurements from in situ buoy and ship observations from 1875 to present and then processed by a sophisticated statistical analysis (empirical orthogonal teleconnections) [52]. Therefore, due to sparser observations prior 1950, it is likely that the accuracy of the SST dataset was affected. This lead–lag relationship is not proof of cause-effect relationship. Thus, the causality analysis (Equation (1)) was applied to both time series.
The rate of information flow from the AMO to the AMM-SST ( T A M O → A M M ) was 0.003 ± 0.001 nats/month, which indicates a cause-effect relationship between the two variabilities. The rate of information flow from the AMM-SST to the AMO ( T A M M → A M O ) was not significantly different from zero at a 95% confidence level, with a value of 0.0004 ± 0.001 nats/month, which indicates no causation, as expected from the correlation analysis. Based on this result, the AMO appears to be part of a mechanism that potentially forces the AMM on decadal time scales. The study of such mechanism would not be explored here, but we should highlight that several studies have pointed out the NAO as an external forcing of the AMM [16,31,34,35,36], hence the connection between AMO and NAO is a potential candidate for the mechanism. Nevertheless, the connection between AMO and NAO is highly complex and remain to be fully understood.
Based on observational datasets, Guan and Nigam [66] reports that the two modes have different temporal variability and they are essentially uncorrelated. On the contrary, recent study have reported their connection, in which the AMO positive phase leads to a negative phase of the NAO in winter [67]. In a multi-model study, Ba et al. [68] shows that the AMOC is the main driver of the AMO but found no linear link on decadal time scales between AMOC and NAO. However, there are modeling studies that find a link between the SSTAs and NAO based on feedback processes between atmosphere and ocean [69,70,71], which implies that the results are model dependent. For instance, Wen et al. [72] used a climate model and found that there is a coupled variability of AMOC and NAO in decadal time scale. This coupling is more effective when compared with the simulations produced by the same with lower resolution.

3.2. Relationship between the AMM and OHC300

As shown in the previous section, the SSTAs variability in the subpolar North Atlantic leads the AMM on a decadal time scale, while the causality analysis is supported by the cause-effect relationship. Nonetheless, we can hypothesize that the ocean subsurface variability in the North Atlantic also exerts influence on the AMM on decadal time scales. A rich body of studies has linked the AMO to the strength of the AMOC, in which the northward transport of warm waters in the upper layers driven by the AMOC impacts the SSTs in the North Atlantic and, together with air-sea heat flux processes, imprints its multidecadal variability [45,73,74,75]. A stronger AMOC leads to warmer SSTs (AMO positive phase) and a weaker AMOC leads to cooler SSTs (AMO negative phase) in the North Atlantic [73]. In general, SSTs are influenced by the ocean-atmosphere interactions on shorter time scales and by large-scale oceanic circulation on longer time scales [76]. Here, our hypothesis assumes that the AMOC can also be an external forcing of the AMM, as it is on the AMO. However, this analysis focuses on the decadal variability of the northward heat transport in the upper layers of the ocean driven by the AMOC over the entire Atlantic basin and not on the strength of the AMOC defined by the latitude/depth plane [77]. The decadal OHC300 is assumed to be an indicator of the decadal variability of the northward heat transport in the upper layers of the ocean. Seidov et al. [48] shows that the decadal OHC is correlated with decadal AMO in the North Atlantic. Nevertheless, the AMOC variability may differentially affect the OHC300 in various North Atlantic regions [48,49]. Zhang [49] shows that the AMO is positively correlated with higher ocean subsurface temperatures in subpolar regions and negatively correlated with ocean subsurface temperatures in the Gulf Stream pathway. The OHC is the integrated ocean temperature at depth, and its anomalies can persist for long periods (from months to years) and potentially imprint an influence on the overlying ocean surface on lower frequencies [78].
To investigate the link between the AMM and Atlantic OHC300 variability on a decadal time scale, we performed an analysis of the zero-lag correlation between low-pass filtered AMM-SST and OHC300 data at each grid point over the Atlantic basin. The spatial correlation pattern is illustrated in Figure 3a. The most extensive areas showing a significant correlation between the AMM-SST and OHC300 lay to the south of Greenland (50°–60° N), extending zonally, and in the subtropical to mid-latitudes in the eastern Atlantic region (5°–35° W; 30°–45° N). In both cases, significant positive correlations indicated that the AMM positive phase correlated with increases in the OHC300 in these regions on a decadal time scale. To further understand the nature of these correlations, two indices were defined based on the spatially averaged OHC300 data for each region, i.e., to the south of Greenland (10°–50° W; 50°–65° N; black box) and in the eastern North Atlantic (10°–30° W; 30°–40° N; purple box), which are called the OHC300-SG and OHC300-ENA indices, respectively. The unfiltered and low-pass filtered time series of the AMM-SST with OHC300-SG and OHC300-ENA are shown in Figure 3b,d, respectively. The lead–lag correlation between the AMM-SST and OHC300-SG shows a slightly antisymmetric structure in which the AMM-SST leads by five to six months (Figure 3c). This result suggests that the OHC300 variability to the south of Greenland does not exert any influence on the AMM variability on a decadal time scale. Concerning the OHC300-ENA, the lead–lag correlation with the AMM-SST shows a symmetric structure around zero lag, suggesting that it was unlikely that the OHC300 variability in the eastern North Atlantic was an AMM forcing (Figure 3e). The same analysis was performed using unfiltered data showed similar results (not shown). Nevertheless, despite the symmetric structure, Figure 3e shows a higher persistence associated with the OHC300 leading. If the OHC300 variability over this region preconditions the AMM phases, it would likely occur via the OHC300 influence on the SSTAs persistence that ultimately affect lower atmosphere, potentially generating conditions to trigger the WES feedback process. Hasanean [79] shows that SSTAs over the tropical North Atlantic influence the sea level pressure of the subtropical high, which leads to trade wind variations that can then influence the SSTAs over the same region. Therefore, to reinforce our conclusion, the causality analysis was applied to the AMM-SST and OHC300-ENA time series. The rate of information flow from the OHC300-ENA to the AMM-SST ( T O H C 300 → A M M ) was −0.0011 ± 0.0017 nats/month, a value that is not significantly different from zero at 95% confidence level, indicating no cause-effect relationship between the two variabilities. The information flow rate from the AMM-SST to the OHC300-ENA ( T A M M → O H C 300 ) also implied no cause-effect relationship, with a value of 0.0002 ± 0.0013 nats/month (not significantly different from zero at 95% confidence level). This result suggests that the AMM decadal variability was not influenced by the decadal variability of the OHC300 in the Atlantic basin.
From Figure 2a and Figure 3a, we observed that both SSTAs and OHC300 variabilities to the south of Greenland significantly correlated with AMM-SST. To analyze the SSTAs and OHC300 relationship, the zero-lag correlation between the OHC300 and the SSTA at each grid point over the Atlantic basin was performed (Figure 4a). For this analysis, the OHC300 dataset was interpolated into the resolution of the SST grid points. The OHC300 was strongly correlated with the SSTAs in the North Atlantic and subpolar eastern North Atlantic. There was also a large area with significant correlations in the western mid-latitudes of the South Atlantic. The unfiltered and low-pass filtered time series for the SSTA (AMO) and OHC300-SG calculated based on the same index region to the south of Greenland are shown in Figure 4b; the respective lead–lag correlations on a decadal time scale are shown in Figure 4c. The SSTA led the OHC300 by roughly 12–15 months. A similar result was reported by Hazeleger et al. [80]. This result suggests that the OHC300 does not lead the SSTAs variability in the region. However, a deeper understanding of their relationship was provided by the causality analysis. The information flow rate from the SSTA to the OHC300 ( T A M O → O H C 300 ) was 0.0083 ± 0.0011 nats/month (significantly different from zero at 95% confidence level) and, on the opposite direction, the information flow rate from the OHC300 to the SSTA ( T O H C 300 → A M O ) was −0.0064 ± 0.0013 nats/month (significantly different from zero at 95% confidence level). The asymmetric causality relationship suggests that the OHC300 stabilized the SSTAs over the subpolar North Atlantic, therefore enhancing the AMO persistence, while the SSTAs variability made the OHC300 variability more uncertain. The result suggests that the OHC300 stabilizes the AMO is in accordance with several studies that reported the dominant role of the ocean heat transport convergence on the AMO [81,82,83]. However, ocean-atmosphere interaction may also play an important role, since dynamic coupling between atmospheric and oceanic circulation patterns appears to be key component modulating the complex processes underlying the North Atlantic SSTAs variability, as recent studies have indicated [84].

4. Conclusions

This article reexamines the link between the AMO and AMM on decadal time scales. The spatial correlation between the variability in the SSTA over the Atlantic basin and the AMM on decadal time scales are more significantly correlated in the region in which the AMO exhibits highest variability (south of Greenland). The SSTA variability over this region leads the AMM by two to three months. These results corroborate the conclusions of Vimont and Kossin [40]. However, such a relationship could indicate that either the AMO modulates the AMM on decadal time scales or that both variabilities are influenced by a third phenomenon. Based on a newly developed causality analysis method, we showed indications that the AMO has causal influence on the AMM on decadal time scales.
We also investigated whether the variability in the ocean heat content in the upper 300 m (OHC300) over the North Atlantic could impact both variabilities. The results showed that there are significant zero-lag statistical correlations between the AMM and OHC300 to the south of Greenland and in the eastern North Atlantic mid-latitudes. Nevertheless, the lead–lag correlations show that the AMM leads the OHC300 in the northern Atlantic region and that there is a symmetrical structure around the zero-lag correlation between the AMM and the OHC300 in the eastern North Atlantic. Moreover, we determined via the causality analysis that there is no causal relationship between the OHC300 variability in the eastern North Atlantic mid-latitudes and the AMM on decadal time scales. Concerning the SSTA variability and the OHC300 variability over the North Atlantic, the lead–lag correlation shows that the SSTA leads the OHC300 on decadal time scales. However, based on the causality analysis result, it is found that the OHC300 drives the SSTAs over the subpolar North Atlantic region, and, therefore, influences the AMO on decadal time scales.

Author Contributions

Conceptualization, S.F.V.; methodology, S.F.V.; formal analysis, S.F.V.; investigation, S.F.V.; writing—original draft preparation, S.F.V.; writing—review and editing, S.F.V. and E.G.; visualization, S.F.V.; supervision, C.A.N. and P.N. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Coordination for High Level Education and Training (CAPES) Grant 88887.197771/2018-00 and Grant 88887.136402/2017-00, National Institute of Science and Technology for Climate Change Phase 2 under CNPq Grant 465501/2014-1 and FAPESP Grants 2014/50848-9.

Acknowledgments

Sandro F. Veiga was supported by a Ph.D. grant funded by the Coordination for Higher Education Personnel Development (CAPES) and now is supported by the Earth League Earth-Doc grant funded by CAPES (88887.197771/2018-00). This work was supported by the National Institute of Science and Technology for Climate Change phase 2, the National Council for Scientific and Technological Development (CNPq), 465501/2014-1, 302218/2016-5, 441227/2017-1; CAPES 88887.136402/2017-00; CAPES/National Water Agency (ANA) 23038.003962/2016-64; Financier of Studies and Projects (Finep) 01.12.0183.00; São Paulo Research Foundation (FAPESP) 2009/50528-6, 2014/50848-9. The Twentieth Century Reanalysis Project data set (20CRv2) was provided by the Office of Science Innovative and Novel Computational Impact on Theory and Experiment (DOE INCITE) program and the Office of Biological and Environmental Research (BER) in the U.S. Department of Energy and by the National Oceanic and Atmospheric Administration Climate Program Office (https://www.esrl.noaa.gov/psd/data/20thC_Rean/). The Extended Reconstructed Sea Surface Temperature (ERSSTv4) data were provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, via their web site at https://www.esrl.noaa.gov/psd/data/gridded/data.noaa.ersst.v4.html. The AMM-SST expansion coefficient from Chiang and Vimont (2004) was provided via the web site https://www.esrl.noaa.gov/psd/data/timeseries/monthly/AMM/. The CHOR_RL Historical Reanalyses data was provided the Centro Euro-Mediterraneo sui Cambiamenti Climatici (CMCC) via their web site http://c-glors.cmcc.it/index/index-3.html?sec=2. We are thankful for the support of Dr. Chunxue Yang for access to the CHOR_RL Historical reanalysis datasets. We also thank Dr. X. San Liang for his guidance on the interpretations of the causality analysis results, and for reading and commenting the manuscript, which helped to improve it. We thank the editor and two anonymous reviewers whose comments led to significant improvements of the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hastenrath, S.; Heller, L. Dynamics of climatic hazards in northeast Brazil. Q. J. R. Meteorol. Soc. 1977, 103, 77–92. [Google Scholar] [CrossRef]
  2. Lamb, P.J. Large-scale Tropical Atlantic surface circulation patterns associated with Subsaharan weather anomalies. Tellus 1978, 30, 240–251. [Google Scholar] [CrossRef] [Green Version]
  3. Hastenrath, S. Decadal-scale changes of the circulation in the tropical Atlantic sector associated with Sahel drought. Int. J. Climatol. 1990, 10, 459–472. [Google Scholar] [CrossRef]
  4. Nobre, P.; Shukla, J. Variation of Sea surface Temperature, Wind Stress, and Rainfall over the Tropical Atlantic and South America. J. Clim. 1996, 9, 2464–2479. [Google Scholar] [CrossRef]
  5. Nobre, P.; De Almeida, R.A.; Malagutti, M.; Giarolla, E. Coupled ocean-atmosphere variations over the South Atlantic Ocean. J. Clim. 2012, 25, 6349–6358. [Google Scholar] [CrossRef]
  6. Xie, S.P.; Carton, J.A. Tropical Atlantic variability: Patterns, mechanisms, and impacts. In Earth’s Climate: The Ocean-Atmosphere Interaction; Geophysical Monograph Series; Wang, C., Xie, S.-P., Carton, J.A., Eds.; AGU: Washington, DC, USA, 2004; volume 147, pp. 121–142. [Google Scholar]
  7. Ham, Y.G.; Kug, J.S.; Park, J.Y. Two distinct roles of Atlantic SSTs in ENSO variability: North Tropical Atlantic SST and Atlantic Niño. Geophys. Res. Lett. 2013, 40, 4012–4017. [Google Scholar] [CrossRef] [Green Version]
  8. Rodríguez-Fonseca, B.; Polo, I.; García-Serrano, J.; Losada, T.; Mohino, E.; Mechoso, C.R.; Kucharski, F. Are Atlantic Niños enhancing Pacific ENSO events in recent decades? Geophys. Res. Lett. 2009, 36, L20705. [Google Scholar] [CrossRef]
  9. Wang, C.; Kucharski, F.; Barimalala, R.; Bracco, A. Teleconnections of the tropical Atlantic to the tropical Indian and Pacific Oceans: A review of recent findings. Meteorol. Zeitschrift. 2009, 18, 445–454. [Google Scholar] [CrossRef] [Green Version]
  10. Wu, L.; He, F.; Liu, Z.; Li, C. Atmospheric teleconnections of tropical Atlantic variability: Interhemispheric, tropical-extratropical, and cross-basin interactions. J. Clim. 2007, 20, 856–870. [Google Scholar] [CrossRef] [Green Version]
  11. Park, J.H.; Li, T.; Yeh, S.W.; Kim, H. Effect of recent Atlantic warming in strengthening Atlantic–Pacific teleconnection on interannual timescale via enhanced connection with the pacific meridional mode. Clim. Dyn. 2019, 53, 371–387. [Google Scholar] [CrossRef]
  12. Okumura, Y.; Xie, S.P.; Numaguti, A.; Tanimoto, Y. Tropical Atlantic air-sea interaction and its influence on the NAO. Geophys. Res. Lett. 2001, 28, 1507–1510. [Google Scholar] [CrossRef] [Green Version]
  13. Kucharski, F.; Bracco, A.; Yoo, J.H.; Molteni, F. Atlantic forced component of the Indian monsoon interannual variability. Geophys. Res. Lett. 2008, 35, L04706. [Google Scholar] [CrossRef] [Green Version]
  14. Pottapinjara, V.; Girishkumar, M.S.; Sivareddy, S.; Ravichandran, M.; Murtugudde, R. Relation between the upper ocean heat content in the equatorial Atlantic during boreal spring and the Indian monsoon rainfall during June-September. Int. J. Climatol. 2016, 36, 2469–2480. [Google Scholar] [CrossRef] [Green Version]
  15. Zebiak, S.E. Air–Sea Interaction in the Equatorial Atlantic Region. J. Clim. 1993, 6, 1567–1586. [Google Scholar] [CrossRef]
  16. Chiang, J.C.H.; Vimont, D.J. Analogous Pacific and Atlantic Meridional Modes of Tropical Atmosphere–Ocean Variability. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
  17. Polo, I.; Rodríguez-Fonseca, B.; Losada, T.; García-Serrano, J. Tropical Atlantic variability modes (1979–2002). Part I: Time-evolving SST modes related to West African rainfall. J. Clim. 2008, 21, 6457–6475. [Google Scholar] [CrossRef] [Green Version]
  18. Moura, A.D.; Shukla, J. On the Dynamics of Droughts in Northeast Brazil: Observations, Theory and Numerical Experiments with a General Circulation Model. J. Atmos. Sci. 1981, 38, 2653–2675. [Google Scholar] [CrossRef] [Green Version]
  19. Chang, P.; Ki, L.; Li, H. A decadal climate variation in the tropical Atlantic Ocean from thermodynamic air-sea interactions. Nature 1997, 385, 516–518. [Google Scholar] [CrossRef]
  20. Xie, S.-P. A Dynamic Ocean–Atmosphere Model of the Tropical Atlantic Decadal Variability. J. Clim. 1999, 12, 64–71. [Google Scholar] [CrossRef]
  21. Chiang, J.C.H.; Kushnir, Y.; Giannini, A. Deconstructing Atlantic ITCZ variability: Influence of the local cross-equatorial SST gradient, and remote forcing from the eastern equatorial Pacific. J. Geophys. Res. Atmos. 2002, 107, 4004. [Google Scholar] [CrossRef]
  22. Xie, S.-P.; Philander, S.G.H. A coupled ocean-atmosphere model of relevance to the ITCZ in the eastern Pacific. Tellus A 1994, 46, 340–350. [Google Scholar] [CrossRef] [Green Version]
  23. Handoh, I.C.; Matthews, A.J.; Bigg, G.R.; Stevens, D.P. Interannual variability of the tropical Atlantic independent of and associated with ENSO: Part I. The North Tropical Atlantic. Int. J. Climatol. 2006, 26, 1937–1956. [Google Scholar] [CrossRef] [Green Version]
  24. Klein, S.A.; Soden, B.J.; Lau, N.-C. Remote Sea Surface Temperature Variations during ENSO: Evidence for a Tropical Atmospheric Bridge. J. Clim. 1999, 12, 917–932. [Google Scholar] [CrossRef] [Green Version]
  25. Saravanan, R.; Chang, P. Interaction between Tropical Atlantic Variability and El Niño–Southern Oscillation. J. Clim. 2000, 13, 2177–2194. [Google Scholar] [CrossRef]
  26. Alexander, M.; Scott, J. The influence of ENSO on air-sea interaction in the Atlantic. Geophys. Res. Lett. 2002, 29, 46-1–46-4. [Google Scholar] [CrossRef] [Green Version]
  27. Saravanan, R.; Chang, P. Thermodynamic Coupling and Predictability of Tropical Sea Surface Temperature. In Earth’s Climate: The Ocean-Atmosphere Interaction; Geophysical Monograph Series; Wang, C., Xie, S.-P., Carton, J.A., Eds.; AGU: Washington, DC, USA, 2004; Volume 147, pp. 171–180. [Google Scholar]
  28. Barreiro, M.; Chang, P.; Ji, L.; Saravanan, R.; Giannini, A. Dynamical elements of predicting boreal spring tropical Atlantic sea-surface temperatures. Dyn. Atmos. Ocean. 2005, 39, 61–85. [Google Scholar] [CrossRef]
  29. Mahajan, S.; Saravanan, R.; Chang, P. Free and forced variability of the tropical Atlantic Ocean: Role of the wind-evaporation-sea surface temperature feedback. J. Clim. 2010, 23, 5958–5977. [Google Scholar] [CrossRef]
  30. Ruiz-Barradas, A.; Carton, J.A.; Nigam, S. Structure of Interannual-to-Decadal Climate Variability in the Tropical Atlantic Sector. J. Clim. 2000, 13, 3285–3297. [Google Scholar] [CrossRef] [Green Version]
  31. Czaja, A.; van der Vaart, P.; Marshall, J. A diagnostic study of the role of remote forcing in tropical Atlantic variability. J. Clim. 2002, 15, 3280–3290. [Google Scholar] [CrossRef]
  32. Liu, Z.; Zhang, Q.; Wu, L. Remote Impact on Tropical Atlantic Climate Variability: Statistical Assessment and Dynamic Assessment. J. Clim. 2004, 17, 1529–1549. [Google Scholar] [CrossRef]
  33. Wu, L.; Zhang, Q.; Liu, Z. Toward understanding tropical Atlantic variability using coupled modeling surgery. In Earth’s Climate: The Ocean-Atmosphere Interaction; Geophysical Monograph Series; Wang, C., Xie, S.-P., Carton, J.A., Eds.; AGU: Washington, DC, USA, 2004; pp. 157–170. [Google Scholar]
  34. Xie, S.-P.; Tanimoto, Y. A pan-Atlantic decadal climate oscillation. Geophys. Res. Lett. 1998, 25, 2185–2188. [Google Scholar] [CrossRef]
  35. Huang, B.; Shukla, J. Ocean–Atmosphere Interactions in the Tropical and Subtropical Atlantic Ocean. J. Clim. 2005, 18, 1652–1672. [Google Scholar] [CrossRef] [Green Version]
  36. Penland, C.; Hartten, L.M. Stochastic forcing of north tropical Atlantic sea surface temperatures by the North Atlantic Oscillation. Geophys. Res. Lett. 2014, 41, 2126–2132. [Google Scholar] [CrossRef]
  37. Wainer, I.; Soares, J. North northeast Brazil rainfall and its decadal-scale relationship to wind stress and sea surface temperature. Geophys. Res. Lett. 1997, 24, 277–280. [Google Scholar] [CrossRef]
  38. Tourre, Y.M.; Rajagopalan, B.; Kushnir, Y.; Tourre, Y.M.; Rajagopalan, B.; Kushnir, Y. Dominant Patterns of Climate Variability in the Atlantic Ocean during the Last 136 Years. J. Clim. 1999, 12, 2285–2299. [Google Scholar] [CrossRef]
  39. Liu, Z. Dynamics of interdecadal climate variability: A historical perspective. J. Clim. 2012, 25, 1963–1995. [Google Scholar] [CrossRef]
  40. Vimont, D.J.; Kossin, J.P. The Atlantic Meridional Mode and hurricane activity. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef] [Green Version]
  41. Smirnov, D.; Vimont, D.J. Extratropical forcing of tropical Atlantic variability during boreal summer and fall. J. Clim. 2012, 25, 2056–2076. [Google Scholar] [CrossRef]
  42. Vimont, D.J. Analysis of the Atlantic meridional mode using linear inverse modeling: Seasonality and regional influences. J. Clim. 2012, 25, 1194–1212. [Google Scholar] [CrossRef]
  43. Delworth, T.L.; Clark, P.U.; Holland, M.; Johns, W.E.; Kuhlbrodt, T.; Lynch-Stieglitz, J.; Morrill, C.; Seager, R.; Weaver, A.J.; Zhang, R. The Potential for Abrupt Change in the Atlantic Meridional Overturning Circulation. Abrupt Climate Change 2008, No. CSSP; Geological Survey: Reston, VA, USA, 2008; pp. 258–359.
  44. Rahmstorf, S.; Box, J.E.; Feulner, G.; Mann, M.E.; Robinson, A.; Rutherford, S.; Schaffernicht, E.J. Exceptional twentieth-century slowdown in Atlantic Ocean overturning circulation. Nat. Clim. Chang. 2015, 5, 475–480. [Google Scholar] [CrossRef] [Green Version]
  45. Knight, J.R.; Allan, R.J.; Folland, C.K.; Vellinga, M.; Mann, M.E. A signature of persistent natural thermohaline circulation cycles in observed climate. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef] [Green Version]
  46. Zhang, L.; Wang, C. Multidecadal North Atlantic sea surface temperature and Atlantic meridional overturning circulation variability in CMIP5 historical simulations. J. Geophys. Res. Ocean. 2013, 118, 5772–5791. [Google Scholar] [CrossRef]
  47. McCarthy, G.D.; Haigh, I.D.; Hirschi, J.J.-M.; Grist, J.P.; Smeed, D.A. Ocean impact on decadal Atlantic climate variability revealed by sea-level observations. Nature 2015, 521, 508–510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  48. Seidov, D.; Mishonov, A.; Reagan, J.; Parsons, R. Multidecadal variability and climate shift in the North Atlantic Ocean. Geophys. Res. Lett. 2017, 44, 4985–4993. [Google Scholar] [CrossRef]
  49. Zhang, R. Coherent surface-subsurface fingerprint of the Atlantic meridional overturning circulation. Geophys. Res. Lett. 2008, 35, L20705. [Google Scholar] [CrossRef] [Green Version]
  50. Liang, X.S. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 52150. [Google Scholar] [CrossRef] [Green Version]
  51. Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [Green Version]
  52. Huang, B.; Banzon, V.F.; Freeman, E.; Lawrimore, J.; Liu, W.; Peterson, T.C.; Smith, T.M.; Thorne, P.W.; Woodruff, S.D.; Zhang, H.-M. Extended reconstructed sea surface temperature version 4 (ERSST.v4). Part I: Upgrades and intercomparisons. J. Clim. 2015, 28, 911–930. [Google Scholar] [CrossRef] [Green Version]
  53. Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The Twentieth Century Reanalysis Project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
  54. Yang, C.; Masina, S.; Storto, A. Historical ocean reanalyses (1900–2010) using different data assimilation strategies. Q. J. R. Meteorol. Soc. 2017, 143, 479–493. [Google Scholar] [CrossRef]
  55. Amaya, D.J.; DeFlorio, M.J.; Miller, A.J.; Xie, S.-P. WES feedback and the Atlantic Meridional Mode: Observations and CMIP5 comparisons. Clim. Dyn. 2017, 49, 1665–1679. [Google Scholar] [CrossRef]
  56. Bretherton, C.S.; Smith, C.; Wallace, J.M. An Intercomparison of Methods for Finding Coupled Patterns in Climate Data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef] [Green Version]
  57. Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like interdecadal variability: 1900–1993. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
  58. Vimont, D.J. The contribution of the interannual ENSO cycle to the spatial pattern of decadal ENSO-like variability. J. Clim. 2005, 18, 2080–2092. [Google Scholar] [CrossRef]
  59. Stips, A.; MacIas, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef] [Green Version]
  60. Vaid, B.H.; Liang, X.S. Tropospheric temperature gradient and its relation to the South and East Asian precipitation variability. Meteorol. Atmos. Phys. 2015, 127, 579–585. [Google Scholar] [CrossRef]
  61. Vaid, B.H.; Liang, X.S. The changing relationship between the convection over the western Tibetan Plateau and the sea surface temperature in the northern Bay of Bengal. Tellus Ser. A Dyn. Meteorol. Oceanogr. 2018, 70, 1–9. [Google Scholar] [CrossRef] [Green Version]
  62. Li, J.; Sun, C.; Jin, F.F. NAO implicated as a predictor of Northern Hemisphere mean temperature multidecadal variability. Geophys. Res. Lett. 2013, 40, 5497–5502. [Google Scholar] [CrossRef]
  63. Pyper, B.J.; Peterman, R.M. Comparison of methods to account for autocorrelation in correlation analyses of fish data. Can. J. Fish. Aquat. Sci. 1998, 55, 2127–2140. [Google Scholar] [CrossRef]
  64. Sun, C.; Kucharski, F.; Li, J.; Jin, F.-F.; Kang, I.-S.; Ding, R. Western tropical Pacific multidecadal variability forced by the Atlantic multidecadal oscillation. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
  65. Goldenberg, S.B.; Landsea, C.W.; Mestas-Nuñez, A.M.; Gray, W.M. The Recent Increase in Atlantic Hurricane Activity: Causes and Implications. Science 2001, 293, 474–479. [Google Scholar] [CrossRef] [Green Version]
  66. Guan, B.; Nigam, S. Analysis of Atlantic SST variability factoring interbasin links and the secular trend: Clarified structure of the Atlantic multidecadal oscillation. J. Clim. 2009, 22, 4228–4240. [Google Scholar] [CrossRef] [Green Version]
  67. Gastineau, G.; Frankignoul, C. Influence of the North Atlantic SST variability on the atmospheric circulation during the twentieth century. J. Clim. 2015, 28, 1396–1416. [Google Scholar] [CrossRef] [Green Version]
  68. Ba, J.; Keenlyside, N.S.; Latif, M.; Park, W.; Ding, H.; Lohmann, K.; Mignot, J.; Menary, M.; Ottera, O.H.; Wouters, B.; et al. A multi-model comparison of Atlantic multidecadal variability. Clim. Dyn. 2014, 43, 2333–2348. [Google Scholar] [CrossRef]
  69. Timmermann, A.; Latif, M. Northern Hemispheric Interdecadal Variability: A Coupled Air-Sea Mode. J. Clim. 1998, 11, 1906–1931. [Google Scholar] [CrossRef] [Green Version]
  70. Farneti, R.; Vallis, G.K. Mechanisms of interdecadal climate variability and the role of ocean-atmosphere coupling. Clim. Dyn. 2011, 36, 289–308. [Google Scholar] [CrossRef] [Green Version]
  71. Gastineau, G.; D’Andrea, F.; Frankignoul, C. Atmospheric response to the North Atlantic Ocean variability on seasonal to decadal time scales. Clim. Dyn. 2013, 40, 2311–2330. [Google Scholar] [CrossRef]
  72. Wen, N.; Frankignoul, C.; Gastineau, G. Active AMOC–NAO coupling in the IPSL-CM5A-MR climate model. Clim. Dyn. 2016, 47, 2105–2119. [Google Scholar] [CrossRef]
  73. Delworth, T.L.; Mann, M.E. Observed and simulated multidecadal variability in the Northern Hemisphere. Clim. Dyn. 2000, 16, 661–676. [Google Scholar] [CrossRef] [Green Version]
  74. Wang, C.; Zhang, L. Multidecadal ocean temperature and salinity variability in the tropical north Atlantic: Linking with the AMO, AMOC, and subtropical cell. J. Clim. 2013, 26, 6137–6162. [Google Scholar] [CrossRef]
  75. Grist, J.P.; Josey, S.A.; Marsh, R.; Good, S.A.; Coward, A.C.; de Cuevas, B.A.; Alderson, S.G.; New, A.L.; Madec, G. The roles of surface heat flux and ocean heat transport convergence in determining Atlantic Ocean temperature variability. Ocean Dyn. 2010, 60, 771–790. [Google Scholar] [CrossRef] [Green Version]
  76. Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea Surface Temperature Variability: Patterns and Mechanisms. Ann. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  77. Lozier, M.S. Overturning in the North Atlantic. Ann. Rev. Mar. Sci. 2012, 4, 291–315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  78. Frajka-Williams, E.; Beaulieu, C.; Duchez, A. Emerging negative Atlantic Multidecadal Oscillation index in spite of warm subtropics. Sci. Rep. 2017, 7, 11224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  79. Hasanean, H.M. Variability of the North Atlantic subtropical high and associations with tropical sea-surface temperature. Int. J. Climatol. 2004, 24, 945–957. [Google Scholar] [CrossRef]
  80. Hazeleger, W.; Wouters, B.; van Oldenborgh, G.J.; Corti, S.; Palmer, T.; Smith, D.; Dunstone, N.; Kröger, J.; Pohlmann, H.; von Storch, J.-S. Predicting multiyear North Atlantic Ocean variability. J. Geophys. Res. Ocean. 2013, 118, 1087–1098. [Google Scholar] [CrossRef] [Green Version]
  81. Zhang, R.; Sutton, R.; Danabasoglu, G.; Delworth, T.L.; Kim, W.M.; Robson, J.; Yeager, S.G. Comment on ‘the Atlantic Multidecadal Oscillation without a role for ocean circulation. Science 2016, 352, 1527. [Google Scholar] [CrossRef] [Green Version]
  82. Delworth, T.L.; Zeng, F.; Zhang, L.; Zhang, R.; Vecchia, G.A.; Yang, X. The central role of ocean dynamics in connecting the North Atlantic oscillation to the extratropical component of the Atlantic multidecadal oscillation. J. Clim. 2017, 30, 3789–3805. [Google Scholar] [CrossRef]
  83. Zhang, R.; Sutton, R.; Danabasoglu, G.; Kwon, Y.; Marsh, R.; Yeager, S.G.; Amrhein, D.E.; Little, C.M. A Review of the Role of the Atlantic Meridional Overturning Circulation in Atlantic Multidecadal Variability and Associated Climate Impacts. Rev. Geophys. 2019, 57, 316–375. [Google Scholar] [CrossRef] [Green Version]
  84. Wills, R.C.J.; Armour, K.C.; Battisti, D.S.; Hartmann, D.L. Ocean-atmosphere dynamical coupling fundamental to the Atlantic multidecadal oscillation. J. Clim. 2019, 32, 251–272. [Google Scholar] [CrossRef]
Atmosphere 11 00003 g001 550
Figure 1. (a) The leading maximum covariance analysis (MCA) mode between sea surface temperature anomaly (SSTA) (shading, °C) and 10-m wind anomalies (arrows, m s−1) over the tropical Atlantic (30° S–30° N). The mode is shown as the SSTA and 10-m wind anomalies regressed onto the SST normalized expansion coefficient (Atlantic meridional mode (AMM)-SST) time series (°C per standard deviation) for the period 1900–2010. The contour interval is 0.05 °C. The squared covariance fraction of the mode is 56.6%. (b) The normalized AMM-SST (red) and AMM-wind (blue) time series. Their correlation is 0.76. (c) The power spectrum of the AMM-SST time series, where the solid red line represents the theoretical red noise spectrum and the dashed and solid gray lines represent the 90% and 95% confidence levels, respectively.
Figure 1. (a) The leading maximum covariance analysis (MCA) mode between sea surface temperature anomaly (SSTA) (shading, °C) and 10-m wind anomalies (arrows, m s−1) over the tropical Atlantic (30° S–30° N). The mode is shown as the SSTA and 10-m wind anomalies regressed onto the SST normalized expansion coefficient (Atlantic meridional mode (AMM)-SST) time series (°C per standard deviation) for the period 1900–2010. The contour interval is 0.05 °C. The squared covariance fraction of the mode is 56.6%. (b) The normalized AMM-SST (red) and AMM-wind (blue) time series. Their correlation is 0.76. (c) The power spectrum of the AMM-SST time series, where the solid red line represents the theoretical red noise spectrum and the dashed and solid gray lines represent the 90% and 95% confidence levels, respectively.
Atmosphere 11 00003 g001
Atmosphere 11 00003 g002 550
Figure 2. (a) Zero-lag spatial correlation pattern between the SSTA at each grid point and the AMM-SST time series. A low-filter was applied to the AMM-SST and SSTA data at each grid point to retain the decadal variability. Dotted areas are statistically significant at the 95% confidence level. (b) AMM-SST filtered (thick black line) and unfiltered (thin black line) time series and Atlantic multidecadal oscillation (AMO) filtered (thick red line) and unfiltered (thin red line) time series. The AMO index was computed by spatially averaging the SSTA in the region to the south of Greenland (black box Figure 2a; 10°–50° W; 50°–65° N). All series were normalized by their respective long-term standard deviations. (c) Lead–lag correlation of the AMM-SST and AMO filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero-lag correlation. It should be noted that the 95% confidence level values changed for each lag correlation performed. However, as the changes in the values were negligible, we chose to display only the 95% confidence level value for the zero-lag correlation.
Figure 2. (a) Zero-lag spatial correlation pattern between the SSTA at each grid point and the AMM-SST time series. A low-filter was applied to the AMM-SST and SSTA data at each grid point to retain the decadal variability. Dotted areas are statistically significant at the 95% confidence level. (b) AMM-SST filtered (thick black line) and unfiltered (thin black line) time series and Atlantic multidecadal oscillation (AMO) filtered (thick red line) and unfiltered (thin red line) time series. The AMO index was computed by spatially averaging the SSTA in the region to the south of Greenland (black box Figure 2a; 10°–50° W; 50°–65° N). All series were normalized by their respective long-term standard deviations. (c) Lead–lag correlation of the AMM-SST and AMO filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero-lag correlation. It should be noted that the 95% confidence level values changed for each lag correlation performed. However, as the changes in the values were negligible, we chose to display only the 95% confidence level value for the zero-lag correlation.
Atmosphere 11 00003 g002
Atmosphere 11 00003 g003a 550Atmosphere 11 00003 g003b 550
Figure 3. (a) Zero-lag spatial correlation pattern between the OHC300 at each grid point and the AMM-SST time series. A low-pass filter was applied to the AMM-SST and OHC300 data at each grid point to retain the decadal variability. Dotted areas are statistically significant at the 95% confidence level. The black boxes represent regions where the OHC300-SG (south of Greenland, 10°–50° W; 50°–65°) and OHC300-ENA (eastern North Atlantic, 10°–30° W; 30°–40° N) indices were computed. (b) AMM-SST filtered (thick black line) and unfiltered (thin black line) time series and OHC300-SG filtered (thick red line) and unfiltered (thin red line) time series. The OHC300-SG indices were computed by spatially averaging the OHC300 in the region to the south of Greenland (black box). All series are normalized by their respective long-term standard deviations. (c) Lead–lag correlation of the AMM-SST and OHC300-SG filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero-lag correlation. (d) AMM-SST filtered (thick black line) and unfiltered (thin black line) time series and OHC300-ENA filtered (thick red line) and unfiltered (thin red line) time series. The OHC300-ENA indices were computed by spatially averaging the OHC300 in the eastern North Atlantic region (purple box). All series were normalized by their respective long-term standard deviations. (e) Lead–lag correlation of the AMM-SST and OHC300-ENA filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero-lag correlation. For (c,e) the 95% confidence level values changed for each lag correlation performed. However, as the changes in the values were negligible, we chose to display only the 95% confidence level value for the zero-lag correlation.
Figure 3. (a) Zero-lag spatial correlation pattern between the OHC300 at each grid point and the AMM-SST time series. A low-pass filter was applied to the AMM-SST and OHC300 data at each grid point to retain the decadal variability. Dotted areas are statistically significant at the 95% confidence level. The black boxes represent regions where the OHC300-SG (south of Greenland, 10°–50° W; 50°–65°) and OHC300-ENA (eastern North Atlantic, 10°–30° W; 30°–40° N) indices were computed. (b) AMM-SST filtered (thick black line) and unfiltered (thin black line) time series and OHC300-SG filtered (thick red line) and unfiltered (thin red line) time series. The OHC300-SG indices were computed by spatially averaging the OHC300 in the region to the south of Greenland (black box). All series are normalized by their respective long-term standard deviations. (c) Lead–lag correlation of the AMM-SST and OHC300-SG filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero-lag correlation. (d) AMM-SST filtered (thick black line) and unfiltered (thin black line) time series and OHC300-ENA filtered (thick red line) and unfiltered (thin red line) time series. The OHC300-ENA indices were computed by spatially averaging the OHC300 in the eastern North Atlantic region (purple box). All series were normalized by their respective long-term standard deviations. (e) Lead–lag correlation of the AMM-SST and OHC300-ENA filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero-lag correlation. For (c,e) the 95% confidence level values changed for each lag correlation performed. However, as the changes in the values were negligible, we chose to display only the 95% confidence level value for the zero-lag correlation.
Atmosphere 11 00003 g003aAtmosphere 11 00003 g003b
Atmosphere 11 00003 g004 550
Figure 4. (a) Zero-lag spatial correlation pattern between the SSTA and the OHC300 in each grid point. The OHC300 datasets were interpolated into the resolution of the SST grid point. A low-pass filter was applied to the data at each grid point to retain the decadal variability. Dotted areas are statistically significant at the 95% confidence level. (b) AMO filtered (thick black line) and unfiltered (thin black line) time series and OHC300-SG filtered (thick red line) and unfiltered (thin red line) time series. Both indices were computed by spatially averaging the data to the south of Greenland region (black box of Figure 4a; 10°–50° W; 50°–65° N). All series are normalized by their respective long-term standard deviation. (c) Lead–lag correlation of AMO and OHC300-SG filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero lag correlation. It should be noted that the 95% confidence level values changed for each lag correlation performed. However, as the changes in the values were negligible, we chose to display only the 95% confidence level value for the zero-lag correlation.
Figure 4. (a) Zero-lag spatial correlation pattern between the SSTA and the OHC300 in each grid point. The OHC300 datasets were interpolated into the resolution of the SST grid point. A low-pass filter was applied to the data at each grid point to retain the decadal variability. Dotted areas are statistically significant at the 95% confidence level. (b) AMO filtered (thick black line) and unfiltered (thin black line) time series and OHC300-SG filtered (thick red line) and unfiltered (thin red line) time series. Both indices were computed by spatially averaging the data to the south of Greenland region (black box of Figure 4a; 10°–50° W; 50°–65° N). All series are normalized by their respective long-term standard deviation. (c) Lead–lag correlation of AMO and OHC300-SG filtered time series. The gray line represents statistical significance at the 95% confidence level value for the zero lag correlation. It should be noted that the 95% confidence level values changed for each lag correlation performed. However, as the changes in the values were negligible, we chose to display only the 95% confidence level value for the zero-lag correlation.
Atmosphere 11 00003 g004

Share and Cite

MDPI and ACS Style

Veiga, S.F.; Giarolla, E.; Nobre, P.; Nobre, C.A. Analyzing the Influence of the North Atlantic Ocean Variability on the Atlantic Meridional Mode on Decadal Time Scales. Atmosphere 2020, 11, 3. https://doi.org/10.3390/atmos11010003

AMA Style

Veiga SF, Giarolla E, Nobre P, Nobre CA. Analyzing the Influence of the North Atlantic Ocean Variability on the Atlantic Meridional Mode on Decadal Time Scales. Atmosphere. 2020; 11(1):3. https://doi.org/10.3390/atmos11010003

Chicago/Turabian Style

Veiga, Sandro F., Emanuel Giarolla, Paulo Nobre, and Carlos A. Nobre. 2020. "Analyzing the Influence of the North Atlantic Ocean Variability on the Atlantic Meridional Mode on Decadal Time Scales" Atmosphere 11, no. 1: 3. https://doi.org/10.3390/atmos11010003

APA Style

Veiga, S. F., Giarolla, E., Nobre, P., & Nobre, C. A. (2020). Analyzing the Influence of the North Atlantic Ocean Variability on the Atlantic Meridional Mode on Decadal Time Scales. Atmosphere, 11(1), 3. https://doi.org/10.3390/atmos11010003

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop