Regional Characteristics of Long-Term Variability of Summer Precipitation in the Poyang Lake Basin and Possible Links with Large-Scale Circulations

Abstract

Understanding the spatiotemporal regime of summer precipitation at local scales plays a key role in regional prevention and mitigation of floods disasters and water resources management. Previous works focused on spatiotemporal characteristics of a region as a whole but left the influence of associated physical factors on sub-regions unexplored. Based on the precipitation data of 77 meteorological stations in the Poyang Lake basin (PYLB) from 1959 to 2013, we have investigated regional characteristics of summer precipitation in the PYLB by integrating the rotated empirical orthogonal function (REOF) analysis with hierarchical clustering algorithm (HCA). Then the long-term variability of summer precipitation in sub-regions of the PYLB and possible links with large-scale circulations was investigated using multiple trend analyses, wavelet analysis and correlation analysis. The results indicate that summer precipitation variations in the PYLB were of very striking regional characteristics. The PYLB was divided into three independent sub-regions based on two leading REOF modes and silhouette coefficient (SC). These sub-regions were located in northern PYLB (sub-region I), central PYLB (sub-region II), and southern PYLB (sub-region III). The summer precipitation in different sub-regions exhibited distinct variation trends and periodicities, which was associated with different factors. All sub-regions show no trends over the whole period 1959–2013, rather they show trends in different periods. Trends per decade in annual summer precipitation in sub-region I and sub-region II were consistent for all periods with different start and end years. The oscillations periods with 2–3 years were found in summer precipitation of all the three sub-regions. Summer precipitation in sub-region I was significantly positively correlated with the previous Indian Ocean Dipole (IOD) event, but negatively correlated with East Asian Summer Monsoon (EASM). While summer precipitation in sub-region II and sub-region III showed weak teleconnections with climate indices. All of the results of this study are conducive to further understand both the regional climate variations in the PYLB and response to circulation patterns variations.

1. Introduction

The Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report indicated that global temperature was likely to rise by 1.5 °C in advance, which would produce violent challenges in the climate of the Earth [1]. The increasing global warming will trigger significant changes in water and heat patterns in many regions of the world and even the frequent occurrence of extreme weather events [2,3]. The increase in surface temperature will also cause higher evapotranspiration rates and force the atmosphere to transport higher amounts of water vapor, thus, in turn, altering the hydrological cycle [4]. Precipitation is one of the most important climatic factors in a region, and the evolution of its distribution pattern has a considerable impact on land surface processes and global ecosystem [5,6]. For example, studies on the basis of observational datasets at the global scale have suggested that extreme precipitation events have increased remarkably over many mid–latitude regions in the Northern Hemisphere, bringing about tremendous impacts of floods hazards [7]. In the wake of global warming, therefore, there is growing concern from public, government, and academic circles about research on exploring the spatiotemporal changes of precipitation and possible influencing factors at the regional scale. For example, spatiotemporal variability of seasonal precipitation in Canada was investigated by employing the cross–wavelet analysis to illustrate insights into the relationship between the seasonal rainfall and the primary factors in the Northern hemisphere [8]. The interannual variability of mean summer rainfall in northern China was studied and then the regional characteristics were revealed by rotated empirical orthogonal function (REOF) [9]. Spatiotemporal and abrupt variations of daily precipitation by concentration index were discovered and their correlations with large–scale atmospheric circulations over Northeast China were investigated [10]. A novel spatial downscaling approach was proposed by integrating precipitation zoning with random forest regression based on satellite–based precipitation [11]. Empirical orthogonal function (EOF)/REOF and Mann–Kendall testing method were used to study spatiotemporal changes of spring precipitation of South China and their relations to atmospheric circulations based on precipitation data and National Centers for Environmental Prediction (NCEP)/National Center for Atmospheric Research (NCAR) reanalysis [12]. Most of these studies investigated the spatiotemporal variations of precipitation in large regions and the influencing factors or physical mechanisms from different perspectives.

Located in the middle and lower reaches of the Yangtze River, the Poyang Lake basin (PYLB) is subjected to the influence of subtropical humid monsoon climate. Historically, frequent droughts and floods disasters took place in the PYLB due to precipitation anomaly, which brought about huge damage to the environment and the agricultural economy [13,14,15,16]. Therefore, in the context of global precipitation pattern changes, the regional response characteristics of precipitation in the PYLB will have an important influence on the regional ecological environment and the sustainable development of social economy. Some scholars have discussed the change characteristics and mechanism of precipitation in the PYLB. Some studies suggested that there was distinct differences between the extreme precipitation from south to north in the PYLB, which were affected by topographic factor [17,18]. Seasonal transitions of precipitation in the PYLB showed different feature according to time spans of study [19,20]. Sub–regions of precipitation in the PYLB can be identified by using REOF method [21]. In addition, possible influence of El Niño-Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), Indian Ocean Dipole (IOD), and Pacific Decadal Oscillation (PDO) on the annual and seasonal precipitation extremes in the PYLB were analyzed in some studies [22,23,24]. A spatiotemporally distributed downscaling model was developed to project precipitation in the Poyang Lake watershed using the MRI-CGCM3 (A New Global Climate Model of the Meteorological Research Institute) [25]. Recently, there have emerged machine learning technology (e.g., hierarchical Bayesian method) to quantify spatiotemporal influences of climate indices on seasonal extreme precipitation in the PYLB [26].

There still exist following problems albeit these studies about precipitation in the PYLB were conducted from different aspects such as spatial distribution, time trend, and influencing factors. Firstly, the number of sites used in some studies is small, which affects the accuracy of the research results. Secondly, time series of some researches are short, which influences the long-term law of rainfall. Thirdly, precipitation in sub-regions of the PYLB and their causes are not conducted in depth. In this case, the objectives of this study are as follows: (1) to obtain objective and reasonable sub-regions of interannual variability of mean summer (June–July–August) precipitation in the PYLB by combining REOF with hierarchical clustering algorithm (HCA); (2) to explore the long-term variability of summer precipitation in each sub-region using multiple trend analysis and wavelet analysis; and (3) to discuss the teleconnections between large-scale atmospheric circulations and summer precipitation in each sub-region. Results of this study will be of significance in providing reference for summer precipitation prediction and water resource allocation management in the PYLB.

2. Study Area and Data

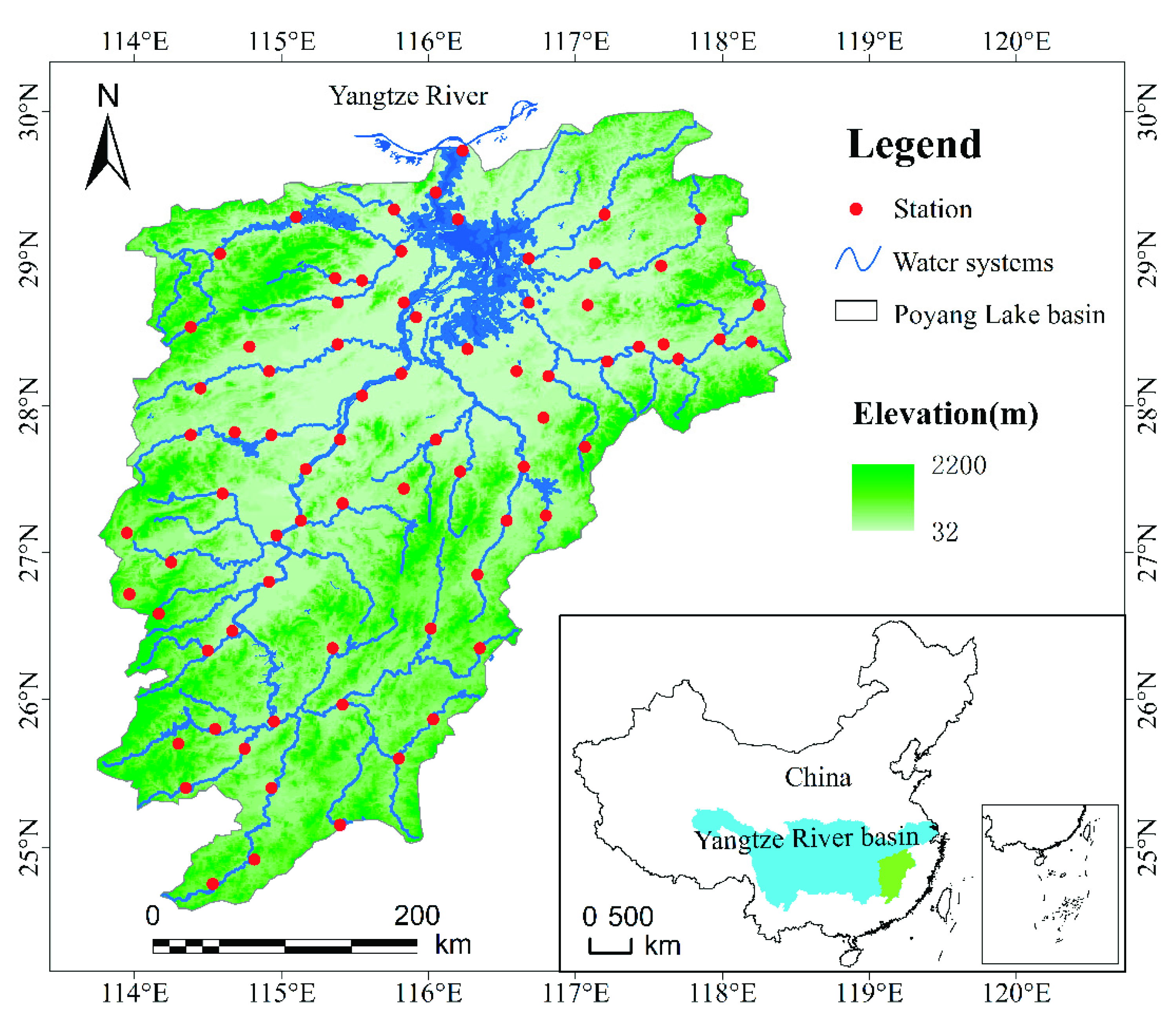
2.1. Description of Study Area

The Poyang Lake basin (24°24′–29°46′ N, 113°23′–118°46′ E, Figure 1) is located in the southeast of the middle-lower reaches of the Yangtze River basin with a drainage area of 1.62 × 10⁵ km² (9% of the Yangtze River basin and 96.6% of Jiangxi province), consisting of the Ganjiang River basin, the Fuhe River basin, the Xinjiang River basin, the Raohe River basin, and the Xiushui River basin [27,28]. The boundary of the basin is highly consistent with that of Jiangxi province, and the overlap area between them attains to 157,000 km², accounting for 94% of Jiangxi province. The PYLB is characterized by a subtropical warm and humid monsoon climate with mean annual temperature of 17.9 °C and mean annual rainfall of 1642 mm. The land cover types of the PYLB are diverse, mainly including woodland, cultivated land, and grassland, accounting for about 64%, 26%, and 4% of the total area of the basin, respectively. The national meteorological stations are distributed over the PYLB (Figure 1), which can stand for the precipitation of the whole basin.

2.2. Data Source and Processing

Precipitation data used in this study is derived from National Meteorological Science Data Center (http://data.cma.cn/). In order to obtain summer rainfall of every station, according to the climatic characteristics of the study area, monthly precipitation (June–July–August) was taken as summer precipitation in this paper. The East Asian Monsoon index (EASMI) is defined as an area–averaged seasonally (June–July–August) dynamical normalized seasonality at 850 hPa within the domain (10°–40° N, 110°–140° E) and the South Asian summer monsoon index (SASMI) is defined as an area–averaged seasonally (June–July–August–September) dynamical normalized seasonality at 850 hPa within the domain (5°–22.5° N, 35°–97.5° E) [29,30]. Both EASMI and SASMI are derived from the website (http://ljp.gcess.cn/dct/page/65540). The Niño3.4 index is one of several El Niño/Southern Oscillation (ENSO) indicators based on sea surface temperatures (SST) in the Niño3.4 region (5° N–5° S, 120–170° W). The NAO index is defined as the normalized pressure difference between the Subtropical (Azores) High and the Subpolar Low, which indicates the intensity of westerlies in the North Atlantic mid–latitudes zone. Both Niño3.4 and NAO indices are obtained from the Climate Prediction Center of National Oceanic and atmospheric administration (https://www.cpc.ncep.noaa.gov/). The IOD index is defined as the sustained changes in the difference between sea surface temperatures of the tropical western (50°–70° E, 10°S–10° N) and eastern Indian Ocean (90°–110° E, 10° S–0° N), which is derived from Japan Agency for Marine–Earth Science and Technology (http://www.jamstec.go.jp/frsgc/research/d1/iod/e/index.html). The PDO index is defined as an SST anomaly pattern of Pacific climate variability (20°N), obtained from Tokyo Climate Center (http://ds.data.jma.go.jp/tcc/tcc/.)

The rotate empirical orthogonal function method (REOF) was conducted by Microsoft Visual Studio 2013 to explore the climate division of summer precipitation in the PYLB. Surfer15 was applied to perform Kriging interpolation of space loads from the results of REOF and draw contour lines. R software (version 3.6.5) was taken to study the correlation between summer precipitation and global climate index with R package pheatmap (version 1.0.1.2). Multiple trend analyses and wavelet analysis were employed to investigate the trend and period of summer precipitation in the PYLB using R software (version 3.6.5) and Matlab 2016b, respectively.

3. Methods

3.1. EOF/REOF

Empirical orthogonal function decomposition (EOF) is widely used in climate diagnosis, which can decompose climatic factors into orthogonal eigenvectors to reflect the spatiotemporal distribution structure of meteorological factors. For Climate variable matrix composed of $m$ stations and $n$ observations, $X_{m\times n}$ can be orthogonally decomposed as a linear combination of p spatial eigenvectors and corresponding time weight coefficients [31,32]:

$$X_{m\times n}=v_{m\times p}{t}_{p\times n}$$

(1)

where $v$ is spatial eigenvector and $t$ is the corresponding time coefficient. Thus, the information of the original variable field is maximized by the first few eigenvectors that pass the North test.

Based on EOF decomposition, the original meteorological variable matrix is rotated orthogonally with maximum variance by rotation empirical orthogonal function decomposition (REOF) so that the high load vector field of the same spatial mode are concentrated in a few variables in some regions. $X_{m\times n}$ can be indicated as form [33,34,35] like,

$$\mathrm{X}={\mathrm{VT}}^{*}+\mathrm{U}$$

(2)

where ${\mathrm{T}}^{*}{}_{p\times n}(p<m)$ is common factor matrix, ${\mathrm{v}}_{p\times p}$ is factor load matrix, and ${\mathrm{u}}_{m\times n}$ is special factor only correlated with $\mathrm{X}$. The common factors of the standardized variables are independent variables with mean value of 0 and variance of 1.

The characteristic field rotated is more stable in time, and the spatial distribution structure is clearer. Therefore, REOF method is an effective tool for regional climatic division.

3.2. Hierarchical Clustering Algorithm

The hierarchical clustering algorithm (HCA) is one of the popular clustering algorithms in machine learning which includes two types of hierarchical clustering: agglomerative (bottom–up) and divisive (top–down) [36]. HCA is an unsupervised clustering algorithm which can divide the dataset into several clusters where data objects in the same cluster have higher similarity than those in different clusters according to distance between all objections. In this study, square Euclidean distance was used to calculate the distance between clustering indexes of each site. Then, Ward method was applied to measure the distance between classes. Finally, the most reasonable clustering number is determined by silhouette coefficient (SC) [37,38]. The value of silhouette coefficient is between −1 and 1. If SC approaches 1, the number of clusters is reasonable. When SC approaches 0, the number of clusters is uncertain. While SC approaches −1, it is unreasonable. In conclusion, the closer the SC value is to 1, the more reasonable the clustering number is.

3.3. Multiple Trend Analyses

The beginning and end years of the investigation period have great influence on the trend of the time series. Multiple trend analyses with different start and end years extend the traditional trend analyses. The non-parametric Mann–Kendall test, with significance levels of 5 and 1%, was performed to explore time series trend at least 30 years in length. Pre-whitened process for the rainfall series is performed to void the lag–1 correlation which may affect the significance test. Changes are presented in terms of precipitation change in mm/decade using Sen’s slope estimate.

3.4. Wavelet Analysis

Wavelet analysis is a time-frequency localization signal analysis method, which is often used for periodic analysis of climatic factors. The continuous wavelet transform [39,40] is defined as

$$wf\left({\mathrm{t}}_0,\mathrm{a}\right)=\frac{1}{\sqrt{\left|a\right|}}\int f\left(t\right)g\left(\frac{t-{\mathrm{t}}_0}{a}\right)dt,$$

(3)

where $wf\left({\mathrm{t}}_0,\mathrm{a}\right)$ is the wavelet transform coefficient, correlated with scale factor and time translation factor b. By means of wavelet transform, a one-dimensional signal is expanded in two directions of time and frequency, and the wavelet coefficients related to time and frequency are obtained. The larger the absolute value of the wavelet coefficient, the more significant the change in the time scale, and the corresponding time scale at the peak is the main period of the sequence.

Cross wavelet transform is a signal processing method combining cross spectrum analysis and wavelet transform, including wavelet cross spectrum and wavelet coherent spectrum, which can analyze the correlation of different time series in time domain and frequency domain. The cross wavelet energy spectrum can reflect the region of the same energy spectrum of two signals after the wavelet analysis, which can reflect the degree of interaction between two signals in different frequency domains. The specific formula [39,40] is

$${\mathrm{W}}_{XY}\left(\mathsf{\alpha },\mathsf{\tau }\right)=\mathrm{CX}\left(\mathsf{\alpha },\mathsf{\tau }\right){\mathrm{C}}^{*}\mathrm{Y}\left(\mathsf{\alpha },\mathsf{\tau }\right)$$

(4)

where W_XY(α,τ) is the cross wavelet spectrum of two signals, CX(α,τ) is the wavelet transform coefficient of the first signal and C*Y (α,τ) is the complex commutation of the wavelet transform coefficients of the second signal. The greater the cross–wavelet power is, the stronger the time series correlation is.

Coherent wavelet can compensate for the shortage of cross wavelet transform by measuring the time-delay correlation of time series in the low energy region. The wavelet coherent spectrum [39,40] of two time series can be defined as

$$R_n^2\left(a\right)=\frac{{\left|S\left(S^{-1}{w}_n^{xy}\left(a\right)\right)\right|}^2}{S\left(S^{-1}{\left|w_n^x\right|}^2\right)S\left(S^{-1}{\left|w_n^y\right|}^2\right)}$$

(5)

where the operator smooths (S) acts as a smoothing agent, and other symbols are the same as the corresponding symbols in the cross spectrum.

4. Results

4.1. Spatial Patterns of Summer Precipitation in the PYLB

Empirical orthogonal function (EOF) decomposition was performed on the normalized summer precipitation during 1959–2013 in the PYLB, and the first two EOFs pass the North test. The two eigenvectors were then rotated and two leading REOFs that make relatively large contributions to the total variance are obtained.

Table 1. The percentage of variance and cumulative variance of two leading modes of empirical orthogonal function (EOF) and rotate empirical orthogonal function (REOF).

Mode	EOF		REOF
	Variance (%)	Cumulative Variance (%)	Variance (%)	Cumulative Variance (%)
1	45.4	45.4	38.8	38.8
2	19.1	64.5	25.7	64.5

presents the variance contribution rates and cumulative variance contribution rates of two leading EOFs and REOFs. As Table 1 shows, the two leading EOFs and REOFs explain 64.5% of the total variance. Both EOF1 and REOF1 are larger than EOF2 and REOF2, indicating EOF1 dominates the change of summer precipitation, and REOF1 is the most optimal mode of summer precipitation. Based on spatial distributions of high loading eigenvectors (the absolute values of the contours larger than 0.5) that correspond to the two leading modes of summer precipitation, two summer precipitation sub-regions separated by 28° N in the PYLB are identified (Figure 2).

As shown in Unal et al. [41], it is quite subjective to select high rotation loading eigenvector critical value, which has an effect on the partition result to a large extent. Here we have taken the REOF eigenvectors as the classification feature to adopt HCA method and determine the optimal clustering number according to silhouette coefficient (SC), so as to obtain a reasonable objective partition of precipitation. As the SC curve (Figure 3) indicates, the maximum value of SC corresponds to a cluster number of 3 (Figure 3). So, it is reasonable to divide the PYLB into three sub-regions (Figure 4), in which the summer precipitation at the same cluster is homogeneous.

According to the HCA results, the regionalization map of summer precipitation in the PYLB and the Thiessen polygon areas calculated by area weight of each station were made. As Figure 4 shows, three sub-regions present obvious spatial consistency with each sub-region distributed zonally from west to east. These sub-regions are northern PYLB (sub-region I), central PYLB (sub-region II), and southern PYLB (sub-region III), respectively. The number, area, and average summer precipitation of meteorological stations in each sub-region are listed in

Table 2. The area and precipitation averaged over the three sub-regions.

Name of Sub-Region	Number of Stations	Area of Sub-Regions/km2	Percentage of Sub-Regions/%	Mean Summer Precipitation/mm
sub-region I	38	75,157.5	47.3	587.8
sub-region II	17	33,331.1	21.0	543.5
sub-region III	22	50,461.7	31.7	533.1

. It can be seen from Table 2 that there are relatively more meteorological stations in sub-region I. Number of stations in sub-region I is approximately the sum of stations in sub-region II and sub-region III. The area ratio of each sub-region to the basin area is around about 2:1:1.5. The mean summer precipitation of each sub-region increases successively from south to north.

4.2. Multi-Time Scale Characteristic of Summer Precipitation of Sub-Regions

Based on the multiple trend analyses, trends in annual summer precipitation for three sub-regions and the whole basin were analyzed. Time series of mean summer precipitation averaged over the three sub-regions and the whole basin (Figure 5) and multiple trend analyses with Sen’s slope estimator for periods with different start and end years are present (Figure 6). The results indicate all sub-regions show no trends over the whole period 1959–2013 but show trends in different periods. For sub-region I and sub-region II, in particular, there were strong significant positive trends in mean summer rainfall in the period from 1974 to 2000. Sub-region III, meanwhile, took on a downward and then upward tendency. Particularly, strong significant negative trends were found in mean summer precipitation from 1959 to late 1970s, and strong significant positive trends in mean summer precipitation from late 1970s to 2000. In addition, we can also conclude that trends in summer rainfall of sub-region I and II were consistent with that of the whole basin.

The wavelet power spectrum structures of summer precipitation time series in different sub-regions and the whole basin are seen in Figure 7. It can be seen from Figure 7 that the mean summer precipitation in the three sub-regions and the whole basin varied with distinct periodicities. Summer precipitation significantly oscillated with periods of 2–3 and 4–6 years in sub-region I, wherein periods of 2–3 years were located in the late 1970s and early 1990s, and periods of 4–6 years were located in 1990s (Figure 7a). Summer precipitation significantly also oscillated with periods of 2–3 and 4–6 years in sub-region III, and both of them are located in the late 1990s (Figure 7c). In sub-region II, summer precipitation exhibited 16 years periods of 2–3 years (Figure 7b), wherein the periods of 2–3 years were located in late 1970s, and where most of wavelet power spectrums of 16 years periods were located outside the conic line due to the influence of the boundary effect. Briefly, the periods at the scale of around 2–3 years in summer precipitation were found in all the three sub-regions; however, wavelet power spectrum were distinctly different with each other.

4.3. The Relationship between Summer Precipitation and Large-Scale Circulations

ENSO, PDO, IOD, NAO, and EASM are dominant climate indices which couple ocean–atmosphere phenomenon with global reach. Many investigations on the possible physical mechanisms of influence of these indices on different regional climate change have been undertaken, e.g., China [22,42], the Yangtze River basin [23,24], America, and the Huaihe River valley [43] etc. Figure 8 presents the correlations of time series of summer precipitation in each sub-region with multiple climate indices. As can be seen from Figure 8, summer precipitation in sub-region I was significantly positive correlated with IOD–1, while it was significantly negative correlated with EASMI. This indicates that the summer precipitation in sub-region I is strongly influenced by the previous IOD events and EASM. The correlation coefficient between IOD–0 and summer precipitation in sub-region II was only 0.23. The correlation coefficient between EASMI and summer precipitation in sub-region III was only 0.26. Although it did not pass the 95% significance level, the correlation coefficient was greater than 0.2, which still indicated that there was weak teleconnection between them. However, they were more likely to be related to other factors, such as the topography and the vast area of the Poyang Lake.

In order to further verify the influence of IOD–1 and EASMI on summer precipitation in sub-region I, wavelet cross spectra and wavelet condensation spectra between them were calculated respectively (Figure 9). The common high–energy region between IOD–1 and the summer precipitation of sub-region I was mainly distributed at the time scale of around 2–4 years, reflecting the strong resonance period between them, in which the cross–wavelet power reached significant levels in 1978–1982 and 1991–1994. The significant correlation between the wavelet coherence spectra of the IOD–1 and summer precipitation of sub-region I in the low energy region was mainly found at the time scale of 0–4 years from 1975 to 1985 and the time scale of >10 years (affected by the boundary). However, the correlation between them was weak in other time-frequency spaces. In these time-frequency spaces with significant consistency, the relationship between IOD–1 and summer precipitation of sub-region I was mainly positive phase, and IOD–1 was one-quarter phase earlier than the summer precipitation of sub-region I. The resonance period between summer precipitation of sub-region I and EASMI was mainly at the time scales of 2–4 years and 4–6 years, and the wavelet crossovers in 1976–1983 and 1985–1991 were significant. The significant wavelet coherence spectra between them was mainly shown at the time scale of 4–6 years from 1965 to 1973 and 1983–1991, respectively, and the time scale of 1–4 years from 1975 to 1985. During the whole study period, the relationship between summer precipitation of sub-region I and EASMI was mainly in inverse phase, showing a constantly changing process. In general, EASMI was prior to summer precipitation, and its location difference increased from <180° at the scale of 4–6 years from 1965 to 1973 to about 180° at the scale of 1–4 years from 1975 to 1985, and >180° at the scale of 4–6 years from 1983 to 1991.

5. Discussion

In this study, the REOF coupled with HCA are applied to the summer precipitation of 77 stations distributed over the PYLB for identifying sub-regions with different precipitation time dynamics and regimes.

The REOF method revealed two sub-regions characterized by different precipitation time variability (Figure 2). However, climate sub-regions based on REOF method is determined by the high loading eigenvector critical value, so the partition results are uncertain with major subjectivity. For example, taking the rotation eigenvector value larger than 0.6 as the boundary of high loading zone, Xie et al. divided the PYLB into three sub-regions for precipitation in flood season [44]. Sun et al. took the absolute value of rotation factor loading value larger than 0.4 as the critical value to divide Jiangxi province into six sub-regions for the flood season rainstorm [45]. Ma et al. divided Jiangxi province into five sub-regions for extreme precipitation by taking the absolute value of rotation factor loading value larger than 0.5 [21]. In this research, we take the critical loading value larger than 0.5 to partition the PYLB for summer rainfall. In order to avoid the subjectivity of REOF method, this paper introduces the machine learning method (HCA) to optimize the objective partition of summer precipitation of the PYLB, which seeks the most reasonable clustering number according to SC value, taking eigenvectors of the REOF decomposition as classification variables (Figure 3).

The summer precipitation in the sub-region I and sub-region II showed an increasing trend, while the summer precipitation in the sub-region III showed a decreasing trend (Figure 5 and Figure 6). This spatial pattern of precipitation changes has a clear dependence on topography of the PYLB. The Poyang Lake basin is high in the southern PYLB with mountainous areas and low with hilly and also low-lying alluvial plains in the northern PYLB. This result is in good line with Zhang et al.’s result that summer precipitation at the stations located in the southern PYLB is in more significant increasing trends when compared to that at the stations located in the northern PYLB [19]. Therefore, this variability of summer precipitation over the PYLB is extremely impacted by topographic characteristics which affects water vapor flux at basin scale. In summer, water vapor fluxes over the PYLB spread from southern and southwestern PYLB, carrying large amounts of water vapor from East or South China Sea by the monsoon circulation in the landward direction, and which can bring about heavy precipitation in the northern PYLB (sub-region I and sub-region II). While weakening in the EASM would limit its northward propagation and result in more and even heavy precipitation in southern PYLB (sub-region III). Many studies also demonstrated that the weakening of the EASM after the end of the 1970s remarkably resulted in increasing summer precipitation in the northern PYLB, which is consistent with the trend of summer precipitation in different sub-regions [24,46,47]. The continuous wavelet analysis demonstrates 2–3 years periods were found in summer rainfall of all the three sub-regions over the PYLB (Figure 7). According to previous studies, summer precipitation in the most parts of China, especially South China, Yangtze River basin, Huaihe River basin, and North China, exhibited a cycle of 2–3 years, which was called QBO feature (i.e., quasi-biennial oscillation) [19,43,48]. This may be related to the QBO characteristics of the East Asian Summer Monsoon.

Correlation analysis indicates that the summer precipitation in sub-region I of the PYLB was positively correlated with IOD–1 and negatively correlated with EASM, respectively. The common resonance period of 2–4 years was found between IOD–1 and summer precipitation in sub-region I of the PYLB, and the positive previous IOD event was one-quarter phase earlier than the summer precipitation of sub-region I. While common resonance periods of 2–4a and 4–6a were found between EASM and summer precipitation in sub-region I of the PYLB, and EASM was prior to summer precipitation with inverse phase. Previous studies have demonstrated the influence of IOD event and EASM on summer rainfall in the PYLB. Yang and Sun et al. indicated that when the high ridge extends westward (retreats eastward), precipitation in the Yangtze River basin tends to increase (decrease), while rainfall in southern China tends to decrease (increase) [49]. Yuan et al. showed that the high ridge of the 500 hPa western pacific subtropical high advances more westward and controls southeast China in the summer after an positive IOD event in the previous year [50]. These are in agreement with Xiao et al.’s results that the positive IOD event at the same year tends to increase the summer precipitation in the southeastern part of the Yangtze River basin [24]. Similar conclusion can be also found in Liu et al. ‘s result that summer precipitation will be above normal in south China in the years of positive IOD occurring independently [51]. The transport of water vapor is determined by the strength of East Asian Summer Monsoon. While East Asian Summer Monsoon has weaken in strength, particularly since the late 1970s, which negatively impacts the northward propagation of the vapor flux, thus leading to more summer precipitation in the middle and lower Yangtze River basin [23,46]. However, the variation of monsoon strength may be related to the anomaly of global sea surface temperature, and specific physical mechanisms needs to be further studied.

6. Conclusions

In this study, we studied the spatial structural patterns and multi–time scale changes in summer precipitation in the PYLB from 1959 to 2013 using REOF, multiple trend analyses, and wavelet analyses. Then, possible links of summer precipitation in sub-regions with large–scale circulations were also discussed. The results are presented as follows.

(1)

Two key precipitation areas in the PYLB were identified by REOF. These key areas were optimally divided into three sub-regions on the basis of the HCA method, which were northern PYLB (sub-region I), central PYLB (sub-region II), and southern PYLB (sub-region III), respectively. The area of sub-region I was lightly less than that of sum of sub-region II and sub-region III. This will help us understand the spatial distribution of water resources in the PYLB, which will also be conducive to make better use of water resources.

(2)

The same trends per decade in annual summer precipitation were found in sub-region I and sub-region II, which was distinctly increasing from 1974 to 2000. Sub-region III, meanwhile, showed summer precipitation apparently in a decreasing trend in the period from 1959 to late 1970s and apparently in an increasing trend from late 1970s to 2000. Summer rainfall in the three sub-regions of the PYLB exhibited distinct periodicities, to be specific, 2–3 and 4–6 years periods in sub-region I and sub-region III, and 16 years and 2–3 years periods in sub-region II. Such results reveal the variation trend and periodic characteristics of summer precipitation in the PYLB and will help to predict drought and flood disasters.

(3)

Summer precipitation in sub-region I was positively correlated with previous IOD events (at 95% significant confidence level) and the common 2–4 years resonance period was found between them. Wavelet coherence spectra showed IOD–1 was one–quarter phase earlier than the summer precipitation of sub-region I. Summer precipitation in sub-region I was negatively correlated with EASM (at 99% significant confidence level) and they exhibited common 2–4 years and 4–6 years resonance periods. Wavelet coherence spectra demonstrates EASM was prior to summer precipitation in sub-region I. Summer precipitation in sub-region II and sub-region III showed weak correlations with multiple indices. The findings of these results may help to better understand the possible influence of circulations on the spatial patterns of summer precipitation.

It is noted that local climatic factors including lake area, changes in land cover, and other human activities, might also have significant influence on regional precipitation, and attempts were not made in this paper to explore them, though correlations between summer precipitation and circulations were discussed comprehensively.