Extending Limited In Situ Mountain Weather Observations to the Baseline Climate: A True Verification Case Study
Abstract
:1. Introduction
2. Data And Methods
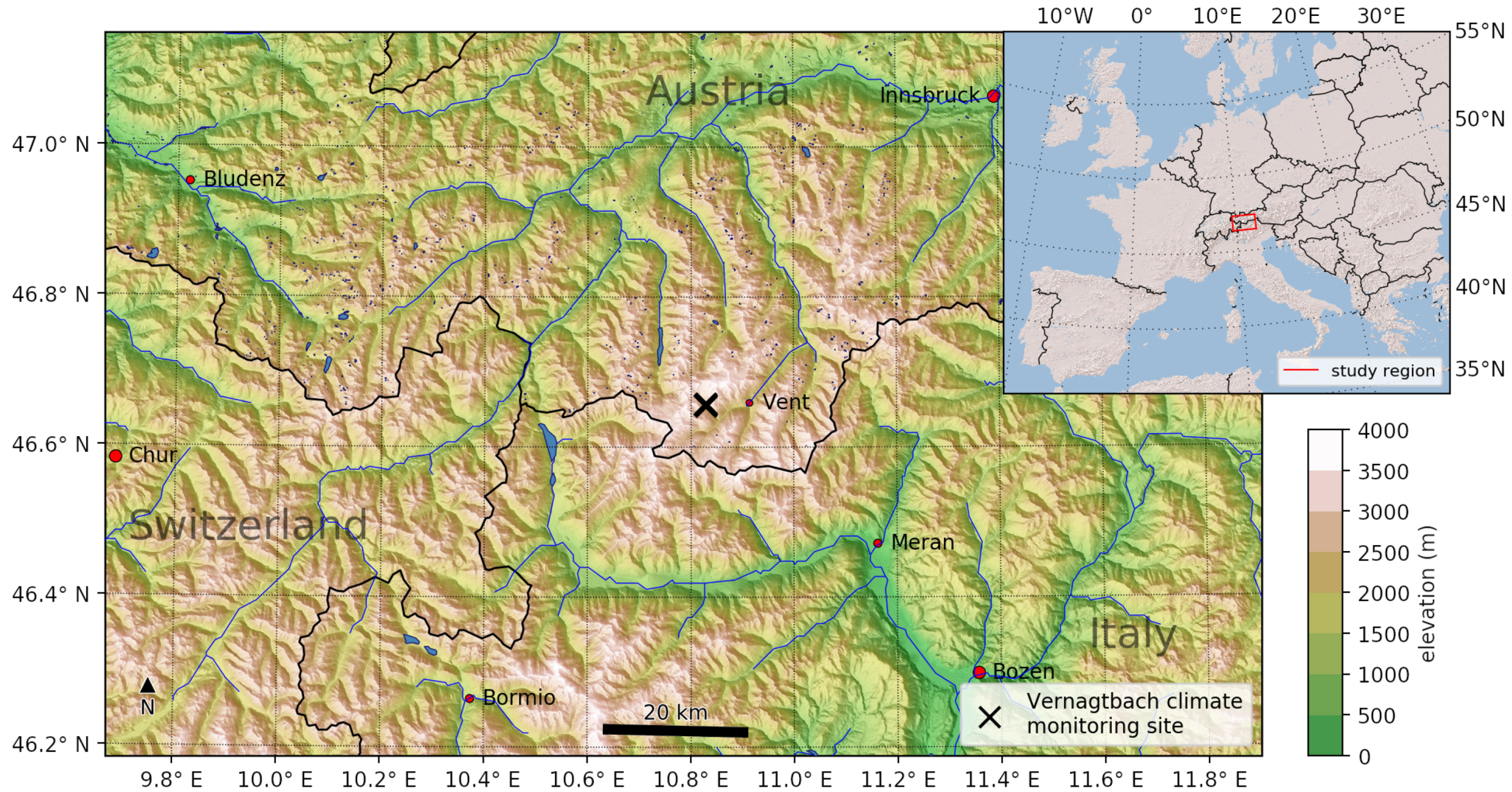
2.1. The Vernagtbach Climate Monitoring Site (VERNAGT)
2.2. sDoG: Statistically Postprocessing Reanalysis Data to the Station Scale (One-Dimensional)
2.3. Evaluation Strategy
2.4. The Reference Data Sets
3. Results
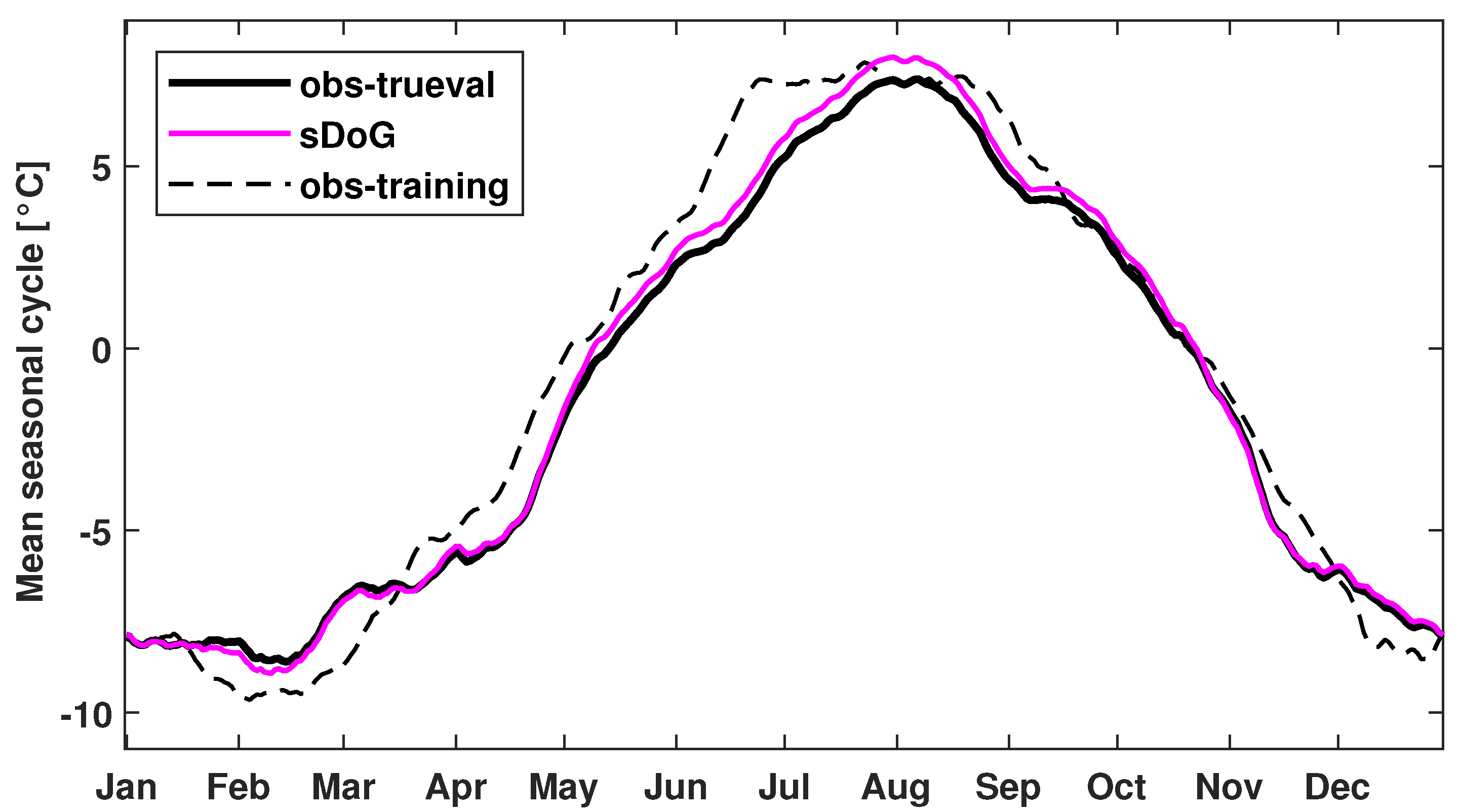
3.1. sDoG Performance at Different Time Scales
3.2. Added Value of sDoG Over the Reference Data Sets
3.3. Verification of the Cross-Validation-Based Uncertainty Estimates of sDoG
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pepin, N.C.; Lundquist, J.D. Temperature trends at high elevations: Patterns across the globe. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Frei, C. Interpolation of temperature in a mountainous region using nonlinear profiles and non-Euclidean distances. Int. J. Climatol. 2014, 1585–1605. [Google Scholar] [CrossRef]
- Isotta, F.A.; Begert, M.; Frei, C. Long-Term Consistent Monthly Temperature and Precipitation Grid Data Sets for Switzerland Over the Past 150 Years. J. Geophys. Res. Atmos. 2019, 124, 3783–3799. [Google Scholar] [CrossRef]
- Escher-Vetter, H.; Braun, L.N.; Siebers, M. Hydrological and Meteorological Records from the Vernagtferner Basin—Vernagtbach Station, for the Years 2002 to 2012. Available online: https://doi.pangaea.de/10.1594/PANGAEA.829516 (accessed on 2 October 2020).
- Cullen, N.J.; Conway, J.P. A 22 month record of surface meteorology and energy balance from the ablation zone of Brewster Glacier, New Zealand. J. Glaciol. 2015, 61, 931–946. [Google Scholar] [CrossRef] [Green Version]
- Carey, M. In the Shadow of Melting Glaciers. Climate Change and Andean Society; Oxford University Press: Oxford, UK, 2010; p. 288. [Google Scholar]
- Juen, I. Glacier Mass Balance and Runoff in the Cordillera Blanca, Peru. Ph.D. Thesis, University of Innsbruck, Innsbruck, Austria, 2006. [Google Scholar]
- Hiebl, J.; Frei, C. Daily temperature grids for Austria since 1961—Concept, creation and applicability. Theor. Appl. Climatol. 2016, 124, 161–178. [Google Scholar] [CrossRef]
- Werner, A.T.; Schnorbus, M.A.; Shrestha, R.R.; Cannon, A.J.; Zwiers, F.W.; Dayon, G.; Anslow, F. A long-term, temporally consistent, gridded daily meteorological dataset for northwestern North America. Sci. Data 2019, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, W.; Berrisford, P.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C.; et al. Global Reanalysis: Goodbye ERA-Interim, Hello ERA5; The European Centre for Medium-Range Weather Forecasts: Reading, UK, 2019; pp. 17–24. [Google Scholar] [CrossRef]
- Kaiser-Weiss, A.K.; Borsche, M.; Niermann, D.; Kaspar, F.; Lussana, C.; Isotta, F.A.; van den Besselaar, E.; van der Schrier, G.; Undén, P. Added value of regional reanalyses for climatological applications. Environ. Res. Commun. 2019, 1, 071004. [Google Scholar] [CrossRef]
- Bazile, E.; Abida, R.; Verrelle, A.; Le Moigne, P.; Szczypta, C. Report for the 55 Years MESCAN-SURFEX Re-Analysis; Technical Report; Météo-France/CNRS: Toulouse, France, 2017. [Google Scholar]
- Giorgi, F.; Jones, C.; Asrar, G. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Shi, X.; Chow, F.K.; Street, R.L.; Bryan, G.H. Key Elements of Turbulence Closures for Simulating Deep Convection at Kilometer-Scale Resolution. J. Adv. Model. Earth Syst. 2019, 11, 818–838. [Google Scholar] [CrossRef] [Green Version]
- Kotlarski, S.; Keuler, K.; Christensen, O.B.; Colette, A.; Déqué, M.; Gobiet, A.; Goergen, K.; Jacob, D.; Lüthi, D.; van Meijgaard, E.; et al. Regional climate modeling on European scales: A joint standard evaluation of the EURO-CORDEX RCM ensemble. Geosci. Model Dev. 2014, 7, 1297–1333. [Google Scholar] [CrossRef] [Green Version]
- Foley, A.; Kelman, I. EURO-CORDEX regional climate model simulation of precipitation on Scottish islands (1971–2000): Model performance and implications for decision-making in topographically complex regions. Int. J. Climatol. 2018, 38, 1087–1095. [Google Scholar] [CrossRef] [Green Version]
- Di Luca, A.; de Elía, R.; Laprise, R. Challenges in the Quest for Added Value of Regional Cloate Dynamical Downscaling. Curr. Clim. Chang. Rep. 2015, 1, 10–21. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change. Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Maraun, D.; Shepherd, T.G.; Widmann, M.; Zappa, G.; Walton, D.; Gutiérrez, J.M.; Hagemann, S.; Richter, I.; Soares, P.M.M.; Hall, A.; et al. Towards process-informed bias correction of climate change simulations. Nat. Clim. Chang. 2017, 7, 764–773. [Google Scholar] [CrossRef] [Green Version]
- Michaelsen, J. Cross-validation in statistical climate forecast models. J. Clim. Appl. Meteorol. 1987, 26, 1589–1600. [Google Scholar] [CrossRef] [Green Version]
- Hofer, M.; Marzeion, B.; Mölg, T. A statistical downscaling method for daily air temperature in data-sparse, glaciated mountain environments. Geosci. Model Dev. 2015, 8, 579–593. [Google Scholar] [CrossRef] [Green Version]
- Hofer, M.; Nemec, J.; Cullen, N.J.; Weber, M. Evaluating Predictor Strategies for Regression-Based Downscaling with a Focus on Glacierized Mountain Environments. J. Appl. Meteorol. Climatol. 2017, 56, 1707–1729. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Cross-validation of bias-corrected climate simulations is misleading. Hydrol. Earth Syst. Sci. 2018, 22, 4867–4873. [Google Scholar] [CrossRef] [Green Version]
- Haerter, J.; Hagemann, S.; Moseley, C.; Piani, C. Climate model bias correction and the role of timescales. Hydrol. Earth Syst. Sci. 2011, 15, 1065–1073. [Google Scholar] [CrossRef] [Green Version]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions “Should we apply bias correction to global and regional climate model data?”. Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef] [Green Version]
- Hewitson, B.C.; Daron, J.; Crane, R.G.; Zermoglio, M.F.; Jack, C. Interrogating empirical-statistical downscaling. Clim. Chang. 2014, 122, 539–554. [Google Scholar] [CrossRef] [Green Version]
- Dixon, K.W.; Lanzante, J.R.; Nath, M.J.; Hayhoe, K.; Stoner, A.; Radhakrishnan, A.; Balaji, V.; Gaitán, C.F. Evaluating the stationarity assumption in statistically downscaled climate projections: Is past performance an indicator of future results? Clim. Chang. 2016, 135, 395–408. [Google Scholar] [CrossRef] [Green Version]
- Barsugli, J.J.; Guentchev, G.; Horton, R.M.; Wood, A.; Mearns, L.O.; Liang, X.Z.; Winkler, J.A.; Dixon, K.; Hayhoe, K.; Rood, R.B.; et al. The Practitioner’s Dilemma: How to Assess the Credibility of Downscaled Climate Projections. Eos Trans. Am. Geophys. Union 2013, 94, 424–425. [Google Scholar] [CrossRef] [Green Version]
- Erlandsen, H.B.; Parding, K.M.; Benestad, R.; Mezghani, A.; Pontoppidan, M. A hybrid downscaling approach for future temperature and precipitation change. J. Appl. Meteorol. Climatol. 2020, 1–46. [Google Scholar] [CrossRef]
- Schmidli, J.; Schmutz, C.; Frei, C.; Wanner, H.; Schär, C. Mesoscale precipitation variability in the region of the European Alps during the 20th century. Int. J. Climatol. 2002, 22, 1049–1074. [Google Scholar] [CrossRef]
- Braun, L.N.; Escher-Vetter, H.; Siebers, M.; Weber, M. Water Balance of the highly Glaciated Vernagt Basin, Ötztal Alps; chapter The Water Balance of the Alps; Innsbruck University Press: Innsbruck, Austria, 2007; Volume 3, pp. 33–42. [Google Scholar]
- Rissel, R. Physikalische Interpretation des Temperatur-Index-Verfahrens zur Berechnung der Eisschmelze am Vernagtferner. Bachelor’s Thesis, Technische Universität Braunschweig, Fakultät Architektur Bauingenieurwesen und Umweltwissenschaften, Braunschweig, Germang, 2012. [Google Scholar]
- Charalampidis, C.; Fischer, A.; Kuhn, M.; Lambrecht, A.; Mayer, C.; Thomaidis, K.; Weber, M. Mass-Budget Anomalies and Geometry Signals of Three Austrian Glaciers. Front. Earth Sci. 2018, 6, 218. [Google Scholar] [CrossRef]
- Escher-Vetter, H.; Oerter, H.; Reinwarth, O.; Braun, L.N.; Weber, M. Hydrological and Meteorological Records from the Vernagtferner Basin—Vernagtbach Station, for the Years 1970 to 2001; PANGAEA: Bremen, Germany, 2012. [Google Scholar] [CrossRef]
- Schneider, T. Analysis of Incomplete Climate Data: Estimation of Mean Values and Covariance Matrices and Imputation of Missing Values. J. Clim. 2001, 14, 853–871. [Google Scholar] [CrossRef]
- Sansom, J.; Tait, A. Estimation of long-term climate information at location with short-term data records. J. Appl. Meteorol. 2003, 43, 915–923. [Google Scholar] [CrossRef]
- Castro, C.L.; Pielke, R.A., Sr.; Leoncini, G. Dynamical downscaling: Assessment of value retained and added using the Regional Atmospheric Modeling System (RAMS). J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Pielke, R.A., Sr.; Wilby, R.L. Regional climate downscaling: What’s the point? Eos Trans. Am. Geophys. Union 2012, 93, 52–53. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; p. 533. [Google Scholar]
- Wilks, D. Statistical Methods in the Atmospheric Sciences, 3rd ed.; International Geophysics; Elsevier Science: Amsterdam, The Netherlands, 2011; p. 704. [Google Scholar]
- Murphy, A.H. Skill Scores Based on the Mean Square Error and Their Relationships to the Correlation Coefficient. Mon. Weather Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Wilks, D.S. Resampling hypothesis tests for autocorrelated fields. J. Clim. 1997, 10, 65–82. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- SMHI. UERRA Data User Guide v 3.0; Copernicus Climate Change Service Climate Data Store: Brussels, Belgium, 2019. [Google Scholar]
- Giot, O.; Termonia, P.; Degrauwe, D.; De Troch, R.; Caluwaerts, S.; Smet, G.; Berckmans, J.; Deckmyn, A.; De Cruz, L.; De Meutter, P.; et al. Validation of the ALARO-0 model within the EURO-CORDEX framework. Geosci. Model Dev. 2016, 9, 1143–1152. [Google Scholar] [CrossRef] [Green Version]
- Strasser, U.; Marke, T.; Braun, L.; Escher-Vetter, H.; Juen, I.; Kuhn, M.; Maussion, F.; Mayer, C.; Nicholson, L.; Niedertscheider, K.; et al. The Rofental: A high Alpine research basin (1890–3770 m a.s.l.) in the Ötztal Alps (Austria) with over 150 years of hydrometeorological and glaciological observations. Earth Syst. Sci. Data 2018, 10, 151–171. [Google Scholar] [CrossRef] [Green Version]
- Thorne, P.W.; Lanzante, J.R.; Peterson, T.C.; Seidel, D.J.; Shine, K.P. Tropospheric temperature trends: History of an ongoing controversy. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 66–88. [Google Scholar] [CrossRef]
- Torma, C.; Giorgi, F.; Coppola, E. Added value of regional climate modeling over areas characterized by complex terrain. In Proceedings of the EGU General Assembly Conference Abstracts, EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2015; p. 709. [Google Scholar] [CrossRef]
- Scherrer, S.C. Temperature monitoring in mountain regions using reanalyses: Lessons from the Alps. Environ. Res. Lett. 2020, 15, 044005. [Google Scholar] [CrossRef]










| Short Name | Data Set | MSL | Period | Grid | Reference |
|---|---|---|---|---|---|
| ERA-Interim | ERA-Interim 750 hPa air temperature (bc) | 1750 m | 1979–2019 | 80 km | [45] |
| ERA5 | ERA5 750 hPa air temperature (bc) | 2426 m | 1979–pres | 31 km | [12] |
| ERA5-Land | ERA5-Land 2 m air temperature (bc) | 2871 m | 1981–pres | 9 km | [12] |
| HARMONIE | HARMONIE 2 m air temperature (bc) | 2710 m | 1961–pres | 11 km | [46] |
| MESCAN-SURFEX | UERRA MESCAN-SURFEX 2 m air temperature (bc) | 2817 m | 1961–2019 | 5.5 km | [14] |
| ALARO | CORDEX ALARO-0 2 m air temperature (bc) | 2843 m | 1979–2010 | 12.5 km | [47] |
| Vent | Vent station 2 m air temperature (bc) | 1905 m | 1935–pres | point | [48] |
| SPARTACUS | SPARTACUS 2 m air temperature (bc) | 2941 m | 1961–2012 | 1 km | [8] |
| Mean Bias [C] | Reduction of Error RE of sDoG (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Short-name | overall | day-to-day | seasonal cycle | year-to-year | |||||
| (see Table 1) | annual | SON | DJF | MAM | JJA | ||||
| obs-training | 0.62 | - | - | - | - | - | - | - | - |
| ERA-Interim | 0.12 (1.15) | 56 | 26 | 76 | 55 | (15) | 61 | (16) | (–17) |
| ERA5 | 0.28 (0.7) | 40 | 24 | (41) | 74 | 42 | 56 | (9) | (–8) |
| ERA5-Land | 0.58 (–2.38) | 83 | 61 | 94 | 91 | 79 | (31) | 66 | (27) |
| HARMONIE | –0.10 (–1.76) | 81 | 66 | 93 | 63 | 72 | 58 | 65 | (–49) |
| MESCAN-SURFEX | –0.62 (–4.12) | 94 | 91 | 98 | 98 | 96 | 98 | 88 | (35) |
| ALARO | 0.18 (–0.89) | 90 | 88 | 90 | 94 | 94 | 92 | 89 | 75 |
| Vent | 0.24 (3.87) | 68 | 52 | 85 | 67 | 66 | (43) | (22) | (–14) |
| SPARTACUS | 0.09 (–2.25) | 50 | 44 | (8) | (8) | 38 | (28) | (0) | (–33) |
| sDoG | 0.21 | - | - | - | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofer, M.; Horak, J. Extending Limited In Situ Mountain Weather Observations to the Baseline Climate: A True Verification Case Study. Atmosphere 2020, 11, 1256. https://doi.org/10.3390/atmos11111256
Hofer M, Horak J. Extending Limited In Situ Mountain Weather Observations to the Baseline Climate: A True Verification Case Study. Atmosphere. 2020; 11(11):1256. https://doi.org/10.3390/atmos11111256
Chicago/Turabian StyleHofer, Marlis, and Johannes Horak. 2020. "Extending Limited In Situ Mountain Weather Observations to the Baseline Climate: A True Verification Case Study" Atmosphere 11, no. 11: 1256. https://doi.org/10.3390/atmos11111256





