Diurnal and Seasonal Variations of Surface Energy and CO2 Fluxes over a Site in Western Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site
2.2. Micrometeorological Measurements
2.2.1. Fast Response Measurements
2.2.2. Slow Response Measurements
2.3. Methods
3. Results
3.1. The Meteorological Background
3.2. Diurnal Variations
3.2.1. Radiation Components
3.2.2. Heat and CO2 Fluxes
3.3. Seasonal Variations
3.3.1. Radiation Components
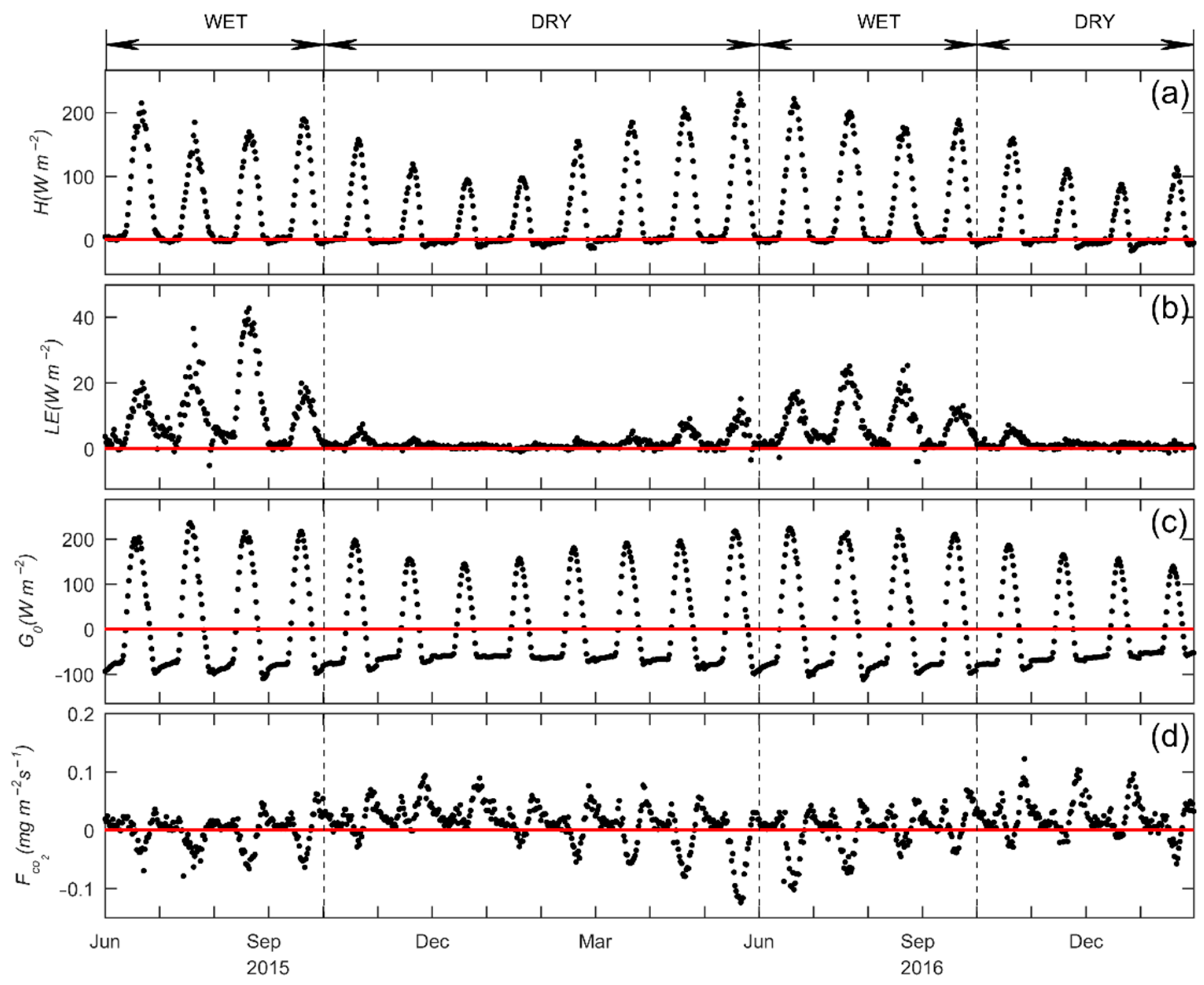
3.3.2. Heat and CO2 Fluxes
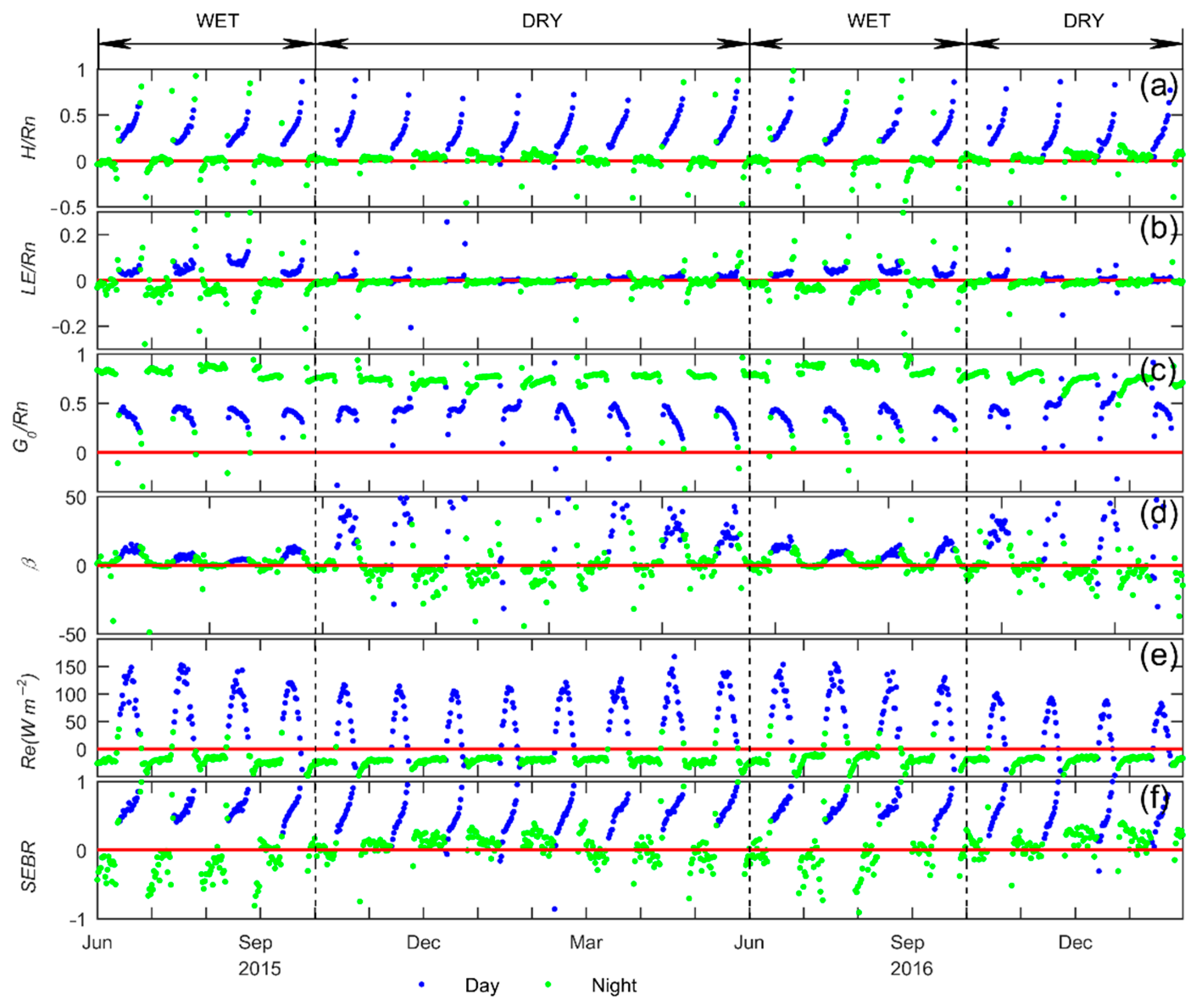
3.4. Energy Partitioning and Energy Balance Closure
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ye, D.Z.; Gao, Y.X. Meteorology of the Qinghai–Xizang Plateau; Science Press: Beijing, China, 1979; pp. 1–278. (In Chinese) [Google Scholar]
- Luo, H.B.; Yanai, M. The large-scale circulation and heat sources over the Tibetan Plateau and surrounding areas during the early summer of 1979. Part Ⅱ: Heat and moisture budgets. Mon. Weather Rev. 1984, 112, 966–989. [Google Scholar] [CrossRef] [Green Version]
- Yanai, M.; Li, C.F.; Song, Z.S. Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon. J. Meteor. Soc. Jpn. Ser. II 1992, 70, 319–351. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.X.; Zhang, Y.S. Tibetan Plateau forcing and the timing of the monsoon onset over South Asia and the South China Sea. Mon. Weather Rev. 1998, 126, 913–927. [Google Scholar] [CrossRef]
- Zhao, P.; Chen, L.X. Climatic features of atmospheric heat source/sink over the Qinghai–Xizang Plateau in 35 years and its relation to rainfall in China. Sci. China Earth Sci. 2001, 44, 858–864. [Google Scholar] [CrossRef]
- Zhao, P.; Chen, L.X. Role of atmospheric heat source/sink over the Qinghai–Xizang Plateau in quasi-4-year oscillation of atmosphere–land–ocean interaction. Chin. Sci. Bull. 2001, 46, 241–245. [Google Scholar] [CrossRef]
- Wu, G.X.; Liu, Y.M.; Wang, T.M.; Wan, R.J.; Liu, X.; Li, W.P.; Wang, Z.Z.; Zhang, Q.; Duan, A.M.; Liang, X.Y. The influence of mechanical and thermal forcing by the Tibetan Plateau on Asian climate. J. Hydrom. 2007, 8, 770–789. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.D.; Lu, C.G.; Shi, X.H.; Gao, S.T. World water tower: An atmospheric perspective. Geophys. Res. Lett. 2008, 35, L20815. [Google Scholar] [CrossRef]
- Zhou, X.J.; Zhao, P.; Chen, J.M.; Chen, L.X.; Li, W.L. Impacts of thermodynamic processes over the Tibetan Plateau on the Northern Hemispheric climate. Sci. China Earth Sci. 2009, 52, 1679–1693. [Google Scholar] [CrossRef]
- Boos, W.R.; Kuang, Z.M. Dominant control of the South Asian monsoon by orographic insulation versus plateau heating. Nature 2010, 463, 218–222. [Google Scholar] [CrossRef]
- Wu, G.X.; Liu, Y.M.; He, B.; Bao, Q.; Duan, A.; Jin, F.F. Thermal controls on the Asian summer monsoon. Sci. Rep. 2012, 2, 404. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Wang, B.; Liu, J.P.; Zhou, X.J.; Chen, J.M.; Nan, S.L.; Liu, G.; Xiao, D. Summer precipitation anomalies in Asia and North America induced by eurasian non-monsoon land heating versus ENSO. Sci. Rep. 2016, 6, 21346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, P.; Xu, X.; Chen, F.; Guo, X.; Zheng, X.; Liu, L.; Hong, Y.; Li, Y.; La, Z.; Peng, H.; et al. The third atmospheric scientific experiment for understanding the earth–atmosphere coupled system over the Tibetan plateau and its effects. Bull. Am. Meteorol. Soc. 2018, 99, 757–776. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Y.; Guo, X.; Xu, X.; Liu, Y.; Tang, S.; Xiao, W.; Shi, C.; Ma, Y.; Yu, X.; et al. The Tibetan Plateau surface-atmosphere coupling system and its weather and climate effects: The Third Tibetan Plateau Atmospheric Science Experiment. J. Meteorol. Res. 2019, 33, 375–399. [Google Scholar] [CrossRef]
- Ye, D.Z. Some characteristics of the summer circulation over the Qinghai–Xizang (Tibet) Plateau and its neighborhood. Bull. Am. Meteorol. Soc. 1981, 62, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Ye, D.Z.; Wu, G.X. The role of the heat source of the Tibetan Plateau in the general circulation. Meteorol. Atmos. Phys. 1998, 67, 181–198. [Google Scholar] [CrossRef]
- Shi, Y.F.; Yu, G.; Liu, X.D.; Li, B.Y.; Yao, T.D. Reconstruction of the 30–40 ka BP enhanced India monsoon climate based on geological record from the Tibetan Plateau. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2001, 169, 69–83. [Google Scholar] [CrossRef]
- Hsu, H.H.; Liu, X. Relationship between the Tibetan Plateau heating and East Asian summer monsoon rainfall. Geophys. Res. Lett. 2003, 30, 2066. [Google Scholar] [CrossRef] [Green Version]
- Sato, T.; Kimura, F. How does the Tibetan Plateau affect the transition of Indian monsoon rainfall? Mon. Weather Rev. 2007, 135, 2006–2015. [Google Scholar] [CrossRef]
- Ma, Y.M.; Kang, S.C.; Zhu, L.P.; Xu, B.Q.; Tian, L.D.; Yao, T.D. Tibetan observation and research platform: Atmosphere–land interaction over a heterogeneous landscape. Bull. Am. Meteorol. Soc. 2008, 89, 1487–1492. [Google Scholar]
- Cui, X.F.; Graf, H.F. Recent land cover changes on the Tibetan Plateau: A review. Clim. Change 2009, 94, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Ye, B.S.; Zhou, D.G.; Wu, B.Y.; Foken, T.; Qin, J.; Zhou, Z.Y. Response of hydrological cycle to recent climate changes in the Tibetan Plateau. Clim. Change 2011, 109, 517–534. [Google Scholar] [CrossRef]
- Duan, A.M.; Wu, G.X.; Liu, Y.M.; Ma, Y.M.; Zhao, P. Weather and climate effects of the Tibetan Plateau. Adv. Atmos. Sci. 2012, 29, 978–992. [Google Scholar] [CrossRef]
- Gu, L.L.; Yao, J.M.; Hu, Z.Y.; Zhao, L. Comparison of the surface energy budget between regions of seasonally frozen ground and permafrost on the Tibetan Plateau. Atmos. Res. 2015, 153, 553–564. [Google Scholar] [CrossRef]
- Karl, T.R.; Trenberth, K.E. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, K.; Tamagawa, I.; Ishikawa, H.; Ma, Y.; Hu, Z. Surface energy budget and closure of the eastern Tibetan Plateau during the GAME-Tibet IOP 1998. J. Hydrol. 2003, 283, 169–183. [Google Scholar] [CrossRef]
- Choi, T.; Hong, J.; Kim, J.; Lee, H.; Asanuma, J.; Ishikawa, H.; Tsukamoto, O.; Gao, Z.Q.; Ma, Y.M.; Ueno, K.; et al. Turbulent exchange of heat, water vapor, and momentum over a Tibetan prairie by eddy covariance and flux variance measurements. J. Geophys. Res. Atmos. 2004, 109, D21. [Google Scholar] [CrossRef]
- Gu, S.; Tang, Y.H.; Cui, X.Y.; Kato, T.; Du, M.Y.; Li, Y.N.; Zhao, X.Q. Energy exchange between the atmosphere and a meadow ecosystem on the Qinghai–Tibetan Plateau. Agric. For. Meteorol. 2004, 129, 175–185. [Google Scholar] [CrossRef]
- Ma, W.Q.; Ma, Y.M. The annual variations on land surface energy in the northern Tibetan Plateau. Environ. Geol. 2007, 51, 1465. [Google Scholar]
- Yao, J.M.; Zhao, L.; Ding, Y.J.; Gu, L.L.; Jiao, K.Q.; Qiao, Y.P.; Wang, Y.Q. The surface energy budget and evapotranspiration in the Tanggula region on the Tibetan Plateau. Cold Reg. Sci. Technol. 2007, 52, 326–340. [Google Scholar] [CrossRef]
- Guo, D.L.; Yang, M.X.; Wang, H.J. Characteristics of land surface heat and water exchange under different soil freeze/thaw conditions over the central Tibetan Plateau. Hydrol. Process. 2011, 25, 2531–2541. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.J.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- You, Q.; Xue, X.; Peng, F.; Dong, S.; Gao, Y. Surface water and heat exchange comparison between alpine meadow and bare land in a permafrost region of the Tibetan Plateau. Agric. For. Meteorol. 2017, 232, 48–65. [Google Scholar] [CrossRef]
- Xin, Y.F.; Chen, F.; Zhao, P.; Barlage, M.; Blanken, P.; Chen, Y.L.; Wang, Y.J. Surface energy balance closure at ten sites over the Tibetan plateau. Agric. For. Meteorol. 2018, 259, 317–328. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P.A. Simple two-dimensional parameterization for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Tanner, C.B.; Thurtell, G.W. Anemoclinometer Measurements of Reynolds Stress and Heat Transport in the Atmospheric Surface Layer; University of Wisconsin: Madison, WI, USA, 1969; p. 82. [Google Scholar]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Moncrieff, J.; Clement, R.; Finnigan, J.; Meyers, T. Averaging, Detrending, and Filtering of Eddy Covariance Time Series. In Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Lee, X., Massman, W., Law, B., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 2004; pp. 7–30. [Google Scholar]
- Zhao, X.R.; Sheng, Z.; Li, J.W.; Yu, H.; Wei, K.J. Determination of the “wave turbopause” using a numerical differentiation method. J. Geophys. Res.: Atmos. 2019, 124, 10592–10607. [Google Scholar] [CrossRef]
- He, Y.; Sheng, Z.; He, M. Spectral Analysis of Gravity Waves from Near Space High-Resolution Balloon Data in Northwest China. Atmosphere 2020, 11, 133. [Google Scholar] [CrossRef] [Green Version]
- Van Wijk, W. Physics of plant environment. Soil Sci. 1964, 98, 69. [Google Scholar] [CrossRef]
- Garratt, J.R. The Atmospheric Boundary Layers; Cambridge University Press: New York, NY, USA, 1992; p. 316. [Google Scholar]
- Franssen, H.J.H. Energy balance closure of eddy-covariance data: A multisite analysis for European FLUXNET stations. Agric. For. Meteorol. 2010, 150, 1553–1567. [Google Scholar] [CrossRef]
- Harazono, Y.; Kim, J.; Miyata, A.; Choi, T.; Yun, J.I. Measurement of energy budget components during the International Rice Experiment (IREX) in Japan. Hydrol. Process. 1998, 12, 2018–2092. [Google Scholar] [CrossRef]
- Burba, G.; Verma, B.S.; Kim, J. Surface energy fluxes of Phragmites australis in a prairie wetland. Agric. For. Meteorol. 1999, 94, 31–51. [Google Scholar] [CrossRef]
- Heitman, J.L.; Xiao, X.; Horton, R.; Sauer, T. Sensible heat measurements indicating depth and magnitude of subsurface soil water evaporation. Water Resour. Res. 2008, 44, W00D05. [Google Scholar] [CrossRef] [Green Version]
- Heitman, J.L.; Horton, R.; Sauer, T.J.; Desutter, T.M. NOTES AND CORRESPONDENCE: Sensible Heat Observations Reveal Soil-Water Evaporation Dynamics. J. Hydrometeorol. 2008, 9, 165–171. [Google Scholar] [CrossRef] [Green Version]
- Heitman, J.L.; Horton, R.; Sauer, T.J.; Ren, T.S.; Xiao, X. Latent heat in soil heat flux measurements. Agric. For. Meteorol. 2010, 150, 1147–1153. [Google Scholar] [CrossRef] [Green Version]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Gu, J.; Smith, E.A.; Merritt, J.D. Testing energy balance closure with GOES-retrieved net radiation and in situ measured eddy correlation fluxes in BOREAS. J. Geophys. Res. 1999, 104, 27881–27893. [Google Scholar] [CrossRef]
- Wilson, K.B. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–234. [Google Scholar] [CrossRef] [Green Version]
- McGloin, R.; Šigut, L.; Havránková, K.; Dušek, J.; Pavelka, M.; Sedlák, P. Energy balance closure at a variety of ecosystems in Central Europe with contrasting topographies. Agric. For. Meteorol. 2018, 248, 418–431. [Google Scholar] [CrossRef]
- Ohtaki, E. Application of an inferred carbon dioxide and humidity instrument to studies of turbulent transport. Bound. Lay. Meteorol. 1984, 29, 85–107. [Google Scholar] [CrossRef]
- Ohtaki, E.; Matsui, T. Infrared device for simultaneous measurement of atmospheric carbon dioxide and water vapor. Bound. Lay. Meteorol. 1982, 24, 109–119. [Google Scholar] [CrossRef]
- Desai, A.R. Influence of vegetation and surface forcing on carbon dioxide fluxes across the Upper Midwest, USA: Implications for regional scaling. Agric. For. Meteorol. 2008, 148, 288–308. [Google Scholar] [CrossRef]
- Ma, Y.; Fan, S.; Ishikawa, H.; Tsukamoto, O.; Yao, T.; Koike, T.; Zuo, H.; Hu, Z.; Su, Z. Diurnal and inter-monthly variation of land surface heat fluxes over the central Tibetan Plateau area. Theor. Appl. Climatol. 2005, 80, 259–273. [Google Scholar] [CrossRef]
- Zhao, X.; Peng, B.; Qin, N.; Wang, W. Characteristics of Energy Transfer and Micrometeorology in Surface Layer in Different Areas of Tibetan Plateau in Summer. Plateau Mt. Meteorol. Res. 2011, 31, 6–11. [Google Scholar]
- Zhao, X.; Li, Y. Seasonal Characteristics of Turbulent Flux and Meteorology Elements in the Atmosphere Surface Layer over the Alpine Meadow on Eastern Slop of Tibetan Plateau. Plateau Mt. Meteorol. Res. 2011, 31, 12–17. [Google Scholar]
- Wohlfahrt, G.; Fenster maker, L.F. A Large annual net ecosystem CO2 uptake of a Mojave Desert ecosystem. Glob.Change Biol. 2008, 1497, 1475–1487. [Google Scholar] [CrossRef]
- Xie, J.; Li, Y. CO2 absorption by alkaline soils and its implication to the global carbon cycle. Environ. Geol. 2009, 56, 953–961. [Google Scholar] [CrossRef]
- Mamtimin, A. Study on Characteristics and Influencing Factors of Carbon Exchange of Desert Area in Xinjiang; NUIST: Nanjing, China, 2015. [Google Scholar]
- Yang, K.; Koike, T. Satellite monitoring of the surface water and energy budget in the central Tibetan Plateau. Adv. Atmos. Sci. 2008, 25, 974–985. [Google Scholar] [CrossRef]
- Guo, D.; Yang, M.; Wang, H. Sensible and latent heat flux response to diurnal variation in soil surface temperature and moisture under different freeze/thaw soil conditions in the seasonal frozen soil region of the central Tibetan Plateau. Environ. Earth Sci. 2011, 63, 97–107. [Google Scholar] [CrossRef]
- Gao, Z. Determination of soil heat flux in a Tibetan short-grass prairie. Boundary-Layer Meteorol. 2005, 114, 165–178. [Google Scholar] [CrossRef]
- Gao, Z.; Bian, L.; Hu, Y.; Wang, L.; Fan, J. Determination of soil temperature in an arid region. J. Arid Environ. 2007, 71, 157–168. [Google Scholar] [CrossRef]
- Gao, Z.; Horton, R.; Liu, H. Impact of wave phase difference between surface soil heat flux and soil surface temperature on land surface energy balance closure. J. Geophys. Res. 2010, 115, D16112. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liu, C.; Yang, N.; Li, Y. Diurnal and Seasonal Variations of Surface Energy and CO2 Fluxes over a Site in Western Tibetan Plateau. Atmosphere 2020, 11, 260. https://doi.org/10.3390/atmos11030260
Zhao X, Liu C, Yang N, Li Y. Diurnal and Seasonal Variations of Surface Energy and CO2 Fluxes over a Site in Western Tibetan Plateau. Atmosphere. 2020; 11(3):260. https://doi.org/10.3390/atmos11030260
Chicago/Turabian StyleZhao, Xingbing, Changwei Liu, Nan Yang, and Yubin Li. 2020. "Diurnal and Seasonal Variations of Surface Energy and CO2 Fluxes over a Site in Western Tibetan Plateau" Atmosphere 11, no. 3: 260. https://doi.org/10.3390/atmos11030260
APA StyleZhao, X., Liu, C., Yang, N., & Li, Y. (2020). Diurnal and Seasonal Variations of Surface Energy and CO2 Fluxes over a Site in Western Tibetan Plateau. Atmosphere, 11(3), 260. https://doi.org/10.3390/atmos11030260





