The Long-Term Change of Latent Heat Flux over the Western Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results
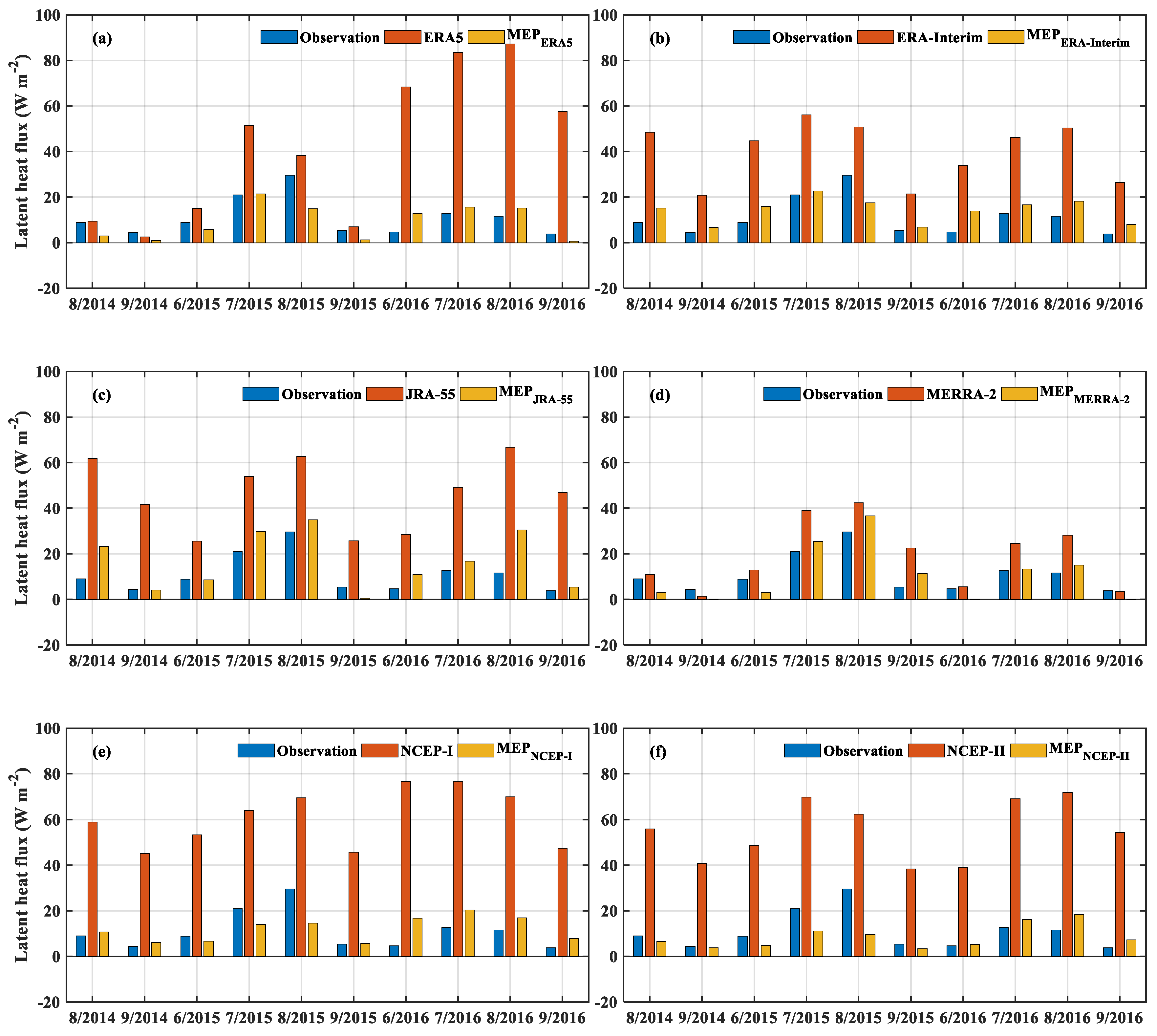
3.1. Estimation of LE by the MEP Model and Observational Data
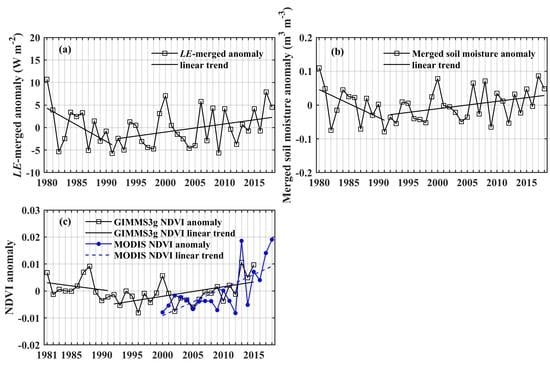
3.2. LE Estimated by the MEP Model and Reanalysis Data and Its Long-Term Variation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, G.X.; Zhang, Y.S. Tibetan plateau forcing and the timing of the monsoon onset over south asia and the south china sea. Mon. Weather Rev. 1998, 126, 913–927. [Google Scholar] [CrossRef]
- Zhao, P.; Chen, L.X. Interannual variability of atmospheric heat source/sink over the Qinghai—Xizang (Tibetan) Plateau and its relation to circulation. Adv. Atmos. Sci. 2001, 18, 106–116. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, B. Summer atmospheric heat sources over the western-central tibetan plateau: An integrated analysis of multiple reanalysis and satellite datasets. J. Clim. 2019, 32, 1181–1202. [Google Scholar] [CrossRef]
- You, Q.; Min, J.; Zhang, W.; Pepin, N.; Kang, S. Comparison of multiple datasets with gridded precipitation observations over the Tibetan Plateau. Clim. Dyn. 2015, 45, 791–806. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Fang, Q.L.; Zhou, L.X.; Zhu, L.P.; Zhang, X.J.; Yang, J.; Zhou, J.; Song, W.W.; Yu, X.J.; Luo, Z.H. Spatiotemporal variation of vegetation dynamics and correlations with climatic factors in the Tibetan Plateau, China. IOP Conf. Ser. Earth Environ. Sci. 2019, 346, 012015. [Google Scholar] [CrossRef]
- Song, L.; Zhuang, Q.; Yin, Y.; Zhu, X.; Wu, S. Spatio-temporal dynamics of evapotranspiration on the Tibetan Plateau from 2000 to 2010. Environ. Res. Lett. 2017, 12, 014011. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, W.; Zhong, L.; Hu, Z.; Li, J.; Zhu, Z.; Han, C.; Wang, B.; Liu, X. Monitoring and modeling the Tibetan Plateau’s climate system and its impact on East Asia. Sci. Rep. 2017, 7, 44574. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Liu, Y.; Li, M.; Hu, Z.; Ding, Z. Assessment of reanalysis flux products based on eddy covariance observations over the Tibetan Plateau. Theor. Appl. Climatol. 2019, 138, 275–292. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.; Liu, H.; Li, Y.; Li, Y.; Hu, Z.; Gao, X.; Ma, Y.; Sun, J.; Lenschow, D.H.; et al. Analysis of land surface parameters and turbulence characteristics over the Tibetan Plateau and surrounding region. J. Geophys. Res. Atmos. 2016, 121, 9540–9560. [Google Scholar] [CrossRef]
- Xin, Y.F.; Chen, F.; Zhao, P.; Barlage, M.; Blanken, P.; Chen, Y.L.; Chen, B.; Wang, Y.J. Surface energy balance closure at ten sites over the Tibetan plateau. Agric. For. Meteorol. 2018, 259, 317–328. [Google Scholar] [CrossRef]
- Zhao, P.; Xu, X.; Chen, F.; Guo, X.; Zheng, X.; Liu, L.; Hong, Y.; Li, Y.; La, Z.; Peng, H.; et al. The third atmospheric scientific experiment for understanding the earth-atmosphere coupled system over the tibetan plateau and its effects. Bull. Am. Meteorol. Soc. 2018, 99, 757–776. [Google Scholar] [CrossRef]
- Shi, Q.; Liang, S. Surface-sensible and latent heat fluxes over the Tibetan Plateau from ground measurements, reanalysis, and satellite data. Atmos. Chem. Phys. 2014, 14, 5659–5677. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Su, Z.; Koike, T.; Yao, T.; Ishikawa, H.; Ueno, K.i.; Menenti, M. On measuring and remote sensing surface energy partitioning over the Tibetan Plateau—From GAME/Tibet to CAMP/Tibet. Phys. Chem. Earth Parts A B C 2003, 28, 63–74. [Google Scholar] [CrossRef]
- Zhao, P.; Chen, L. Study on climatic features of surface turbulent heat exchange coefficients and surface thermal sources over the Qinghai-Xizang Plateau. Acta Meteorol. Sin. 2000, 2000, 13–29. [Google Scholar]
- Ma, Y.; Fan, S.; Ishikawa, H.; Tsukamoto, O.; Yao, T.; Koike, T.; Zuo, H.; Hu, Z.; Su, Z. Diurnal and inter-monthly variation of land surface heat fluxes over the central Tibetan Plateau area. Theor. Appl. Climatol. 2004, 80, 259–273. [Google Scholar] [CrossRef]
- Ma, Y.; Zhong, L.; Wang, B.; Ma, W.; Chen, X.; Li, M. Determination of land surface heat fluxes over heterogeneous landscape of the Tibetan Plateau by using the MODIS and in situ data. Atmos. Chem. Phys. 2011, 11, 10461–10469. [Google Scholar] [CrossRef] [Green Version]
- Han, C.; Ma, Y.; Chen, X.; Su, Z. Estimates of land surface heat fluxes of the Mt. Everest region over the Tibetan Plateau utilizing ASTER data. Atmos. Res. 2016, 168, 180–190. [Google Scholar] [CrossRef]
- Huang, S.; Deng, Y.; Wang, J. Revisiting the global surface energy budgets with maximum-entropy-production model of surface heat fluxes. Clim. Dyn. 2016, 49, 1531–1545. [Google Scholar] [CrossRef]
- Li, N.; Zhao, P.; Wang, J.; Deng, Y. Estimation of surface heat fluxes over the central tibetan plateau using the maximum entropy production model. J. Geophys. Res. Atmos. 2019, 124, 6827–6840. [Google Scholar] [CrossRef] [Green Version]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, S0960148118303677. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Kistler, R.; Kalnay, E.; Woollen, J.; Chelliah, M.; Ebisuzaki, W.; Kousky, V.; Dool, H.V.D.; Collins, W.; Saha, S.; White, G.; et al. The NCEP-NCAR 50-year reanalysis: Monthly means CD-ROM and documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–268. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J. NCEP–DOE AMIP-II reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Wang, J.; Bras, R.L. A model of evapotranspiration based on the theory of maximum entropy production. Water Resour. Res. 2011, 47, W03521. [Google Scholar] [CrossRef]
- Huang, S.; Wang, J. A coupled force-restore model of surface temperature and soil moisture using the maximum entropy production model of heat fluxes. J. Geophys. Res. Atmos. 2016, 121, 7528–7547. [Google Scholar] [CrossRef]
- Ge, F.; Sielmann, F.; Zhu, X.H.; Fraedrich, K.; Zhi, X.F.; Peng, T.; Wang, L. The link between Tibetan Plateau monsoon and Indian summer precipitation: A linear diagnostic perspective. Clim. Dyn. 2017, 49, 4201–4215. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coronato, F.R.; Bertiller, M.B. Precipitation and landscape related effects on soil moisture in semi-arid rangelands of Patagonia. J. Arid Environ. 1996, 34, 1–9. [Google Scholar] [CrossRef]
- Yang, K.; Qin, J.; Guo, X.; Zhou, D.; Ma, Y. method development for estimating sensible heat flux over the Tibetan Plateau from CMA Data. J. Appl. Meteorol. Climatol. 2009, 48, 2474–2486. [Google Scholar] [CrossRef]
- Brunke, M.A.; Wang, Z.; Zeng, X.; Bosilovich, M.; Shie, C.L. An assessment of the uncertainties in ocean surface turbulent fluxes in 11 reanalysis, satellite-derived, and combined global datasets. J. Clim. 2011, 24, 5469–5493. [Google Scholar] [CrossRef]
- Xie, J.; Yu, Y.; Li, J.; Ge, J.; Liu, C. Comparison of surface sensible and latent heat fluxes over the Tibetan Plateau from reanalysis and observations. Meteorol. Atmos. Phys. 2018, 131, 567–584. [Google Scholar] [CrossRef]
- Han, C.; Ma, Y.; Chen, X.; Su, Z. Trends of land surface heat fluxes on the Tibetan Plateau from 2001 to 2012. Int. J. Climatol. 2017, 37, 4757–4767. [Google Scholar] [CrossRef]
- Guo, D.; Yang, M.; Wang, H. Sensible and latent heat flux response to diurnal variation in soil surface temperature and moisture under different freeze/thaw soil conditions in the seasonal frozen soil region of the central Tibetan Plateau. Environ. Earth Sci. 2011, 63, 97–107. [Google Scholar] [CrossRef]
- Wu, S.; Yin, Y.; Du, Z.; Yang, Q.J. Climatic trends over the Tibetan Plateau during 1971–2000. J. Geogr. Sci. 2007, 17, 141–151. [Google Scholar] [CrossRef]
- Bibi, S.; Wang, L.; Li, X.; Zhou, J.; Chen, D.; Yao, T. Climatic and associated cryospheric, biospheric, and hydrological changes on the Tibetan Plateau: A review: Review on climate change and its effects on spheres on Tibetan Plateau. Int. J. Climatol. 2018, 38, e1–e17. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Luo, W.; Chen, W.; Zheng, G. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.; Pu, J.; Lu, A.; Wang, Y.; Yu, W. Recent glacial retreat and its impact on hydrological processes on the Tibetan Plateau, china, and surrounding regions. Arct. Antarct. Alp. Res. 2007, 39, 642–650. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Zhou, T.; Liu, M.; Chen, Y.; Shang, H.; Zhu, L.; Shedayi, A.A.; Yu, H.; Cheng, G.; Liu, G.; et al. Linkages of the dynamics of glaciers and lakes with the climate elements over the Tibetan Plateau. Earth Sci. Rev. 2018, 185, 308–324. [Google Scholar] [CrossRef]
- Ma, W.; Ma, Y. Modeling the influence of land surface flux on the regional climate of the Tibetan Plateau. Theor. Appl. Climatol. 2016, 125, 45–52. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, J.; Zhang, L.; Wang, Y.; Li, Y.; Wang, X. NDVI dynamic changes and their relationship with meteorological factors and soil moisture. Environ. Earth Sci. 2018, 77, 582. [Google Scholar] [CrossRef]
- Li, W.K.; Qiu, B.; Guo, W.D.; Zhu, Z.W.; Hsu, P.C. Intraseasonal variability of Tibetan Plateau snow cover. Int. J. Climatol. 2019, 1–16. [Google Scholar] [CrossRef] [Green Version]






| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SHEC (W/m2) | 22.0 | 31.7 | 45.6 | 62.4 | 69.5 | 64.8 | 52.6 | 53.4 | 52.1 | 39.3 | 24.1 | 16.1 |
| LEEC (W/m2) | 0.22 | 0.57 | 1.37 | 0.54 | 1.78 | 6.77 | 16.86 | 16.69 | 4.56 | 1.51 | 0.24 | 0.04 |
| ERA5 | ERA-Interim | JRA-55 | MERRA-2 | NCEP-I | NCEP-II | |
|---|---|---|---|---|---|---|
| β | 1.1 | 2.4 | 4.0 | 8.2 | 4.1 | 3.5 |
| LE | R2 | RMSE (W m−2) | MBE (W m−2) | |
|---|---|---|---|---|
| ERA5 | Reanalysis | 0.07 | 46.8 | 31.0 |
| MR | 0.43 | 11.2 | −3.5 | |
| ERA-Interim | Reanalysis | 0.14 | 33.7 | 28.8 |
| MR | 0.15 | 12.8 | −0.9 | |
| JRA-55 | Reanalysis | 0.13 | 42.3 | 36.1 |
| MR | 0.34 | 19.1 | 5.6 | |
| MERRA-2 | Reanalysis | 0.38 | 15.8 | 8.4 |
| MR | 0.54 | 10.1 | −0.34 | |
| NCEP-I | Reanalysis | 0.01 | 52.1 | 49.3 |
| MR | 0.14 | 12.8 | 0.10 | |
| NCEP-II | Reanalysis | 0.09 | 48.4 | 44.5 |
| MR | 0.11 | 13.2 | 0.20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Zhao, P.; Wang, J.; Deng, Y. The Long-Term Change of Latent Heat Flux over the Western Tibetan Plateau. Atmosphere 2020, 11, 262. https://doi.org/10.3390/atmos11030262
Li N, Zhao P, Wang J, Deng Y. The Long-Term Change of Latent Heat Flux over the Western Tibetan Plateau. Atmosphere. 2020; 11(3):262. https://doi.org/10.3390/atmos11030262
Chicago/Turabian StyleLi, Na, Ping Zhao, Jingfeng Wang, and Yi Deng. 2020. "The Long-Term Change of Latent Heat Flux over the Western Tibetan Plateau" Atmosphere 11, no. 3: 262. https://doi.org/10.3390/atmos11030262
APA StyleLi, N., Zhao, P., Wang, J., & Deng, Y. (2020). The Long-Term Change of Latent Heat Flux over the Western Tibetan Plateau. Atmosphere, 11(3), 262. https://doi.org/10.3390/atmos11030262