A Budget-Based Turbulence Length Scale Diagnostic
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Spectral TKE Equation
2.2. Formulation of the New Turbulence Length Scale
3. Method and Data
3.1. Estimation of the New Turbulence Length Scale
3.2. LES Simulations
3.3. Fit of Turbulence Length Scale
3.4. Computation of Turbulence Fluxes
3.5. Gravity Waves
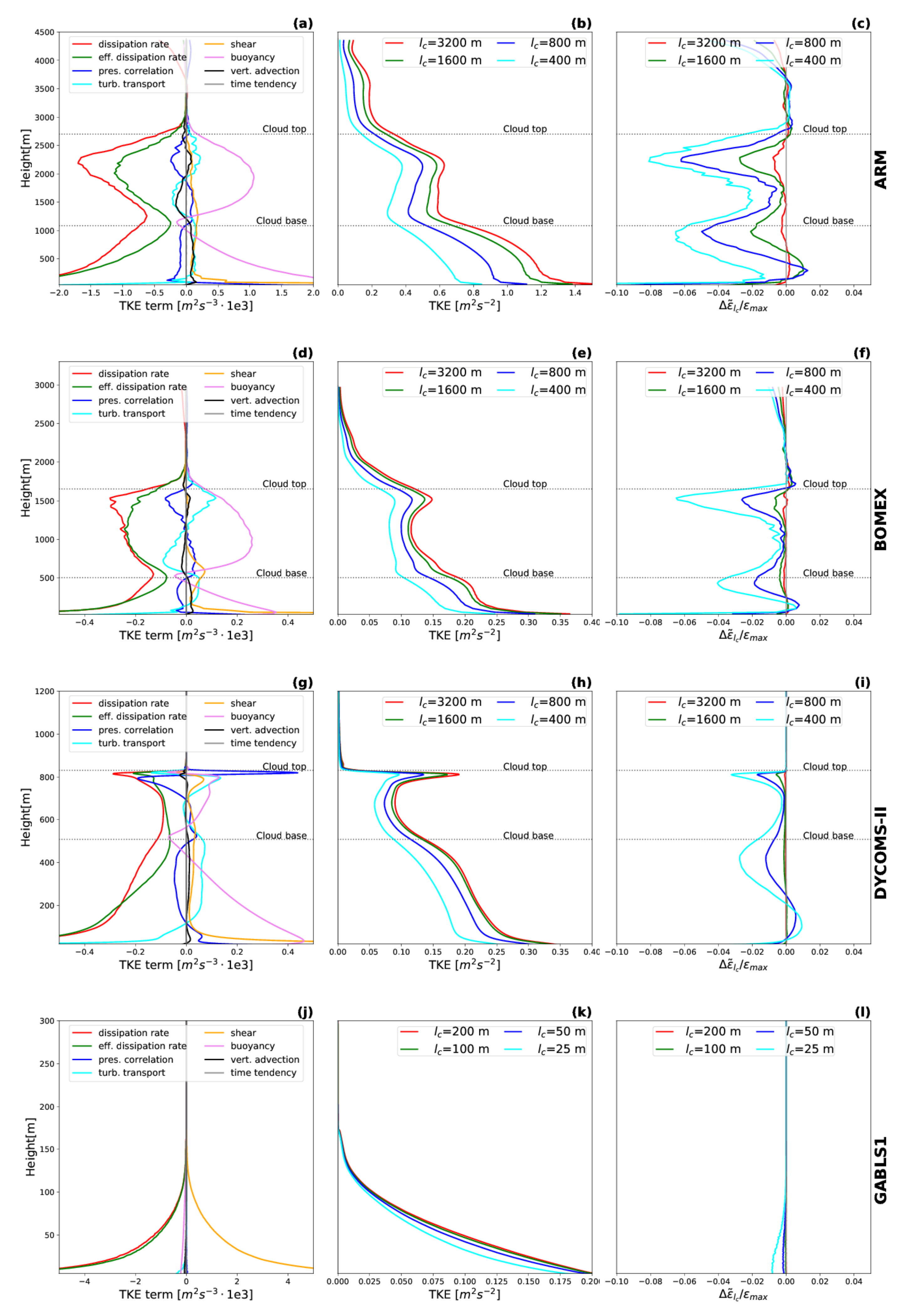
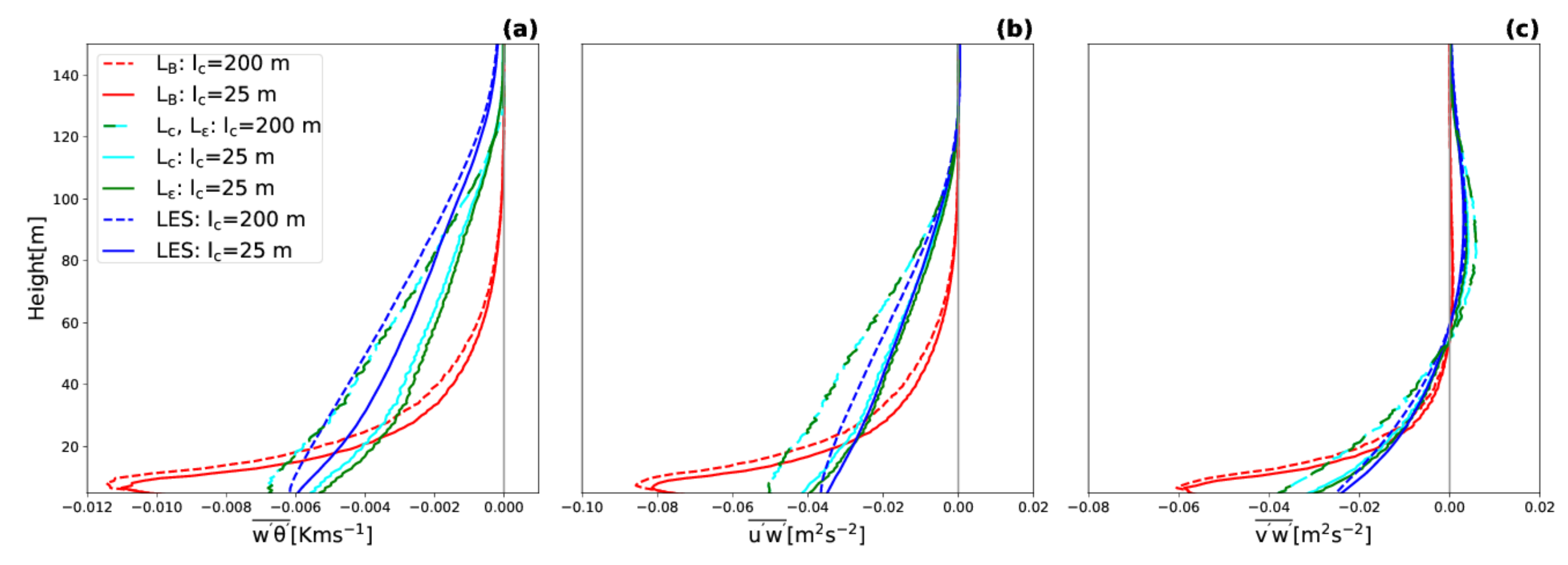
4. Results
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric Boundary Layer |
| ARM | Atmospheric Radiation Measurement |
| BOMEX | Barbados Oceanographic and Meteorological Experiment |
| DYCOMS-II | second Dynamics and Chemistry of Marine Stratocumulus |
| GABLS | GEWEX Atmospheric Boundary Layer Study |
| GC | Global Circulation |
| LES | Large Eddy Simulation |
| NWP | Numerical Weather Prediction |
| TKE | Turbulence Kinetic Energy |
References
- Wyngaard, J.C. Toward Numerical Modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Honnert, R.; Masson, V.; Couvreux, F. A Diagnostic for Evaluating the Representation of Turbulence in Atmospheric Models at the Kilometric Scale. J. Atmos. Sci. 2011, 68, 3112–3131. [Google Scholar] [CrossRef]
- Honnert, R. Representation of the grey zone of turbulence in the atmospheric boundary layer. Adv. Sci. Res. 2016, 13, 63–67. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Mellor, G.L.; Yamada, T. A Hierarchy of Turbulence Closure Models for Planetary Boundary Layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef] [Green Version]
- Golaz, J.C.; Larson, V.E.; Cotton, W.R. A PDF-Based Model for Boundary Layer Clouds. Part I: Method and Model Description. J. Atmos. Sci. 2002, 59, 3540–3551. [Google Scholar] [CrossRef] [Green Version]
- Mironov, D.V.; Machulskaya, E. A Turbulence Kinetic Energy—Scalar Variance Turbulence Parameterization Scheme. 2017. Available online: www.cosmo-model.org (accessed on 18 April 2020).
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Redelsperger, J.L.; Mahé, F.; Carlotti, P. A Simple And General Subgrid Model Suitable Both For Surface Layer And Free-Stream Turbulence. Bound.-Layer Meteorol. 2001, 101, 375–408. [Google Scholar] [CrossRef]
- Cheng, Y.; Canuto, V.; Howard, A. An Improved Model for the Turbulent PBL. J. Atmos. Sci. 2002, 59, 1550–1565. [Google Scholar] [CrossRef] [Green Version]
- Bašták Ďurán, I.; Geleyn, J.F.; Váňa, F. A Compact Model for the Stability Dependency of TKE Production-Destruction-Conversion Terms Valid for the Whole Range of Richardson Numbers. J. Atmos. Sci. 2014, 71, 3004–3026. [Google Scholar] [CrossRef]
- Lenderink, G.; Holtslag, A.A.M. An updated length-scale formulation for turbulent mixing in clear and cloudy boundary layers. Q. J. R. Meteorol. Soc. 2004, 130, 3405–3427. [Google Scholar] [CrossRef] [Green Version]
- Sáanchez, E.; Cuxart, J. A buoyancy-based mixing-length proposal for cloudy boundary layers. Q. J. R. Meteorol. Soc. 2004, 130, 3385–3404. [Google Scholar] [CrossRef]
- Nakanishi, M. Improvement of the Mellor–Yamada Turbulence Closure Model Based on Large-Eddy Simulation Data. Bound.-Layer Meteorol. 2001, 99, 349–378. [Google Scholar] [CrossRef]
- Kitamura, Y. Estimating Dependence of the Turbulent Length Scales on Model Resolution Based on a Priori Analysis. J. Atmos. Sci. 2015, 72, 750–762. [Google Scholar] [CrossRef]
- Bašták Ďurán, I.; Geleyn, J.F.; Váňa, F.V.; Schmidli, J.; Brožková, R. A Turbulence Scheme with Two Prognostic Turbulence Energies. J. Atmos. Sci. 2018, 75, 3381–3402. [Google Scholar] [CrossRef]
- Blackadar, A.K. The vertical distribution of wind and turbulent exchange in a neutral atmosphere. J. Geophys. Res. (1896–1977) 1962, 67, 3095–3102. [Google Scholar] [CrossRef] [Green Version]
- Cedilnik, J. Parallel Suites Documentation. 2005. Available online: http://www.https.com//www.rclace.eu/file/physics/2005 (accessed on 18 April 2020).
- Von Karman, T. Mechanische Ähnlichkeit und Turbulenz. Nachr. Ges. Wiss. Göttingen 1930, 58–76, also Proceedings of the Third International Congress of Applied Mechanics. Stockholm 1930. [Google Scholar]
- Prandtl, L. Zur turbulenten Stromung in Rohren und langs Platten. Ergebnisse der Aerodynamischen Versuchsanstalt zu GöTtingen 1932, 4, 18–29. [Google Scholar]
- Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Teixeira, J.; Cheinet, S. A Simple Mixing Length Formulation for the Eddy-Diffusivity Parameterization of Dry Convection. Bound.-Layer Meteorol. 2004, 110, 435–453. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an Improved Turbulence Closure Model for the Atmospheric Boundary Layer. J. Meteorol. Soc. Jpn. Ser. II 2009, 87, 895–912. [Google Scholar] [CrossRef] [Green Version]
- Bogenschutz, P.A.; Krueger, S.K. A simplified PDF parameterization of subgrid-scale clouds and turbulence for cloud-resolving models. J. Adv. Model. Earth Syst. 2013, 5, 195–211. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of Orography-Induced Turbulence in a Mesobeta–Scale Model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
- Kantha, L.H. The length scale equation in turbulence models. Nonlinear Process. Geophys. 2004, 11, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Zilitinkevich, S.; Elperin, T.; Kleeorin, N.; Rogachevskii, I.; Esau, I. A Hierarchy of Energy- and Flux-Budget (EFB) Turbulence Closure Models for Stably-Stratified Geophysical Flows. Bound.-Layer Meteor. 2013, 146, 341–373. [Google Scholar] [CrossRef] [Green Version]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Kolmogorov, A. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. USSR Acad. Sci. 1941, 30, 299–303. (In Russian) [Google Scholar]
- de Roode, S.R.; Duynkerke, P.G.; Jonker, H.J.J. Large-Eddy Simulation: How Large is Large Enough? J. Atmos. Sci. 2004, 61, 403–421. [Google Scholar] [CrossRef]
- Cuxart, J.; Bougeault, P.; Redelsperger, J.L. A turbulence scheme allowing for mesoscale and large-eddy simulations. Q. J. R. Meteorol. Soc. 2000, 126, 1–30. [Google Scholar] [CrossRef]
- Peña, A.; Gryning, S.E.; Mann, J. On the length-scale of the wind profile. Q. J. R. Meteorol. Soc. 2010, 136, 2119–2131. [Google Scholar] [CrossRef]
- Weinstock, J. On the Theory of Turbulence in the Buoyancy Subrange of Stably Stratified Flows. J. Atmos. Sci. 1978, 35, 634–649. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Li, Q.; Argentini, S.; Sayde, C.; Gentine, P. Turbulence Spectra in the Stable Atmospheric Boundary Layer. arXiv 2018, arXiv:1801.05847v3. [Google Scholar]
- O’Connor, E.J.; Illingworth, A.J.; Brooks, I.M.; Westbrook, C.D.; Hogan, R.J.; Davies, F.; Brooks, B.J. A Method for Estimating the Turbulent Kinetic Energy Dissipation Rate from a Vertically Pointing Doppler Lidar, and Independent Evaluation from Balloon-Borne In Situ Measurements. J. Atmos. Ocean. Technol. 2010, 27, 1652–1664. [Google Scholar] [CrossRef] [Green Version]
- Hatlee, S.C.; Wyngaard, J.C. Improved Subfilter-Scale Models from the HATS Field Data. J. Atmos. Sci. 2007, 64, 1694–1705. [Google Scholar] [CrossRef]
- Zhou, B.; Zhu, K.; Xue, M. A Physically Based Horizontal Subgrid-Scale Turbulent Mixing Parameterization for the Convective Boundary Layer. J. Atmos. Sci. 2017, 74, 2657–2674. [Google Scholar] [CrossRef]
- Zhang, X.; Bao, J.W.; Chen, B.; Grell, E.D. A Three-Dimensional Scale-Adaptive Turbulent Kinetic Energy Scheme in the WRF-ARW Model. Mon. Weather Rev. 2018, 146, 2023–2045. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Stevens, B. A two Turbulence Kinetic Energy model as a scale-adaptive approach to modeling the planetary boundary layer. J. Adv. Model. Earth Syst. 2016, 8, 224–243. [Google Scholar] [CrossRef] [Green Version]
- Boutle, I.A.; Eyre, J.E.J.; Lock, A.P. Seamless Stratocumulus Simulation across the Turbulent Gray Zone. Mon. Weather Rev. 2014, 142, 1655–1668. [Google Scholar] [CrossRef]
- Efstathiou, G.A.; Beare, R.J. Quantifying and improving sub-grid diffusion in the boundary-layer grey zone. Q. J. R. Meteorol. Soc. 2015, 141, 3006–3017. [Google Scholar] [CrossRef]
- Kurowski, M.J.; Teixeira, J. A Scale-Adaptive Turbulent Kinetic Energy Closure for the Dry Convective Boundary Layer. J. Atmos. Sci. 2018, 75, 675–690. [Google Scholar] [CrossRef]
- Lilly, D. The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences, New York, NY, USA, 14–16 November 1967; pp. 195–210. [Google Scholar]
- Heinze, R.; Mironov, D.; Raasch, S. Second-moment budgets in cloud topped boundary layers: A large-eddy simulation study. J. Adv. Model. Earth Syst. 2015, 7, 510–536. [Google Scholar] [CrossRef]
- O’Neill, P.; Nicolaides, D.; Honnery, D.; Soria, J. Autocorrelation functions and the determination of integral length with reference to experimental and numerical data. In Proceedings of the Fifteenth Australasian Fluid Mechanics Conference, Sydney, Australia, 13–17 December 2004; Behnia, M., Lin, W., McBain, G., Eds.; The University of Sydney: Sydney, Australia, 2004; pp. 1–4. [Google Scholar]
- Stevens, B.; Moeng, C.H.; Ackerman, A.S.; Bretherton, C.S.; Chlond, A.; de Roode, S.; Edwards, J.; Golaz, J.C.; Jiang, H.; Khairoutdinov, M.; et al. Evaluation of Large-Eddy Simulations via Observations of Nocturnal Marine Stratocumulus. Mon. Weather Rev. 2005, 133, 1443–1462. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.R.; Cederwall, R.T.; Chlond, A.; Duynkerke, P.G.; Golaz, J.C.; Khairoutdinov, M.; Lewellen, D.C.; Lock, A.P.; MacVean, M.K.; Moeng, C.H.; et al. Large-eddy simulation of the diurnal cycle of shallow cumulus convection over land. Q. J. R. Meteorol. Soc. 2002, 128, 1075–1093. [Google Scholar] [CrossRef] [Green Version]
- Lenderink, G.; Siebesma, A.P.; Cheinet, S.; Irons, S.; Jones, C.G.; Marquet, P.; Müller, F.M.; Olmeda, D.; Calvo, J.; Sánchez, E.; et al. The diurnal cycle of shallow cumulus clouds over land: A single-column model intercomparison study. Q. J. R. Meteorol. Soc. 2004, 130, 3339–3364. [Google Scholar] [CrossRef] [Green Version]
- Siebesma, A.P.; Bretherton, C.S.; Brown, A.; Chlond, A.; Cuxart, J.; Duynkerke, P.G.; Jiang, H.; Khairoutdinov, M.; Lewellen, D.; Moeng, C.H.; et al. A Large Eddy Simulation Intercomparison Study of Shallow Cumulus Convection. J. Atmos. Sci. 2003, 60, 1201–1219. [Google Scholar] [CrossRef]
- Holtslag, B. Preface: GEWEX Atmospheric Boundary-layer Study (GABLS) on Stable Boundary Layers. Bound.-Layer Meteorol. 2006, 118, 243–246. [Google Scholar] [CrossRef]
- Beare, R.J.; Macvean, M.K.; Holtslag, A.A.M.; Cuxart, J.; Esau, I.; Golaz, J.C.; Jimenez, M.A.; Khairoutdinov, M.; Kosovic, B.; Lewellen, D.; et al. An Intercomparison of Large-Eddy Simulations of the Stable Boundary Layer. Bound.-Layer Meteorol. 2006, 118, 247–272. [Google Scholar] [CrossRef] [Green Version]
- Cuxart, J.; Holtslag, A.A.M.; Beare, R.J.; Bazile, E.; Beljaars, A.; Cheng, A.; Conangla, L.; Ek, M.; Freedman, F.; Hamdi, R.; et al. Single-Column Model Intercomparison for a Stably Stratified Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2006, 118, 273–303. [Google Scholar] [CrossRef] [Green Version]
- van Heerwaarden, C.C.; van Stratum, B.J.H.; Heus, T.; Gibbs, J.A.; Fedorovich, E.; Mellado, J.P. MicroHH 1.0: A computational fluid dynamics code for direct numerical simulation and large-eddy simulation of atmospheric boundary layer flows. Geosci. Model Dev. 2017, 10, 3145–3165. [Google Scholar] [CrossRef] [Green Version]
- van Heerwaarden, C.; van Stratum, B.; Heus, T. microhh/microhh: 1.0.0. Zenodo 2017. [Google Scholar] [CrossRef]
- Pressel, K.G.; Mishra, S.; Schneider, T.; Kaul, C.M.; Tan, Z. Numerics and subgrid-scale modeling in large eddy simulations of stratocumulus clouds. J. Adv. Model. Earth Syst. 2017, 9, 1342–1365. [Google Scholar] [CrossRef]
- Shi, X.; Enriquez, R.M.; Street, R.L.; Bryan, G.H.; Chow, F.K. An Implicit Algebraic Turbulence Closure Scheme for Atmospheric Boundary Layer Simulation. J. Atmos. Sci. 2019, 76, 3367–3386. [Google Scholar] [CrossRef]
- Bastak Duran, I.; Schmidli, J.; Bhattacharya, R. Data for A budget-based turbulence length scale diagnostic. Zenodo 2020. [Google Scholar] [CrossRef]


| Case | Hor. Domain Size | Hor. Resol. | Ver. Domain Size | Ver. Resol. | Integration Time |
|---|---|---|---|---|---|
| ARM | 12.8 km × 12.8 km | 12.5 m | 1500 m | 31.125 m | 10 h |
| BOMEX | 12.8 km × 12.8 km | 12.5 m | 3000 m | 23.44 m | 6 h |
| DYCOMS-II | 12.8 km × 12.8 km | 12.5 m | 1500 m | 2.93 m | 4 h |
| GABLS1 | 800 m × 800 m | 0.78125 m | 400 m | 0.78125 m | 6 h |
| Fitting Constant | First Guess | Minimal Value | Maximal Value |
|---|---|---|---|
| 1000 m | 0 m | 2000 m | |
| 350 m | 0 m | 1000 m | |
| 5.5 | 0 | 100 | |
| 3.0 | 0 | 100 | |
| 0.02 | −0.2 | 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bašták Ďurán, I.; Schmidli, J.; Bhattacharya, R. A Budget-Based Turbulence Length Scale Diagnostic. Atmosphere 2020, 11, 425. https://doi.org/10.3390/atmos11040425
Bašták Ďurán I, Schmidli J, Bhattacharya R. A Budget-Based Turbulence Length Scale Diagnostic. Atmosphere. 2020; 11(4):425. https://doi.org/10.3390/atmos11040425
Chicago/Turabian StyleBašták Ďurán, Ivan, Juerg Schmidli, and Ritthik Bhattacharya. 2020. "A Budget-Based Turbulence Length Scale Diagnostic" Atmosphere 11, no. 4: 425. https://doi.org/10.3390/atmos11040425





