Characteristics of Raindrop Size Distribution on the Eastern Slope of the Tibetan Plateau in Summer
Abstract
:1. Introduction
2. Data and Methods
2.1. Experiment, Instrument, and Measurements
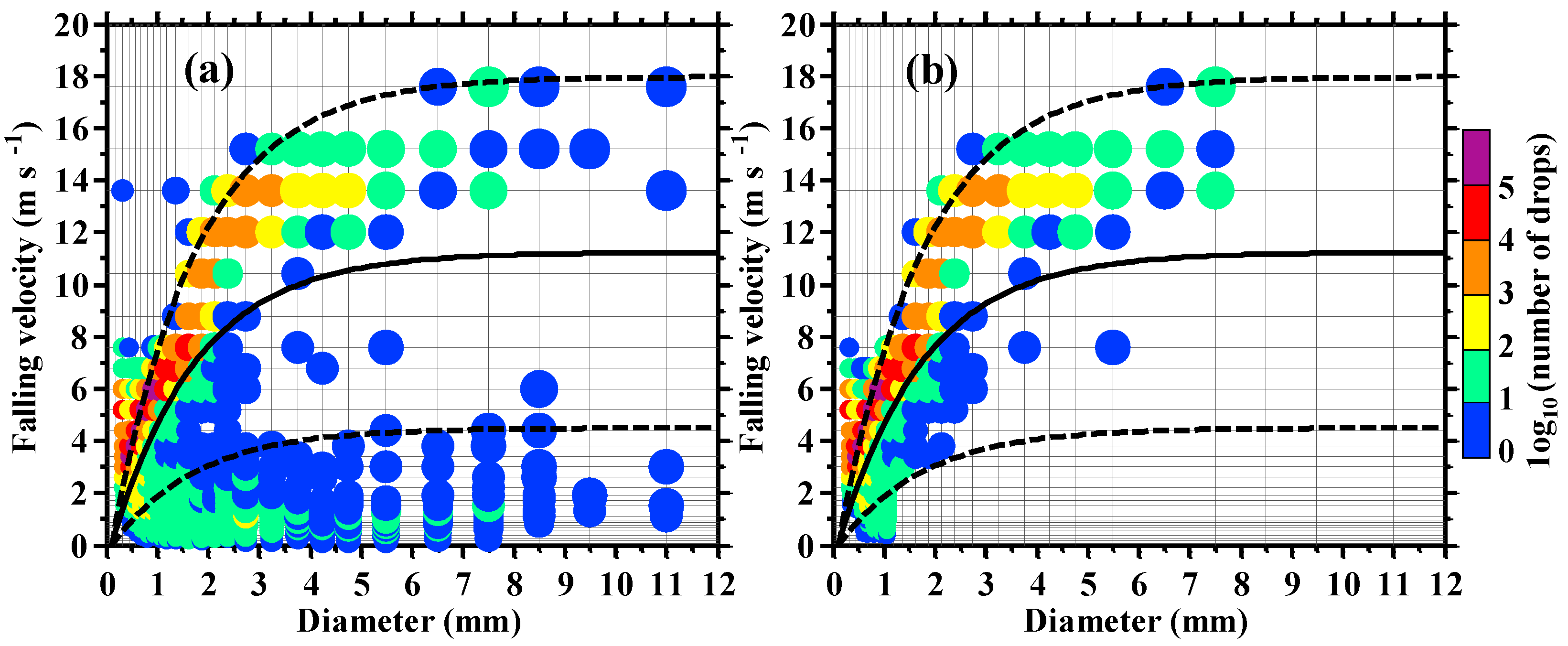
2.2. Data QC and Rainfall Physical Quantity Calculation
2.3. Rain Type Classification
3. Results
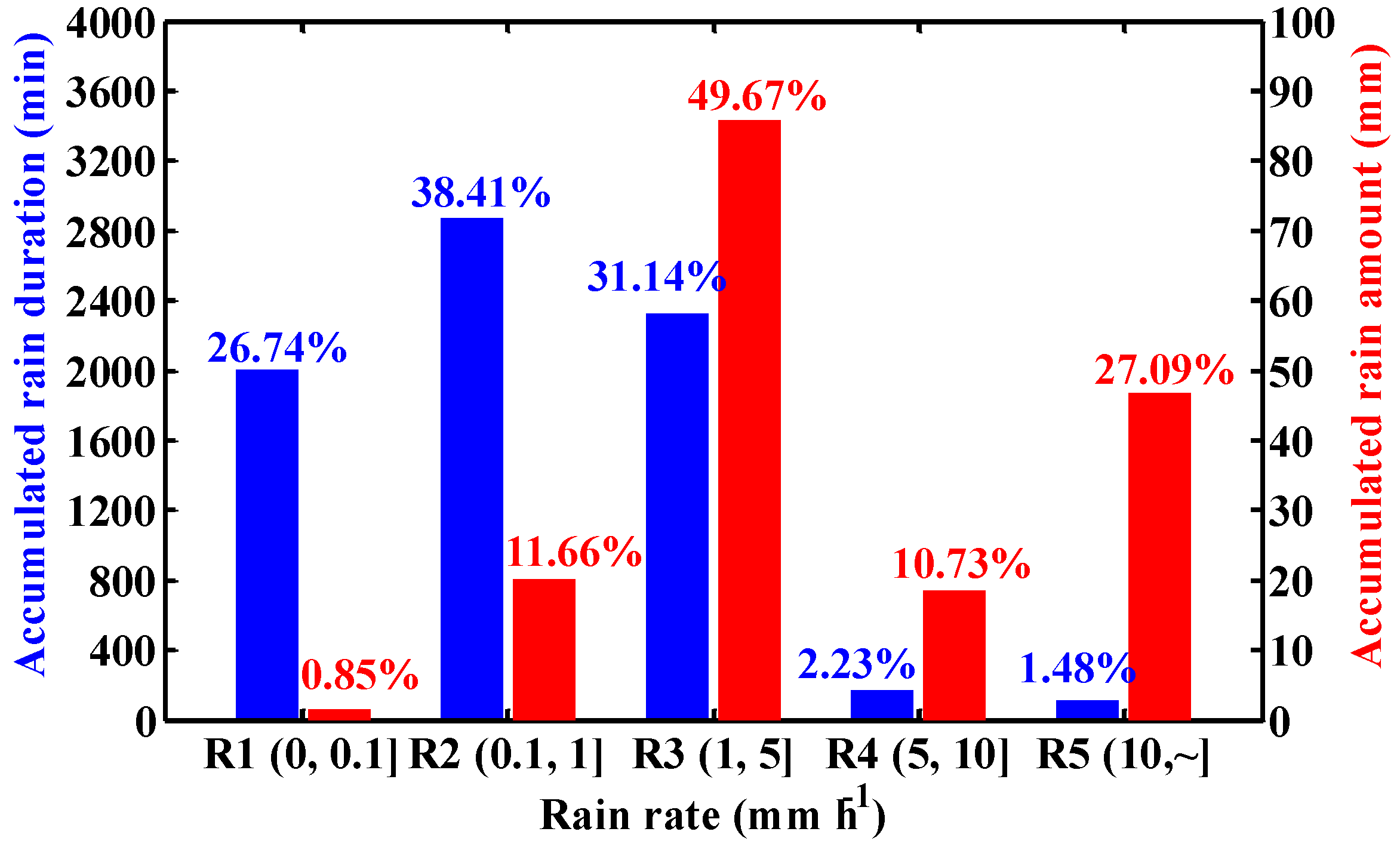
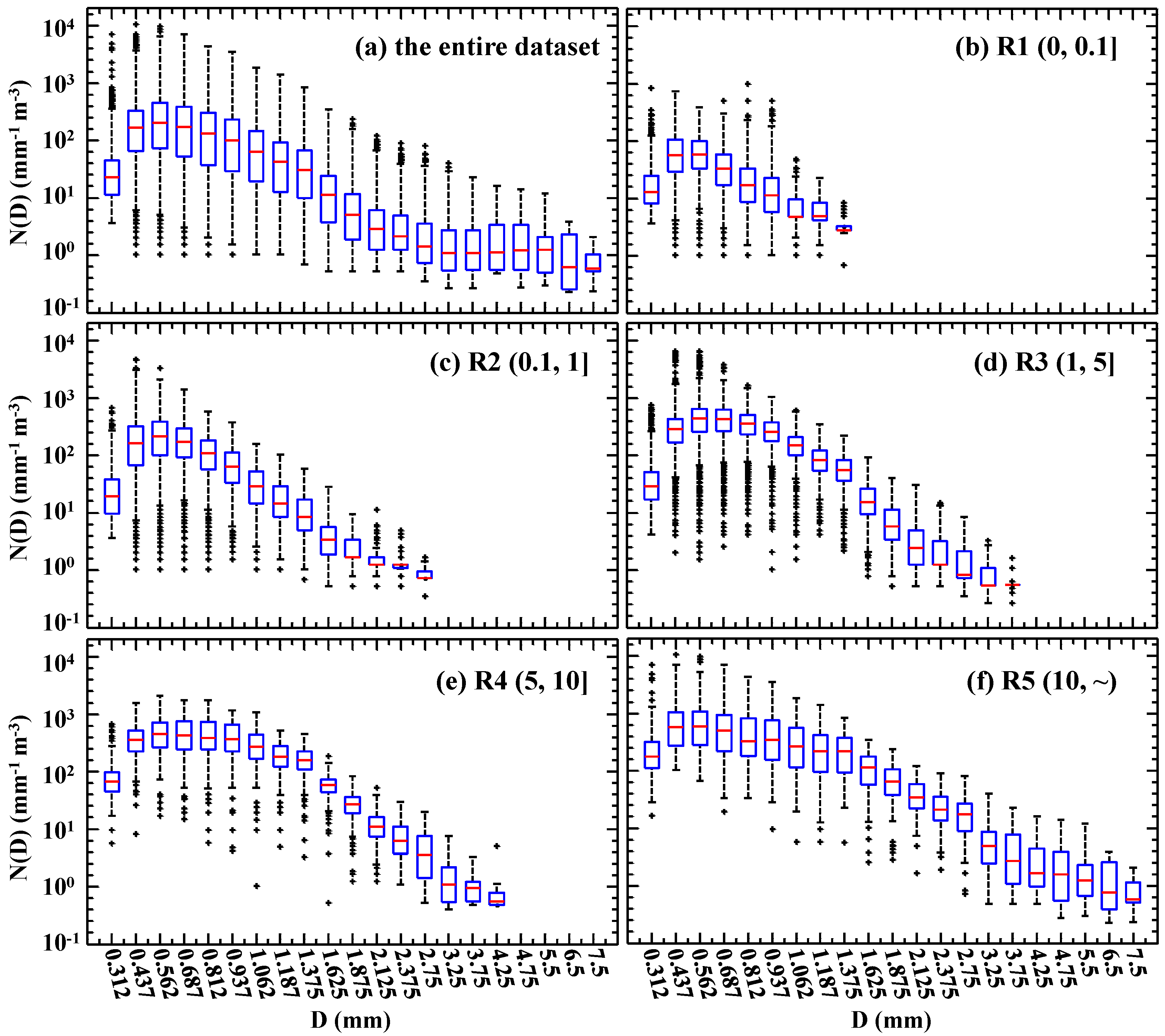
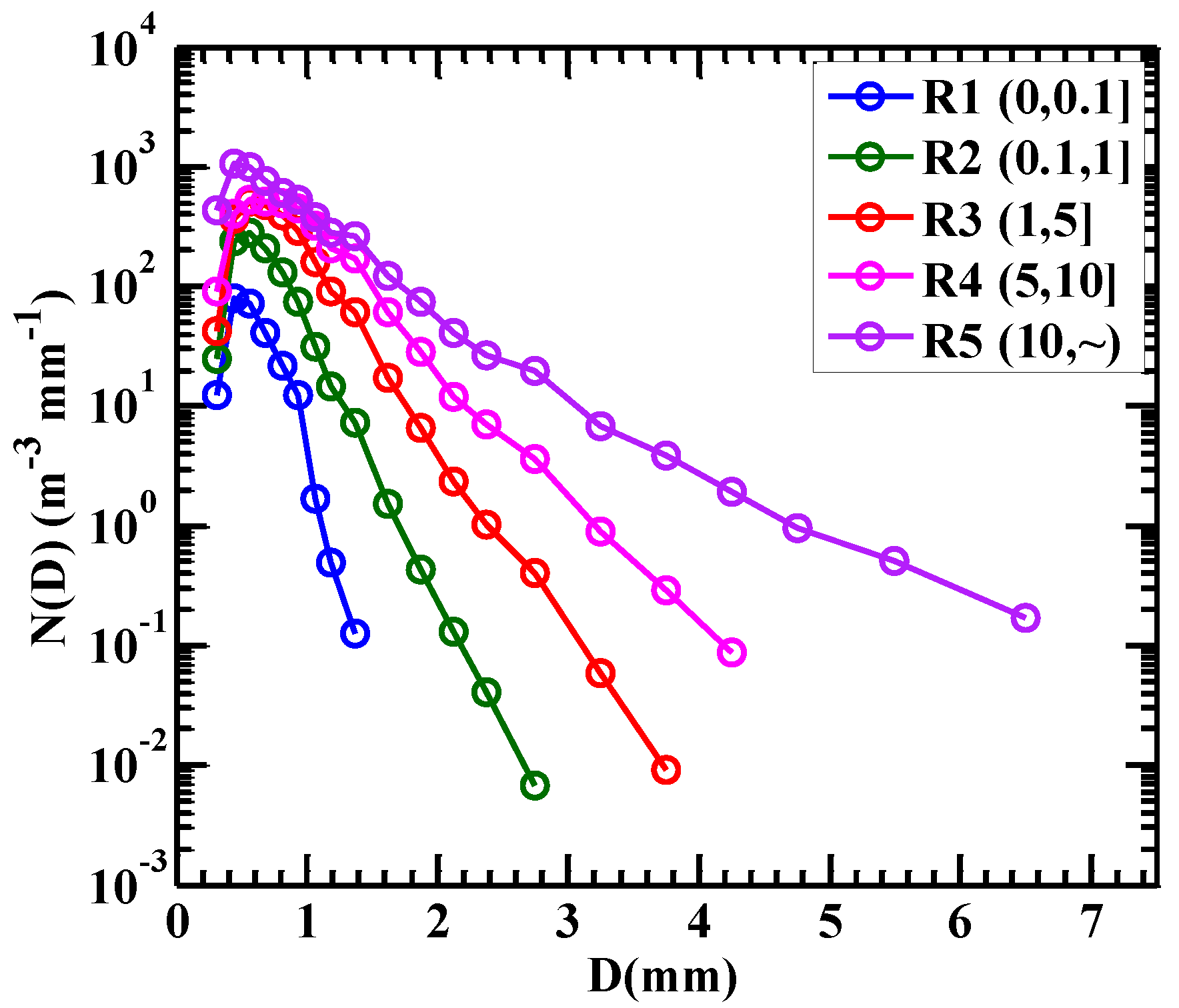
3.1. DSD Characteristics for Different Rain Rates
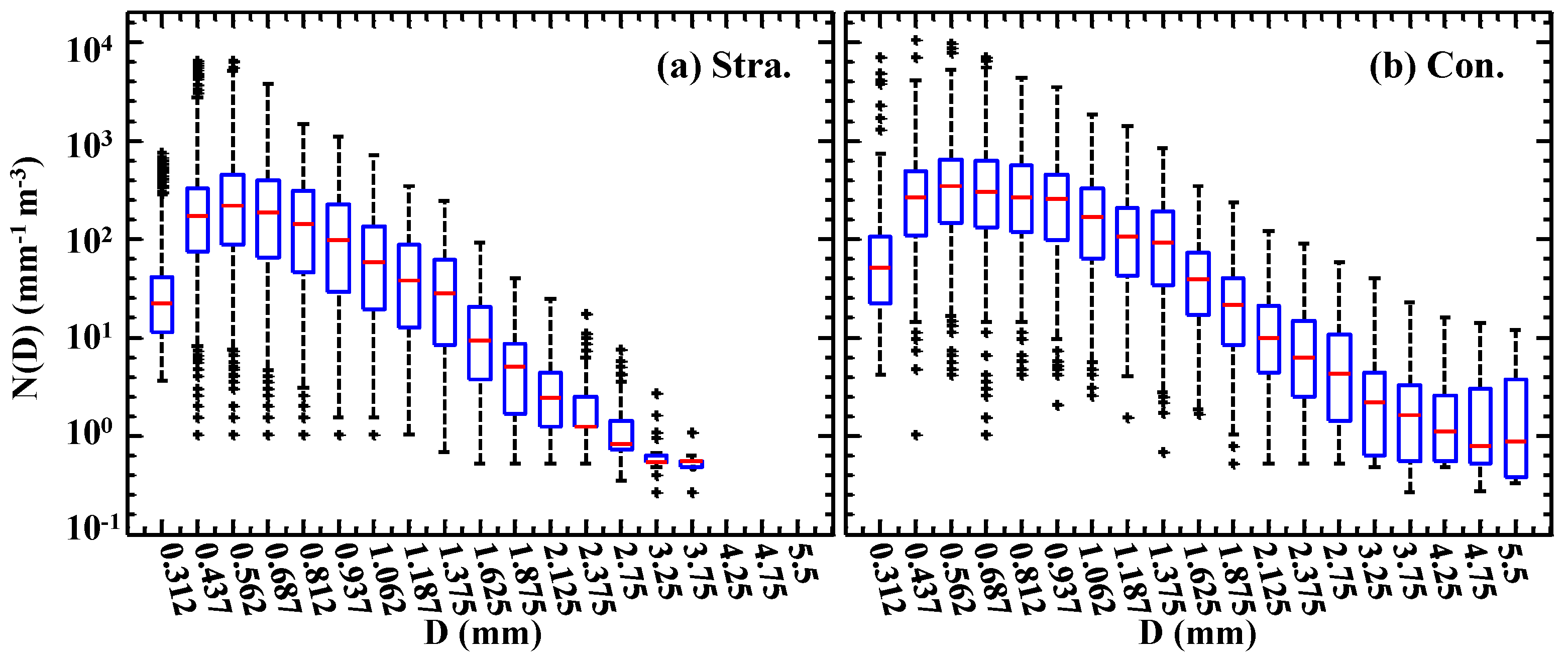
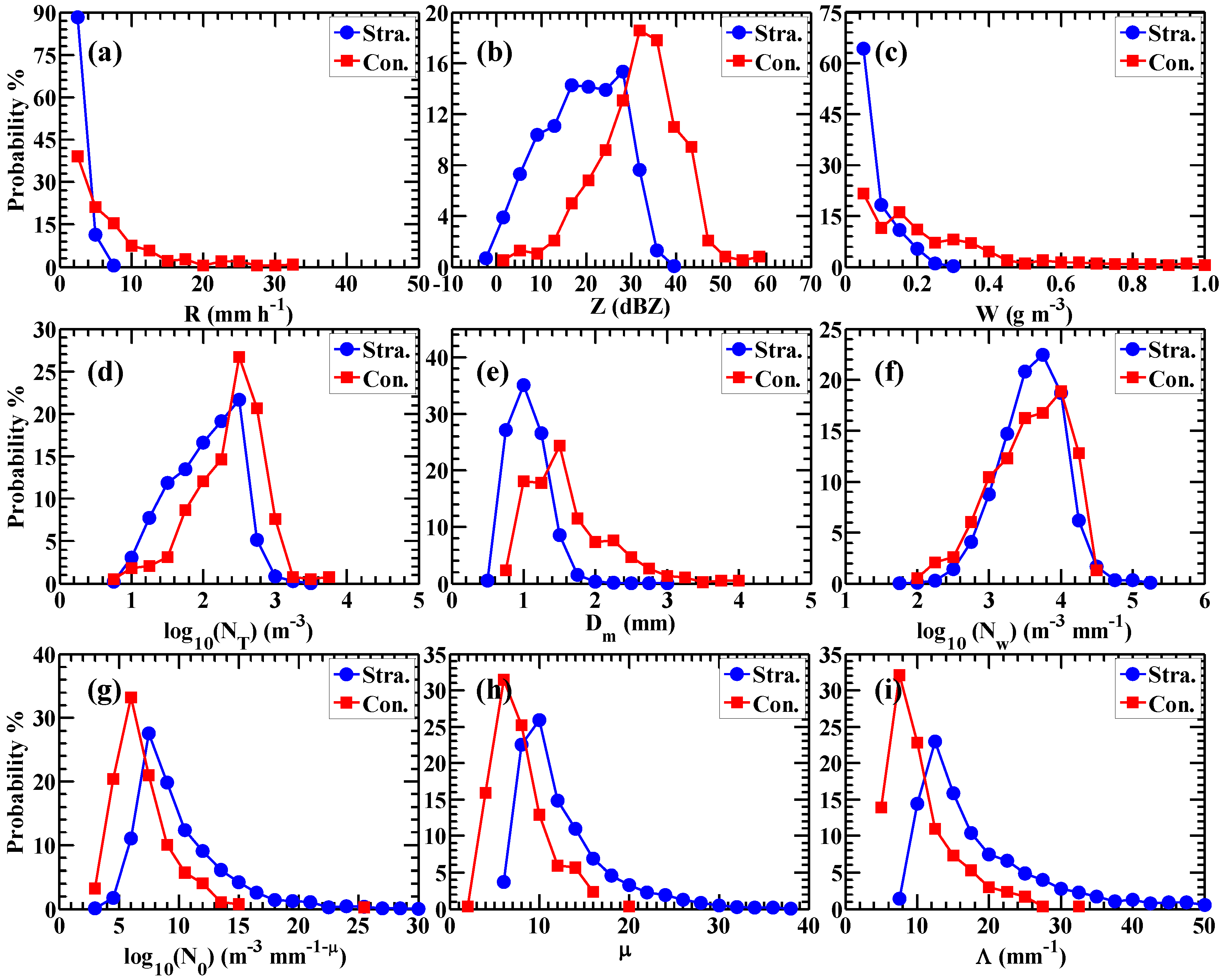
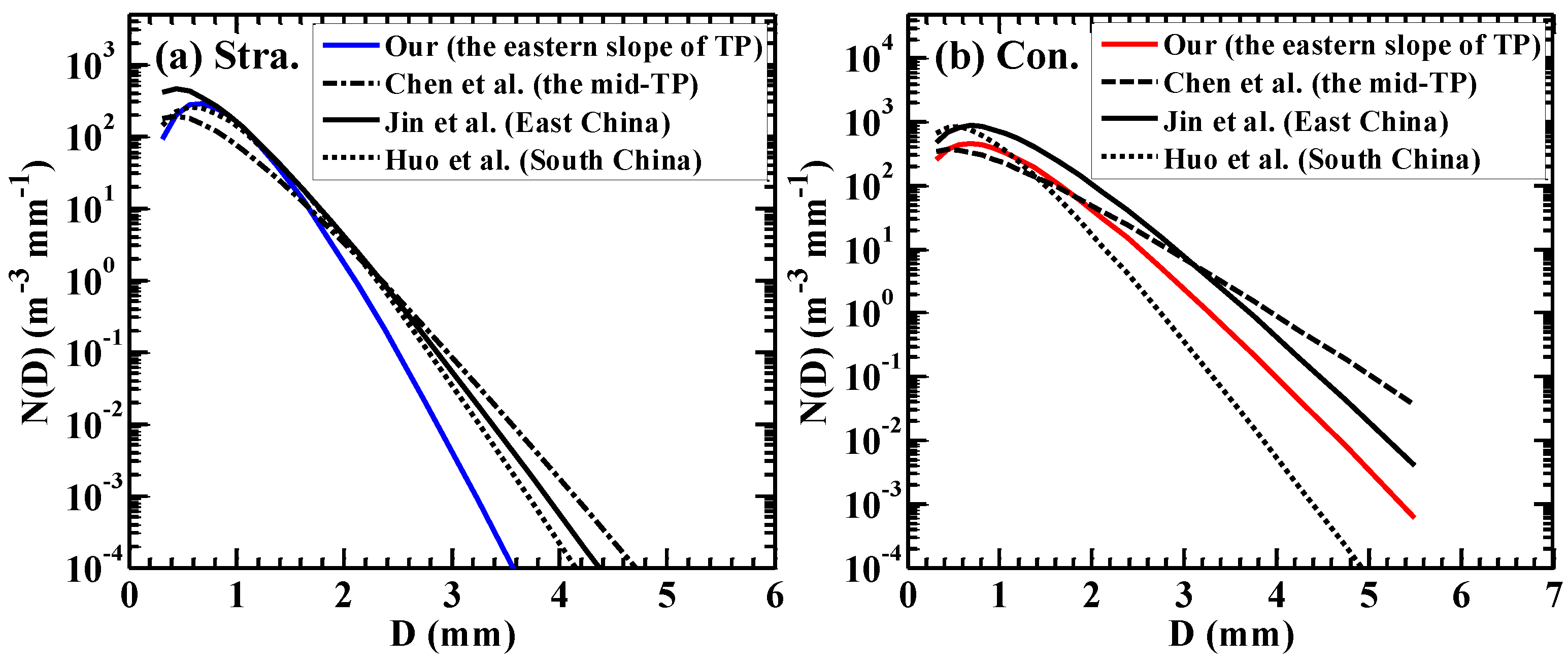
3.2. DSD Characteristics for Different Rain Types
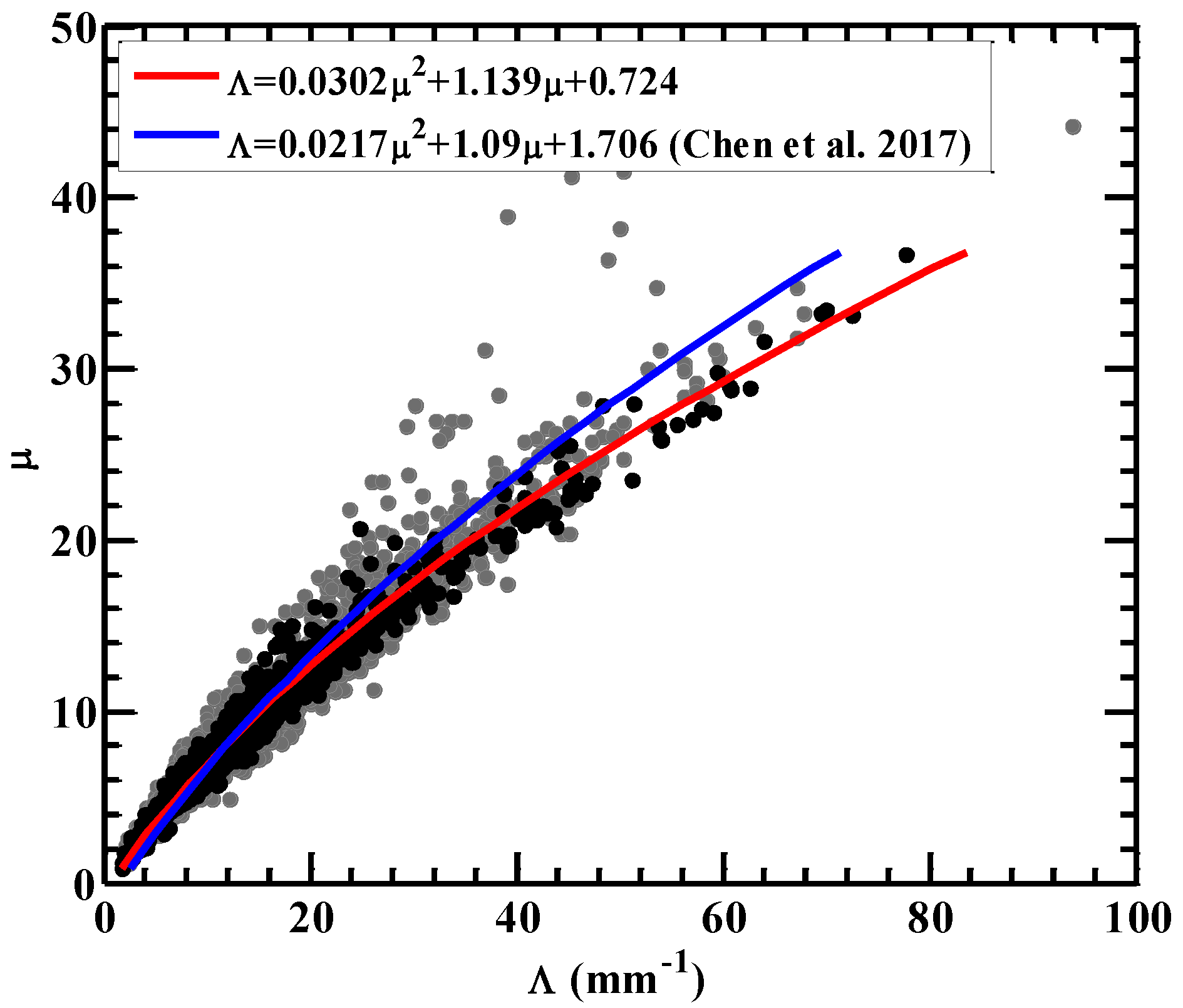
3.3. Relationship of
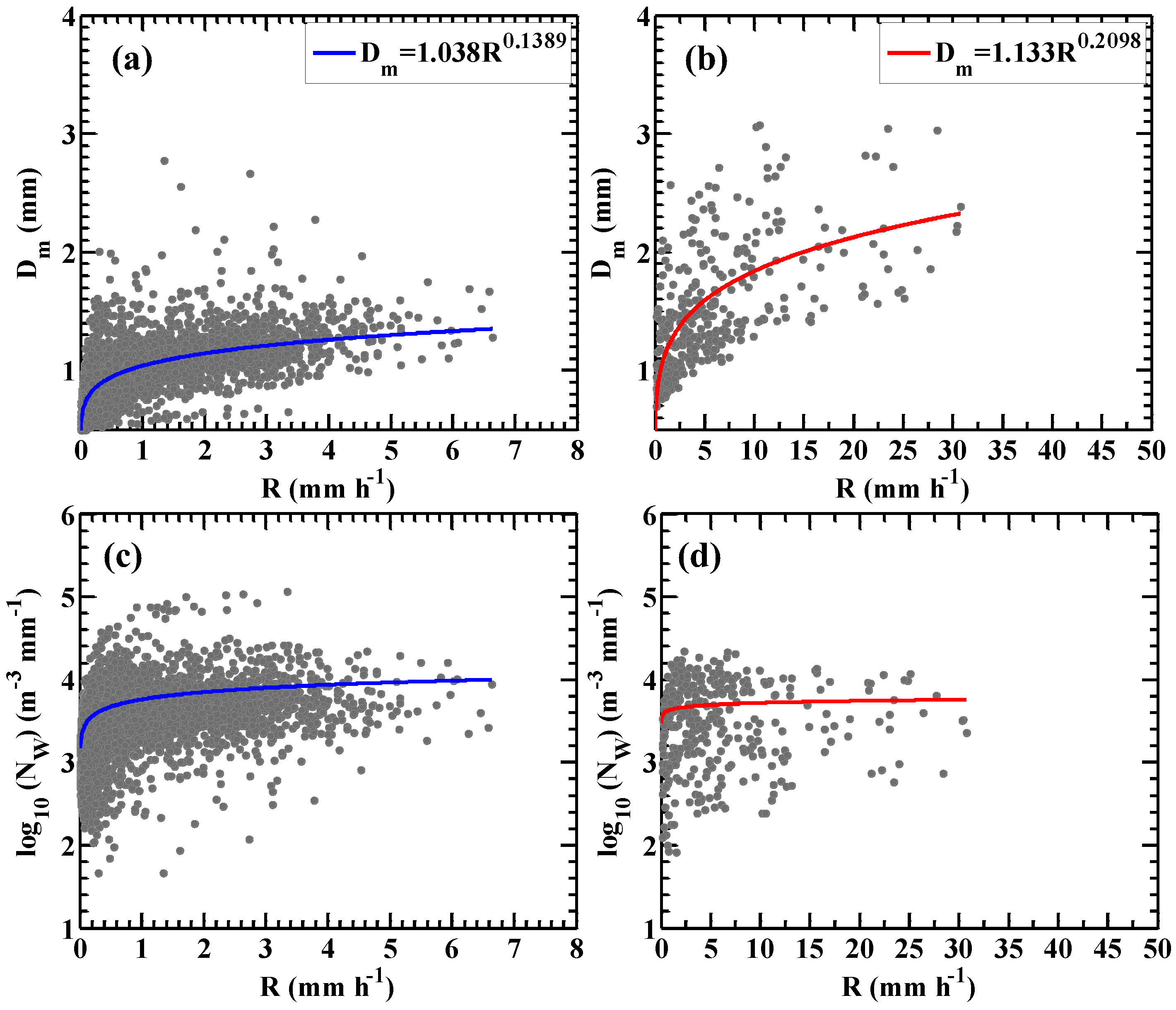
3.4. Relationships of and
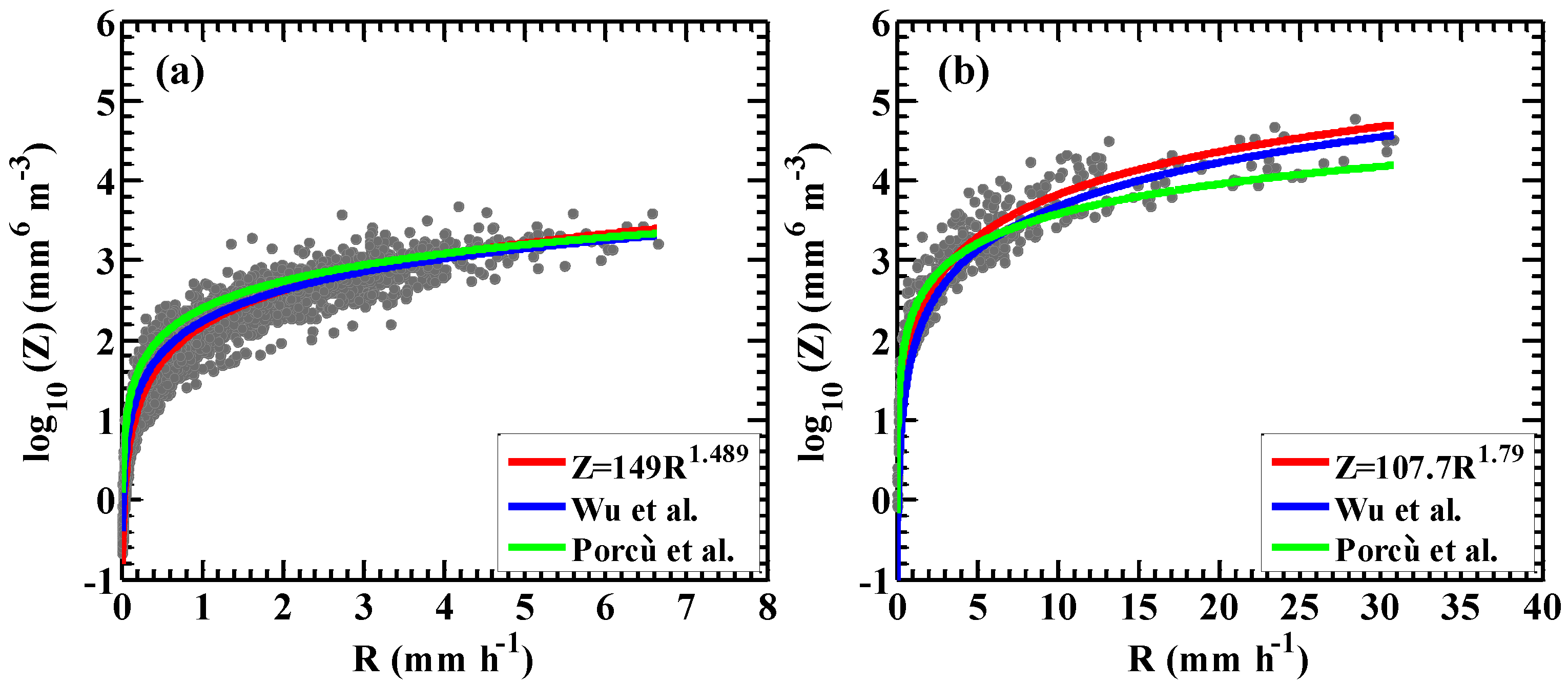
3.5. Relationship of
4. Discussion
4.1. Comparison of DSD Characteristics
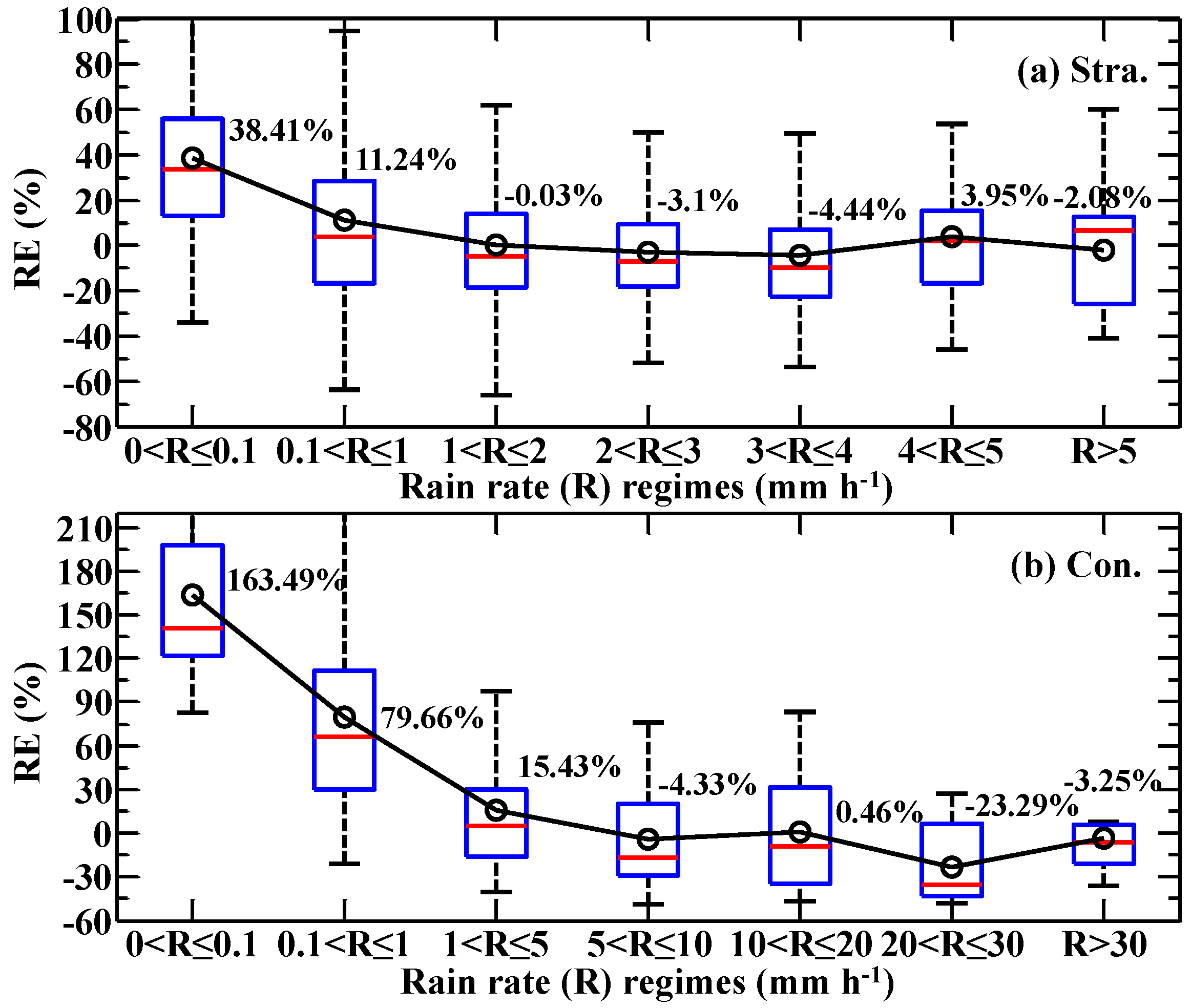
4.2. Biases of ML Method and Relationship
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, G.; Zhang, Y. Tibetan plateau forcing and the timing of the monsoon onset over South Asia and the South China Sea. Mon. Weather Rev. 1998, 126, 913–927. [Google Scholar] [CrossRef]
- Zhao, P.; Xu, X.D.; Chen, F.; Guo, X.L.; Zheng, X.D.; Liu, L.P.; Hong, Y.; Li, Y.Q.; La, Z.; Peng, H.; et al. The third atmospheric scientific experiment for understanding the earth-atmosphere coupled system over the tibetan plateau and its effects. Bull. Am. Meteorol. Soc. 2018, 99, 757–776. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E.A.; Meneghini, R.; Kozu, T. The shape–slope relation in observed gamma raindrop size distributions: Statistical error or useful information? J. Atmos. Ocean. Technol. 2003, 20, 1106–1119. [Google Scholar] [CrossRef] [Green Version]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G.; Brandes, E.; Schuur, T.; Ryzhkov, A.; Ikeda, K. Analysis of video disdrometer and polarimetric radar data to characterize rain microphysics in Oklahoma. J. Appl. Meteorol. Clim. 2008, 47, 2238–2255. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, D.; Ulbrich, C.W. Cloud microphysical properties, processes, and rain fall estimation opportunities. Meteorol. Monogr. 2003, 30, 237–258. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef] [Green Version]
- Ulbrich, C.W.; Atlas, D. Microphysics of raindrop size spectra: Tropical continental and maritime storms. J. Appl. Meteorol. Clim. 2007, 46, 1777–1791. [Google Scholar] [CrossRef]
- Brawn, D.; Upton, G. Estimation of an atmospheric gamma drop size distribution using disdrometer data. Atmos. Res. 2008, 87, 66–79. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; May, P.T. CPOL radar-derived drop size distribution statistics of stratiform and convective rain for two regimes in Darwin, Australia. J. Atmos. Ocean. Technol. 2010, 27, 932–942. [Google Scholar] [CrossRef]
- Kumar, L.S.; Lee, Y.H.; Ong, J.T. Two-parameter gamma drop size distribution models for Singapore. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3371–3380. [Google Scholar] [CrossRef]
- Chen, B.; Yang, J.; Pu, J. Statistical characteristics of raindrop size distribution in the Meiyu season observed in eastern China. J. Meteorol. Soc. Jpn. 2013, 91, 215–227. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, K.; Zhang, G.; Xue, M.; Zhou, B.; Liu, S.; Chen, X. Statistical characteristics of raindrop size distributions observed in East China during the Asian summer monsoon season using 2-D video disdrometer and micro rain radar data. J. Geophys. Res. Atmos. 2016, 121, 2265–2282. [Google Scholar] [CrossRef] [Green Version]
- Uijlenhoet, R.; Smith, J.A.; Steiner, M. The microphysical structure of extreme precipitation as inferred from ground-based raindrop spectra. J. Atmos. Sci. 2003, 60, 1220–1238. [Google Scholar] [CrossRef]
- Barthes, L.; Mallet, C. Vertical evolution of raindrop size distribution: Impact on the shape of the DSD. Atmos. Res. 2013, 119, 13–22. [Google Scholar] [CrossRef]
- Kirankumar, N.V.P.; Narayana, R.T.; Radhakrishna, B.; Rao, D.N. Statistical characteristics of raindrop size distribution in southwest monsoon season. J. Appl. Meteorol. Clim. 2008, 47, 576–590. [Google Scholar] [CrossRef]
- Niu, S.; Jia, X.; Sang, J.; Liu, X.; Lu, C.; Liu, Y. Distributions of raindrop sizes and fall velocities in a semiarid plateau climate: Convective versus stratiform rains. J. Appl. Meteorol. Clim. 2010, 49, 632–645. [Google Scholar] [CrossRef]
- Chen, B.; Hu, Z.; Liu, L.; Zhang, G. Raindrop size distribution measurements at 4,500 m on the Tibetan Plateau during TIPEX-III. J. Geophys. Res. Atmos. 2017, 122, 11092–11106. [Google Scholar] [CrossRef]
- Geoffroy, O.; Siebesma, A.P.; Burnet, F. Characteristics of the raindrop distributions in RICO shallow cumulus. Atmos. Chem. Phys. 2014, 14, 10897–10909. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Yin, Y.; Shan, Y.P.; Jin, Q. Statistical characteristics of raindrop size distribution for stratiform and convective precipitation at different altitudes in Mt. Huangshan. Chin. J. Atmos. Sci. 2018, 42, 268–280. [Google Scholar] [CrossRef]
- Bao, X.; Wu, L.; Tang, B.; Ma, L.; Wu, D.; Tang, J.; Chen, H.; Wu, L. Variable Raindrop Size Distributions in Different Rainbands Associated with Typhoon Fitow (2013). J. Geophys. Res. Atmos. 2019. [Google Scholar] [CrossRef]
- Stoelinga, M.T.; Hobbs, P.V.; Mass, C.F.; Locatelli, J.D.; Colle, B.A.; Houze, R.A., Jr.; Rangno, A.L.; Bond, N.A.; Smull, B.F.; Rasmussen, R.M.; et al. Improvement of microphysical parameterization through observational verification experiment. Bull. Am. Meteorol. Soc. 2003, 84, 1807–1826. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, J.; Brandes, E.A. Improving Parameterization of Rain Microphysics with Disdrometer and Radar Observations. J. Atmos. Sci. 2006, 63, 1273–1290. [Google Scholar] [CrossRef] [Green Version]
- Shan, Y.; Wilcox, E.M.; Gao, L.; Lin, L.; Mitchell, D.L.; Yin, Y.; Zhao, T.; Zhang, L.; Shi, H.; Gao, M. Evaluating Errors in Gamma-Function Representations of the Raindrop Size Distribution: A Method for Determining the Optimal Parameter Set for Use in Bulk Microphysics Schemes. J. Atmos. Sci. 2020, 77, 513–529. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Meneghini, R.; Zawadzki, I. Global and local precipitation measurements by radar. Meteorol. Monogr. 2003, 52, 215–236. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Giangrande, S.E.; Schuur, T.J. Rainfall Estimation with a Polarimetric Prototype of WSR-88D. J. Appl. Meteorol. 2005, 44, 502–515. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.P.; Zheng, J.F.; Ruan, Z.; Cui, Z.H.; Hu, Z.Q.; Wu, S.H.; Dai, G.Y.; Wu, Y.H. Comprehensive radar observations of clouds and precipitation over the Tibetan Plateau and preliminary analysis of cloud properties. J. Meteorol. Res. 2015, 29, 546–561. [Google Scholar] [CrossRef]
- Chang, Y.; Guo, X. Characteristics of convective cloud and precipitation during summer time at Naqu over Tibetan Plateau (in Chinese). Chin. Sci. Bull. 2016, 61, 1706–1720. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.H.; Liu, L.P. Statistical characteristics of raindrop size distribution in the Tibetan Plateau and southern China. Adv. Atmos. Sci. 2017, 34, 727–736. [Google Scholar] [CrossRef]
- Porcù, F.; D’Adderio, L.P.; Prodi, F.; Caracciolo, C. Rain drop size distribution over the Tibetan Plateau. Atmos. Res. 2014, 150, 21–30. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Experimental quantification of the sampling uncertainty associated with measurements from PARSIVEL disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL snow observations: A critical assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Yuter, S.E.; Kingsmill, D.E.; Nance, L.B.; Löffler-Mang, M. Observations of precipitation size and fall speed characteristics within coexisting rain and wet snow. J. Appl. Meteorol. 2006, 45, 1450–1464. [Google Scholar] [CrossRef] [Green Version]
- Huo, Z.; Ruan, Z.; Wei, M.; Ge, R.; Li, F.; Ruan, Y. Statistical characteristics of raindrop size distribution in south China summer based on the vertical structure derived from VPR-CFMCW. Atmos. Res. 2019, 222, 47–61. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Checa, R.; de Castro, M. An experiment to measure the spatial variability of rain drop size distribution using sixteen laser disdrometers. Geophys. Res. Lett. 2010, 37, L16803. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Quantification of the small-scale spatial structure of the raindrop size distribution from a network of disdrometers. J. Appl. Meteorol. Climatol. 2012, 51, 941–953. [Google Scholar] [CrossRef]
- Friedrich, K.; Higgins, S.; Masters, F.J.; Lopez, C.R. Articulating and stationary PARSIVEL disdrometer measurements in conditions with strong winds and heavy rainfall. J. Atmos. Ocean. Technol. 2013, 30, 2063–2080. [Google Scholar] [CrossRef]
- Kalina, E.A.; Friedrich, K.; Ellis, S.M.; Burgess, D.W. Comparison of disdrometer and X-band mobile radar observations in convective precipitation. Mon. Weather Rev. 2014, 142, 2414–2435. [Google Scholar] [CrossRef] [Green Version]
- Konwar, M.; Das, S.K.; Deshpande, S.M.; Chakravarty, K.; Goswami, B.N. Microphysics of clouds and rain over the Western Ghat. J. Geophys. Res. Atmos. 2014, 119, 6140–6159. [Google Scholar] [CrossRef]
- Zhang, A.; Hu, J.; Chen, S.; Hu, D.; Liang, Z.; Huang, C.; Xiao, L.; Min, C.; Li, H. Statistical Characteristics of Raindrop Size Distribution in the Monsoon Season Observed in Southern China. Remote Sens. 2019, 11, 432. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Lin, P.; Chang, W.; Seela, B.K.; Janapati, J. Microphysical characteristics and types of precipitation for different seasons over north Taiwan. J. Meteorol. Soc. Jpn. 2019, 97, 841–865. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.; Xiao, H.; Yang, H.; Chen, H.; Guo, J.; Sun, Y.; Feng, L. Raindrop size distribution and microphysical characteristics of a great rainstorm in 2016 in Beijing, China. Atmos. Res. 2020, 239. [Google Scholar] [CrossRef]
- Hopper, L.J.; Schumacher, C.; Humes, K.; Funk, A. Drop-size distribution variations associated with different storm types in southeast Texas. Atmosphere 2019, 11, 8. [Google Scholar] [CrossRef] [Green Version]
- Serio, M.A.; Carollo, F.G.; Ferro, V. Raindrop size distribution and terminal velocity for rainfall erosivity studies. A review. J. Hydrol. 2019, 576, 210–228. [Google Scholar] [CrossRef]
- Ma, Y.; Ni, G.; Chandra, C.V.; Tian, F.; Chen, H. Statistical characteristics of raindrop size distribution during rainy seasons in the Beijing urban area and implications for radar rainfall estimation. Hydrol. Earth Syst. Sci. 2019, 23, 4153–4170. [Google Scholar] [CrossRef] [Green Version]
- Villalobospuma, E.; Martinezcastro, D.; Floresrojas, J.L.; Saavedrahuanca, M.; Silvavidal, Y. Diurnal cycle of raindrops size distribution in a valley of the Peruvian Central Andes. Atmosphere 2019, 11, 38. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Zhang, Y.; Lei, H.; Xie, Y.; Gao, T.; Zhang, L.; Wang, C.; Huang, Y. Microphysical characteristics of precipitation during pre-monsoon, monsoon, and post-monsoon periods over the South China Sea. Adv. Atmos. Sci. 2019, 36, 1103–1120. [Google Scholar] [CrossRef]
- Checa-Garcia, R.; Tokay, A.; Tapiador, F. Binning effects on in-situ raindrop size distribution measurements. Atmos. Meas. Tech. 2014, 7, 2339–2379. [Google Scholar] [CrossRef] [Green Version]
- Campos, E.; Zawadzki, I. Instrumental uncertainties in Z-R Relations. J. Appl. Meteorol. 1969, 39, 1088–1102. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An optical disdrometer for measuring size and velocity of hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Sheppard, B.; Joe, P. Comparison of raindrop size distribution measurements by a Joss-Waldvogel disdrometer, a PMS 2DG spectrometer, and a POSS doppler radar. J. Atmos. Ocean. Technol. 1994, 11, 874–887. [Google Scholar] [CrossRef]
- Mallet, C.; Barthes, L. Estimation of gamma raindrop size distribution parameters: Statistical fluctuations and estimation errors. J. Atmos. Ocean. Technol. 2009, 26, 1572–1584. [Google Scholar] [CrossRef]
- Tokay, A.; Petersen, W.A.; Gatlin, P.; Wingo, M. Comparison of raindrop size distribution measurements by collocated disdrometers. J. Atmos. Ocean. Technol. 2013, 30, 1672–1690. [Google Scholar] [CrossRef]
- De Moraes Frasson, R.P.; da Cunha, L.K.; Krajewski, W.F. Assessment of the Thies optical disdrometer performance. Atmos. Res. 2011, 101, 237–255. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, K.; Zhang, G.; Liu, S.; Chen, G. Impacts of instrument limitations on estimated raindrop size distribution, radar parameters, and model microphysics during Mei-Yu season in East China. J. Atmos. Ocean. Technol. 2017, 34, 1021–1037. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Kruger, A.; Caracciolo, C.; Golé, P.; Barthes, L.; Creutin, J.-D.; Delahaye, J.-Y.; Nikolopoulos, E.I.; Ogden, F.; Vinson, J.-P. DEVEX-disdrometer evaluation experiment: Basic results and implications for hydrologic studies. Adv. Water Resour. 2006, 29, 311–325. [Google Scholar] [CrossRef]
- Thurai, M.; Gatlin, P.; Bringi, V.N.; Petersen, W.; Kennedy, P.; Notaroš, B.; Carey, L. Toward completing the raindrop size spectrum: Case studies involving 2D-video disdrometer, droplet spectrometer, and polarimetric radar measurements. J. Appl. Meteorol. Clim. 2017, 56, 877–896. [Google Scholar] [CrossRef]
- Guyot, A.; Pudashine, J.; Protat, A.; Uijlenhoet, R.; Pauwels, V.R.N.; Seed, A.; Walker, J.P. Effect of disdrometer type on rain drop size distribution characterisation: A new dataset for south-eastern Australia. Hydrol. Earth Syst. Sci. 2019, 23, 4737–4761. [Google Scholar] [CrossRef] [Green Version]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. Space Phys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Johnson, R.W.; Kliche, D.V.; Smith, P.L. Comparison of estimators for parameters of gamma distributions with left-truncated samples. J. Appl. Meteorol. Climatol. 2011, 50, 296–310. [Google Scholar] [CrossRef]
- Johnson, R.W.; Kliche, D.V.; Smith, P.L. Maximum likelihood estimation of gamma parameters for coarsely binned and truncated raindrop size data. Q. J. R. Meteorol. Soc. 2013, 140, 1245–1256. [Google Scholar] [CrossRef]
- Smith, P.L.; Kliche, D.V. The bias in moment estimators for parameters of drop-size distribution functions: Sampling from exponential distributions. J. Appl. Meteorol. 2005, 44, 1195–1205. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteorol. 1996, 35, 355–371. [Google Scholar] [CrossRef] [Green Version]
- Testud, J.; Oury, S.; Amayenc, P.; Black, R.A. The concept of “normalized” distributions to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Nzeukou, A.; Sauvageot, H.; Ochou, A.D.; Kebe, C.M.F. Raindrop size distribution and radar parameters at Cape Verde. J. Appl. Meteorol. 2004, 43, 90–105. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Rainfall microphysics and radar properties: Analysis methods for drop size spectra. J. Appl. Meteorol. 1998, 37, 912–923. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. An evaluation of a drop distribution–based rainfall estimator. J. Appl. Meteorol. 2003, 42, 652–660. [Google Scholar] [CrossRef]
- Sharma, S.; Konwar, M.; Sarma, D.K.; Kalapureddy, M.C.R.; Jain, A.R. Characteristics of rain integral parameters during tropical convective, transition, and stratiform rain at gadanki and its application in rain retrieval. J. Appl. Meteorol. Clim. 2009, 48, 1245–1266. [Google Scholar] [CrossRef] [Green Version]
- Jin, Q.; Yuan, Y.; Liu, H.J.; Shi, C.E.; Li, J.B. Analysis of microphysical characteristics of the raindrop spectrum over the area between the Yangtze River and the Huaihe River during summer. Acta Meteorol. Sin. 2015, 73, 778–788. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Fulton, R.A.; Breidenbach, J.P.; Seo, D.-J.; Miller, D.A. The WSR-88D rainfall algorithm. Weather Forecast 1998, 13, 377–395. [Google Scholar] [CrossRef]
- Maki, M.; Keenan, T.D.; Sasaki, Y. Characteristics of the raindrop size distribution in tropical continental squall lines observed in Darwin, Austrialia. J. Appl. Meteorol. 2001, 40, 1393–1412. [Google Scholar] [CrossRef]
- Moumouni, S.; Gosset, M.; Houngninou, E. Main features of rain drop size distributions observed in Benin, West Africa, with optical disdrometers. Geophys. Res. Lett. 2008, 35, L23807. [Google Scholar] [CrossRef]
- Chen, B.; Hu, W.; Pu, J. Characteristics of the raindrop size distribution for freezing precipitation observed in southern China. J. Geophys. Res. 2011, 116, D06201. [Google Scholar] [CrossRef]
- Ji, L.; Chen, H.; Li, L.; Chen, B.; Xiao, X.; Chen, M.; Zhang, G. Raindrop size distributions and rain characteristics observed by a PARSIVEL disdrometer in Beijing, Northern China. Remote Sens. 2019, 11, 1479. [Google Scholar] [CrossRef] [Green Version]




| Class (mm−1) | () | |||||||
|---|---|---|---|---|---|---|---|---|
| Total | 175.24 | 30.18 | 0.0617 | 1.415 | 4.399 | 6.529 | 6.454 | 10.141 |
| R1 (0, 0.1] | 30.12 | 5.25 | 0.0038 | 0.723 | 4.009 | 11.088 | 12.951 | 24.364 |
| R2 (0.1, 1] | 127.84 | 17.24 | 0.0252 | 0.906 | 4.630 | 8.928 | 9.791 | 16.589 |
| R3 (1, 5] | 311.95 | 27.40 | 0.1086 | 1.177 | 4.868 | 6.858 | 6.817 | 10.203 |
| R4 (5, 10] | 436.34 | 35.26 | 0.2662 | 1.552 | 4.803 | 5.445 | 4.704 | 6.447 |
| R5 (10, ~) | 758.18 | 47.10 | 0.7594 | 2.541 | 4.472 | 4.541 | 2.526 | 3.995 |
| Rainfall Quantities and Gamma Parameters | Rain Types | 5th | 25th | Median | Average | 75th | 95th |
|---|---|---|---|---|---|---|---|
| (mm h−1) | Stra. | 0.026 | 0.121 | 0.454 | 0.944 | 1.432 | 3.261 |
| Con. | 0.168 | 1.314 | 3.818 | 7.453 | 7.706 | 23.437 | |
| (g m−3) | Stra. | 0.002 | 0.008 | 0.028 | 0.049 | 0.074 | 0.159 |
| Con. | 0.009 | 0.066 | 0.154 | 0.265 | 0.311 | 0.786 | |
| (dBZ) | Stra. | 0.286 | 9.246 | 16.559 | 16.115 | 23.804 | 29.281 |
| Con. | 12.005 | 23.767 | 30.767 | 29.585 | 35.916 | 43.002 | |
| (mm) | Stra. | 0.575 | 0.734 | 0.899 | 0.932 | 1.099 | 1.377 |
| Con. | 0.803 | 1.073 | 1.379 | 1.496 | 1.812 | 2.666 | |
| Stra. | 1.201 | 1.664 | 2.081 | 2.023 | 2.407 | 2.656 | |
| Con. | 1.408 | 2.062 | 2.446 | 2.356 | 2.683 | 2.992 | |
| (m−3 mm−1) | Stra. | 2.717 | 3.193 | 3.498 | 3.467 | 3.774 | 4.111 |
| Con. | 2.481 | 3.097 | 3.494 | 3.437 | 3.874 | 4.131 | |
| () | Stra. | 5.301 | 6.671 | 8.146 | 9.236 | 10.878 | 16.844 |
| Con. | 3.184 | 4.572 | 5.663 | 6.123 | 7.084 | 10.859 | |
| Stra. | 5.055 | 7.009 | 9.164 | 10.646 | 12.959 | 21.147 | |
| Con. | 1.999 | 3.429 | 5.271 | 6.009 | 7.775 | 12.837 | |
| (mm−1) | Stra. | 7.173 | 10.132 | 13.847 | 16.453 | 20.692 | 34.061 |
| Con. | 2.663 | 4.805 | 7.027 | 8.581 | 11.018 | 20.015 |
| Rain Types | R | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Stra. | 0.85 | 172.73 | 22.98 | 0.0490 | 1.094 | 4.649 | 5.746 | 5.282 | 8.167 |
| Con. | 6.21 | 390.07 | 39.01 | 0.2573 | 1.911 | 4.475 | 4.272 | 2.622 | 3.947 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zheng, J.; Cheng, Z.; Wang, B. Characteristics of Raindrop Size Distribution on the Eastern Slope of the Tibetan Plateau in Summer. Atmosphere 2020, 11, 562. https://doi.org/10.3390/atmos11060562
Wang Y, Zheng J, Cheng Z, Wang B. Characteristics of Raindrop Size Distribution on the Eastern Slope of the Tibetan Plateau in Summer. Atmosphere. 2020; 11(6):562. https://doi.org/10.3390/atmos11060562
Chicago/Turabian StyleWang, Yingjue, Jiafeng Zheng, Zhigang Cheng, and Bingyun Wang. 2020. "Characteristics of Raindrop Size Distribution on the Eastern Slope of the Tibetan Plateau in Summer" Atmosphere 11, no. 6: 562. https://doi.org/10.3390/atmos11060562
APA StyleWang, Y., Zheng, J., Cheng, Z., & Wang, B. (2020). Characteristics of Raindrop Size Distribution on the Eastern Slope of the Tibetan Plateau in Summer. Atmosphere, 11(6), 562. https://doi.org/10.3390/atmos11060562







