Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches
Abstract
:1. Introduction
2. Study Area and Data
Data Used
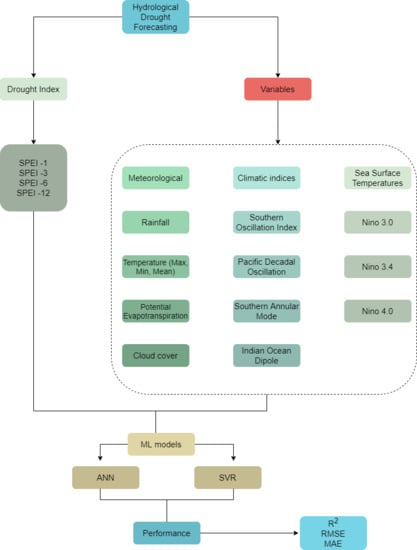
3. Methodology
3.1. Drought Index Calculation
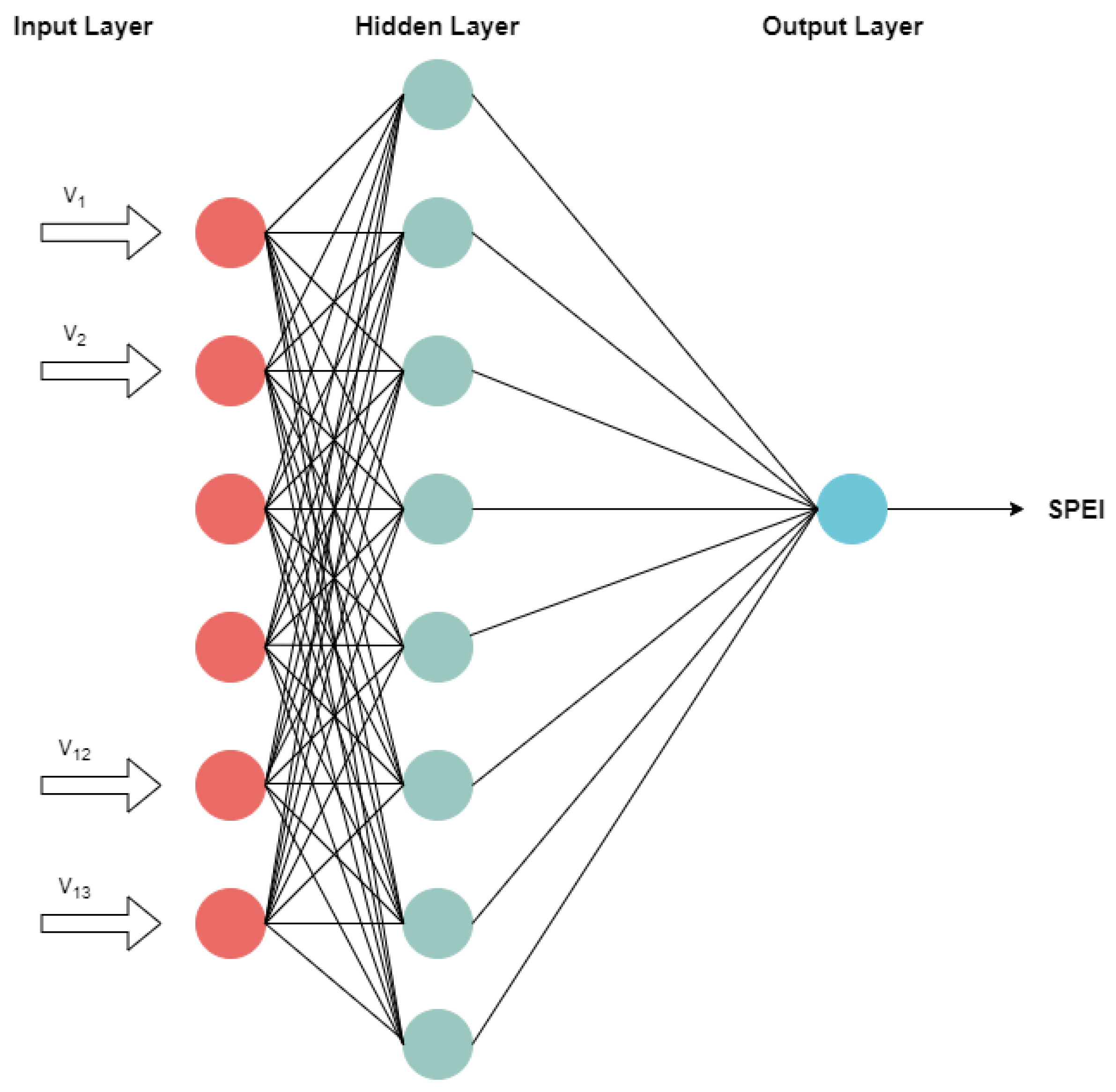
3.2. Artificial Neural Networks
3.3. Support Vector Regression
3.4. Performance Metrics
4. Results and Discussions
5. Conclusions
- The ANN models proved to be significantly better than SVR models at all the time scales studied. In addition, in both cases, forecasting at longer time scales provided better R2 values, suggesting these models be used for long-term forecasting rather than short-term.
- The study used various input variable categories. The relative importance of these variables determined from using the ANN model suggested that sea surface temperatures may not have a significant effect on the temporal aspect of drought as compared to the other meteorological and climatic indices.
- The present study is the first of its kind using a global climatological dataset for NSW. It is likely that future research will increasingly employ such datasets. Further study needs to be conducted on understanding the effect of variables at a spatial scale and in forecasting using more advanced computational approaches.
Author Contributions
Funding
Conflicts of Interest
References
- Belayneh, A.; Adamowski, J.; Khalil, B. Short-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet transforms and machine learning methods. Sustain. Water Resour. Manag. 2015, 2, 87–101. [Google Scholar] [CrossRef]
- Fung, K.; Huang, Y.; Koo, C.; Soh, Y. Drought forecasting: A review of modelling approaches 2007–2017. J. Water Clim. Chang. 2019, 1–29. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Mishra, A.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Cancelliere, A.; Di Mauro, G.; Bonaccorso, B.; Rossi, G. Drought forecasting using the Standardized Precipitation Index. Water Resour. Manag. 2006, 21, 801–819. [Google Scholar] [CrossRef]
- Rossi, G.; Vega, T.; Bonaccorso, B. Methods and Tools for Drought Analysis and Management; Springer Science & Business Media: Berlin, Germany, 2007; Volume 62. [Google Scholar]
- Sheffield, J.; Wood, E.F. Drought: Past Problems and Future Scenarios; Routledge: Abingdon, UK, 2012. [Google Scholar]
- Yihdego, Y.; Vaheddoost, B.; Al-Weshah, R.A. Drought indices and indicators revisited. Arab. J. Geosci. 2019, 12, 69. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, January 1993; pp. 179–184. [Google Scholar]
- Beguería, S.; Vicente-Serrano, S.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Clim. 2013, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.; Beguería, S.; I López-Moreno, J. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Manzano, A.; Clemente, M.A.; Morata, A.; Luna, M.Y.; Beguería, S.; Vicente-Serrano, S.M.; Martín, M.L. Analysis of the atmospheric circulation pattern effects over SPEI drought index in Spain. Atmos. Res. 2019, 230, 104630. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.; Luo, L.; Ye, A.; Duan, Q. Seasonal drought predictability and forecast skill in the semi-arid endorheic Heihe River basin in northwestern China. Hydrol. Earth Syst. Sci. 2018, 22, 5697–5709. [Google Scholar] [CrossRef] [Green Version]
- Hudson, D.; Alves, O.; Hendon, H.H.; Marshall, A.G. Bridging the gap between weather and seasonal forecasting: Intraseasonal forecasting for Australia. Q. J. R. Meteorol. Soc. 2011, 137, 673–689. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Pradhan, B.; Segoni, S.; Alamri, A.M. Rainfall Induced Landslide Studies in Indian Himalayan Region: A Critical Review. Appl. Sci. 2020, 10, 2466. [Google Scholar] [CrossRef] [Green Version]
- Deo, R.C.; Şahin, M. Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia. Atmos. Res. 2015, 161, 65–81. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sachindra, D.A.; Kanae, S. Machine learning for downscaling: The use of parallel multiple populations in genetic programming. Stoch. Environ. Res. Risk Assess. 2019, 33, 1497–1533. [Google Scholar] [CrossRef] [Green Version]
- Khan, N.; Sachindra, D.; Shahid, S.; Ahmed, K.; Shiru, M.S.; Nawaz, N. Prediction of droughts over Pakistan using machine learning algorithms. Adv. Water Resour. 2020, 139, 103562. [Google Scholar] [CrossRef]
- Feng, P.; Wang, B.; Liu, D.L.; Yu, Q. Machine learning-based integration of remotely-sensed drought factors can improve the estimation of agricultural drought in South-Eastern Australia. Agric. Syst. 2019, 173, 303–316. [Google Scholar] [CrossRef]
- Ortiz-Garcia, E.; Salcedo-Sanz, S.; Casanova-Mateo, C. Accurate precipitation prediction with support vector classifiers: A study including novel predictive variables and observational data. Atmos. Res. 2014, 139, 128–136. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R.; Singh, V.P. Drought Forecasting Using a Hybrid Stochastic and Neural Network Model. J. Hydrol. Eng. 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Haidary, A.; Amiri, B.J.; Adamowski, J.; Fohrer, N.; Nakane, K. Assessing the Impacts of Four Land Use Types on the Water Quality of Wetlands in Japan. Water Resour. Manag. 2013, 27, 2217–2229. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V. Drought forecasting using feed-forward recursive neural network. Ecol. Model. 2006, 198, 127–138. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Clim. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Barua, S.; Ng, A.; Perera, C. Artificial Neural Network–Based Drought Forecasting Using a Nonlinear Aggregated Drought Index. J. Hydrol. Eng. 2012, 17, 1408–1413. [Google Scholar] [CrossRef]
- Marj, A.F.; Meijerink, A.M.J. Agricultural drought forecasting using satellite images, climate indices and artificial neural network. Int. J. Remote Sens. 2011, 32, 9707–9719. [Google Scholar] [CrossRef]
- Xiang, B.; Lin, S.J.; Zhao, M.; Johnson, N.C.; Yang, X.; Jiang, X. Subseasonal week 3–5 surface air temperature prediction during boreal wintertime in a GFDL model. Geophys. Res. Lett. 2019, 46, 416–425. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.; Silva, M.C.; Pulido-Calvo, I. Spring drought prediction based on winter NAO and global SST in Portugal. Hydrol. Process. 2012, 28, 1009–1024. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Ensemble prediction of regional droughts using climate inputs and the SVM–copula approach. Hydrol. Process. 2013, 28, 4989–5009. [Google Scholar] [CrossRef]
- Dey, R.; Lewis, S.C.; Arblaster, J.; Abram, N.J. A review of past and projected changes in Australia’s rainfall. Wiley Interdiscip. Rev. Clim. Chang. 2019, 10, e577. [Google Scholar] [CrossRef]
- Hope, P.; Timbal, B.; Fawcett, R. Associations between rainfall variability in the southwest and southeast of Australia and their evolution through time. Int. J. Clim. 2009, 30, 1360–1371. [Google Scholar] [CrossRef]
- Timbal, B.; Arblaster, J.; Braganza, K.; Fernandez, E.; Hendon, H.; Murphy, B.; Raupach, M.; Rakich, C.; Smith, I.; Whan, K. Understanding the Anthropogenic Nature of the Observed Rainfall Decline across South Eastern Australia. Available online: https://www.cawcr.gov.au/technical-reports/CTR_026.pdf (accessed on 30 April 2020).
- Verdon-Kidd, D.C.; Kiem, A.S. Nature and causes of protracted droughts in southeast Australia: Comparison between the Federation, WWII, and Big Dry droughts. Geophys. Res. Lett. 2009, 36, 36. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Van Der Schrier, G.; Jones, P.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2013, 4, 17–22. [Google Scholar] [CrossRef]
- Cai, W.; Van Rensch, P.; Cowan, T.; Hendon, H.H. Teleconnection Pathways of ENSO and the IOD and the Mechanisms for Impacts on Australian Rainfall. J. Clim. 2011, 24, 3910–3923. [Google Scholar] [CrossRef]
- Meneghini, B.; Simmonds, I.H.; Smith, I.N. Association between Australian rainfall and the Southern Annular Mode. Int. J. Clim. 2006, 27, 109–121. [Google Scholar] [CrossRef]
- Latif, M.; Kleeman, R.; Eckert, C. Greenhouse Warming, Decadal Variability, or El Niño? An Attempt to Understand the Anomalous 1990s. J. Clim. 1997, 10, 2221–2239. [Google Scholar] [CrossRef] [Green Version]
- Hanley, D.E.; Bourassa, M.; O’Brien, J.J.; Smith, S.; Spade, E.R. A Quantitative Evaluation of ENSO Indices. J. Clim. 2003, 16, 1249–1258. [Google Scholar] [CrossRef]
- Huang, B.; L’Heureux, M.L.; Lawrimore, J.; Liu, C.; Zhang, H.-M.; Banzon, V.; Hu, Z.; Kumar, A. Why Did Large Differences Arise in the Sea Surface Temperature Datasets across the Tropical Pacific during 2012? J. Atmos. Ocean. Technol. 2013, 30, 2944–2953. [Google Scholar] [CrossRef]
- Hendon, H.H.; Thompson, D.W.J.; Wheeler, M. Australian Rainfall and Surface Temperature Variations Associated with the Southern Hemisphere Annular Mode. J. Clim. 2007, 20, 2452–2467. [Google Scholar] [CrossRef]
- Duc, H.N.; Rivett, K.; Macsween, K.; Le-Anh, L. Association of climate drivers with rainfall in New South Wales, Australia, using Bayesian Model Averaging. Theor. Appl. Clim. 2015, 127, 169–185. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Rim, C.-S. The implications of geography and climate on drought trend. Int. J. Clim. 2012, 33, 2799–2815. [Google Scholar] [CrossRef]
- Martins, V.S.; Novo, E.; Lyapustin, A.; Aragão, L.E.; Freitas, S.R.; Barbosa, C.C.F. Seasonal and interannual assessment of cloud cover and atmospheric constituents across the Amazon (2000–2015): Insights for remote sensing and climate analysis. ISPRS J. Photogramm. Remote Sens. 2018, 145, 309–327. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Revuelto, J.; I López-Moreno, J.; Gonzalez-Hidalgo, J.C.; Morán-Tejeda, E.; Espejo, F. Reference evapotranspiration variability and trends in Spain, 1961–2011. Glob. Planet. Chang. 2014, 121, 26–40. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.; Beguería, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; I López-Moreno, J.; Azorin-Molina, C.; Revuelto, J.; Morán-Tejeda, E.; Sanchez-Lorenzo, A. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Interact. 2012, 16, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Beguería, S.; Vicente-Serrano, S.M.; Beguería, M.S. Package ‘SPEI’. 2017. Available online: https://cran.r-project.org/web/packages/SPEI/SPEI.pdf (accessed on 30 April 2020).
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Hagan, M.; Menhaj, M. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Wilamowski, B.M. Levenberg-marquardt training. Ind. Electron. Handb. 2011, 5, 1. [Google Scholar]
- Wanas, N.; Auda, G.; Kamel, M.S.; Karray, F. On the optimal number of hidden nodes in a neural network. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No. 98TH8341), Vancouver, BC, Canada, 24–28 May 1998; pp. 918–921. [Google Scholar]
- Bourdin, D.R.; Fleming, S.W.; Stull, R.B. Streamflow Modelling: A Primer on Applications, Approaches and Challenges. Atmos. Ocean 2012, 50, 507–536. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Kisi, O.; Çimen, M. A wavelet-support vector machine conjunction model for monthly streamflow forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Paulescu, M.; Paulescu, E.; Stefu, N. A temperature-based model for global solar irradiance and its application to estimate daily irradiation values. Int. J. Energy Res. 2011, 35, 520–529. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Chatterjee, C. Development of an accurate and reliable hourly flood forecasting model using wavelet–bootstrap–ANN (WBANN) hybrid approach. J. Hydrol. 2010, 394, 458–470. [Google Scholar] [CrossRef]
- Lima, A.R.; Cannon, A.J.; Hsieh, W.W. Nonlinear regression in environmental sciences by support vector machines combined with evolutionary strategy. Comput. Geosci. 2013, 50, 136–144. [Google Scholar] [CrossRef]
- Chevalier, R.F.; Hoogenboom, G.; McClendon, R.W.; Paz, J.O. Support vector regression with reduced training sets for air temperature prediction: A comparison with artificial neural networks. Neural Comput. Appl. 2010, 20, 151–159. [Google Scholar] [CrossRef]




| Meteorological Factors | Climatic Indices | Sea Surface Temperature |
|---|---|---|
| Monthly mean precipitation | Southern Oscillation Index | Nino 3.4 SST (5° N–5° S,170° W–120° W) |
| Monthly mean air temperature | Pacific Decadal Oscillation | Nino 4.0 SST (5° N–5° S, 160° E–150° W) |
| Monthly maximum air temperature | Southern Annular Mode | Nino 3.0 SST (5° N–5° S,150° W–90° W) |
| Monthly minimum air temperature | Indian Ocean Dipole | |
| Potential evapotranspiration | ||
| Cloud cover |
| SPEI Classifications | Categories |
|---|---|
| ≤−2.0 | Extremely Dry |
| −1.99 to −1.5 | Severely Dry |
| −1.49 to −1.0 | Moderately Dry |
| −0.99 to 0.99 | Near Normal |
| 1.0 to 1.49 | Moderately Wet |
| 1.5 to 1.99 | Severely Wet |
| ≥2.0 | Extremely Wet |
| Prediction | R2 | RMSE | MAE |
|---|---|---|---|
| SPEI 1 | 0.61 | 0.94 | 0.93 |
| SPEI 3 | 0.72 | 0.68 | 0.65 |
| SPEI 6 | 0.74 | 0.62 | 0.59 |
| SPEI 12 | 0.75 | 0.58 | 0.55 |
| Prediction | R2 | RMSE | MAE |
|---|---|---|---|
| SPEI 1 | 0.72 | 0.68 | 0.65 |
| SPEI 3 | 0.75 | 0.62 | 0.59 |
| SPEI 6 | 0.81 | 0.54 | 0.51 |
| SPEI 12 | 0.86 | 0.24 | 0.23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dikshit, A.; Pradhan, B.; Alamri, A.M. Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches. Atmosphere 2020, 11, 585. https://doi.org/10.3390/atmos11060585
Dikshit A, Pradhan B, Alamri AM. Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches. Atmosphere. 2020; 11(6):585. https://doi.org/10.3390/atmos11060585
Chicago/Turabian StyleDikshit, Abhirup, Biswajeet Pradhan, and Abdullah M. Alamri. 2020. "Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches" Atmosphere 11, no. 6: 585. https://doi.org/10.3390/atmos11060585
APA StyleDikshit, A., Pradhan, B., & Alamri, A. M. (2020). Temporal Hydrological Drought Index Forecasting for New South Wales, Australia Using Machine Learning Approaches. Atmosphere, 11(6), 585. https://doi.org/10.3390/atmos11060585