Assessment of Meteorological Drought and Wet Conditions Using Two Drought Indices Across KwaZulu-Natal Province, South Africa
Abstract
:1. Introduction
2. Description of the Study Area
2.1. Location and Physiography
2.2. Climate and Regional Moisture Sources
3. Methodology and Data
3.1. Precipitation Data
3.2. Drought Indices Used
- Percentage of Normal Precipitation Index (PNI):
- Rainfall Anomaly Index (RAI):
3.3. Statistical Analyses
- Mann–Kendall Test
- Sen’s Slope Estimator Test
4. Results
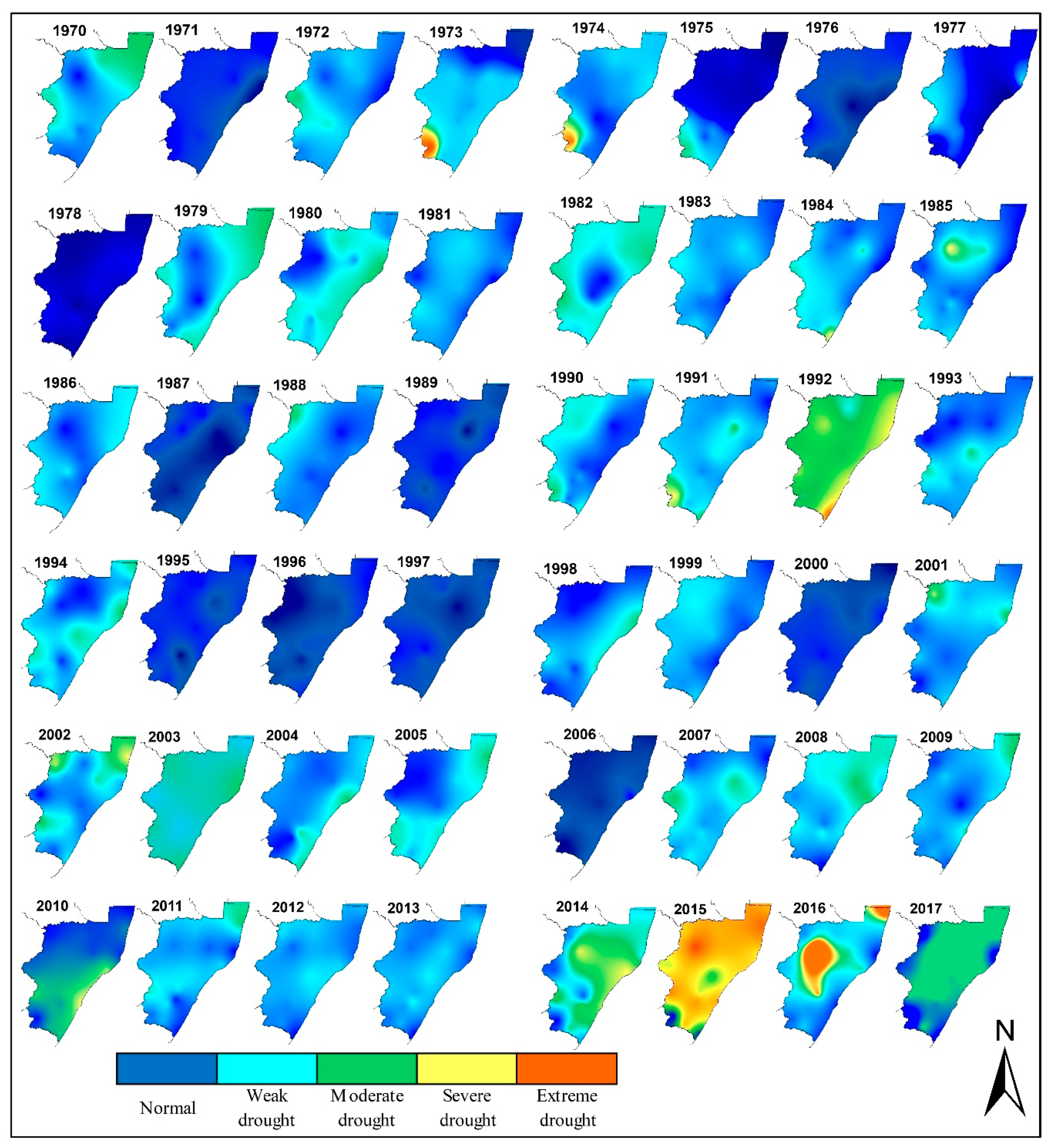
4.1. Frequency and Spatial Distribution of Drought and Wet Conditions
4.2. Statistical Trend Analysis of Drought Indices
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix
Appendix A
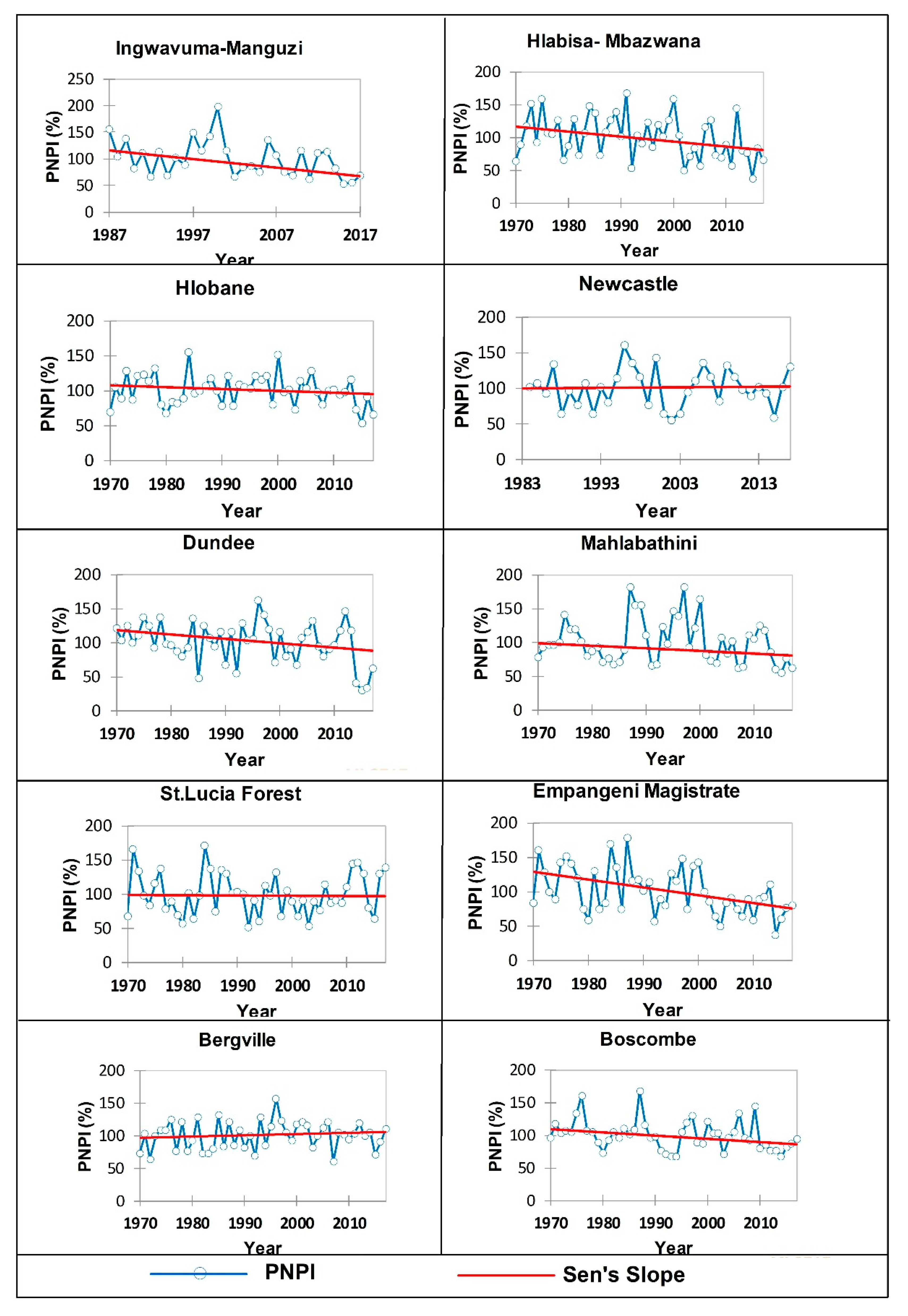

Appendix B
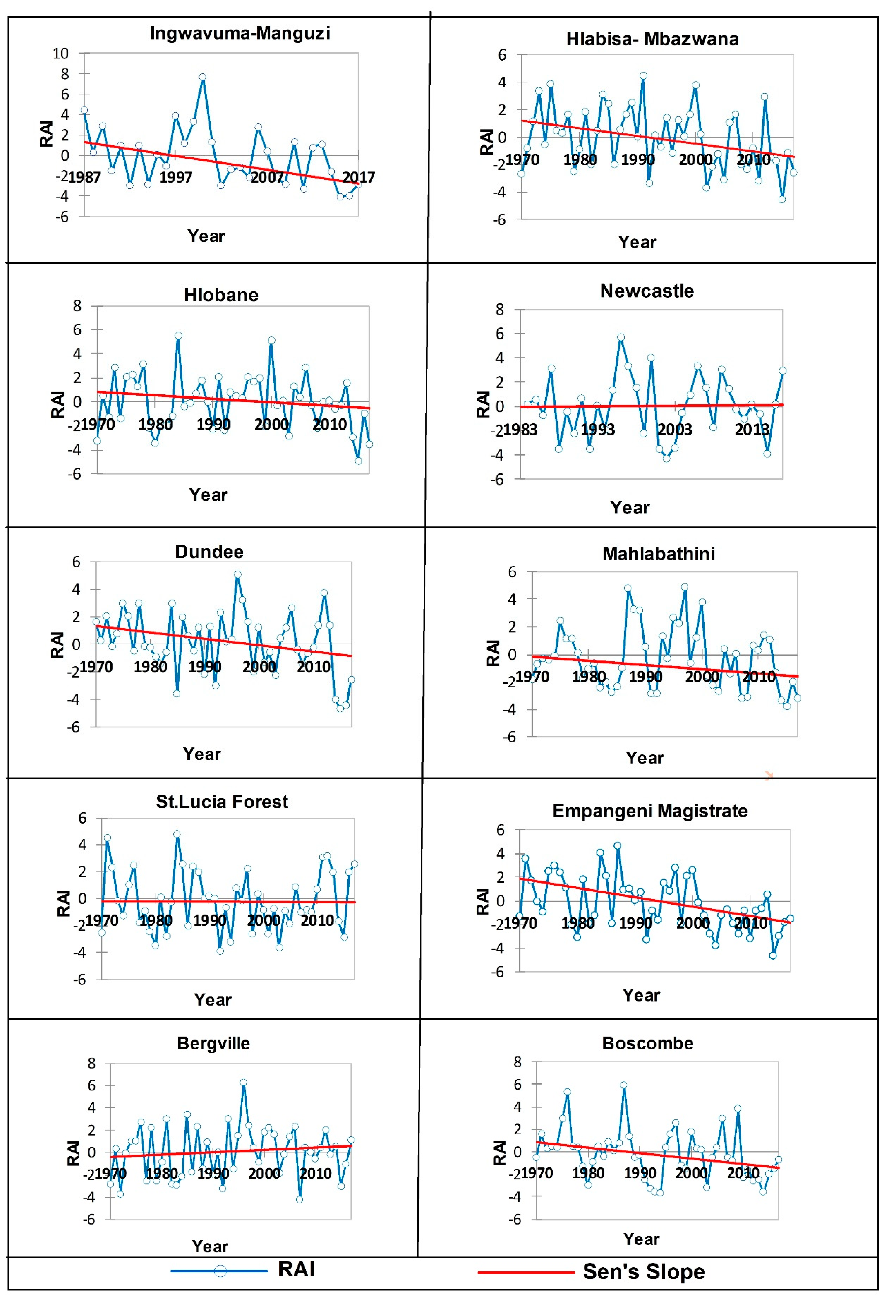
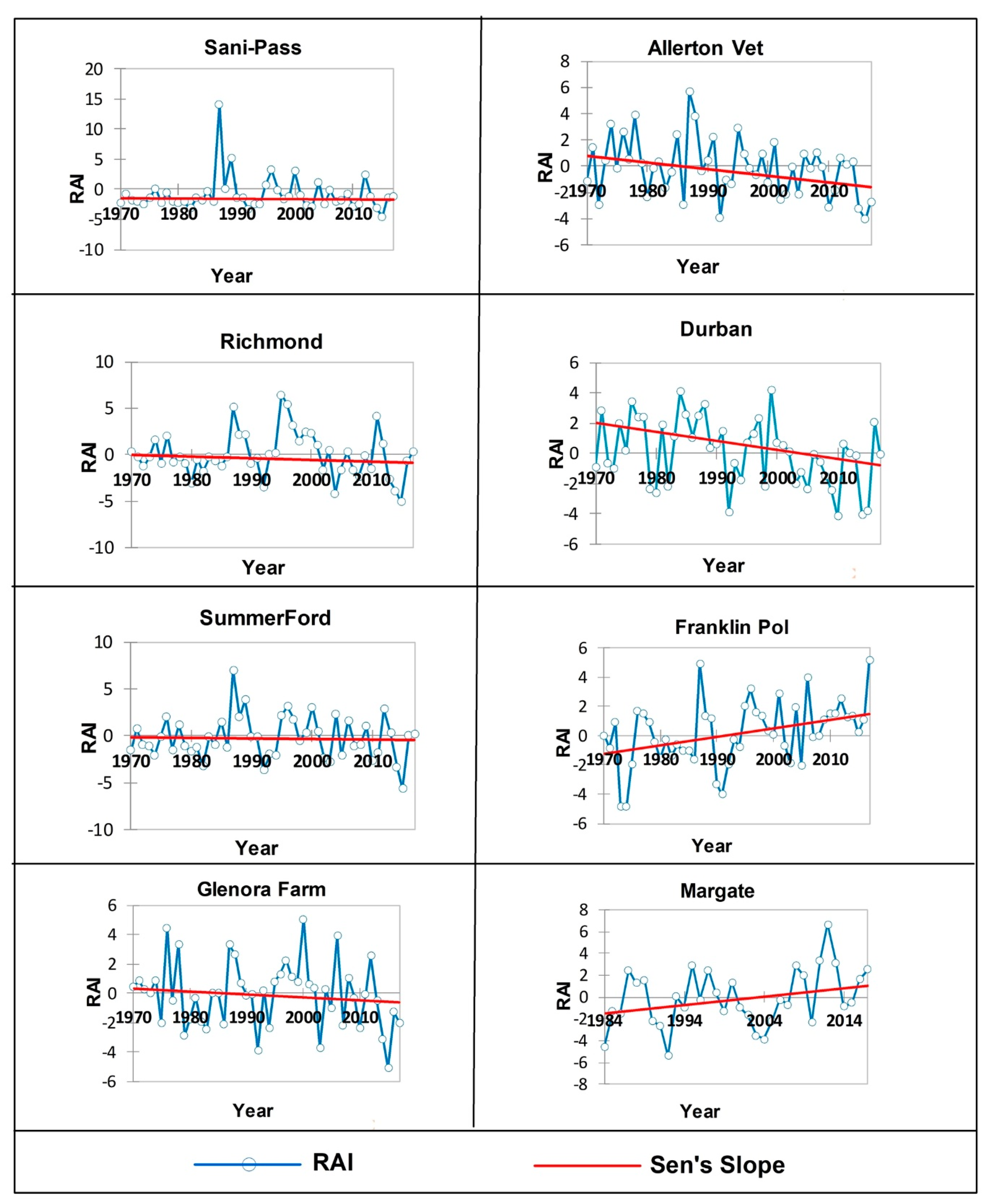
References
- Department of Water Affairs and Forestry. National Groundwater Strategy; Department of Water Affairs and Forestry: Pretoria, South Africa, 2010.
- World Meteorological Organization (WMO). International Meteorological Vocabulary, 2nd ed.; World Meteorological Organization: Geneva, Switzerland, 1992. [Google Scholar]
- Department of Water and Sanitation. Drought Status Report: November 2015; Department of Water and Sanitation: Pretoria, South Africa, 2015.
- Hove, L.; Kambanje, C. Lessons from the El Nino–induced 2015/16 drought in the Southern Africa region. Curr. Dir. Water Scarcity Res. 2019, 33–54. [Google Scholar] [CrossRef]
- Tyson, P.D.; Preston-Whyte, R.A. The Weather and Climate of Southern Africa, 2nd ed.; Oxford University Press Southern Africa: Cape Town, South Africa, 2000; pp. 228–236. [Google Scholar]
- Nicholson, S.E.; Leposo, D.; Grist, J. The relationship between El Niño and drought over Botswana. J. Clim. 2001, 14, 323–335. [Google Scholar] [CrossRef]
- Rouault, M.; Richard, Y. Intensity and spatial extension of drought in South Africa at different time scales. Water Sa 2003, 29, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Ratnam, J.V.; Behera, S.K.; Masumoto, Y.; Yamagata, T. Remote effects of El Niño and Modoki events on the Austral Summer Precipitation of Southern Africa. J. Climatol. 2014, 27, 3802–3815. [Google Scholar] [CrossRef]
- Dieppois, B.; Rouault, M.; New, M. The impact of ENSO on Southern African rainfall in CMIP5 ocean atmosphere coupled climate models. Clim. Dyn. 2015, 45, 2425–2442. [Google Scholar] [CrossRef] [Green Version]
- Walker, N.D.; Lindesay, J.A. Preliminary observations of oceanic influences on the February–March 1988 floods in central SouthAfrica. S. Afr. J. Sci. 1989, 85, 164–169. [Google Scholar]
- Reason, C.J.C.; Mulenga, H. Relationships between South African rainfall and SST anomalies in the south west Indian Ocean. Int. J. Climatol. 1999, 19, 1651–1673. [Google Scholar] [CrossRef]
- Camberlin, P.; Diop, M. Inter-relationships between groundnut yield in Senegal, interannual rainfall variability and sea-surface temperatures. Theor. Appl. Climatol. 1999, 63, 163–181. [Google Scholar] [CrossRef]
- Fauchereau, N.; Trzaska, S.; Richard, Y.; Roucou, P.; Camberlin, P. Sea-surface temperature co-variability in the Southern Atlantic and Indian Oceans and its connections with the atmospheric circulation in the Southern Hemisphere. Int. J. Climatol. 2003, 23, 663–677. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Kim, J. The relationship of the El Niño–Southern Oscillation to African rainfall. Int. J. Climatol. 1997, 17, 117–135. [Google Scholar] [CrossRef]
- Hewitson, B.C.; Tenant, W.; Walawege, R. Atmospheric moisture transport and sources for South Africa; WRC Report, No. 1024/1/04; 2004; WRC: Pretoria, South Africa. [Google Scholar]
- Botai, C.M.; Botai, J.O.; Dlamini, L.C.; Zwane, N.S.; Phaduli, E. Characteristics of Droughts in South Africa: A Case Study of Free State and North West Provinces. Water 2017, 8, 439. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2000, 83, 1167–1180. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Moghaddasi, M. Comparison of seven meteorological indices for drought monitoring in Iran. Int. J. Climatol. 2006, 26, 971–985. [Google Scholar] [CrossRef]
- Salehnia, N.; Alizadeh, A.; Sanaeinejad, H.; Bannayan, M.; Zarrin, A.; Hoogenboom, G. Estimation of meteorological drought indices based on AgMERRA precipitation data and station-observed precipitation data. J. Arid Land 2017, 9, 797–809. [Google Scholar] [CrossRef] [Green Version]
- Afzalia, A.; Keshtkarb, H.; Pakzada, S.; Moazamia, N.; Azizabadi Farahania, E.A.; Golpaygania, A.; Khosrojerdia, E.; Yousefia, Z.; Taghi Naghiloua, M. Spatio-Temporal Analysis of Drought Severity Using Drought Indices and Deterministic and Geostatistical Methods (Case Study: Zayandehroud River Basin). Deserts 2016, 21, 165–172. [Google Scholar]
- Wilhite, D.A.; Glantz, M. Understanding the drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–112. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D. Drought: A Global Assessment; Routledge: New York, NY, USA, 2000; p. 752. [Google Scholar]
- World Meteorological Organization. Drought Monitoring and Early Warning: Concepts, Progress and Future Challenges; WMO-No. 1006; World Meteorological Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Asefjah, B.F.; Fanian, Z.; Feizi, A.; Abolhasani, H.; Paktinat, M.; Naghilou, A.; Molaei Atani, M.; Asadollahi, M.; Babakhani, A.; Kouroshnia, F.; et al. Drought monitoring by using several meteorological drought indices (Case study: Salt Lake Basin of Iran). Desert 2014, 19, 155–165. [Google Scholar]
- Palmer, W.C. Meteorological Drought; Research Paper, No. 45; U.S. Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Shafer, B.A.; Dezman, L.E. Development of a Surface Water Supply Index (SWSI) to assess the severity of drought conditions in snowpack runoff areas. In Proceedings of the Western Snow Conference, Colorado State University, Fort Collins, CO, USA, 19–23 April 1982; pp. 164–175. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time steps. Preprints. In In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 22 January 1993; pp. 179–184. [Google Scholar]
- Willeke, G.; Hosking, J.R.M.; Wallis, J.R.; Guttman, N.B. The National Drought Atlas; Institute for Water Resources Report 94-NDS-4; U.S. Army Corps of Engineers: San Francisco, CA, USA, 1994.
- Van Rooy, M.P. A rainfall anomaly index independent of time and space. Notos 1965, 14, 43–48. [Google Scholar]
- Meyer, S.J.; Hubbard, K.G.; Wilhite, D.A. A crop-specific drought index for corn. Model development and validation. Agron. J. 1993, 85, 388–395. [Google Scholar] [CrossRef]
- Barua, S.; Ng, A.W.M.; Perera, B.J.C. Comparative Evaluation of Drought Indexes: A Case Study on the Yarra River Catchment in Australia. J. Water Resour. Plan. Manag. 2011, 137, 215–226. [Google Scholar] [CrossRef]
- Sneyer, R. On the Statistical Analysis of Series of Observations; Technical Note, no. 143, WMO No. 415; World Meteorological Organization: Geneva, Switzerland, 1990. [Google Scholar]
- Subash, N.; Gangwar, B. Statistical analysis of Indian rainfall and rice productivity anomalies over the last decades. Int. J. Climatol. 2013, 34, 2378–2392. [Google Scholar] [CrossRef]
- StatsSA. Mid-Year Population Estimates: Statistics South Africa. P0302; Statistics South Africa: Pretoria, South Africa, 2016; 17p.
- Department of Water and Sanitation. Digital Elevation Model; Department of Water and Sanitation: Durban, South Africa, 2016.
- Cook, C.; Reason, C.J.C.; Hewitson, B.C. West and dry spells within particularly wet and dry summers in the South African summer rainfall region. Clim. Res. 2004, 26, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Fetter, C.W. Applied Hydrogeology, 4th ed.; Prentice-Hall, Inc.: Upper Sadlle River, NJ, USA, 2001; 589p. [Google Scholar]
- Singh, V.P. Elementary Hydrology; Prentice Hall of India: New Delhi, India, 1994; 973p. [Google Scholar]
- Ostad-Ali-Askari, K.; Eslamian, S.; Singh, V.P.; Dalezios, N.R.; Ghane, M.; Yihdego, Y.; Motouq, M. A review of drought index. Int. J Constr. Res. Civ. Eng. 2017, 3, 48–66. [Google Scholar]
- Javan, K.; Azzizadeh, M.R.; Yousefi, S. An Investigation and Assessment of meteorological drought in Lake Urma Basin using drought indices and probabilistic methods. Nat. Environ. Chang. 2016, 2, 153–164. [Google Scholar]
- Mann, H.B. Non-parametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Wilks, D.S. Hypothesis Testing. In Statistical Methods in the Atmospheric Sciences; Academic Press: New York, NY, USA, 1995; pp. 160–176. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, S.; Fu, S.; Liu, J.; Wang, G.; Zhou, G. Trends of precipitation in Beijiang River Basin, Guangdong province, China. Hydrol. Process. 2008, 22, 2377–2386. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef] [Green Version]
- Dube, L.T.; Jury, M.R. Meteorological structure of the 1992/93 drought over eastern South Africa from ECMWF and satellite OLR analyses. S. Afr. Geogr. J. 2002, 84, 170–181. [Google Scholar] [CrossRef]
- Terry, A.K. The impact of the 2015-16 El Nino drought on the irrigated home gardens of the Komati downstream development project, Swaziland. S. Afr. Geogr. J. 2019. [Google Scholar] [CrossRef]
- Malherbe, J.; Dieppois, B.; Maluleke, P.; Van Staden, M.; Pillay, D.L. South African droughts and decadal variability. Nat. Hazards 2016, 80, 657–681. [Google Scholar] [CrossRef]
- Reason, C.J.C. Sensitivity of the southern African circulation to dipole sea-surface-temperature patterns in the south Indian Ocean. Int. J. Climatol. 2002, 22, 377–393. [Google Scholar] [CrossRef]
- Lakhraj-Govender, R.; Grab, S.W. Assessing the impact of El Niño-Southern Oscillation on South African temperatures during austral summer. Int. J. Climatol. 2018. [Google Scholar] [CrossRef] [Green Version]
- Jury, M.R.; Pathack, B.; Wang, B.; Powell, M.; Raholitao, N. A destructive Tropical cyclone season in the SW Indian Ocean: January–February 1984. S. Afr. Geogr. J. 1993, 75, 53–59. [Google Scholar] [CrossRef]
- Matondo, J.I.; Msibi, K.M. Estimation of the impact of climate change on hydrology and water resources in Swaziland. Water Int. 2001, 26, 425–434. [Google Scholar] [CrossRef]
- Reason, C.J.C.; Keibel, A. Tropical cyclone Eline and its usual penetration and impacts over the South African mainland. Am. Meteorol. Soc. 2004, 19, 789–805. [Google Scholar]
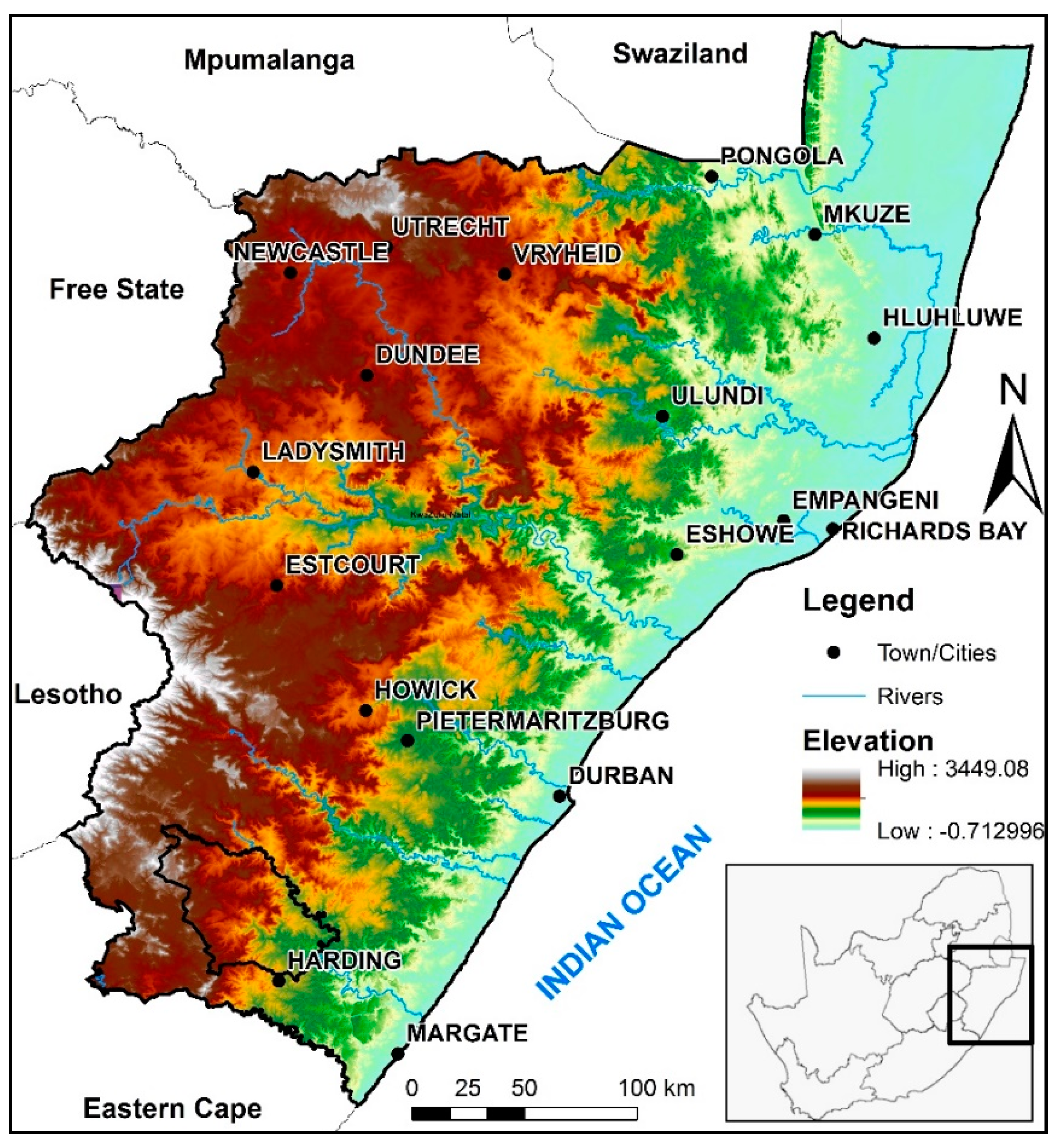
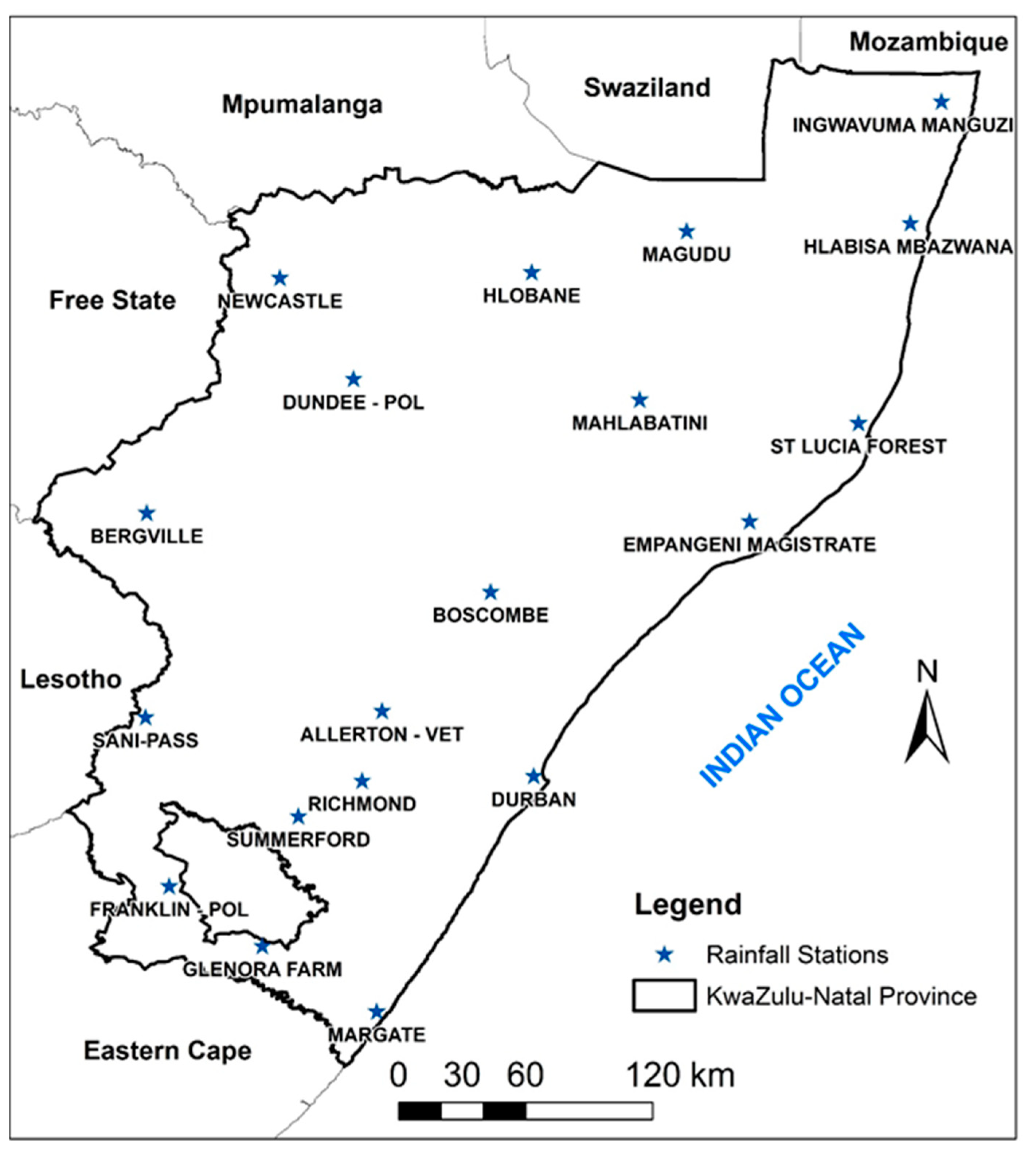


| Station | Location | Altitude (m amsl) | Record Period | Mean Rainfall (mm) | |
|---|---|---|---|---|---|
| Lat | Long | ||||
| Ingwavuma-Manguzi | −26.9830 | 32.7329 | 69 | 1987–2017 | 827.9 |
| Hlabisa- Mbazwana | −27.5000 | 32.6000 | 55 | 1970–2017 | 839.1 |
| Hlobane | −27.7089 | 30.9914 | 1294 | 1970–2017 | 860.6 |
| Newcastle | −27.7322 | 29.9211 | 1241 | 1984–2017 | 846.7 |
| Dundee | −28.1619 | 30.2339 | 1256 | 1970–2017 | 720.8 |
| Mahlabathini | −28.2500 | 31.4500 | 757 | 1970–2017 | 788.3 |
| St.Lucia Forest | −28.3500 | 32.3800 | 44 | 1970–2017 | 1168.3 |
| Empangeni Magistrate | −28.7670 | 31.9170 | 74 | 1970–2017 | 997.5 |
| Bergville | −28.7319 | 29.3550 | 1145 | 1970–2017 | 775.1 |
| Boscombe | −29.0670 | 30.8170 | 1151 | 1970–2017 | 965.4 |
| Sani-Pass | −29.6000 | 29.3500 | 2063 | 1970–2017 | 1049.2 |
| Allerton Vet | −29.5736 | 30.3556 | 711 | 1970–2017 | 963.9 |
| Richmond | −29.8700 | 30.2700 | 864 | 1970–2017 | 947.8 |
| Durban | −29.8500 | 31.0000 | 76 | 1970–2017 | 964.2 |
| SummerFord | −30.0208 | 29.9994 | 1233 | 1970–2017 | 871.9 |
| Franklin Pol | −30.3175 | 29.4508 | 1532 | 1970–2017 | 711.6 |
| Glenora Farm | −30.5714 | 29.8458 | 872 | 1970–2017 | 824.7 |
| Margate | −30.8500 | 30.3330 | 127 | 1984–2017 | 1381.8 |
| Category | Index (%) |
|---|---|
| Normal | >80 |
| Weak drought | 70–80 |
| Moderate drought | 50–70 |
| Severe drought | 40–50 |
| Extreme drought | <40 |
| Category | RAI |
|---|---|
| Extremely wet | ≥3.0 |
| Very Wet | 2.0 to 2.99 |
| Moderately wet | 1.0 to 1.99 |
| Slightly wet | 0.50 to 0.99 |
| Near Normal | 0.49 to −0.49 |
| Slightly dry | −0.50 to −0.99 |
| Moderately dry | −1.0 to −1.99 |
| Very dry | −2.0 to −2.99 |
| Extremely dry | ≤−3.00 |
| Rainfall Station | Altitude | S-Value | p-Value | Sen’s Slope | |
|---|---|---|---|---|---|
| (m amsl) | RAI | PNPI | |||
| Ingwavuma-Manguzi | 69 | −131 | 0.026 | −0.137 | −1.617 |
| Hlabisa- Mbazwana | 55 | −256 | 0.023 | −0.056 | −0.787 |
| Hlobane | 1294 | −130 | 0.253 | −0.028 | −0.271 |
| Newcastle | 1241 | 17 | 0.814 | 0.005 | 0.056 |
| Dundee | 1256 | −212 | 0.061 | −0.046 | −0.613 |
| Mahlabathini | 757 | −156 | 0.169 | −0.032 | −0.409 |
| St.Lucia Forest | 44 | 0 | 0.993 | −9.8 × 10−5 | −0.001 |
| Empangeni Magistrate | 74 | −336 | 0.003 | −0.079 | −1.135 |
| Bergville | 1145 | 78 | 0.496 | 0.021 | 0.194 |
| Boscombe | 1151 | −286 | 0.011 | −0.048 | −0.484 |
| Sani-Pass | 2063 | −20 | 0.867 | −0.003 | −0.038 |
| Allerton Vet | 711 | −221 | 0.049 | −0.051 | −0.467 |
| Richmond | 864 | −71 | 0.528 | −0.017 | −0.233 |
| Durban | 76 | −288 | 0.01 | −0.06 | −0.708 |
| SummerFord | 1233 | −20 | 0.867 | −0.005 | −0.046 |
| Franklin Pol | 1532 | 304 | 0.007 | 0.058 | 0.765 |
| Glenora Farm | 872 | −134 | 0.239 | −0.02 | −0.193 |
| Margate | 127 | 123 | 0.07 | 0.078 | 0.879 |
| Rainfall Station | Minimum | Maximum | Mean | σ | ||
|---|---|---|---|---|---|---|
| Ingwavuma-Manguzi | 52.94 | (2015) | 197.17 | (2000) | 100.0 | 33.8 |
| Hlabisa- Mbazwana | 37.29 | (2015) | 167.58 | (1991) | 100.0 | 32.2 |
| Hlobane | 53.57 | (2015) | 154.88 | (1994) | 100.0 | 21.7 |
| Newcastle | 54.99 | (2002) | 159.63 | (1996) | 100.0 | 26.4 |
| Dundee | 30.10 | (2015) | 161.67 | (1996) | 100.0 | 29.6 |
| Mahlabathini | 54.29 | (2015) | 181.81 | (1987) | 100.0 | 32.4 |
| St.Lucia Forest | 50.35 | (1992) | 170.15 | (1984) | 100.0 | 30.0 |
| Empangeni Magistrate | 37.70 | (2014) | 177.74 | (1987) | 100.0 | 33.6 |
| Bergville | 59.34 | (2007) | 157.23 | (1996) | 100.0 | 20.8 |
| Boscombe | 66.38 | (2014) | 167.39 | (1987) | 100.0 | 22.7 |
| Sani-Pass | 44.25 | (2015) | 144.54 | (1987) | 83.1 | 17.9 |
| Allerton Vet | 64.27 | (2016) | 159.05 | (1987) | 100.0 | 20.8 |
| Richmond | 49.43 | (2015) | 165.42 | (1996) | 99.5 | 24.4 |
| Durban | 48.21 | (2014) | 147.65 | (1999) | 100.0 | 26.1 |
| SummerFord | 53.25 | (2015) | 173.92 | (1987) | 100.0 | 21.6 |
| Franklin Pol | 28.81 | (1974) | 162.61 | (1987) | 100.6 | 29.1 |
| Glenora Farm | 55.16 | (2015) | 149.80 | (2000) | 100.0 | 20.5 |
| Margate | 39.74 | (1992) | 179.75 | (2012) | 100.0 | 30.2 |
| Rainfall Station | Minimum | Maximum | Mean | σ | ||
|---|---|---|---|---|---|---|
| Ingwavuma-Manguzi | −4.09 | (2015) | 7.75 | (2000) | −0.10 | 2.79 |
| Hlabisa- Mbazwana | −4.55 | (2015) | 4.45 | (1991) | −0.09 | 2.22 |
| Hlobane | −4.88 | (2015) | 5.51 | (1994) | −0.04 | 2.23 |
| Newcastle | −4.24 | (2002) | 5.74 | (1996) | 0.02 | 2.52 |
| Dundee | −4.69 | (2015) | 5.08 | (1996) | 0.18 | 2.18 |
| Mahlabathini | −3.81 | (2015) | 4.86 | (1987) | −0.31 | 2.22 |
| St.Lucia Forest | −3.91 | (1992) | 4.81 | (1984) | −0.12 | 2.19 |
| Empangeni Magistrate | −4.64 | (2014) | 4.67 | (1987) | −0.20 | 2.22 |
| Bergville | −4.24 | (2007) | 6.30 | (1996) | 0.05 | 2.23 |
| Boscombe | −3.66 | (2014) | 5.92 | (1987) | −0.18 | 2.18 |
| Sani-Pass | −4.47 | (2015) | 14.10 | (1987) | −0.88 | 2.87 |
| Allerton Vet | −4.03 | (2016) | 5.71 | (1987) | −0.13 | 2.16 |
| Richmond | −5.06 | (2015) | 6.44 | (1996) | −0.02 | 2.40 |
| Durban | −4.14 | (2014) | 4.21 | (1999) | 0.09 | 2.19 |
| SummerFord | −5.68 | (2015) | 6.99 | (1987) | −0.22 | 2.27 |
| Franklin Pol | −4.84 | (1974) | 5.21 | (1987) | 0.21 | 2.18 |
| Glenora Farm | −5.09 | (2015) | 5.06 | (2000) | −0.09 | 2.19 |
| Margate | −5.42 | (1992) | 6.68 | (2012) | −0.08 | 2.62 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndlovu, M.S.; Demlie, M. Assessment of Meteorological Drought and Wet Conditions Using Two Drought Indices Across KwaZulu-Natal Province, South Africa. Atmosphere 2020, 11, 623. https://doi.org/10.3390/atmos11060623
Ndlovu MS, Demlie M. Assessment of Meteorological Drought and Wet Conditions Using Two Drought Indices Across KwaZulu-Natal Province, South Africa. Atmosphere. 2020; 11(6):623. https://doi.org/10.3390/atmos11060623
Chicago/Turabian StyleNdlovu, Minenhle Siphesihle, and Molla Demlie. 2020. "Assessment of Meteorological Drought and Wet Conditions Using Two Drought Indices Across KwaZulu-Natal Province, South Africa" Atmosphere 11, no. 6: 623. https://doi.org/10.3390/atmos11060623
APA StyleNdlovu, M. S., & Demlie, M. (2020). Assessment of Meteorological Drought and Wet Conditions Using Two Drought Indices Across KwaZulu-Natal Province, South Africa. Atmosphere, 11(6), 623. https://doi.org/10.3390/atmos11060623





