Using High-Density Rain Gauges to Validate the Accuracy of Satellite Precipitation Products over Complex Terrains
Abstract
:1. Introduction
2. Study Area and Datasets
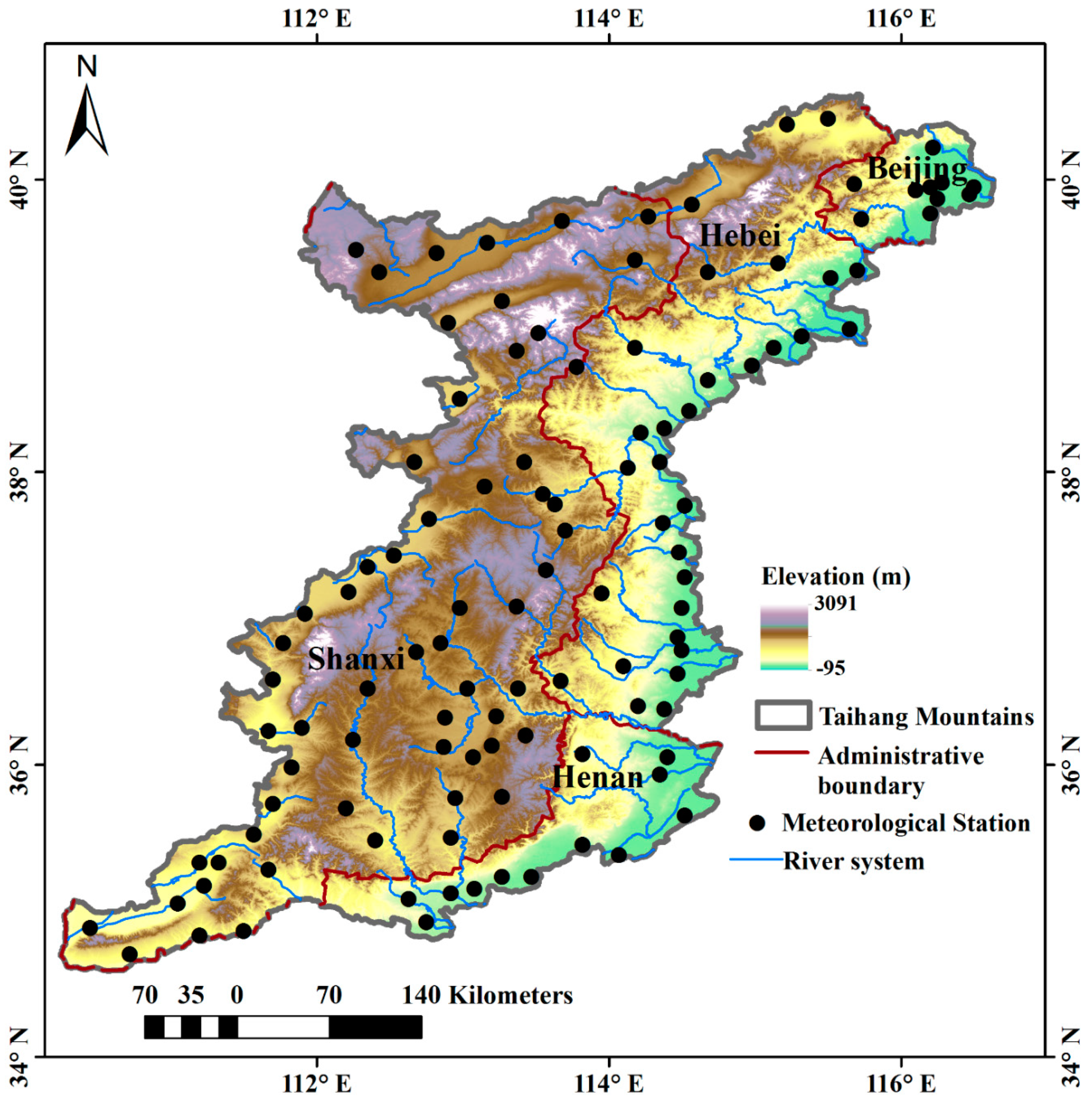
2.1. Study Area
2.2. Rain Gauge Dataset
2.3. Satellite-Based Datasets
2.3.1. CMORPH CRT
2.3.2. TRMM 3B42V7
2.3.3. GPM IMERG
3. Methodology
3.1. Methodology for Data Comparison
3.2. Classification of Elevation Group and Precipitation Intensity (PI)
3.3. Statistical Analysis
3.4. Regression Models
- (1)
- Find the minimum value of via fitting ;
- (2)
- The predicted value is
4. Results
4.1. Overall Performance in Different Elevation Regions
4.2. Reliability of the Performance of SPPs on Elevation
4.3. Reliability of the Performance of SPPs on Precipitation Intensity in Different Elevation Regions
5. Discussion
6. Conclusions
- Over the whole regions, the three SPPs provided overall larger daily precipitation estimates than rain gauges, and 3B42 slightly outperformed CRT and IMERG. In the different elevation groups, the three products showed better performance accuracy in the 0–500 m regions. The three SPPs showed a similar precipitation detection performance over the whole area, and exhibited good precipitation detecting ability in high-elevation (>1000 m) regions.
- The errors of 3B42 and CRT showed a significant positive (p < 0.01) correlation with elevation. Precipitation detection performance of three products was gradually improved with the rise in elevation.
- Over the whole regions, three SPPs slightly overestimated the frequency of heavy rain events (6.9 < PI ≤ 19.6 mm/d). CRT and 3B42 tended to underestimate the frequency of no rain events (PI < 0.1 mm/d), while IMERG overestimated the frequency of no rain events. Our study infers that the precipitation detection performances of the three SPPs become worse with the increase of precipitation intensity.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xia, T.; Wang, Z.J.; Zheng, H. Topography and data mining based methods for improving satellite precipitation in mountainous areas of China. Atmosphere 2015, 6, 983–1005. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Tang, G.; Han, Z.; Guo, X.; Hong, Y. Global intercomparison and regional evaluation of GPM IMERG version-03, version-04 and its latest version-05 precipitation products: Similarity, difference and improvements. J. Hydrol. 2018, 564, 342–356. [Google Scholar] [CrossRef]
- Pan, M.; Li, H.; Wood, E. Assessing the skill of satellite-based precipitation estimates in hydrologic applications. Water Resour. Res. 2010, 46, 201–210. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, Y.; Hu, B.; Liang, Z.; Shi, Z. Downscaling annual precipitation with TMPA and land surface characteristics in China. Int. J. Clim. 2017, 37, 5105–5119. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Multi time-scale evaluation of high-resolution satellite-based precipitation products over northeast of Austria. Atmos. Res. 2018, 206, 46–63. [Google Scholar] [CrossRef]
- Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.; Hong, Y. Global view of real-time TRMM multisatellite precipitation analysis: Implications for its successor global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2015, 96, 283–296. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Magginoi, V.; Meyers, P.C.; Robinson, M.D. A review of merged high-resolution satellite. Precipitation product accuracy during the tropical rainfall measuring mission (TRMM) era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 1–15. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef] [Green Version]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef] [Green Version]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, W06526. [Google Scholar] [CrossRef]
- Song, H.J.; Sohn, B.J. Two Heavy Rainfall Types over the Korean Peninsula in the Humid East Asian Summer Environment: A Satellite Observation Study. Mon. Weather. Rev. 2015, 143, 363–382. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y.P. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7 and NCEP-CFSR over humid regions in China. Hydrological. Processes 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V.; Turk, J.; Ferraro, R. Satellite precipitation measurements for water resource monitoring. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 567–579. [Google Scholar] [CrossRef]
- Wang, K.; Guan, Q.; Chen, N.; Tong, D.; Hu, C.; Peng, Y.; Dong, X.; Yang, C. Optimizing the configuration of precipitation stations in a space-ground integrated sensor network based on spatial-temporal coverage maximization. J. Hydrol. 2017, 548, 625–640. [Google Scholar] [CrossRef]
- Aires, F.; Prigent, C.; Bernardo, F.; Jiménez, C.; Saunders, R.; Brunel, P. A Tool to Estimate Land-Surface Emissivities at Microwave frequencies (TELSEM) for use in numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 137, 690–699. [Google Scholar] [CrossRef] [Green Version]
- Carr, N.; Kirstetter, P.E.; Hong, Y.; Gourley, J.J.; Schwaller, M.; Petersen, W.; Wang, N.; Ferraro, R.R.; Xue, X. The influence of surface and precipitation characteristics on TRMM microwave imager rainfall retrieval uncertainty. J. Hydrometeorol. 2015, 16, 1596–1614. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa complex topography. Int. J. Remote. Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Gottschalck, J.; Meng, J.; Rodell, M.; Houser, P. Analysis of multiple precipitation products and preliminary assessment of their impact on global land data assimilation system land surface states. J. Hydrometeorol. 2005, 6, 573–598. [Google Scholar] [CrossRef]
- Bharti, V.; Singh, C. Evaluation of error in TRMM 3B42V7 precipitation estimates over the Himalayan region. J. Geophys. Res. Atmos. 2015, 120, 12458–12473. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Zhang, L.; Hao, Z. Tibetan plateau precipitation as depicted by gauge observations, reanalyses and satellite retrievals. Int. J. Climatol. 2014, 34, 265–285. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef] [Green Version]
- Cinco, T.A.; Guzman, R.G.; Hilario, F.D.; Wilson, D.M. Long-term trends and extremes in observed in daily precipitation and near surface air temperature in the Philippines for the period 1951–2010. Atmos. Res. 2014, 145–146, 12–26. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Li, J.; Singh, V.P.; Sun, P. Impact of urbanization on nonstationarity of annual and seasonal precipitation extremes in China. J. Hydrol. 2019, 575, 638–655. [Google Scholar] [CrossRef]
- Vu, T.M.; Mishra, A.K. Nonstationary frequency analysis of recent extreme precipitation events in the United States. J. Hydrol. 2019, 575, 999–1010. [Google Scholar] [CrossRef]
- Sarkar, S.; Maity, R. Increase in probable maximum precipitation in a changing climate over India. J. Hydrol. 2020, 585, 124806. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Li, J.; Singh, V.P.; Wang, Z. Topography-based spatial patterns of precipitation of precipitation extremes in the Poyang Lake basin, China: Changing properties and causes. J. Hydrol. 2014, 512, 229–239. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Singh, V.P.; Liu, L.; Shi, P. Spatiotemporal patterns of annual and seasonal precipitation extremes distributions across China and potential impact of tropical cyclones. Int. J. Climatol. 2017, 37, 4186–4198. [Google Scholar] [CrossRef]
- Fu, T.; Han, L.; Gao, H.; Liang, H.; Li, X.; Liu, J. Pedodiversity and its controlling factors in mountain regions—A case study of Taihang Mountain, China. Geoderma 2018, 310, 230–237. [Google Scholar] [CrossRef]
- Fu, T.; Han, L.; Gao, H.; Liang, H.; Liu, J. Geostatistical analysis of pedodiversity in Taihang Mountain region in North China. Geoderma 2018, 328, 91–99. [Google Scholar] [CrossRef]
- Tang, G.; Carroll, R.W.H.; Lutz, A.; Lin, S. Regulation of precipitation-associated vegetation dynamics on catchment water balance in a semiarid and arid mountainous watershed. Ecohydrology 2016, 9, 1248–1262. [Google Scholar] [CrossRef]
- Ding, Y.; Chan, J.C.L. The East Asian summer monsoon: An overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar] [CrossRef]
- Yang, M.; Yao, T.; Guo, X.; Wang, H.; Hao, L. Comparison analysis of the summer monsoon precipitation between northern and southern slopes of Tanggula Mountains, Qinghai-Xizang (Tibetan) plateau: A case study in summer 1998. Hydrol. Process. 2006, 21, 1841–1847. [Google Scholar] [CrossRef]
- Briggs, P.R.; Cogley, J.G. Topographic bias in mesoscale precipitation networks. J. Clim. 1996, 9, 205–218. [Google Scholar] [CrossRef]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Climatol. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global. precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 287–296. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM multi-satellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimate at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T. TRMM and other data precipitation date set documentation. In NASA Global Change Master Directory Doc; Mesoscale Atmospheric Processes Laboratory: Greenbelt, MD, USA, 2013; pp. 1–44. Available online: https://www.researchgate.net/publication/228892338 (accessed on 13 June 2020).
- Hou, A.Y.; Skofronick-Jackson, G.; Kummerow, C.D.; Shepherd, J.M. Global Precipitation Measurement. Part II: Precipitation: Advances in Measurement, Estimation and Prediction; Springer: Berlin/Heidelberg, Germany, 2008; Volumes 131–169. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Lguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Simonović, P.S. Floods in a Changing Climate. Risk Management, 1st ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of TRMM-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Sohn, B.J.; Ryu, G.H.; Song, H.J.; Ou, M.L. Characteristic features of warm-type rain producing heavy rainfall over the Korean Peninsula inferred from TRMM measurements. Mon. Weather Rev. 2013, 141, 3873–3888. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Hong, Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Kirstetter, P.E.; Hong, Y.; Gourley, J.J.; Schwaller, M.; Petersen, W.; Zhang, J. Comparison of TRMM 2A25 products, version 6 and version 7, with NOAA/NSSL ground radar–based national mosaic QPE. J. Hydrometeorol. 2013, 14, 661–669. [Google Scholar] [CrossRef] [Green Version]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1998, 83, 596–610. [Google Scholar] [CrossRef]
- Anders, A.M.; Roe, G.H.; Hallet, B.; Montgomery, D.R.; Finnegan, N.J.; Putkonen, J. Spatial patterns of precipitation and topography in the Himalaya. Geol. Soc. Am. Spec. Pap. 2006, 398, 39–53. [Google Scholar] [CrossRef] [Green Version]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Santos Villar, D.; Silvestre, D.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
- Mantas, V.M.; Liu, Z.; Caro, C.; Pereira, A. Validation of TRMM multi-satellite precipitation analysis (TMPA) products in the Peruvian Andes. Atmos. Res. 2015, 163, 132–145. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the dependence of satellite rainfall uncertainty on topography and climate for hydrologic model simulation. IEEE Trans. Geosci. Remote. Sens. 2013, 5, 704–718. [Google Scholar] [CrossRef]
- EI Kenaway, A.M.; Lopez-Moreno, J.I.; McCabe, M.F.; Vicente-Serrano, S.M. Evaluation of the TMPA-3B42 precipitation product using a high-density rain gauge network over complex terrain in northeastern Iberia. Glob. Planet. Chang. 2015, 133, 188–200. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Yang, D.; Gao, B.; Jiao, Y.; Hong, Y.; Xu, T. Multiscale hydrologic applications of the latest satellite precipitation products in the Yangtze River basin using a distributed hydrologic model. J. Hydrometeorol. 2015, 16, 407–426. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N. Evaluation of global satellite rainfall products over continental Europe. J. Hydrometeorol. 2012, 13, 588–603. [Google Scholar] [CrossRef]
- Dembélé, M.; Zwart, S. Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote. Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef] [Green Version]
- Arkin, P.A. The relationship between fractional coverage of high cloud and rainfall accumulations during GATE over the B-scale array. Mon. Weather Rev. 1979, 107, 1382–1387. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Liu, X.; Huang, K.; Li, X.; Shi, X.; Chen, Y.; Li, J. Improved snow depth retrieval by integrating microwave brightness temperature and visible/infrared reflectance. Remote. Sens. Environ. 2015, 156, 500–509. [Google Scholar] [CrossRef]
- Chokngamwong, R.; Chiu, L.S. Thailand daily rainfall and comparison with TRMM products. J. Hydrometeorol. 2008, 9, 256–266. [Google Scholar] [CrossRef]
- Prakash, S.; Gairola, R.M. Validation of TRMM-3B42 precipitation product over the tropical Indian Ocean using rain gauge data from the RAMA buoy array. Theor. Appl. Climatol. 2014, 115, 451–460. [Google Scholar] [CrossRef]
- Blacutt, L.A.; Herdies, D.L.; Gonçalves, L.G.G.; Vila, D.A.; Marcoe, A. Precipitation comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme dataset in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef] [Green Version]





| Dataset | Full Name | Latitudinal Coverage | Spatial Resolution | Temporal Coverage | References |
|---|---|---|---|---|---|
| CMORPH | NOAA Climate Prediction Center (CPC) MORPHing technique | 60° N–60° S | 8 km, 0.25° | January 1998–present | [38] |
| TRMM 3B42V7 | TRMM Multi-satellite Precipitation Analysis research product 3B42 Version 7 | 50° N–50° S | 0.25° | January 1998–December 2019 | [39] |
| GPM IMERG | GPM Integrated Multi-satelliteE Retrievals Version 05 | 60° N–60° S | 0.1° | June 2014–present | [41,42] |
| Statistic Metrics | Equation | Perfect Value |
|---|---|---|
| Correlation Coefficient (CC) | 1 | |
| Bias Ratio (β) | 1 | |
| Variability Ratio (γ) | 1 | |
| Modified KGE (KGE’) | 1 | |
| Root Mean Squared Error (RMSE) | 0 | |
| Probability of Detection (POD) | 1 | |
| False Alarm Ratio (FAR) | 0 | |
| Critical Success Index (CSI) | 1 |
| Elevation (m) | Total Gauges | Mean Rain (mm/d) | CC | β | γ | RMSE (mm) | KGE’ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CRT | IMERG | 3B42 | CRT | IMERG | 3B42 | CRT | IMERG | 3B42 | CRT | IMERG | 3B42 | CRT | IMERG | 3B42 | |||
| Whole regions | 104 | 1.63 | 0.36 | 0.52 | 0.48 | 1.04 | 1.05 | 1.06 | 0.80 | 0.81 | 0.77 | 7.43 | 7.06 | 7.29 | 0.33 | 0.48 | 0.43 |
| <100 | 30 | 1.68 | 0.37 | 0.49 | 0.43 | 0.95 | 1.04 | 1.02 | 0.73 | 0.77 | 0.72 | 9.43 | 8.87 | 9.09 | 0.31 | 0.43 | 0.37 |
| 100–500 | 20 | 1.59 | 0.46 | 0.57 | 0.52 | 1.15 | 1.12 | 1.11 | 0.76 | 0.76 | 0.73 | 7.68 | 6.79 | 7.15 | 0.39 | 0.49 | 0.44 |
| 500–1000 | 40 | 1.60 | 0.47 | 0.54 | 0.51 | 1.09 | 1.03 | 1.06 | 0.85 | 0.85 | 0.83 | 6.42 | 5.89 | 6.07 | 0.45 | 0.52 | 0.47 |
| >1000 | 14 | 1.65 | 0.47 | 0.54 | 0.51 | 1.11 | 1.02 | 1.05 | 0.94 | 0.96 | 0.97 | 6.39 | 5.79 | 6.06 | 0.46 | 0.54 | 0.51 |
| Elevation (m) | Total Gauges | POD | FAR | CSI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CRT | IMERG | 3B42 | CRT | IMERG | 3B42 | CRT | IMERG | 3B42 | ||
| Whole regions | 104 | 0.58 | 0.53 | 0.57 | 0.49 | 0.41 | 0.48 | 0.37 | 0.38 | 0.38 |
| <100 | 30 | 0.55 | 0.53 | 0.53 | 0.53 | 0.45 | 0.48 | 0.34 | 0.37 | 0.35 |
| 100–500 | 20 | 0.57 | 0.54 | 0.57 | 0.51 | 0.42 | 0.51 | 0.36 | 0.39 | 0.35 |
| 500–1000 | 40 | 0.60 | 0.52 | 0.59 | 0.48 | 0.40 | 0.47 | 0.39 | 0.39 | 0.39 |
| >1000 | 14 | 0.59 | 0.52 | 0.59 | 0.44 | 0.35 | 0.43 | 0.40 | 0.40 | 0.41 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Zhang, Y.; Yang, Y. Using High-Density Rain Gauges to Validate the Accuracy of Satellite Precipitation Products over Complex Terrains. Atmosphere 2020, 11, 633. https://doi.org/10.3390/atmos11060633
Yu L, Zhang Y, Yang Y. Using High-Density Rain Gauges to Validate the Accuracy of Satellite Precipitation Products over Complex Terrains. Atmosphere. 2020; 11(6):633. https://doi.org/10.3390/atmos11060633
Chicago/Turabian StyleYu, Linfei, Yongqiang Zhang, and Yonghui Yang. 2020. "Using High-Density Rain Gauges to Validate the Accuracy of Satellite Precipitation Products over Complex Terrains" Atmosphere 11, no. 6: 633. https://doi.org/10.3390/atmos11060633
APA StyleYu, L., Zhang, Y., & Yang, Y. (2020). Using High-Density Rain Gauges to Validate the Accuracy of Satellite Precipitation Products over Complex Terrains. Atmosphere, 11(6), 633. https://doi.org/10.3390/atmos11060633






