Formation of Multilayered Sporadic E under an Influence of Atmospheric Gravity Waves (AGWs)

Abstract

The formation of multilayered sporadic E by atmospheric gravity waves (AGWs), propagating in the mid-latitude lower thermosphere, is shown theoretically and numerically. AGWs with a vertical wavelength smaller than the width of the lower thermosphere lead to the appearance of vertical drift velocity nodes (regions where the ions’ vertical drift velocity, caused by these waves, is zero) of heavy metallic ions (Fe⁺). The distance between the nearest nodes is close to the AGWs’ vertical wavelength. When the divergence of the ion vertical drift velocity at its nodes has a minimal negative value, then these charged particles can accumulate into Es-type thin layers and the formation of multilayered sporadic E is possible. We showed the importance of the ions’ ambipolar diffusion in the formation of Es layers and control of their densities. Oblique downward or upward propagation of AGWs causes downward or upward motion of the ion vertical drift velocity nodes by the vertical propagation phase velocity of these waves. In this case, the formed Es layers also descend or move upward with the same phase velocity. The condition, when the horizontal component of AGWs’ intrinsic phase velocity (phase velocity relative to the wind) and background wind velocity have same magnitudes but opposite directions, is favorable for the formation of the multilayered sporadic E at fixed heights of the sublayers. When the AGWs are absent, then horizontal homogeneous wind causes the formation of sporadic E but with a single peak. In the framework of the suggested theory, it is shown that, in the lower thermosphere, the wind direction, magnitude, and shear determine the development of the processes of ion/electron convergence into the Es-type layer, as well as their density divergence. Consideration of arbitrary height profiles of the meridional and zonal components of the horizontal wind velocity, in case of AGW propagation, should be important for the investigation of the distribution and behavior of heavy metallic ions on regional and global scales.

1. Introduction

The lower thermosphere is a weakly ionized medium and the behavior of the charged particles at the global and regional scales should be significantly determined by neutral wind. Neutral wind and its significant variations can be determined by atmospheric gravity waves (AGWs), planetary waves, and tidal motion [1,2]. The sporadic E is an ionospheric irregular structure observed in the lower thermosphere, which can be a manifestation of neutral atmosphere–ionosphere coupling in the presence of horizontal wind. The wind shear caused by tidal motion or atmospheric waves and instabilities, as well as wind and electric field directions, influence the formation and behavior of the Es layers [3,4,5,6,7].

In this study, the observed additional peak or sublayers (multilayered structures) in sporadic E [8,9,10] can be caused by vertical/oblique propagation of AGWs or tidal winds. Here, unlike the previous studies [11,12,13], homogeneous horizontal wind can cause single peak sporadic E (Es layer), but the presence of AGWs with vertical wavelengths smaller than the width of the height region between about 90 and 150 km can cause additional sublayers (Es layers). In this case, the vertical changes in the wind direction, magnitude, and shear causes the appearance of nodes of ion vertical drift velocity—heights where the ion vertical drift velocity, caused by the AGWs, is zero. When in these regions of nodes, the drift velocity divergence has minimal negative values, and then the ions/electrons converge in the Es-type thin layer. The distances between such nodes and the sporadic E sublayers are close to the AGWs’ vertical wavelength. In this case, the Es layer densities are also controlled by ion ambipolar diffusion. When the ion vertical drift velocity divergence has maximal positive values at the region of its nodes, then the ion/electron density is depleted. The charged particles’ density depletion is also an irregular/sporadic phenomenon, with increased interest of investigation [14].

According to the present theoretical study, the development of ion convergence processes and the formation of Es-type layers in a given mid-latitude lower thermosphere region, as well as their localization, are determined by horizontal wind direction, magnitude, and shear. In the framework of the presented theory, these processes are more predictable than by the windshear theory [15,16,17,18,19]. According to the windshear theory, the sporadic E is formed at heights, where, e.g., for the northern hemisphere, due to wind velocity vertical shear, the southward wind changes to the northward one, or the eastward wind to the westward one [19]. Our study shows that the Es layers do not always form in the regions where horizontal wind changes direction to the opposite, which is an observed phenomenon [8,20,21]. We show analytically that the tendency of formation of the sporadic E can be caused by a certain direction, magnitude, and shear of arbitrary horizontal wind. In the presence of AGWs, the horizontal wind height profile is assumed as the sum of its homogeneous and variable parts caused by the AGWs (or tidal wind). This theoretical consideration will be followed by corresponding numerical simulations showing (1) the possibility of formation of multilayered sporadic E and its sublayers under influence of AGWs; (2) Es layers located at the ion vertical drift velocity nodes; (3) the importance of the effect of homogeneous horizontal wind on the ion/electron convergence processes; and (4) the possibility of formation of sporadic E by homogeneous winds. Considering the horizontal wind at about the 120 km height region, determined by the sum of the background wind and the AGW velocities, compared to the values of the Horizontal Wind Model 2014 (HWM14) and some measured data [1,22], we noted the importance of these waves in the formation of Es layers, at the region where they are frequently observed (below 120 km). The analytically obtained condition of formation and localization of the Es layers, which was applied to the linear AGWs, also includes the possibility of its development in case of various horizontal wind height profiles, which can be caused by both linear and nonlinear waves.

We demonstrate the applicability of the presented theory, describing heavy metallic ion behavior in the lower thermosphere, including the phenomena of sporadic E formation and ion depletion under influence of horizontal wind, taking into account the propagation of the AGWs. The applicability of this theory shows its importance for the investigation of regional and global peculiarities of heavy metallic ion distribution [23,24].

2. Theory of Sporadic E Formation under the Influence of AGWs and Background Horizontal Wind

In this section, we describe the theory of the formation of sporadic E in the nighttime mid-latitude lower thermosphere. For simplicity, we consider a case when the heavy metallic ions Fe⁺ are dominant. Due to the quick quenching of molecular ions after sunset [10], the quasi neutrality in the region is mainly determined by the density of these metallic ions. The approximate analytical solution of the continuity equation for the ion/electron density height profile shows the possibility of formation of multilayered sporadic E in case of the presence of background horizontal wind and oblique propagation of the AGWs.

We study the mid-latitude lower thermosphere where the formation of sporadic E is mostly observed. The thermospheric wind influences the development of ion convergence/divergence processes via combined action of the Lorentz forcing and ion-neutral collision. Here, the ion ambipolar diffusion also influences the ion/electron motion and formation of a narrow and dense Es-type layer. We consider the horizontal neutral wind velocity $V(V_x, V_y, 0)$ with arbitrary height profiles of the meridional $V_x(z)$ and zonal $V_y(z)$ components. We take a right-handed set of coordinates (x, y, z) with x directed to the magnetic north, y to the west, and z vertically upwards.

2.1. Equation for Ion/Electron Density Height Profile Behavior under Influence of Horizontal Wind with AGWs

In the suggested study, the meridional $V_x$ and zonal $V_y$ components of the wind velocity (V) are represented by the sum of the background homogeneous wind velocity with meridional $V_{ox}$ and zonal $V_{oy}$ components and AGWs with velocities $V_{gx}(z,t), V_{gy}(z,t)\propto e^{\frac{z-z_o}{2H}}\mathrm{Real}\left\{\exp i[-\omega (t-t_o)+k_z(z-z_o)+k_x(x-x_o)+k_y(y-y_o)]\right\}$ ($i=\sqrt{-1}$ is the unit imaginary number), and can be described by the following equations [25,26]:

$$V_x(z,t)=V_{ox}+V_{gx}(z,t)$$

(1)

$$V_y(z,t)=V_{oy}+V_{gy}(z,t)$$

(2)

where

$$V_{gx}(z,t)=A_x{e}^{\frac{z-z_o}{2H}}\cos [-\omega (t-t_o)+k_z(z-z_o)+k_x(x-x_o)+k_y(y-y_o)]$$

(3)

$$V_{gy}(z,t)=A_y{e}^{\frac{z-z_o}{2H}}\cos [-\omega (t-t_o)+k_z(z-z_o)+k_x(x-x_o)+k_y(y-y_o)]$$

(4)

Here, $t_o\left(t\ge t_o\right)$ is some initial time. $A_x$ and $A_y$ are amplitudes of wind velocity perturbations, caused by waves, at the point $x=x_o$, $y=y_o$ and $z=z_o$. It is assumed that the vertical component of wind velocity is much smaller than the horizontal components given in Equations (1) and (2), and its influence on the ion vertical drift velocity is negligibly small [5,19]. In Equations (3) and (4), $\omega$ is the observed wave frequency at the given mid-latitude region of the lower thermosphere, which, in the case of homogeneous background horizontal wind $V_o(V_{ox}, V_{oy}, 0)$, is determined by the dispersion equation [27]:

$${\left(\omega -k_x{V}_{ox}-k_y{V}_{oy}\right)}^2={\omega }_g^2$$

(5)

Here, ${\omega }_g$ is the AGWs intrinsic frequency (frequency relative to the background wind) and has the following form [25]:

$${\omega }_g^2=\frac{1}{2}{c}_s^2\left({\left|\mathit{k}\right|}^2+\frac{1}{4H^2}\right)-\sqrt{\frac{1}{4}{c}_s^4{\left({\left|\mathit{k}\right|}^2+\frac{1}{4H^2}\right)}^2-{\omega }_b^2{c}_s^2\left(k_x^2+k_y^2\right)}$$

(6)

where $H$ is the atmospheric scale height; ${\omega }_b$ is the Brunt–Väisälä frequency; $c_s={(\gamma gH)}^{0.5}$ is the speed of sound; $\gamma$ is the specific heat ratio; $\mathit{k}=\mathit{k}(k_x,k_y,k_z)$ is the wavenumber where $\left|k_x\right|=\frac{2\pi }{{\lambda }_x}$; $\left|k_y\right|=\frac{2\pi }{{\lambda }_y}$; $\left|k_z\right|=\frac{2\pi }{{\lambda }_z}$; ${\lambda }_x,{\lambda }_y$; and ${\lambda }_z$ are the meridional, zonal, and vertical wavelengths, respectively.

Note that, for the horizontal wavelengths ${\lambda }_x$ and ${\lambda }_y$ of about 100–200 km, the horizontal wind velocity in the lower thermosphere of about 50–150 m/s [1], which significantly influences the AGWs’ frequency (Equations (3) and (4)), and can lead to stationary ($\omega =0$) velocity profiles (Equations (1) and (2)) over the considered mid-latitude region. Such a stationary condition for propagation of the AGWs is similar to the case of tidal winds for which the horizontal wavelengths and period are expected to be much greater than those of the AGWs.

The dependence of ions’ vertical drift velocity ${\mathrm{w}}_i$ on the meridional $V_x$ and zonal $V_y$ components of the neutral particles horizontal wind velocity $V(V_x, V_y, 0)$ and ambipolar diffusion $D_a$ can be described by the following equations [6,13,28]:

$${\mathrm{w}}_i={\mathrm{w}}_{iv}-D_a(z)\frac{1}{N_i}\frac{\partial N_i}{\partial z}$$

(7)

and

$${\mathrm{w}}_{iv}=-C_x(z)V_x-C_y(z)V_y$$

(8)

where ${\mathrm{w}}_{iv}$ is the ion vertical drift velocity caused by only horizontal wind via combined action of the Lorentz forcing and ion-neutral collisions [19]. In Equations (7) and (8),

$$C_x(z)=\frac{1}{1+{\kappa }^2(z)}\sin I\cos I$$

(9)

$$C_y(z)=\frac{\kappa (z)}{1+{\kappa }^2(z)}\cos I$$

(10)

and

$$D_a(z)=\frac{{\kappa }^2(z)+{\sin }^{2}I}{1+{\kappa }^2(z)}\frac{2k_{B}T}{M_i{\nu }_{in}(z)}$$

(11)

Here, $\kappa (z)={\nu }_{in}(z)/{\omega }_i$; ${\nu }_{in}(z)$ is the ion-neutral collision frequency; ${\omega }_i={eB/M}_i$ is the metallic ion (Fe⁺) gyrofrequency (${\omega }_i=80 s^{-1}$); $B(B\cos I,0,-B\sin I)$ is the Earth’s magnetic field vector; I is the magnetic dip angle; $M_i$ is the ion mass; $D_a(z)$ is the ambipolar diffusion coefficient; $T=(T_e+T_i)/2$ is the mean plasma temperature; $T_e$ and $T_i$ are ions and electrons temperatures, respectively; and $k_B$ is the Boltzmann constant. In this study, Fe⁺ is assumed as the dominant ion in the nighttime lower thermosphere [10,16,18,19]. The $C_x(z)$ and $C_y(z)$ coefficients determine the influence of the meridional $V_x$ and zonal $V_y$ components of the horizontal wind velocity $V$ on the ions’ vertical drift velocities ${\mathrm{w}}_i$ and ${\mathrm{w}}_{iv}$ (Equations (7) and (8)). These coefficients in ${\mathrm{w}}_{iv}$ (Equation (8)) significantly change with height in the lower thermosphere between heights of about 100 km and 140 km. This height dependence is mainly caused by ${\nu }_{in}(z)$, which in turn is determined by the height profiles of the neutral particle densities ($[N_2](z)$, $[O_2](z)$ and $[O](z)$) dominating in this region [29]:

$${\nu }_{in}(z)=\left(2.62[N_2](z)+2.61 [O_2](z)+1.43[O](z)\right)\times {10}^{-10} s^{-1}$$

(12)

To investigate the behavior of the height profile of the ion/electron density $N_e(z,t)$ (assuming quasi-neutrality $N_e=N_i(F{e}^{+})$) under the influence of the horizontal wind with velocity $V(V_x, V_y, 0)$, we apply the continuity equation, taking into account the ions’ vertical drift velocity ${\mathrm{w}}_i$ as per Equations (7)–(10):

$$\frac{\partial N_e}{\partial t}=(C_v^{\prime }+C_{sh}^{\prime })N_e-w_{iv}\frac{\partial N_e}{\partial z}+\frac{\partial }{\partial z}\left(D_a\frac{\partial N_e}{\partial z}\right)$$

(13)

where

$$C_v^{\prime }=V_x\frac{\partial C_x}{\partial z}+V_y\frac{\partial C_y}{\partial z}$$

(14)

$$C_{sh}^{\prime }=C_x\frac{\partial V_x}{\partial z}+C_y\frac{\partial V_y}{\partial z}$$

(15)

In the continuity Equation (13), the production and loss rates of the long-lived metallic ion Fe⁺ or the electrons for the characteristic time of sporadic E formation (e.g., about 1 h) are neglected [30]. Here, the behavior of $N_e(z,t)$ under the influence of the meridional $V_x$ and zonal $V_y$ components of the horizontal wind velocity (V) and their vertical shears ($\frac{\partial V_x}{\partial z}\ne 0,\frac{\partial V_y}{\partial z}\ne 0$) is described in terms of the parameters $C_v^{\prime }(z)$, Equation (14), and $C_{sh}^{\prime }(z)$, Equation (15). The ions’ ambipolar diffusion, Equation (11), is also taken into account. Here, for a given wind velocity magnitude and direction, the vertical changes ($\frac{\partial C_x}{\partial z}\ne 0,\frac{\partial C_y}{\partial z}\ne 0$) of the ion drift velocity coefficients $C_x(z)$ and $C_y(z)$ determine the height profile of the $C_v^{\prime }\ne 0$ parameter (Equation (14)). On the basis of Equations (9) and (10), we can state that unlike the windshear effect, determined by $C_{sh}^{\prime }(z)$, the $C_v^{\prime }(z)$ coefficient is important only in the lower thermosphere. According to Equations (10), (11), and (13), the value of $C_v^{\prime }(z)$ both above the top of the lower thermosphere of about z > 150 km ($V_x\frac{\partial C_x}{\partial z}\propto [V_{ox}+A_x{e}^{\frac{z-z_o}{2H}}]e^{-\frac{2(z-z_o)}{H}},V_y\frac{\partial C_y}{\partial z}\propto [V_{oy}+A_y{e}^{\frac{z-z_o}{2H}}]e^{-\frac{z-z_o}{H}}$) and below its bottom of about z < 90 km ($V_x\frac{\partial C_x}{\partial z}\propto [V_{ox}+A_x{e}^{\frac{z-z_o}{2H}}]e^{\frac{2(z-z_o)}{H}},V_y\frac{\partial C_y}{\partial z}\propto [V_{oy}+A_y{e}^{\frac{z-z_o}{2H}}]e^{\frac{z-z_o}{H}}$) decreases by at least one order of magnitude compared to its value at height about $z=z_o=120 \mathrm{km}$, even for the maximal values of the total wind about $V_{ox}+A_x\le 150 \mathrm{m}/\mathrm{s}$. Here, we assumed the barometric approach in the neutrals density vertical distribution $\propto e^{-\frac{(z-z_o)}{H}}$ and correspondingly for the ion-neutral collisional frequency ${\nu }_{in}(z)\propto \kappa (z)\propto e^{-\frac{(z-z_o)}{H}}$ (Equation (10)). $\kappa \approx 1$ (ion gyrofrequency equal to the ion-neutral frequency) occurs at a height of about z = 121 km.

2.2. Analytical Approach for Ion/Electron Density Height Profile Behavior and Condition of Sporadic E Formation under Influence of Horizontal Wind

To show the importance of the $C_v^{\prime }(z)$ and $C_{sh}^{\prime }(z)$ parameters on the behavior of ion/electron density $N_e(z,t)$, Equations (14) and (15), we solve Equation (13) approximately. The approximated analytical solution of Equation (13), for small time $t-t_o<<H_{ic}^2/2D_a$ and heights ${(z-z_{om})}^2<<H_{ic}^2$, has the following form:

$$N_e(z,t)\approx N_{om}\exp \left\{\left[-\frac{2D_a}{H_{ic}^2}+C_v^{\prime }+C_{sh}^{\prime }\right](t-t_o)-{\left(\frac{z-[z_{om}+w_{iv}(t-t_o)]}{H_{ic}}\right)}^2\right\}$$

(16)

At the initial time of $t=t_o$, Equation (16) corresponds to the ion/electron Gaussian-type distribution layer with maximal density $N_{om}$ (peak density) at the corresponding $z=z_{om}$ height (peak height). In case of the absence of wind ($w_{iv}=0$, $C_v^{\prime }, C_{sh}^{\prime }=0$), the ion/electron density at peak height $z=z_{om}$ decreases due to ambipolar diffusion. $H_{ic}$ is the characteristic scale height of the ions, which determines the ion/electron main layer thickness ($2H_{ic}$) and height region $z-z={}^{om}\pm H_{ic}$ at some initial time t = to, where their density decreases by e.

According to Equation (16), when, at the peak height of the ion/electron density initial layer, ($z=z_{om}$) $C_v^{\prime }+C_{sh}^{\prime }>\frac{2D_a}{H_{ic}^2}$ occurs, then the charged particles density in this region tends to increase ($N_e/N_{om}>1$). When, at this peak height, $C_v^{\prime }+C_{sh}^{\prime }<\frac{2D_a}{H_{ic}^2}$, then the ion/electron density decreases in this region ($N_e/N_{om}<1$). Here, it is important to note that, when the parameter $C_v^{\prime }(z)+C_{sh}^{\prime }(z)>0$ has its maximal values at certain heights, then the ion/electron convergence into a thin horizontal layer becomes possible. The assumed dominance of the long-lived heavy metallic ions Fe⁺ in the nighttime lower thermosphere also assumes the negligibly small changes in total electron content (TEC). If, in this case, the relatively big increase in ion/electron density $N_e(z,t)/N_{om}>1$ at the height region with $(C_v^{\prime }+C_{sh}^{\prime })\max >0$ exceeds their diffusive displacement, then the ion/electron convergence into a thin layer and the sporadic E may be formed. So, according to Equation (16), the condition necessary for the formation of sporadic E is:

$$(C_v^{\prime }+C_{sh}^{\prime })\max >\frac{2D_a}{H_{ic}^2}$$

(17)

According to Equations (7)–(10), (14), and (15), when $\left|C_v^{\prime }+C_{sh}^{\prime }\right|>>\left|\frac{\partial }{\partial z}\left(D_a\frac{1}{N_i}\frac{\partial N_i}{\partial z}\right)\right|$ then the ion vertical drift velocity divergence is $\frac{\partial w_i}{\partial z}\approx \frac{\partial w_{iv}}{\partial z}=-C_v^{\prime }-C_{sh}^{\prime }$. In this case, the condition (17) of the ion/electron convergence into a thin layer (when $N_e/N_{om}$ increases) takes place at the region where the ion drift velocity divergence has a minimal negative value ($\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$). The dependence of the convergence of the ion/electron into a thin layer on the ions’ ambipolar diffusion (diffusive control $\propto \frac{2D_a}{H_{ic}^2}$), as per Equation (17), will appear for a narrow layer of these charged particles ($H_{ic}<H$), as well as for the upper heights of the lower thermosphere, where this diffusion increases. The case of $(C_v^{\prime }+C_{sh}^{\prime })\min <0$ corresponds to the maximal positive divergence of the ion vertical drift velocity $(\partial w_{iv}/\partial z)\max >0$ and, according to Equation (17), the ion/electron density depletion ($N_e/N_{om}<1$) may happen for the given height region of the lower thermosphere. Hereafter, the coefficients $C_v^{\prime }$, Equation (14), and $C_{sh}^{\prime }$, Equation (15), will be referred to as the ion convergence ($C_v^{\prime }>0$, $C_{sh}^{\prime }>0$) or divergence ($C_v^{\prime }<0$,$C_{sh}^{\prime }<0$) rates, respectively, caused by the horizontal wind (V) and its vertical shear.

2.3. Vertical Motion of Es Layers and Their Localization during Presence of Homogeneous Wind and AGWs

According to Equation (16), the development of the ion/electron convergence processes ($\frac{\partial N_e}{\partial t}\propto -\frac{2D_a}{H_{ic}^2}+C_v^{\prime }+C_{sh}^{\prime }>0$ or $(C_v^{\prime }+C_{sh}^{\prime })\max >\frac{2D_a}{H_{ic}^2}$) and the formation of the Es layer is also possible during the drift of its peak height $z_m=z_{om}+w_{iv}(t-t_o)$ downward ($w_{iv}<0$) or upward ($w_{iv}>0$) by velocity $w_{iv}$. In this case, taking into account the vertical changes of the ion drift velocity $w_{iv}$, the Es layers upward ($w_{iv}>0$) or downward ($w_{iv}<0$) motion will continue until its localization either at the region of the ion drift velocity node or at the one where it vanishes. Here, under the ion vertical drift velocity $w_{iv}$ (Equation (8)) nodes, we assume the height region with $w_{iv}=0$ ($C_x{V}_{ox}+C_y{V}_{oy}=0$) heights, where this drift velocity modulation by the AGWs is zero ($C_x{V}_{gx}+C_y{V}_{gy}=0$). Later, in numerical simulations, we will consider the case where the $w_{iv}$ nodes are determined by the AGWs and the certain directed homogeneous wind can cause the Es-type layer localization at height regions with $w_{iv}\to 0$.

In the lower thermosphere, at the height region 90–150 km, for the modeled [1] and observed [22] horizontal wind height profiles, the region with $C_v^{\prime }\ne 0$ always occurs determined by the wind direction and magnitude (Equation (14)), and/or the one with $C_{sh}^{\prime }\ne 0$, determined by the wind vertical shear (Equation (15)). The windshear theory takes into account the effect of direction changes of the meridional wind (with $\frac{\partial V_x}{\partial z}>0$) or/and zonal wind (with $\frac{\partial V_y}{\partial z}>0$) on the formation of sporadic E [19]. In case of only a windshear effect (with $C_{sh}^{\prime }>0$ and $C_v^{\prime }=0$), for the given height profiles of the meridional $V_x(z)$ and zonal $V_y(z)$ components of the horizontal wind velocity, the condition $(C_{sh}^{\prime })\max >\frac{2D_a}{H_{ic}^2}$, Equation (17), is the more precise criteria for the formation of the Es layer than the condition $C_{sh}^{\prime }>0$ (or $(\partial w_{iv}/\partial z)<0$).

According to the height profile of the horizontal wind, given by Equations (1)–(4), the presence of homogeneous background wind ($V_o$) can determine the effect of the wind direction and magnitude on the ion convergence ($C_v^{\prime }>0$) or divergence ($C_v^{\prime }<0$) processes. According to Equations (9)–(11), for the horizontal wind velocity 30–60 m/s at the height region of about 115–125 km, the condition $(C_v^{\prime })\max >\frac{2D_a}{H_{ic}^2}$ is valid for $H_{ic}\le 3 \mathrm{km}$ and, therefore, the formation of a high density thin Es-type layer by only the wind magnitude and direction effect is also possible. During propagation of AGWs, the wind direction, magnitude ($C_v^{\prime }\ne 0$), and shear ($C_{sh}^{\prime }\ne 0$) are expected to influence on the development of the ion convergence ($(C_v^{\prime }+C_{sh}^{\prime })\max >0$) or divergence ($(C_v^{\prime }+C_{sh}^{\prime })\max <0$) processes as well. Here, the character of changes in the wind direction and magnitude with height depends on the vertical wavelength ${\lambda }_z$. When ${\lambda }_z\le 30 \mathrm{km}$, then several regions of the ion vertical drift velocity nodes (caused by AGWs) occurs (Equations (1)–(4) and (8)), where $(C_v^{\prime }+C_{sh}^{\prime })\max >0$; therefore, the formation of the multilayered sporadic E is possible.

Using numerical simulations for solution of Equation (13) we will show the formation of multilayered sporadic E by AGWs, taking into account the background homogeneous horizontal wind (Equations (1)–(4)) [31,32,33,34]. In these simulations, the Gaussian height profile $N_e(z,t=t_o)$ is used as the initial condition for the electron density, which corresponds to the analytical solution (14). The numerically obtained $N_e(z,t)$ allows us to estimate at some time $t (t>t_o)$ the peak densities $N_{em}$, its heights $z_m$ (or $h_m$), and the characteristic scale height of ions $H_{ic}$, which also changes with time. The formation of sporadic E is considered in the case of the constant TEC.

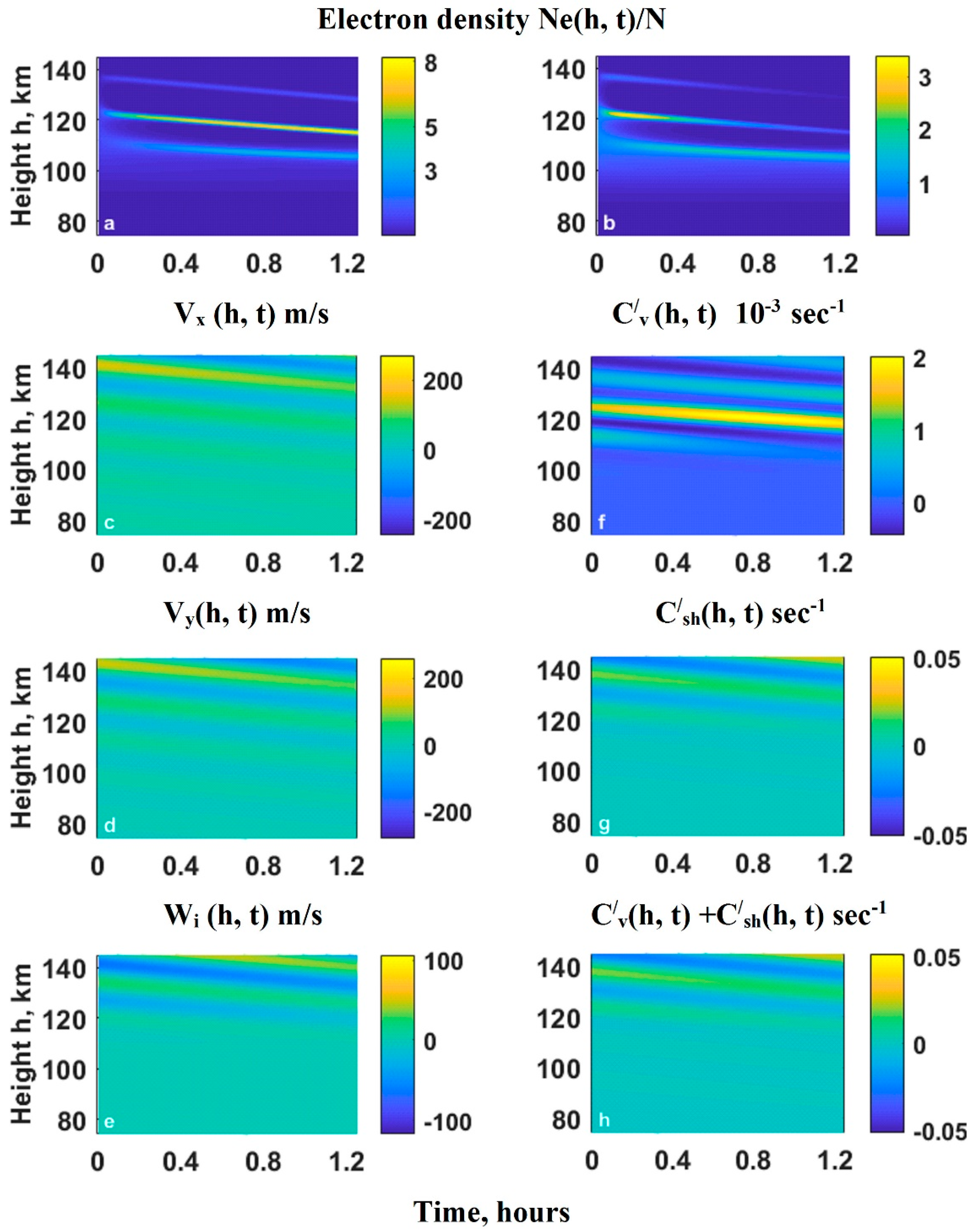
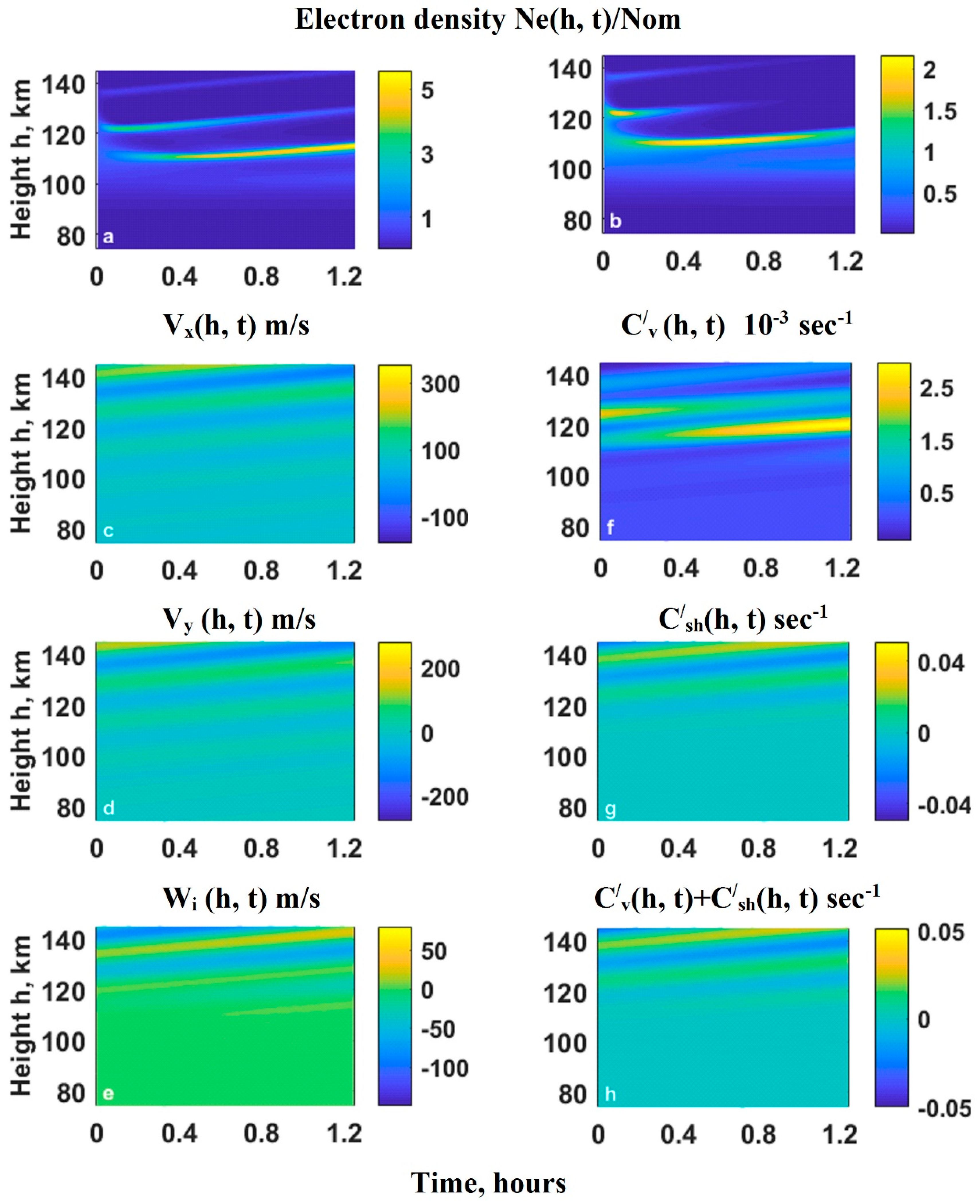
3. Results and Discussion

By numerical solutions of Equation (13), we demonstrated the behavior of the height profile of the normalized electron density $N_e(h,t)/N_{om}$, showing the formation of multilayered sporadic E by AGWs. This phenomenon was demonstrated theoretically in the previous section. We consider AGWs with a vertical wavelength (${\lambda }_z=15 \mathrm{km}$) of about a quarter of the width of the lower thermosphere height region (90–150 km). These waves can form sporadic E with two or more sublayers. The background homogeneous wind with a certain velocity $V_o(V_{ox}, V_{oy}, 0)$, Equations (1) and (2), also can form the Es layer, in cases when there are no atmospheric waves. In the presented simulation, the neutral densities of the lower thermosphere are used from the NRLMSISE-00 model [35], for the midlatitude regions 45° ± 2° N, 45° ± 2° E, and I = 61° ± 2°. The results can be extended for other mid-latitude regions of the northern or/and southern hemispheres, as well as for various directions and magnitudes of the horizontal wind.

3.1. Formation of Es Layers at the Fixed Heights by Stationary AGWs

At the beginning, we considered how the AGWs with observed frequency $\omega =0$ (stationary AGWs), as per Equations (5) and (6), influence on the behavior of the ion/electron density and formation of sporadic E. In this case, the northward wind velocity $V_{ox}>0$ is opposite and equal to the southward intrinsic phase velocity $\frac{{\omega }_g}{k_x}<0$ ($V_{ox}=-\frac{{\omega }_g}{k_x}$) of the AGWs. In this case the height profiles of the meridional $V_x$ and zonal $V_y$ wind velocities are stationary (Equations (1)–(4)). Respectively, the location of the nodes of ion drift velocity $w_{iv}$ ($C_x{V}_{gx}+C_y{V}_{gy}=0$), Equation (8), does not change. When the ion/electron total convergence rate $C_v^{\prime }+C_{sh}^{\prime }>0$ reaches its maximal value at this region, then the formation and localization of the Es layer should be more noticeable.

Figure 1 shows the formation of multilayered sporadic E, with sublayers at fixed heights, by the AGWs and background horizontal wind (panels a and b). The heavy metallic ion/electron content in the initial layer ($H_{ic}=16 \mathrm{km}, z_{om}=h_{mo}=120 \mathrm{km}$) is redistributed and in this case ($\omega =0$, ${\lambda }_x={\lambda }_y=150 \mathrm{km}$, ${\lambda }_z=15 \mathrm{km}$, $A_x=A_y=30m/s (h=120 \mathrm{km})$, $V_{ox}=-\frac{{\omega }_g}{k_x}=55 \mathrm{m}/\mathrm{s}$, $V_{oy}=0$), the four Es-type relative thin dense layers (panel a) are formed with $H_{ic1}=8.2 \mathrm{km} (N_{m1}/N_{om}=0.4)$, $H_{ic2}=0.8 \mathrm{km} (N_{m2}/N_{om}=6.8)$, $H_{ic3}=0.8 \mathrm{km} (N_{m3}/N_{om}=5.8)$, and $H_{ic4}=1 \mathrm{km} (N_{m4}/N_{om}=0.8)$. As it was predicted by the theoretical model in Section 2, these layers are localizing in the regions of ion vertical drift velocity nodes at $h_{m1}=99 \mathrm{km}$, $h_{m2}=109 \mathrm{km}$, $h_{m3}=122 \mathrm{km}$, and $h_{m4}=137 \mathrm{km}$ (panel d). The ion total convergence rates ($C_v^{\prime }+ C_{sh}^{\prime }>0$) in the vicinity of these regions have maximal values $3·{10}^{-5}{\mathrm{s}}^{-1}$, $1.2·{10}^{-3}{\mathrm{s}}^{-1}$, $1·{10}^{-2}{\mathrm{s}}^{-1}$, and $1.9·{10}^{-2}{\mathrm{s}}^{-1}$, respectively (panel e). The comparison of the parameters corresponding to panels a and b show that the combined effect of the wind velocity magnitude, direction (with $C_v^{\prime }>0$), and shear (with $C_{sh}^{\prime }>0$) on the ion total convergence rates ($C_v^{\prime }+ C_{sh}^{\prime }>0$), leading to the significantly higher peak densities ($N_{m1}/N_{om}=0.7$, $N_{m2}/N_{om}=6.8$, $N_{m3}/N_{om}=5.8$, and $N_{m4}/N_{om}=1.3$) of the formed Es layers (panel a), than only the windshear effect ($C_v^{\prime }=0, C_{sh}^{\prime }>0$), where $N_{m1}/N_{om}=0.4$, $N_{m2}/N_{om}=3.1$, $N_{m3}/N_{om}=2.5$, and $N_{m4}/N_{om}=0.6$ (panel b).

Ion drift velocity also has nodes in the regions between the Es layers, where $(C_v^{\prime }+C_{sh}^{\prime })\min <0$ and density depletions $N_e(t=t_o)/N_e(t-t_o=1.2h)<<1$ occur in the vicinity of heights 108 km, 120 km, and 133 km. When the wind direction, magnitude (with $C_v^{\prime }<0$), and shear (with $C_{sh}^{\prime }<0$) effect on the ion total divergence rate ($(C_v^{\prime }+C_{sh}^{\prime })\min <0$), then these depletions are more noticeable (panel a) than during the shear effect only (panel b). The directions of the wind velocity ($\angle Vx$) at the peak heights are 12° (at 99 km), 357° (at 109 km), 322° (at 122 km), and 296° (at 137 km). Those at the ion depletion region are 340° (at 104 km), 21° (at 115 km), and 30° (at 128 km). A single peak sporadic E (panel c) is formed under the influence of the horizontal wind only when there are no AGWs.

The initial phase of AGWs (Equations (3) and (4)) slightly influences the formation process and behavior of the Es layers in the lower thermosphere. Changes of the initial phase can shift the height of the ion drift velocity nodes.

Figure 1a,b also show that ion ambipolar diffusion has a significant effect on the formed Es layers densities (Equations (11), (16), and (17)). In this case, at $h_{m2}=109 \mathrm{km}$ and $h_{m3}=122 \mathrm{km}$, for $H_{ic}\approx 0.8 \mathrm{km}$ the increase in densities caused by the AGWs after about t-to > 0.6 h is balanced by diffusive displacement ($C_v^{\prime }+ C_{sh}^{\prime }\approx 2D_a/H_{ic}^2$), and their densities have tendency of saturation (Figure 1a). In case of only windshear effect, the diffusion (with condition $2D_a/H_{ic}^2>C_{sh}^{\prime }$) leads to a bigger decrease of the Es densities (Figure 1b).

Note that, according to the analytical solution (16), the location of the initial ion/electron layer peak height $h_{mo}$ close to the ion drift velocity node (caused by AGWs) is more favorable for formation of a relatively high density Es layer than its other locations. These various cases are not demonstrated for brevity. Figure 1c shows that the only homogeneous meridional (northward) wind with velocity $V_{ox}=55 \mathrm{m}/\mathrm{s}$, for which $C_v^{\prime }>0$ and $C_{sh}^{\prime }=0$ (panel f), causes accumulation of the initial ion/electron layer into a single dense ($N_{em}/N_{om}=5.1$) Es-type layer ($H_{ic}=2 \mathrm{km}$) at the region of about $h_m=111 \mathrm{km}$ (panel c), where ion drift velocity $w_{iv}\to 0$ (panel d). The thickness of this single layer is wider ($H_{ic}=2 \mathrm{km}$) than those of the multilayered sporadic E sublayers ($H_{ic}\le 1.2 \mathrm{km}$) formed by the AGWs. The formation of the high-density Es layer ($N_{m2}/N_{om}=6.8$) at the height region around 108–114 km is caused by a combined effect of the background horizontal wind and AGWs (panels a and c) on the ion/electron convergence. The additional Es layers above and below the height region 112–114 km are caused by the AGWs.

We see that the condition $\omega =0$ (or $V_{ox}=-{\omega }_g/k_x$) corresponding to the stationary meridional and zonal velocity height profiles caused by the AGWs, Equations (1) and (2), is favorable for formation of the high density Es layers at a fixed height near the region where $C_x{V}_{gx}+C_y{V}_{gy}=0$. Next, we consider the behavior of ion/electron density caused by the AGWs propagating obliquely upward ($\omega /k_z>0$) and downwards ($\omega /k_z<0$). Such propagation of the AGWs cause wave-like variations in the height of the ion drift velocity nodes and its convergence (or divergence) rates as well.

3.2. Descending Es Layers Formed by Oblique Downward Propagating AGWs

Figure 2 shows the possibility of formation of multilayered sporadic E by AGWs propagating obliquely downward, with vertical phase velocity $\frac{\omega }{k_z}=-0.2 \mathrm{m}/\mathrm{s}$ ($V_{ox}=-\frac{{\omega }_g}{k_x}+20 \mathrm{m}/\mathrm{s}$ and $\frac{\omega }{k_z}=-20\left|\frac{k{}^x}{k_z}\right|\mathrm{m}/\mathrm{s}$). In this case, the Es layers initial peak height is located at the same region as in Figure 1a. Here, the Es layers are descending (panel a and b) with the speed about equal to the wave vertical phase velocity (−0.2m/s). In this case the ion drift velocity nodes are also descending by the speed close to the AGWs’ vertical phase velocity (panel e). Here the regions with maximal (or minimal) ion convergence (or divergence) rates $C_v^{\prime }(h,t)$ (panel f), $C_{sh}^{\prime }(h,t)$ (panel g), and $C_v^{\prime }(h,t)+C_{sh}^{\prime }(h,t)$ (panel h), determined by the meridional $V_x(h,t)$ (panel c) and zonal $V_y(h,t)$ (panel d) wind velocity height profiles, are also shifting, similarly to the downward motion of the waves. This is expectable from Equations (1)–(10), (14), and (15). In this case, the descending regions of the ion/electron convergence (along with descending nodes) also cause accumulation of the charged particles into thin layers. These formed Es-type layers follow the nodes and convergence regions, so they move downward with the AGWs’ vertical phase velocity ($\frac{\omega }{k_z}=-0.2 \mathrm{m}/\mathrm{s}$). Here, unlike the case of a stationary wave wind velocity ($\omega =0$) profile (Figure 1), the descending converged layers, caused by the AGWs propagating obliquely downward, cross their maximal convergence regions only for a certain time. The total maximal densities of the formed Es layers are smaller than those during their formation by the waves with the same amplitude and $\omega =0$ (Figure 1a,b).

In the case of the descending layers, the formation of one high-density layer at about 120 km and below occurs, where the portion of homogeneous wind in the value of $C_v^{\prime }(h,t)+ C_{sh}^{\prime }(h,t)>0$ is significant. In the case of absence of wind direction and a value effect (with $C_v^{\prime }=0$) in the ion/electron total convergence rate $C_v^{\prime }(h,t)+C_{sh}^{\prime }(h,t)>0$, the peak densities of the Es-type layers are significantly smaller (Figure 2b) than during both wind velocity and shear effects (Figure 2a). In this case, unlike the one when $\omega =0$, the sporadic E formed mostly with three sublayers is descending to the region with $w_i\to 0$ and $C_v^{\prime }(h,t)+ C_{sh}^{\prime }(h,t)\to 0$. This causes the lower peak ($h_{m1}=99 \mathrm{km}$) of the Es layer to vanish (panels a and b).

3.3. Upward Motion of Es Layers Formed by Oblique Upward Propagating AGWs

The formation of multilayered sporadic E by oblique upward propagating AGWs is also possible, similarly to the case of oblique downward propagating AGWs (Figure 3).

Figure 3 shows that the multilayered sporadic E formed similarly to the one in Figure 2, but by oblique upward propagating AGWs, with a vertical phase velocity $\frac{\omega }{k_z}=0.2 \mathrm{m}/\mathrm{s}$ ($V_{ox}=-\frac{{\omega }_g}{k_x}-20 \mathrm{m}/\mathrm{s}$ and $\frac{\omega }{k_z}=20\left|\frac{k{}^x}{k_z}\right|\mathrm{m}/\mathrm{s}$). Here, the height regions of the maximal (or minimal) ion convergence (or divergence) rates $C_v^{\prime }(h,t)$, $C_{sh}^{\prime }(h,t)$ and, $C_v^{\prime }(h,t)+C_{sh}^{\prime }(h,t)$ (panels f, g and h, respectively), and the ion vertical drift velocity nodes (regions with $C_x{V}_{gx}+C_y{V}_{gy}+0$) determined by the meridional $V_x(h,t)$ (c) and zonal $V_y(h,t)$ (panel d) wind velocity height profiles, also move upward by a speed equal to the vertical phase velocity of the wave ($0.2 \mathrm{m}/\mathrm{s}$). In this case the Es layers (three) follow the convergence regions with $C_x{V}_{gx}+C_y{V}_{gy}=0$ (like on Figure 2), and they move upwards (panel a and b) by the speed close to the vertical phase velocity of the wave (0.2 m/s). In this case the formed Es layers density is also smaller than during the AGWs with $\omega =0$ (Figure 1). Here, the effect of wind total convergence on the Es layers’ density (Figure 3a) is bigger than the wind shear effect only (Figure 3b).

Figure 3 also shows the importance of ambipolar diffusion on the formation of the Es layers. In the case of upward motion of the Es layers, the density peaks are more noticeable at the lower heights (from 99 km) (Figure 3a,b). The upper peak is vanishing due to an increase in ion ambipolar diffusion. Here, the density in the upper peak is less than in case of the AGWs with an observed frequency $\omega =0$ (Figure 1a,b).

3.4. Discussion

According to the presented theoretical mechanism, the multilayered sporadic E, which is an observed phenomenon [8,9,10], can be formed by AGWs (Figure 1, Figure 2 and Figure 3). We have showed that the formation of these layers can happen at the ion vertical drift velocity nodes, where vertical drift velocity divergence ($\frac{\partial w_{iv}}{\partial z}=-(C_v^{\prime }+C_{sh}^{\prime })$) has a minimal negative value or the total convergence rate $(C_v^{\prime }+C_{sh}^{\prime })>0$ is maximal. In this case, the distances between the Es layers and also the regions of ion/electron depletion (with $(C_v^{\prime }+C_{sh}^{\prime })\min =\left(-\frac{\partial w_{iv}}{\partial z}\right)\min <0$) are almost the same as the AGWs’ vertical wavelength. The downward (Figure 2) or upward (Figure 3) motions of the Es sublayers should correspond to the wave propagation in the lower thermosphere in case of the presence of homogeneous horizontal wind. Homogeneous background horizontal wind with a certain direction, in case of the absence of AGWs, can form a single-peak sporadic E (Figure 1c). Such behavior of ion/electron density (Figure 1, Figure 2 and Figure 3) is predictable by Equation (16). In this case, the ion/electron total convergence rate $C_v^{\prime }+C_{sh}^{\prime }$, for the considered case of the presence of homogeneous meridional wind (with velocity $V_{ox}$) and AGWs (with meridional $A_x$ and zonal $A_y$ wind velocity amplitudes), taking into account Equations (14) and (15), can be described by the following equation:

$$C_v^{\prime }+C_{sh}^{\prime }=f_o(z)V_{ox}+f_w(z)\cos [-\omega (t-t_o)+k_z(z-z_o)+\psi (z)]$$

(18)

where

$$f_o=\frac{\partial C_x}{\partial z}$$

(19)

$$f_w=e^{\frac{z-z_o}{2H}}{\left[{(A_x\frac{\partial C_x}{\partial z}+A_y\frac{\partial C_y}{\partial z}+\frac{A_x{C}_x+A_y{C}_y}{2H})}^2+k_z^2{(A_x{C}_x+A_y{C}_y)}^2\right]}^{1/2}$$

(20)

$$\psi =arctang\left[\frac{k_z(A_x{C}_x+A_y{C}_y)}{A_x\frac{\partial C_x}{\partial z}+A_y\frac{\partial C_y}{\partial z}+\frac{A_x{C}_x+A_y{C}_y}{2H}}\right]$$

(21)

The first term ($f_o(z)V_{ox}$) in Equation (18) determines the part of homogeneous wind with velocity $V_{ox}$ in the ion total convergence/divergence rate, while the second one determines the oscillated part with amplitude $f_w$ caused by the AGWs. Equations (18)–(21) show that condition (17) is necessary for the development of ion/electron convergence into a thin layer, and in case of the absence of AGWs ($C_{sh}^{\prime }=0$), will be $(f_o(z)V_{ox})\max >\frac{2D_a}{H_{ic}^2}$. The latter occurs at heights where $\frac{\partial C_x}{\partial z}$ have maximal values. If we assume the barometric approach for the height distribution of neutral particles density, $[N_2](z), [O_2](z)\propto \exp (-z/H)$, then, in case of homogeneous northward wind ($V_{ox}>0$), $(C_v^{\prime })\max =(\frac{\partial C_x}{\partial z})\max ·V_{ox}\approx \frac{V_{ox}}{2H}\sin \theta \cos \theta$. This maximum in ion/electron convergence rate occurs at about the 121 km height where the ion gyrofrequency is equal to the ion-neutral collision frequency ($\kappa \approx 1$). These theoretical estimations of $(C_v^{\prime })\max$ ($\approx 1.4\times {10}^{-3}{s}^{-1}$) and its location ($\approx 121 \mathrm{km}$) for $V_{ox}=55 \mathrm{m}/\mathrm{s}$, as well as atmospheric scale height of about H = 8 km, correspond to the numerical results given in Figure 1f. During southward wind ($V_{ox}<0$ and $(C_v^{\prime })\min \approx \frac{V_{ox}}{2H}\sin \theta \cos \theta <0$), at the region of about 121 km, the opposite phenomenon of depletion of ion content should take place, which for brevity is not demonstrated.

The vertical changes in the total convergence rate $C_v^{\prime }+C_{sh}^{\prime }$, Equation (18), caused by the AGWs (Equations (1)–(4)) at some mid-latitude region ($x=x_o=0$ and $y=y_o=0$), are shifted from the changes in the ion vertical drift velocity by the phase $\psi (z)+\pi$. The ion vertical drift velocity (22) is obtained from Equation (8), in case of the northward meridional wind ($V_{ox}>0$ and $V_{oy}=0$). Here, the ion drift velocity nodes are determined by the condition $\cos [-\omega (t-t_o)+k_z(z-z_o)]=0$ (for $A_x{C}_x+A_y{C}_y\ne 0$). There can be four nodes for the vertical wavelength ${\lambda }_z=15 \mathrm{km}$ of the AGWs in the height region of about 90–150 km. In this case, the maximal positive (or minimal negative) values in the total convergence rates $C_v^{\prime }+C_{sh}^{\prime }$ at the ion drift velocity nodes also could be four. So, these nodes and maximal positive (or minimal negative) values of the ion/electron convergence rate should be localized by the vertical wavelength distances from each other, as was obtained in the numerical results of the formation of the Es layers (Figure 1, Figure 2 and Figure 3).

$$w_{iv}=-C_x{V}_{ox}-e^{\frac{z-z_o}{2H}}(A_x{C}_x+A_y{C}_y)\cos [-\omega (t-t_o)+k_z(z-z_o)]$$

(22)

Equations (18)–(21) also show that the downward ($\frac{\omega }{k_z}<0$) or upward ($\frac{\omega }{k_z}>0$) propagation of the waves causes a similar downward (Figure 2) or upward (Figure 3) change in the value of ion/electron total convergence/divergence rate $C_v^{\prime }+C_{sh}^{\prime }$. The latter causes the downward ($\frac{\omega }{k_z}<0$) or upward ($\frac{\omega }{k_z}>0$) motion of the Es layers and ion/electron depletion regions by the wave vertical phase velocity. Here, for the considered parameters of AGWs, the changes in the distances of the Es layer peak heights, due to the vertical changes of the phase $\psi (z)$, as per Equation (21), are relatively small (Figure 1, Figure 2 and Figure 3). Equations (18)–(21) also show the possibility of accumulation of ions/electrons into the Es layers at almost fixed heights (Figure 1), in case of a stationary wave ($\omega =0$).

During propagation of AGWs with greater values in the vertical phase velocity, the time of ion/electron density accumulation into the Es-type layers will be smaller than in case of stationary waves.

Planetary-scale tidal winds or atmospheric waves (with $\omega <<{\omega }_g$, ${\lambda }_z<<{\lambda }_x$ and $\left|\frac{1}{V_x}\frac{\partial V_x}{\partial z}\right|<<\frac{1}{H}$ or ${\lambda }_z>>H$) resemble the homogeneous horizontal wind. In this case, the condition of $(C_v^{\prime })\max >>(C_{sh}^{\prime })\max$ can take place in the region of the greater horizontal wind velocity and the formation of single-peak sporadic E by homogeneous wind is possible (Figure 1c). Therefore, the formation of double-peak sporadic E by tidal wind only or by planetary waves should be rarer than during the propagation of AGWs. The similar horizontal wind profiles of Equations (3) and (4) also have been used for investigation of the formation of the Es layers under the influence of tidal wind [36].

We have used the non-dissipative linear AGW model with exponential growth of the amplitude, Equations (3)–(6) [25], to study the formation of multilayered sporadic E. According to the present theory, using Equations (16) and (17), the formation of the Es layers can be investigated for various height profiles of the linear and nonlinear atmospheric wave velocities. The magnitude of the horizontal wind velocity at about 120 km height, determined by the sum of the background and AGWs velocities ($\left|V_o+V_g\right|\approx 30-90 \mathrm{m}/\mathrm{s}$) (Equations (1)–(4)), is comparable with the HWM14 and other measured data [1,22]. The AGWs velocity amplitudes $A_x=30 \mathrm{m}/\mathrm{s}$ and $A_y=30 \mathrm{m}/\mathrm{s}$ are about twice smaller than those of the meridional or zonal direction phase velocities $\frac{{\omega }_g}{k_{x,y}}=55 \mathrm{m}/\mathrm{s}$ ($T_g=\frac{2\pi }{{\omega }_g}=45\min$). In case of wave propagation in the meridional direction and the presence of a homogeneous wind with velocity $V_{ox}$, the value of $\left|\omega -k_x{V}_{ox}\right|={\omega }_g$ (Equation (5)) is about twice greater than in case of the nonlinear effect ($V_{gx}\frac{\partial V_{gx}}{\partial x}$), determined by the parameter $k_x{A}_x$ at a height about z = 120 km. (Such nonlinear and dissipative processes for the considered time interval of the Es layers formation (Figure 1, Figure 2 and Figure 3) include 1–2 AGWs’ period $T_g=45\min$, and were not taken into account. We assume that, at the region of about 120 km or above, the nonlinear decay of the considered AGWs is also important, especially for the relatively big time. In this case, the AGWs decay into the short scale linear waves increases the number of the ion vertical drift velocity nodes above 120 km. The newly formed convergence nodes in turn result in the ion/electron content redistribution into these nodes and the Es layers peak densities should be smaller above the 120 km height than during its formation in case of the absence of nonlinear processes. Taking into account the observed high values in the horizontal wind below 120 km [22], which, in addition to the tidal wind, can be caused by AGWs, shows the important role of AGWs in more frequent formation of Es layers below 120 km.

AGWs with short wavelengths (${\lambda }_x,{\lambda }_y,{\lambda }_z=O(H)$) also can be important for the formation of the quasi-periodic echo-like structures [37]. In this case, one can also take into account the influence of the vertical component of velocity perturbation, caused by short-period and small-scale AGWs, on the ion vertical drift velocity, as it was done in [13]. As we have shown, the oblique upward propagation of the AGWs can influence the upward motion of the heavy metallic ion layers (Figure 3); therefore, the extension of the presented theory for equatorial regions should be important to study the formation of the bubble-like structures of plasma [38].

The obtained results stimulate the study of the observed coupling of Es layer formation with tectonic events [39] and thunderstorms [24], by generation and propagation of the atmospheric waves from the troposphere to the lower thermosphere. In this case, the presence of linear, nonlinear, and ducted-type AGWs [26] during the formation of the Es layers can be taken into account.

The above study shows the important influence of the AGWs and the background horizontal wind on the behavior of the mid-latitude lower thermosphere heavy metallic ions [2]. Here, for the given height profiles of meridional and zonal wind velocity, the development of heavy metallic ion convergence (or divergence) processes is possible. The localization regions of the Es layers can be predicted theoretically. Development of this theory should be important for investigation of heavy metallic ion distribution at the global and regional scales. It is important to take into account the AGWs’ propagation from the troposphere to the lower thermosphere for understanding of the regional peculiarities of sporadic E formation and, correspondingly, the heavy metallic ion distribution [23,24,40]. In this case, considering the background electric field, causing the ions’ additional drift perpendicular to the geomagnetic field [36,41], also will be important for predictability of Es layers formation and Fe⁺ ion distribution at the mid-latitude and equatorial regions. It is also important to consider ion horizontal transport caused by atmospheric waves and tidal motion, which is the goal of a future study.

4. Conclusions

We showed the formation of multilayered sporadic E by atmospheric gravity waves (AGWs) propagating in the mid-latitude lower thermosphere at about a 90–150 km height. We have used the non-dissipative linear AGW model with exponential growth of the amplitude. In this study, we have not taken into account the possible collapse of these waves during their interaction and propagation in the atmosphere. Such AGWs with a vertical wavelength smaller than the width of this region lead to appearance of the heavy metallic ion (Fe⁺) vertical drift velocity nodes (height regions with $C_x{V}_{gx}+C_y{V}_{gy}=0$). When the ion vertical drift velocity divergence at its nodes has a minimal negative value, then these charged particles can accumulate into the Es-type thin layers and the formation of multilayered sporadic E becomes possible. Here, the importance of the ions’ ambipolar diffusion in the formation of Es layers and the control of their densities were shown. When at regions of ion drift velocity nodes, its divergence is positive and have maximal values, then the opposite phenomenon—density depletion—occurs. The distance between the nearest ion/electron convergence nodes is close to the AGWs’ vertical wavelength. In case of horizontal homogeneous wind, the Es-type layer is localized at the ion drift velocity nodes or at the region where it vanishes.

It was demonstrated that the AGWs with a vertical wavelength of about a quarter of the width of the lower thermosphere (e.g., ${\lambda }_z=15 \mathrm{km}$) can form sporadic E with four sub-E-type layers. Here, significant depletion in ion/electron density between the two nearest Es-type layers was noted. According to the suggested theory and corresponding numerical results, when the horizontal component of the AGWs’ intrinsic phase velocity (phase velocity relative to wind) and background wind velocity have the same magnitudes and opposite directions, it is favorable for the formation of multilayered sporadic E with sub-layers at fixed heights. During upward propagation of the AGWs, the Es layer densities are smaller than during its downward propagation. This case corresponds to the stationary height profiles of wind velocity. We have shown that the oblique downward or upward propagation of the AGWs causes the downward or upward motion of the ion vertical drift velocity nodes by the vertical propagation phase velocity of these waves. A horizontal homogeneous wind can form only a single-peak sporadic E.

Considering the horizontal wind at about the 120 km height region, determined by the sum of the background and AGW velocities, comparable to the values of the HWM14 and some measured data [1,22], we noted the importance of these waves in the formation of Es layers, at the region where they are frequently observed (below 120 km).

Within the suggested theory, the development of the processes of ion/electron convergence into an Es-type layer and its localization, determined by the wind direction, magnitude, and shear, is more predictable than in case of a windshear effect only. The applicability of this theory to horizontal wind considering propagation of AGWs, which was shown in this study, indicates its importance for investigation of the peculiarities of heavy metallic ion distribution on regional and global scales.