Concepts and New Implements for Modified Physiologically Equivalent Temperature
Abstract
1. Introduction
2. Concepts and Strategies of Modifications
2.1. Concepts to Modify Thermo-Physiological Model
- is the actually metabolic rate (W/m);
- is the actually convective heat fluxes (W/m);
- is the actually radiant heat fluxes (W/m);
- is the actual heat fluxes of the skin diffusion (W/m);
- is the actual heat fluxes of the sweating evaporation (W/m);
- is the actually respiratory heat fluxes (W/m);
- is the actual storage heat fluxes inside body (W/m);
- is the metabolic rate of the reference (W/m);
- is the convective heat fluxes based on the value of mPET (W/m);
- is the heat fluxes of the skin diffusion corresponded to 12 hPa vapor pressure (W/m);
- is the radiant heat fluxes based on the value of mPET (W/m);
- is the respiratory heat fluxes based on the value of mPET (W/m).
2.2. Bio-Heat Equation and Solution for Thermo-Physiological Model
- is the tissue conductivity (W/(mK));
- is the tissue temperature (C);
- r is the radius of tissue (m);
- is the metabolic rate (W/m);
- is the density of blood (kg/m);
- is the geometry factor of the tissue ;
- is the blood perfusion rate (1/s);
- is the heat capacity of blood (J/(kg·K));
- is the arterial blood temperature (C);
- is the density of the tissue (kg/m);
- is the heat capacity of the tissue (J/(kg·K));
- t is the time (s).
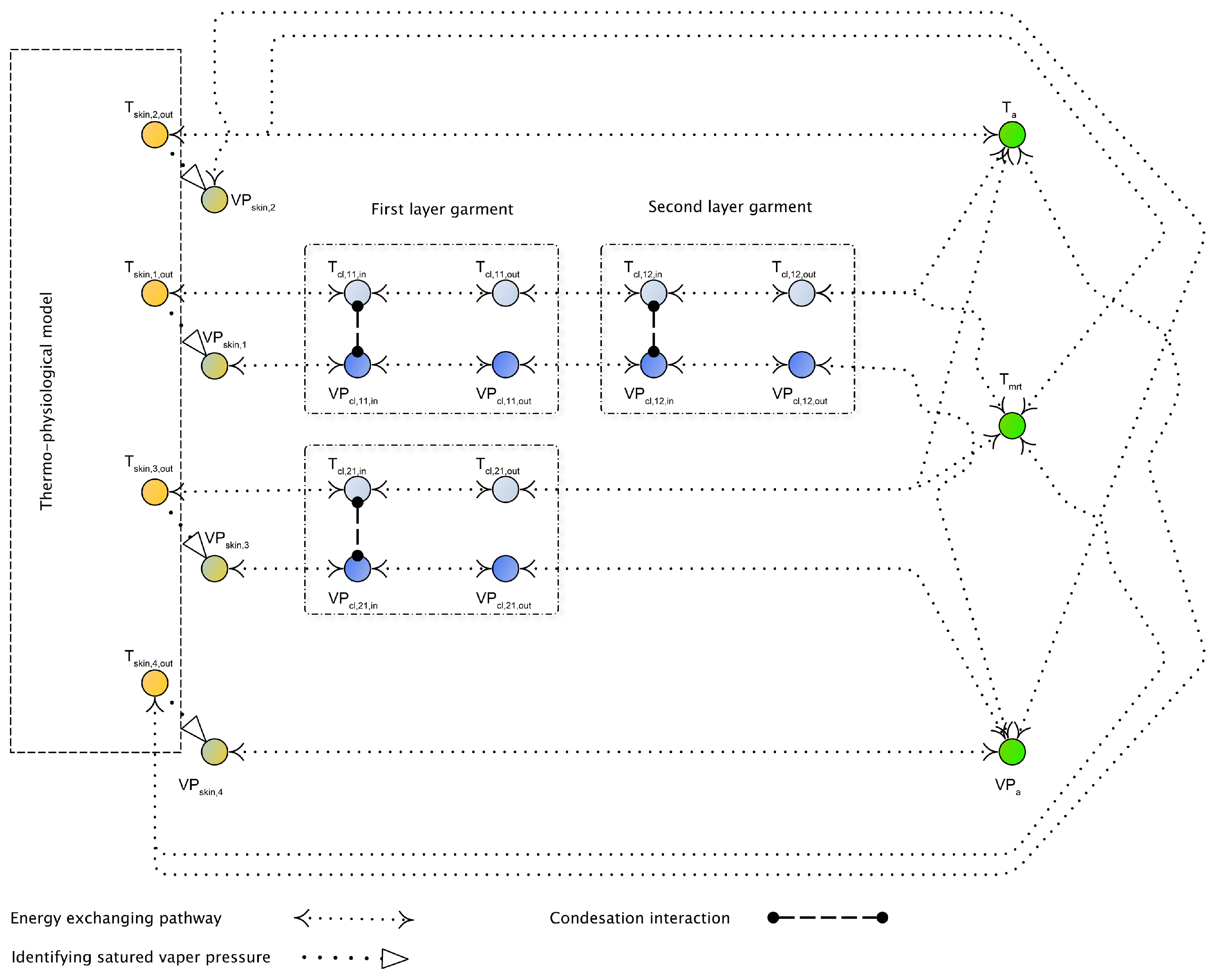
2.3. Modifications of Clothing Model
2.4. Mechanisms of Latent Fluxes
- is the latent heat fluxes (W/m);
- is the gender factor of sweating rate ;
- is the evaporative energy of the liquid water per gram (W/kg);
- is the skin surface area (m);
- is the sweating rate (kg/s);
- is the ratio of skin moisture ;
- is the saturated skin vapor pressure (hPa);
- is the actual air vapor pressure (hPa);
- is the skin resistance of the vapor pressure (hPa·m/W);
- is the clothing factor of vapor pressure resistance in the PET-model .
- is the latent heat fluxes (W/m);
- is the actual skin vapor pressure (hPa);
- is the actual air vapor pressure (hPa);
- is the clothing resistance of the vapor pressure (hPa·m/W);
- is the skin resistance of the vapor pressure (hPa·m/W);
- is the gender factor of sweating rate ;
- is the evaporative energy of the liquid water per gram (W/kg);
- is the skin surface area (m);
- is the sweating rate (kg/s);
- is the saturated skin vapor pressure (hPa).
3. Comparison of PETs
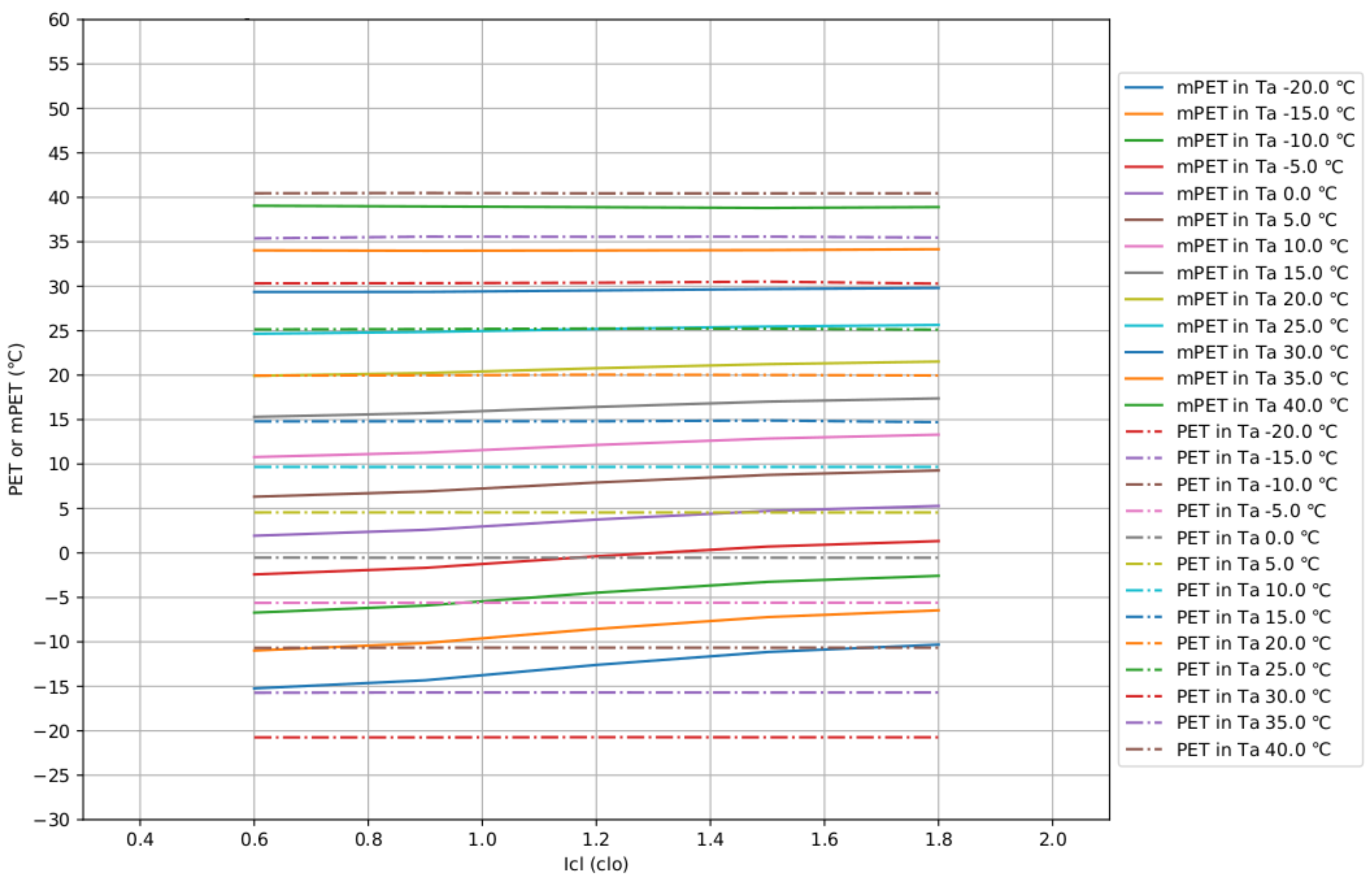
3.1. Sensitivity Tests of the Thermally Environmental Variables
3.2. Clothing Influences
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Höppe, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef]
- Höppe, P. Different aspects of assessing indoor and outdoor thermal comfort. Energy Build. 2002, 34, 661–665. [Google Scholar] [CrossRef]
- Coccolo, S.; Kämpf, J.; Scartezzini, J.L.; Pearlmutter, D. Outdoor human comfort and thermal stress: A comprehensive review on models and standards. Urban Clim. 2016, 18, 33–57. [Google Scholar] [CrossRef]
- Parsons, K. Humam Thermal Environments; Taylor & Francis e-Library: London, UK, 2003; p. 635. [Google Scholar]
- Steadman, R.G. The assessment of sultriness. Part I. A temperature-humidity index based on human physiology and clothing science. J. Appl. Meteorol. 1979, 18, 861–873. [Google Scholar] [CrossRef]
- Steadman, R.G. A universal scale of apparent temperature. J. Clim. Appl. Meteorol. 1984, 23, 1674–1687. [Google Scholar] [CrossRef]
- Fröhlich, D.; Matzarakis, A. Spatial Estimation of Thermal Indices in Urban Areas—Basics of the SkyHelios Model. Atmosphere 2018, 9, 209. [Google Scholar] [CrossRef]
- Fröhlich, D.; Gangwisch, M.; Matzarakis, A. Effect of radiation and wind on thermal comfort in urban environments—Application of the RayMan and SkyHelios model. Urban Clim. 2019, 27, 1–7. [Google Scholar] [CrossRef]
- Zare, S.; Hasheminejad, N.; Shirvan, H.E.; Hemmatjo, R.; Sarebanzadeh, K.; Ahmadi, S. Comparing Universal Thermal Climate Index (UTCI) with selected thermal indices/environmental parameters during 12 months of the year. Weather Clim. Extrem. 2018, 19, 49–57. [Google Scholar] [CrossRef]
- Fanger, P.O. Calculation of Thermal Comfort, Introduction of a Basic Comfort Equation. ASHRAE Trans. 1967, 73, III.4.1–III.4.20. [Google Scholar]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1972; Volume 3, p. 181. [Google Scholar] [CrossRef]
- de Dear, R.J.; Brager, G.S. Developing an adaptive model of thermal comfort and preference. ASHRAE Trans. 1998, 104, 145–167. [Google Scholar]
- Gagge, A.P. Rational temperature indices of man’s thermal environment and their use with a 2 node model of his temperature regulation. Fed. Proc. 1973, 32, 1572–1582. [Google Scholar] [PubMed]
- Gagge, A.P.; Fobelets, A.P.; Berglund, L.G. Standard Predictive Index of Human Response to the Thermal Environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- Bröde, P.; Fiala, D.; Błażejczyk, K.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Tinz, B.; Havenith, G. Deriving the operational procedure for the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2012, 56, 481–494. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A computer model of human thermoregulation for a wide range of environmental conditions: The passive system. J. Appl. Physiol. 1999, 87, 1096–1102. [Google Scholar] [CrossRef]
- Fiala, D.; Lomas, K.J.; Stohrer, M. Computer prediction of human thermoregulatory and temperature responses to a wide range of environmental conditions. Int. J. Biometeorol. 2001, 45, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Fiala, D.; Havenith, G.; Bröde, P.; Kampmann, B.; Jendritzky, G. UTCI-Fiala multi-node model of human heat transfer and temperature regulation. Int. J. Biometeorol. 2012, 56, 429–441. [Google Scholar] [CrossRef]
- Jendritzky, G.; Staiger, H.; Bucher, K.; Grätz, A.; Laschewski, G. The Perceived Temperature: The Method of the Deutscher Wetterdienst for the Assessment of Cold Stress and Heat Load for the Human Body. Available online: http://www.utci.org/isb/documents/perceived_temperature.pdf (accessed on 30 June 2020).
- Staiger, H.; Laschewski, G.; Grätz, A. The perceived temperature—A versatile index for the assessment of the human thermal environment. Part A: Scientific basics. Int. J. Biometeorol. 2012, 56, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Budd, G.M. Wet-bulb globe temperature (WBGT)-its history and its limitations. J. Sci. Med. Sport 2008, 11, 20–32. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.Y.; Chien, Y.Y.; Su, C.J.; Kueh, M.T.; Lung, S.C. Climate variability of heat wave and projection of warming scenario in Taiwan. Clim. Chang. 2017, 145, 305–320. [Google Scholar] [CrossRef]
- Weatherly, J.W.; Rosenbaum, M.A. Future projections of heat and fire-risk indices for the contiguous United States. J. Appl. Meteorol. Climatol. 2017, 56, 863–876. [Google Scholar] [CrossRef]
- Yi, W.; Chan, A. Effects of Heat Stress on Construction Labor Productivity in Hong Kong: A Case Study of Rebar Workers. Int. J. Environ. Res. Public Health 2017, 14, 1055. [Google Scholar] [CrossRef] [PubMed]
- d’Ambrosio Alfano, F.R.; Palella, B.I.; Riccio, G. The role of measurement accuracy on the thermal environment assessment by means of PMV index. Build. Environ. 2011, 46, 1361–1369. [Google Scholar] [CrossRef]
- ISO 7730. ISO 7730: Ergonomics of the thermal environment Analytical determination and interpretation of thermal comfort using calculation of the PMV and PPD indices and local thermal comfort criteria. Management 2005. [Google Scholar] [CrossRef]
- Fröhlich, D.; Matzarakis, A. A quantitative sensitivity analysis on the behaviour of common thermal indices under hot and windy conditions in Doha, Qatar. Theor. Appl. Climatol. 2016, 124, 179–187. [Google Scholar] [CrossRef]
- Ketterer, C.; Matzarakis, A. Human-biometeorological assessment of the urban heat island in a city with complex topography—The case of Stuttgart, Germany. Urban Clim. 2014, 10, 573–584. [Google Scholar] [CrossRef]
- Matzarakis, A.; Fröhlich, D. Influence of urban green on human thermal bioclimate—Application of thermal indices and micro-scale models. Acta Hortic. 2018, 1215, 1–10. [Google Scholar] [CrossRef]
- Matzarakis, A.; Muthers, S.; Rutz, F. Application and comparison of UTCI and PET in temperate climate conditions. Finisterra 2015, 49, 21–31. [Google Scholar] [CrossRef]
- Staiger, H.; Laschewski, G.; Matzarakis, A. Selection of Appropriate Thermal Indices for Applications in Human Biometeorological Studies. Atmosphere 2019, 10, 18. [Google Scholar] [CrossRef]
- Urban, A.; Kyselý, J. Comparison of UTCI with Other Thermal Indices in the Assessment of Heat and Cold Effects on Cardiovascular Mortality in the Czech Republic. Int. J. Environ. Res. Public Health 2014, 11, 952–967. [Google Scholar] [CrossRef] [PubMed]
- Vanos, J.K.; Warland, J.S.; Gillespie, T.J.; Kenny, N.A. Review of the physiology of human thermal comfort while exercising in urban landscapes and implications for bioclimatic design. Int. J. Biometeorol. 2010, 54, 319–334. [Google Scholar] [CrossRef]
- Stolwijk, J.A.; Hardy, J.D. Temperature regulation in man—A theoretical study. Pflügers Archiv für die Gesamte Physiologie des Menschen und der Tiere 1966, 291, 129–162. [Google Scholar] [CrossRef] [PubMed]
- Wissler, E.H.; Havenith, G. A simple theoretical model of heat and moisture transport in multi-layer garments in cool ambient air. Eur. J. Appl. Physiol. 2009, 105, 797–808. [Google Scholar] [CrossRef] [PubMed]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Wissler, E.H. 50 years of JAP: Pennes’ 1948 paper revisited. J. Appl. Physiol. 1998, 85, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.C.; Matzarakis, A. Modified physiologically equivalent temperature—Basics and applications for western European climate. Theor. Appl. Climatol. 2018, 132, 1275–1289. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Huizenga, C.; Hui, Z.; Arens, E. A model of human physiology and comfort for assessing complex thermal environments. Build. Environ. 2001, 36, 691–699. [Google Scholar] [CrossRef]
- Tanabe, S.I.; Kobayashi, K.; Nakano, J.; Ozeki, Y.; Konishi, M. Evaluation of thermal comfort using combined multi-node thermoregulation (65MN) and radiation models and computational fluid dynamics (CFD). Energy Build. 2002, 34, 637–646. [Google Scholar] [CrossRef]
- Wyon, D.P. Use of thermal manikins in environmental ergonomics. Scand. J. Work. Environ. Health 1989, 15, 84–94. [Google Scholar] [PubMed]
- Havenith, G.; Fiala, D.; Błazejczyk, K.; Richards, M.; Bröde, P.; Holmér, I.; Rintamaki, H.; Benshabat, Y.; Jendritzky, G. The UTCI-clothing model. Int. J. Biometeorol. 2012, 56, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.P.; Yang, S.R.; Chen, Y.C.; Matzarakis, A. The potential of a modified physiologically equivalent temperature (mPET) based on local thermal comfort perception in hot and humid regions. Theor. Appl. Climatol. 2019, 135, 873–876. [Google Scholar] [CrossRef]






| PET | SET* | UTCI | |
|---|---|---|---|
| Physiological factors | 2 nodes body model with variable parameters | 2 nodes body model with standardized conditions | A regression function based on data and multiple-segment body model |
| Clothing adaption | Independently variable | adjusted by metabolic rate | Auto changing by |
| Environmental factors | , , , v | , , , v | , , , v |
| Advantages | Good in , , v | Good in , , | Good in , |
| Disadvantages | Weak in , | Weak in , v | Weak in v, and no performance on |
| Clothing Insulation (clo) | Single Layer | Double Layer | Triple Layer | Cap | Uncovered |
|---|---|---|---|---|---|
| 0.3~0.6 | 62% | - | - | - | 38% |
| 0.6~0.9 | 36% | 45% | - | - | 19% |
| 0.9~1.2 | 42% | 45% | - | - | 13% |
| 1.2~1.6 | 30% | 22% | 35% | - | 13% |
| 1.6~2.0 | 26% | 22% | 45% | - | 7% |
| 2.0~2.5 | 12% | 25% | 55% | 5% | 3% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-C.; Chen, W.-N.; Chou, C.C.-K.; Matzarakis, A. Concepts and New Implements for Modified Physiologically Equivalent Temperature. Atmosphere 2020, 11, 694. https://doi.org/10.3390/atmos11070694
Chen Y-C, Chen W-N, Chou CC-K, Matzarakis A. Concepts and New Implements for Modified Physiologically Equivalent Temperature. Atmosphere. 2020; 11(7):694. https://doi.org/10.3390/atmos11070694
Chicago/Turabian StyleChen, Yung-Chang, Wei-Nai Chen, Charles C.-K. Chou, and Andreas Matzarakis. 2020. "Concepts and New Implements for Modified Physiologically Equivalent Temperature" Atmosphere 11, no. 7: 694. https://doi.org/10.3390/atmos11070694
APA StyleChen, Y.-C., Chen, W.-N., Chou, C. C.-K., & Matzarakis, A. (2020). Concepts and New Implements for Modified Physiologically Equivalent Temperature. Atmosphere, 11(7), 694. https://doi.org/10.3390/atmos11070694





