Measurements of Cloud Radiative Effect across the Southern Ocean (43° S–79° S, 63° E–158° W)
Abstract
:1. Introduction
2. Experiments
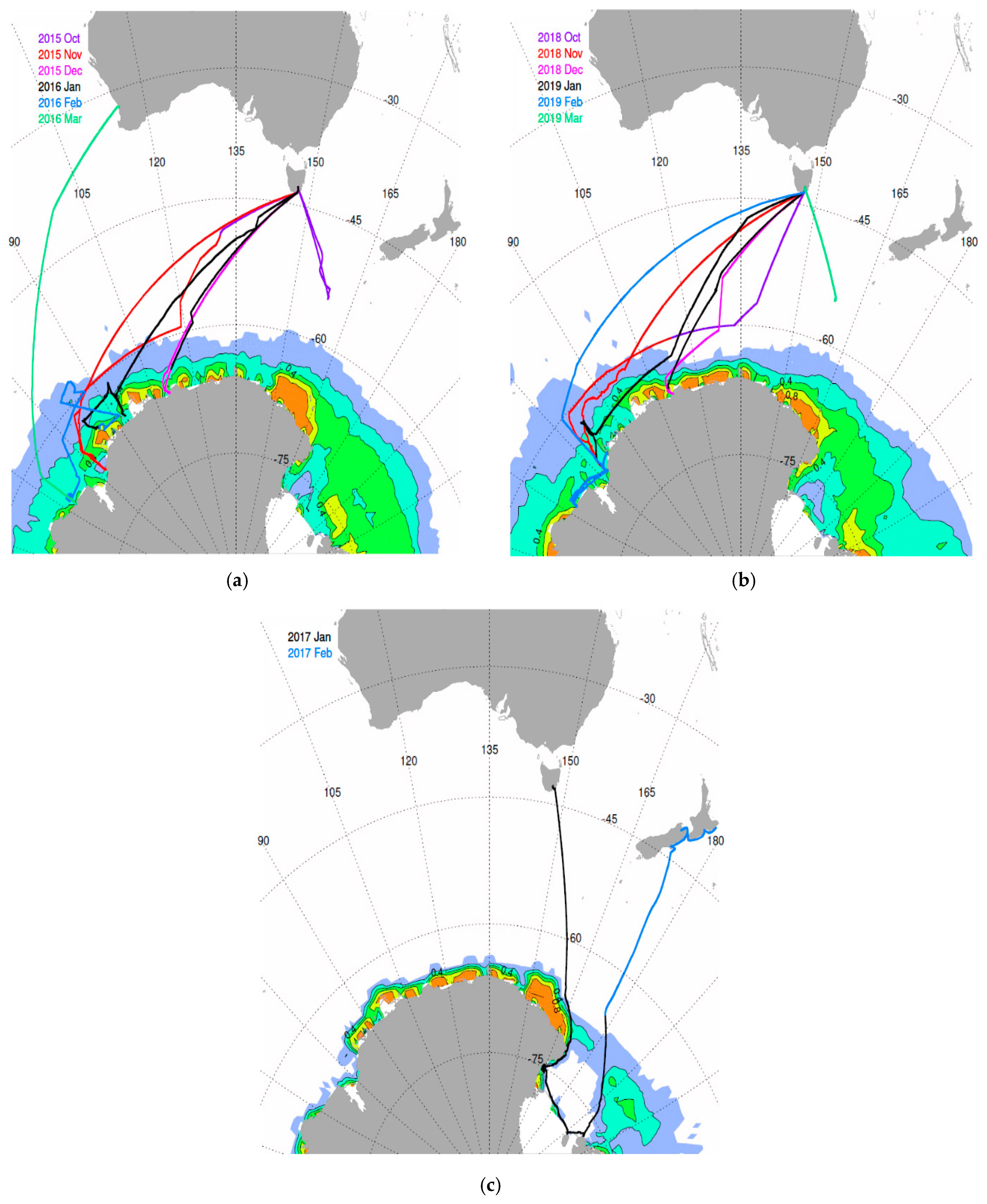
2.1. Overview of Voyage Data
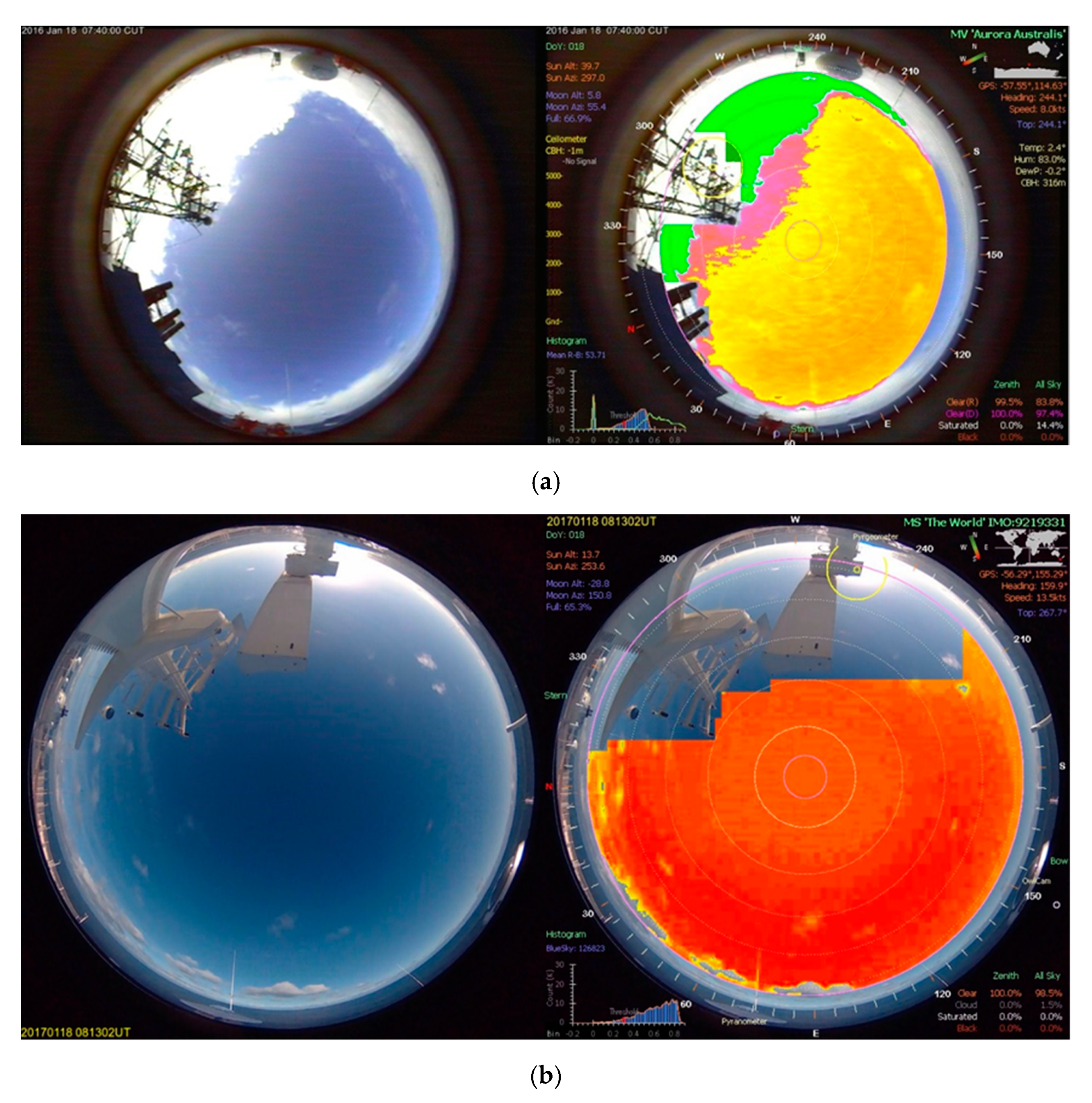
2.2. Cloud Imagers
2.3. Radiometers
2.4. Meteorological Reanalysis
2.5. Sea Ice Information
2.6. Measurement Intervals and Averaging
2.7. Models for Clear Sky Radiation
3. Results
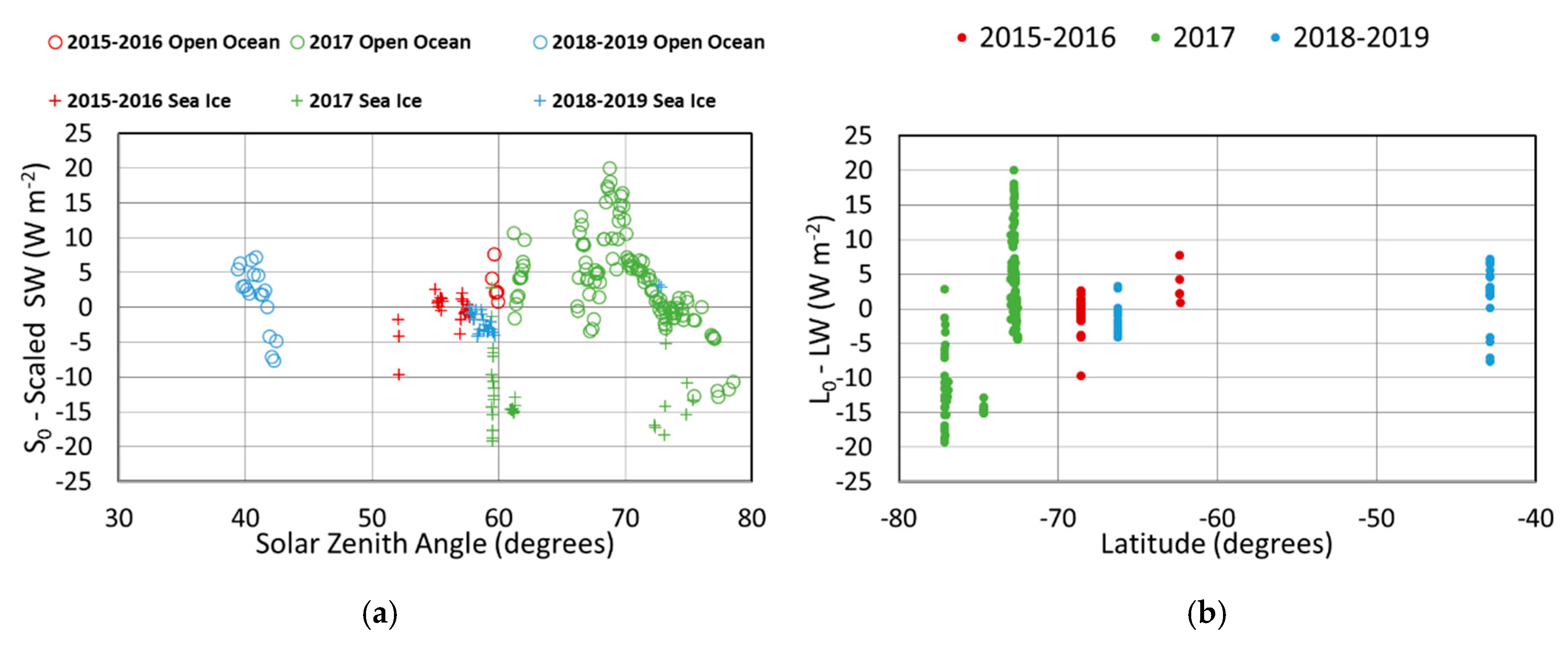
3.1. Meridional Variation of CRE
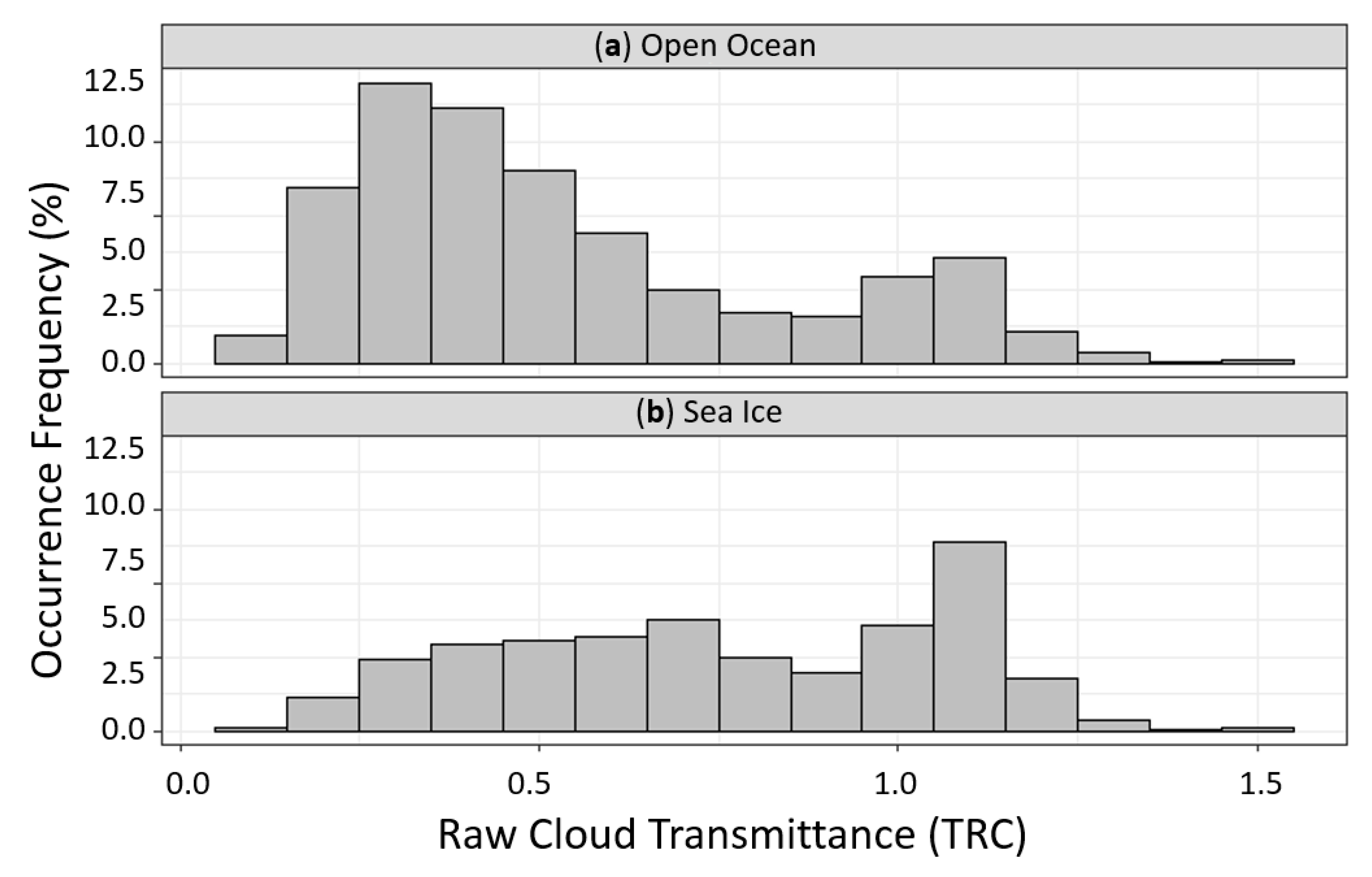
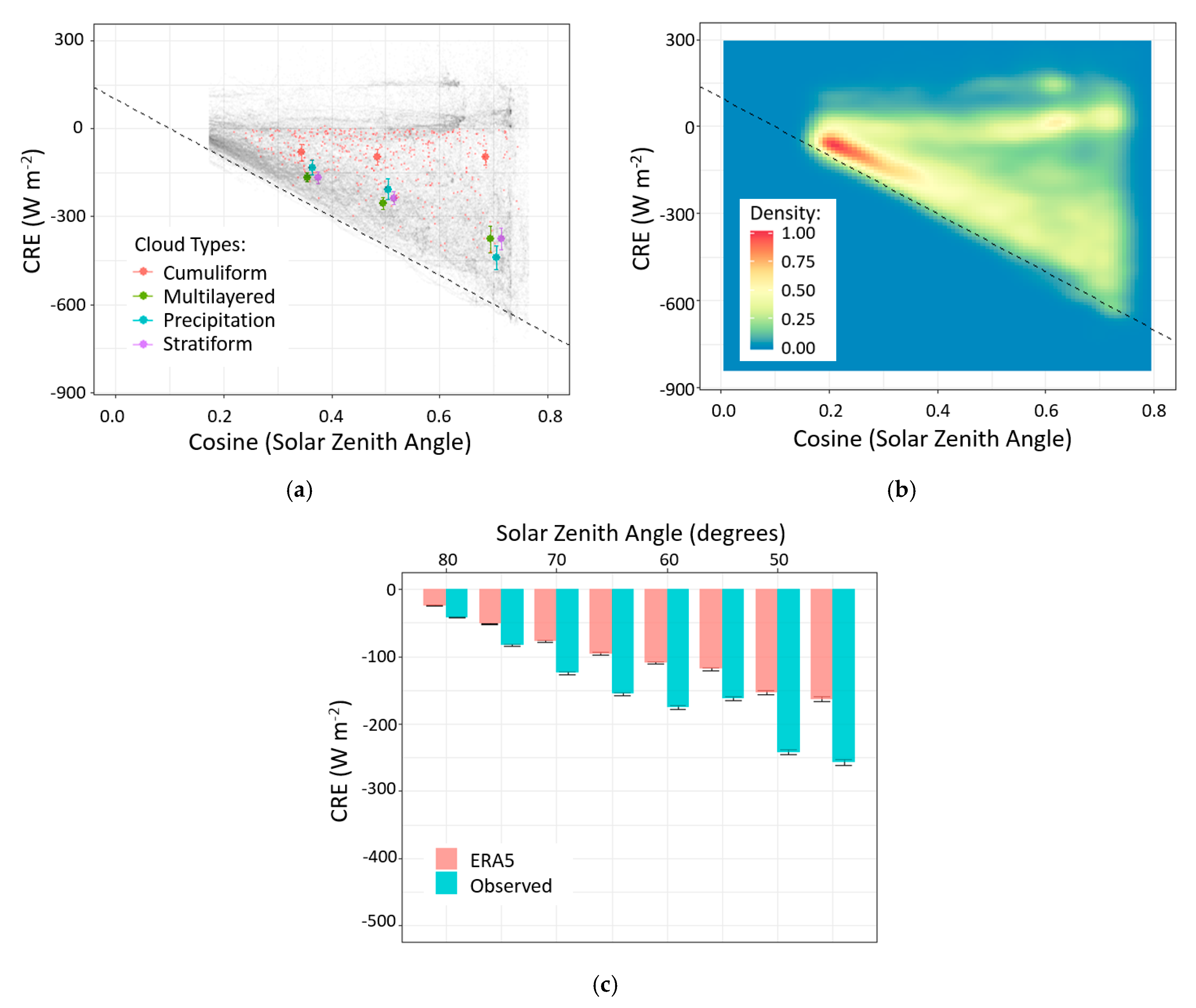
3.2. Cloud Fraction and CRE
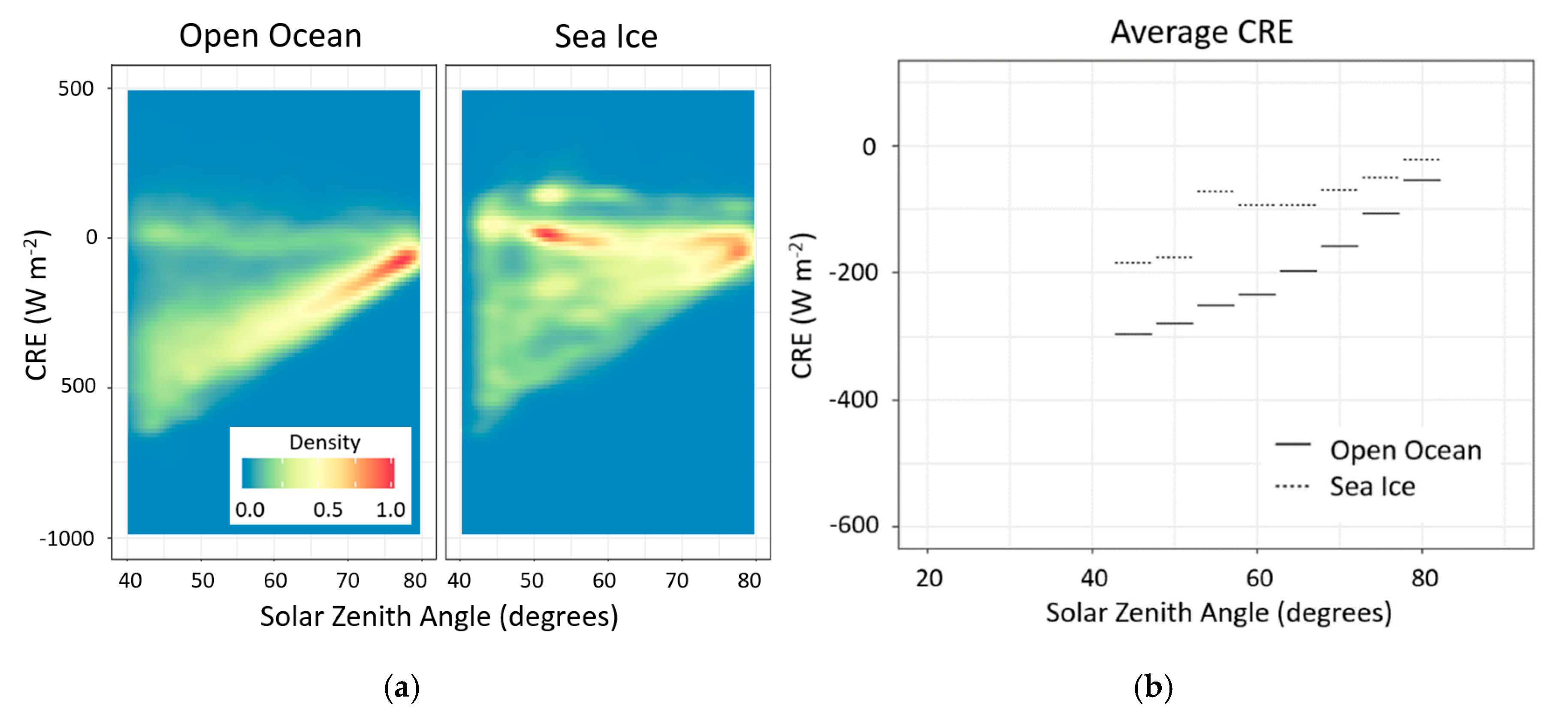
3.3. Effect of Sea Ice on CRE
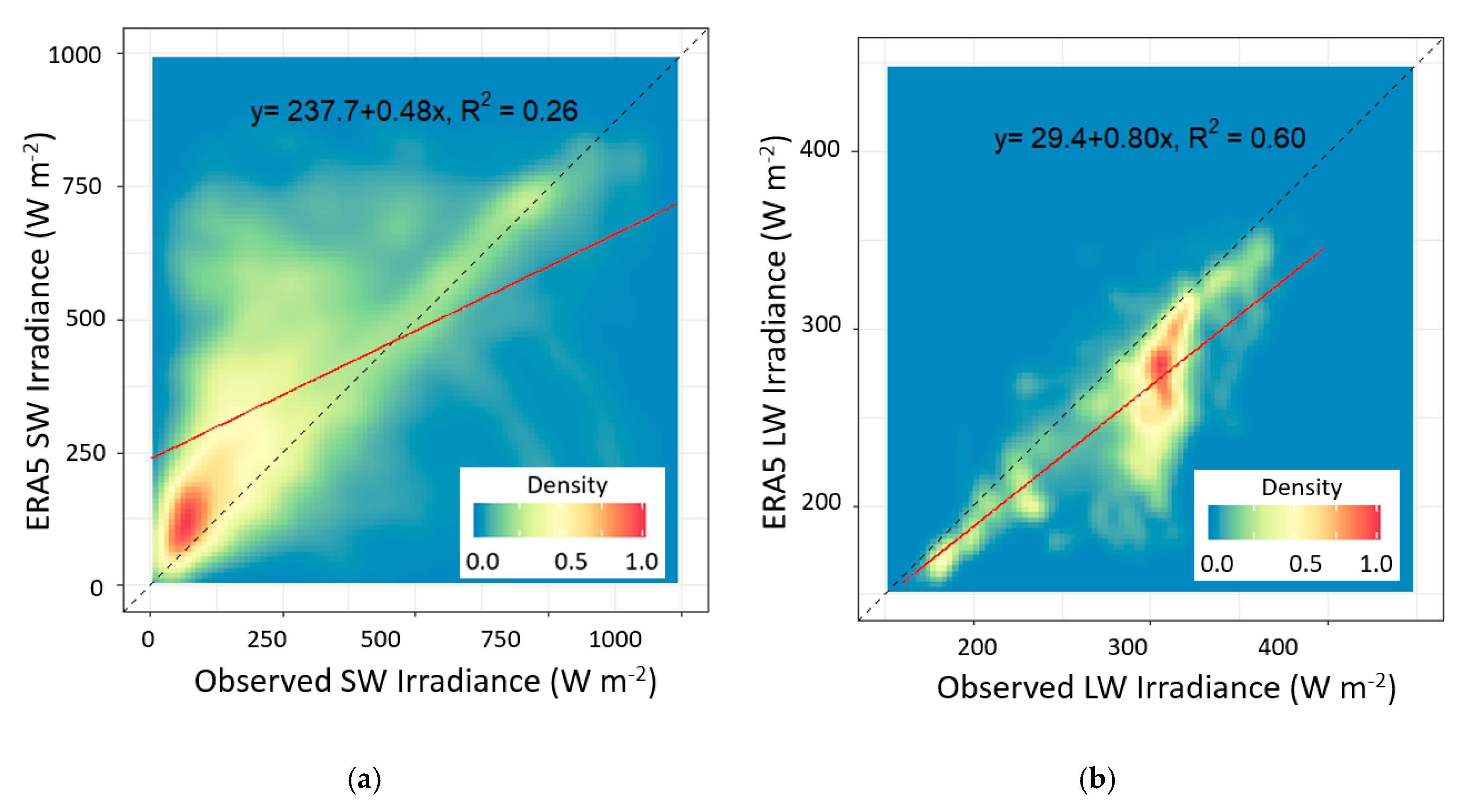
3.4. Comparison with ERA5 Radiation Data
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smith, K.L.; Previdi, M.; Polvani, L.M. The Antarctic Atmospheric Energy Budget. Part II: The Effect of Ozone Depletion and its Projected Recovery. J. Clim. 2013, 26, 9729–9744. [Google Scholar] [CrossRef] [Green Version]
- Haynes, J.M.; Jakob, C.; Rossow, W.B.; Tselioudis, G.; Brown, J. Major Characteristics of Southern Ocean Cloud Regimes and Their Effects on the Energy Budget. J. Clim. 2011, 24, 5061–5080. [Google Scholar] [CrossRef] [Green Version]
- Aebi, C.; Gröbner, J.; Kämpfer, N.; Vuilleumier, L. Cloud radiative effect, cloud fraction and cloud type at two stations in Switzerland using hemispherical sky cameras. Atmos. Meas. Tech. 2017, 10, 4587–4600. [Google Scholar] [CrossRef] [Green Version]
- Arking, A. The Radiative Effects of Clouds and their Impact on Climate. Bull. Am. Meteorol. Soc. 1991, 72, 795–814. [Google Scholar] [CrossRef]
- Liou, K. An Introduction to Atmospheric Radiation; Academic Press: Amsterdam, The Netherlands, 2002; pp. 444–454. [Google Scholar]
- Dommenget, D.; Flöter, J. Conceptual understanding of climate change with a globally resolved energy balance model. Clim. Dyn. 2011, 37, 2143–2165. [Google Scholar] [CrossRef]
- Shupe, M.D.; Intrieri, J.M. Cloud Radiative Forcing of the Arctic Surface: The Influence of Cloud Properties, Surface Albedo, and Solar Zenith Angle. J. Clim. 2004, 17, 616–628. [Google Scholar] [CrossRef]
- Key, E.L.; Minnett, P.J. Implications of shortwave cloud forcing and feedbacks in the Southern Ocean. Ann. Glaciol. 2006, 44, 15–22. [Google Scholar] [CrossRef]
- Cogley, J.; Henderson-Sellers, A. Effects of Cloudiness on the High-Latitude Surface Radiation Budget. Mon. Weather. Rev. 1984, 112. [Google Scholar] [CrossRef] [Green Version]
- Sedlar, J.; Tjernström, M. Clouds, warm air, and a climate cooling signal over the summer Arctic. Geophys. Res. Lett. 2017, 44, 1095–1103. [Google Scholar] [CrossRef]
- Parise, C.K.; Pezzi, L.P.; Hodges, K.I.; Justino, F. The Influence of Sea Ice Dynamics on the Climate Sensitivity and Memory to Increased Antarctic Sea Ice. J. Clim. 2015, 28, 9642–9668. [Google Scholar] [CrossRef]
- Brandt, R.E.; Warren, S.G.; Worby, A.P.; Grenfell, T.C. Surface Albedo of the Antarctic Sea Ice Zone. J. Clim. 2005, 18, 3606–3622. [Google Scholar] [CrossRef] [Green Version]
- Fitzpatrick, M.F.; Warren, S.G. Transmission of Solar Radiation by Clouds over Snow and Ice Surfaces. Part II: Cloud Optical Depth and Shortwave Radiative Forcing from Pyranometer Measurements in the Southern Ocean. J. Clim. 2005, 18, 4637–4648. [Google Scholar] [CrossRef] [Green Version]
- Hyder, P.; Edwards, J.M.; Allan, R.P.; Hewitt, H.T.; Bracegirdle, T.J.; Gregory, J.M.; Wood, R.A.; Meijers, A.J.S.; Mulcahy, J.; Field, P.; et al. Critical Southern Ocean climate model biases traced to atmospheric model cloud errors. Nat. Commun. 2018, 9, 3625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trenberth, K.E.; Fasullo, J.T. Simulation of Present-Day and Twenty-First-Century Energy Budgets of the Southern Oceans. J. Clim. 2010, 23, 440–454. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Gille, S.T.; Bitz, C.; Carlson, D.; Cerovecki, I.; Clayson, C.A.; Cronin, M.F.; Drennan, W.M.; Fairall, C.W.; Hoffman, R.N.; et al. High-Latitude Ocean and Sea Ice Surface Fluxes: Challenges for Climate Research. Bull. Am. Meteorol. Soc. 2013, 94, 403–423. [Google Scholar] [CrossRef]
- Marchand, R.; Ackerman, T.; Smyth, M.; Rossow, W.B. A review of cloud top height and optical depth histograms from MISR, ISCCP, and MODIS. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Ceppi, P.; Hwang, Y.-T.; Frierson, D.M.W.; Hartmann, D.L. Southern Hemisphere jet latitude biases in CMIP5 models linked to shortwave cloud forcing. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Ho, C.-H.; Park, C.-E.; Storelvmo, T.; Tan, I. Influence of cloud phase composition on climate feedbacks. J. Geophys. Res. Atmos. 2014, 119, 3687–3700. [Google Scholar] [CrossRef]
- Huang, Y.; Siems, S.T.; Manton, M.J.; Thompson, G. An Evaluation of WRF Simulations of Clouds over the Southern Ocean with A-Train Observations. Mon. Weather. Rev. 2014, 142, 647–667. [Google Scholar] [CrossRef]
- McCoy, D.T.; Hartmann, D.L.; Grosvenor, D.P. Observed Southern Ocean Cloud Properties and Shortwave Reflection. Part I: Calculation of SW Flux from Observed Cloud Properties *. J. Clim. 2014, 27, 8836–8857. [Google Scholar] [CrossRef]
- McCluskey, C.S.; Hill, T.C.J.; Humphries, R.S.; Rauker, A.M.; Moreau, S.; Strutton, P.G.; Chambers, S.D.; Williams, A.G.; McRobert, I.; Ward, J.; et al. Observations of Ice Nucleating Particles Over Southern Ocean Waters. Geophys. Res. Lett. 2018, 45, 11989–11997. [Google Scholar] [CrossRef]
- Lawson, R.P.; Gettelman, A. Impact of Antarctic mixed-phase clouds on climate. Proc. Natl. Acad. Sci. USA 2014, 111, 18156–18161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Listowski, C.; Delanoë, J.; Kirchgaessner, A.; Lachlan-Cope, T.; King, J. Antarctic clouds, supercooled liquid water and mixed phase, investigated with DARDAR: Geographical and seasonal variations. Atmos. Chem. Phys. 2019, 19, 6771–6808. [Google Scholar] [CrossRef] [Green Version]
- Murray, B.J.; O’Sullivan, D.; Atkinson, J.D.; Webb, M.E. Ice nucleation by particles immersed in supercooled cloud droplets. Chem. Soc. Rev. 2012, 41, 6519–6554. [Google Scholar] [CrossRef] [Green Version]
- Bodas-Salcedo, A.; Williams, K.D.; Ringer, M.A.; Beau, I.; Cole, J.N.S.; Dufresne, J.-L.; Koshiro, T.; Stevens, B.; Wang, Z.; Yokohata, T. Origins of the Solar Radiation Biases over the Southern Ocean in CFMIP2 Models. J. Clim. 2014, 27, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Mace, G.G. Cloud properties and radiative forcing over the maritime storm tracks of the Southern Ocean and North Atlantic derived from A-Train. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Kuma, P.; McDonald, A.J.; Morgenstern, O.; Alexander, S.P.; Cassano, J.J.; Garrett, S.; Halla, J.; Hartery, S.; Harvey, M.J.; Parsons, S.; et al. Evaluation of Southern Ocean cloud in the HadGEM3 general circulation model and MERRA-2 reanalysis using ship-based observations. Atmos. Chem. Phys. 2020, 20, 6607–6630. [Google Scholar] [CrossRef]
- Matthews, J.B.R. Comparing historical and modern methods of sea surface temperature measurement–Part 1: Review of methods, field comparisons and dataset adjustments. Ocean. Sci. 2013, 9, 683–694. [Google Scholar] [CrossRef]
- Protat, A.; Schulz, E.; Rikus, L.; Sun, Z.; Xiao, Y.; Keywood, M. Shipborne observations of the radiative effect of Southern Ocean clouds. J. Geophys. Res. Atmos. 2017, 122, 318–328. [Google Scholar] [CrossRef]
- Klekociuk, A.R.; French, W.J.R.; Alexander, S.P.; Kuma, P.; McDonald, A.J. The state of the atmosphere in the 2016 southern Kerguelen Axis campaign region. Deep Sea Res. Part II Top. Stud. Oceanogr. 2020, 174. [Google Scholar] [CrossRef]
- Cox, C.J.; Walden, V.P.; Rowe, P.M.; Shupe, M.D. Humidity trends imply increased sensitivity to clouds in a warming Arctic. Nat. Commun. 2015, 6, 10117. [Google Scholar] [CrossRef] [Green Version]
- Gras, J.L.; Keywood, M. Cloud condensation nuclei over the Southern Ocean: Wind dependence and seasonal cycles. Atmos. Chem. Phys. 2017, 17, 4419–4432. [Google Scholar] [CrossRef] [Green Version]
- Ghonima, M.S.; Urquhart, B.; Chow, C.W.; Shields, J.E.; Cazorla, A.; Kleissl, J. A method for cloud detection and opacity classification based on ground based sky imagery. Atmos. Meas. Tech. 2012, 5, 2881–2892. [Google Scholar] [CrossRef] [Green Version]
- Jayadevan, V.T.; Rodriguez, J.J.; Cronin, A.D. A New Contrast-Enhancing Feature for Cloud Detection in Ground-Based Sky Images. J. Atmos. Ocean. Technol. 2015, 32, 209–219. [Google Scholar] [CrossRef]
- Li, Q.; Lu, W.; Yang, J. A Hybrid Thresholding Algorithm for Cloud Detection on Ground-Based Color Images. J. Atmos. Ocean. Technol. 2011, 28, 1286–1296. [Google Scholar] [CrossRef]
- Saito, M.; Iwabuchi, H. Cloud Discrimination from Sky Images Using a Clear-Sky Index. J. Atmos. Ocean. Technol. 2016, 33, 1583–1595. [Google Scholar] [CrossRef]
- Yabuki, M.; Shiobara, M.; Nishinaka, K.; Kuji, M. Development of a cloud detection method from whole-sky color images. Polar Sci. 2014, 8, 315–326. [Google Scholar] [CrossRef] [Green Version]
- Kipp and Zonen CMP21 Pyranometer. Available online: https://www.kippzonen.com/Product/14/CMP21-Pyranometer (accessed on 1 July 2020).
- Kipp and Zonen CGR4 Pyrgeometer. Available online: https://www.kippzonen.com/Product/17/CGR4-Pyrgeometer (accessed on 1 July 2020).
- Campbell Scientific CR3000 Micrologger. Available online: https://www.campbellsci.com.au/cr3000 (accessed on 1 July 2020).
- Watts, D.J. A Database of Scientific Voyages of the Australian Antarctic Programme. Available online: https://data.aad.gov.au/metadata/records/DB_Voyages (accessed on 1 July 2020).
- Middleton Class B Solar Total Pyranometer. Available online: https://www.middletonsolar.com/products/product4.htm (accessed on 1 July 2020).
- Eppley Precision Infrared Radiometer. Available online: http://www.eppleylab.com/instrument-list/precision-infared-radiometer/ (accessed on 1 July 2020).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 1–51. [Google Scholar] [CrossRef]
- Bracegirdle, T.J.; Marshall, G.J. The Reliability of Antarctic Tropospheric Pressure and Temperature in the Latest Global Reanalyses. J. Clim. 2012, 25, 7138–7146. [Google Scholar] [CrossRef] [Green Version]
- ERA5 Hourly Data on Single Levels from 1979 to Present. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form (accessed on 1 July 2020).
- NOAA Optimum Interpolation (OI) Sea Surface Temperature (SST) V2. Available online: https://psl.noaa.gov/data/gridded/data.noaa.oisst.v2.html (accessed on 1 July 2020).
- Cronin, T.W. Reply to “Comments on ‘On the Choice of Average Solar Zenith Angle’”. J. Atmos. Sci. 2017, 74, 1677–1680. [Google Scholar] [CrossRef]
- R Package for Insolation Model by J. G. Corripio. Available online: https://meteoexploration.com/R/insol/index.html (accessed on 1 July 2020).
- Bird, R.E.; Hulstrom, R.L. A Simlified Clear Sky Model of Dirrect and Diffuse Insolation on Horizontal Surfaces; SER/TR-642-761; Solar Energy Research Institute: Golden, CO, USA, 1981.
- Idso, S.B. A set of equations for full spectrum and 8- to 14-μm and 10.5- to 12.5-μm thermal radiation from cloudless skies. Water Resour. Res. 1981, 17, 295–304. [Google Scholar] [CrossRef]
- Naud, C.M.; Booth, J.F.; Del Genio, A.D. Evaluation of ERA-Interim and MERRA Cloudiness in the Southern Ocean. J. Clim. 2014, 27, 2109–2124. [Google Scholar] [CrossRef]
- Minnett, P.J. The Influence of Solar Zenith Angle and Cloud Type on Cloud Radiative Forcing at the Surface in the Arctic. J. Clim. 1999, 12, 147–158. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, S.; Wang, G.; Yao, Y.; Jiang, B.; Cheng, J. Evaluation of the Reanalysis Surface Incident Shortwave Radiation Products from NCEP, ECMWF, GSFC, and JMA Using Satellite and Surface Observations. Remote. Sens. 2016, 8, 225. [Google Scholar] [CrossRef] [Green Version]
- Silber, I.; Verlinde, J.; Wang, S.-H.; Bromwich, D.H.; Fridlind, A.M.; Cadeddu, M.; Eloranta, E.W.; Flynn, C.J. Cloud Influence on ERA5 and AMPS Surface Downwelling Longwave Radiation Biases in West Antarctica. J. Clim. 2019, 32, 7935–7949. [Google Scholar] [CrossRef] [Green Version]
- Alexander, S.P.; Protat, A. Vertical Profiling of Aerosols With a Combined Raman-Elastic Backscatter Lidar in the Remote Southern Ocean Marine Boundary Layer (43–66° S, 132–150° E). J. Geophys. Res. Atmos. 2019, 124, 12107–12125. [Google Scholar] [CrossRef]





| Season | Vessel 1 | m | Number of Measurements | R |
|---|---|---|---|---|
| 2015–2016 | AA | 0.9574 ± 0.0008 | 28 | 0.999 |
| 2017 | TW | 1.0356 ± 0.0019 | 153 | 0.999 |
| 2018–2019 | AA | 0.9863 ± 0.0008 | 41 | 0.999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Klekociuk, A.R.; French, W.J.R.; Alexander, S.P.; Warner, T.A. Measurements of Cloud Radiative Effect across the Southern Ocean (43° S–79° S, 63° E–158° W). Atmosphere 2020, 11, 949. https://doi.org/10.3390/atmos11090949
Wang H, Klekociuk AR, French WJR, Alexander SP, Warner TA. Measurements of Cloud Radiative Effect across the Southern Ocean (43° S–79° S, 63° E–158° W). Atmosphere. 2020; 11(9):949. https://doi.org/10.3390/atmos11090949
Chicago/Turabian StyleWang, Haoran, Andrew R. Klekociuk, W. John R. French, Simon P. Alexander, and Tom A. Warner. 2020. "Measurements of Cloud Radiative Effect across the Southern Ocean (43° S–79° S, 63° E–158° W)" Atmosphere 11, no. 9: 949. https://doi.org/10.3390/atmos11090949
APA StyleWang, H., Klekociuk, A. R., French, W. J. R., Alexander, S. P., & Warner, T. A. (2020). Measurements of Cloud Radiative Effect across the Southern Ocean (43° S–79° S, 63° E–158° W). Atmosphere, 11(9), 949. https://doi.org/10.3390/atmos11090949






