Electret Filters—From the Influence of Discharging Methods to Optimization Potential
Abstract
:1. Introduction
2. Experiments
2.1. Electret Filter Media
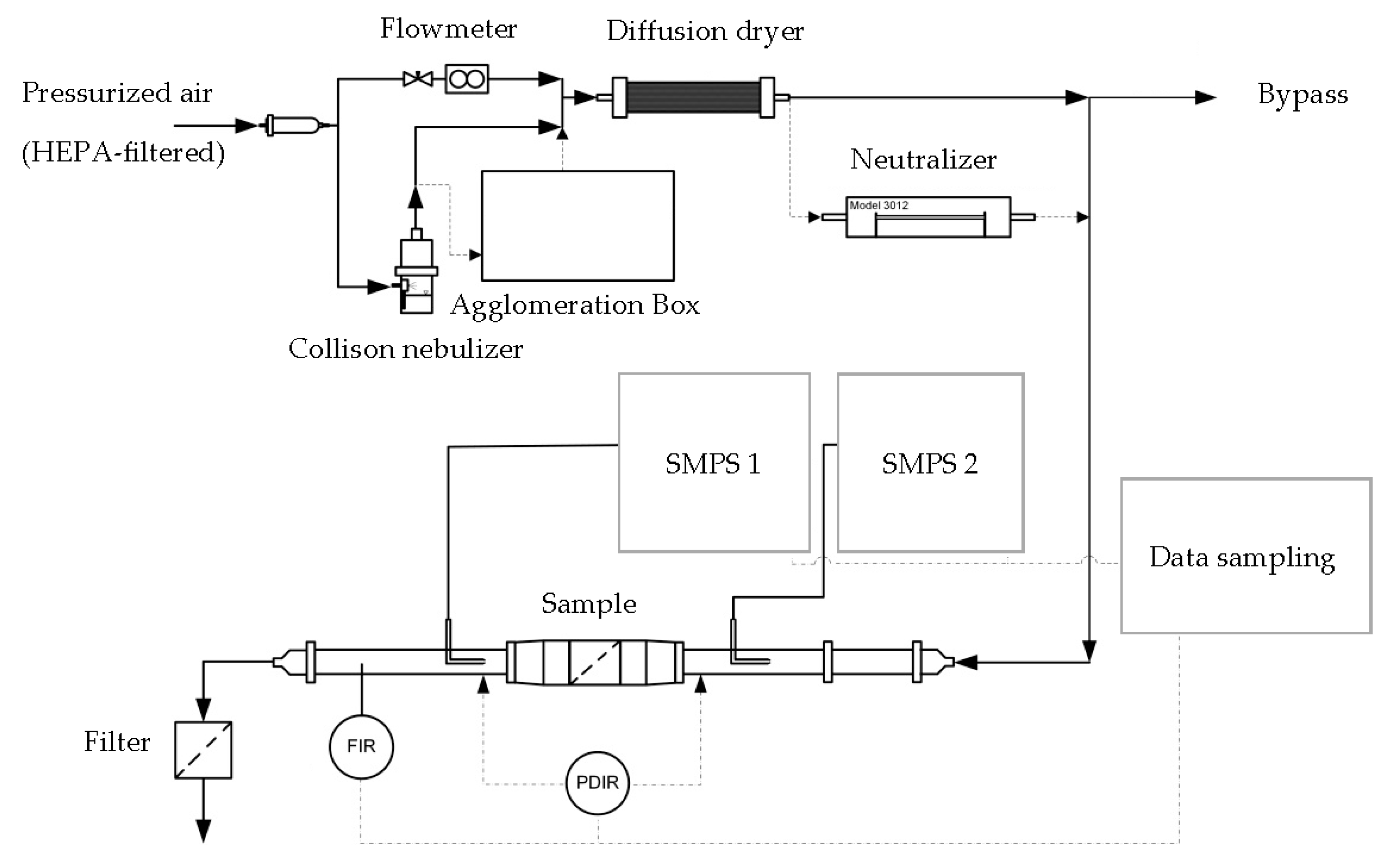
2.2. Test Setup
2.3. Discharging Methods
2.4. Results
3. Direct Numerical Simulations
3.1. 3D Model Generation
3.2. Computation of Gas Flow, Electric Field, and Particle Movement
3.3. Results
3.3.1. Fiber Charge Properties
3.3.2. Fibrous Structure Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lathrache, R.; Fissan, H.J. Enhancement of particle deposition in filters due to electrostatic effects. Filtr. Sep. 1987, 24, 418–422. [Google Scholar]
- Lathrache, R.; Fissan, H.J.; Neumann, S. Deposition of submicron particles on electrically charged fibers. J. Aerosol Sci. 1986, 17, 446–449. [Google Scholar] [CrossRef]
- Lathrache, R.; Fissan, H. Fractional Penetrations for Electrostatically Charged Fibrous Filters in the Submicron Particle Size Range. Part. Part. Syst. Charact. 1986, 3, 74–80. [Google Scholar] [CrossRef]
- Baumgartner, H.; Löffler, F. The collection perfomance of electret filters in the particle size range 10 nm-10µm. J. Aerosol Sci. 1986, 17, 438–445. [Google Scholar] [CrossRef]
- Baumgartner, H.; Löffler, F.; Umhauer, H. Deep-Bed Electret Filters: The Determination of Single Fiber Charge and Collection Efficiency. IEEE Trans. Electr. Insul. 1986, EI-21, 477–486. [Google Scholar] [CrossRef]
- Löffler, F. Staubabscheiden; Geor Thieme Verlag: Stuttgart, Germany; New York, NY, USA, 1988. [Google Scholar]
- Wang, C.-S. Electrostatic forces in fibrous filters—A review. Powder Technol. 2001, 118, 166–170. [Google Scholar] [CrossRef]
- Sanchez, A.L.; Hubbard, J.A.; Dellinger, J.G.; Servantes, B.L. Experimental Study of Electrostatic Aerosol Filtration at Moderate Filter Face Velocity. Aerosol Sci. Technol. 2013, 47, 606–615. [Google Scholar] [CrossRef]
- Kerner, M.; Schmidt, K.; Hellmann, A.; Schumacher, S.; Pitz, M.; Asbach, C.; Ripperger, S.; Antonyuk, S. Numerical and experimental study of submicron aerosol deposition in electret microfiber nonwovens. J. Aerosol Sci. 2018, 122, 32–44. [Google Scholar] [CrossRef]
- Walsh, D.C.; Stenhouse, J.I.T. The effect of particle size, charge and composition on the loading characteristics of an electrically active fibrous filter material. J. Aerosol Sci. 1997, 28, 307–321. [Google Scholar] [CrossRef]
- Otani, Y.; Emi, H.; Mori, J. Initial Collection Efficiency of Electret Filters and Its Durability for Solid and Liquid Particles. Kona Powder Part. J. 1993, 207–214. [Google Scholar] [CrossRef] [Green Version]
- Walsh, D.C.; Stenhouse, J.I.T. Parameters Affecting the Loading Behavior and Degradation of Electrically Active Filter Materials. Aerosol Sci. Technol. 1998, 29, 419–432. [Google Scholar] [CrossRef]
- Kerner, M.; Schmidt, K.; Schumacher, S.; Puderbach, V.; Asbach, C.; Antonyuk, S. Evaluation of electrostatic properties of electret filters for aerosol deposition. Sep. Purif. Technol. 2020, 116548. [Google Scholar] [CrossRef]
- Schumacher, S.; Spiegelhoff, D.; Schneiderwind, U.; Finger, H.; Asbach, C. Performance of New and Artificially Aged Electret Filters in Indoor Air Cleaners. Chem. Eng. Technol. 2018, 41, 27–34. [Google Scholar] [CrossRef]
- Ji, J.H.; Bae, G.N.; Kang, S.H.; Hwang, J. Effect of particle loading on the collection performance of an electret cabin air filter for submicron aerosols. J. Aerosol Sci. 2003, 34, 1493–1504. [Google Scholar] [CrossRef]
- Jasper, W.; Hinestroza, J.; Mohan, A.; Kim, J.; Shiels, B.; Gunay, M.; Thompson, D.; Barker, R. Effect of xylene exposure on the performance of electret filter media. J. Aerosol Sci. 2006, 37, 903–911. [Google Scholar] [CrossRef]
- Choi, H.-J.; Park, E.-S.; Kim, J.-U.; Kim, S.H.; Lee, M.-H. Experimental Study on Charge Decay of Electret Filter Due to Organic Solvent Exposure. Aerosol Sci. Technol. 2015, 49, 977–983. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Lee, W.-M.G.; Huang, H.-L.; Huang, Y.-C.; Luo, C.-H.; Wu, C.-C.; Yu, K.-P. Aerosol penetration properties of an electret filter with submicron aerosols with various operating factors. J. Environ. Sci. Health A Tox. Hazard. Subst. Environ. Eng. 2007, 42, 51–57. [Google Scholar] [CrossRef]
- Motyl, E.; Lowkis, B. Effect of Air Humidity on Charge Decay and Lifetime of PP Electret Nonwovens. Fibres Text. East. Eur. 2006, 14, 39–42. [Google Scholar]
- DIN EN 779. Partikel-Luftfilter für die Allgemeine Raumlufttechnik—Bestimmung der Filterleistung. 2012. Available online: https://www.beuth.de/en/standard/din-en-779/136851927 (accessed on 3 January 2021).
- ISO 16890-4:2016. Air Filters for General Ventilation—Part 4: Conditioning Method to Determine the Minimum Fractional Test Efficiency. Available online: https://www.iso.org/standard/57867.html (accessed on 3 January 2021).
- Xiao, H.; Song, Y.; Chen, G. Correlation between charge decay and solvent effect for melt-blown polypropylene electret filter fabrics. J. Electrost. 2014, 72, 311–314. [Google Scholar] [CrossRef]
- Tang, M.; Thompson, D.; Chen, S.-C.; Liang, Y.; Pui, D.Y.H. Evaluation of different discharging methods on HVAC electret filter media. Build. Environ. 2018, 141, 206–214. [Google Scholar] [CrossRef]
- Biermann, A.H.; Lum, B.Y.; Bergman, W. Evaluation of permanently charged electrofibrous filters. In Proceedings of the 17th Doe Nucelar Air Cleaning Conference-Proccedings, Livemore, CA, USA, 1 August 1982. [Google Scholar]
- Tronvill, P.; Rivers, R. Looking for the minimum efficiency of fibrous air filters during their sercive life. In Proceedings of the 11th World Filtration Congress, Graz, Austria, 16–20 March 2012. [Google Scholar]
- Myers, D.L.; Arnold, B.D. Electret Media for HVAC Filtration Applications. INJ Winter 2003, 12, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Sun, C. Implication of Discharging Condtitioning on Air Filter Media. In Proceedings of the International Nonwovens Technical Conference (INTC), Denver, CO, USA, 21–24 September 2009. [Google Scholar]
- Kim, J.; Hinestroza, J.P.; Jasper, W.; Barker, R.L. Effect of Solvent Exposure on the Filtration Performance of Electrostatically Charged Polypropylene Filter Media. Text. Res. J. 2009, 79, 343–350. [Google Scholar] [CrossRef]
- Kerner, M.; Schmidt, K.; Schumacher, S.; Asbach, C.; Antonyuk, S. Ageing of electret filter media due to deposition of submicron particles—Experimental and numerical investigations. Sep. Purif. Technol. 2020, 251, 117299. [Google Scholar] [CrossRef]
- Oh, Y.-W.; Jeon, K.-J.; Jung, A.-I.; Jung, Y.-W. A Simulation Study on the Collection of Submicron Particles in a Unipolar Charged Fiber. Aerosol Sci. Technol. 2002, 36, 573–582. [Google Scholar] [CrossRef]
- Rief, S.; Latz, A.; Wiegmann, A. Research note: Computer simulation of air filtration including electric surface charges in 3-dimensional fibrous microstructures. Filtr. Solut. 2006, 6, 169–172. [Google Scholar]
- Schober, C. Modeling and Simulation of Cabin Air Filtration with Focus on Electrostatic Effects. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2019. [Google Scholar]
- Mohan, A. Effect of Organic Solvent Exposure on Electret Filtration; Raleigh. 2005. Available online: http://www.lib.ncsu.edu/resolver/1840.16/2168 (accessed on 3 January 2021).
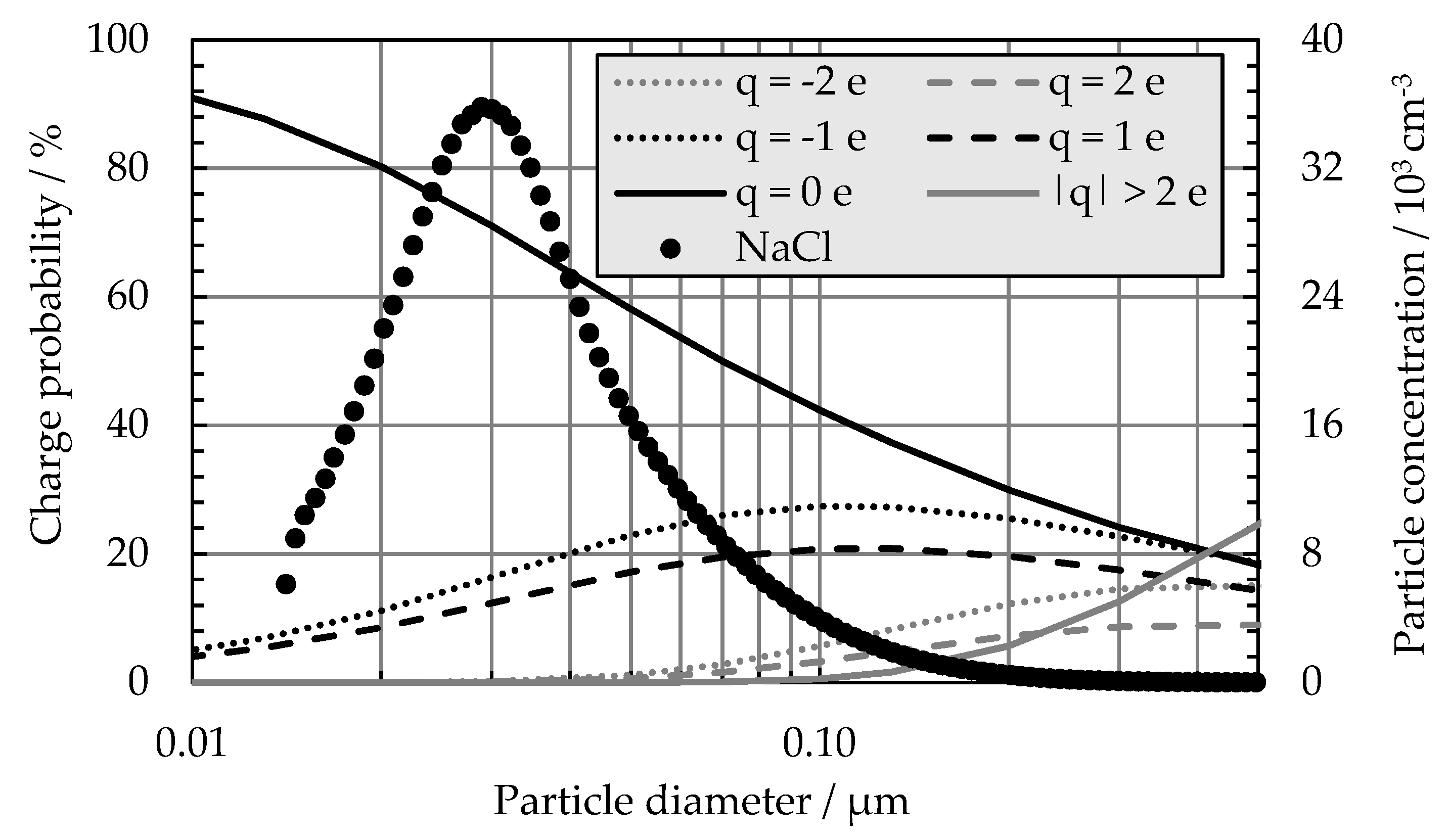
- Wiedensohler, A. An approximation of the bipolar charge distribution for particles in the submicron size range. J. Aerosol Sci. 1988, 19, 387–389. [Google Scholar] [CrossRef]
- Schmidt, K. Dreidimensionale Modellierung von Filtermedien und Simulation der Partikelabscheidung auf der Mikroskala. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 2011. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Brown, R.C. Air Filtration—An Integrated Approach to the Theory and Applications of Fibrous Filters, 1st ed.; Pergamin Press: Oxford, UK, 1993. [Google Scholar]
- Kim, J.C.; Otani, Y.; Noto, D.; Namiki, N.; Kimura, K. Initial Collection Performance of Resin Wool Filters and Estimation of Charge Density. Aerosol Sci. Technol. 2005, 39, 501–508. [Google Scholar] [CrossRef] [Green Version]
- Chang, D.-Q.; Chen, S.-C.; Fox, A.R.; Viner, A.S.; Pui, D.Y.H. Penetration of Sub-50 nm Nanoparticles Through Electret HVAC Filters Used in Residence. Aerosol Sci. Technol. 2015, 49, 966–976. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Otani, Y.; Namiki, N.; Emi, H. Prediction of Collection Efficiency of High-performance Electret Filters. J. Chem. Eng. Jpn. JCEJ 2002, 35, 57–62. [Google Scholar] [CrossRef]
- Chen, S.-C.; Wang, J.; Bahk, Y.K.; Fissan, H.; Pui, D.Y.H. Carbon Nanotube Penetration Through Fiberglass and Electret Respirator Filter and Nuclepore Filter Media: Experiments and Models. Aerosol Sci. Technol. 2014, 48, 997–1008. [Google Scholar] [CrossRef] [Green Version]

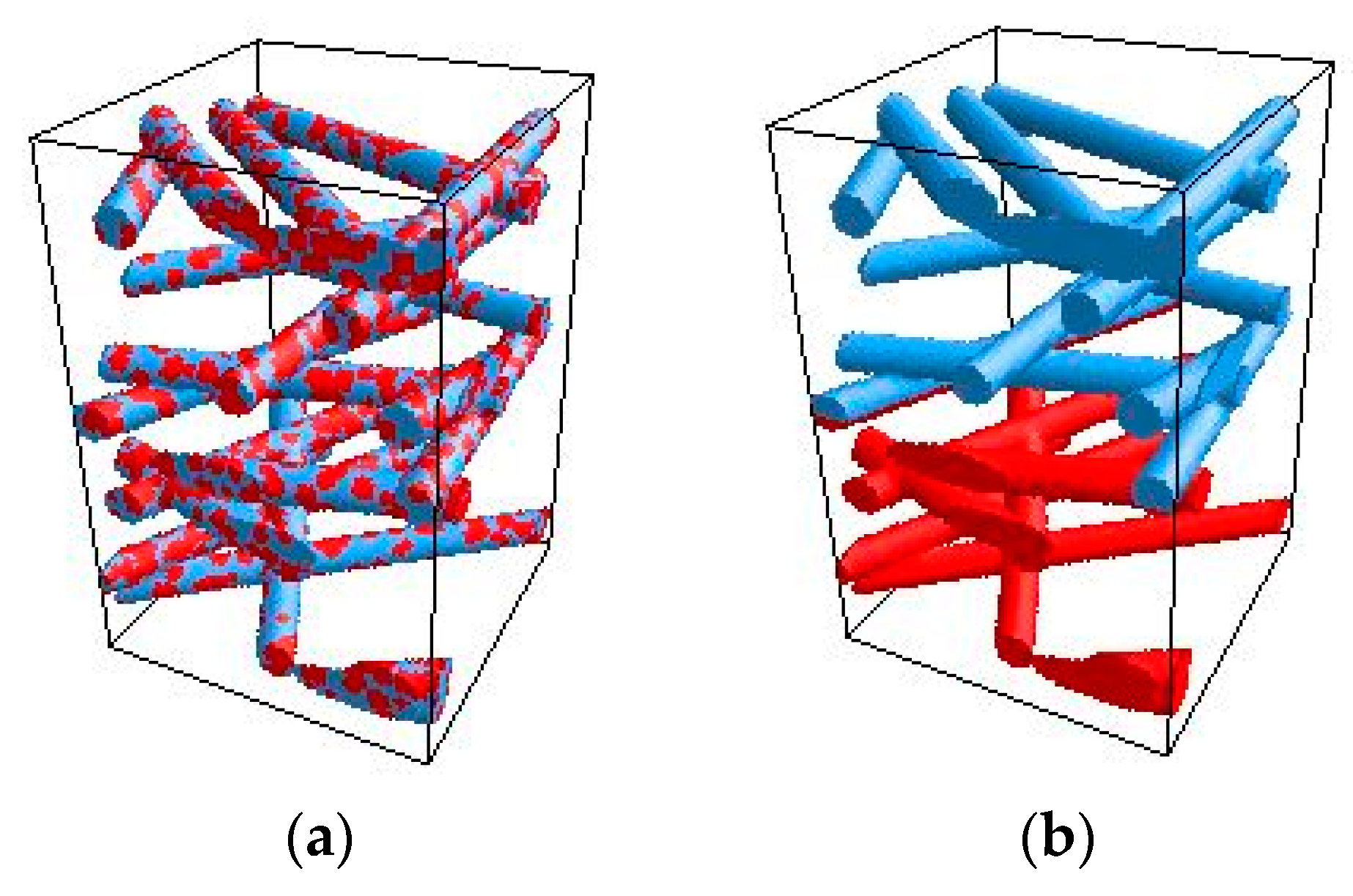


| Filter Medium | Material | Manufacturing Process | Charging Method |
|---|---|---|---|
| 1 | Polypropylene | N/A | Corona charged |
| 2 | N/A | Meltblown | N/A |
| 3 | Polypropylene | Meltblown | Corona charged |
| 4 | Polyamide nanofiber layer, Polyethylene/Polypropylene supporting layer, | Spunbond (supporting layer) | Corona charged |
| 5 | Polypropylene, Polyethylene terephthalate supporting layer, | Meltblown (supportinglayer) | Corona-charged |
| 6 | Polypropylene | Spunbond | N/A |
| 7 | Polymer-Blend | N/A | Triboelectrically charged |
| 8 | Polymer-Blend | N/A | Triboelectrically charged |
| 9 | Polymer-Blend | N/A | Triboelectrically charged |
| 10 | Polymer-Blend | N/A | Triboelectrically charged |
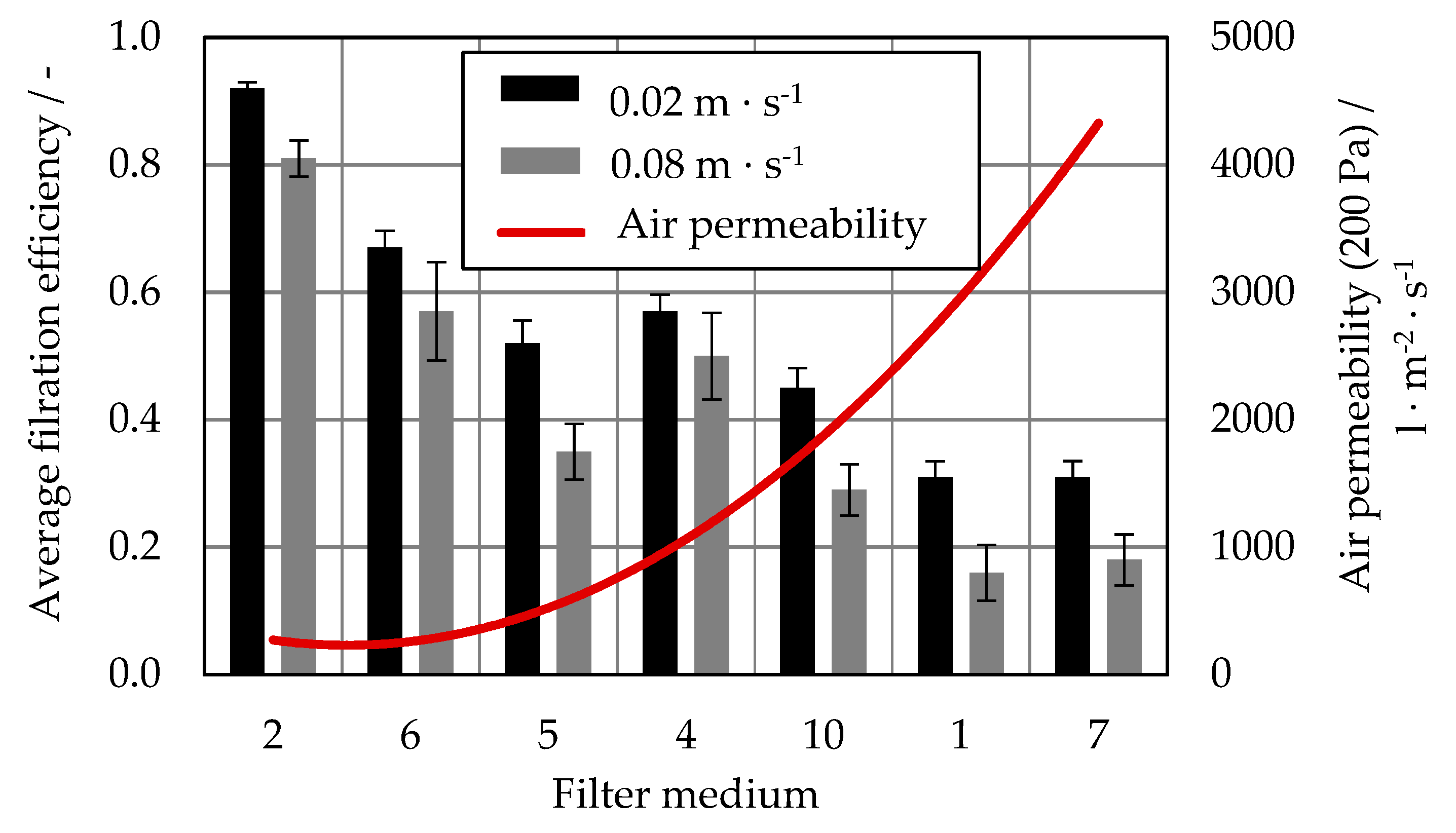
| Filter Medium | Basis Weight | Air Permeability (200 Pa) | Porosity | Thickness | Arithmetic Mean Value of Fiber Diameter Distribution | Modal Value of Fiber Diameter Distribution | ||
|---|---|---|---|---|---|---|---|---|
| g∙m−2 | L∙m−2∙s−1 | % | µm | µm | µm | |||
| Upstream | Downstream | Upstream | Downstream | |||||
| 1 | 133 ± 7 | 2527 ± 227 | 77.2 ± 0.2 | 646.8 ± 37.0 | 31.8 ± 1.5 | 32.8 ± 1.5 | 32.5 | 32.5 |
| 2 | 51 ± 3 | 101 ± 3 | 87.3 ± 0.1 | 447.1 ± 97.7 | 1.9 ± 1.1 | 1.5 ± 0.7 | 1.1 | 1.1 |
| 3 | 152 ± 8 | 705 ± 13 | 79.4 ± 0.1 | 847.4 ± 74.7 | 14.4 ± 3.7 | 13.7 + 4.8 | 11.3 | 11.3 |
| 4 | 108 ± 3 | 895 ± 177 | 86.7 ± 0.2 | 934.2 ± 58.7 | 20.4 ± 3.8 0.1 (Nanofiber layer) | 22.6 ± 1.5 | 21.3 | 23.8 |
| 5 | 114 ± 4 | 712 ± 44 | 85.8 ± 0.1 | 654.7 ± 92.0 | 3.4 ± 2.2 | 28.9 ± 12.0 | 1.5 | 16.3 41.3 |
| 6 | 153 ± 6 | 444 ± 56 | 92.6 ± 0.1 | 2377.0 ± 214.3 | 15.6 ± 9.0 | 17.1 ± 1.6 | 12.5 | 16.3 |
| 7 | 56 ± 1 | 4473 ± 111 | 96.2 ± 0.3 | 1739.0 ± 33.3 | 18.2 ± 2.4 | 19.2 ± 2.2 | 18.8 | 18.8 |
| 8 | 67 ± 1 | 4407 ± 222 | 96.1 ± 0.2 | 1603.3 ± 95.5 | 18.8 ± 3.7 | 18.0 ± 2.1 | 18.8 | 18.8 |
| 9 | 99 ± 14 | 3105 ± 408 | 95.8 ± 0.4 | 2467.7 ± 11.3 | 19.3 ± 3.9 | 18.0 ± 3.0 | 18.8 | 18.8 |
| 10 | 149 ± 4 | 1889 ± 121 | 95.3 ± 0.2 | 3261.0 ± 110.6 | 18.0 ± 4.1 | 18.2 ± 4.3 | 18.8 | 18.8 |
| Filter Medium | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| Face velocity of 0.02 m·s−1 | |||||||||
| Untreated | 0.77 | 1.00 | 0.97 | 0.97 | 0.85 | 0.93 | 0.90 | 0.97 | 0.99 |
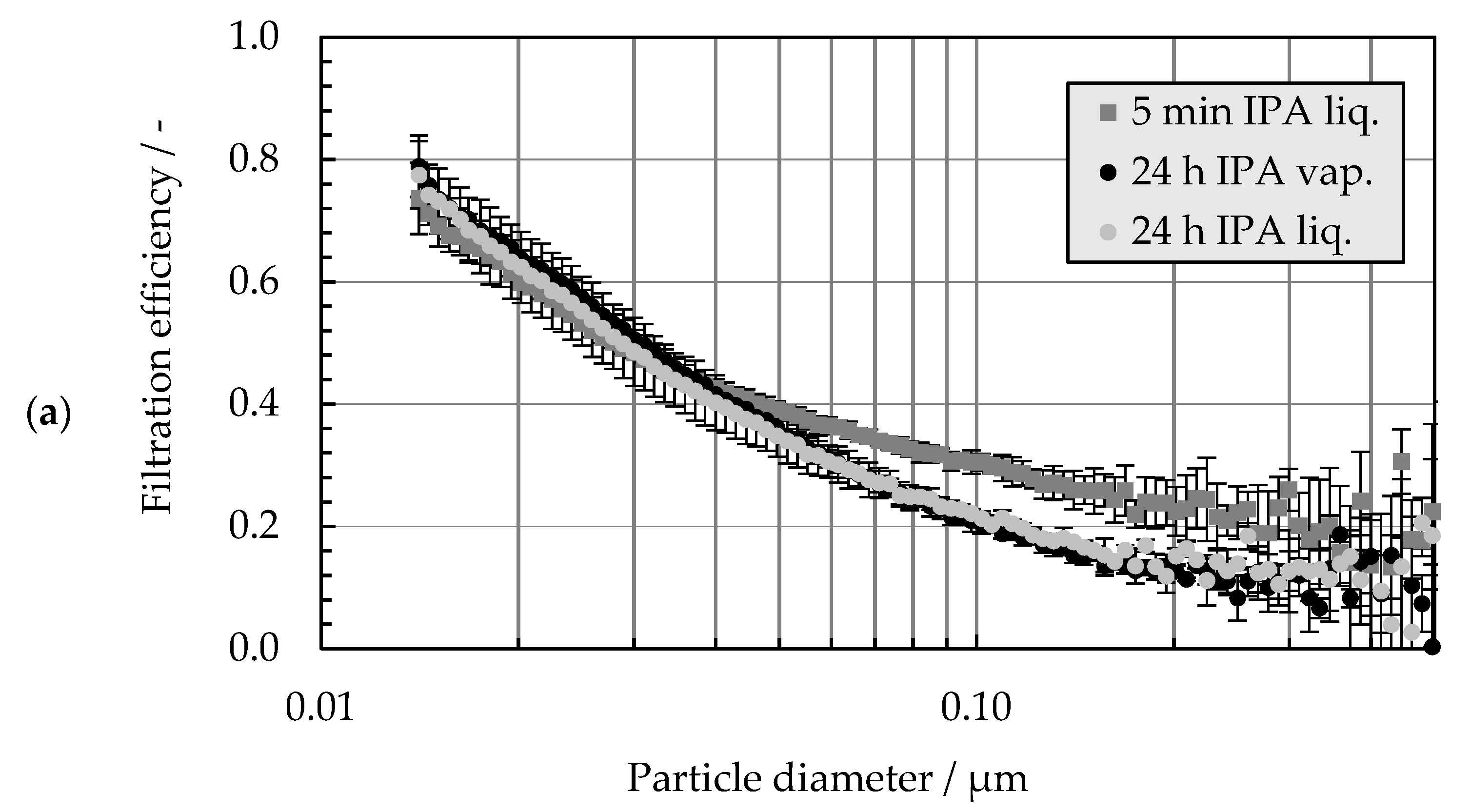
| 5 min IPA liq. | 0.26 | 0.95 | 0.36 | 0.47 | 0.67 | 0.11 | 0.19 | 0.19 | 0.43 |
| 24 h IPA liq. | 0.13 | 0.87 | 0.35 | 0.55 | 0.09 | 0.35 | |||
| 24 h IPA vap. | 0.13 | 0.80 | 0.21 | 0.42 | 0.13 | 0.10 | |||
| Face velocity of 0.08 m·s−1 | |||||||||
| Untreated | 0.48 | 1.00 | 0.77 | 0.81 | 0.51 | 0.60 | 0.60 | 0.78 | 0.91 |
| 5 min IPA liq. | 0.06 | 0.85 | 0.15 | 0.22 | 0.41 | 0.07 | 0.11 | 0.07 | 0.14 |
| 24 h IPA liq. | 0.08 | 0.85 | 0.05 | 0.41 | 0.09 | 0.05 | |||
| 24 h IPA vap. | 0.08 | 0.63 | 0.09 | 0.42 | 0.10 | 0.09 | |||
| Thickness | Porosity | Fiber Diameter | Spot Size |
|---|---|---|---|
| µm | - | µm | µm |
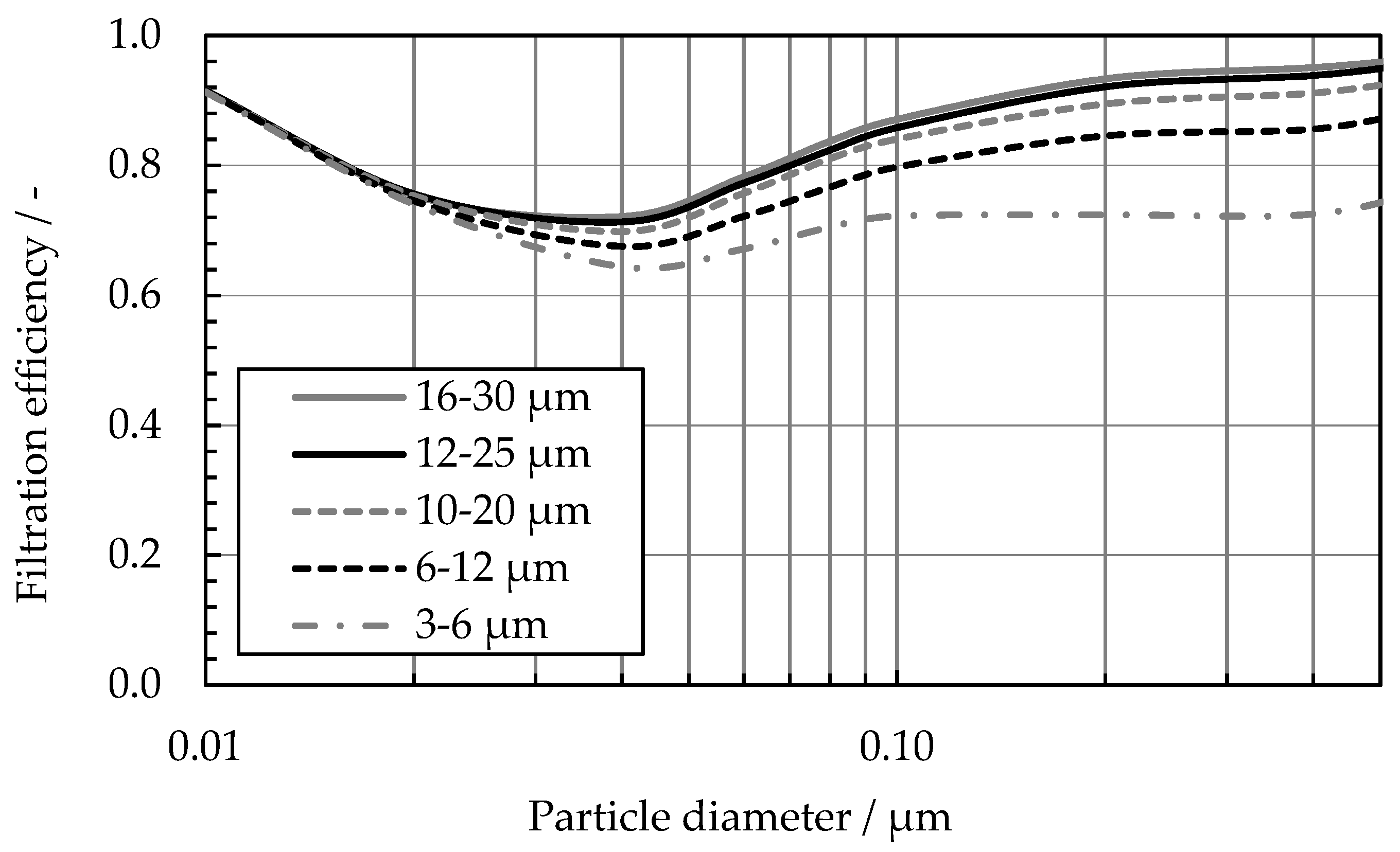
| 500 | 0.7 | 10 | 3–6 |
| 600 | 0.75 | 20 | 6–12 |
| 675 | 0.79 | 32 | 10–20 |
| 800 | 0.85 | 40 | 12–25 |
| 900 | 0.9 | 50 | 16–30 |
| Temperature | K | 293.15 |
| Pressure | mbar | 1013 |
| Gas viscosity | kg·m−1·s−1 | 18.1 × 10−6 |
| Gas density | kg·m−3 | 1.2 |
| Particle density | kg·m−3 | 2160 |
| Relative dielectric constant of particles | - | 5.9 |
| Air velocity | m·s−1 | 0.02 |
| Surface charge density | µC·m−2 | 100 |
| Thickness/µm | 500 | 600 | 675 | 800 | 900 |
|---|---|---|---|---|---|
| No charge | 0.28 | 0.32 | 0.32 | 0.37 | 0.39 |
| Divided | 0.87 | 0.91 | 0.91 | 0.93 | 0.94 |
| 0.59 | 0.59 | 0.59 | 0.57 | 0.56 | |
| Spherical spots | 0.80 | 0.84 | 0.84 | 0.88 | 0.89 |
| 0.52 | 0.52 | 0.52 | 0.51 | 0.51 | |
| Porosity/− | 0.70 | 0.75 | 0.79 | 0.85 | 0.90 |
| No charge | 0.43 | 0.37 | 0.32 | 0.28 | 0.21 |
| Divided | 0.96 | 0.94 | 0.91 | 0.88 | 0.80 |
| 0.53 | 0.56 | 0.59 | 0.61 | 0.60 | |
| Spherical spots | 0.92 | 0.88 | 0.84 | 0.79 | 0.68 |
| 0.50 | 0.51 | 0.52 | 0.52 | 0.48 | |
| Fiber Diameter/µm | 10 | 20 | 32 | 40 | 50 |
| No charge | 0.84 | 0.50 | 0.32 | 0.27 | 0.22 |
| Divided | 1.00 | 0.98 | 0.91 | 0.88 | 0.80 |
| 0.16 | 0.48 | 0.59 | 0.60 | 0.58 | |
| Spherical Spots | 1.00 | 0.94 | 0.84 | 0.80 | 0.74 |
| 0.15 | 0.44 | 0.52 | 0.53 | 0.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerner, M.; Schmidt, K.; Schumacher, S.; Asbach, C.; Antonyuk, S. Electret Filters—From the Influence of Discharging Methods to Optimization Potential. Atmosphere 2021, 12, 65. https://doi.org/10.3390/atmos12010065
Kerner M, Schmidt K, Schumacher S, Asbach C, Antonyuk S. Electret Filters—From the Influence of Discharging Methods to Optimization Potential. Atmosphere. 2021; 12(1):65. https://doi.org/10.3390/atmos12010065
Chicago/Turabian StyleKerner, Maximilian, Kilian Schmidt, Stefan Schumacher, Christof Asbach, and Sergiy Antonyuk. 2021. "Electret Filters—From the Influence of Discharging Methods to Optimization Potential" Atmosphere 12, no. 1: 65. https://doi.org/10.3390/atmos12010065








