Significance of Absorbing Fraction of Coating on Absorption Enhancement of Partially Coated Black Carbon Aerosols
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Blocking Effect of Absorbing Coatings on BC Absorption Enhancement
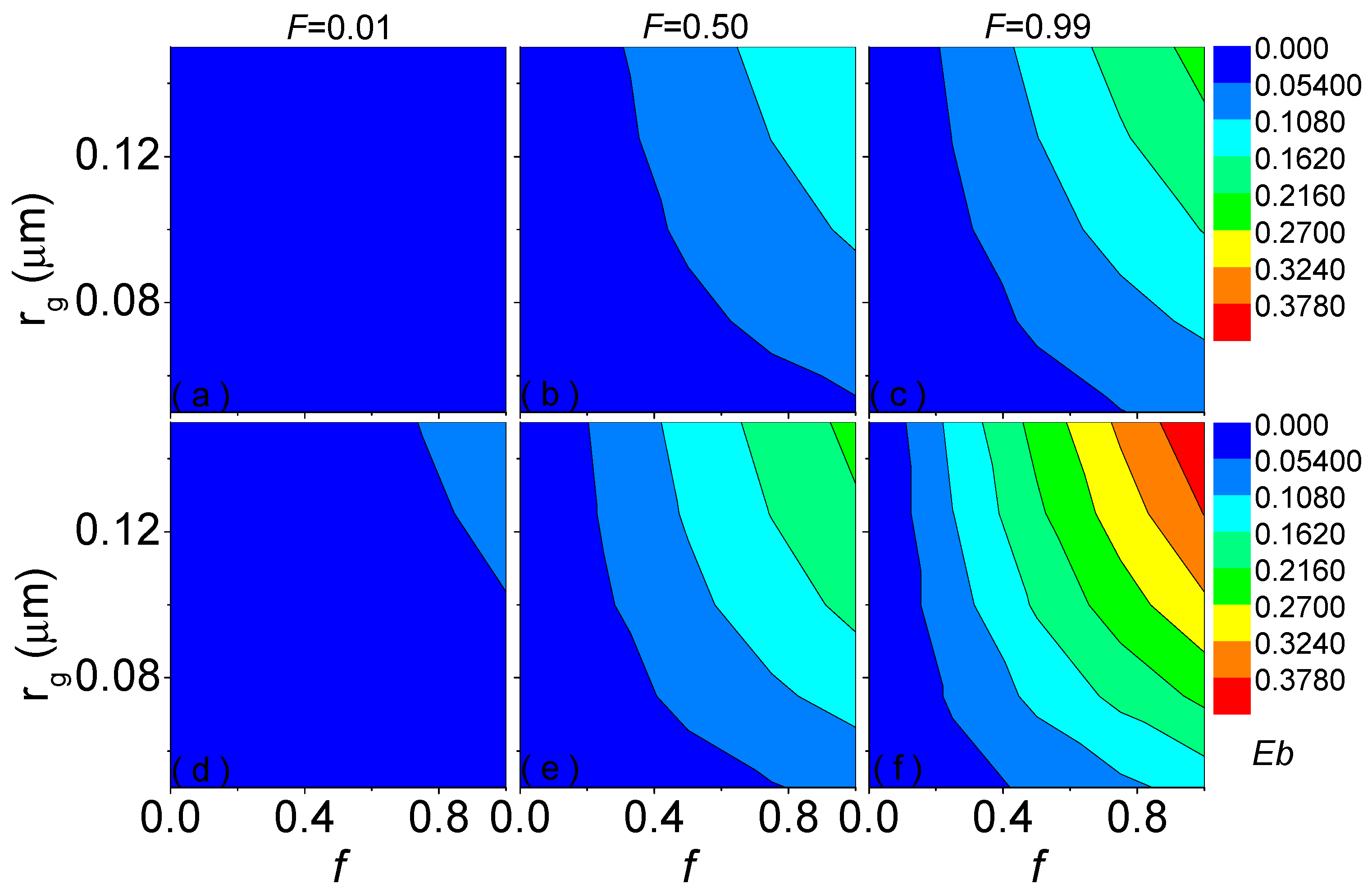
3.2. Influence of Coating Absorbing Volume Fraction on Blocking Effect
3.3. Empirical Formula for Blocking Effect Influenced by Absorbing Volume Fraction of Coating
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Curci, G.; Alyuz, U.; Barò, R.; Bianconi, R.; Bieser, J.; Christensen, J.H.; Colette, A.; Farrow, A.; Francis, X.; Jiménez-Guerrero, P.; et al. Modelling black carbon absorption of solar radiation: Combining external and internal mixing assumptions. Atmos. Chem. Phys. Discuss. 2019, 19, 181–204. [Google Scholar] [CrossRef] [Green Version]
- Mao, M.; Sun, H.; Zhang, X. Air pollution characteristics and health risks in the Yangtze river economic belt, China during winter. Int. J. Environ. Res. Public Health 2020, 17, 9172. [Google Scholar] [CrossRef]
- Jin, S.; Ma, Y.; Zhang, M.; Gong, W.; Lei, L.; Ma, X. Comparation of aerosol optical properties and associated radiative effects of air pollution events between summer and winter: A case study in January and July 2014 over Wuhan, central China. Atmos. Environ. 2019, 218, 117004. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, M.; Jin, S.; Gong, W.; Chen, N.; Chen, Z.; Jin, Y.; Shi, Y. Long-term investigation of aerosol optical and radiative characteristics in a typical megacity of central China during winter haze periods. J. Geophys. Res. 2019, 124, 12093–12106. [Google Scholar] [CrossRef]
- Ma, Y.; Fan, R.; Jin, S.; Ma, X.; Zhang, M.; Gong, W.; Liu, B.; Shi, Y.; Zhang, Y.; Li, H. Black carbon over Wuhan, China: Seasonal variations in its optical properties, radiative forcing and contribution to atmospheric aerosols. Remote Sens. 2021, 13, 3620. [Google Scholar] [CrossRef]
- Zhang, X.; Rao, R.; Huang, Y.; Mao, M.; Berg, M.J.; Sun, W. Black carbon aerosols in urban central China. J. Quant. Spectrosc. Radiat. Transf. 2015, 150, 3–11. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kaercher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, P.; Peng, J.; Zhang, R.; Jiang, J.H.; Easter, R.C.; Yung, Y.L. Constraining aging processes of black carbon in the community atmosphere model using environmental chamber measurements. J. Adv. Model. Earth Syst. 2018, 10, 2514–2526. [Google Scholar] [CrossRef] [Green Version]
- Zuberi, B.; Johnson, K.S.; Aleks, G.K.; Molina, L.T.; Molina, M.J.; Laskin, A. Hydrophilic properties of aged soot. Geophys. Res. Lett. 2005, 32, 01807. [Google Scholar] [CrossRef]
- Zhang, R.; Khalizov, A.F.; Pagels, J.; Zhang, D.; Xue, H.; McMurry, P.H. Variability in morphology, hygroscopicity, and optical properties of soot aerosols during atmospheric processing. Proc. Natl. Acad. Sci. USA 2008, 105, 10291–10296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riemer, N.; West, M.; Zaveri, R.; Easter, R. Estimating black carbon aging time-scales with a particle-resolved aerosol model. J. Aerosol Sci. 2010, 41, 143–158. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Li, Q.; Liou, K.-N.; Qi, L.; Tao, S.; Schwarz, J.P. Microphysics-based black carbon aging in a global CTM: Constraints from HIPPO observations and implications for global black carbon budget. Atmos. Chem. Phys. Discuss. 2016, 16, 3077–3098. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Hu, M.; Guo, S.; Du, Z.; Zheng, J.; Shang, D.; Zamora, M.L.; Zeng, L.; Shao, M.; Wu, Y.-S.; et al. Markedly enhanced absorption and direct radiative forcing of black carbon under polluted urban environments. Proc. Natl. Acad. Sci. USA 2016, 113, 4266–4271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Heald, C.L.; Liu, J.; Weber, R.J.; Campuzano-Jost, P.; Jimenez, J.L.; Schwarz, J.P.; Perring, A.E. Exploring the observational constraints on the simulation of brown carbon. Atmos. Chem. Phys. 2018, 18, 635–653. [Google Scholar] [CrossRef] [Green Version]
- Moteki, N.; Kondo, Y.; Miyazaki, Y.; Takegawa, N.; Komazaki, Y.; Kurata, G.; Shirai, T.; Blake, D.R.; Miyakawa, T.; Koike, M. Evolution of mixing state of black carbon particles: Aircraft measurements over the western Pacific in March 2004. Geophys. Res. Lett. 2007, 34, 11803. [Google Scholar] [CrossRef] [Green Version]
- Shiraiwa, M.; Kondo, Y.; Moteki, N.; Takegawa, N.; Miyazaki, Y.; Blake, D.R. Evolution of mixing state of black carbon in polluted air from Tokyo. Geophys. Res. Lett. 2007, 34, 16803. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.S.; Zuberi, B.; Molina, L.T.; Molina, M.J.; Iedema, M.J.; Cowin, J.P.; Gaspar, D.J.; Wang, C.; Laskin, A. Processing of soot in an urban environment: Case study from the Mexico City Metropolitan Area. Atmos. Chem. Phys. Discuss. 2005, 5, 3033–3043. [Google Scholar] [CrossRef] [Green Version]
- Kondo, Y.; Matsui, H.; Moteki, N.; Sahu, L.; Takegawa, N.; Kajino, M.; Zhao, Y.; Cubison, M.J.; Jimenez, J.L.; Vay, S.; et al. Emissions of black carbon, organic, and inorganic aerosols from biomass burning in North America and Asia in 2008. J. Geophys. Res. Space Phys. 2011, 116, 08204. [Google Scholar] [CrossRef] [Green Version]
- Khalizov, A.; Cruz-Quinones, M.; Zhang, R. Heterogeneous reaction of NO2 on fresh and coated soot surfaces. J. Phys. Chem. A 2010, 114, 7516–7524. [Google Scholar] [CrossRef]
- Zhang, R.; Khalizov, A.; Wang, L.; Hu, M.; Xu, W. Nucleation and growth of nanoparticles in the atmosphere. Chem. Rev. 2012, 112, 1957–2011. [Google Scholar] [CrossRef]
- Kirchstetter, T.W.; Thatcher, T.L. Contribution of organic carbon to wood smoke particulate matter absorption of solar radiation. Atmos. Chem. Phys. 2012, 12, 6067–6072. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Mao, M.; Chen, H. Characterization of optically effective complex refractive index of black carbon composite aerosols. J. Atmos. Sol.-Terr. Phys. 2020, 198, 105180. [Google Scholar] [CrossRef]
- Coz, E.; Leck, C. Morphology and state of mixture of atmospheric soot aggregates during the winter season over Southern Asia—A quantitative approach. Tellus B 2011, 63, 107–116. [Google Scholar] [CrossRef]
- Srivastava, R.; Ramachandran, S. The mixing state of aerosols over the Indo-Gangetic Plain and its impact on radiative forcing. Q. J. R. Meteorol. Soc. 2013, 139, 137–151. [Google Scholar] [CrossRef]
- He, C. Radiative properties of atmospheric black carbon (soot) particles with complex structures. In Springer Series in Light Scattering; Kokhanovsky, A., Ed.; Springer: Cham, Switzerland, 2019; Volume 4, pp. 219–254. [Google Scholar]
- Kahnert, M.; Kanngiesser, F. Modelling optical properties of atmospheric black carbon aerosols. J. Quant. Spectrosc. Radiat. Transf. 2020, 244, 106849. [Google Scholar] [CrossRef]
- Liu, D.; He, C.; Schwarz, J.P.; Wang, X. Lifecycle of light-absorbing carbonaceous aerosols in the atmosphere. NPJ Clim. Atmos. Sci. 2020, 3, 40. [Google Scholar] [CrossRef]
- Cappa, C.D.; Onasch, T.B.; Massoli, P.; Worsnop, D.R.; Bates, T.S.; Cross, E.S.; Davidovits, P.; Hakala, J.; Hayden, K.L.; Jobson, B.T.; et al. Radiative absorption enhancements due to the mixing state of atmospheric black carbon. Science 2012, 337, 1078–1081. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Whitehead, J.; Alfarra, R.; Reyes-Villegas, E.; Spracklen, D.V.; Reddington, C.; Kong, S.; Williams, P.; Ting, Y.-C.; Haslett, S.; et al. Black-carbon absorption enhancement in the atmosphere determined by particle mixing state. Nat. Geosci. 2017, 10, 184–188. [Google Scholar] [CrossRef]
- Chakrabarty, R.K.; Heinson, W.R. Scaling laws for light absorption enhancement due to nonrefractory coating of atmospheric black carbon aerosol. Phys. Rev. Lett. 2018, 121, 218701. [Google Scholar] [CrossRef] [Green Version]
- You, R.; Radney, J.; Zachariah, M.R.; Zangmeister, C.D. Measured wavelength-dependent absorption enhancement of internally mixed black carbon with absorbing and nonabsorbing materials. Environ. Sci. Technol. 2016, 50, 7982–7990. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.; Wang, X.; Yang, L.; Chen, B.; Chen, J.; Andersson, A.; Gustafsson, Ö. Radiative absorption enhancement from coatings on black carbon aerosols. Sci. Total Environ. 2016, 551-552, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Bai, Z.; Cui, X.; Chen, J.; Andersson, A.; Gustafsson, Ö. Light absorption enhancement of black carbon from urban haze in northern China winter. Environ. Pollut. 2017, 221, 418–426. [Google Scholar] [CrossRef]
- Scarnato, B.V.; Vahidinia, S.; Richard, D.T.; Kirchstetter, T.W. Effects of internal mixing and aggregate morphology on optical properties of black carbon using a discrete dipole approximation model. Atmos. Chem. Phys. 2013, 13, 5089–5101. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Zhao, J.; Liu, L. Morphological effects on the radiative properties of soot aerosols in different internally mixing states with sulfate. J. Quant. Spectrosc. Radiat. Transf. 2015, 165, 43–55. [Google Scholar] [CrossRef]
- He, C.; Liou, K.-N.; Takano, Y.; Zhang, R.; Zamora, M.L.; Yang, P.; Li, Q.; Leung, L.R. Variation of the radiative properties during black carbon aging: Theoretical and experimental intercomparison. Atmos. Chem. Phys. Discuss. 2015, 15, 11967–11980. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Mao, M.; Yin, Y.; Wang, B. Absorption enhancement of aged black carbon aerosols affected by their microphysics: A numerical investigation. J. Quant. Spectrosc. Radiat. Transf. 2017, 202, 90–97. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, M.; Yin, Y.; Wang, B. Numerical investigation on absorption enhancement of black carbon aerosols partially coated with nonabsorbing organics. J. Geophys. Res. Atmos. 2018, 123, 1297–1308. [Google Scholar] [CrossRef]
- Cheng, Y.; He, K.-B.; Du, Z.-Y.; Engling, G.; Liu, J.-M.; Ma, Y.-L.; Zheng, M.; Weber, R.J. The characteristics of brown carbon aerosol during winter in Beijing. Atmos. Environ. 2016, 127, 355–364. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Y.; Wang, F.; Zhang, Q. Effects of brown coatings on the absorption enhancement of black carbon: A numerical investigation. Atmos. Chem. Phys. Discuss. 2018, 18, 16897–16914. [Google Scholar] [CrossRef] [Green Version]
- China, S.; Mazzoleni, C.; Gorkowski, K.; Aiken, A.; Dubey, M. Morphology and mixing state of individual freshly emitted wildfire carbonaceous particles. Nat. Commun. 2013, 4, 2122. [Google Scholar] [CrossRef] [Green Version]
- China, S.; Scarnato, B.; Owen, R.C.; Zhang, B.; Ampadu, M.T.; Kumar, S.; Dzepina, K.; Dziobak, M.P.; Fialho, P.; Perlinger, J.A.; et al. Morphology and mixing state of aged soot particles at a remote marine free troposphere site: Implications for optical properties. Geophys. Res. Lett. 2015, 42, 1243–1250. [Google Scholar] [CrossRef]
- Li, W.; Sun, J.; Xu, L.; Shi, Z.; Riemer, N.; Sun, Y.; Fu, P.; Zhang, J.; Lin, Y.; Wang, X.; et al. A conceptual framework for mixing structures in individual aerosol particles. J. Geophys. Res. Atmos. 2016, 121, 13784–13798. [Google Scholar] [CrossRef]
- Sorensen, C.M. Light scattering by fractal aggregates: A review. Aerosol Sci. Technol. 2001, 35, 648–687. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Cheng, Y.; Su, H.; Kecorius, S.; Wang, Z.; Wu, Z.; Hu, M.; Zhu, T.; Wiedensohler, A.; et al. Measuring the morphology and density of internally mixed black carbon with SP2 and VTDMA: New insight into the absorption enhancement of black carbon in the atmosphere. Atmos. Meas. Tech. 2016, 9, 1833–1843. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Taylor, J.W.; Young, D.E.; Flynn, M.J.; Coe, H.; Allan, J.D. The effect of complex black carbon microphysics on the determination of the optical properties of brown carbon. Geophys. Res. Lett. 2015, 42, 613–619. [Google Scholar] [CrossRef]
- Skorupski, K.; Mroczka, J.; Wriedt, T.; Riefler, N. A fast and accurate implementation of tunable algorithms used for generation of fractal-like aggregate models. Phys. A Stat. Mech. Appl. 2014, 404, 106–117. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, M.; Yin, Y.; Tang, S. The absorption Ångstrom exponent of black carbon with brown coatings: Effects of aerosol microphysics and parameterization. Atmos. Chem. Phys. Discuss. 2020, 20, 9701–9711. [Google Scholar] [CrossRef]
- Mackowski, D. A general superposition solution for electromagnetic scattering by multiple spherical domains of optically active media. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 264–270. [Google Scholar] [CrossRef]
- Yu, F.; Luo, G. Simulation of particle size distribution with a global aerosol model: Contribution of nucleation to aerosol and CCN number concentrations. Atmos. Chem. Phys. Discuss. 2009, 9, 7691–7710. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; O’Donnell, D.; Kazil, J.; Stier, P.; Kinne, S.; Lohmann, U.; Ferrachat, S.; Croft, B.; Quaas, J.; Wan, H.; et al. The global aerosol-climate model ECHAM-HAM, version 2: Sensitivity to improvements in process representations. Atmos. Chem. Phys. Discuss. 2012, 12, 8911–8949. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Mao, M.; Chen, H.; Yin, Y.; Tang, S. Lensing effect of black carbon with brown coatings: Dominant microphysics and parameterization. J. Geophys. Res. Atmos. 2021, 126, e2020JD033549. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, M.; Yin, Y. Optically effective complex refractive index of coated black carbon aerosols: From numerical aspects. Atmos. Chem. Phys. Discuss. 2019, 19, 7507–7518. [Google Scholar] [CrossRef] [Green Version]
- Kirchstetter, T.W.; Novakov, T.; Hobbs, P.V. Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon. J. Geophys. Res. Space Phys. 2004, 109, 21208. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarty, R.K.; Moosmüller, H.; Chen, L.-W.A.; Lewis, K.; Arnott, W.P.; Mazzoleni, C.; Dubey, M.K.; Wold, C.E.; Hao, W.M.; Kreidenweis, S.M. Brown carbon in tar balls from smoldering biomass combustion. Atmos. Chem. Phys. Discuss. 2010, 10, 6363–6370. [Google Scholar] [CrossRef] [Green Version]
- Bond, T.; Bergstrom, R.W. Light absorption by carbonaceous particles: An investigative review. Aerosol Sci. Technol. 2006, 40, 27–67. [Google Scholar] [CrossRef]
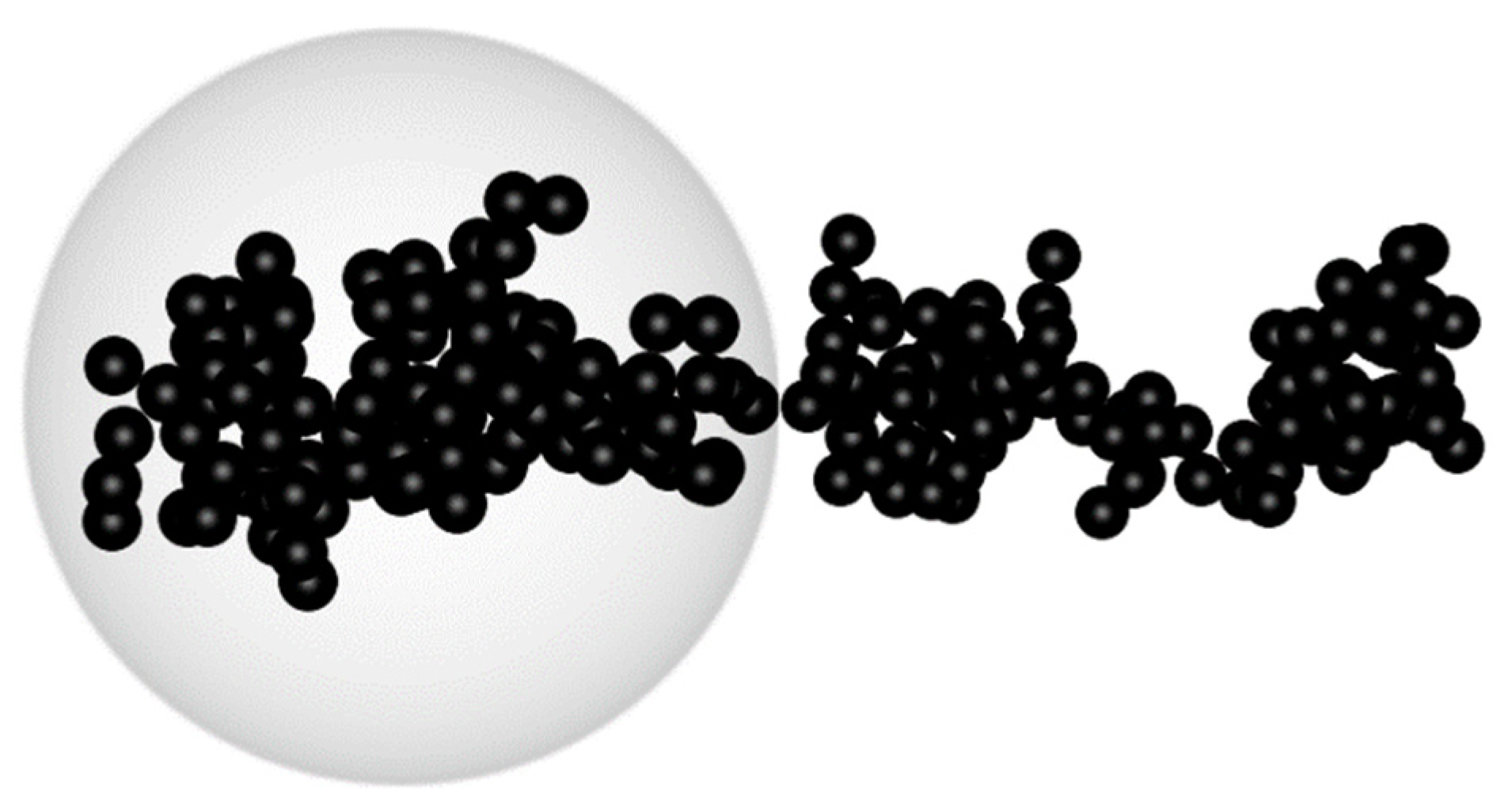

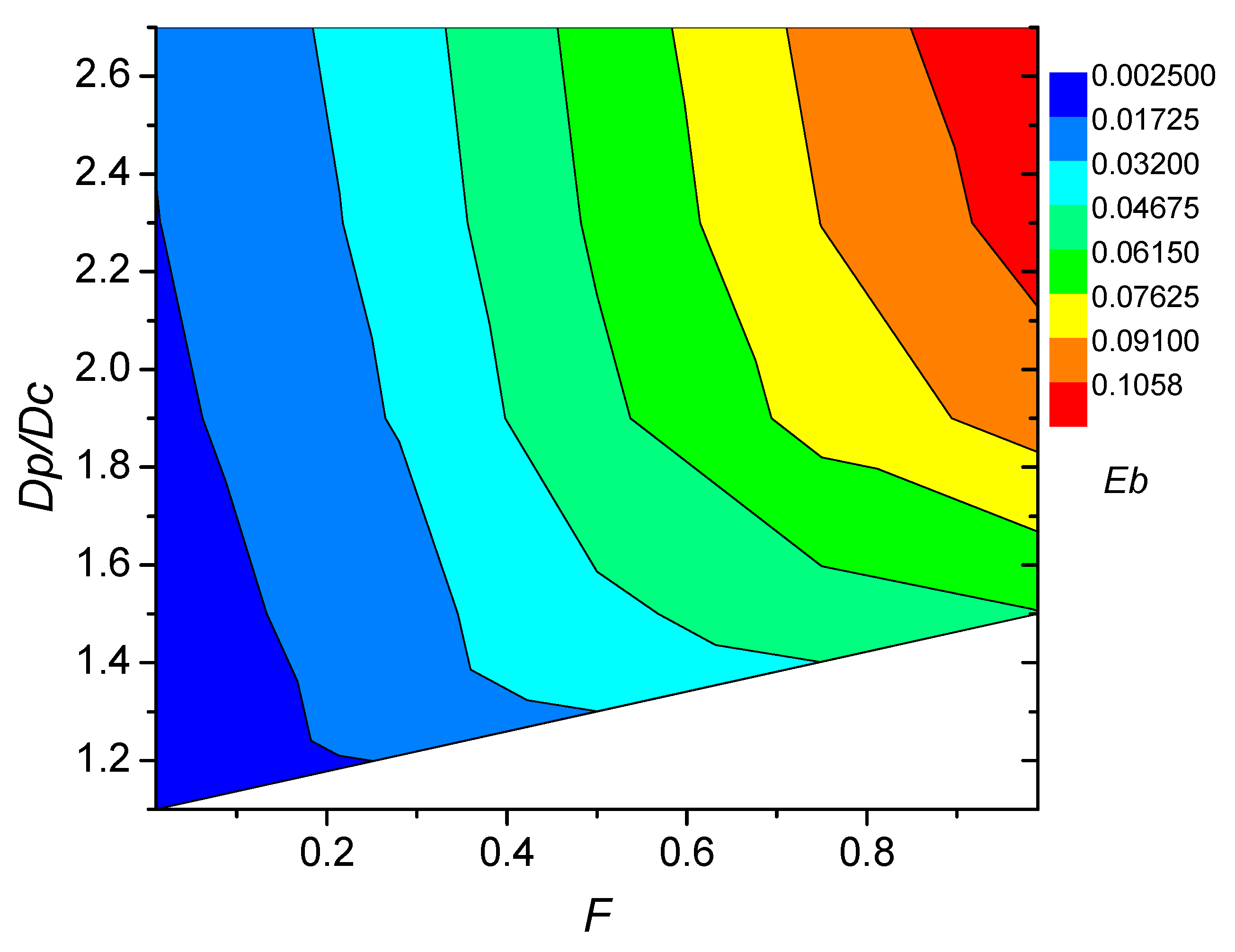
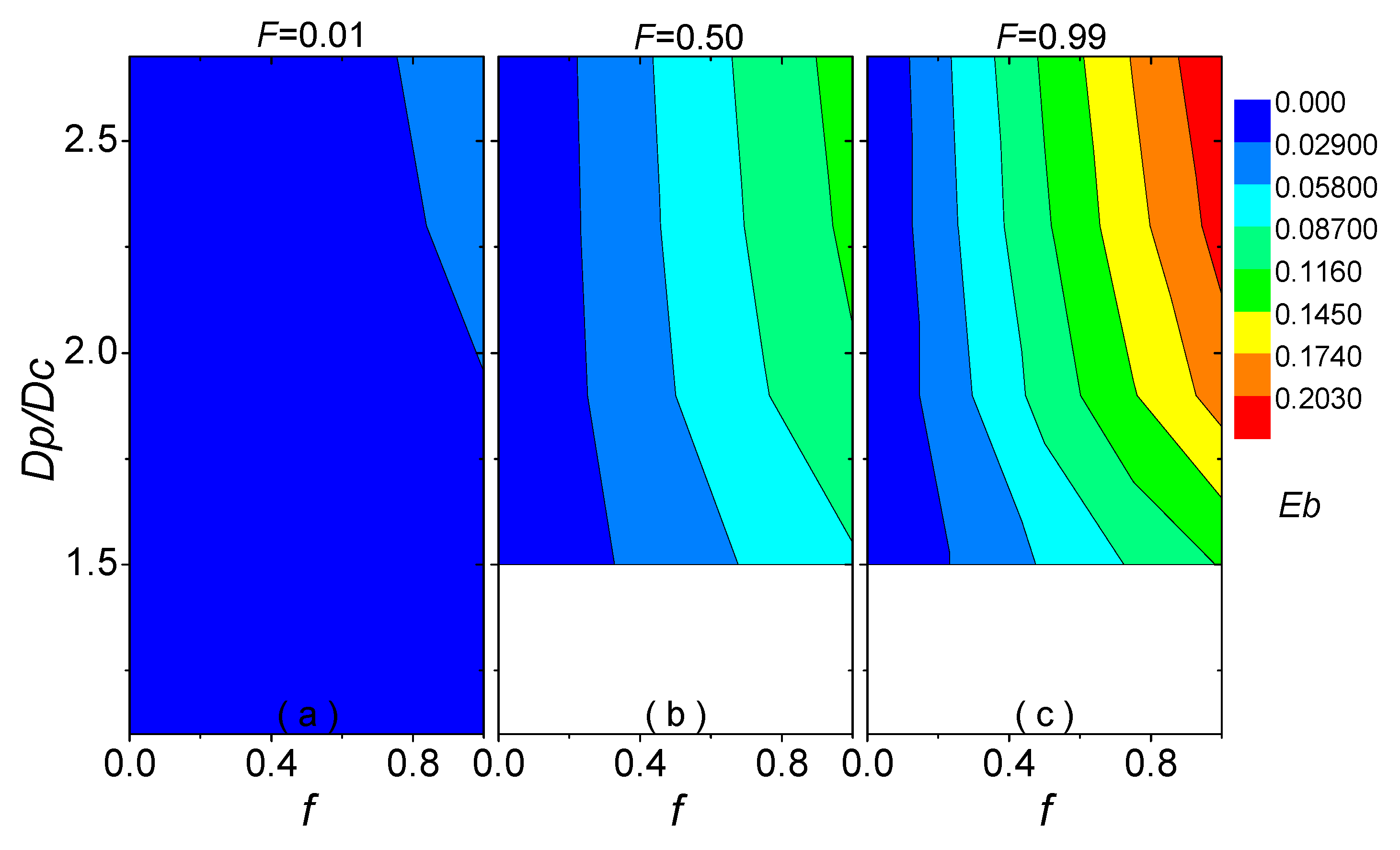
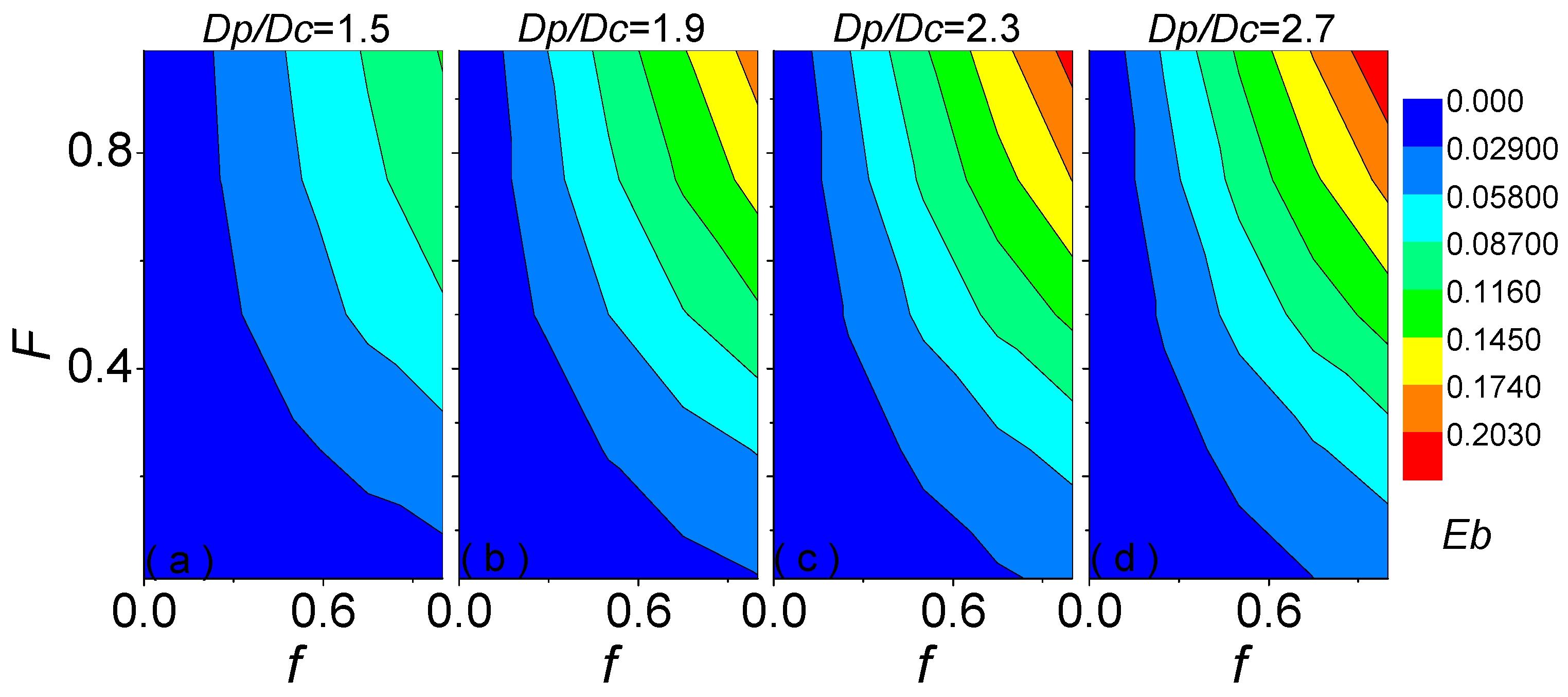

| Parameters | Used Values | |
|---|---|---|
| Df of BC | 1.8, 2.8 | |
| Dp/Dc | 1.1, 1.5, 1.9, 2.3, 2.7 | |
| F | 0.01, 0.25, 0.5, 0.75, 0.99 | |
| Size distribution | rg, μm | 0.075 (0.05–0.15) |
| σg | 1.59 | |
| Abbreviated Parameters | Meaning |
|---|---|
| Df | Fractal dimension |
| Dp/Dc | Shell/core ratio |
| F | Coated volume fraction of BC |
| f | Absorbing volume fraction of coating |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, Y.; Zhou, Y.; Wang, J.; Mao, M. Significance of Absorbing Fraction of Coating on Absorption Enhancement of Partially Coated Black Carbon Aerosols. Atmosphere 2021, 12, 1422. https://doi.org/10.3390/atmos12111422
Zhang X, Wang Y, Zhou Y, Wang J, Mao M. Significance of Absorbing Fraction of Coating on Absorption Enhancement of Partially Coated Black Carbon Aerosols. Atmosphere. 2021; 12(11):1422. https://doi.org/10.3390/atmos12111422
Chicago/Turabian StyleZhang, Xiaolin, Yuanzhi Wang, Yu Zhou, Junyao Wang, and Mao Mao. 2021. "Significance of Absorbing Fraction of Coating on Absorption Enhancement of Partially Coated Black Carbon Aerosols" Atmosphere 12, no. 11: 1422. https://doi.org/10.3390/atmos12111422
APA StyleZhang, X., Wang, Y., Zhou, Y., Wang, J., & Mao, M. (2021). Significance of Absorbing Fraction of Coating on Absorption Enhancement of Partially Coated Black Carbon Aerosols. Atmosphere, 12(11), 1422. https://doi.org/10.3390/atmos12111422








