Statistical Modeling to Predict Climate Change Effects on Watershed Scale Evapotranspiration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Landsat Imagery
2.2.2. Weather Data
2.2.3. Gridded Climate Data
2.2.4. Climate Projection Data
2.2.5. Elevation and Land Use Data
2.2.6. Crop Data
2.3. METRIC Model
2.4. Random Forest Model
2.5. Model Development
2.6. Projecting Future Evapotranspiration
3. Results
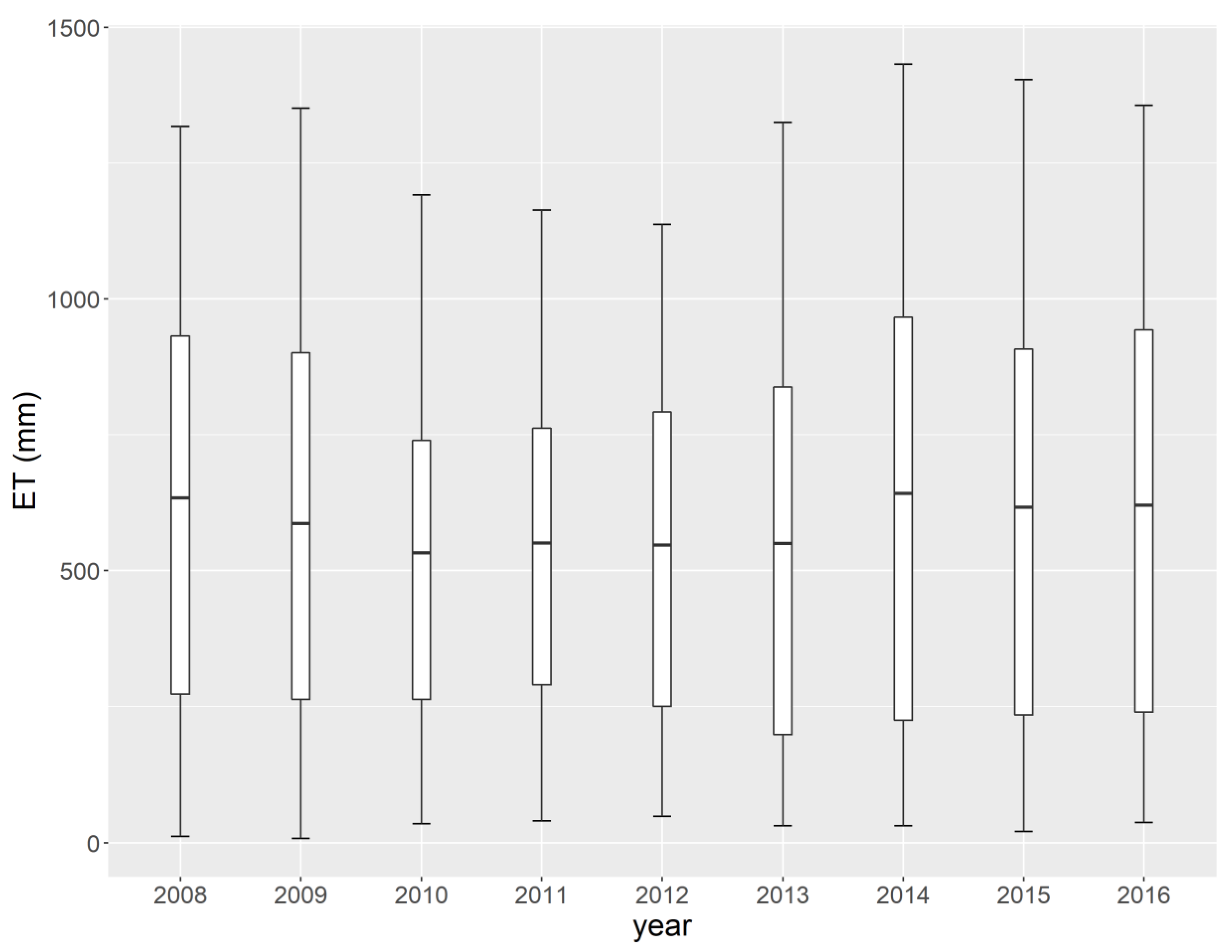
3.1. Historical ET
3.2. Important Predictors of Watershed ET
3.3. Model Evaluation
3.4. Historical and Projected Climate
3.5. Change in Consumptive Use of Water under Future Projected Climate
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDL | Cropland Data Layer |
| Specific heat of air | |
| DEM | Digital Elevation Model |
| dT | Temperature gradient |
| ET | Evapotranspiration |
| ETr | Reference evapotranspiration |
| G | Sensible heat flux conducted into the ground |
| GCM | General Circulation Model |
| GEE | Google Earth Engine |
| H | Sensible heat flux convected to the air |
| Kc | Crop coefficient |
| LE | Latent Energy |
| maxnodes | Maximum number of terminal nodes |
| METRIC | Mapping Evapotranspiration at Internalized Calibration |
| MSE | Mean Square Error |
| mtry | Number of variables used in splitting |
| NASS | National Agriculture Statistics Service |
| ntree | Number of trees for the forest |
| OOB | Out-of-bag |
| PDSI | Palmer Drought Severity Index |
| RCP | Representative Concentration Pathway |
| R2 | R-square |
| RF | Random Forest |
| Rn | Net Radiation |
| SEBAL | Surface Energy Balance Algorithm for Land |
| SEE | Standard Error of Estimate |
| SWE | Snow Water Equivalent |
| Ts | Surface temperature |
| TSEB | Two-Source Energy Balance |
| USBR | US Bureau of Reclamation |
| USDA | US Department of Agriculture |
| Albedo | |
| Density of air |
References
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global Water Resources: Vulnerability from Climate Change and Population Growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [Green Version]
- Flörke, M.; Schneider, C.; McDonald, R.I. Water competition between cities and agriculture driven by climate change and urban growth. Nat. Sustain. 2018, 1, 51–58. [Google Scholar] [CrossRef]
- Crossman, J.; Futter, M.; Oni, S.; Whitehead, P.; Jin, L.; Butterfield, D.; Baulch, H.; Dillon, P. Impacts of climate change on hydrology and water quality: Future proofing management strategies in the Lake Simcoe watershed, Canada. J. Great Lakes Res. 2012, 39, 19–32. [Google Scholar] [CrossRef]
- Rajagopalan, K.; Chinnayakanahalli, K.J.; Stockle, C.O.; Nelson, R.L.; Kruger, C.E.; Brady, M.P.; Malek, K.; Dinesh, S.T.; Barber, M.E.; Hamlet, A.F.; et al. Impacts of Near-Term Climate Change on Irrigation Demands and Crop Yields in the Columbia River Basin. Water Resour. Res. 2018, 54, 2152–2182. [Google Scholar] [CrossRef]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.-L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term Climate Change: Projections, Commitments and Irreversibility. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1029–1136. [Google Scholar] [CrossRef]
- Pease, M.; Snyder, T. Model Water Transfer Mechanisms as a Drought Preparation System. J. Contemp. Water Res. Educ. 2017, 161, 66–80. [Google Scholar] [CrossRef] [Green Version]
- Rey, D.; Holman, I.P.; Knox, J.W. Developing drought resilience in irrigated agriculture in the face of increasing water scarcity. Reg. Environ. Chang. 2017, 17, 1527–1540. [Google Scholar] [CrossRef] [Green Version]
- Yoder, J.; Adam, J.; Brady, M.; Cook, J.; Katz, S.; Johnston, S.; Malek, K.; McMillan, J.; Yang, Q. Benefit-Cost Analysis of Integrated Water Resource Management: Accounting for Interdependence in the Yakima Basin Integrated Plan. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 456–477. [Google Scholar] [CrossRef]
- Khanal, R.; Brady, M.P.; Stöckle, C.O.; Rajagopalan, K.; Yoder, J.; Barber, M.E. The Economic and Environmental Benefits of Partial Leasing of Agricultural Water Rights. Water Resour. Res. 2021, 57. [Google Scholar] [CrossRef]
- Grafton, Q.; Libecap, G.; McGlennon, S.; Landry, C.; O’Brien, B. An Integrated Assessment of Water Markets: A Cross-Country Comparison. Rev. Environ. Econ. Policy 2011, 5, 219–239. [Google Scholar] [CrossRef] [Green Version]
- Knox, J.; Kay, M.; Weatherhead, E. Water regulation, crop production, and agricultural water management—Understanding farmer perspectives on irrigation efficiency. Agric. Water Manag. 2012, 108, 3–8. [Google Scholar] [CrossRef]
- Luo, B.; Maqsood, I.; Yin, Y.Y.; Huang, G.H.; Cohen, S.J. Adaption to Climate Change through Water Trading under Uncertainty An Inexact Two-Stage Nonlinear Programming Approach. J. Environ. Inform. 2015, 2, 58–68. [Google Scholar] [CrossRef]
- Schaible, G.; Aillery, M. Water Conservation in Irrigated Agriculture: Trends and Challenges in the Face of Emerging Demands. SSRN Electron. J. 2012. [Google Scholar] [CrossRef] [Green Version]
- D’Odorico, P.; Chiarelli, D.D.; Rosa, L.; Bini, A.; Zilberman, D.; Rulli, M.C. The global value of water in agriculture. Proc. Natl. Acad. Sci. USA 2020, 117, 21985–21993. [Google Scholar] [CrossRef]
- Syed, T.H.; Webster, P.J.; Famiglietti, J.S. Assessing variability of evapotranspiration over the Ganga river basin using water balance computations. Water Resour. Res. 2014, 50, 2551–2565. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.K.; Senay, G.B.; Velpuri, N.M.; Bohms, S.; Scott, R.L.; Verdin, J.P. Actual Evapotranspiration (Water Use) Assessment of the Colorado River Basin at the Landsat Resolution Using the Operational Simplified Surface Energy Balance Model. Remote Sens. 2013, 6, 233–256. [Google Scholar] [CrossRef] [Green Version]
- Xue, B.-L.; Wang, L.; Li, X.; Yang, K.; Chen, D.; Sun, L. Evaluation of evapotranspiration estimates for two river basins on the Tibetan Plateau by a water balance method. J. Hydrol. 2013, 492, 290–297. [Google Scholar] [CrossRef]
- Torres, A.F.; Walker, W.R.; McKee, M. Forecasting daily potential evapotranspiration using machine learning and limited climatic data. Agric. Water Manag. 2011, 98, 553–562. [Google Scholar] [CrossRef]
- Hirschi, M.; Michel, D.; Lehner, I.; Seneviratne, S.I. A site-level comparison of lysimeter and eddy covariance flux measurements of evapotranspiration. Hydrol. Earth Syst. Sci. 2017, 21, 1809–1825. [Google Scholar] [CrossRef] [Green Version]
- Ding, R.; Kang, S.; Li, F.; Zhang, Y.; Tong, L.; Sun, Q. Evaluating eddy covariance method by large-scale weighing lysimeter in a maize field of northwest China. Agric. Water Manag. 2010, 98, 87–95. [Google Scholar] [CrossRef]
- Mobilia, M.; Longobardi, A. Prediction of Potential and Actual Evapotranspiration Fluxes Using Six Meteorological Data-Based Approaches for a Range of Climate and Land Cover Types. ISPRS Int. J. Geo-Inf. 2021, 10, 192. [Google Scholar] [CrossRef]
- Tian, D.; Martinez, C.J. Forecasting Reference Evapotranspiration Using Retrospective Forecast Analogs in the Southeastern United States. J. Hydrometeorol. 2012, 13, 1874–1892. [Google Scholar] [CrossRef]
- Mawdsley, J.A.; Ali, M.F. Estimating Nonpotential Evapotranspiration by Means of the Equilibrium Evaporation Concept. Water Resour. Res. 1985, 21, 383–391. [Google Scholar] [CrossRef]
- Mobilia, M.; Schmidt, M.; Longobardi, A. Modelling Actual Evapotranspiration Seasonal Variability by Meteorological Data-Based Models. Hydrology 2020, 7, 50. [Google Scholar] [CrossRef]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Malek, K.; Stöckle, C.; Chinnayakanahalli, K.; Nelson, R.; Liu, M.; Rajagopalan, K.; Barik, M.; Adam, J.C. VIC–CropSyst-v2: A regional-scale modeling platform to simulate the nexus of climate, hydrology, cropping systems, and human decisions. Geosci. Model. Dev. 2017, 10, 3059–3084. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; González-Dugo, M.P.; Cammalleri, C.; D’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, B. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Dile, Y.T.; Ayana, E.K.; Worqlul, A.W.; Xie, H.; Srinivasan, R.; Lefore, N.; You, L.; Clarke, N. Evaluating satellite-based evapotranspiration estimates for hydrological applications in data-scarce regions: A case in Ethiopia. Sci. Total. Environ. 2020, 743, 140702. [Google Scholar] [CrossRef] [PubMed]
- Dhungel, S. Predicting Watershed-scale Agricultural Water Consumption Using Statistical and Cropping System Models with Satellite-Based Remote Sensing. University of Utah. 2019. Available online: https://www.proquest.com/openview/6127c38237edeb338b37ef083e159a52/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 23 November 2021).
- Famiglietti, J.S.; Wood, E.F. Multiscale modeling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef] [Green Version]
- Solomatine, D.P.; Shrestha, D.L. A novel method to estimate model uncertainty using machine learning techniques. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2010, 29, 11–25. [Google Scholar] [CrossRef]
- Jain, S.K.; Nayak, P.C.; Sudheer, K.P. Models for estimating evapotranspiration using artificial neural networks, and their physical interpretation. Hydrol. Process. 2008, 22, 2225–2234. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating Different Machine Learning Methods for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Bodesheim, P.; Jung, M.; Gans, F.; Mahecha, M.D.; Reichstein, M. Upscaled diurnal cycles of land–atmosphere fluxes: A new global half-hourly data product. Earth Syst. Sci. Data 2018, 10, 1327–1365. [Google Scholar] [CrossRef] [Green Version]
- Bachour, R.; Walker, W.R.; Ticlavilca, A.M.; McKee, M.; Maslova, I. Estimation of Spatially Distributed Evapotranspiration Using Remote Sensing and a Relevance Vector Machine. J. Irrig. Drain. Eng. 2014, 140, 04014029. [Google Scholar] [CrossRef]
- Hindman, M. Building Better Models: Prediction, Replication, and Machine Learning in the Social Sciences. Ann. Am. Acad. Political Soc. Sci. 2015, 659, 48–62. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef] [Green Version]
- Thorp, K.R.; Thompson, A.L.; Harders, S.J.; French, A.N.; Ward, R.W. High-Throughput Phenotyping of Crop Water Use Efficiency via Multispectral Drone Imagery and a Daily Soil Water Balance Model. Remote Sens. 2018, 10, 1682. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R. A Landsat-based energy balance and evapotranspiration model in Western US water rights regulation and planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
- Liaqat, U.W.; Choi, M. Surface energy fluxes in the Northeast Asia ecosystem: SEBS and METRIC models using Landsat satellite images. Agric. For. Meteorol. 2015, 214-215, 60–79. [Google Scholar] [CrossRef]
- Hillman, B.; Douglas, E.M.; Terkla, D. An analysis of the allocation of Yakima River water in terms of sustainability and economic efficiency. J. Environ. Manag. 2012, 103, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Dhungel, S.; Barber, M.E. Estimating Calibration Variability in Evapotranspiration Derived from a Satellite-Based Energy Balance Model. Remote Sens. 2018, 10, 1695. [Google Scholar] [CrossRef] [Green Version]
- PRISM Climate Group, Oregon State University. Available online: http://prism.oregonstate.edu (accessed on 23 November 2021).
- Abatzoglou, J.T.; Brown, T.J. A comparison of statistical downscaling methods suited for wildfire applications. Int. J. Clim. 2011, 32, 772–780. [Google Scholar] [CrossRef]
- Herger, N.; Abramowitz, G.; Knutti, R.; Angélil, O.; Lehmann, K.; Sanderson, B.M. Selecting a climate model subset to optimise key ensemble properties. Earth Syst. Dyn. 2018, 9, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Meehl, G.A.; Hu, G.A.M.A.; Santer, B.D.; Xie, S.-P. Contribution of the Interdecadal Pacific Oscillation to twentieth-century global surface temperature trends. Nat. Clim. Chang. 2016, 6, 1005–1008. [Google Scholar] [CrossRef]
- Knutti, R. The end of model democracy? Clim. Chang. 2010, 102, 395–404. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Attorre, F.; Alfò, M.; de Sanctis, M.; Francesconi, F.; Valenti, R.; Vitale, M.; Bruno, F. Evaluating the effects of climate change on tree species abundance and distribution in the Italian peninsula. Appl. Veg. Sci. 2011, 14, 242–255. [Google Scholar] [CrossRef]
- Evans, J.S.; Murphy, M.A.; Holden, Z.A.; Cushman, S.A. Modeling Species Distribution and Change Using Random Forest. In Predictive Species and Habitat Modeling in Landscape Ecology: Concepts and Applications; Drew, C.A., Wiersma, Y.F., Huettmann, F., Eds.; Springer: New York, NY, USA, 2011; pp. 139–159. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Nitze, I.; Barrett, B.; Cawkwell, F. Temporal optimisation of image acquisition for land cover classification with Random Forest and MODIS time-series. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. Forest 2002, 23, 18–22. [Google Scholar]
- Watts, J.; Lawrence, R. Merging random forest classification with an object-oriented approach for analysis of agricultural lands. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 579–582. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing 2020; Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Abatzoglou, J.; Rupp, D.E.; Mote, P.W. Seasonal Climate Variability and Change in the Pacific Northwest of the United States. J. Clim. 2014, 27, 2125–2142. [Google Scholar] [CrossRef]
- Lane, B.A.; Rosenberg, D.E. Promoting In-Stream Flows in the Changing Western US. J. Water Resour. Plan. Manag. 2020, 146, 02519003. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]








| Site Descriptors | HRHW | LEGW |
|---|---|---|
| Latitude (N) | 46.38472 | 46.20527 |
| Longitude (W) | 120.57444 | 118.93611 |
| Elevation (m) | 259.1 | 176.784 |
| Data availability period | 1987–current | 1986–current |
| Source of data | USBR Agrimet | USBR Agrimet |
| S.N. | Variable Name | Variable Description | Variable Acronym | Source |
|---|---|---|---|---|
| 1 | Apples area | Crop area of apple | Apples_ac | USDA, CDL |
| 2 | Alfalfa area | Crop area of alfalfa | Alfalfa_ac | USDA, CDL |
| 3 | Corn area | Crop area of corn | Corn_ac | USDA, CDL |
| 4 | Grapes area | Crop area of grapes | Grapes_ac | USDA, CDL |
| 5 | Hops area | Crop area of hops | Hops_ac | USDA, CDL |
| 6 | Aspect | Aspect | Asp | USGS, NED |
| 7 | Elevation | Elevation | Elev | USGS, NED |
| 8 | Slope | Slope | Slp | USGS, NED |
| 9 | Spring precipitation | Average precipitation of March, April and May | pptMAM | PRISM |
| 10 | Summer precipitation | Average precipitation of June, July and August | pptJJA | PRISM |
| 11 | Fall precipitation | Average precipitation of September, October and November | pptSON | PRISM |
| 12 | Winter precipitation | Average precipitation of December, January and February | pptDJF | PRISM |
| 13 | Precipitation standard deviation | Standard deviation of annual precipitation | ppt_sd | PRISM |
| 14 | Sum precipitation | Annual precipitation | sumppt | PRISM |
| 15 | Spring maximum temperature | Average maximum temperature of March, April and May | tmaxMAM | PRISM |
| 16 | Summer maximum temperature | Average maximum temperature of June, July and August | tmaxJJA | PRISM |
| 17 | Fall maximum temperature | Average maximum temperature of September, October and November | tmaxSON | PRISM |
| 18 | Winter maximum temperature | Average maximum temperature of December, January and February | tmaxDJF | PRISM |
| 19 | Maximum temperature standard deviation | Standard deviation of annual maximum temperature | tmax_sd | PRISM |
| 20 | Spring minimum temperature | Average minimum temperature of March, April and May | tminMAM | PRISM |
| 21 | Summer minimum temperature | Average minimum temperature of June, July and August | tminJJA | PRISM |
| 22 | Fall minimum temperature | Average minimum temperature of September, October and November | tminSON | PRISM |
| 23 | Winter minimum temperature | Average minimum temperature of December, January and February | tminDJF | PRISM |
| 24 | Minimum temperature standard deviation | Standard deviation of annual minimum temperature | tmin_sd | PRISM |
| 25 | Spring maximum vapor pressure deficit | Average maximum vapor pressure deficit of March, April and May | vpdmaxMAM | PRISM |
| 26 | Summer maximum vapor pressure deficit | Average maximum vapor pressure deficit of June, July and August | vpdmaxJJA | PRISM |
| 27 | Fall maximum vapor pressure deficit | Average maximum vapor pressure deficit of September, October and November | vpdmaxSON | PRISM |
| 28 | Winter maximum vapor pressure deficit | Average maximum vapor pressure deficit of December, January and February | vpdmaxDJF | PRISM |
| 29 | Spring minimum vapor pressure deficit | Average minimum vapor pressure deficit of March, April and May | vpdminMAM | PRISM |
| 30 | Summer minimum vapor pressure deficit | Average minimum vapor pressure deficit of June, July and August | vpdminJJA | PRISM |
| 31 | Fall minimum vapor pressure deficit | Average minimum vapor pressure deficit of September, October and November | vpdminSON | PRISM |
| 32 | Winter minimum vapor pressure deficit | Average minimum vapor pressure deficit of December, January and February | vpdminDJF | PRISM |
| 33 | Sum of monthly temperature | Sum of total monthly temperature | dailyTsum | PRISM |
| 34 | Evapotranspiration | Total growing seasonal evapotranspiration | ET | METRIC |
| S.N. | Variable Name | (2008–2014) | 2015 | 2016 |
|---|---|---|---|---|
| Mean, Sd | Mean, Sd | Mean, Sd | ||
| 1 | Apples area | 306.65, 334.60 | 306.06, 382.35 | 335.88, 403.90 |
| 2 | Alfalfa area | 114.72, 151.80 | 148.11, 219.25 | 156.00, 212.04 |
| 3 | Corn area | 182.28, 286.31 | 193.29, 327.81 | 192.94, 307.522 |
| 4 | Grapes area | 272.438, 391.80 | 256.01, 421.42 | 263.92, 441.73 |
| 5 | Hops area | 85.56, 179.02 | 138.86, 275.71 | 172.88, 320.87 |
| 6 | Aspect | 175.10, 101.60 | 175.10, 101.60 | 175.10, 101.60 |
| 7 | Elevation | 342.57, 154.12 | 342.57, 154.12 | 342.57, 154.12 |
| 8 | Slope | 6.51, 7.58 | 6.51, 7.58 | 6.51, 7.58 |
| 9 | Spring precipitation | 18.78, 2.19 | 19.24, 2.6 | 18.78, 4.61 |
| 10 | Summer precipitation | 9.33, 1.51 | 0.21, 0.44 | 4.89, 1.39 |
| 11 | Fall precipitation | 15.96, 1.85 | 11.21, 2.08 | 32.49, 3.40 |
| 12 | Winter precipitation | 23.13, 4.30 | 23.20, 5.57 | 44.93, 9.62 |
| 13 | Precipitation standard deviation | 12.84, 1.45 | 21.29, 4.22 | 21.38, 3.17 |
| 14 | Sum precipitation | 171.25, 18.88 | 128.54, 16.67 | 227.40, 27.57 |
| 15 | Spring maximum temperature | 16.93, 1.09 | 19.62, 1.13 | 19.63, 1.06 |
| 16 | Summer maximum temperature | 29.45, 0.97 | 31.96, 0.93 | 29.44, 0.94 |
| 17 | Fall maximum temperature | 17.66, 0.86 | 18.19, 0.86 | 17.74, 0.87 |
| 18 | Winter maximum temperature | 4.76, 0.67 | 6.78, 0.63 | 5.99, 0.76 |
| 19 | Maximum temperature standard deviation | 9.81, 0.16 | 9.97, 0.17 | 9.54, 0.17 |
| 20 | Spring minimum temperature | 2.79, 0.85 | 4.58, 0.74 | 5.17, 0.77 |
| 21 | Summer minimum temperature | 12.25, 1.06 | 14.11, 1.05 | 11.96, 1.09 |
| 22 | Fall minimum temperature | 4.00, 0.87 | 4.45, 0.96 | 5.68, 0.94 |
| 23 | Winter minimum temperature | −3.95, 0.59 | −0.78, 0.58 | −1.66, 0.9 |
| 24 | Minimum temperature standard deviation | 6.47, 0.26 | 6.12, 0.26 | 5.92, 0.19 |
| 25 | Spring maximum vapor pressure deficit | 1.57, 0.13 | 1.64, 0.40 | 1.50, 0.47 |
| 26 | Summer maximum vapor pressure deficit | 3.58, 0.60 | 5.11, 1.88 | 3.59, 1.42 |
| 27 | Fall maximum vapor pressure deficit | 1.43, 0.39 | 1.33, 0.54 | 0.96, 0.49 |
| 28 | Winter maximum vapor pressure deficit | 3.58, 0.28 | 3.77, 0.34 | 3.42, 0.40 |
| 29 | Spring minimum vapor pressure deficit | 1.57, 0.13 | 1.64, 0.40 | 1.50, 0.47 |
| 30 | Summer minimum vapor pressure deficit | 3.58, 0.60 | 5.11, 1.88 | 3.59, 1.42 |
| 31 | Fall minimum vapor pressure deficit | 1.43, 0.39 | 1.33, 0.54 | 0.96, 0.49 |
| 32 | Winter minimum vapor pressure deficit | 0.41, 0.06 | 0.40, 0.14 | 0.22, 0.07 |
| 33 | Sum of monthly temperature | 3363.00, 179.02 | 3729.19, 151.30 | 3547.07, 162.77 |
| 34 | Evapotranspiration | 572.32, 337.07 | 609.24, 390.13 | 626.23, 391.09 |
| Variable | Season | Observed, 2008-14 | RCP4.5, 2008-14 | RCP8.5, 2008-14 | RCP4.5, 20051-60 | RCP8.5, 20051-60 |
|---|---|---|---|---|---|---|
| Maximum Temperature | Winter | 4.76 | 6.49 | 6.26 | 7.49 | 7.84 |
| Spring | 16.93 | 19.79 | 19.65 | 20.42 | 20.76 | |
| Summer | 29.45 | 30.65 | 30.84 | 32.88 | 33.93 | |
| Fall | 17.66 | 17.13 | 17.21 | 19.73 | 20.91 | |
| Minimum Temperature | Winter | −3.95 | −2.06 | −2.18 | −0.70 | −0.26 |
| Spring | 2.79 | 5.31 | 5.24 | 6.02 | 6.38 | |
| Summer | 12.25 | 13.26 | 13.44 | 15.10 | 15.98 | |
| Fall | 4.00 | 3.93 | 3.93 | 5.99 | 6.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanal, R.; Dhungel, S.; Brewer, S.C.; Barber, M.E. Statistical Modeling to Predict Climate Change Effects on Watershed Scale Evapotranspiration. Atmosphere 2021, 12, 1565. https://doi.org/10.3390/atmos12121565
Khanal R, Dhungel S, Brewer SC, Barber ME. Statistical Modeling to Predict Climate Change Effects on Watershed Scale Evapotranspiration. Atmosphere. 2021; 12(12):1565. https://doi.org/10.3390/atmos12121565
Chicago/Turabian StyleKhanal, Rajendra, Sulochan Dhungel, Simon C. Brewer, and Michael E. Barber. 2021. "Statistical Modeling to Predict Climate Change Effects on Watershed Scale Evapotranspiration" Atmosphere 12, no. 12: 1565. https://doi.org/10.3390/atmos12121565
APA StyleKhanal, R., Dhungel, S., Brewer, S. C., & Barber, M. E. (2021). Statistical Modeling to Predict Climate Change Effects on Watershed Scale Evapotranspiration. Atmosphere, 12(12), 1565. https://doi.org/10.3390/atmos12121565








