1. Introduction
Understanding precipitation amounts and patterns is essential for sustainable water management and monitoring the hydrological cycle [
1]. In complex mountainous regions characterized by high spatiotemporal variability, coarse networks of operational precipitation gauge stations are often lacking. The spatiotemporal variability, combined with lack of gauge data, makes the time series and area-averaged rainfall analysis more complicated in these regions [
2]. This also applies to the complex topography of the Andes in Ecuador.
Early satellite-based rainfall retrieval efforts estimated rainfall from geostationary infrared (IR) data, using the indirect relationship between precipitation rate and the temperature of cloud on top [
3]. Hence, the algorithms and the product accuracy were limited to the top of the cloud’s characteristics. Unlike IR, microwave (MW) sensors measure thermal radiance from actual precipitation particles in the clouds; consequently, MW retrieval generally provides superior precipitation information [
4].
A recent result of the continuous technological improvement of low-Earth-orbiting passive MW satellites and spaceborne radars in the MW band is the Global Precipitation Measurement (GPM) mission [
5]. GPM was launched in 2014 as post Tropical Rainfall Measuring Mission (TRMM) [
6]. Compared with TRMM, the GPM improved sensitivity to light precipitation and distribution of rain and snow. These improvements have achieved by a two-frequencies precipitation radar (Ku band (13.6 GHz) and Ka-band (35.5 GHz)) as well as the GPM multi-channel microwave imager (GMI) that accommodates higher spectral resolution at frequencies of 10.65, 18.7, 23.8, 26.5, 89, 165.5, and 183.3 GHz [
5,
7,
8].
However, several studies showed that machine learning could improved the regionally calibrated retrievals using simply passive IR data from geostationary orbit (GEO) [
3,
8,
9,
10,
11,
12,
13]. Compared to the passive MW and radar sensors, the GEO systems provide the high temporal (10–30 min) and spatial (2–4 km
2) resolution. It is essential to capture the short-term characteristics of rainfall systems in the retrieval [
8]
A few studies have investigated the performance of satellite-based rainfall products over Ecuadorian areas. The Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN) [
14] shows low agreement with rain gauge in daily resolution [
2] in rain area detection. Manz et al. [
15] investigated the performance of the integrated multi-satellite retrievals for GPM (IMERG) [
5] and TRMM multi-satellite precipitation analysis (TMPA) [
6] against gauge data with different temporal resolutions (hourly, 3 h, and daily). In their study, IMERG showed better agreement than TMPA, especially on the high elevation of Andes. Erazo et al. [
16] reported that at high elevations in the Andes, TRMM 3B43 Version 7 retrievals showed a higher correlation (R
2 = 0.82) on monthly compared with interpolated gauge data at a spatial resolution of 27.75 km
2. The result of the validation of the regionally developed algorithm in Ecuador, the random forest-based rainfall (RF-based rainfall) of Turini et al. [
3] with an 11 km
2 resolution, obtained a median Heike skill score (HSS) around 0.35 for daily gauge stations, meanwhile the lower performance of the IR-only from the IMERG (IR-only IMERG) showed by HSS = 0.2. In their method, they used the Random forest algorithm to retrieve rainfall. In this text, the RF-based rainfall stands for the rainfall retrieval from random forest algorithm [
3]. The RF-based rainfall retrieval performed in estimating the rainfall rate with correlation coefficient (r) values 0.34 [
3].
To improve satellite-based products’ overall performance, understanding the sources of error on the highest possible temporal resolution is crucial [
6,
17]. Given the high spatiotemporal variability of rainfall in Ecuador, spatiotemporally high-resolution validation sources for rainfall are lacking. Therefore, as stated before, only a couple of studies have investigated the performance of satellite-based rainfall products at higher spatiotemporal resolution [
15,
18].
Different studies have found that, due to the variability of weather and climate in complex terrain, the satellite retrievals are posed to challenges both in IR and MW products [
3,
8,
12,
13,
19]. Dinku et al. [
19] evaluated the impact of topography on IR-based Tropical Applications of Meteorology using Satellite and ground-based observation (TAMSAT) [
20] in East Africa for 1998–2012, comprising five different countries: Uganda, Kenya, Tanzania, Rwanda, and Burundi. In the study, the elevation varied between 1500 and 4500 m [
19]. TAMSAT showed an underestimation. Dinku et al. [
19] argued that the underestimation corresponded mainly to convective and orographic rainfall during the rainy season (March, April, and May), mostly in the windward exposition.
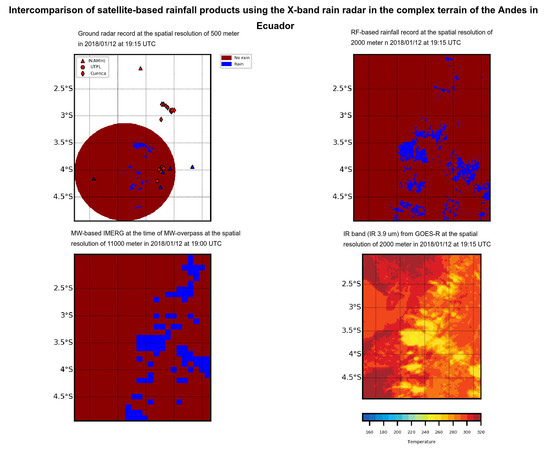
In this work, we aimed to validate different satellite-based rainfall products to identify and understand sources of errors in the complex elevation of the Andes in Ecuador on a sub-daily time scale. Our aim was not just to compare satellite-based rainfall products with ground measurements but also to identify the sources of the differences between the satellite-based rainfall products and ground measurements. Therefore, in this study, we evaluated the performance of MW-based IMERG in comparison with RF-based rainfall and IR-only IMERG against high-spatiotemporal-resolution data from ground based radar network and high temporal resolution of meteorological stations to characterize the impact of climatic and topographic conditions on satellite-based rainfall products at the time of MW overpass. We also assessed the performance of regionally trained RF-based rainfall in Ecuador on the subdaily time scale (30 min) and high spatial resolution (2 km
2) with the aim of finding the source of possible errors for further development. Following a description of the climatology of the study area, the satellite-based rainfall products, ground based radar data and meteorological stations are described in
Section 2.1.
Section 2.2 introduces the evaluation methodology with a focus on rain area detection and rain estimation. The results are presented in
Section 3 and discussed in
Section 4. Finally, the important findings are summarized in
Section 5.
4. Discussion
In
Section 3.1, satellite-based rainfall products at the time of MW overpasses from IMERG were assessed using radar data. We evaluated the satellite-based products in grid cells at the time of MW overpasses and a spatial resolution of 11 km
2.
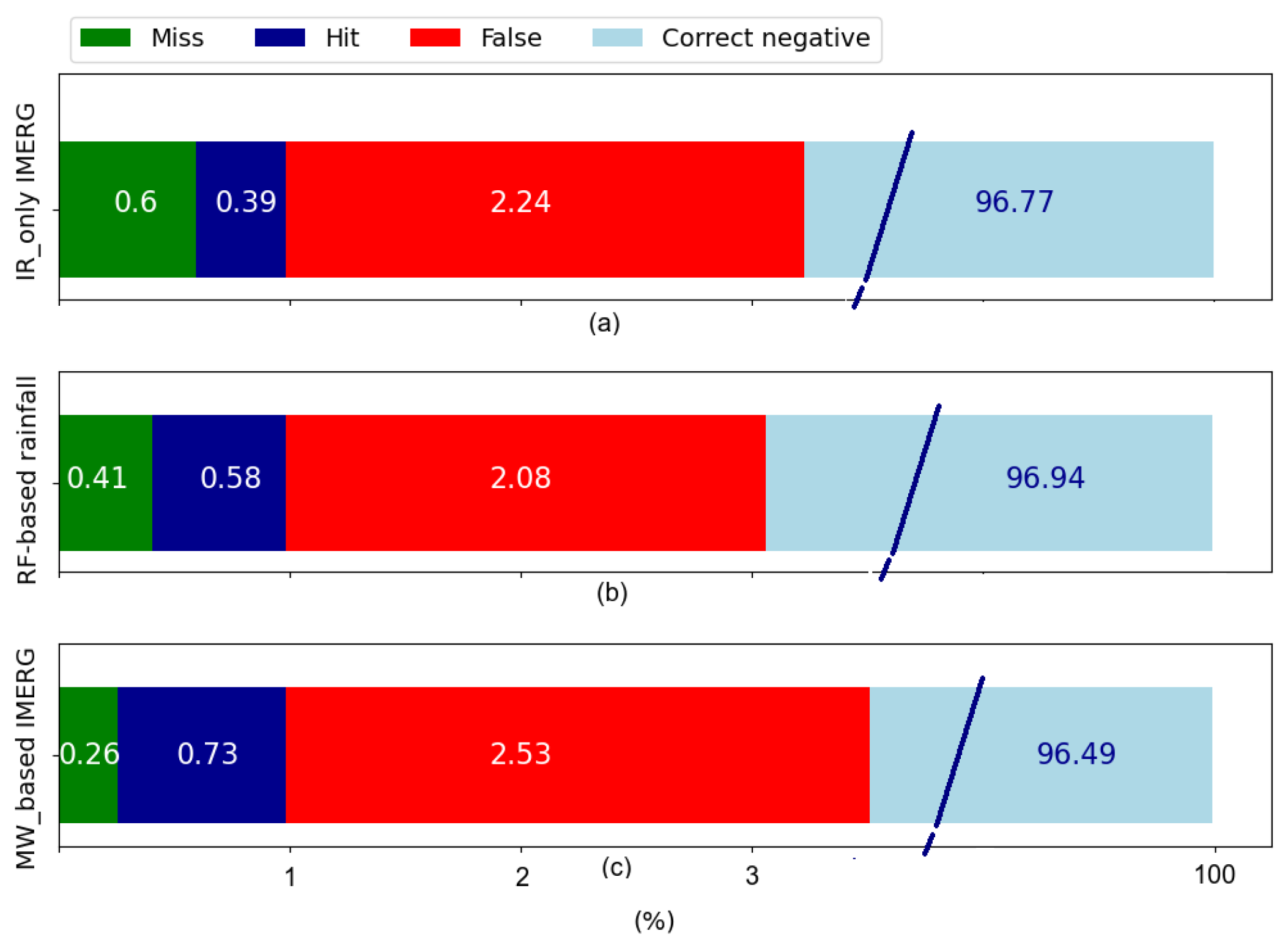
The verification scores for rain area delineation revealed that the MW-based IMERG has superior performance in estimating rain area (POD = 0.74, HSS = 0.33). RF-based rainfall, which is trained based on MW-based IMERG, has slightly lower performance compared to MW-based IMERG data (HSS = 0.31). IR-only IMERG performed the worst in Ecuador. This is in line with the findings of Kolbe et al. [
12], Kolbe et al. [
13], Turini et al. [
8], and Turini et al. [
3]. It shows that multispectral GEO data has more potential than using one IR channel only for rainfall retrieval.
The frequent false alarm is one of the most noticeable issues identified in the present study. This agrees well with the result of IMERG-V06 validation in the west African forest zone [
17] and confirms the previous investigation of IMERG-v05 by Manz et al. [
15] in the Andes region. In our study, around 60% of the false alarms were related to rain rates less than 1 mm/h for all products (
Figure 9), which was found to be the dominant rainfall intensity in this region of the world [
39]. We also note that the radar potentially underestimated rainfall [
40,
41,
42,
43]. This was also reported elsewhere for the radars in Ecuador [
23]. In MW-based IMERG and RF-based rainfall, with increasing the rainfall rate, the FAR decreases while POD does not change (
Figure 8).
The results of the topography-based evaluation indicated the high detection accuracy of MW-based IMERG and RF-based rainfall in different topographical regions. Moreover, the highest errors occurred for coastal areas and foothills (0–1500 m.a.s.l) and high mountains regions (>3000 m.a.s.l) compared to the other topographical regions. All the products experienced challenges in estimating rainfall at high elevation in the Andes (
Figure 10). In Ecuador, high-elevation areas and volcanoes have two issues for rainfall retrieval algorithms: (i) They are regularly covered by ice, which generates errors in MW-based IMERG [
29,
44]; (ii) the drizzle on the high elevation is hard to be captured by MW and IR channels. This conclusion is in agreement with the findings of study conducted by Prakash et al. [
45], who assessed the performance of IMERG products in monsoon-dominated regions in India. Their results showed that IMERG was affected by the orographic process, which leads to higher errors in mountainous areas. Another study by Kim et al. [
46] revealed the disadvantage of IMERG products over mountainous and coastal regions. Similar results were obtained by Turini et al. [
3] in Ecuador for RF-based rainfall. They argued that because of local topography, the subscale convective rainfall systems probably could not be captured by GOES data and IMERG [
3,
37]. Altogether, at the elevation of 0–750 m.a.s.l, RF-based rainfall showed the best performance of all products (
Figure 7 and
Figure 10).
Concerning rainfall rate validation, the overall variability in all the products is high, suggesting rainfall rate estimation and/or timing issues. Different studies discuss a possible time lag between the satellite-based rainfall products and the ground-based rainfall measurements as a source of degrading validation results [
17,
38,
47,
48,
49]. The time lag is defined as the time shift when satellite observation and surface precipitation rate from ground data obtain to their optimum correlation. This time lag might be due to the time it takes for the precipitation detected by the satellite to reach the ground [
17,
47]. You et al. [
38] related the precipitation time from GMI to the environmental temperature and storm top height. They found that when the storm is taller, the lag time increases to obtain the optimum correlation between the GMI and ground truth data. This is due to the long way of raindrops from the storm top to the gauge.
Ignoring the corresponding time steps in the Q–Q plots shows that the MW-based IMERG and RF-based (
Figure 9b,h) rainfall rates are distributed up to 5 mm/h evenly. The positive values in MW-based IMERG at higher rainfall rates are more evident. Conversely, the rainfall rate distribution between the radar and IR-only IMERG shows more discrepancies (
Figure 9e). The validation of satellite-based rainfall products against the gauges show lower consistency (
Table 5). However, in the term of rain area delineation (
Table 4), the RF-based rainfall product shows better performance than IMERG-IR-only, which confirms the potential to use multispectral GEO data.
The validation of satellite-based rainfall show a slight overestimation of rainfall totals for all products (
Table 5).
It should be noted that the evaluation of satellite-based products against only a few gauges has high uncertainties [
8,
36], especially in areas with high small-scale precipitation variability in mainly convective environments, like the Ecuadorian Andes, where point based observations at weather stations cannot properly represent the spatial rainfall distribution.
The validation of RF-based rainfall retrieval at high spatiotemporal resolution for all the available rain events is shown in
Table 6. The RF-based rainfall is calibrated locally for Ecuador. The importance of local calibration, which involves determining relevant climatic parameters, including the selection of appropriate temperature thresholds for clouds and a local correlation systematic biases that may not have been adjusted in global products, have been mentioned in different studies [
50,
51,
52].
RF-based rainfall for 2 km
2 and 30 min shows a lower HSS compared to the RF-based rainfall for 11 km
2 at the time of MW overpass. This was expected because the errors at higher temporal resolutions may cancel each other out following the aggregation to a lower temporal resolution [
50]. However, in terms of rainfall estimation, RF-based rainfall performs better at higher spatial resolution (
Table 3). This result needs to be interpreted with caution, since the rainfall events at the time of MW overpasses differ from the validation of the RF-based rainfall at 2 km
2 and 30 min.
An event-based analysis was then used to investigate the source of error in the RF-based rainfall product. Shifting the RF-based rainfall backward by one to two time steps (i.e., 30 min) resulted in the more accurate detection of rainfall around 10% (
Figure 11b) by lowering the misses. RF-based rainfall rates are lower than their counterparts in radar, as shown in
Figure 12d. We speculate that this lag appears due to the lag time between the time of MW overpass and the GOES-16 scan time. The RF-based rainfall algorithm relies on the precipitation information from MW-based IMERG and IR data from GOES-16.
However, RF-based rainfall also has a high FAR. The event-based spatial analysis reduced the FAR by 8.5% (
Figure 11e), but the challenge remains the same. High FAR values occur for all the different types of rain with different intensities (
Figure 12c,d). The reason for the high FAR in RF-based rainfall might be (i) the high amount of FAR from MW-based IMERG in Ecuador (
Table 2), which is used as a reference for calibrating of RF-based rainfall; (ii) A bias in IR retrievals that classify cold cloud pixels as rainy. They experience difficulties in defining the correct rainfall cloud and profile, thus producing error in statistical-physical rainfall algorithms.
By increasing the temporal resolution of the RF-based rainfall product, the performance of the product increased. However, the FAR (60% in daily resolution) remains a main challenge.