Experimental Determination of Pedestrian Thermal Comfort on Water-Retaining Pavement for UHI Adaptation Strategy
Abstract
:1. Introduction
2. Experiments
2.1. Material
2.2. Methods
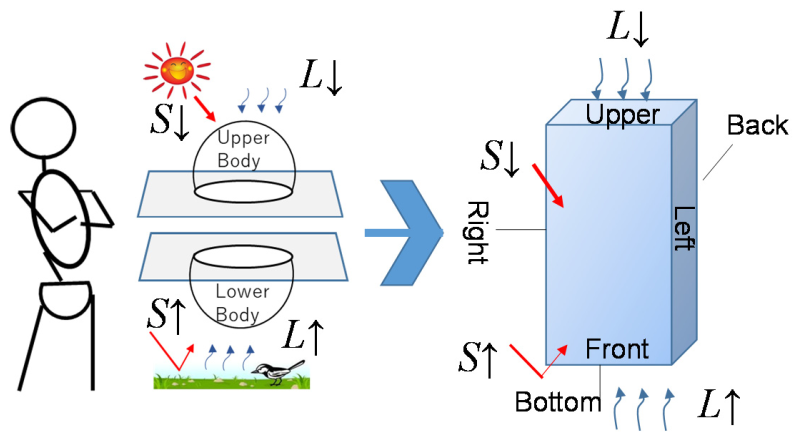
2.2.1. Experimental Setup
2.2.2. Climatic Observation
2.2.3. Pavement Conditions
2.2.4. Human Thermal States on Pavements
2.2.5. Human Perceptions
2.2.6. Data Analysis
3. Results
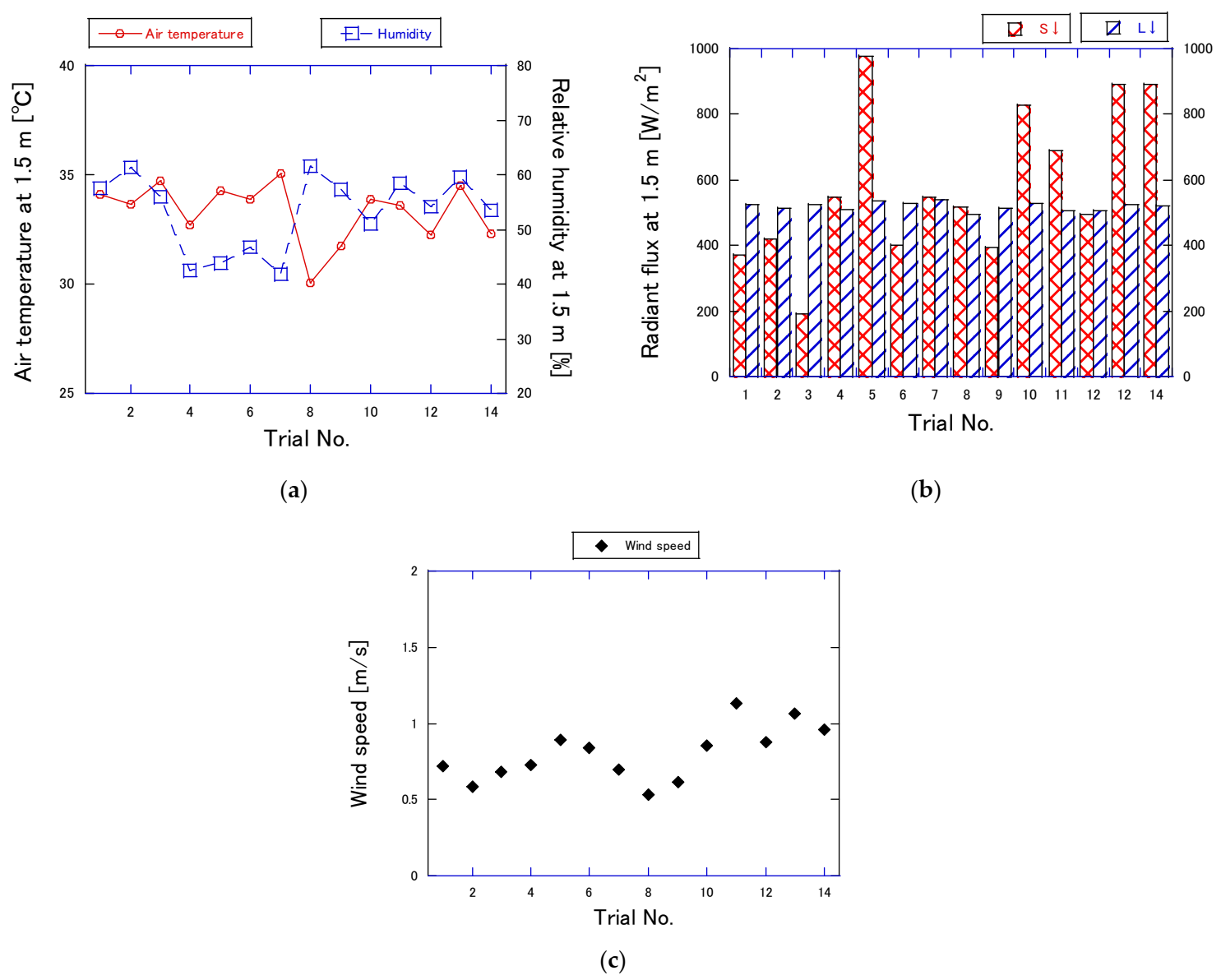
3.1. Experimental Conditions
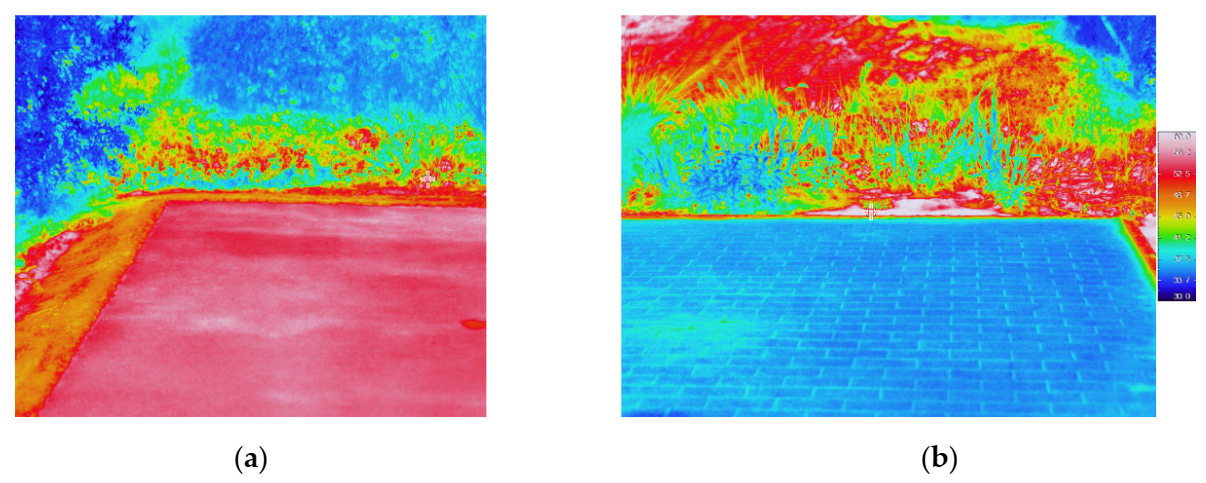
3.2. Pavement Conditions
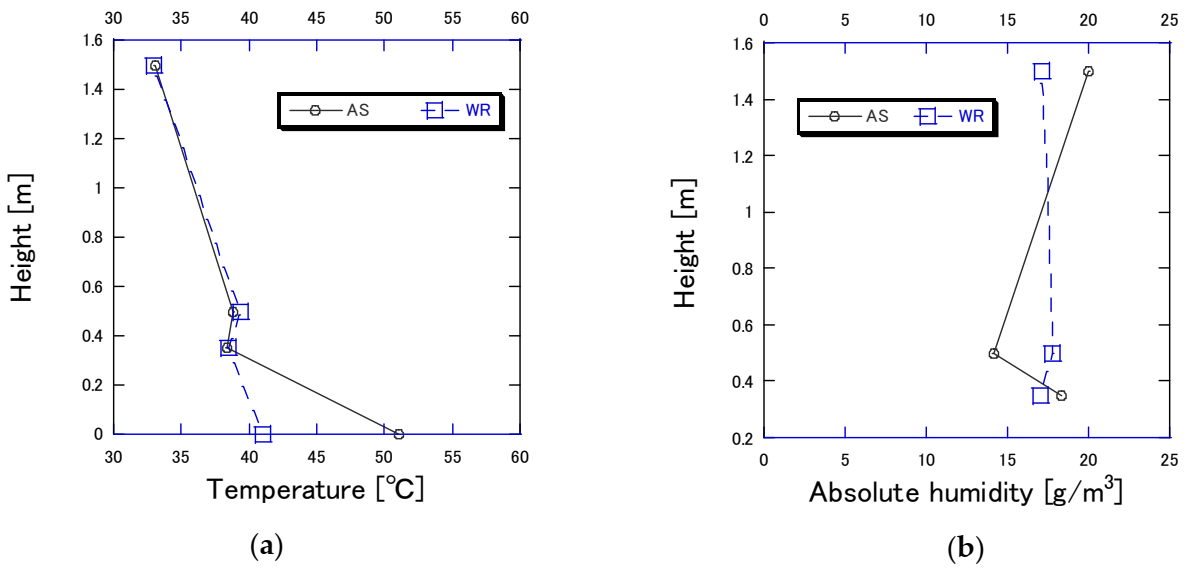
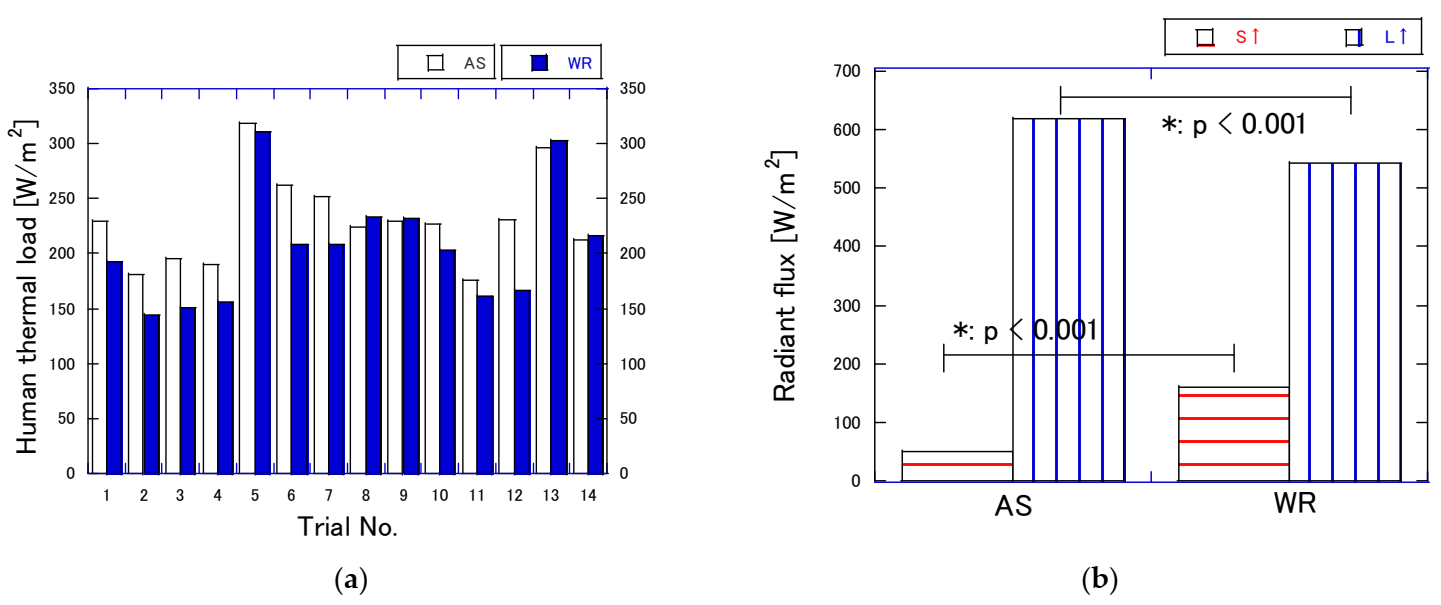
3.3. Human Thermal Condition at a Height of 1.5 m
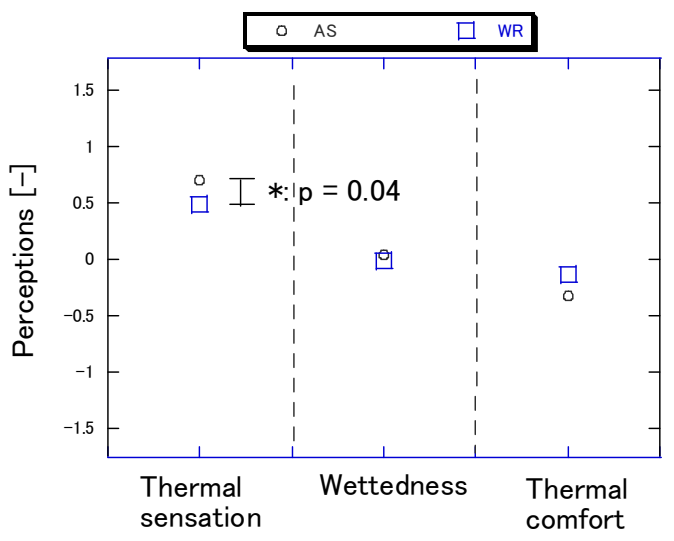
3.4. Human Perceptions
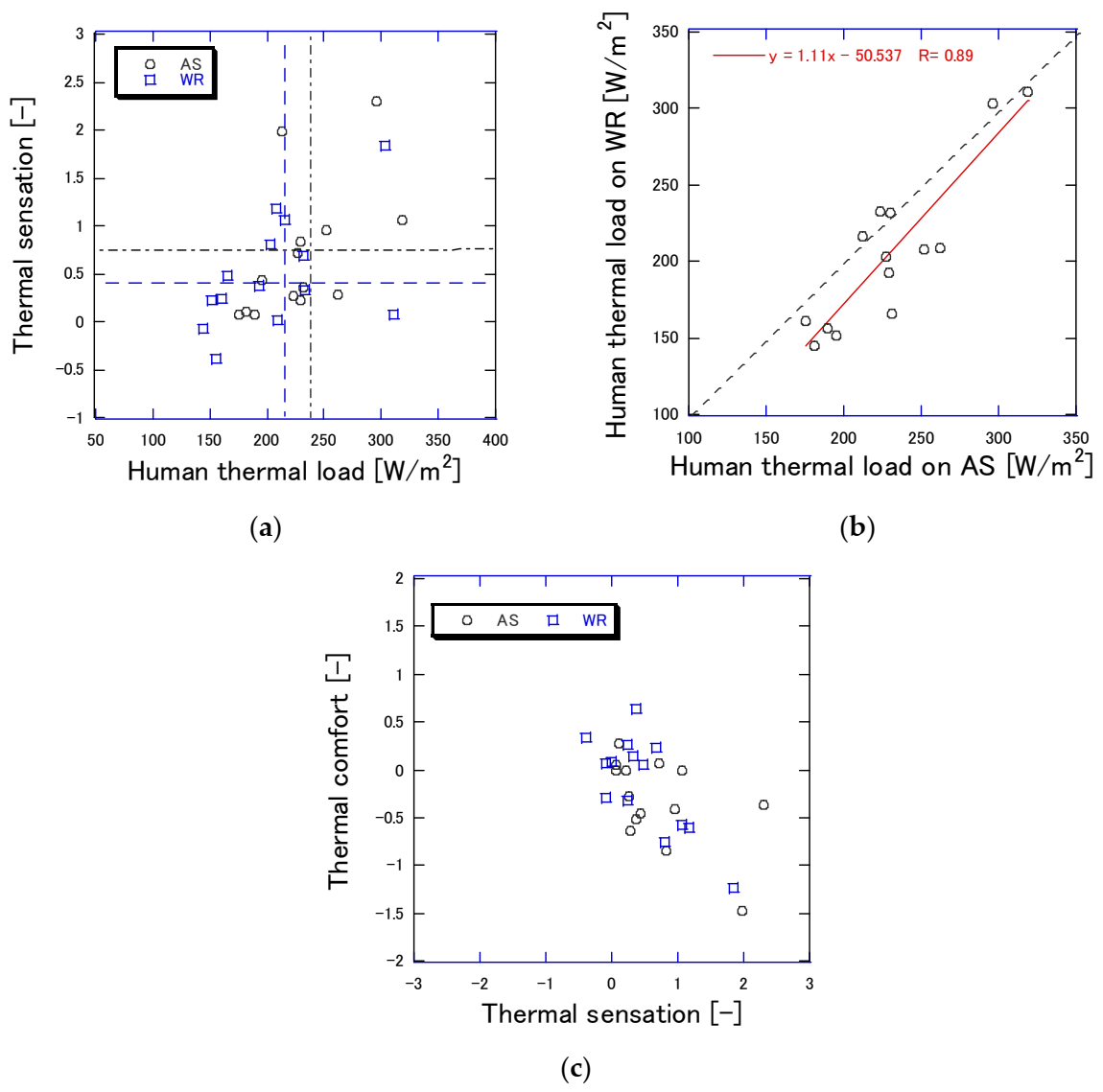
4. Discussion
4.1. Effects of Properties of WR on Human Thermal Environment
4.2. Human Thermal States and Perceptions
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akbari, H.; Konopacki, S.; Pomerantz, M. Cooling energy savings potential of reflective roofs for residential and commercial buildings in the United States. Energy 1999, 24, 391–407. [Google Scholar] [CrossRef]
- Qin, Y. A review on the development of cool pavements to mitigate urban heat island effect. Renew. Sustain. Energy Rev. 2015, 52, 445–459. [Google Scholar] [CrossRef]
- Bretz, S.; Akbari, H.; Rosenfeld, A. Practical issues for using solar-reflective materials to mitigate urban heat islands. Atmos. Environ. 1998, 32, 95–101. [Google Scholar] [CrossRef] [Green Version]
- Doulos, L.; Santamouris, M.; Livada, I. Passive cooling of outdoor urban spaces. The role of materials. Sol. Energy 2004, 77, 231–249. [Google Scholar] [CrossRef]
- Chen, J.; Wang, H.; Zhu, H. Analytical approach for evaluating temperature field of thermal modified asphalt pavement and urban heat island effect. Appl. Therm. Eng. 2017, 113, 739–748. [Google Scholar] [CrossRef]
- Takebayashi, H.; Moriyama, M. Study on surface heat budget of various pavements for urban heat island mitigation. Adv. Mater. Sci. Eng. 2012, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Nakayama, T.; Fujita, T. Cooling effect of water-holding pavements made of new materials on water and heat budgets in urban areas. Landsc. Urban Plan. 2010, 96, 57–67. [Google Scholar] [CrossRef]
- Higashiyama, H.; Sano, M.; Nakanishi, F.; Takahashi, O.; Tsukuma, S. Field measurements of road surface temperature of several asphalt pavements with temperature rise reducing function. Case Stud. Constr. 2016, 4, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Kinoshita, S.; Yoshida, A.; Okuno, N. Evaporation performance analysis for water-retentive material-Based on outdoor heat-budget and transport properties. J. Heat Isl. Inst. Int. 2012, 7, 222–230. [Google Scholar]
- Höppe, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef]
- Jendritzky, G.; De Dear, R.; Havenith, G. UTCI-Why another thermal index? Int. J. Biometeorol. 2012, 56, 421–428. [Google Scholar] [CrossRef] [Green Version]
- Takebayashi, H.; Okubo, M.; Danno, H. Thermal environment map in street canyon for implementing extreme high temperature measures. Atmosphere 2020, 11, 550. [Google Scholar] [CrossRef]
- Nicol, J.F.; Humphreys, M.A. Adaptive thermal comfort and sustainable thermal standards for buildings. Energy Build. 2002, 34, 563–572. [Google Scholar] [CrossRef]
- De Dear, R.; Xiong, J.; Kim, J.; Cao, B. A review of adaptive thermal comfort research since 1998. Energy Build. 2020, 214, 109893. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, Z. Standard effective temperature based adaptive-rational thermal comfort model. Appl. Energy 2020, 246, 114723. [Google Scholar] [CrossRef]
- Junyan, Y.; Beixiang, S.; Geyang, X.; Qin, X.; Shi-Jie, C. Impacts of urban form on thermal environment near the surface region at pedestrian height: A case study based on high-density built-up areas of Nanjing City in China. Sustainability 2020, 12, 1737. [Google Scholar] [CrossRef] [Green Version]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Shimazaki, Y.; Yoshida, A.; Satsumoto, Y.; Taketani, S. Effect of properties of sports surface and clothing materials on human thermal load under hot environment. Procedia Eng. 2014, 72, 502–507. [Google Scholar] [CrossRef] [Green Version]
- Shimazaki, Y.; Yoshida, A.; Suzuki, R.; Kawabata, T.; Imai, D.; Kinoshita, S. Application of human thermal load into unsteady condition for improvement of outdoor thermal comfort. Build. Environ. 2011, 46, 1716–1724. [Google Scholar] [CrossRef]
- ISO. ISO 8996:2004—Ergonomics of the Thermal Environment—Determination of Metabolic Rate; ISO: Geneva, Switzerland, 2004. [Google Scholar]
- Weir, J. New methods for calculating metabolic rate with special reference to protein metabolism. J. Physiol. 1949, 109, 1–9. [Google Scholar] [CrossRef]
- Kurazumi, Y.; Horikoshi, T.; Tsuchikawa, T.; Matsubara, N. The body surface area of Japanese. Jpn. J. Biometeorol. 1994, 31, 5–29. (In Japanese) [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). Chapter 9: Thermal comfort. In 2009 ASHRAE Handbook—Fundamentals; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- Marino, C.; Nucara, A.; Pietrafesa, M.; Polimeni, E. The effect of the short-wave radiation and its reflected components on the mean radiant temperature: Modelling and preliminary experimental results. J. Build. Eng. 2017, 9, 41–51. [Google Scholar] [CrossRef]
- Fernández-Cuevas, I.; Bouzas Marins, J.C.; Arnáiz Lastras, J.; Gómez Carmona, P.M.; Piñonosa Cano, S.; García-Concepción, M.Á.; Sillero-Quintana, M. Classification of factors influencing the use of infrared thermography in humans: A review. Infrared Phys. Technol. 2015, 71, 28–55. [Google Scholar] [CrossRef]
- ISO. ISO 9886:2004—Ergonomics—Evaluation of Thermal Strain by Physiological Measurements; ISO: Geneva, Switzerland, 2004. [Google Scholar]
- Hardy, J.D.; Du Bois, E.F.; Soderstrom, G.F. The technic of measuring radiation and convection. J. Nutr. 1938, 15, 461–475. [Google Scholar] [CrossRef]
- Udagawa, M.; Kimura, K. The estimation of direct solar radiation from global radiation. J. Archit. Plan. 1978, 267, 83–90. (In Japanese) [Google Scholar]
- Burton, A.C.; Edholm, O.G. Man in a cold environment—Physiological and pathological effects of exposure to low temperatures. Q. Rev. Biol. 1956, 31, 151–152. [Google Scholar]
- Yang, J.H.; Kato, S.; Seo, J. Evaluation of the convective heat transfer coefficient of the human body using the wind tunnel and thermal manikin. J. Asian Archit. Build. Eng. 2009, 8, 563–569. [Google Scholar] [CrossRef] [Green Version]
- ISO. ISO 9920:2007 Ergonomics of the Thermal Environment—Estimation of Thermal Insulation and Water Vapor Resistance of a Clothing Ensemble; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Gagge, A.P.; Stolwijk, J.A.J.; Nishi, Y. An effective temperature scale based on a simple model of human physiological regulatory response. ASHRAE Trans. 1971, 77, 247–262. [Google Scholar]
- Gagge, A.P.; Fobelets, A.P.; Berglund, L.G. A standard predictive index of human response to the thermal environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- AIJ. Standards for Measurement of Psychological and Physiological Responses to Thermal Environments; Maruzen Publishing: Tokyo, Japan, 2014. (In Japanese) [Google Scholar]
- Santamouris, M. Using cool pavements as a mitigation strategy to fight urban heat island—A review of the actual developments. Renew. Sustain. Energy Rev. 2013, 26, 224–240. [Google Scholar] [CrossRef]



| Body Region i | Weighting Factor Fi |
|---|---|
| 1: Forehead | 0.07 |
| 2: Abdomen | 0.35 |
| 3: Forearm | 0.14 |
| 4: Back of hand | 0.05 |
| 5: Thigh | 0.19 |
| 6: Leg | 0.13 |
| 7: Back of Foot | 0.07 |
| Value | Thermal Sensation | Wettedness | Thermal Comfort |
|---|---|---|---|
| 3 | Hot | - | - |
| 2 | Warm | Wet | Comfortable |
| 1 | Slightly warm | Slightly wet | Slightly comfortable |
| 0 | Neutral | Neutral | Neutral |
| −1 | Slightly cool | Slightly dry | Slightly uncomfortable |
| −2 | Cool | Dry | Uncomfortable |
| −3 | Cold | - | - |
| Parameter | Accuracy | Instrument |
|---|---|---|
| Air temperature | ±0.3 °C (0–50 °C) | TR-73U, T&D |
| Relative humidity | ±5% R.H. (10–95% R.H.) | TR-73U, T&D |
| Wind speed | ±2% or 0.02 m/s | Model-6531, Kanomax |
| Surface temperature | ±1.5 °C (−40–375 °C) | Thermocouple, J-type |
| Ventilatory gas | ±0.1% for O2/ ±0.2% for CO2 | VO2000, MGC Diagnostics |
| Body temperature | ±0.2 °C (0–70 °C) | N543R, Nikkiso-Therm |
| Body weight | ±10 g | GP-100K, A&D |
| Heartrate | ±1% or 1 bpm | RS800CX, Polar |
| AS | WR | |
|---|---|---|
| Reflectance 1 | 0.085 ± 0.010 | 0.253 ± 0.029 |
| Component | AS | WR |
|---|---|---|
| Metabolic rate | 87 ± 2 | 87 ± 2 |
| Workload | 0 | 0 |
| Net radiation | 193 ± 42 | 181 ± 55 |
| Convective heal loss | 15 ± 6 | 18 ± 4 |
| Evaporative heat loss | 29 ± 3 | 35 ± 5 |
| Human thermal load * | 237 ± 38 | 215 ± 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimazaki, Y.; Aoki, M.; Nitta, J.; Okajima, H.; Yoshida, A. Experimental Determination of Pedestrian Thermal Comfort on Water-Retaining Pavement for UHI Adaptation Strategy. Atmosphere 2021, 12, 127. https://doi.org/10.3390/atmos12020127
Shimazaki Y, Aoki M, Nitta J, Okajima H, Yoshida A. Experimental Determination of Pedestrian Thermal Comfort on Water-Retaining Pavement for UHI Adaptation Strategy. Atmosphere. 2021; 12(2):127. https://doi.org/10.3390/atmos12020127
Chicago/Turabian StyleShimazaki, Yasuhiro, Masashige Aoki, Jumpei Nitta, Hodaka Okajima, and Atsumasa Yoshida. 2021. "Experimental Determination of Pedestrian Thermal Comfort on Water-Retaining Pavement for UHI Adaptation Strategy" Atmosphere 12, no. 2: 127. https://doi.org/10.3390/atmos12020127
APA StyleShimazaki, Y., Aoki, M., Nitta, J., Okajima, H., & Yoshida, A. (2021). Experimental Determination of Pedestrian Thermal Comfort on Water-Retaining Pavement for UHI Adaptation Strategy. Atmosphere, 12(2), 127. https://doi.org/10.3390/atmos12020127





