Modeling Low Intensity Fires: Lessons Learned from 2012 RxCADRE
Abstract
:1. Introduction
2. Experimental Data
2.1. Fuels
2.2. Winds
2.2.1. Temporal Wind Variability
2.2.2. Spatial Wind Variability
3. Modeling Methods
3.1. FIRETEC Domain Setup
3.2. Wind Initial and Boundary Conditions
- Adequately representing the spatial and temporal variability of the winds, including the dynamic wind events that influence fire behavior within the S5 plot.
- Using the 3.3 m high anemometer data to estimate winds aloft.
3.3. Ignition
4. Modeling Results and Discussion
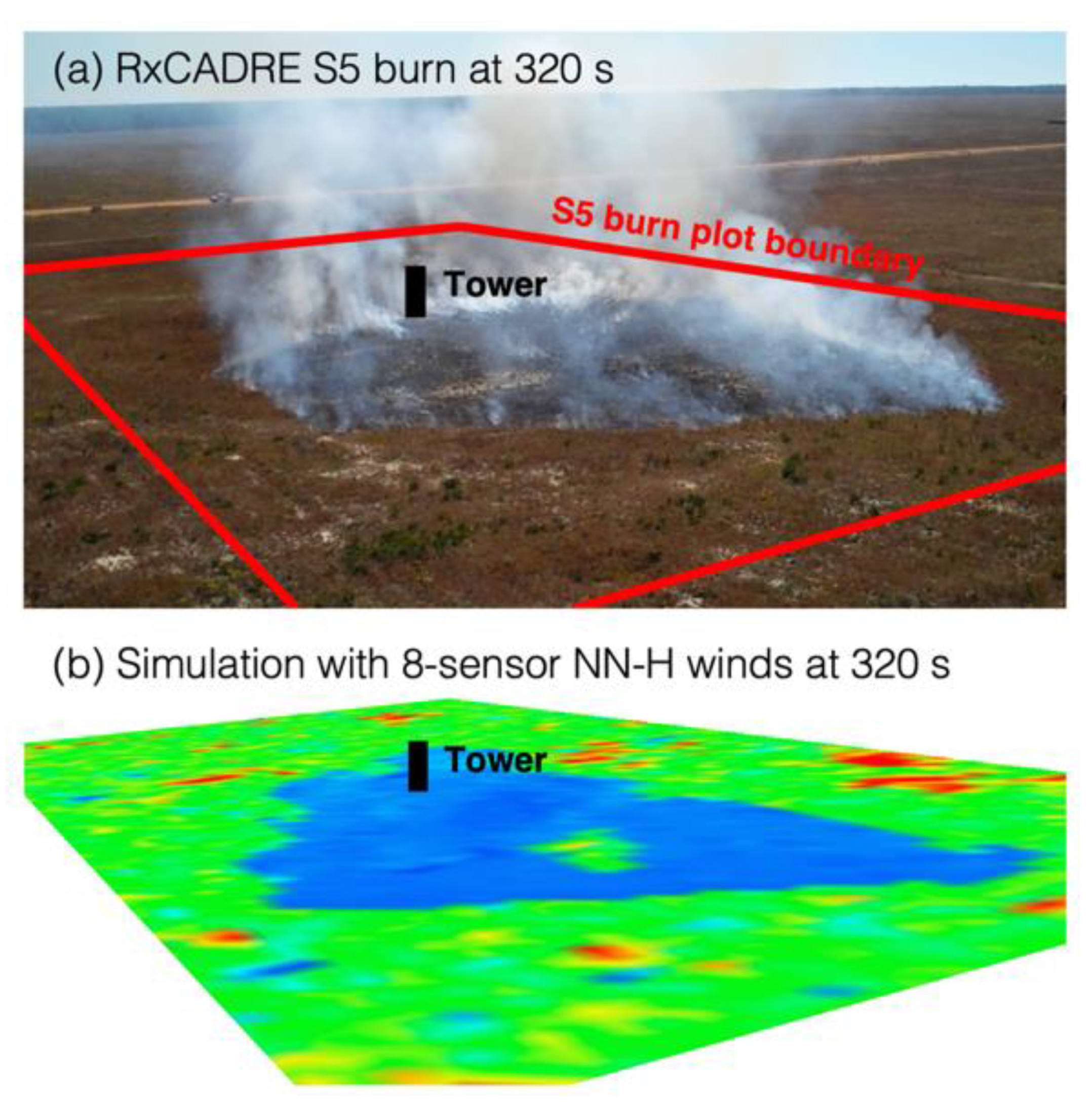
Fire Spread
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffman, C.; Sieg, C.; Linn, R.; Mell, W.; Parsons, R.; Ziegler, J.; Hiers, J. Advancing the Science of Wildland Fire Dynamics Using Process-Based Models. Fire 2018, 1, 32. [Google Scholar] [CrossRef] [Green Version]
- Hiers, J.K.; O’Brien, J.J.; Varner, J.M.; Butler, B.W.; Dickinson, M.; Furman, J.; Gallagher, M.; Godwin, D.; Goodrick, S.L.; Hood, S.M.; et al. Prescribed fire science: The case for a refined research agenda. Fire Ecol. 2020, 16, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Jonko, A.; Yedinak, K.; Linn, R.; Parsons, R.; Atchley, A.; Conley, J. Sensitivity of grassfires to small perturbations in the turbulent wind field. J. Geophys. Res. Atmos. In review.
- Ottmar, R.D.; Hiers, J.K.; Butler, B.W.; Clements, C.B.; Dickinson, M.B.; Hudak, A.T.; O’Brien, J.J.; Potter, B.E.; Rowell, E.M.; Strand, T.M.; et al. Measurements, datasets and preliminary results from the RxCADRE project-2008, 2011 and 2012. Int. J. Wildl. Fire 2016, 25, 114. [Google Scholar] [CrossRef]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. Int. J. Wildl. Fire 2009, 18, 349–368. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, A.L. Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. Int. J. Wildl. Fire 2009, 18, 369–386. [Google Scholar] [CrossRef] [Green Version]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels. 1972. Available online: https://www.fs.fed.us/rm/pubs_int/int_rp115.pdf (accessed on 15 January 2020).
- Burgan, R.E.; Rothermel, R.C. BEHAVE: Fire Behavior Prediction and Fuel Modeling System-FUEL Subsystem. 1984. Available online: https://www.fs.usda.gov/treesearch/pubs/29616 (accessed on 15 January 2020).
- Hiers, J.K.; Stauhammer, C.L.; O’Brien, J.J.; Gholz, H.L.; Martin, T.A.; Hom, J.; Starr, G. Fine dead fuel moisture shows complex lagged responses to environmental conditions in a saw palmetto (Serenoa repens) flatwoods. Agric. For. Meteorol. 2019, 266–267, 20–28. [Google Scholar] [CrossRef]
- Chiodi, A.M.; Larkin, N.S.; Varner, J.M. An analysis of Southeastern US prescribed burn weather windows: Seasonal variability and El Niño associations. Int. J. Wildl. Fire 2018, 27, 176–189. [Google Scholar] [CrossRef]
- Wade, D.D.; Lunsford, J.D.; Dixon, M.J.; Mobley, H.E. A Guide for Prescribed Fire in Southern Forests; US Department of Agriculture: Washington, DC, USA, 1989. [Google Scholar]
- Zhou, X.; Mahalingam, S.; Weise, D. Modeling of marginal burning state of fire spread in live chaparral shrub fuel bed. Combust. Flame. 2005, 143, 183–198. [Google Scholar] [CrossRef]
- Hoffman, C.M.; Linn, R.; Parsons, R.; Sieg, C.; Winterkamp, J. Modeling spatial and temporal dynamics of wind flow and potential fire behavior following a mountain pine beetle outbreak in a lodgepole pine forest. Agric. For. Meteorol. 2015, 204, 79–93. [Google Scholar] [CrossRef]
- Overholt, K.J.; Kurzawski, A.J.; Cabrera, J.; Koopersmith, M.; Ezekoye, O.A. Fire behavior and heat fluxes for lab-scale burning of little bluestem grass. Fire Saf. J. 2014, 67, 70–81. [Google Scholar] [CrossRef]
- Overholt, K.J.; Cabrera, J.; Kurzawski, A.; Koopersmith, M.; Ezekoye, O.A. Characterization of Fuel Properties and Fire Spread Rates for Little Bluestem Grass. Fire Technol. 2014, 50, 9–38. [Google Scholar] [CrossRef]
- Mueller, E.; Mell, W.; Simeoni, A. Large eddy simulation of forest canopy flow for wildland fire modeling. Can. J. For. Res. 2014, 44, 1534–1544. [Google Scholar] [CrossRef]
- Dupuy, J.-L.; Pimont, F.; Linn, R.R.; Clements, C.B. FIRETEC evaluation against the FireFlux experiement: Preliminary results. In Advances in Forest Fire Research. Proceedings of the 7th ICFFR; Viegas, D.X., Ed.; Coimbra University Press: Coimbra, Portugal, 2014. [Google Scholar]
- Kochanski, A.K.; Jenkins, M.A.; Mandel, J.; Beezley, J.D.; Clements, C.B.; Krueger, S. Evaluation of WRF-SFIRE performance with field observations from the FireFlux experiment. Geosci. Model Dev. 2013, 6, 1109–1126. [Google Scholar] [CrossRef] [Green Version]
- Linn, R.R.; Cunningham, P. Numerical simulations of grass fires using a coupled atmosphere-fire model: Basic fire behavior and dependence on wind speed. J. Geophys. Res. Atmos. 2005, 110, 1–19. [Google Scholar] [CrossRef]
- Linn, R.; Anderson, K.; Winterkamp, J.; Brooks, A.; Wotton, M.; Dupuy, J.-L.; Pimont, F.; Edminster, C. Incorporating field wind data into FIRETEC simulations of the International Crown Fire Modeling Experiment (ICFME): Preliminary lessons learned. Can. J. For. Res. 2012, 42, 879–898. [Google Scholar] [CrossRef]
- Mallia, D.V.; Kochanski, A.K.; Urbanski, S.P.; Lin, J.C. Optimizing Smoke and Plume Rise Modeling Approaches at Local Scales. Atmosphere 2018, 9, 166. [Google Scholar] [CrossRef] [Green Version]
- Mallia, D.V.; Kochanski, A.K.; Urbanski, S.P.; Mandel, J.; Farguell, A.; Krueger, S.K. Incorporating a Canopy Parameterization within a Coupled Fire-Atmosphere Model to Improve a Smoke Simulation for a Prescribed Burn. Atmosphere 2020, 11, 832. [Google Scholar] [CrossRef]
- Alexander, M.E.; Cruz, M.G. Are the applications of wildland fire behaviour models getting ahead of their evaluation again? Environ. Model. Softw. 2013, 41, 65–71. [Google Scholar] [CrossRef]
- Davis, A.Y.; Ottmar, R.; Liu, Y.; Goodrick, S.; Achtemeier, G.; Gullett, B.; Aurell, J.; Stevens, W.; Greenwald, R.; Hu, Y.; et al. Fire emission uncertainties and their effect on smoke dispersion predictions: A case study at Eglin Air Force Base, Florida, USA. Int. J. Wildl. Fire 2015, 24, 276–285. [Google Scholar] [CrossRef] [Green Version]
- Achtemeier, G.L.; Goodrick, S.A.; Liu, Y. Modeling multiple-core updraft plume rise for an aerial ignition prescribed burn by coupling daysmoke with a cellular automata fire model. Atmosphere 2012, 3, 352–376. [Google Scholar] [CrossRef] [Green Version]
- O’Brien, J.J.; Loudermilk, E.L.; Hornsby, B.; Hudak, A.T.; Bright, B.C.; Dickinson, M.B.; Hiers, J.K.; Teske, C.; Ottmar, R.D. High-resolution infrared thermography for capturing wildland fire behaviour: RxCADRE 2012. Int. J. Wildl. Fire 2016, 25, 62–75. [Google Scholar] [CrossRef]
- Hudak, A.T.; Dickinson, M.B.; Bright, B.C.; Kremens, R.L.; Loudermilk, E.L.; O’Brien, J.J.; Hornsby, B.S.; Ottmar, R.D. Measurements relating fire radiative energy density and surface fuel consumption-RxCADRE 2011 and 2012. Int. J. Wildl. Fire 2016, 25, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Clements, C.B.; Lareau, N.P.; Seto, D.; Contezac, J.; Davis, B.; Teske, C.; Zajkowski, T.J.; Hudak, A.T.; Bright, B.C.; Dickinson, M.B.; et al. Fire weather conditions and fire–atmosphere interactions observed during low-intensity prescribed fires–RxCADRE 2012. Int. J. Wildl. Fire 2016, 25, 90–101. [Google Scholar] [CrossRef]
- Linn, R.R. A Transport Model for Prediction of Wildfire Behavior. Doctoral Thesis, New Mexico State University, Las Cruces, NM, USA, 1997. [Google Scholar]
- Linn, R.R.; Harlow, F.H. Computational Technologies for Fluid/Structural/Chemical Systems With Industrial Applications; Kleijn, C.R., Kawano, S., Kudriavtsev, V.V., Eds.; ASME: New York, NY, USA, 1998; pp. 161–168. [Google Scholar]
- Linn, R.R.; Reisner, J.; Colman, J.J.; Winterkamp, J.L. Studying wildfire behavior using FIRETEC. Int. J. Wildl. Fire 2002, 11, 233. [Google Scholar] [CrossRef]
- Cunningham, P.; Linn, R.R. Numerical simulations of grass fires using a coupled atmosphere-fire model: Dynamics of fire spread. J. Geophys. Res. 2007, 112, D05108. [Google Scholar] [CrossRef]
- Dupuy, J.-L.; Linn, R.R.; Konovalov, V.; Pimont, F.; Vega, J.A.; Jiménez, E. Exploring three-dimensional coupled fire—Atmosphere interactions downwind of wind-driven surface fires and their influence on backfires using the HIGRAD-FIRETEC model. Int. J. Wildl. Fire 2011, 20, 734. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A physics-based approach to modelling grassland fires. Int. J. Wildl. Fire 2007, 16, 1. [Google Scholar] [CrossRef]
- Accary, G.; Meradji, S.; Morvan, D.; Bessonov, O.; Fougere, D. FireStar3D: 3D finite volume model for the prediction of wildfires. In Proceedings of the VII International Conference of Forest Fire Research, Coimbra, Portugal, 17–20 November 2014. [Google Scholar]
- Rowell, E.M.; Seielstad, C.A.; Ottmar, R.D. Development and validation of fuel height models for terrestrial lidar-RxCADRE 2012. Int. J. Wildl. Fire 2016, 25, 38–47. [Google Scholar] [CrossRef]
- Hudak, A.T.; Bright, B.C. RxCADRE 2011 and 2012: Predicted Surface Fuel Maps; Forest Service Research Data Archive: Fort Collins, CO, USA, 2018. [Google Scholar] [CrossRef]
- Hudak, A.T.; Bright, B.C.; Williams, B.W.; Hiers, J.K. RxCADRE 2011 and 2012: Ignition Data; Forest Service Research Data Archive: Fort Collins, CO, USA, 2018. [Google Scholar] [CrossRef]
- Seto, D.; Clements, C.B. RxCADRE 2012: In-Site Wind, Air Temperature, Barometric Pressure, and Heat Flux Time Series Data; Forest Service Research Data Archive: Fort Collins, CO, USA, 2015. [Google Scholar] [CrossRef]
- Hiers, J.K.; O’Brien, J.J.; Mitchell, R.J.; Grego, J.M.; Loudermilk, E.L. The wildland fuel cell concept: An approach to characterize fine-scale variation in fuels and fire in frequently burned longleaf pine forests. Int. J. Wildl. Fire 2009, 18, 315. [Google Scholar] [CrossRef]
- Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, S.; Seielstad, C.; Queen, L.L.; O’Brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling terrestrial laser scanning with 3D fuel biomass sampling for advancing wildland fuels characterization. For. Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
- Reisner, J.; Wynne, S.; Margolin, L.; Linn, R.R. Coupled Atmospheric–Fire Modeling Employing the Method of Averages. Mon. Weather Rev. 2000, 128, 3683–3691. [Google Scholar] [CrossRef]
- Nadiga, B.T.; Hecht, M.W.; Margolin, L.G.; Smolarkiewicz, P.K. On simulating flows with multiple time scales using a method of averages. Theor. Comput. Fluid Dyn. 1997, 9, 281–292. [Google Scholar] [CrossRef] [Green Version]
- Cheney, N.; Gould, J.; Catchpole, W. The Influence of Fuel, Weather and Fire Shape Variables on Fire-Spread in Grasslands. Int. J. Wildl. Fire 1993, 3, 31. [Google Scholar] [CrossRef]
- Linn, R.; Winterkamp, J.; Colman, J.J.; Edminster, C.; Bailey, J.D. Modeling interactions between fire and atmosphere in discrete element fuel beds. Int. J. Wildl. Fire 2005, 14, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Pimont, F.; Dupuy, J.-L.; Linn, R.R. Coupled slope and wind effects on fire spread with influences of fire size: A numerical study using FIRETEC. Int. J. Wildl. Fire 2012, 21, 828. [Google Scholar] [CrossRef]
- Canfield, J.M.; Linn, R.R.; Sauer, J.A.; Finney, M.; Forthofer, J. A numerical investigation of the interplay between fireline length, geometry, and rate of spread. Agric. For. Meteorol. 2014. [Google Scholar] [CrossRef]
- Atchley, A.L.; Linn, R.R.; Jonko, A.; Hoffman, C.M.; Hyman, J.D.; Pimont, F.; Sieg, C.; Middleton, R. Effects of fuel spatial distribution on wildland fire behavior. Int. J. Wildl. Fire 2021, WF20093. [Google Scholar]
- Prichard, S.; Larkin, N.; Ottmar, R.; French, N.; Baker, K.; Brown, T.; Clements, C.; Dickinson, M.; Hudak, A.; Kochanski, A.; et al. The Fire and Smoke Model Evaluation Experiment—A Plan for Integrated, Large Fire–Atmosphere Field Campaigns. Atmosphere 2019, 10, 66. [Google Scholar] [CrossRef] [Green Version]





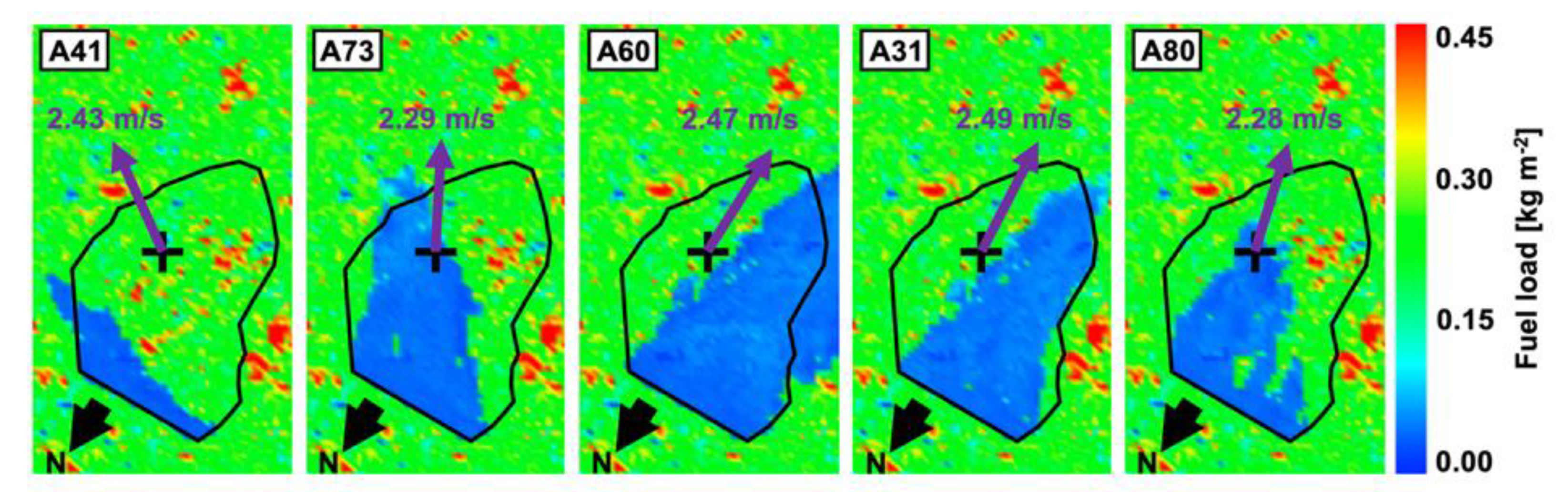
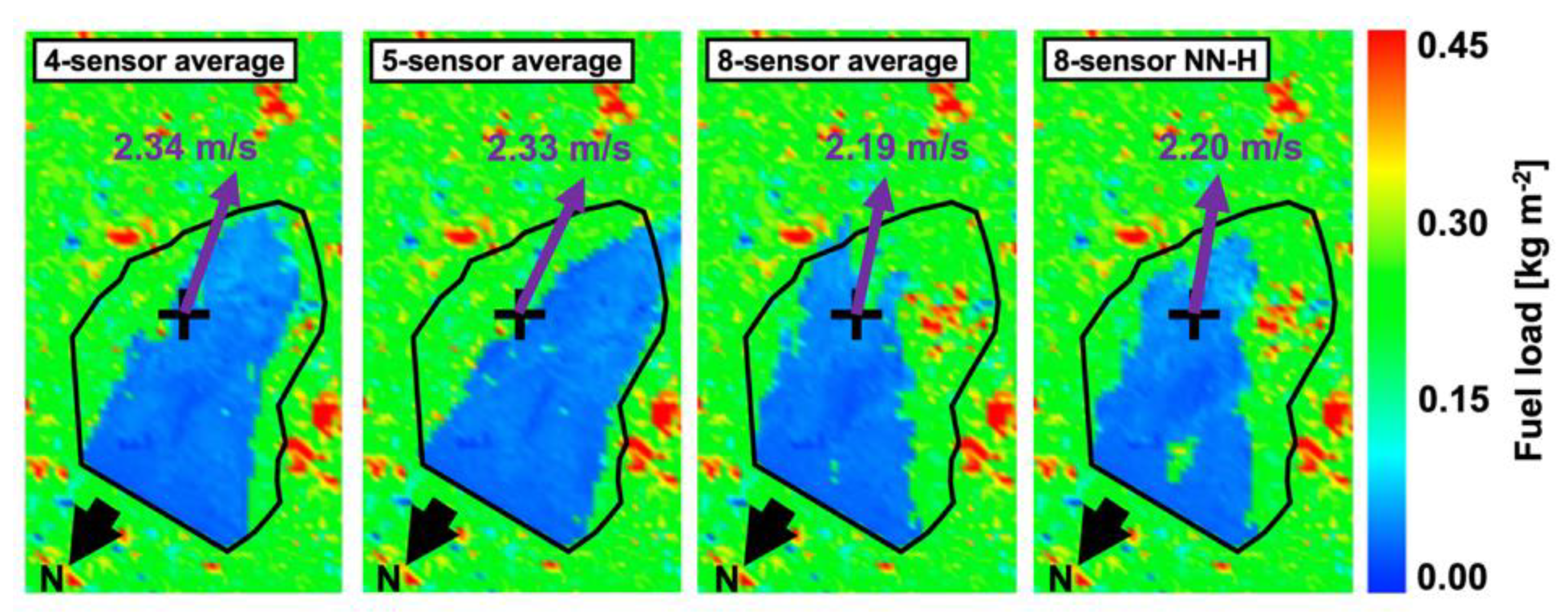

| Sensor | (ms−1) | (ms−1) | (ms−1) | (ms−1) | (ms−1) | MKE (m2/s2) | TKE (m2/s2) | |
|---|---|---|---|---|---|---|---|---|
| A81 | 2.17 ± 0.81 | 3.91 ± 18.10 | 0.76 | 0.80 | −0.15 ± 0.79 | −2.17 ± 0.77 | 2.35 | 0.60 |
| A26 | 2.35 ± 0.91 | −3.95 ± 21.72 | 0.92 | 0.86 | 0.16 ± 0.85 | −2.35 ± 0.92 | 2.77 | 0.79 |
| A80 | 2.28 ± 0.84 | −15.55 ± 20.05 | 0.86 | 0.73 | 0.61 ± 0.76 | −2.19 ± 0.83 | 2.58 | 0.64 |
| A31 | 2.49 ± 0.87 | −5.79 ± 14.06 | 0.90 | 0.48 | 0.25 ± 0.52 | −2.48 ± 0.87 | 3.11 | 0.52 |
| A60 | 2.47 ± 0.85 | −1.26 ± 10.52 | 0.86 | 0.38 | 0.05 ± 0.39 | −2.47 ± 0.86 | 3.05 | 0.44 |
| A73 | 2.29 ± 0.78 | −29.66 ± 16.16 | 0.78 | 0.62 | 1.13 ± 0.56 | −1.99 ± 0.83 | 2.62 | 0.50 |
| A41 | 2.43 ± 0.81 | −56.24 ± 18.23 | 0.85 | 0.62 | 2.02 ± 0.64 | −1.35 ± 0.84 | 2.95 | 0.56 |
| A42 | 2.44 ± 0.78 | −54.66 ± 17.49 | 0.79 | 0.69 | 1.99 ± 0.60 | −1.41 ± 0.86 | 2.97 | 0.55 |
| Simulation | Surface Wind | Fuels | ||||
|---|---|---|---|---|---|---|
| A80 | A80 | Heterogeneous | 2.28 | −15.55 | 2.20 | 0.61 |
| A31 | A31 | Heterogeneous | 2.49 | −5.79 | 2.48 | 0.25 |
| A60 | A60 | Heterogeneous | 2.47 | −1.26 | 2.47 | 0.05 |
| A73 | A73 | Heterogeneous | 2.29 | −29.66 | 1.99 | 1.13 |
| A41 | A41 | Heterogeneous | 2.43 | −56.24 | 1.35 | 2.02 |
| 4S_avg | 4-sensor average | Heterogeneous | 2.34 | −12.61 | 2.28 | 0.51 |
| 5S_avg | 5-sensor average | Heterogeneous | 2.33 | −4.56 | 2.32 | 0.19 |
| 8S_avg | 8-sensor average | Heterogeneous | 2.19 | −20.34 | 2.05 | 0.76 |
| 8NN-H | Nearest neighbor | Heterogeneous | 2.20 | −22.68 | 2.03 | 0.85 |
| 8NN-U | Nearest neighbor | Uniform (averaged) | 2.20 | −22.68 | 2.03 | 0.85 |
| Simulation | ROSSSWind (m s−1) | ROS8avg (m s−1) | Area Burned 320 s after Ignition (m2) |
|---|---|---|---|
| A80 | 0.279 | 0.278 | 2676 |
| A31 | 0.359 | 0.347 | 4108 |
| A60 | 0.504 | 0.476 | 5424 |
| A73 | 0.324 | 0.320 | 3592 |
| A41 | 0.118 | 0.096 | 1212 |
| 4S_avg | 0.380 | 0.377 | 4260 |
| 5S_avg | 0.392 | 0.378 | 4404 |
| 8S_avg | 0.322 | 0.322 | 3452 |
| 8NN-H | 0.413 | 0.413 | 3444 |
| 8NN-U | 0.531 | 0.531 | 5540 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linn, R.R.; Winterkamp, J.L.; Furman, J.H.; Williams, B.; Hiers, J.K.; Jonko, A.; O’Brien, J.J.; Yedinak, K.M.; Goodrick, S. Modeling Low Intensity Fires: Lessons Learned from 2012 RxCADRE. Atmosphere 2021, 12, 139. https://doi.org/10.3390/atmos12020139
Linn RR, Winterkamp JL, Furman JH, Williams B, Hiers JK, Jonko A, O’Brien JJ, Yedinak KM, Goodrick S. Modeling Low Intensity Fires: Lessons Learned from 2012 RxCADRE. Atmosphere. 2021; 12(2):139. https://doi.org/10.3390/atmos12020139
Chicago/Turabian StyleLinn, Rodman R., Judith L. Winterkamp, James H. Furman, Brett Williams, J. Kevin Hiers, Alexandra Jonko, Joseph J. O’Brien, Kara M. Yedinak, and Scott Goodrick. 2021. "Modeling Low Intensity Fires: Lessons Learned from 2012 RxCADRE" Atmosphere 12, no. 2: 139. https://doi.org/10.3390/atmos12020139
APA StyleLinn, R. R., Winterkamp, J. L., Furman, J. H., Williams, B., Hiers, J. K., Jonko, A., O’Brien, J. J., Yedinak, K. M., & Goodrick, S. (2021). Modeling Low Intensity Fires: Lessons Learned from 2012 RxCADRE. Atmosphere, 12(2), 139. https://doi.org/10.3390/atmos12020139






