Assessment of Morelian Meteoroid Impact on Mexican Environment
Abstract
:1. Introduction
2. Brief Review of Previous Meteoroid Events
3. Background Conditions
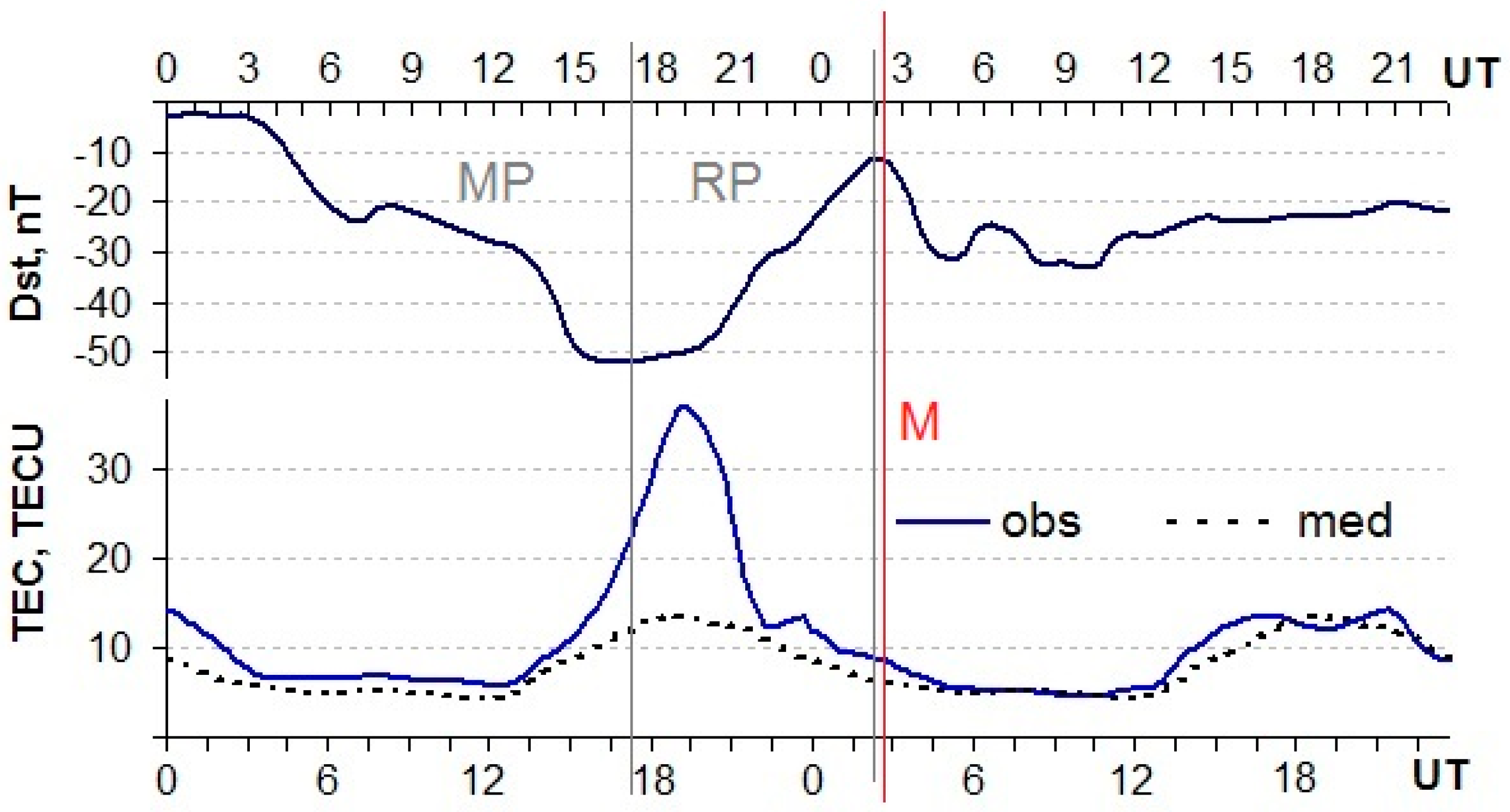
3.1. Space Weather
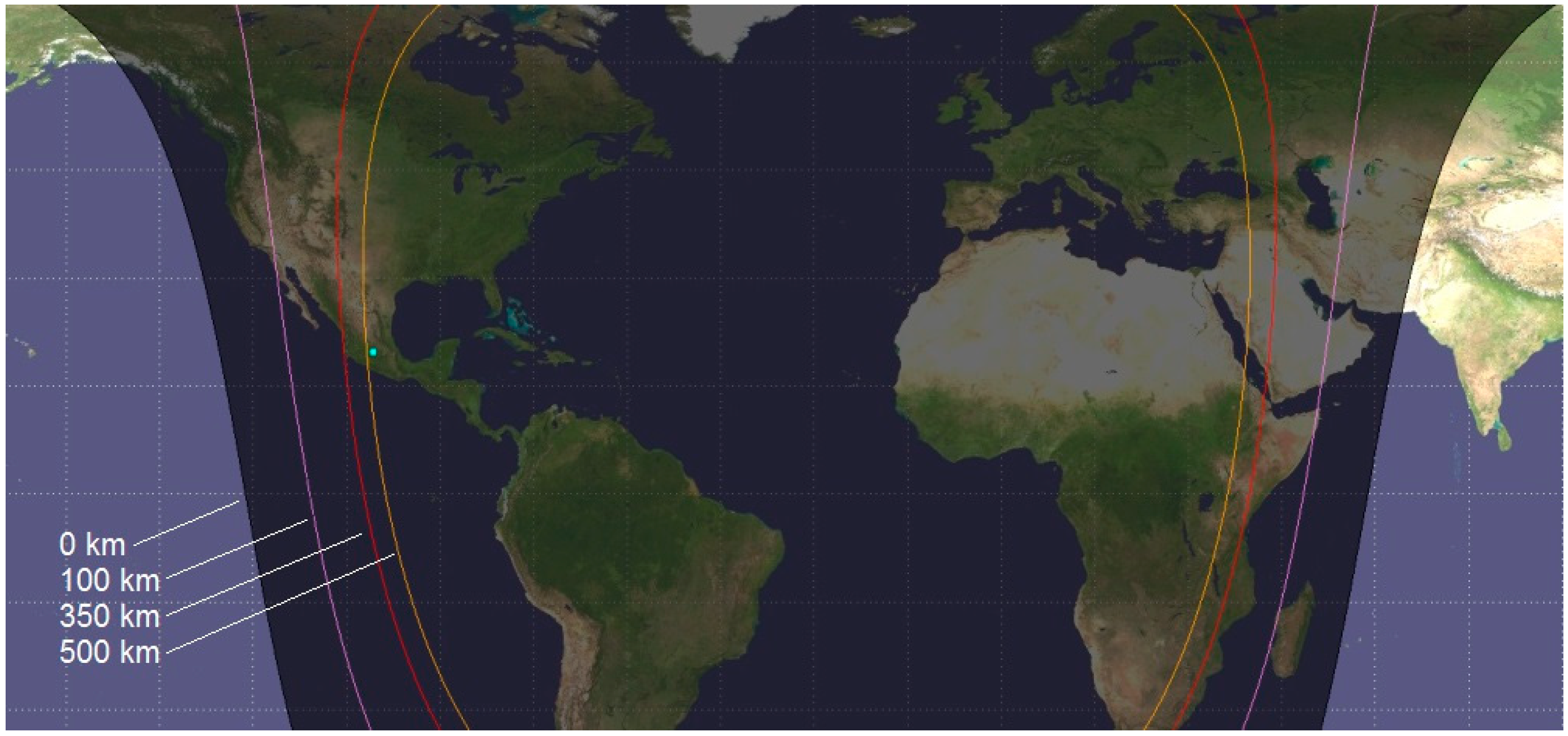
3.2. Terminator
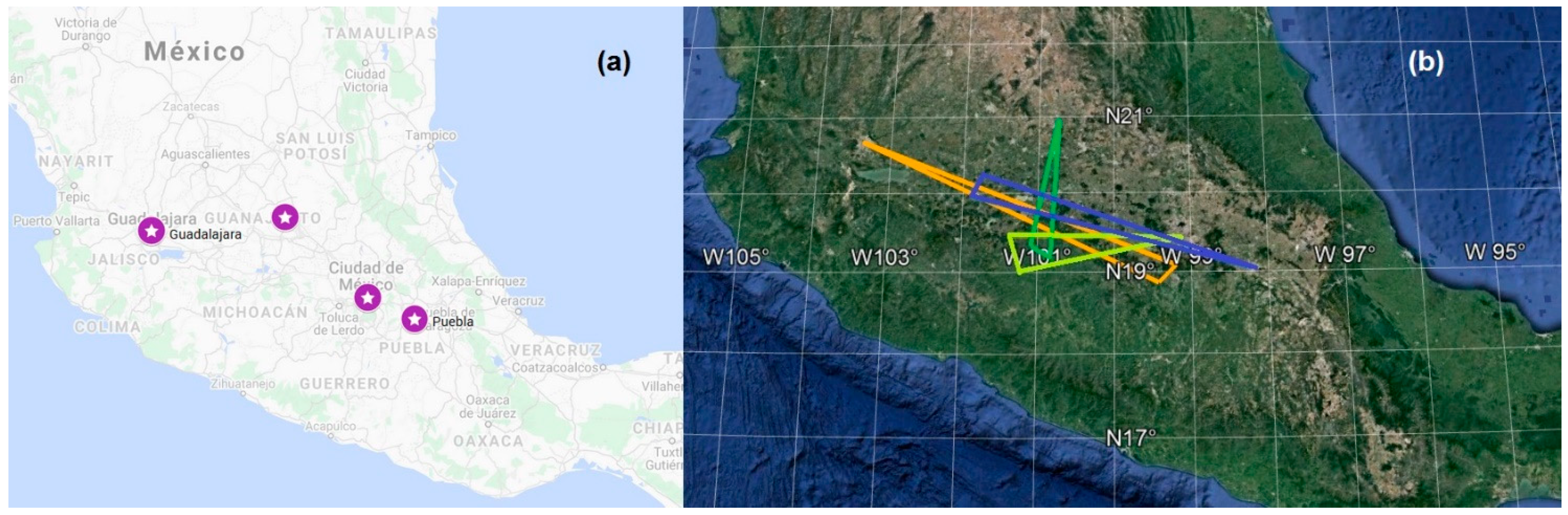
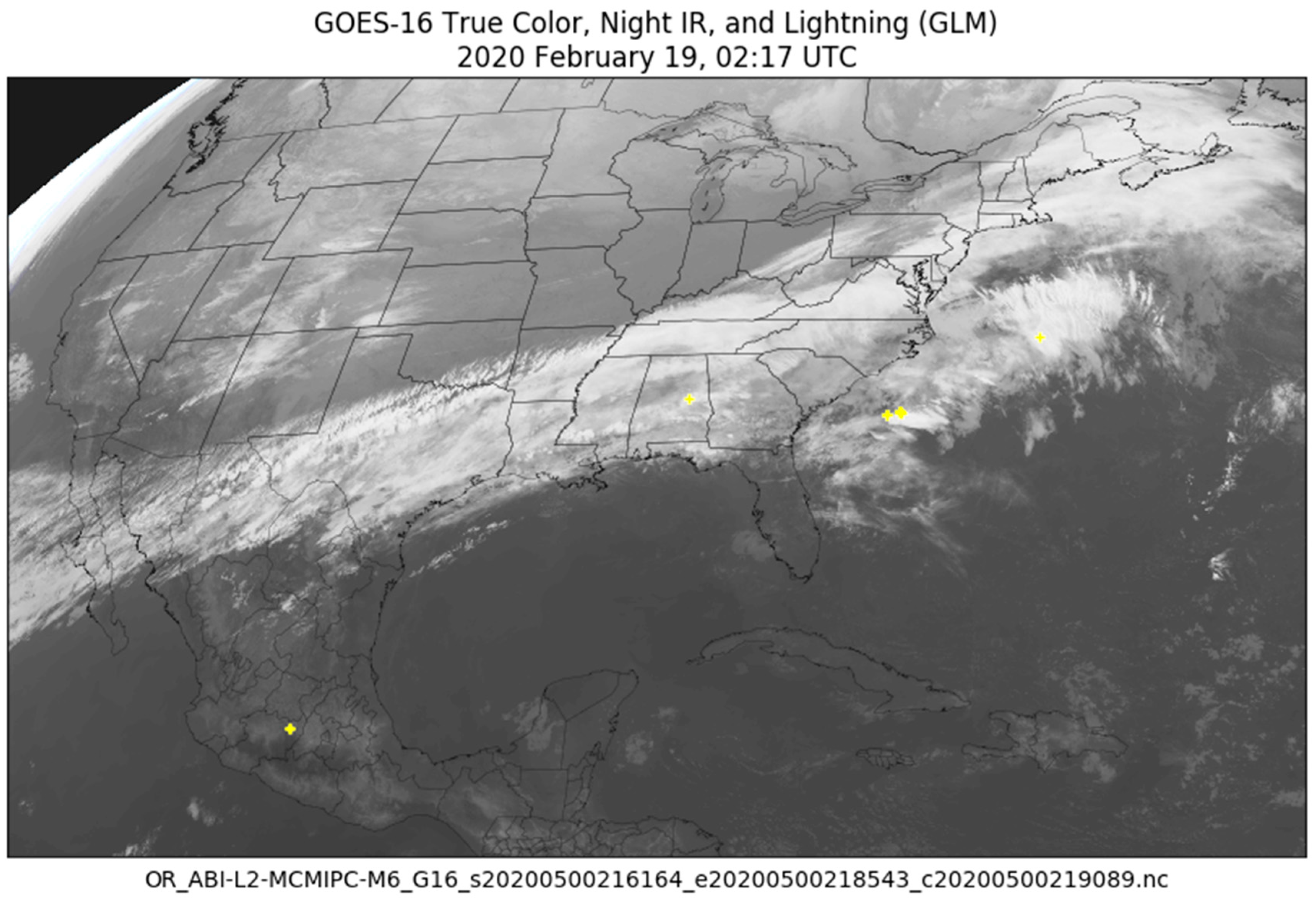
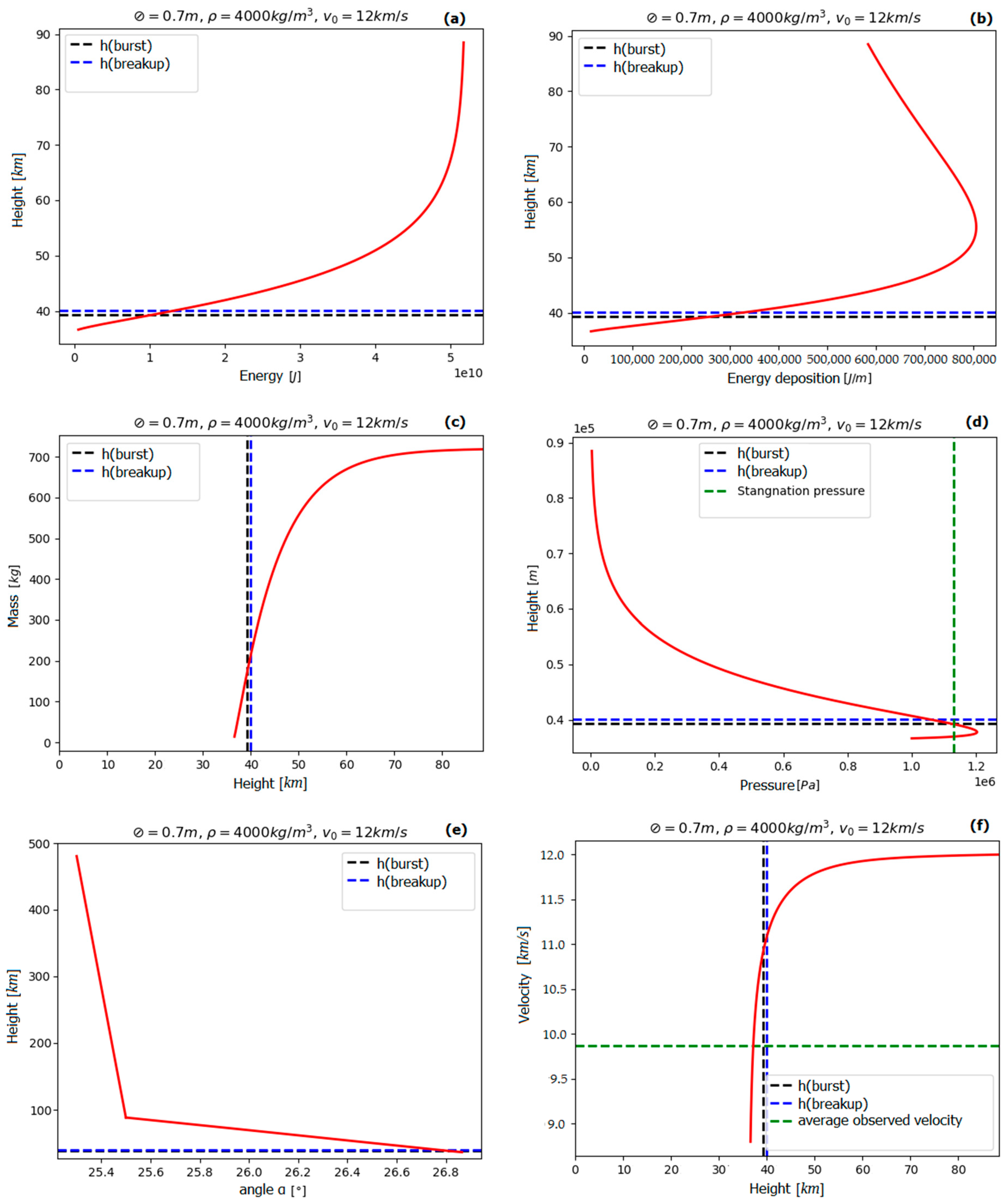
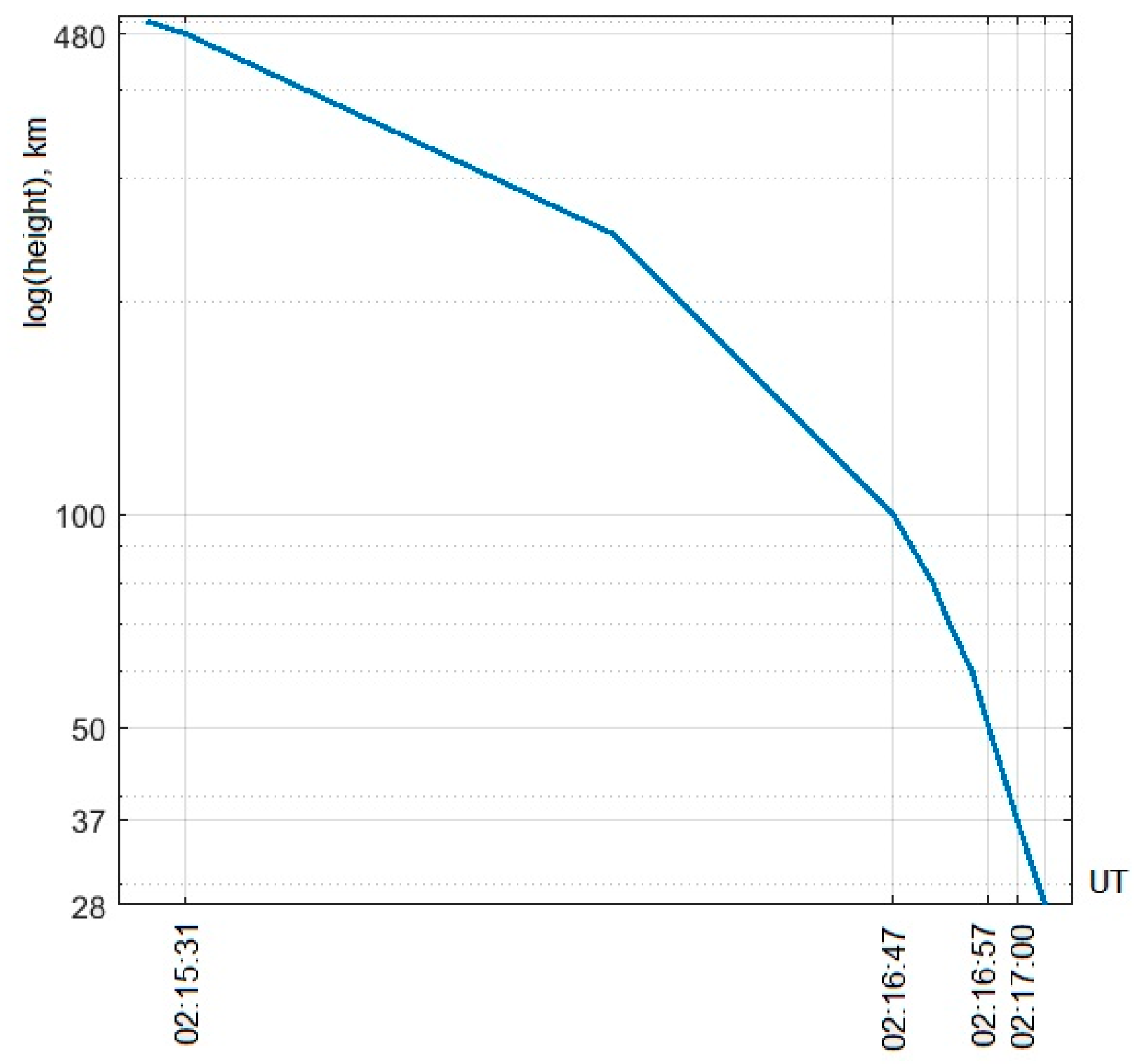
4. Meteor Trajectory Estimation
- RA 13.96 ± 9.085°, Dec −0.64° ± 0.16°; θ = ~ 242°;
- Meteor trajectory:
- Initial point: 19.500° N, 100.983° W, h1 = ~50 km (02:18:46 UT, 19 February 2020);
- Explosion point: 19.619° N, 100.764° W, h2 = ~36.8 km (02:18:49 UT, 19 February 2020);
- End point: 19.700° N, 100.617° W, h3 = ~28 km (02:18:51 UT, 19 February 2020)
- Angle to the horizontal: α = ~26.46°.
- The average observed meteor velocity: υ(visible) = ~9.87 km/s.
5. Modeling Results
6. Possible Ionospheric Impact: Results of Observations
6.1. General Considerations and Methods (Approaches) Used
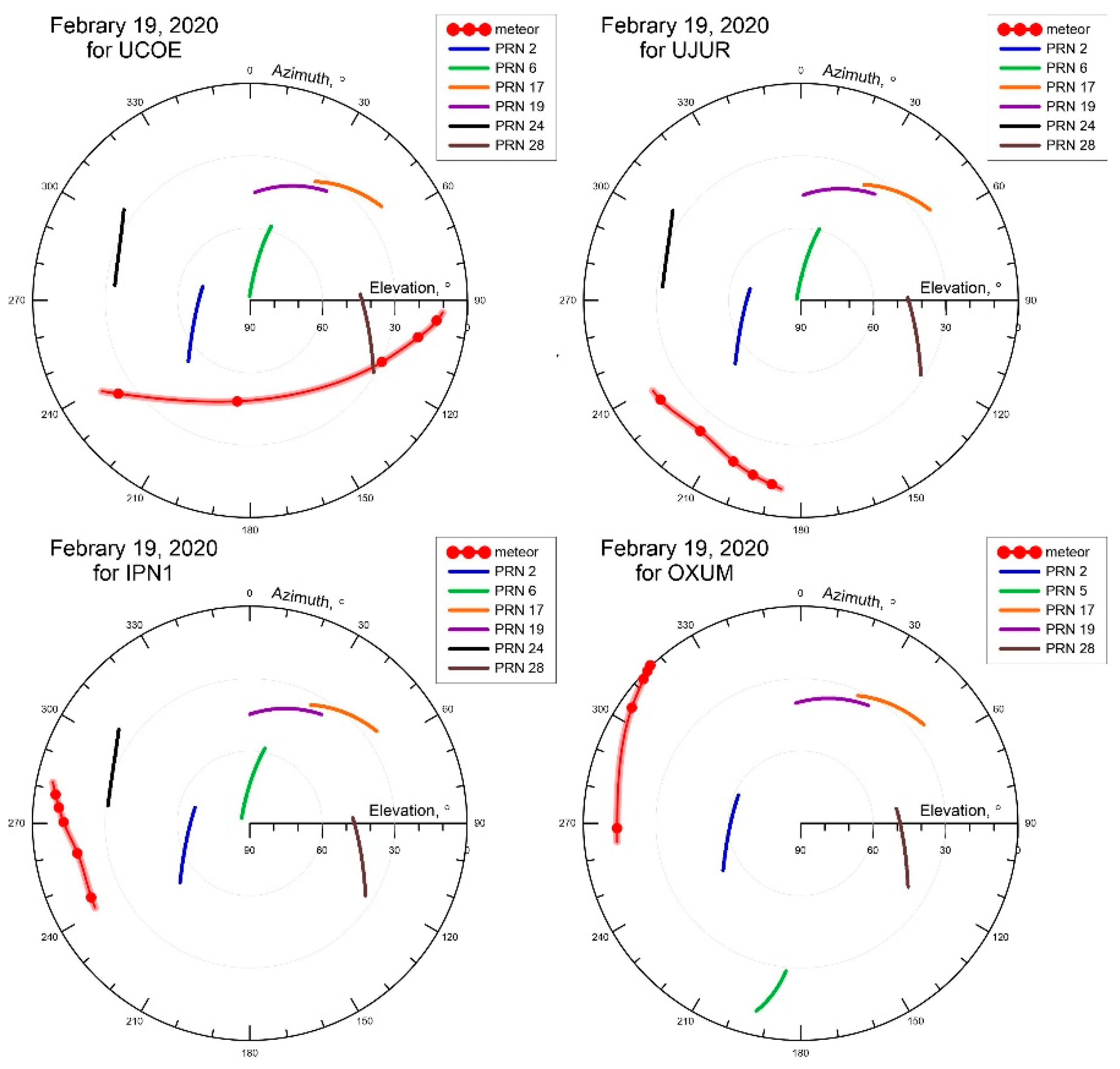
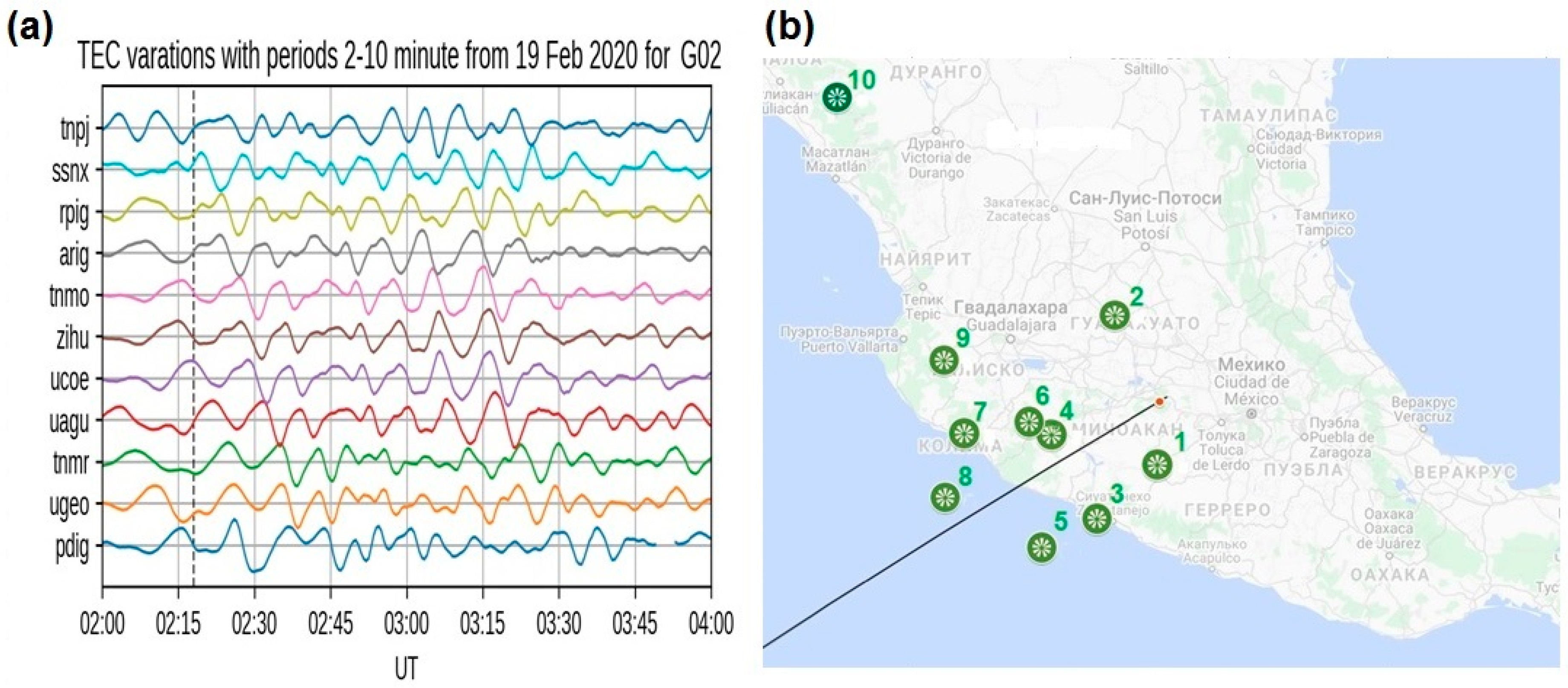
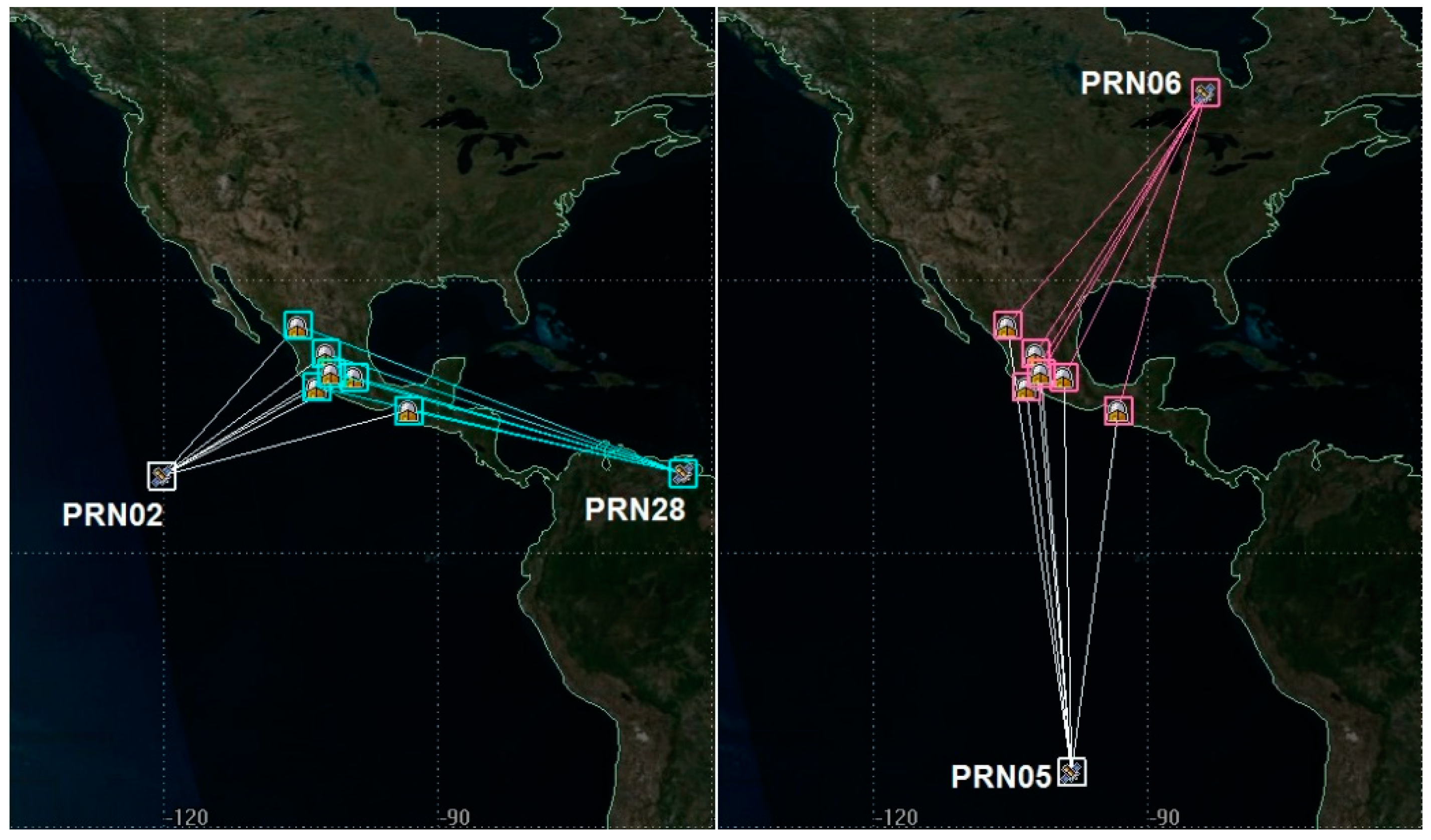
6.2. Data Used
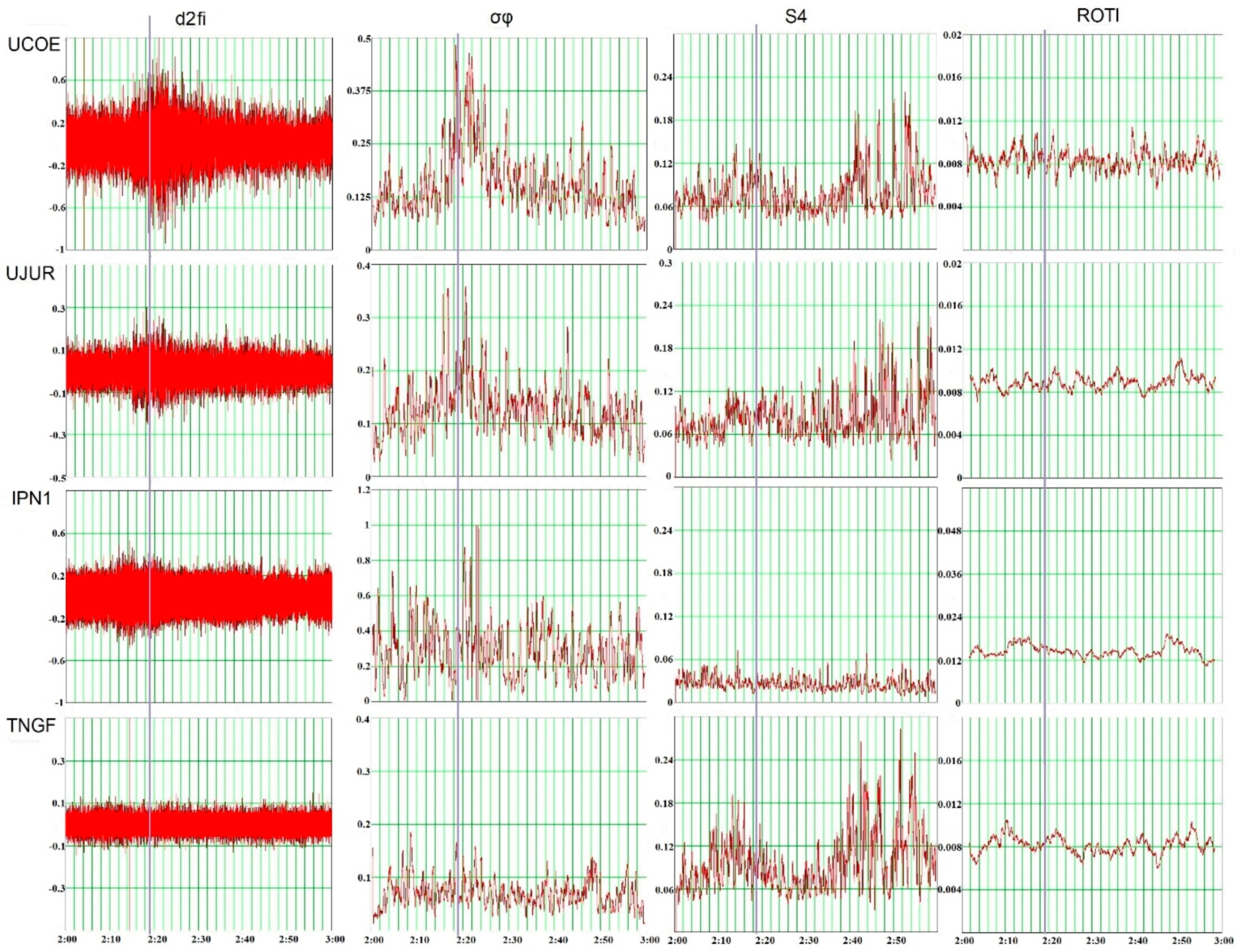
6.3. Ionospheric Response Registered by Scintillation Indices
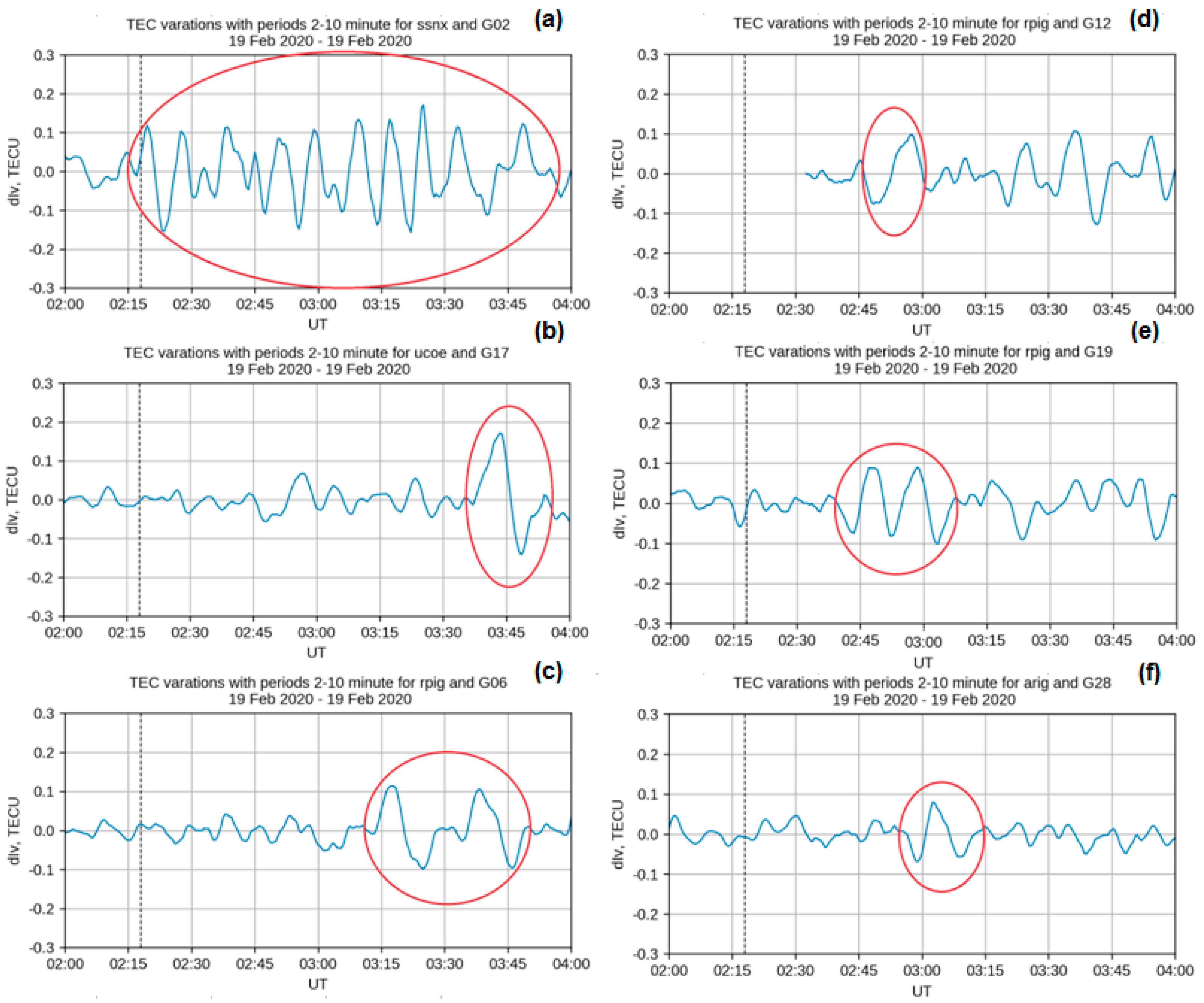
6.4. Ionospheric Response Registered by dIv Data
6.5. Comparative Analysis of Results by Two Methods
7. Possibility of Other Effects
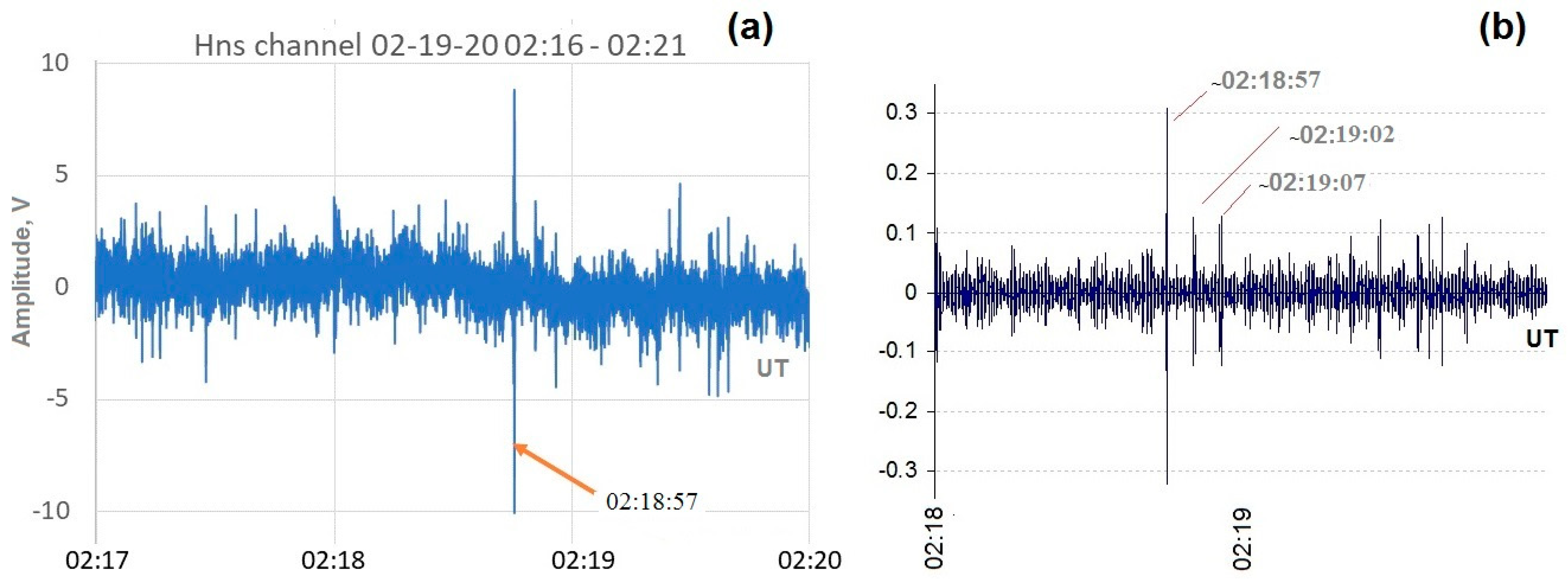
7.1. Possible Schumann Resonance Effect
7.2. Possible Seismic Effect
7.3. Possible Magnetic Effects
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| SAW | shock-acoustic wave |
| GW | gravity wave |
| TID | Travelling Ionospheric Disturbance |
| Dst | disturbance storm time index of global magnetic activity |
| Kp | planetary three-hour index of global magnetic activity |
| sTEC | slant Total Electron Content |
| vTEC | vertical Total Electron Content |
| δvTEC | vTEC deviation from its median value |
| VIS | Vertical Ionospheric Sounding |
| foF2 | critical frequency of F2 layer |
| RA | right ascension for topocentric radiant |
| Dec | declination for topocentric radiant |
| PRN | number of the pseudo-random noise code sequence unique for each satellite |
| GLM | Geostationary Lightning Mapper |
| h(breakup) | height of break-up |
| h(burst) | height of explosion |
| LoS | line-of-sight |
| dIv | sTEC variations converted to equivalent vertical variations |
Appendix B
Appendix C
References
- Mokhnatkin, A.; Molotov, I.; Perez Tijerina, E.G.; Perez Leon, J.E.; Kokina, T.; Schildknecht, T. Implementing of the ISON project in Northern Mexico. Open Astron. 2018, 27, 167–174. [Google Scholar] [CrossRef]
- Chernogor, L.F. Physical effects of the Romanian meteoroid. 1. Space Sci. Technol. 2018, 24, 1. [Google Scholar] [CrossRef]
- Chernogor, L.F. Physical effects of the Romanian meteoroid. 2. Space Sci. Technol. 2018, 24, 2. [Google Scholar] [CrossRef]
- Silber, E.A.; Boslough, M.; Hocking, W.K.; Gritsevich, M.; Whitaker, R.W. Physics of meteor generated shock waves in the Earth’s atmosphere—A review. Adv. Space Res. 2018, 62, 489–532. [Google Scholar] [CrossRef] [Green Version]
- Cander, L.R. Lonospheric Space Weather; Springer Geophysics: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Hocke, K.; Schlegel, K. A review of atmospheric gravity waves and travelling ionospheric disturbances: 1982–1995. Ann. Geophys. 1996, 14, 917–940. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Perevalova, N.P. GPS Monitoring of Earth upper Atmosphere; Russian Academy of Sciences Siberian Branch: Irkutsk, Russia, 2006; 460p, ISBN 5-98277-033-7. [Google Scholar]
- ElGabry, M.N.; Korrat, I.M.; Hussein, H.M.; Hamamaa, I.H. Infrasound detection of meteors. NRIAG J. Astron. Geophys. 2017, 6, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Gordeev, E.I.; Kulichkov, S.N.; Firstov, P.P.; Popov, O.E.; Chunchuzov, I.P.; Budilov, D.I.; Chebrov, D.V. Infrasonic waves and assessment of energy of explosion of Beringovomorsky meteoroid on December 19, 2018. Acad. Sci. Rep. 2019, 489, 409–413. [Google Scholar] [CrossRef]
- Trigo-Rodrıguez, J.M.; Lyytinen, E.; Gritsevich, M.; Moreno-Ibanez, M.; Bottke, W.F.; Williams, I.; Lupovka, V.; Dmitriev, V.; Kohout, T.; Grokhovsky, V. Orbit and dynamic origin of the recently recovered Annama’s H5 chondrite. Mon. Not. R. Astron. Soc. 2015, 449, 2119–2127. [Google Scholar] [CrossRef] [Green Version]
- Cherniakov, S.M.; Turyansky, V.A.; Gomonov, A.D. Ionospheric effects of meteor explosion over North Finland on November 2017. Physics of Auroral Phenomena. In Proceedings of the XLI Annual Seminar, Apatity, Russia, 12–16 March 2018; pp. 102–105. [Google Scholar] [CrossRef]
- Cherniakov, S.M.; Nikolashkin, S.V.; Tereshchenko, V.A. Siberian meteors: Ionospheric and geomagnetic effects in the lower ionosphere of high latitudes, Physics of Auroral Phenomena. In Proceedings of the XL Annual Seminar, Apatity, Russia, 13–17 March 2017; pp. 104–107. [Google Scholar]
- Perevalova, N.P.; Shestakov, N.V.; Voeykov, S.V.; Takahashi, H.; Guojie, M. Ionospheric disturbances in the vicinity of the Chelyabinsk meteoroid explosive disruption as inferred from dense GPS observations. Geophys. Res. Lett. 2015, 42, 6535–6543. [Google Scholar] [CrossRef]
- Ruzhin, Y.Y.; Kuznetsov, V.D.; Smirnov, V.M. The Ionosphere Effects of the Chelyabinsk Meteoroid Explosion. Int. J. Electron. Appl. Res. 2014, 1, 39–60. [Google Scholar]
- Yang, Y.-M.; Komjathy, A.; Langley, R.B.; Vergados, P.; Butala, M.D.; Mannucci, A.J. The 2013 Chelyabinsk Meteor Ionospheric Impact Studied Using GPS Measurements. Radio Sci. 2014, 49, 341–350. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Galkin, I.A. Global ionospheric radio observatory (GIRO). Earth Planets Space 2011, 63, 377–381. [Google Scholar] [CrossRef] [Green Version]
- Sergeeva, M.A.; Maltseva, O.A.; Gonzalez-Esparza, J.A.; De la Luz, V.; Corona-Romero, P. Features of TEC behaviour over the low-latitude North-American region during the period of medium solar activity. Adv. Space Res. 2017, 60, 1594–1605. [Google Scholar] [CrossRef]
- Sergeeva, M.A.; Maltseva, O.A.; Gonzalez-Esparza, J.-A.; Mejia-Ambriz, J.C.; De la Luz, V.; Corona-Romero, P.; Gonzalez, L.X.; Gatica-Acevedo, V.J.; Romero-Hernandez, E.; Rodriguez-Martinez, M.; et al. TEC behavior over the Mexican region. Ann. Geophys. 2018, 61, 104. [Google Scholar] [CrossRef]
- Somsikov, V.M. Solar Terminator and Dynamic Phenomena in the Atmosphere: A Review. Geomagn. Aeron. 2011, 51, 707–719. [Google Scholar] [CrossRef]
- Gural, P.S. A new method of meteor trajectory determination applied to multiple unsynchronized video cameras. Meteorit. Planet. Sci. 2012, 47, 1405–1418. [Google Scholar] [CrossRef]
- Ceplecha, Z. Geometric, Dynamic, orbital and photometric data on meteoroids from photographic fireball networks. Bull. Astron. Inst. Czechoslov. 1987, 38, 222–234. [Google Scholar]
- Bruning, E.; Tillier, C.E.; Edgington, S.F.; Rudlosky, S.D.; Zajic, J.; Gravelle, C.; Foster, M.; Calhoun, K.M.; Campbell, P.A.; Stano, G.T.; et al. Meteorological imagery for the geostationary lightning mapper. J. Geophys. Res. Atmos. 2019, 124, 14258–14309. [Google Scholar] [CrossRef]
- Rudlosky, S.D.; Goodman, S.J.; Virts, K.L.; Bruning, E.C. Initial Geostationary Lightning Mapper Observations. Geophys. Res. Lett. 2019, 46, 1097–1104. [Google Scholar] [CrossRef]
- Wheeler, L.F.; Register, P.J.; Mathias, D.L. A fragment-cloud model for asteroid breakup and atmospheric energy deposition. Icarus 2017, 295, 149–169. [Google Scholar] [CrossRef]
- Register, P.J.; Mathias, D.L.; Wheeler, L.F. Asteroid fragmentation approaches for modeling atmospheric energy deposition. Icarus 2017, 284, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Mathias, D.L.; Wheeler, L.F.; Dotson, J.L. A probabilistic asteroid impact risk model: Assessment of sub-300 m impacts. Icarus 2017, 289. [Google Scholar] [CrossRef]
- Collins, G.S.; Melosh, H.J.; Marcus, R.A. Earth Impact Effects Program: A web-based computer program for calculating the regional environmental consequences of a meteoroid impact on Earth. Meteorit. Planet. Sci. 2005, 40, 817–840. [Google Scholar] [CrossRef] [Green Version]
- Ferrier, L.; Verant, J.L.; Moschetta, J.M. Aerothermodynamical study for the entry of an Apophis-like asteroid. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef]
- Hills, J.G.; Goda, M.P. The fragmentation of small asteroids in the atmosphere. Astron. J. 1993, 105, 1114–1144. [Google Scholar] [CrossRef]
- Chyba, C.; Thomas, P.; Zahnle, K. The 1908 Tunguska explosion: Atmospheric disruption of a stony asteroid. Nature 1993, 361, 40–44. [Google Scholar] [CrossRef]
- Borovicka, J.; Spurny, P.; Grigore, V.I.; Svoren, J. The January 7, 2015, superbolide over Romania and structural diversity of meter-sized asteroids. Planet Space Sci. 2017, 143, 147–158. [Google Scholar] [CrossRef] [Green Version]
- Pricopi, D.; Dascalu, M.; Badescu, O.; Nedelcu, A.; Popescu, M.; Sonka, A.; Suran, D. Orbit reconstruction for the meteoroid of the meteorite-producting fireball that exploded over Romania on January 7, 2015. Proc. Rom. Acad. Ser. A 2016, 17, 133–136. [Google Scholar]
- Aarons, J. Global morphology of ionospheric scintillations. Proc. IEEE 1982, 70, 360. [Google Scholar] [CrossRef]
- Doherty, P.H.; Delay, S.H.; Valladares, C.E.; Klobuchar, J.A. Ionospheric Scintillation Effects in the Equatorial and Auroral Regions. Navig. J. Inst. Navig. 2003, 50, 235–245. [Google Scholar] [CrossRef]
- Juan, J.M.; Sanz, J.; González-Casado, G.; Rovira-Garcia, A.; Camps, A.; Riba, J.; Barbosa, J.; Blanch, E.; Altadill, D.; Orus, R. Feasibility of precise navigation in high and low latitude regions under scintillation conditions. J. Space Weather Space Clim. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Hayakawa, M.; Molchanov, O.A. Seismo Electromagnetics: Lithosphere–Atmosphere–Ionosphere Coupling; Terra Sci.: Tokyo, Japan, 2008; p. 477. [Google Scholar]
- Perevalova, N.P.; Shestakov, N.V.; Zhupityayeva, A.S.; Yasyukevich, Y.V.; Voeikov, S.V.; Kutelev, K.A. Dynamics of Total Electron Content during the passage and explosion of Chelyabinsk meteoroid. Sol. Terr. Phys. 2013, 24, 36–41. [Google Scholar]
- Afraimovich, E.L.; Perevalova, N.P.; Plotnikov, A.V.; Uralov, A.M. The shock-acoustic waves generated by earthquakes. Ann. Geophys. 2001, 19, 395–409. [Google Scholar] [CrossRef] [Green Version]
- Chou, M.-Y.; Shen, M.-H.; Lin, C.C.H.; Yue, J.; Chen, C.-H.; Liu, J.-Y.; Lin, J.-T. Gigantic circular shock acoustic waves in the ionosphere triggered bythe launch of FORMOSAT-5 satellite. Space Weather 2018, 16, 172–184. [Google Scholar] [CrossRef]
- Demyanov, V.; Sergeeva, M.; Fedorov, M.; Ishina, T.; Gatica-Acevedo, V.J.; Cabral-Cano, E. Comparison of TEC Calculations Based on Trimble, Javad, Leica, and Septentrio GNSS Receiver Data. Remote Sens. 2020, 12, 3268. [Google Scholar] [CrossRef]
- Demyanov, V.V.; Sergeeva, M.A.; Yasyukevich, A.S. GNSS High-Rate Data and the Efficiency of Ionospheric Scintillation Indices. In Satellites Missions and Technologies for Geosciences; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Pi, X.; Mannucci, A.J.; Lindqwister, U.J.; Ho, C.M. Monitoring of global ionospheric irregularities using the worldwide GPS-network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Tiwari, R.; Strangeways, H.J. Regionally based alarm index to mitigate ionospheric scintillation effects for GNSS receivers. Space Weather 2015, 13, 72–85. [Google Scholar] [CrossRef] [Green Version]
- Yasyukevich, Y.V.; Kiselev, A.V.; Zhivetiev, I.V.; Edemskiy, I.K.; Syrovatskii, S.V.; Maletckii, B.M.; Vesnin, A.M. SIMuRG: System for Ionosphere Monitoring and Research from GNSS. GPS Solut. 2020, 24. [Google Scholar] [CrossRef]
- Kazimirovsky, E.S.; Kokourov, V.D.; Vergasova, G.V. Dynamical climatology of the upper mesosphere, lower thermosphere and ionosphere. Surv. Geophys. 2006, 27, 211–255. [Google Scholar] [CrossRef]
- Hargreaves, J.K. The Upper Atmosphere and Solar Terrestrial Relations: An Introduction to the Aerospace Environment; Van Nostrand Reinhold: New York, NY, USA, 1979. [Google Scholar]
- Kazimirovsky, E.; Herraiz, M.; De la Morena, B.A. Effects on the ionosphere due to phenomena occurring below it. Surv. Geophys. 2003, 24, 139–184. [Google Scholar] [CrossRef]
- Afraimovich, E.; Astafyeva, E.; Demyanov, V.; Edemskiy, I.; Gavrilyuk, N.; Ishin, A.B.; Kosogorov, E.A.; Leonovich, L.A.; Lesyuta, O.S.; Palamartchouk, K.S.; et al. A review of GPS/GLONASS studies of the ionospheric response to natural and anthropogenic processes and phenomena. J. Space Weather Space Clim. 2013, 3. [Google Scholar] [CrossRef] [Green Version]
- Sierra, F.P.; Vázquez, H.S.; Andrade, M.E.; Mendoza, B.; Rodríguez-Osorio, D. Development of a Schumann-resonance station in Mexico: Preliminary measurements. IEEE Trans. Propag. Mag. 2014, 56, 112–119. [Google Scholar] [CrossRef]
- Chernogor, L.F. Geomagnetic field effects of the Chelyabinsk meteoroid. Geomagn. Aeron. 2014, 54, 613–624. [Google Scholar] [CrossRef]
- Cabral-Cano, E.; Pérez-Campos, X.; Márquez-Azúa, B.; Sergeeva, M.A.; Salazar-Tlaczani, L.; DeMets, C.; Adams, D.; Galetzka, J.; Feaux, K.; Serra, Y.L.; et al. TLALOCNet: A Continuous GPS-Met Backbone in Mexico for Seismotectonic, and Atmospheric Research. Seismol. Res. Lett. 2018, 89, 373–381. [Google Scholar] [CrossRef]
- Gonzalez-Esparza, J.A.; Sergeeva, M.A.; Corona-Romero, P.; Mejia-Ambriz, J.C.; Gonzalez, L.X.; De la Luz, V.; Aguilar-Rodriguez, E.; Romero-Hernandez, E. Space Weather Events, Hurricanes, and Earthquakes in Mexico in September 2017. Space Weather 2018, 16, 2038–2051. [Google Scholar] [CrossRef]
- Pérez-Campos, X.; Espíndola, V.H.; Pérez, J.; Estrada, J.A.; Cárdenas Monroy, C.; Bello, D.; González-López, A.; González Ávila, D.; Contreras Ruiz Esparza, M.G.; Maldonado, R.; et al. The Mexican National Seismological Service: An Overview. Seismol. Res. Lett. 2018, 89, 318–323. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Mylnikova, A.A.; Polyakova, A.S. Estimating the total electron content absolute value from the GPS/GLONASS data. Results Phys. 2015, 5, 32–33. [Google Scholar] [CrossRef] [Green Version]





| № | Geographical Coordinates (Lat, Lon)° | Data of Event (DD.MM.YYYY, HH:MM) | VIS Data | δvTEC, % at the Site of Explosion/Meteor | Region |
|---|---|---|---|---|---|
| 1 | 68.70, 23.8 | 16.11.2017, 16:40 | (+) | −30 | Northern Finland |
| 2 | 65.95, 29.72 | 19.04.2014, 22:14 | (+) | −10 | Annama |
| 3 | 64.30, 123.1 | 04.03.2014, 21:29 | (+) | −17.9 | Vilyuisk |
| 4 | 56.90, 172.4 | 18.12.2018, 23:48 | −3 | Bering Strait | |
| 5 | 55.00, 61 | 15.02.2013, 03:20 | (+) | −15 | Chelyabinsk |
| 6 | 45.70, 27.1 | 07.01.2015, 01:06 | −7.8 | Romania |
| Station | Distance to The Explosion Ground Projection Point, km | Data Time Resolution | Geographic | Geomagnetic | ||
|---|---|---|---|---|---|---|
| Lat°,N | Lon°,W | Lat°,N | Lon°,W | |||
| High-rate data | ||||||
| UCOE (Trimble) | 99.7 | 20 Hz | 19.8 | 101.68 | 27.88 | 31.11 |
| UJUR (Trimble) | 125 | 50 Hz | 20.7 | 100.44 | 28.83 | 29.85 |
| TNGF (Trimble) | 171 | 50 Hz | 19.32 | 99.17 | 27.56 | 28.37 |
| IPN1 (Leica) | 172 | 50 Hz | 19.29 | 99.64 | 27.54 | 28.89 |
| OXUM (Trimble) | 632 | 5 Hz | 15.66 | 96.49 | 24.13 | 25.22 |
| Low-rate data | ||||||
| UCOE | 99.7 | 15s | 19.8 | 101.68 | 27.88 | 31.11 |
| TNMO | 54 | 15s | 19.65 | 101.29 | 27.72 | 30.65 |
| ARIG | 155 | 30s | 18.28 | 100.35 | 26.43 | 29.52 |
| SSNX | 171 | 30s | 19.33 | 99.18 | 27.57 | 28.38 |
| ZIHU | 235 | 30s | 17.6 | 101.47 | 25.67 | 30.64 |
| RPIG | 265 | 30s | 21.89 | 99.98 | 30.04 | 29.48 |
| UGEO | 293 | 15s | 20.69 | 103.35 | 28.57 | 32.94 |
| UAGU | 302 | 15s | 21.92 | 102.31 | 29.88 | 31.97 |
| TNMR | 308 | 30s | 18.28 | 103.35 | 26.18 | 32.69 |
| PDIG | 769 | 30s | 25.04 | 105.4 | 32.69 | 35.63 |
| TNPJ | 915 | 30s | 15.7 | 93.22 | 24.38 | 21.78 |
| Station | PRN28 | PRN02 | PRN24 * | PRN06 | PRN19 | PRN17 | |
|---|---|---|---|---|---|---|---|
| d2fi | UCOE | + | + | + | + | + | + |
| UJUR | + | +/- | + | +/- | +/- | +/- | |
| IPN1 | + | - | + | +/- | + | +^ | |
| TNGF | - | - | - | - | - | - | |
| OXUM | - | - | - | - | - | - | |
| σφ | UCOE | + | + | + | + | + | + |
| UJUR | + | + | + | + | + | + | |
| IPN1 | + | + | + | + | + | + | |
| TNGF | - | - | - | - | - | - | |
| OXUM | + | - | no data | - | + | + | |
| S4 | UCOE | + | +^ | + | + | + | +/- |
| UJUR | + | +^ | +^ | + | +/- | + | |
| IPN1 | - | - | - | - | - | +^ | |
| TNGF | + | +-^ | - | +/- | - | - | |
| OXUM | +/- | + | + | - | - | + | |
| ROTI | UCOE | + | - | - | + | + | +/- |
| UJUR | - | - | - | - | + | - | |
| IPN1 | +/- | - | - | +/- | + | +/- | |
| TNGF | - | - | - | - | + | - | |
| OXUM | - | - | - | - | + | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sergeeva, M.A.; Demyanov, V.V.; Maltseva, O.A.; Mokhnatkin, A.; Rodriguez-Martinez, M.; Gutierrez, R.; Vesnin, A.M.; Gatica-Acevedo, V.J.; Gonzalez-Esparza, J.A.; Fedorov, M.E.; et al. Assessment of Morelian Meteoroid Impact on Mexican Environment. Atmosphere 2021, 12, 185. https://doi.org/10.3390/atmos12020185
Sergeeva MA, Demyanov VV, Maltseva OA, Mokhnatkin A, Rodriguez-Martinez M, Gutierrez R, Vesnin AM, Gatica-Acevedo VJ, Gonzalez-Esparza JA, Fedorov ME, et al. Assessment of Morelian Meteoroid Impact on Mexican Environment. Atmosphere. 2021; 12(2):185. https://doi.org/10.3390/atmos12020185
Chicago/Turabian StyleSergeeva, Maria A., Vladislav V. Demyanov, Olga A. Maltseva, Artem Mokhnatkin, Mario Rodriguez-Martinez, Raul Gutierrez, Artem M. Vesnin, Victor Jose Gatica-Acevedo, Juan Americo Gonzalez-Esparza, Mark E. Fedorov, and et al. 2021. "Assessment of Morelian Meteoroid Impact on Mexican Environment" Atmosphere 12, no. 2: 185. https://doi.org/10.3390/atmos12020185
APA StyleSergeeva, M. A., Demyanov, V. V., Maltseva, O. A., Mokhnatkin, A., Rodriguez-Martinez, M., Gutierrez, R., Vesnin, A. M., Gatica-Acevedo, V. J., Gonzalez-Esparza, J. A., Fedorov, M. E., Ishina, T. V., Pazos, M., Gonzalez, L. X., Corona-Romero, P., Mejia-Ambriz, J. C., Gonzalez-Aviles, J. J., Aguilar-Rodriguez, E., Cabral-Cano, E., Mendoza, B., ... Orrala-Legorreta, I. D. (2021). Assessment of Morelian Meteoroid Impact on Mexican Environment. Atmosphere, 12(2), 185. https://doi.org/10.3390/atmos12020185










