Application of Dynamically Constrained Interpolation Methodology in Simulating National-Scale Spatial Distribution of PM2.5 Concentrations in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region and Data
2.2. Dynamically Constrained Interpolation Methodology
2.2.1. The Dynamic Model
2.2.2. Parameter Optimization by the Adjoint Method
2.2.3. Default Settings of the Dynamical Model
2.2.4. The Process of DCIM
2.3. The OPF Method Based on Chebyshev Basis Functions
3. Results and Analysis
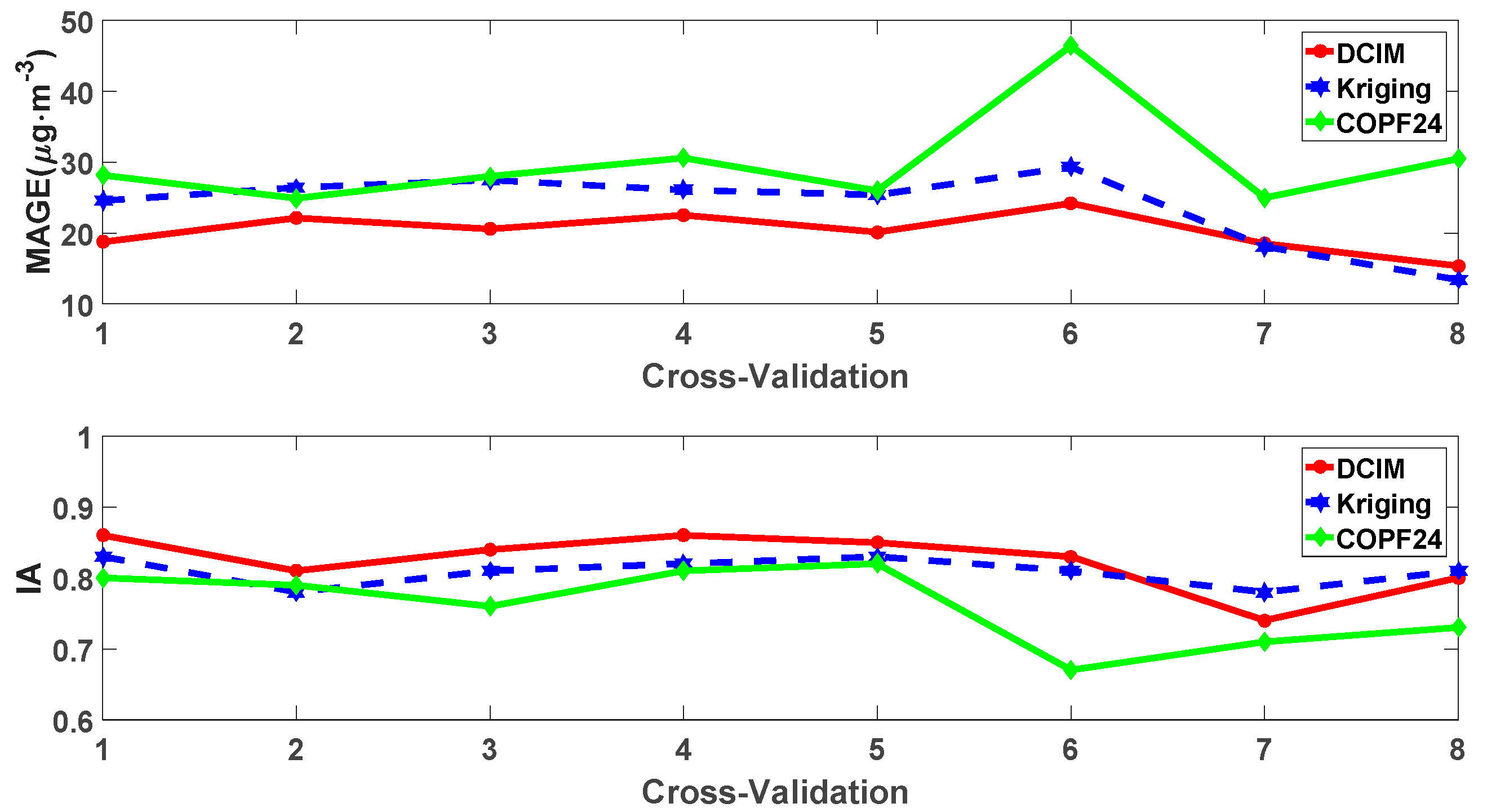
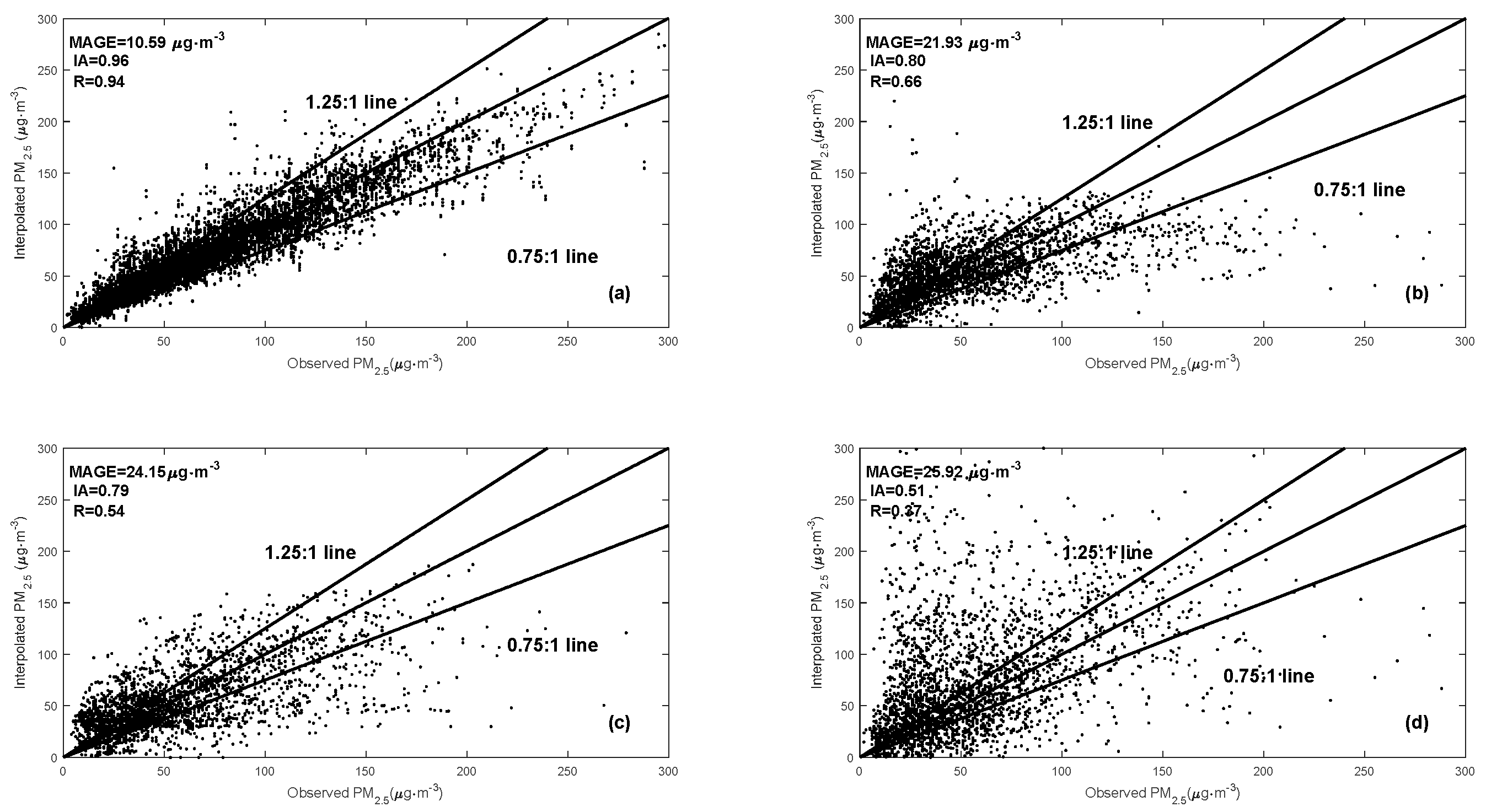
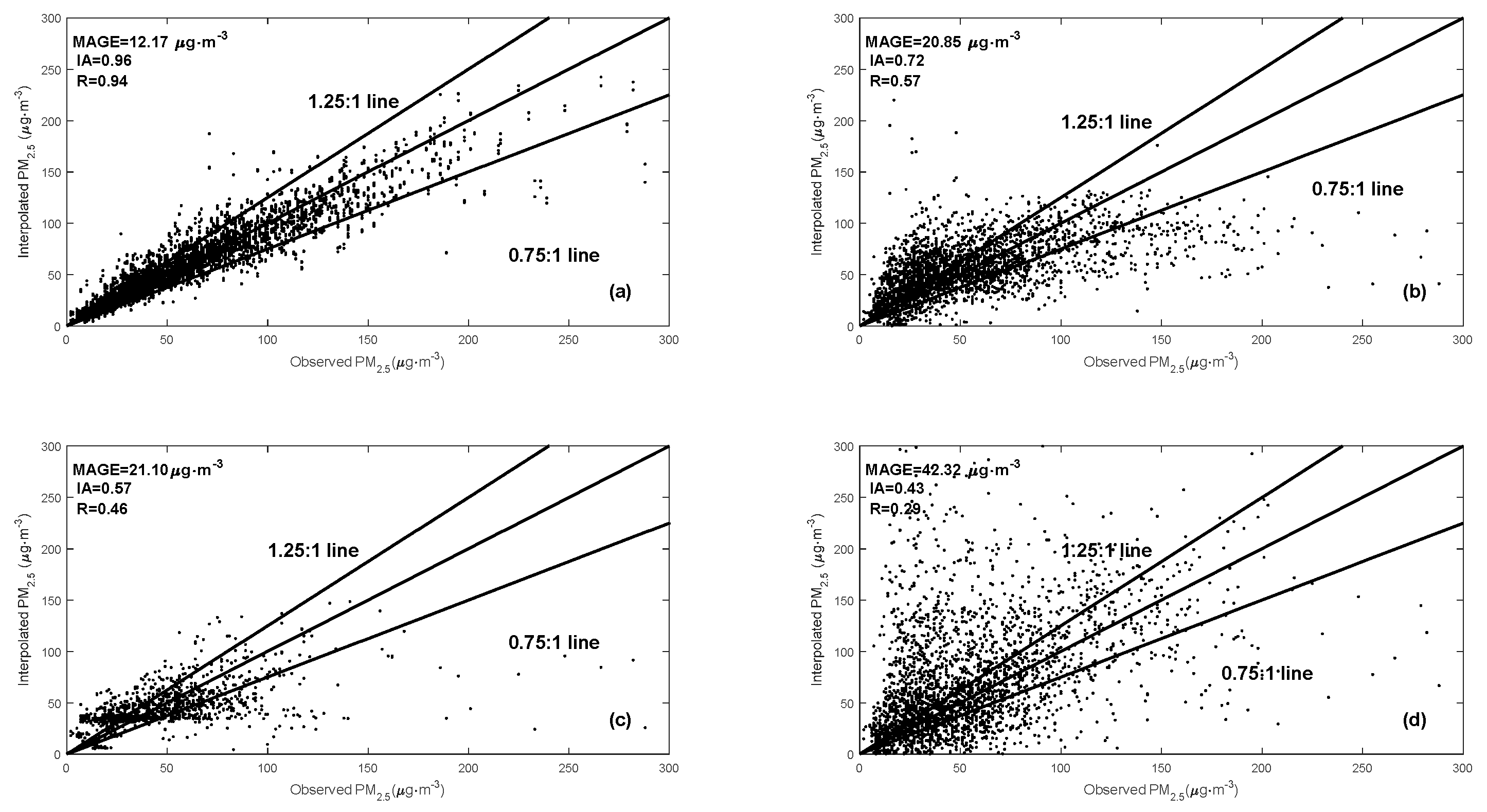
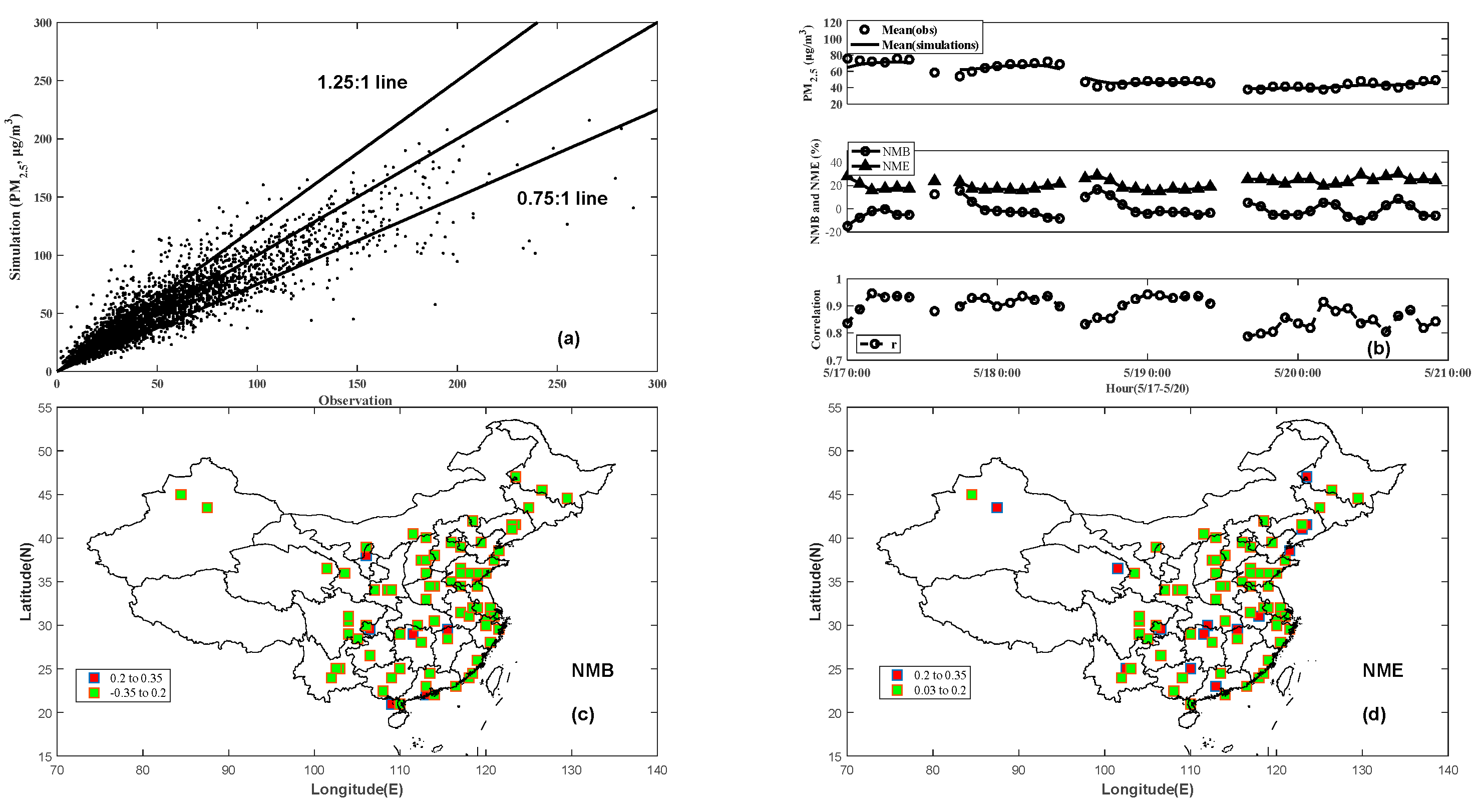
3.1. Verification and Evaluation of DCIM
3.2. Performance of the DCIM
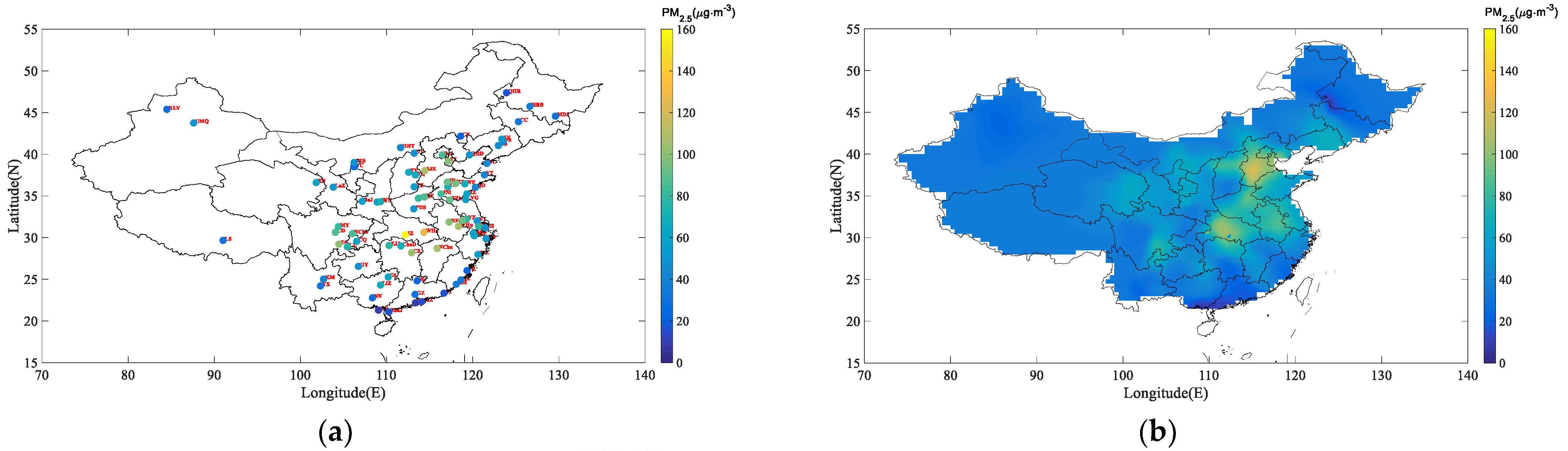
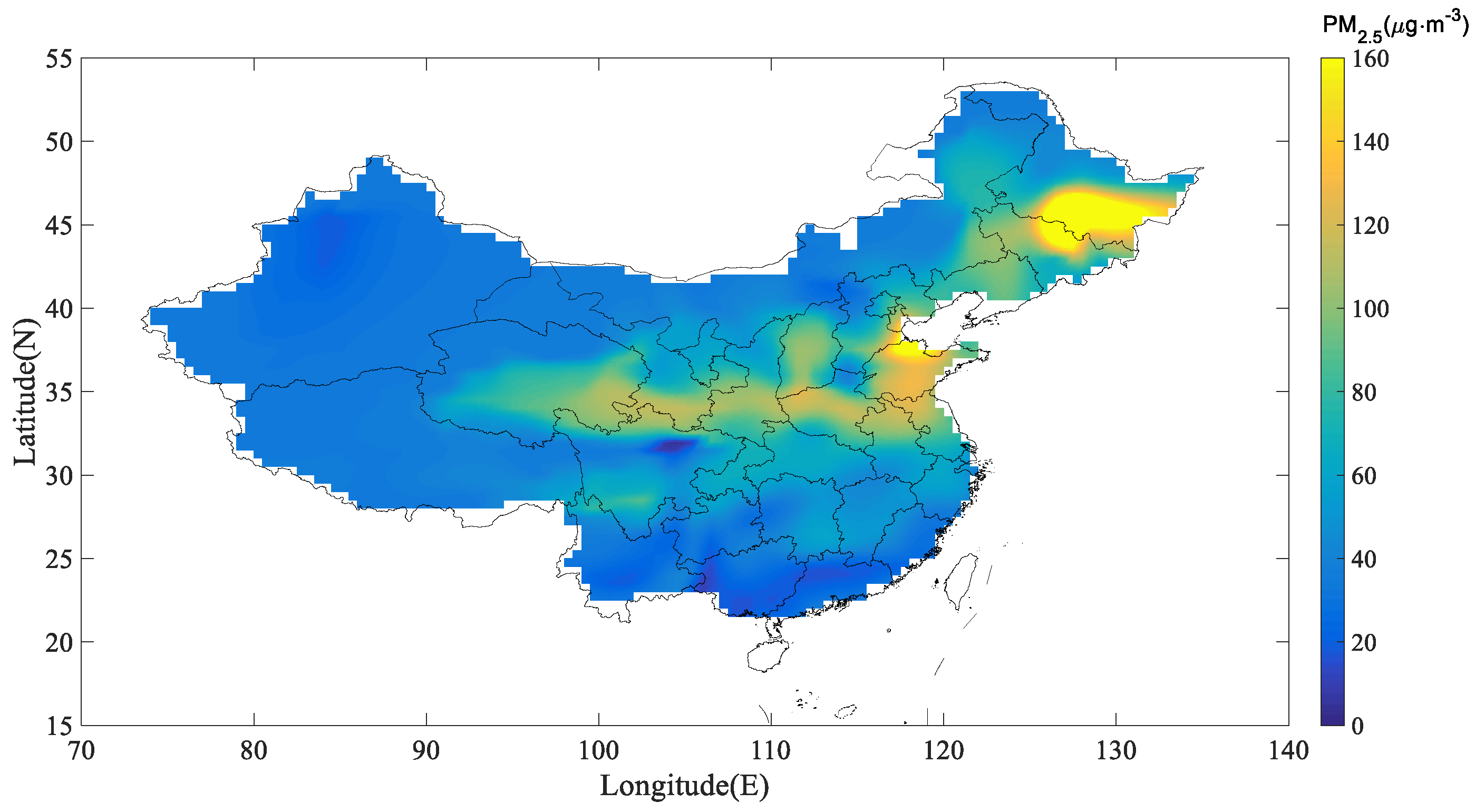
3.3. Mapping of the Mean PM2.5 Simulations
4. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, F.K.; He, K.B.; Ma, Y.L.; Yang, F.M.; Yu, X.C.; Cadle, S.H.; Chan, T.; Mulawa, P.A. Concentration and chemical characteristics of PM2.5 in Beijing, China: 2001–2002. Sci. Total Environ. 2006, 355, 264–275. [Google Scholar] [CrossRef]
- Han, B.; Zhang, R.; Yang, W.; Bai, Z.P.; Ma, Z.Q.; Zhang, W.J. Heavy haze episodes in Beijing during January 2013: Inorganic ion chemistry and source analysis using highly time-resolved measurements from an urban site. Sci. Total Environ. 2016, 544, 319–329. [Google Scholar] [CrossRef]
- Chang, H.H.; Hu, X.; Liu, Y. Calibrating MODIS aerosol optical depth for predicting daily PM2.5 concentrations via statistical downscaling. J. Expo. Sci. Environ. Epidemiol. 2014, 24, 198–404. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.L.; Wang, Z.F.; Fu, P.Q.; Yang, T.; Jiang, Q.; Dong, H.B.; Li, J.J.; Jia, J.J. Aerosol composition, sources and processes during wintertime in Beijing. China. Atmos. Chem. Phys. 2013, 13, 4577–4592. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.T.; Primbs, T.; Tao, S.; Simonich, S.L.M. Atmospheric particulate matter pollution during the 2008 Beijing Olympics. Environ. Sci. Technol. 2009, 43, 5314–5320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Park, R.J.; Jacob, D.J.; Li, Q.B.; Kilaru, V.; Sarnat, J.A. Mapping annual mean ground-level PM2.5 concentrations using Multiangle Imaging Spectroradiometer aerosol optical thickness over the contiguous United States. J. Geophys. Res. Atmos. 2004, 109, D22. [Google Scholar]
- VanDonkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environment. Environ. Health Persp. 2010, 118, 847–855. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Schichtel, B.; Koutrakis, P. Estimating particle sulfate concentrations using MISR retrieved aerosol properties. IEEE J. STARS 2009, 2, 176–184. [Google Scholar] [CrossRef]
- Song, W.Z.; Jia, H.F.; Huang, J.F.; Zhang, Y.Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China. Remote. Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Li, T.W.; Shen, H.F.; Yuan, Q.Q.; Zhang, X.C. Estimating Ground-Level PM2.5 by Fusing Satellite and Station Observations: A Geo-Intelligent Deep Learning Approach. Geophys. Res. Lett. 2017. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Li, Q.; Zhu, Y.J.; Hou, J.X.; Jin, L.Y.; Wang, J.J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Li, T.W.; Shen, H.F.; Zeng, C.; Yuan, Q.Q.; Zhang, L.P. Point-surface fusion of station measurements and satellite observations for mapping PM2.5 distribution in China: Methods and assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef] [Green Version]
- Hrust, L.; Klaic, Z.B.; Krizan, J.; Antonic, O.; Hercog, P. Neural network forecasting of air pollutants hourly concentrations using optimized temporal averages of meteorological variables and pollutant concentrations. Atmos. Environ. 2009, 43, 5588–5596. [Google Scholar] [CrossRef]
- Niska, H.; Rantamaki, M.; Hiltuinen, T.; Karppinen, A.; Kukkonen, J.L.; Ruuskanen, J.; Kolehmainen, M. Evaluation of an integrated modeling system containing a multi-layer perceptron model and the numerical weather prediction model HIRLAM for the forecasting of urban airborne pollutant concentrations. Atmos. Environ. 2005, 39, 6524–6536. [Google Scholar] [CrossRef]
- Zhang, H.F.; Wang, Z.H.; Zhang, W.Z. Exploring spatiotemporal patterns of PM2.5 in China based on ground level observations for 190 cities. Environ. Pollut. 2016, 216, 559–567. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.L.; Cobourn, W.G.; Bai, Y.Q. Development of nonlinear empirical models to forecast daily PM2.5 and ozone levels in three large Chinese cities. Atmos. Environ. 2016, 147, 209–223. [Google Scholar] [CrossRef]
- Physick, W.L.; Cope, M.E.; Lee, S.; Hurley, P.J. An approach for estimating exposure to ambient concentrations. J. Expo. Sci. Environ. Epidemiol. 2007, 17, 76–83. [Google Scholar] [CrossRef]
- Lv, B.L.; Hu, Y.T.; Howard, H.C.; Armistead, G.R.; Cai, J.; Xu, B.; Bai, Y.Q. Daily estimation of ground-level PM2.5 concentrations at 4 km resolution over Beijing-Tianjin-Hebei by fusing MODIS AOD and ground observations. Sci. Total Environ. 2017, 580, 235–244. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Pan, H.D.; Fan, W.; Lv, X.Q. Application of surface spline interpolation in inversion of bottom friction coefficients. J. Atmos. Ocean. Technol. 2017, 34, 2021–2028. [Google Scholar] [CrossRef]
- Li, B.T.; Liu, Y.Z.; Wang, X.Y.; Fu, Q.J.; Lv, X.Q. Application of the Orthogonal Polynomial Fitting Method in Estimating PM2.5 Concentrations in Central and Southern Regions of China. Int. J. Environ. Res. Public Health 2019, 16, 1418. [Google Scholar] [CrossRef] [Green Version]
- Lebedev, K.; Yaremchuk, M.; Mitsudera, H.; Nakano, I.; Yuan, G. Monitoring the Kuroshio Extension with dynamically constrained synthesis of the acoustic tomography, satellite altimeter and in situ data. J. Phys. Oceanogr. 2003, 59, 7. [Google Scholar] [CrossRef]
- Zheng, Q.X.; Li, X.N.; Lv, X.Q. Application of Dynamically Constrained Interpolation Methodology to the Surface Nitrogen Concentration in the Bohai Sea. Int. J. Environ. Res. Public Health 2019, 16, 2400. [Google Scholar] [CrossRef] [Green Version]
- Qu, W.J.; Arimoto, R.; Zhang, X.Y. Spatial distribution and interannual variation of surface PM10 concentrations over eighty-six Chinese cities. Atmos. Chem. Phys. 2010, 10, 5641–5662. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part I: History, techniques, and current status. Atmos. Environ. 2012, 60, 632–655. [Google Scholar] [CrossRef]
- Wang, D.S.; Li, N.; Shen, Y.L.; Lv, X.Q. The Parameters Estimation for a PM2.5 Transport Model with the Adjoint Method. Adv. Meteorol. 2016, 9, 1–13. [Google Scholar]
- Li, N.; Lv, X.Q.; Zhang, J.C. Application of Surface Spline Interpolation Method in Parameter Estimation of a PM2.5 Transport Adjoint Model. Math. Probl. Eng. 2018, 6, 1–11. [Google Scholar] [CrossRef]
- Henze, D.; Seinfeld, J.; Shindell, D. Inverse modeling and mapping US air quality influences of inorganic PM2.5 precursor emissions using the adjoint of GEOS-Chem. Atmos. Chem. Phys. 2009, 9, 5877–5903. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Liu, L.; Zhao, Y. Source attribution of PM2.5 pollution over North China using the adjoint method. AGU Fall Meet. Abstr. 2014, 1, 4. [Google Scholar]
- Capps, S.; Henze, D.; Russell, A. Quantifying relative contributions of global emissions to PM2.5 air quality attainment in the US. AGU Fall Meet. Abstr. 2011, 1, 7. [Google Scholar]
- Van, D.A.; Martin, R.V.; Brauer, M.; Hus, C.N.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global estimates of fine particulate matter using a combined geophysical-statistical method with information from satellites, models, and monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar]
- Wei, J.; Li, Z.; Alexei, L.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Maureen, C. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021. [Google Scholar] [CrossRef]





| Expt | K1 a (µg/m3) | K2 a | K3 a (µg/m3) | K4 a | ||||
|---|---|---|---|---|---|---|---|---|
| Initial | Final | Initial (%) | Final (%) | Initial | Final | Initial (%) | Final (%) | |
| PE_1 | 41.23 | 11.66 | 61.89 | 22.35 | 43.31 | 23.86 | 65.72 | 57.16 |
| PE_2 | 41.79 | 12.62 | 61.89 | 22.47 | 39.31 | 26.01 | 65.64 | 59.26 |
| PE_3 | 39.91 | 10.21 | 63.05 | 24.58 | 52.61 | 26.73 | 57.34 | 50.10 |
| PE_4 | 42.76 | 10.60 | 59.80 | 23.26 | 32.29 | 22.04 | 80.78 | 70.19 |
| PE_5 | 40.02 | 10.40 | 64.06 | 24.86 | 46.77 | 23.86 | 49.97 | 41.13 |
| PE_6 | 42.51 | 11.60 | 63.72 | 24.75 | 39.47 | 24.20 | 47.03 | 43.62 |
| PE_7 | 43.56 | 13.59 | 64.05 | 24.68 | 19.50 | 17.66 | 60.97 | 57.35 |
| PE_8 | 45.33 | 16.01 | 59.96 | 23.45 | 13.90 | 12.41 | 79.47 | 67.11 |
| Expt | K1 a | K2 a | K3 a | K4 a |
|---|---|---|---|---|
| PE_1 | 0.97 | 0.95 | 0.88 | 0.77 |
| PE_2 | 0.96 | 0.93 | 0.82 | 0.70 |
| PE_3 | 0.97 | 0.96 | 0.85 | 0.73 |
| PE_4 | 0.98 | 0.96 | 0.88 | 0.78 |
| PE_5 | 0.96 | 0.93 | 0.87 | 0.76 |
| PE_6 | 0.96 | 0.93 | 0.84 | 0.70 |
| PE_7 | 0.96 | 0.94 | 0.79 | 0.69 |
| PE_8 | 0.96 | 0.94 | 0.83 | 0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Xu, J.; Lv, X. Application of Dynamically Constrained Interpolation Methodology in Simulating National-Scale Spatial Distribution of PM2.5 Concentrations in China. Atmosphere 2021, 12, 272. https://doi.org/10.3390/atmos12020272
Li N, Xu J, Lv X. Application of Dynamically Constrained Interpolation Methodology in Simulating National-Scale Spatial Distribution of PM2.5 Concentrations in China. Atmosphere. 2021; 12(2):272. https://doi.org/10.3390/atmos12020272
Chicago/Turabian StyleLi, Ning, Junli Xu, and Xianqing Lv. 2021. "Application of Dynamically Constrained Interpolation Methodology in Simulating National-Scale Spatial Distribution of PM2.5 Concentrations in China" Atmosphere 12, no. 2: 272. https://doi.org/10.3390/atmos12020272
APA StyleLi, N., Xu, J., & Lv, X. (2021). Application of Dynamically Constrained Interpolation Methodology in Simulating National-Scale Spatial Distribution of PM2.5 Concentrations in China. Atmosphere, 12(2), 272. https://doi.org/10.3390/atmos12020272





