The Impact of the Variation in Weather and Season on WRF Dynamical Downscaling in the Pearl River Delta Region
Abstract
:1. Introduction
2. Data and Method
2.1. WRF Model Design
2.2. Meteorological Data
2.3. Model Evaluation
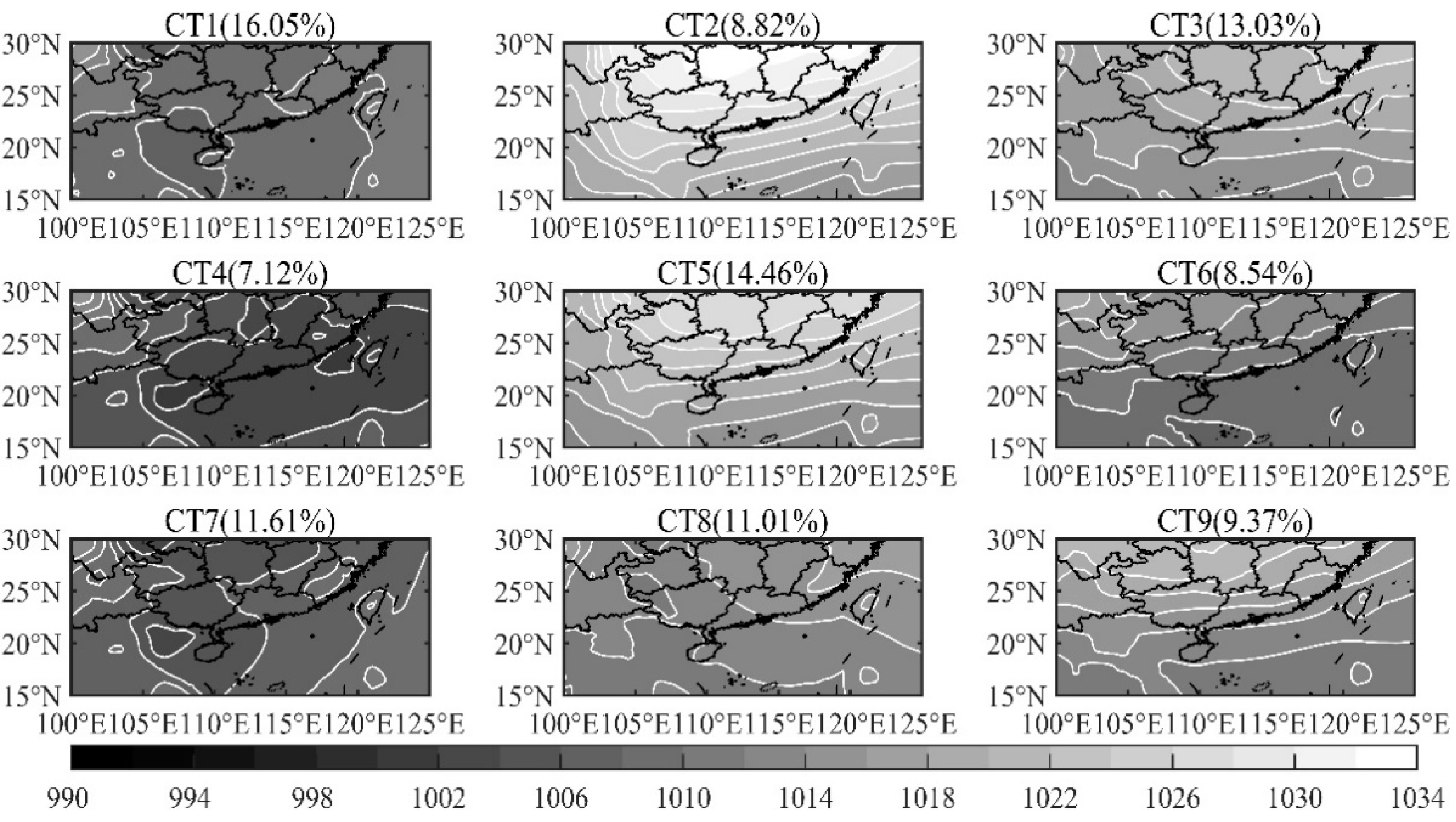
2.4. Circulation Classification
3. Results and Discussion
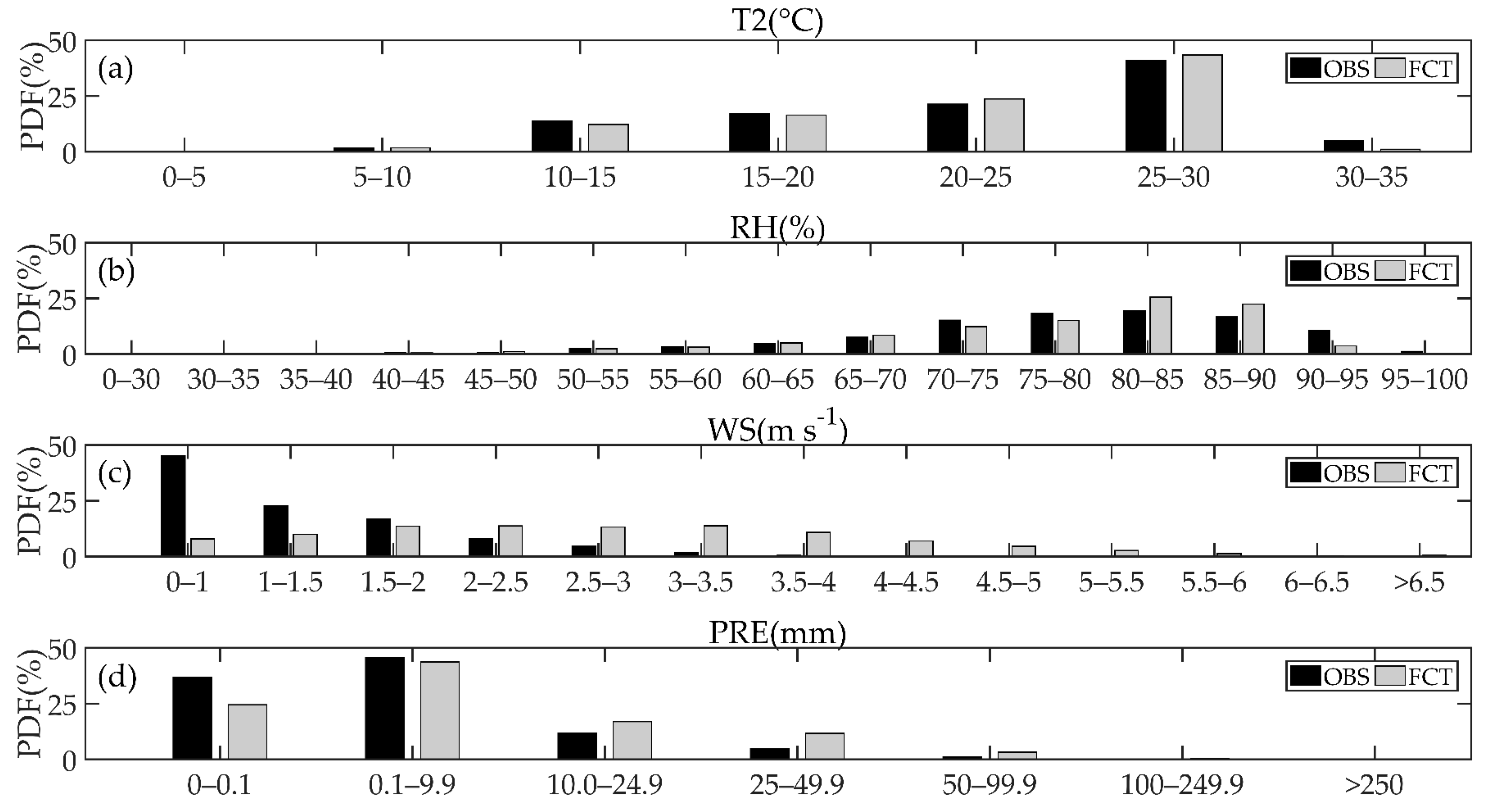
3.1. Overall Performance
3.2. The Performance in Different Seasons
3.3. The Performance in Different Circulation Types
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, K. Characteristics and Comparison of Different Downscaling Methods in Global Climate Model. Meteorol. Environ. Res. 2020, 11, 44–48. [Google Scholar] [CrossRef]
- Wang, J.; Zhi, X.F.; Chen, Y.W. Probabilistic Multimodel Ensemble Prediction of Decadal Variability of East Asian Surface Air Temperature Based on IPCC-AR5 Near-term Climate Simulations. Adv. Atmos. Sci. 2013, 30, 1129–1142. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W.; Barrow, E.M. SDSM-A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K.; Chen, L.J.; Ren, H.L. An operational statistical downscaling prediction model of the winter monthly temperature over China based on a multi-model ensemble. Atmos. Res. 2021, 249, 105262. [Google Scholar] [CrossRef]
- Kumar, B.; Chattopadhyay, R.; Singh, M.; Chaudhari, N.; Kodari, K.; Barve, A. Deep learning–based downscaling of summer monsoon rainfall data over Indian region. Theor. Appl. Climatol. 2021, 143, 1–12. [Google Scholar] [CrossRef]
- Pan, X.D.; Li, X.; Shi, X.K.; Han, J.N.; Luo, L.H.; Wang, L.X. Dynamic downscaling of near-surface air temperature at the basin scale using WRF-a case study in the Heihe River Basin, China. Front. Earth Sci. 2012, 6, 314–323. [Google Scholar] [CrossRef]
- Tong, C.H.; Yim, S.H.; Rothenberg, D.; Wang, C.; Lin, C.Y.; Chen, Y.D.; Lau, N.C. Assessing the impacts of seasonal and vertical atmospheric conditions on air quality over the Pearl River Delta region. Atmos. Environ. 2018, 180, 69–78. [Google Scholar] [CrossRef]
- You, C.; Fung, C.H. Characteristics of Sea-breeze Circulation in the Pearl River Delta Region and Its Dynamical Diagnosis. J. Appl. Meteorol. Climatol. 2019, 58, 741–755. [Google Scholar] [CrossRef]
- Mooney, P.A.; Mulligan, F.J.; Fealy, R. Evaluation of the sensitivity of the weather research and forecasting model to parameterization schemes for regional climates of Europe over the period 1990-95. J. Clim. 2013, 26, 1002–1017. [Google Scholar] [CrossRef] [Green Version]
- Otte, T.L.; Nolte, C.G.; Otte, M.J.; Bowden, J.H. Does Nudging Squelch the Extremes in Regional Climate Modeling? J. Clim. 2012, 25, 7046–7066. [Google Scholar] [CrossRef]
- Wang, B.; Yang, H.W. Hydrological issues in lateral boundary conditions for regional climate modeling: Simulation of east asian summer monsoon in 1998. Clim. Dyn. 2008, 31, 477–490. [Google Scholar] [CrossRef]
- Guo, J.; Huang, G.; Wang, X.; Li, Y.; Lin, Q. Investigating future precipitation changes over China through a high-resolution regional climate model ensemble. Earth Future 2017, 5, 285–303. [Google Scholar] [CrossRef]
- Qiu, Y.; Hu, Q.; Zhang, C. WRF simulation and downscaling of local climate in Central Asia. Int. J. Climatol. 2017, 37, 513–528. [Google Scholar] [CrossRef]
- Gao, X.J.; Zhao, Z.C.; Ding, Y.H.; Huang, R.H.; Giorgi, F. Climate change due to greenhouse effects in China as simulated by a regional climate model. Acta Meteorol. Sin. 2003, 17, 417–427. [Google Scholar] [CrossRef]
- Jiménez, P.A.; González-Rouco, J.F.; García-Bustamante, E. Surface Wind Regionalization over Complex Terrain: Evaluation and Analysis of a High-Resolution WRF Simulation. J. Appl. Meteorol. Climatol. 2008, 49, 268–287. [Google Scholar] [CrossRef] [Green Version]
- He, J.J.; Yu, Y.; Liu, N.; Zhao, S.P. Impact of land surface information on WRFs performance in complex terrain area. Chin. J. Atmos. Sci. 2014, 38, 484–498. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Powers, J.G. A Description of the Advanced Research WRF Version 3. Univ. Corp. Atmos. Res. 2008. [Google Scholar] [CrossRef]
- Pérez, J.C.; Díaz, J.P.; González, A.; Expósito, J.; Taima, D. Evaluation of WRF Parameterizations for Dynamical Downscaling in the Canary Islands. J. Clim. 2013, 27, 5611–5631. [Google Scholar] [CrossRef]
- Yu, L.J.; Yin, C.M.; Lin, Y.C.; He, J.J. Study of Dynamical Downscaling on Near Surface Wind Speed over China. J. Arid Meteorol. 2017, 35, 23–28. [Google Scholar] [CrossRef]
- Lopes, D.; Ferreira, J.; Hoi, K.I.; Miranda, A.I.; Yuen, K.V.; Mok, K.M. Weather research and forecasting model simulations over the Pearl River Delta Region. Air Qual. Atmos. Health 2019, 12, 115–125. [Google Scholar] [CrossRef]
- Wen, J.; Chen, J.; Lin, W.; Jiang, B.; Xu, S.; Lan, J. Impacts of Anthropogenic Heat Flux and Urban Land-Use Change on Frontal Rainfall near Coastal Regions: A Case Study of a Rainstorm over the Pearl River Delta, South China. J. Appl. Meteorol. Climatol. 2020, 59, 363–379. [Google Scholar] [CrossRef]
- Wang, E.T.; Sun, H.J.; Jian, Q. A Quick Report on a Dynamical Downscaling Simulation over China Using the Nested Model. Atmos. Ocean. Sci. Lett. 2010, 3, 325–329. [Google Scholar] [CrossRef]
- Zhang, B.H.; Liu, S.H.; Liu, H.P.; Ma, Y.J. The effect of MYJ and YSU schemes on the simulation of boundary layer meteorological factors of WRF. Chin. J. Geophys 2012, 55, 2239–2248. [Google Scholar] [CrossRef]
- Bowden, J.H.; Nolte, C.G.; Otte, T.L. Simulating the impact of the large-scale circulation on the 2-m temperature and precipitation climatology. Clim. Dyn. 2013, 40, 1903–1920. [Google Scholar] [CrossRef]
- Stauffer, D.R.; Seaman, N.L. Multiscale Four-Dimensional Data Assimilation. J. Appl. Meteorol. 1994, 33, 416–434. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.H.; Min, S.K.; Zhang, X.; Zwiers, F.; Alexander, L.V.; Donat, M.G.; Tung, Y.S. Attribution of extreme temperature changes during 1951–2010. Clim. Dyn. 2016, 46, 1769–1782. [Google Scholar] [CrossRef]
- Xie, P.P.; Yatagai, A.; Chen, M.Y.; Hayasaka, T.; Fukushima, Y.; Liu, C.M.; Yang, S. A Gauge-Based Analysis of Daily Precipitation over East Asia. J. Hydrometeor. 2007, 8, 607. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J. Improving the Representation of Resolved and Unresolved Topographic Effects on Surface Wind in the WRF Model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef] [Green Version]
- Soares, P.M.M.; Cardoso, R.M.; Miranda, P.M.A.; de Medeiros, J.; Belo-Pereira, M.; Espirito-Santo, F. WRF high resolution dynamical downscaling of ERA-Interim for Portugal. Clim. Dyn. 2012, 39, 2497–2522. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, J.A.; Holbrook, N.J.; Mcaneney, J. Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Conner, M.; Petty, G. Validation and Intercomparison of SSM/I Rain-Rate Retrieval Methods over the Continental United States. J. Appl. Meteorol. 1998, 37, 679–700. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Ocean. 1985, 90, 8995–9005. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Gong, S.; Zhou, C.; Lu, S.; Wu, L.; Chen, Y.; Yu, Y.; Zhao, S.; Yu, L.; Yin, C. Analyses of winter circulation types and their impacts on haze pollution in Beijing. Atmos. Environ. 2018, 192, 94–103. [Google Scholar] [CrossRef] [Green Version]
- Porras, I.; Arasa, R.; Ángeles, M.; Jésica, G.; Bernat, P. Defining a Standard Methodology to Obtain Optimum WRF Configuration for Operational Forecast: Application over the Port of Huelva (Southern Spain). Atmos. Clim. Sci. 2016, 6, 329–350. [Google Scholar] [CrossRef] [Green Version]
- Jiang, P.; Liu, X.R.; Zhu, H.N.; Zhu, Y.; Zeng, W.X. Idealized Numerical Simulation of Local Mountain-Valley Winds over Complex Topography. Plateau Meteorol. 2019, 38, 1272–1282. [Google Scholar] [CrossRef]
- Shimada, S.; Ohsawa, T.; Chikaoka, S.; Kozai, K. Accuracy of the Wind Speed Profile in the Lower PBL as Simulated by the WRF Model. Entific Online Lett. Atmos. SOLA 2011, 7, 109–112. [Google Scholar] [CrossRef] [Green Version]
- Mei, Q.; Zhi, X.F.; Wang, J. Verification and consensus experiments of rainstorm forecasting using different cloud parameterization schemes in WRF model. Trans. Atmos. Sci. 2018, 41, 731–742. [Google Scholar] [CrossRef]
- Huang, D.L.; Gao, S.B. Impact of different reanalysis data on WRF dynamical downscaling over China. Atmos. Res. 2018, 200, 25–35. [Google Scholar] [CrossRef]
- Zhang, D.L.; Shou, Y.X.; Dickerson, R.R. Upstream urbanization exacerbates urban heat island effects. Geophys. Res. Lett. 2009, 36, 88–113. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Xue, Y.; Peng, W.; Kang, H.-S. Assessment of dynamic downscaling of the extreme rainfall over East Asia using a regional climate model. Adv. Atmos. Sci. 2011, 28, 1077–1098. [Google Scholar] [CrossRef]
- Zhao, S.P.; Yu, Y.; Qin, D.H.; Yin, D.Y.; He, J.J. Assessment of long-term and large-scale even-odd license plate controlled plan effects on urban air quality and its implication. Atmos. Environ. 2017, 170, 82–95. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, L.; Dong, W. Land-atmosphere coupling and summer climate variability over East Asia. J. Geophys. Res. Atmos. 2011, 116, D05117. [Google Scholar] [CrossRef]
- Davis, C.; Bosart, L.F. Numerical Simulations of the Genesis of Hurricane Diana (1984). Part II: Sensitivity of Track and Intensity Prediction. Mon. Weather. Rev. 2002, 130, 1100–1124. [Google Scholar] [CrossRef]
- Zhao, C.L.; Zhang, T.J.; Wang, W.; Liu, Y.P.; Zeng, D.W.; Li, Y.H. Impacts of Land-use Data on the Simulation of 10 m Wind Speed in Northwest China. J. Arid Meteorol. 2018, 36, 397–404. [Google Scholar] [CrossRef]
- Zhang, J.P.; Zhu, T.; Zhang, Q.H.; Li, C.C.; Shu, H.L.; Ying, Y.; Dai, Z.P.; Wang, X.; Liu, X.Y.; Liang, A.M. The impact of circulation patterns on regional transport pathways and air quality over Beijing and its surroundings. Atmos. Chem. Phys. 2012, 11, 33465–33509. [Google Scholar] [CrossRef] [Green Version]
- Hon, K.K. Tropical cyclone track prediction using a large-area WRF model at the Hong Kong Observatory. Trop. Cyclone Res. Rev. 2020, 9, 64–74. [Google Scholar] [CrossRef]
- Ojrzyska, H.; Kryza, M.; Waaszek, K.; Szymanowski, M.; Werner, M.; Dore, A.J. High-Resolution Dynamical Downscaling of ERA-Interim Using the WRF Regional Climate Model for the Area of Poland. Part 2: Model Performance with Respect to Automatically Derived Circulation Types. Pure Appl. Geophys. 2017, 174, 527–550. [Google Scholar] [CrossRef] [Green Version]
- Miao, S.; Chen, F.; Lemone, M.A.; Tewari, M.; Wang, Y. An Observational and Modeling Study of Characteristics of Urban Heat Island and Boundary Layer Structures in Beijing. J. Appl. Meteorol. Climatol. 2009, 48, 484–501. [Google Scholar] [CrossRef]
- Vuillaume, J.F.; Hearth, S. Dynamic downscaling based on weather types classification: An application to extreme rainfall in south-east Japan. J. Flood Risk Manag. 2018, 11, e12340. [Google Scholar] [CrossRef] [Green Version]

| ID | Indicator Name | Definitions | UNITS |
|---|---|---|---|
| TXx | Max Tmax | Monthly maximum value of daily maximum temperature | °C |
| TNx | Max Tmin | Monthly maximum value of daily minimum temperature | °C |
| TXn | Min Tmax | Monthly minimum value of daily maximum temperature | °C |
| TNn | Min Tmin | Monthly minimum value of daily minimum temperature | °C |
| DTR | Mean diurnal temperature range | The diurnal range of temperature in a day | °C |
| SDII | Simple daily intensity index | Annual total precipitation/rainy days | mm/day |
| R10 | Number of heavy precipitation days | The number of days precipitation ≥ 10 mm in all year | day |
| R20 | Number of very heavy precipitation days | The number of days precipitation ≥ 20 mm in all year | day |
| R95t | Contribution rate of extreme precipitation | The sum of extreme precipitation (the number of days precipitation ≥ the 95th percentile) as a percentage of all annual precipitation | % |
| Rx1day | Maximum daily precipitation | Annual maximum daily precipitation | mm |
| Designation | TAG | Formula |
|---|---|---|
| Correlation Coefficient | R | |
| Root Mean Square Error | RMSE | |
| Hit Rate | HR | |
| Standard Deviation | STD | |
| Index of Agreement | IA | |
| Mean Bias | MB | |
| Probability of Detection | POD | |
| False Alarm Rate | FAR | |
| Heidke Skill Score | HSS |
| R | RMSE | HR/(%) | STDf * | STDo * | IA | MB | ||
|---|---|---|---|---|---|---|---|---|
| T2 | WRF | 0.98 | 1.15 °C | 92.66 | 5.97 °C | 6.03 °C | 0.99 | −0.21 °C |
| FNL | 0.81 | 4.67 °C | 64.23 | 5.99 °C | 6.00 °C | 0.86 | −2.71 °C | |
| RH2 | WRF | 0.88 | 5.17% | 93.98 | 10.27% | 10.59% | 0.94 | −0.48% |
| FNL | 0.74 | 8.32% | 80.84 | 10.57% | 10.56% | 0.85 | 0.02% | |
| WS | WRF | 0.82 | 1.70 m s−1 | 26.78 | 1.30 m s−1 | 0.74 m s−1 | 0.60 | 1.50 m s−1 |
| FNL | 0.32 | 3.16 m s−1 | 47.74 | 2.60 m s−1 | 0.75 m s−1 | 0.29 | 1.82 m s−1 | |
| WD | WRF | \ | 69.97° | 76.78 | \ | \ | \ | \ |
| FNL | \ | 89.42° | 59.50 | \ | \ | \ | \ | |
| PRE | WRF | 0.54 | 18.81 mm | \ | 21.43 mm | 10.61 mm | 0.59 | 5.26 mm |
| Precipitation Grade | POD | FAR | HSS |
|---|---|---|---|
| No rain (<0.1 mm) | 0.59 | 0.11 | 0.59 |
| Light rain (0.1–9.9 mm) | 0.59 | 0.38 | 0.28 |
| Light to moderate rain (5.0–16.9 mm) | 0.29 | 0.75 | 0.10 |
| Moderate rain (10.0–24.9 mm) | 0.27 | 0.81 | 0.10 |
| Moderate rain to heavy rain (17.0–37.9 mm) | 0.45 | 0.76 | 0.23 |
| Heavy rain or above (>25 mm) | 0.69 | 0.73 | 0.33 |
| Indicator Name | OBS * | FCT * | MB | Percentage Error |
|---|---|---|---|---|
| TXx | 36.6 °C | 35.7 °C | −1.0 °C | −2.6% |
| TNx | 28.1 °C | 26.9 °C | −0.6 °C | −6.1% |
| TXn | 9.3 °C | 8.7 °C | −1.2 °C | −4.2% |
| TNn | 4.4 °C | 2.3 °C | −2.1 °C | −47.6% |
| DTR | 16.8 °C | 18.8 °C | 2.0 °C | 11.9% |
| SDII | 11.6 mm day−1 | 17.5 mm day−1 | 5.9 mm day−1 | 50.6% |
| R10 | 63.8 day | 115.8 day | 52.0 day | 81.5% |
| R20 | 29.2 day | 70.8 day | 41.6 day | 142.5% |
| R95t | 74.2% | 91.2% | 17.0% | 22.9% |
| RX1day | 81.8 mm | 204.1 mm | 122.3 mm | 149.5% |
| T2 | RH2 | WS | WD | PRE | ||
|---|---|---|---|---|---|---|
| MAM | R | 0.96 | 0.85 | 0.61 | \ | 0.37 |
| RMSE | 1.32 °C | 4.7% | 1.70 m s−1 | 60.81° | 30.3 mm | |
| HR/(%) | 86.96 | 96.09 | 28.91 | 68.26 | \ | |
| STDf * | 3.75 °C | 7.81% | 1.09 m s−1 | \ | 32.13 mm | |
| STDo * | 4.25 °C | 8.39% | 0.61 m s−1 | \ | 12.11 mm | |
| IA | 0.97 | 0.91 | 0.46 | \ | 0.40 | |
| MB | 0.43 °C | −1.58% | 1.46 m s−1 | \ | 5.10 mm | |
| JJA | R | 0.74 | 0.77 | 0.80 | \ | 0.68 |
| RMSE | 1.03 °C | 4.40% | 1.56 m s−1 | 67.78° | 18.21 mm | |
| HR/(%) | 96.96 | 97.39 | 34.78 | 72.17 | \ | |
| STDf * | 1.00 °C | 4.54% | 1.19 m s−1 | \ | 18.52 mm | |
| STDo * | 1.46 °C | 6.55% | 0.62 m s−1 | \ | 11.69 mm | |
| IA | 0.81 | 0.84 | 0.55 | \ | 0.66 | |
| MB | −0.31 °C | 1.38% | 1.35 m s−1 | \ | 12.08 mm | |
| SON | R | 0.98 | 0.85 | 0.90 | \ | 0.68 |
| RMSE | 1.02 °C | 5.43% | 1.76 m s−1 | 76.66° | 11.46 mm | |
| HR/(%) | 97.14 | 93.41 | 25.27 | 80.88 | \ | |
| STDf * | 3.91 °C | 9.57% | 1.48 m s−1 | \ | 14.70 mm | |
| STDo * | 3.98 °C | 10.04% | 0.79 m s−1 | \ | 8.73 mm | |
| IA | 0.98 | 0.92 | 0.61 | \ | 0.73 | |
| MB | −0.52 °C | −0.48% | 1.55 m s−1 | \ | 3.73 mm | |
| DJF | R | 0.96 | 0.89 | 0.87 | \ | 0.77 |
| RMSE | 1.18 °C | 6.01% | 1.78 m s−1 | 73.72° | 4.99 mm | |
| HR/(%) | 89.58 | 88.91 | 17.96 | 86.03 | \ | |
| STDf * | 3.74 °C | 12.75% | 1.32 m s−1 | \ | 6.53 mm | |
| STDo * | 3.60 °C | 12.75% | 0.86 m s−1 | \ | 7.71 mm | |
| IA | 0.97 | 0.94 | 0.60 | \ | 0.86 | |
| MB | −0.44 °C | −1.25% | 1.63 m s−1 | \ | 0.03 mm |
| CT1 | CT2 | CT3 | CT4 | CT5 | CT6 | CT7 | CT8 | CT9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| T2 | R | 0.86 | 0.91 | 0.94 | 0.76 | 0.95 | 0.94 | 0.80 | 0.94 | 0.97 |
| RMSE (°C) | 1.02 | 1.44 | 1.20 | 1.10 | 1.3 | 1.05 | 1.03 | 1.19 | 1.12 | |
| HR (%) | 96.25 | 82.61 | 90.34 | 95.38 | 91.29 | 96.79 | 96.70 | 92.04 | 91.81 | |
| STDf (°C) * | 1.32 | 2.96 | 3.16 | 1.27 | 3.38 | 2.24 | 1.01 | 2.66 | 4.15 | |
| STDo (°C) * | 1.81 | 2.72 | 3.44 | 1.64 | 3.57 | 2.66 | 1.59 | 3.21 | 4.42 | |
| IA | 0.89 | 0.93 | 0.97 | 0.85 | 0.97 | 0.95 | 0.83 | 0.96 | 0.98 | |
| MB (°C) | −0.15 | −0.80 | 0.13 | −0.22 | −0.28 | −0.43 | −0.27 | 0.11 | −0.21 | |
| RH2 | R | 0.77 | 0.87 | 0.83 | 0.80 | 0.86 | 0.84 | 0.78 | 0.79 | 0.84 |
| RMSE (%) | 4.07 | 6.82 | 5.38 | 4.99 | 6.22 | 4.45 | 3.99 | 3.94 | 6.11 | |
| HR (%) | 99.32 | 84.47 | 93.28 | 93.08 | 87.88 | 97.44 | 99.53 | 0.99 | 90.64 | |
| STDf (%) * | 4.16 | 10.85 | 8.82 | 5.92 | 10.25 | 6.50 | 4.11 | 5.19 | 8.96 | |
| STDo (%) * | 6.22 | 12.73 | 9.14 | 7.71 | 10.91 | 8.01 | 6.11 | 6.43 | 10.93 | |
| IA | 0.83 | 0.91 | 0.91 | 0.86 | 0.91 | 0.90 | 0.84 | 0.88 | 0.90 | |
| MB (%) | 0.37 | −2.58 | −0.96 | 1.97 | −2.81 | 1.09 | 0.91 | −0.09 | −1.13 | |
| WS | R | 0.69 | 0.88 | 0.73 | 0.82 | 0.90 | 0.84 | 0.80 | 0.61 | 0.87 |
| RMSE (m s−1) | 1.67 | 2.12 | 1.38 | 1.37 | 1.85 | 1.53 | 1.85 | 1.49 | 1.87 | |
| HR (%) | 30.72 | 4.97 | 32.35 | 51.54 | 11.74 | 42.31 | 22.64 | 38.31 | 14.62 | |
| STDf (m s−1) * | 1.10 | 1.17 | 0.88 | 1.31 | 1.24 | 1.47 | 1.29 | 1.04 | 1.33 | |
| STDo (m s−1) * | 0.50 | 0.80 | 0.53 | 0.76 | 0.86 | 0.73 | 0.70 | 0.53 | 0.80 | |
| IA | 0.43 | 0.50 | 0.50 | 0.67 | 0.58 | 0.63 | 0.52 | 0.47 | 0.56 | |
| MB (m s−1) | 1.44 | 2.04 | 1.24 | 1.09 | 1.75 | 1.21 | 1.65 | 1.24 | 1.72 | |
| WD | RMSE (°) | 53.29 | 48.06 | 57.14 | 114.80 | 73.57 | 116.82 | 53.47 | 50.91 | 57.29 |
| HR (%) | 68.60 | 96.27 | 71.85 | 59.32 | 92.05 | 71.79 | 75.94 | 64.18 | 89.47 | |
| PRE | R | 0.52 | 0.69 | 0.69 | 0.60 | 0.78 | 0.61 | 0.44 | 0.60 | 0.81 |
| RMSE (mm) | 18.77 | 5.58 | 6.09 | 22.53 | 3.95 | 14.39 | 43.44 | 9.75 | 6.47 | |
| STDf (mm) * | 18.15 | 4.11 | 7.50 | 21.31 | 5.91 | 16.38 | 44.88 | 10.53 | 10.62 | |
| STDo (mm) * | 12.40 | 7.51 | 7.92 | 13.49 | 5.89 | 9.08 | 12.41 | 10.33 | 9.65 | |
| IA | 0.60 | 0.73 | 0.82 | 0.61 | 0.88 | 0.66 | 0.36 | 0.75 | 0.83 | |
| MB (mm) | 10.09 | −0.58 | 0.39 | 14.66 | −0.05 | 6.35 | 14.40 | 2.73 | 0.99 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; He, J.; Lai, X.; Liu, Y.; Che, H.; Gong, S. The Impact of the Variation in Weather and Season on WRF Dynamical Downscaling in the Pearl River Delta Region. Atmosphere 2021, 12, 409. https://doi.org/10.3390/atmos12030409
Zhang C, He J, Lai X, Liu Y, Che H, Gong S. The Impact of the Variation in Weather and Season on WRF Dynamical Downscaling in the Pearl River Delta Region. Atmosphere. 2021; 12(3):409. https://doi.org/10.3390/atmos12030409
Chicago/Turabian StyleZhang, Chengwei, Jianjun He, Xin Lai, Yilin Liu, Huizheng Che, and Sunling Gong. 2021. "The Impact of the Variation in Weather and Season on WRF Dynamical Downscaling in the Pearl River Delta Region" Atmosphere 12, no. 3: 409. https://doi.org/10.3390/atmos12030409
APA StyleZhang, C., He, J., Lai, X., Liu, Y., Che, H., & Gong, S. (2021). The Impact of the Variation in Weather and Season on WRF Dynamical Downscaling in the Pearl River Delta Region. Atmosphere, 12(3), 409. https://doi.org/10.3390/atmos12030409








