An Advanced Artificial Intelligence System for Investigating Tropical Cyclone Rapid Intensification with the SHIPS Database

Abstract

Currently, most tropical cyclone (TC) rapid intensification (RI) prediction studies are conducted based on a subset of the SHIPS database using a relatively simple model structure. However, variables (features) in the SHIPS database are built upon human expertise in TC intensity studies based on hard and subjective thresholds, and they should be explored thoroughly to make full use of the expertise. Based on the complete SHIPS data, this study constructs a complicated artificial intelligence (AI) system that handles feature engineering and selection, imbalance, prediction, and hyper parameter-tuning, simultaneously. The complicated AI system is used to further improve the performance of the current studies in RI prediction, and to identify other essential SHIPS variables that are ignored by previous studies with variable importance scores. The results outperform most of the earlier studies by approximately 21–50% on POD (Probability Of Detection) with reduced FAR (False Alarm Rate). This study built a baseline for future work on new predictor identification with more complicated AI techniques.

1. Introduction

Prediction of tropical cyclone (TC) behaviors is important for potential risk mitigation. A major difficulty in TC intensity prediction is rapid intensification (RI) [1,2,3], which results in larger intensity prediction errors [4].

RI was defined by Kaplan and DeMaria [1] (hereafter, KD03) as a maximum sustained surface wind speed increase of 30 kt or more over a 24-h period. KD03 derived the first version of the Rapid Intensification Index (RII) based on the Statistical Hurricane Intensity Prediction Scheme (SHIPS) database for the Atlantic basin. A two-sided t-test was utilized in KD03 for SHIPS variables in distinguishing between RI and non-RI instances. Eleven significant variables were identified, and five of them with the highest individual RI prediction power were used to estimate the RII.

Kaplan et al. [5] (hereafter, KDK10) employed linear discriminant analysis to derive a revised SHIPS-RII for the Atlantic. In the revised RII for the Atlantic, KDK10 added one large-scale variable, and three satellite-derived variables, to four variables (except for SST among the five) selected in KD03, resulting in eight variables.

Kaplan et al. [6] (hereafter, KRD15) reevaluated the variables for RI with 20–55 knots intensity changes in 12 to 48 h (seven combinations) for both the Atlantic basin and the eastern North Pacific and selected ten variables (replaced two and added two in comparison to those in KDK10). They then used the linear discriminant analysis technique to develop an enhanced SHIPS-RII. The enhanced SHIPS-RII model, along with the logistic regression model and the Bayesian classification model by Rozoff and Kossin [7], were fed into a probabilistic model and resulted in a better RI prediction.

In spite of the limited success in RI prediction, the variable selection in the above studies was a one-by-one t-test, a trial-and-error process on individual factors. There are possibilities that a single variable may be insignificantly correlated to the response, but multiple variables together may have a significant impact on the prediction skill [8]. Furthermore, only a few variables (usually less than 20) were selected for these studies, among many potential variables in the SHIPS database. Therefore, more systematic methods are needed to conduct an exhaustive search for the most influential factors contributing to RI. Such efforts were made by [3,9,10], with the association rules technique for feature selection among the eleven variables identified by KD03. Yang et al. [3] mined out a three variables association rule with 47.6% RI probability, better than the five variables rule searched out by KD03 with 41% probability.

Furthermore, Yang [11] (hereafter, Y16) employed WEKA [12], a machine-learning toolbox, to conduct an exhaustive and systematic examination for classification-based RI prediction with various models, subset features, and cost values for imbalance handling. Y16 split the entire dataset into a training dataset for model fitting and test dataset for model evaluation. Although the performance of the best model in Y16 achieved a decent training result, the performance on test data was not as good. Apparently, the commonly known overfitting [13] caused an accuracy discrepancy.

The algorithms in Y16 could be improved by tweaking the so-called hyperparameters, a group of model parameters set before the training process. In Y16, only the default hyperparameter setting was used. Moreover, Y16 only employed a cost-effective approach to handle the highly imbalanced RI/non-RI classes.

To improve the performance of previous RI prediction research and to build a baseline for including newly derived features in future, this study constructs a well-tailored artificial intelligence (AI) system with the whole SHIPS database, adopts a customized data sampler for overcoming the imbalance, employs a very powerful state-of-the-art classifier, and tweaks the hyperparameters for optimal results. The structure of the proposed AI system is displayed in Figure 1. There are four major components: a SHIPS data filter, a Gaussian mixture model synthetic minority oversampling technique (GMM-SMOTE)-based sampler, a classifier based on distributed gradient boosting tree model (XGBoost), and a hyperparameter tuning process.

The original SHIPS dataset for input comes from case-based ASCII blocks. The SHIPS data filter will be used to convert the source data into the commonly used attribute-relation format and to filter the variables to generate a reduced variable set as the input for the data sampler. The GMM-SMOTE data sampler will up-sample RI (minority) instances and down-sample non-RI (majority) instances accordingly, leading to a balanced augmented dataset. The XGBoost classifier will then classify the balanced data into RI or non-RI instances. Although the hyperparameter tuning is displayed as one component in Figure 1, the process could take place in multiple steps, either independently for one component such as for the SHIPS data filtering alone or jointly such as for data augmentation and classification together.

The outline of the remainder of this paper is constructed as follows. In Section 2, the SHIPS dataset is introduced. Section 3 specifies the data filter, data sampler, and classifier of the system. Hyperparameter tuning is discussed in Section 4. Section 5 delivers the results and discusses variable importance. Section 6 concludes the study and outlines future research.

2. Data

At the moment, SHIPS Developmental Data is the most complete dataset with parameters known to be related to TC intensity changes [14]. The ASCII SHIPS data consist of instance blocks with parameter names and their values from the current time up to 120 h in a 6-h interval. The SHIPS parameters include well-known TC-related parameters such as climatological SST (sea surface temperature), relative humidity averaged over a ring in 200–800 km from TC centers, satellite-based average brightness temperature in 0–200 km circular areas around TCs, and many others derived from model analysis and satellite observation data. Every year, instances from the previous year are added, while the variable set may be updated. The 2018 version of SHIPS Developmental Data used in this study has 141 lines in each block with TC instances from 1982 to 2017 in the Atlantic basin [15]. All the lines can be divided into three categories: (1) special notations denote start/end of a block and time; (2) one-time variable lines give values not time-dependent; (3) regular variable lines give variable values from −12 h to 120 h [16]. The SHIPS data filter will extract relevant information based on line categories and output the data in an attribute-relation table.

3. Data Filter, Sampler, and Classifier

3.1. SHIPS Data Filter

3.1.1. Ascii Text to Attribute-Relation Table

For classification analysis, the input data model is usually entity-relation tables commonly used for relational databases. Therefore, each SHIPS instance block should be transformed into one entry in an attribute-relation table. During the conversion, special notations, one-time variables, and time-dependent variables are handled differently and are described below in detail. The number of variables for each category is also listed for tracking purposes only.

• Special notations (3 lines in total: HEAD (original abbreviations used in SHIPS are used here. A shorten version of the SHIPS Predictor Description file [16] is provided in the Supplementary Materials), LAST, and TIME): The HEAD line has ten elements: TC name (NAME), year (YEAR), month (MONTH), date (DATE), universal time coordinated (UTC), maximum surface wind, center latitude, center longitude, minimum sea level pressure (SLP), and the US NOAA-specified ATCF ID number (ATCF). Only six values are extracted from the HEAD line: NAME, YEAR, MONTH, DATE, UTC, and ATCF. No information is retrieved from the TIME and LAST lines (6 variables).
• One-time variables (7 lines: HIST, IRXX, IR00, IRM1, IRM3, PSLV, and MTPW): We just take the values of those variables by adding “_x” to the variable names, where “x” measures the position corresponding to the time column with “_0” to the current time (TIME = 0). The leading position (TIME = 0) for IRXX, IR00, IRM1, and IRM3 and the last three spaces for PSLV are empty. As a result, we have HIST_0, HIST_1, …, HIST_20, MTPW_0, …, MTPW_20; IRXX_1, …, IRXX_20, IR00_1, …, IR00_20, IRM1_1, …, IR M1_20, IRM3_1, …, IRM3_20; PSLV_1, …, PSLV_18 (140 variables).
• Time-dependent variables (the remaining 131 lines (three lines, PC00, PCM1, PCM3 were mistreated as time-dependent initially. See details in the main text)): The current value of a time-dependent parameter is taken with the corresponding TC instance. The values for other times are not considered unless they are used to derive other variables for data preprocessing (131 variables; total 277 variables).

In SHIPS, three lines, PC00, PCM1, and PCM3, give the first nine principal components (PCs) for IR imageries at the current time, 1.5 h before, and 3 h before. Initially, we misinterpret the variables as time-dependent variables and keep the current PC00, PCM1, and PCM3 values only. Although it is not a correct treatment for those values, fortunately, the kept values are for the 2nd principal components, which are the only important components identified by previous studies (KRD15).

3.1.2. Preprocessing of the Ships Attribute-Relation Table

The raw attribute-relation table obtained above is hard to be used directly due to variable natures, i.e., irrelevant variables, heavy missing values (9999 in original SHIPS files), scaling issue, and the inter-correlation between variables. In addition, some potential variables, such as Julian date and intensity changes in near past, are not available directly from the simple conversion procedure. As a result, preprocessing is performed on the raw attribute-relation table.

Adding Additional Variables Based on Variable Natures

Based on previous studies (e.g., [2]), intensity change in the near past is critical for rapid intensification prediction. Therefore, previous 6-h intensity change (BD06) is calculated as subtracting the current intensity by the intensity 6 h before, and BD06 for the first instance of each TC is set as missing. Previous 12-h intensity change (BD12) and 18-h intensity change (BD18) are calculated similarly. The first two (three) instances of each TC for BD12 (BD18) are set as missing. Since BD06 and BD12 contain the information of DELV and INCV, the latter two are removed (3 variables added and 2 removed resulting in 1 more variable, so 277 + 3 − 2 = 278 variables remained in total).

To include the temporal variation of RI, Julian day (jd) is created to combine the information of MONTH and DATE, while MONTH, DATE, and UTC are removed (278 + 1 − 3 = 276 variables).

Removing Unrelated Variables

Some variables, such as the first four letters of storm names (NAME), useful for tracing but unrelated to the RI prediction, should be removed. Other removed variables due to lack of RI prediction potential are ATCF, YEAR, TYPE (1 or 2 for tropical or subtropical TCs and is not used in SHIPS model), and PSLV_8 to PSLV_18, which give optimal weights for different vertical layers in matching environmental flow. (276 − 15 = 261 variables).

IRXX should only be used when IR00 values are missing. Therefore, missing values in IR00_1, …, IR00_20, are replaced with the corresponding values in IRXX_1, …, IRXX_20, respectively, and then IRXX_1, …, IRXX_20 are removed (261 − 20 = 241 variables).

Removing Variables with Heavy Missing Values

There are variables with filled missing values when the right values are not available. The missing values are screened for each feature, and the missing value percentages are recorded. Since variables with a large percentage of missing values are not expected to give much information in the RI prediction, a threshold of 50% is selected here, and 10 variables with more than 50% missing values are removed. After this removal, the remaining missing values are coded as “NA,” a notation that can be easily handled later for sampling and classification (241 − 10 = 231 variables).

Value Scaling

To make the data internally consistent, valid numerical values for all variables are scaled to values between 0 and 1 with

$$\frac{Valu{e}_{variable}-Mi{n}_{variable}}{Ma{x}_{variable}-Mi{n}_{variable}}$$

(1)

where Value_variable represents an instance value of a particular variable, $Ma{x}_{variable}$ and $Mi{n}_{variable}$ represent the maximum and minimum values of that particular variable across all instances.

Removal of Highly Correlated Variables

Although highly correlated input variables will not affect the prediction accuracy for classifiers such as the XGBoost, they could influence the accuracy of the variable importance evaluation. Therefore, among highly correlated variables in the SHIPS dataset, only one variable from the group should be kept while others are removed.

The definition of “highly correlated” depends on a pre-defined correlation threshold, which determines the number of variables to be removed (or kept). This correlation threshold is one of the so-called hyperparameters.

As the first step, pairwise Pearson’s r correlations of all the variables are calculated and compared with the correlation threshold. For each variable, its highly correlated variables (correlation higher than the threshold) are identified and placed in a group started with that variable. Therefore, there is a group that started with each of the 231 variables. All groups are sorted descending based on the number of variables they have, and if the lengths of the two groups are the same, the sorting is alphabetically based on the leading variable names. Then, starting from the first group, all following groups starting with any current group members are eliminated, and then, member variables are also removed from all other remaining groups to guarantee that each variable will appear only once. This process continues until the last group is reached. After that, the first variables in all remaining groups are selected as filtered variables.

For example,

Table 1. Correlation values for pairs among BD06, BD12, and BD18 and the corresponding raw groups for highly correlated variables (correlation higher than the threshold, 0.8).

	BD06	BD12	BD18	Group List
BD06	1.00	0.86	0.75	BD06, BD12
BD12	0.86	1.00	0.92	BD12, BD06, BD18
BD18	0.75	0.92	1.00	BD18, BD12

displays the correlation values between BD06, BD12, and BD18 and the highly correlated groups with an arbitrarily selected 0.8 correlation threshold. The group leading with BD12 has other two correlated variables, BD06 and BD18, while the BD06 and BD18 groups have only one correlated member, BD12 each. Therefore, after sorting, the BD12’s group is placed before the BD06’s and BD18’s. In removing procedure, from the BD12’s group, we know that the groups leading by BD06 and BD18 should be removed. Finally, only the group starting with BD12 is kept, and variable BD12 is kept. If there are any other following groups in an extended case, variable BD06 and BD18 are supposed to be removed from all other groups.

The final result from the above procedure should be sensitive to the to-be-tuned hyperparameter, correlation threshold. If the threshold is too low, the accuracy of the model is reduced because important variables could be removed. On the contrary, if the threshold is too high, too many highly correlated variables will be kept; hence collinearity could happen and result in inaccurate variable importance evaluation. In this study, 0.7, 0.8, 0.9, and 0.95 are predetermined as the searching space to tune (find the best value for) this hyperparameter.

3.2. GMM-SMOTE

Only approximately 5% of TC instances undergo RI, and hence, the dataset is significantly imbalanced, which is a major issue for RI prediction with classification. There are several ways to overcome the imbalance issue for classification, and one of them is resampling. We can up-sample the minority (RI) cases and down-sample the majority (non-RI) cases. To improve the sampling process, the research communities have developed many algorithms. For example, instead of conducting sampling in the whole dataset, clustering methods are used first, and sampling will be carried out in each cluster, and some clusters with very few minority cases will be ignored. In addition to direct sampling, new minority instances could also be created based on neighboring instances around the existing minority instances. Recently, one of the most popular algorithms to handle the imbalance problem is a modified version of the synthetic minority over-sampling technique (SMOTE) [17] and is used for this study. The technical details are presented below.

The original SMOTE is modified by [18] to up-sample only the danger minority class instances, which are difficult to classify. To avoid the influence of the extreme values in the sampling process, and to make the resample process more efficient, Last et al. [19] proposed the K-means SMOTE to group instances into clusters, and only up-sample the minority instances in “dangerous” clusters.

However, K-means does not work efficiently on data with complex geometrical shapes, especially in a high dimensional space. K-means SMOTE does not handle missing values in variables either. Therefore, in this study, the Gaussian mixture model (GMM) with a weighted Euclidean distance is used for clustering the high-dimensional SHIPS data. Additionally, the Bayesian information criterion (BIC) [20] is used to determine the best number of clusters in GMM.

In other words, a GMM-SMOTE combination approach is designed in this study as the data sampler to resample the unbalanced RI dataset. The sampler employs the BIC to determine the number of clusters from a pre-defined range between 2 and 10 and then employs the GMM to cluster all the instances. Every cluster is defined as safe, noise, or dangerous based on the instance imbalance rate (IIR), i.e., the ratio of the minority instances in the cluster divided by the ratio for the entire population. For example, if there are 3% minority instances in a cluster and 5% minority instance in the population, IIR = 3/5% = 0.6 for this cluster. When a cluster is composed of mainly majority instances, the classification of all instances would be majority class no matter the actual instance is the minority or not. Those clusters cannot make any contribution to improve the classification accuracy and are termed as noise clusters. Similarly, a cluster is defined as safe when its minority instances are dominant in the cluster and are less possible to be misclassified. In this study, 0.2 (5) of IIR value is set as the threshold, and any clusters with IIR ≤ 0.2 (≥5) are termed noise (safe). Otherwise (0.2 < IIR < 5), the classification of the minority is difficult, and the cluster is termed dangerous. Furthermore, instances can also be identified as safe, noise, or danger based on the number of minority instances in their m_neighbors neighbors. An instance is termed as noise (safe) if none (more than half) of its neighbors is in the minority class, otherwise, as danger. Only danger instances in dangerous clusters are up-sampled with SMOTE following

$$u_{new}= u_c+w\times \left(u_n-u_c\right), w ~ U\left(0,1\right) if u_n is minority class; otherwise w ~ U\left(0,0.5\right)$$

(2)

where $\mathrm{instance}c$presents the selected minority class instance that needs to be augmented, $\mathrm{instance}n$ presents the randomly selected neighbor of $c$ using k nearest neighbor in the same cluster with k = k_neighbors, another to-be-determined hyperparameter. Variable u denotes the value of any one feature, and $U\left(0,1\right)$ and $U\left(0,0.5\right)$ present random numbers with a uniform distribution between 0 and 1 and 0 and 0.5, respectively. Because the number of majority instances is much larger than that of the minority instance, the increase in m_neighbors will result in the increase in the number of majority neighbors, for instance, leading to the increased possibility of the instance is classified as noise; hence, the instance is less likely to be up-sampled. Therefore, the number of instances that are up-sampled are fewer, and the variety of the up-sampled instances is decreased. Similarly, smaller k_neighbors will lead to a smaller variety because fewer neighbors will be selected for the up-sampling. Smaller (larger) variety represents less (more) coverage in the parameter space and would more likely result in an underfitted (overfitted) model, or a conservative (aggressive) model. Therefore, large (small) m_neighbors and small (large) k_neighbors will lead to conservative (aggressive) models.

Each danger instance in dangerous clusters is augmented N_a times where N_a is defined as the integer part of

$$0.75\times \frac{\mathrm{The}\mathrm{number}\mathrm{of}\mathrm{majority}\mathrm{instance}\mathrm{in}\mathrm{the}\mathrm{population}}{\mathrm{The}\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{minority}\mathrm{instances}\mathrm{need}\mathrm{to}\mathrm{be}\mathrm{augmented}}-1$$

(3)

which makes the final number of minority instances be approximately 75% of the majority instance number assuming most of the minority instances will be augmented. Then, as the final step of the resampling, 25% instances in majority class are randomly removed (down-sampled) to make the majority class and minority class have similar number of instances [19,21].

3.3. XGBoost Classifier

One of the most popular classifications and prediction models in the machine-learning community is the classification and regression tree model (CART) [22]. The trees are grown via different division thresholds (see Figure 2 as an example). At the leaves (end of a tree), a numerical score for a specific classification such as RI is assigned, and a decision could be made based on such classification scores. However, a single CART usually is a weak classifier, and only slightly better than random guessing. One way for the prediction accuracy improvement is the so-called boosting approach. Instead of using a single tree for a classification decision, a large set of weak classifiers could be built, and classification scores from the individual trees are integrated together to boost classification performance. However, boosting is usually based on a complicated structure, and such a structure would lead to overfitting. Many strategies are used for the tree growth and for the growth regularizations to control structure and overfitting. The state-of-the-art boosting tree growth model is the gradient boosting tree (GBT) [7], and a regularized distributed GBT, XGBoost, is applied for the RI prediction in this work. The tedious details are elaborated below.

The gradient-boosting process trains a series of weak CART classifiers iteratively. Each classifier is constructed on the remaining errors of previous classifiers, and new classifiers are trained to correct the mistake made by the previous classifiers. The output of each classifier is a leaf level score, as shown in Figure 2 as an example of RI prediction. An instance with attributes A and B lands at leaf A1 of Tree 1 based on the A value and leaf B1 of Tree 2 based on the B value. The raw classification score for being a RI instance is a weighted sum, w₁ × S1 + w₂ × S3, with w₁ and w₂ being the weights for Tree 1 and Tree 2, respectively. The raw score is rescaled to a value between 0 and 1 using a sigmoid function [8]. In the binary classification in this study, 0 and 1 are used to encode non-RI and RI classes. If the rescaled score is less than a decision threshold, which is a to-be-tuned hyperparameter, and preselected as 0.5, the instance is predicted as non-RI; otherwise, the instance is predicted as RI. A greedy algorithm like GBT may generate too many weak classifiers fitting in the residuals that the total model can be easily overfitted, and a regularized distributed GBT, i.e., XGBoost, is designed to control the overfitting [23].

XGBoost generates weaker classifiers iteratively by minimizing an objective function, consisting of a loss function and a regularization function. The loss function is based on the errors between the predicted classes and the ground truth classes for all instances. The regularization function is a function of classifiers, and its purpose is to control the overfitting of the final classification. In short, the strategy in XGBoost is to have the best prediction (minimum loss function) with the regularized complexity of the tree structure (to avoid overfitting).

The regularization constraints can be roughly divided into two categories. The first category is on the overall structure outside individual classifier, which includes shrinkage ratio (shrinkage), the number of classifiers (n_estimator), subsample ratio, and features ratio. The second category is on the individual CART (classifier) level, which includes L1 regularization and L2 regularization, minimum loss reduction required to make a split (Split criteria, aka, gamma) and the minimum sum of instance weight in a split, and the maximum depth of the CART.

In the first category, since the subsequent classifiers are iteratively fitted into the remained error from the previous classifiers, the subsequent classifiers contribute less and less as boosted trees go deeper. Therefore, similar to gradient descent algorithm with decreasing steps for better approximation [8], we decrease the contribution of each weak classifiers with a rate of shrinkage, a hyperparameter within (0, 1]. Additionally, similar to the gradient descent algorithm, a too-small shrinkage will result in overfitting. Empirically, XGBoost was found to perform best with the shrinkage around 0.1, and the search space is defined as 0 to 0.3 here. While more classifiers would result in better accuracy, too many classifiers will result in overfitting. Therefore, the number of classifiers, n_estimator, is limited in (100,2000) and will be searched in that range to avoid underfitting and overfitting simultaneously. In addition to the classifier number, overfitting can also be reduced by using only a reduced set of datasets and variables [8]. Subsample ratio (subsample) and features ratio (colsample) are used to control the sizes of randomly selected reduced datasets and feature sets, and the search spaces are defined as 0.5 (50% instances) to 1 and 0.4 (40% features) to 1, respectively. In total, four constrains: shrinkage, n_estimator, subsample, and colsample are adopted as hyperparameters for overall constraints in the classification process.

In the second category, the concern is the same, to avoid overfitting by similar strategies but on individual trees. Although the number of features is reduced by colsample, that process is random. The number of the features are further controlled by L1 regularization and L2 regularization based on their importance, where L1 regularization (reg_alpha) and L2 regularization (reg_lambda) are similar to Ridge and Lasso [8] in linear regression but apply on CART to reduce the impact of less predictive features. The search spaces of L1 and L2 regularization are specified as 0.5 to 20 and 0.1 to 20, respectively. Another tree-level constraint is to limit tree growth. This can be achieved by setting minimum loss reduction required to make a split (gamma) and a minimum sum of instance weight in a split (min_child_weight), and 0 to 10 and 0.5 to 5 are defined as their search space, respectively. Finally, the maximum depth (max_depth) is used to control the depth of a CART and is searched in the space from 3 to 10.

Details of all hyperparameters are specified in

Table 2. Hyperparameters, their searching space defined by the minimum and maximum, and the initial values.

Hyperparameter	Component	Explanation	Min	Max	Initial Value
n_cluster	GMM-SMOTE	The maximum number of clusters in the Gaussian mixture model	2	10	2
m_neighbors	GMM-SMOTE	The number of nearest neighbors used to determine if a minority sample is in danger	3	10	10
k_neighbors	GMM-SMOTE	The number of nearest neighbors used to construct synthetic samples	3	14	5
shrinkage	XGBoost	Shrinkage ratio for each feature	0	0.3	0.1
n_estimator	XGBoost	The number of CART to grow	100	2000	100
subsample	XGBoost	Subsample ratio of the training instances	0.5	1	1
colsample	XGBoost	Subsample ratio of columns for creating each classifier	0.5	1	1
reg_alpha	XGBoost	L1 regularization term on weights	0	20	0
reg_lambda	XGBoost	L2 regularization term on weights	0.5	20	1
gamma	XGBoost	Minimum loss reduction required to make a further partition on a CART node	0	10	0
min_child_weight	XGBoost	Minimum sum of instance weight in a split	0.5	5	1
max_depth	XGBoost	Max depth of each CART model in XGBoost	3	10	3
decision threshold	XGBoost	Decision threshold on the XGBoost classifier output	0	1	0.5

. For a short note, lower m_neighbors, k_neighbors, shrinkage, n_estimators, subsample, colsample, max_depth, and higher reg_alpha, reg_lambda, gamma, min_child_weight lead to a more conservative model; while n_cluster and decision threshold will not influence the conservativeness of the model.

4. Hyperparameter Tuning Process

Hyperparameter tuning is based on pre-defined measures of classification performance, and all performance measures are derived from the elements of the so-called confusion matrix, as shown in

Table 3. Confusion matrix.

	Predicted Positive	Predicted Negative
Actual positive	Truth positive (TP)	False negative (FN)
Actual negative	False positive (FP)	Truth negative (TN)

. The commonly used accuracy, (TP + TN)/(TP + FP + FN + TN), is not a good measure for the unbalanced RI cases. Instead, POD (Probability Of Detection), FAR (False Alarm Rate), Peirce’s skill score (PSS), and kappa scores are often used in RI prediction evaluations [6,11,24].

POD (aka recall) is defined as TP/(TP + FN), or the ratio of correct positive prediction cases to all the positive cases. FAR is defined as FP/(TP + FP) measuring the false positive prediction ratio compared to all the positive predictions. PSS, defined as TP/(TP + FN) − FP/(FP + TN), can be interpreted as the sum of the class level accuracy. Additionally, the kappa score, defined as 2 × (TP × TN – FN × FP)/[(TP + FN)(FN + TN) − (TP + FP)(FP + TN)], is conceptually the same as Brier skill score (BSS), measuring the relative improvement of the prediction against the prediction based on samples without any models [24]. In this study, the kappa score is mainly used for the hyperparameters tuning because it is a single metric and widely used for this purpose. Other measures are used mostly to report the performance of the prediction and to compare it with previous studies.

To find the optimal values of the hyperparameter set (maximizing the kappa score in this study), a grid search is performed in most previous works, but the grid search is too time-consuming, especially with a large number of hyperparameters in the model. Bayesian optimization (BO) is then designed to reduce the time consumption, which uses an iteration procedure to search the global optimum. In reality, it is difficult for BO to find the global optimum, and instead, the BO will converge to local optima and diverge in the global optimum searching process. Therefore, the iteration should stop at a pre-defined maximum iteration number to avoid an almost never-ending global optimum search [25,26]. In this study, BO is used with a pre-defined range for each parameter.

5. Experiment and Results

In data mining and machine learning, a dataset is usually divided into training dataset, validation dataset, and test dataset. The training dataset is used to train and fit the model, the validation dataset is adopted for hyperparameter tuning, and the test dataset is employed to provide the assessment of the final model [27].

In this study, the whole dataset is divided into 90% for the training validation and 10% for the test. The training validation dataset is again split into ten mutually exclusive equal-sized subsets. One of the subsets is reserved as the validation dataset, and the other nine subsets are used for training, and each of the subsets is used for validation once in ten turns. This is defined as 10-fold cross-validation [28]. The hyperparameters are tuned based on the mean kappa score over the ten validation datasets.

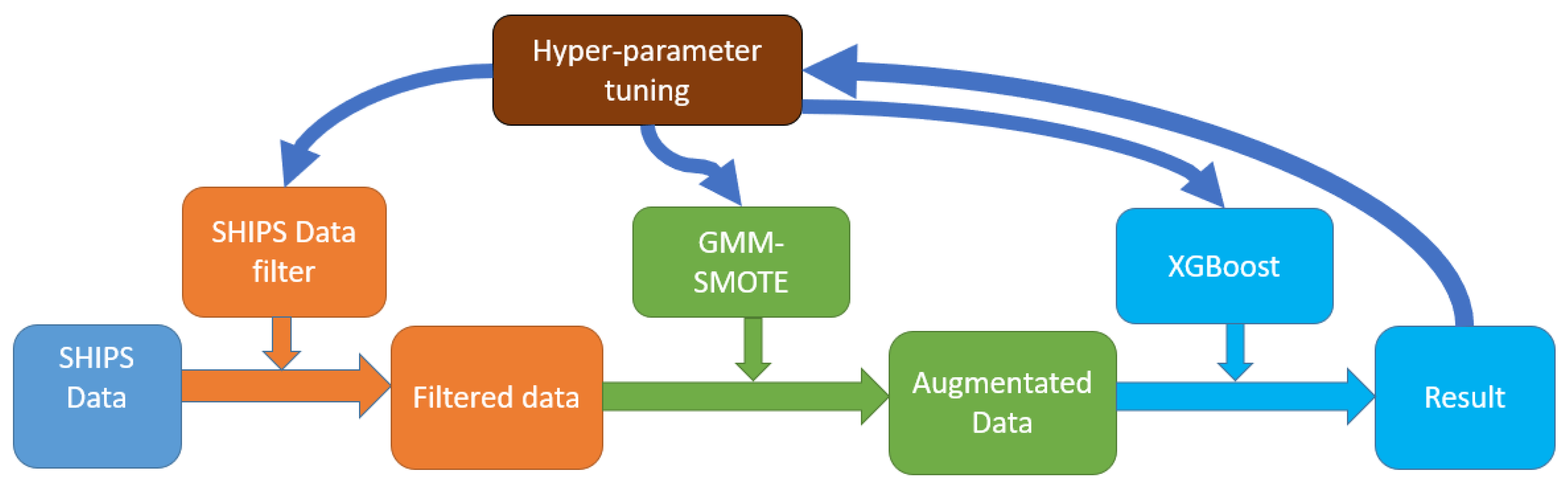
When the study is first conducted, there were 11,317 instances (cases) from 1982 to 2016, and 571 (approximately 5.0%) were under rapid intensification (RI). A random stratified sampling process based on TC cases with consideration of RI/non-RI ratio is performed. In other words, a TC is included in either the training set or the testing set with all the instances for the same TC to avoid autocorrelation for instances in the same TCs. This division process resulted in 10,185 instances (including 523 RI cases, 5.1%) in the training validation set, and 1132 instances (48 RI cases, 4.2%) were in the test dataset.

After the training was done, however, 465 instances in 2017 and the last tropical cyclone in 2016 are added to the SHIPS developmental database, and all of these instances are added to the test dataset. The test dataset proportion ends up with 1597 (14.1%) instances in total with 95 RI instances (5.9%).

All algorithms, including those for data processing, data visualization, and data mining and machine learning in this study, are performed with R (version 3.5.1), python base (v3.7.0), python multiprocessing package (v2.5), scikit-learn package (v1.9.2), XGBoost package (v0.83), and pyspark package (Spark API) (v2.21).

5.1. Hyperparameter Tuning for Model Selection

5.1.1. Hyperparameters Tuning for SHIPS Data Filter

The correlation threshold in SHIPS data filter is tuned based on trial-and-error with four values, 0.7, 0.8, 0.9, and 0.95. For each of the correlation threshold, variables are first filtered as discussed before. Then, Bayesian optimization with 40 iterations is used to tune hyperparameters in Table 2 without clustering and the preset 0.5 classification decision threshold. With each iteration, a 10 cross-validation kappa score is recorded with a corresponding set of hyperparameter values, and the top five out of 40 kappa scores for each threshold are listed in

Table 4. Kappa scores of the 5 best 10-fold cross-validation results and their mean for different correlation thresholds. The name of the 1st to 5th indicate the 1st to 5th best kappa scores. The “number variables selected” is the number of variables kept after highly correlated variables removal.

Correlation Threshold	5th	4th	3rd	2nd	1st	Mean	Number Variables Selected
0.7	0.314	0.321	0.334	0.352	0.392	0.343	56
0.8	0.404	0.407	0.411	0.417	0.418	0.411	72
0.9	0.402	0.403	0.405	0.415	0.419	0.409	99
0.95	0.387	0.397	0.401	0.409	0.411	0.401	136

. By considering both the mean kappa scores and the numbers of non-correlated variables (favoring fewer, which lowers overfitting probability), 0.8 is selected as the correlation threshold. There are 72 highly correlated variable groups that passed the filtering (see

Table A1. The highly correlated parameter group list.

No.	Parameters
1	IRM1_16, IR00_10, IR00_13, IR00_15, IR00_16, IR00_2, IR00_4, IR00_6, IR00_7, IR00_8, IR00_9, IRM1_10, IRM1_12, IRM1_13, IRM1_15, IRM1_2, IRM1_4, IRM1_6, IRM1_7, IRM1_8, IRM1_9, IRM3_10, IRM3_12, IRM3_13, IRM3_15, IRM3_16, IRM3_2, IRM3_4, IRM3_6, IRM3_7, IRM3_8, IRM3_9
2	E000, CSST, DSST, DSTA, ENEG, ENSS, EPOS, MTPW_10, MTPW_12, MTPW_14, MTPW_16, MTPW_20, MTPW_2, MTPW_4, MTPW_6, MTPW_8, PW03, PW05, PW07, PW09, PW11, PW13, PW15, PW17, PW21, RSST, T000, XDST, XNST, XTMX
3	HIST_8, HIST_9, HIST_10, HIST_11, HIST_12, HIST_13, HIST_14, HIST_2, HIST_3, HIST_4, HIST_5, HIST_6, HIST_7
4	PW14, MTPW_11, MTPW_13, MTPW_15, MTPW_3, MTPW_5, PW04, PW06, PW12, PW16
5	CD26, CD20, COHC, ND26, XD20, XD22, XD24, XD26, XO20, XOHC
6	MTPW_19, MTPW_0, MTPW_18, PW01, PW19, PW20,
7	HIST_15, HIST_16, HIST_17, HIST_18, HIST_19, HIST_20
8	IRM3_19, IRM1_18, IRM1_19, IRM1_20, IRM3_18, IRM3_20
9	PW08, MTPW_9, MTPW_17, PW10, PW18
10	PSLV_4, PSLV_2, PSLV_6, U200, U20C
11	IRM1_5, IR00_5, IRM1_3, IRM3_3, IRM3_5
12	SHRD, SHDC, SHGC, SHRG
13	V850, TWAC, V000, V500
14	IRM3_11, IR00_11, IRM1_11
15	RHMD, RHHI, RHLO
16	IR00_20, IR00_18, IR00_19
17	DTL, LON, TLON
18	PSLV_3, PSLV_5, PSLV_7
19	PENV, PENC, Z000
20	VVAC, VMFX, VVAV
21	BD12, BD06, BD18
22	T250, T200
23	NSST, NTMX
24	HIST_1, HIST_0
25	NOHC, RHCN
26	RD26, RD20
27	XD18, XD16
28	D200, DIVC
29	PC00, IR00_1
30	OAGE, NAGE
31	NTFR, XTFR
32	PCM1, IRM1_1
33	HE07, HE05
34	PEFC, V20C
35	PCM3, IRM3_1
36	VMAX, MSLP
37	TLAT, LAT
38	MTPW_1, PW02
39	O500, O700
40	NDFR, XDFR
41	IR00_12
42	VMPI
43	IR00_3
44	ND20
45	EPSS
46	TWXC
47	G150
48	SHTD
49	NDTX
50	XDML
51	Z850
52	CFLX
53	XDTX
54	SHTS
55	SDDC
56	jd
57	SHRS
58	IR00_14
59	IR00_17
60	G250
61	G200
62	REFC
63	PSLV_1
64	V300
65	IRM1_17
66	T150
67	TGRD
68	TADV
69	IRM3_14
70	R000
71	IRM3_17
72	IRM1_14

in Appendix A), and the first variable in each group makes up the selected variable set for the following steps.

5.1.2. The Number of Clusters Selected in GMM-SMOTE

After the correlation threshold is determined, the hyperparameters for GMM-SMOTE and XGBoost still need to be tuned for the best results. In GMM tuning for the “optimal” cluster numbers, BIC is chosen as the selection criterion, and the BIC values with the different number of clusters are displayed in Figure 3. The BIC values decrease with the cluster number first and then increase. The BIC stops falling for the next two consecutive iterations at n_cluster = 6, and therefore, 6 is selected as the best cluster number for the GMM clustering.

The clustering result is displayed in

Table 5. The number of minority and total cases, and the IIR (with population RI ratio at 5.1%) for the 6 clusters generated by GMM.

Cluster	1	2	3	4	5	6	Total
Minority instance	84	69	12	235	5	118	523
Total instance	2275	1481	1255	2390	1146	1638	10,185
IIR	0.724	0.914	0.187	1.928	0.086	1.413	1

with the numbers of minority (RI) and total instances, and IIR in each cluster. As we defined danger clusters with 0.2–5 IIR range, Clusters 3 and 5 could be excluded due to too few minority cases in the following augmentation, which removed a total of 2401 instances with 17 RI cases (0.71%).

5.1.3. Other Hyperparameters Tuning for GMM-SMOTE and XGboost

While the correlation threshold in the SHIPS data filter and the cluster number are tuned separately, all other eleven hyperparameters except for the decision threshold are tuned together by BO. Those parameters are listed in Table 2 with the pre-defined searching spaces and initial values.

Figure 4 shows the change in the 10-fold cross-validation kappa scores, the tuning criterion, over a total 40 BO iterations. The kappa score is fluctuating over the iterations. For example, BO process helps the model reach a local optimum at iteration 8 and diverges from the local optimum to look for the global optimum and reach another local optimum after iteration 11. This process continues until the global optimum is found, which is barely possible, or the maximum iteration, 40 preset in this case, is reached. Since the trend with the iteration is unpredictable, hyperparameter sets when the best five kappa scores are selected, and the scores and hyperparameter values are displayed in

Table 6. Top performed hyperparameter sets, the corresponding cross-validation kappa scores, and specific values of the tuned hyperparameters. The numbers after “M” denoting the iteration numbers.

Name	M38	M11	M25	M36	M14
Kappa score	0.405	0.407	0.411	0.417	0.418
m_neighbors	4	3	3	3	5
k_neighbors	6	11	9	10	10
shrinkage	0.29	0.23	0.3	0.3	0.21
n_estimators	2000	572	2000	376	1510
subsample	0.75	0.5	0.5	0.5	0.67
colsample	0.99	0.78	0.99	0.9	0.99
reg_alpha	0.5	1.34	0.5	0.5	0.5
reg_lambda	20	20	20	18.91	20
gamma	0	0	0	0	0
min_child_weight	0.5	0.5	2.12	1.26	0.91
max_depth	7	8	7	7	10

. The five sets are denoted as MX with X being the iteration numbers. For example, M11 implies the parameter set is selected after the 11th iteration.

To find a balanced model based on the five hyperparameter sets, a system is designed to score the conservativeness of the hyperparameter set. The scores are based on a 1 (the least conservative) to 5 (the most conservative) scale associated with the hyperparameter value ranks, as listed in

Table 7. The descending value ranking of individual hyperparameter among the top 5 performing cases, and the corresponding conservativeness ranking scores in parentheses. The parameters with normal font are those favoring smaller values for conservativeness, and those italicized favoring larger values.

Name	M38	M11	M25	M36	M14
m_neighbors	2 (4)	3 (1)	3 (1)	3 (1)	1 (5)
k_neighbors	5 (5)	1 (1)	4 (4)	2 (2)	2 (2)
shrinkage	3 (3)	4 (4)	1 (1)	1 (1)	5 (5)
n_estimators	1 (1)	4 (4)	1 (1)	5 (5)	3 (3)
subsample	1 (1)	3 (3)	3 (3)	3 (3)	2 (2)
colsample	1 (1)	2 (2)	1 (1)	3 (3)	1 (1)
reg_alpha	2 (1)	1 (5)	2 (1)	2 (1)	2 (1)
reg_lambda	1 (2)	1 (2)	1 (2)	2 (1)	1 (2)
gamma	1 (1)	1 (1)	1 (1)	1 (1)	1 (1)
min_child_weight	4 (1)	4 (1)	1 (5)	2 (4)	3 (3)
max_depth	3 (3)	2 (2)	3 (3)	3 (3)	1 (1)
Total score	23	26	23	25	26

. For hyperparameters favoring smaller values for conservativeness (k_neighbors, shrinkage, n_estimators, subsample, colsample, max_depth), the scores are the same as the descending parameter value ranks. When a tie appears, the tied values will have the same rank (score), and the next rank value depends on how many ties. For example, in k_neighbors, M11 has the largest value, 11; hence, M11 is scored 1. M36 and M14 have the second largest value, 10; hence, they are scored 2. The next largest value, 9, is ranked the 4th (instead of the 3rd) in M25 and is scored 4. For other hyperparameters (m_neighbors, reg_alpha, reg_lambda, gamma, and min_child_weight), the conservativeness ranking scores are opposite to the descending value ranks. After the ranking scores are assigned to all of the 11 hyperparameters in the five local optimal cases, the scores are summed up for the five cases (Table 7). Since our goal is to choose a model neither conservative nor aggressive, the parameter set M36 with the middle conservativeness ranking score is chosen for following implementation and discussion.

5.1.4. Hyperparameters Tuning for XGboost Decision Threshold

The last tuned hyperparameter is the decision threshold on the XGBoost classifier output, which was set as 0.5 before tuning. To tune this hyperparameter, we use a graphic method based on the relative values of POD and FAR as well as the kappa score. Since POD and FAR are monotonically decreasing function with the decision threshold, we instead use precision (1-FAR) for identifying a threshold that balances the POD and FAR.

Figure 5a displays the variations of precision and POD as functions of the decision threshold with the 10-fold cross-validation classification results. The precision and POD curves cross each other around 0.2 of the threshold value, a relatively balanced point for POD and FAR. At the same point, the kappa scores shown in Figure 5b is close to the highest value, 0.35. As a result, 0.2 is selected as the decision threshold, which is expected to balance the POD and FAR and, therefore, could minimize the overfitting effect in the final classification results.

5.2. Classification Results

5.2.1. Model Results on Test Data

In the cross-validation training process, all training validation data contribute to the final prediction model. Due to this fact, the real independent evaluation of the prediction should be on the test data only. The confusion matrix for the test data, before hyperparameter tuning (MB), and after hyperparameter tuning (MA) is displayed in

Table 8. Confusion matrix values after [MA] (before [MB]) hyperparameter tuning with the test data.

	Predicted RI	Predicted Non-RI	Actual Total
Actual RI	39 (33)	56 (62)	95
Actual non-RI	64 (55)	1438 (1447)	1502
Predicted total	103 (88)	1494 (1509)

. The hyperparameter set of MB except n_cluster is displayed in the last column of Table 2 (initial values set by the software) with the decision threshold as 0.5, n_cluster as 1 (without clustering), and the MA is with the hyperparameter set of M36 (Table 6) with the 0.2 decision threshold and six clusters.

Kappa, PSS, POD, and FAR are used for the model evaluation, and their values for MB and MA are elaborated in

Table 9. Performance comparisons: MB and MA denote the models before and after the hyperparameter tuning. NA represents “value not available.” The improvement percentages are based on the corresponding values for MA against the reference values. The numbers for KRD15 were estimated from Figure 8 of KRD15.

Model	Kappa	PSS	POD	FAR
MB	0.315	0.293	0.326	0.617
MA	0.354	0.368	0.411	0.621
Y16	0.275	NA	0.340	0.711
KRD15	NA	0.225	0.275	0.675
Improvement Y16	28.7%	NA	20.9%	−12.7%
Improvement KRD15	NA	63.6%	49.5%	−8.0%

along with the available values from Y16 and KRD15. The POD and FAR values for MB and MA cases demonstrated the importance of hyperparameter tuning. After tuning, POD increases 26.1% from 0.326 to 0.411, while FAR only increase from 0.617 to 0.621, almost nil (0.6%). That is, the benefit of higher correct RI prediction is much larger than the cost of false alarm with the hyperparameter tuning. The PSS and kappa scores also increased by 25.6 and 12.4%, respectively.

5.2.2. Model Performance Comparison

Two works, i.e., the best model in Y16 and KRD15, are used to compare with the performance of our model.

In Y16, all classification experiments for RI prediction were conducted based on the WEKA environment, and the best result is achieved by C4.5 decision tree (kappa 27.5%) for data in 1982–2009. In addition, the consensus model developed in KRD15 outperforms most of the other operational models in terms of Peirce’s skill score (PSS) (approximately 0.225).

The values in Table 9 show that our model is significantly better than the other two models with all the performance measures even without the hyperparameter tuning. To be specific, after tuning, the kappa score in our model is improved by 28.7% from Y16 (0.275 to 0.354), and the PSS is improved by 63.6% from KRD15 (0.225 to 0.368). Similarly, POD in our model (0.411) is 20.9 and 49.5% better than those in Y16 (0.340) and KRD15 (0.275), respectively. FAR in our model (0.621) is 12.7 and 8.0% lower than those in the best model in Y16 (0.711) and KRD15 (0.675), respectively.

The numbers above show that our model largely improves the performance of the RI prediction vs. previous studies. However, it is worth noting that RI cases in different periods show certain heterogeneous behaviors, and the quantitative values of those metrics would be different if the testing was performed on the same datasets in previous studies. Nevertheless, due to the relatively large improvement amounts, the overall trend should be the same.

5.3. Feature Importance

Generally, the variable (feature) importance is used to leverage the variable contribution and is defined as a quantitative score. The higher the score is, the more the variable contributes, and the more useful that variable is for classifying RI. The classifier used in this study, XGBoost, provides the scaled importance scores with the sum of all scores being one.

Table 10. Features of top ten importance, their importance scores, and feature description from [16].

Variable	Importance	Description
BD12	0.0362	The past 12-h intensity change
DTL	0.0217	The distance to nearest major land
CFLX	0.0207	Dry air predictor based on the difference in surface moisture flux between air with the observed (GFS) RH value, and with RH of air mixed from 500 hPa to the surface.
SHRD	0.0206	850–200 hPa shear magnitude (kt *10) vs time (200–800 km)
G150	0.0205	Temperature perturbation at 150 hPa due to the symmetric vortex calculated from the gradient thermal wind. Averaged from r = 200 to 800 km centered on input lat/lon
jd	0.0204	Julian day
VMAX	0.0201	Maximum surface wind
IRM1_5	0.0199	Predictors from GOES data for r = 100–300 km but at 1.5 h before initial time
PW08	0.0191	600–800 km TPW standard deviation
VMPI	0.0190	Maximum potential intensity from Kerry Emanuel equation

displays the variables with the top 10 importance scores and their definition [16]. The full list of the 72 variables is given in

Table A2. The full variable important list including rankings, variable names, and the importance scores.

Ranking	Variable	Score
1	BD12	0.0362
2	DTL	0.0217
3	CFLX	0.0207
4	SHRD	0.0206
5	G150	0.0205
6	jd	0.0204
7	VMAX	0.0199
8	IRM1_5	0.0199
9	PW08	0.0191
10	VMPI	0.019
11	SHTD	0.0187
12	IR00_12	0.0183
13	HE07	0.018
14	MTPW_1	0.0177
15	XD18	0.0177
16	SHTS	0.0175
17	PW14	0.0173
18	TWXC	0.0172
19	R000	0.0168
20	V300	0.0167
21	OAGE	0.0165
22	PSLV_1	0.0162
23	Z850	0.0161
24	SHRS	0.0161
25	SDDC	0.0157
26	VVAC	0.0156
27	PCM3	0.0156
28	TGRD	0.0154
29	T150	0.0153
30	CD26	0.0153
31	TADV	0.0152
32	V850	0.0151
33	PSLV_4	0.0148
34	PSLV_3	0.0145
35	REFC	0.0145
36	RD26	0.0142
37	MTPW_19	0.014
38	ND20	0.0138
39	XDML	0.0138
40	PENV	0.0137
41	EPSS	0.0137
42	G200	0.0136
43	IR00_3	0.0134
44	D200	0.0131
45	NTFR	0.013
46	T250	0.0124
47	O500	0.0124
48	IR00_20	0.0124
49	NSST	0.012
50	IRM1_16	0.0119
51	TLAT	0.0119
52	E000	0.0115
53	IRM3_17	0.0112
54	IRM3_11	0.0112
55	HIST_1	0.0109
56	G250	0.0109
57	RHMD	0.0109
58	NDFR	0.0106
59	IR00_17	0.0104
60	IRM1_17	0.0099
61	NOHC	0.0098
62	PEFC	0.0089
63	IR00_14	0.0083
64	IRM3_14	0.0075
65	PCM1	0.0063
66	IRM1_14	0.0057
67	NDTX	0.0052
68	HIST_8	0.0043
69	XDTX	0.0041
70	PC00	0.0031
71	IRM3_19	0.0023
72	HIST_15	0.0019

. The past 12-h intensity change, BD12, has the largest importance score, 0.0362, which almost doubles the importance score of the second important variable. Because BD18 and BD06 are highly correlated with BD12 (see Table A1), we can safely assume that they are as important as BD12. This result confirms the findings of KD03 and Yang et al. [3] and means RI takes place more likely when a TC is in a relatively long-term intensification phase. The second most important variable is DTL, the distance from a TC to the nearest major land. The importance of DTL is slightly higher than the third to seventh most important variables, CFLX, SHRD, G150, jd, and VMAX, which are related to dry air, vertical wind shear magnitude between 850–200 hPa, the temperature perturbation at 150 hPa, annual Julian day, and the current TC intensity, respectively. The eighth to ninth variables are IRM1_5 and PW08.

It is interesting to note that IRM1_5, the standard deviation (STD) of GOES (Geostationary Operational Environmental Satellite) [29] BT (brightness temperature) in 100–300 km radius 1.5 h before the initial time, is more important than the average BT value itself (IRM1_2). The phenomenon plausibly says that the non-uniform BT distribution around the TC center plays a greater role than the uniform BT level for the RI. The same thing takes place with PW08, the 600–800 km total precipitable water (TPW) standard deviation from the GFS analysis [30], which is more important than the corresponding TPW value, PW07 represented by the highly correlated RHMD (Table A1). This finding is consistent with the relationship between TC intensity and the symmetricity of the TC structure. Asif et al. [31] used the STD and other statistics of BT in centric bands to establish a relationship with TC intensity, and those statistics play a similar role of the variance of the deviation angle described by Piñeros et al. [32] and Ritchie et al. [33]. A careful checking of the roles of the STDs of IRM1_5 and PW08 found that the means for RI cases are smaller than those means for non-RI cases, or a negative impact to RI. That means smaller STDs or more symmetric cloud features favor RI, consistent with the findings on symmetric convective structure related to shear direction [34,35,36]. The tenth most important variable is VMPI, the maximum potential intensity, which ranked higher in other RI studies.

A two-side t-test is used for variable selection in KD03, and the KD03 model was built based on the five variables, DVMX (intensity change during the previous 12 h), SST, POT (maximum potential intensity (MPI)–maximum sustained surface wind speed), SHR (850–200 hPa vertical shear averaged from r = 200–800 km), and RHLO (850–700 hPa relative humidity averaged from r = 200–800 km), which are found significant in a 99.9% level and with the highest individual RI prediction power. In the first 10 importance variables identified by our model, BD12 (ranked 1st), SHRD (4th), VMPI (10th), and VMAX (7th) (POT = VMPI − VMAX) are consistent with the selected variables in KD03. The missed variables in the top ten compared with the top five in KD03 are SST and RHLO. SST is highly correlated with the selected E000, which is listed 52nd in the importance ranks. RHLO is highly correlated with RHMD, which is listed 57th in the importance ranks (Table A1 and Table A2).

Compared with variables selected by KD03, in KDK10, SST is removed, and four additional variables, D200 (time averaged 200 hPa divergence within a 1000-km radius), OHC (time averaged oceanic heat content), SDBT (STD of GOES-IR BT (t = 0 h) within a 50–200 km radius), and PX30 (the percentage area from 50 to 200 km radius covered by IR cloud-top BT of −30 °C or colder), are added. Among the four new variables, D200 is ranked 44th with a 0.0131 importance score (Table A2). The OHC related parameters include COHC, NOHC, and RHCN, and among them, the highest importance score is achieved by COHC, which is highly correlated with CD26 ranked 30th with a score of 0.0153. The PX30 is corresponding to IR00_8, which is highly correlated with IRM1_16 ranked 50th with a 0.0119 score value. The only caught new KRD10 variable in our top ten is the SDBT by IRM1_5 (ranked 8th), representing GOES BT STD within the 100–300 km around the TC centers but 1.5 h before the current time.

KRD15 replaced RHLO with TPW (percentage of an area with TPW < 45 mm within a 500-km radius and ±45° of the up-shear SHIPS wind direction (t = 0 h)), and PX30 with PC2 (the second principal component of GOES-IR imagery within a 440 km radius (t = 0 h)), and added two new variables, inner-core dry-air (ICDA) predictor (time avg), and VMX0 (max sustained wind (t = 0 h)), comparing with variable used in KDK10. Among the four new variables, VMX0 is consistent with VMAX, ranked 7th in the importance list. ICDA is not directly included in SHIPS data, but the related parameter found is CFLX, the dry air predictor except for a factor of VMX0 in KRD15, and CFLX is ranked the 3rd in the top 10 parameter list. The definition of TPW is the same as MTPW_19 in the SHIPS, which ranked only 37th with an importance score of 0.014. The PC2 equivalent parameter in SHIPS is PC00, which ranked only 70th.

In summary, variables used by KD03, KDK10, and KRD15 for RI prediction are mostly consistent with our top 10 variables. The missed variables in KD03 are RHLO and SST, and RHLO was actually replaced by TPW later (KRD15), and TPW is ranked 37th in our list, much more important than the RHLO via the highly correlated RHMD at the 57th place. Among the four newly added parameters in KDK10, three, OHC, D200, and PX30, are outside the top 10 list. There are several variables in SHIPS representing the OHC. The most important one is found to be climatological OHC via the highly correlated parameter CD26 at the 30th rank. KRD15 mentioned that OHC works well only when the other two variables POT and ICDA are included in a model. D200 was introduced to SHIPS in 1998 [37], but it was eliminated in 2001 and added back in 2002 [2]. DeMaria et al. [2] also found that the role of this divergence in TC intensity forecasting is sensitive to the data sources. Therefore, it is not very unusual if this model did not rank this predictor high. The last parameter not in the top 10 list, PX30, was replaced by PC2 in KRD15. Actually, PC2 is ranked 70th in this study, and it is hard to interpret the result. It is very unfortunate that the GOES-IR principal components were mistreated initially in this work, and we missed the opportunity to rank the importance of other PCs among the first nine PCs. The other missed parameter in KRD15 is the TPW, ranked only 37th. It is plausible that the humidity effects are also reflected in the 3rd ranked parameter CFLX.

In contrast to the missed parameters in the top 10 list, four out of the 10 variables, DTL, G150, jd, and PW08, are not included in the cited RI studies. The first such variable is the DTL, the distance to nearest major landmass, ranked the 2nd, which was introduced in the original SHIPS [38] but removed in 1994 from the model. Since most RI events take place over the ocean, no other model includes this parameter. One reason for the importance of DTL is possibly that we did not remove TCs near land or landfall TCs. A detailed DTL distribution for RI and non-RI cases (not shown) demonstrates a complex role of DTL on RI. When DTL is less than ~700 km, a larger distance favors RI, not a surprising result. On the contrary, when the DTL is relatively large, the DTL for RI cases is smaller than that for the non-RI cases. Actually, it is not totally unexpected, because most weak TCs in their early lives are far from the landmass. G150 was added to the SHIPS database in 2015 without many direct applications/discussions in the relevant literature [16]. It could be related to the tropopause temperature anomaly [39,40] and the height of the tropopause, and the related tropospheric stability (the authors thank one anonymous reviewer for this point). The Julian day, jd, was introduced in the first version of SHIPS [38] with respect to the peak date, but it was found that the coefficients in the multiple linear regressions are not statistically significant for less than 48 h forecasting. Since 2003, the Julian day term in SHIPS was modified to a Gaussian function of the day with a 25-day scale to reduce the penalty on the very early and very late TCs [2]. The Gaussian modification of jd in SHIPS and the important finding in this work possibly say that the Julian day has an influence on the RI, but its role may be nonlinear. It is interesting to notice that PW08 (the same as MPTW_8), the 600–800 km environmental TPW STD from the GFS analysis, is a more important feature than the corresponding TPW mean value (PW07). That means the variation of TPW in that range is more important than TPW amount, which also says the outer structure of TCs plays a role in the RI process.

6. Conclusions and Discussion

To improve RI prediction with modern techniques, this study constructs a well-tailored artificial intelligence (AI) system that goes back to the SHIPS database, the most complete dataset with parameters known to be related to TC intensity changes. This system consists of four major components, a SHIPS data filter to remove parameters unrelated to RI, reduce parameters among highly correlated parameters, and screen out variables with high missing value rates; a customized sampler to up-sample the minority (RI) instances and to down-sample majority instances simultaneously based on a combined GMM-SMOTE approach; a very powerful state-of-the-art classifier, the XGBoost, to classify instances into RI and non-RI and to evaluate variable importance based on the information gain; a hyperparameter tuning procedure tweaks hyperparameters appearing in all of the three above components, within pre-defined value ranges.

The entire SHIPS dataset is split into a training/validation and a test set, where the former is used to fit our model and to tune the hyperparameters, and the latter is used for the performance evaluation and comparison. The performance of our model on the test data shows improvement in the RI prediction with hyperparameter tuning.

It is found that our model outperforms Y16 and KRD15 by 20.9 and 49.5% on POD, while reducing the FAR by 12.7 and 8.0%, respectively. Our model also improves the kappa score of 28.7% vs. Y16 and the PSS 63.6% against KRD15. With the difficulties in RI prediction and the slow improvement rates in previous studies (KD03, KDK10, KRD15, Y16), we believe the improvement by this work is substantial.

The variable importance is also evaluated, and BD12, the past 12-h intensity change, is found to have the largest importance score and contributes significantly more than other variables. Other important variables are DTL, CFLX, SHRD, G150, jd, VMAX, IRM1_5, PW08, and VMPI. Comparing with the important variables used by the significance tests in KD03, KDK10, and KRD15, most variables are consistent with our top 10 variables with some exceptions. The variables in our top 10 list but not considered in other RI studies may be useful for future RI studies, especially for DLT, jd, G150, and PW08, to help understand the mechanism of the TC intensification.

So far, SHIPS data are the only major data source for RI studies with data analysis method, and parameters in SHIPS are based on knowledge accumulated in past TC intensity studies. Since the RI prediction is of the high priority in NHC, there have been many investigations on identifying impact factors for the RI. For example, Wadler et al. [41] investigate the case of Hurricane Michael (2018) with observation air–ocean data from aircraft missions, which lead them to consider the warm waters in the left-of-shear quadrants important for RI. In another case study, Alvey et al. [42] used ensemble simulations of Hurricane Edouard (2014) to study the relationship among vortex alignment, precipitation structure, and TC intensity change and found that precipitation symmetrization and alignment interact to each other, and this interaction precedes and continues through RI. Other recent case studies for RI factors include sub-vortex asymmetries of energy [43], precipitation symmetricities, vortex tilt, humidity [44], eyewall replacement cycles [45], and precipitation symmetrization under shear condition [46]. On the other end of the analysis method, against the case studies, composite analysis was also employed to identify the favorable conditions for RI. For example, Wu et al. [47] composite data from CloudSat profile radar in 2006–2015 and a high-resolution hurricane forecasting model prediction to confirm that high ice water content (IWC) is related to RI. Su et al. [40] composite satellite observations of surface precipitation rate, IWC, and tropical tropopause layer temperature to improve the RI prediction. In addition to case studies and composite analysis with TC-related data, AI, with the capabilities to distill features from a vast amount of data, is potentially helpful in identifying new features related to TC intensity changes in general and RI in particular [48,49]. We plan to work on ERA interim data [50] with AI data filters such as deep learning to identify new parameters and combine the newly found features with the existing features in SHIPS as the next step for the RI prediction. That is, we will try to mine out new features from the gridded data, not noticed before for TC intensity prediction and RI. This study provides a baseline for this direction because once the improvement by the modern classifiers is assessed, the further improvement by the newly mined features can be easily distinguished.