Predicting Major Storm Surge Levels

Abstract

The National Atmospheric and Oceanic Administration (NOAA) calculates the surge probability distribution along the coast from their long-term tidal stations. This process is sufficient for predicting the surge from common storms but tends to underestimate large surges. Across 23 long-term tidal stations along the East Coast of the United States, 100-year surges were observed 49 times, although they should have occurred only 23 times. We hypothesize that these 100-year surges are not the tail outcome from common storms but are actually caused by major hurricanes. Matching these 100-year surges with major hurricanes revealed that major hurricanes caused 43 of the 49 surges. We consequently suggest a revised approach to estimating the surge probability distribution. We used tidal data to estimate the probability of common surges but analyzed major hurricane surges separately, using the return rate of major hurricanes and the observed surge from each major hurricane to predict hurricane surges. The revision reveals that expected coastal flooding damage is higher than we thought, especially in the southeast United States.

1. Introduction

In order to conduct careful analysis of expected flood damage, it is important to measure the probability distribution of storm surges in coastal areas. The surges’ cumulative probability distribution provides the cumulative probability of experiencing a surge of different heights. This is commonly expressed in terms of the return rate (1/cumulative probability) or average number of years it takes to see a surge of a specific height. Coupled with information about the location and value of low lying property, one can calculate the expected flood damage and the benefits of flood protection [1,2,3,4]. Finally, the definition of a fair premium for flood insurance is the expected flood damage. Coupled with future sea level rise and storm projections, it is also critical for determining the future coastal damage from climate change [5,6]. Because of the central role the flood probability distribution plays in all these calculations and policy issues, it is important that the flood probability distribution be as unbiased and as accurate as possible.

The National Atmospheric and Oceanic Administration (NOAA) has taken important steps towards accurately estimating the surge probability function in the United States. It has built and operated a set of long standing coastal tidal stations beginning after the Civil War. This study relies on 23 coastal tidal stations along the Atlantic and Gulf Coast that have been in operation since before 1940. The study relies on the maximum annual tides observed each year at each station [7] to calculate a flood probability distribution between the height of each surge versus its return rate (1/probability) for each site [8].

NOAA follows best practices in estimating these surge probability distributions. The data are first adjusted for sea level rise at each station using a linear regression of mean sea level on time. Adjusting for sea level rise removes the effect of rising global temperatures on mean sea level over time. A generalized extreme value function is then fit to the data in order to measure the flood probability distribution. For common storms, this procedure accurately captures the relationship between the probability of a storm and the height of the storm surge. However, this procedure tends to underestimate the magnitude and probability of the largest observed surges. The largest observed surges lie outside the 95% confidence interval too often, and there are too many surges with a 1% cumulative probability. The GEV model appears to be consistently underestimating either the frequency or size of large surges.

This paper hypothesizes that the GEV model is calibrated to fit common storms and frequent small tropical cyclones, but that it is not able to capture the effects of major tropical cyclones. Examining the errors of the GEV model reveals that the model is excellent at capturing the tides caused by common storms and small tropical cyclones. However, when we look at the surges caused by major hurricanes, we find that the GEV model consistently underestimates their observed surge and produces large positive errors. Similarly, we find that the GEV model consistently underestimates how often these large surges occur, especially in the southeastern United States. Because these large surges cause a disproportionate amount of flood damage, these errors cause GEV models to underestimate expected damage.

We propose a new approach to measuring expected flood damage, using the traditional GEV analysis to study surges from common storms and small tropical cyclones (CAT1 and 2). Then, we rely on tropical cyclone climatology to predict the return rate of major hurricanes using a combination of historic data and modeling. Then, we combine this return rate with an estimated surge height caused by major hurricanes (CAT3+). This can be measured from past major hurricanes at each station. The return rate and height can then be added to the results from common storms to measure expected flood damage. This will lead to higher expected flood damage along the East Coast but especially in the southeast and Gulf states.

2. Data and Methods

It is critical to have long-term tidal data in order to estimate surge probability functions. The United States has successfully measured tides by building tidal stations beginning in the Civil War era but expanding stations rapidly since 1930 [7]. This study relies on the surge data from the 23 coastal stations along the East Coast that have been operating since 1940. The long record of maximum annual tides from these stations provide the data that underlie the calculations of the flood probability distribution.

The methodology for calculating flood probability functions is well developed [9,10]. The analysis is based on either the observed maximum annual tide every year or the monthly maximums [9,10]. The data must first be adjusted for sea level rise (SLR). Mean sea level is regressed on time at each station [11]. SLR captures the effect of rising ocean temperatures. Tidal-station-specific SLR also captures the effect of land subsidence. The regression measures the average relative SLR at each station. These measures are ideal for making decisions about flood and coastal protection, because these all depend on relative sea level heights. However, it should be noted that the relative SLR is not the same as the absolute change in ocean height. Adding the relative SLR back on top of past maximum tides updates past records to current mean sea levels. These adjustments are intended to make the underlying surge probability distribution equivalent over time.

Using these corrected maximum tides, a generalized extreme value (GEV) cumulative function is estimated to measure the cumulative probability of observing the maximum annual tide height. It is intended to capture the shape of the extreme end of an underlying tidal probability distribution. In this case, the model captures the shape of the distribution of extreme high tides. The GEV cumulative function has three parameters, the location (μ), scale (σ), and the shape (ξ):

F(x; μ, σ, ξ) = exp { −[ 1 + ξ(x − μ)/σ ] − 1/ξ }

(1)

Using maximum likelihood, the estimated GEV model leads to an exceedance probability curve for surge by height. The exceedance probability curve measures the height of the surge versus its return rate (1/probability). The return rate is the expected number of years that must pass before one sees a surge in a specific height or more. For example, a popular cumulative probability to study is 1/100 or 1%. The return rate in this case is 100 years. The predicted surge height with a 1% cumulative probability is the 100-year surge.

The fitted GEV model is used to predict the 95% confidence interval around the exceedance probability curve. There are many observations of relatively low surge heights. The 95% confidence interval is quite tight around the expected prediction of common surges. However, as one moves towards the tail of the surge distribution, there are very few observations, and the 95% confidence interval becomes much wider. Even with over 90 years of data, there is considerable uncertainty surrounding the 100-year surge, since it often happens only once over that entire period.

NOAA has estimated the exceedance probability curve for each of the 23 longstanding eastern coastal stations in this study, and they are available online [8]. The exceedance probability functions that have been estimated by NOAA do a very good job of predicting common storms. This can be seen by how tightly the actual observations fit around the expected curve. However, there is a consistent problem at many stations revealing that the highest surges are well above the expected curve. The current approach by NOAA is underestimating these surges.

This paper tests whether these extreme surges are due to a different phenomenon than common surges. Specifically, the analysis examines whether these extreme surges are coming from major tropical cyclones. The paper looks at the place and date of each 100-year surge and examines whether the extreme surges were caused by a major tropical cyclone hitting that site. The results reveal that almost all of these 100-year surges are caused by major tropical cyclones.

The paper then develops a method that would capture these underestimated surges accurately. The paper suggests that surges from major tropical cyclones be dropped from the GEV analysis. The resulting GEV function will continue to do a good job of measuring the shape of the exceedance probability function of common surges.

In order to capture the outliers, the paper suggests turning to the climatology of tropical cyclones to estimate a return rate of major hurricanes [12]. Hurricane experts already predict the return rate of major hurricanes across the Atlantic coastline [13]. Hurricane experts could also calculate the 95% confidence interval of this return rate at each site as well. The distribution of surge heights of major storms can then be taken from the observed surges of the major hurricanes that happen to strike each tidal station. A simplistic approach would be to take the mean storm surge height from all past major tropical cyclone strikes at each site. A more sophisticated alternative is to calculate the probability of a range of surge heights from major tropical cyclone strikes at each site. For example, a site might have a return rate of a major tropical cyclone every 32 years. Over a 90-year period, they would likely see three actual storms. Suppose these storms caused surges of 2, 2.5, and 3 m. The average approach would argue that major hurricanes will have a return rate of 32 years with an average surge of 2.5 m. The distribution approach would argue that individual major hurricanes would each have a return rate of 96 (3 × 32) years, one with a surge of 2 m, one with a surge of 2.5 m, and one with a surge of 3 m. Because flood damage is a nonlinear function of surge height, the distribution approach would provide an unbiased estimate of flood damage.

Future research could explore alternative methods that combine information across sites to estimate the range of surge heights caused by major tropical cyclones. For example, it might be possible to use the characteristics of sites to predict this range. The surge heights from multiple storms could then be used to calibrate the tropical cyclone surge height model. The climatology would then generate estimates of the surge height of tropical cyclones. The climatology may well be able to capture the effects of both small and large tropical cyclones, leaving just common storms in the GEV analysis.

Ultimately, the exceedance probability distribution of the surge from normal storms and the exceedance probability distribution from major tropical cyclones would both be used to predict expected flood damage. This would take full advantage of what is known about common storms from tidal data as well as what is known about major tropical cyclones from their climatology and actual surges.

3. Results

The 23 NOAA coastal (saltwater) tidal stations along the eastern coast of the United States that have been in operation at least since 1940 provide a useful record of how frequently each site has been flooded.

Table 1. Recorded 1/100 year storms by tidal station.

City	Date	Height Above MHHW	Hurricane	Category
Galveston, TX	1915	2.5 m	Galveston	4
	2018	3.3 m	Ike	4
Pensacola, FL	1926	2.2 m	Miami	4
	2004	2.9 m	Ivan	3
Cedar Key, FL	2017	1.8 m	Irma	5
Key West, FL	1947	0.5 m	Florida	4
	1965	0.6 m	Betsy	3
	2005	1.0 m	Wilma	5
	2017	0.8 m	Irma	5
Mayport, FL	1945	0.6 m	Homestead	4
	1964	0.6 m	Dora	4
	2017	1.0 m	Irma	5
	2019	0.8 m	Doria	4
Jacksonville, FL	1899	2.1 m	San Ciriaco	4
(Fernandino Beach)	1945	1.1 m	Homestead	4
	1964	1.2 m	Dora	4
	2017	1.3 m	Irma	5
Savannah, GA	1940	0.9 m	South Carolina	2
(Fort Polaski)	1945	1.1 m	Homestead	4
	2017	1.5 m	Irma	5
	2019	1.4 m	Doria	4
Charleston, SC	1940	1.3 m	South Carolina	2
	1989	2.1 m	Hugo	4
Wilmington, NC	1954	1.1 m	Hazel	4
	2016	1.1 m	Matthew	5
Norfolk, VA (Sewells Point)	1935	1.6 m	Labor Day	5
Solomon Island, MD	1955	0.8 m	Connie	2
	2003	1.6 m	Isabel	5
Annapolis, MD	1933	1.4 m	Chesapeake	4
	2003	1.7 m	Isabel	5
Baltimore, MD	1933	1.8 m	Chesapeake	4
	2003	2.0 m	Isabel	5
Atlantic City, NJ	1944	1.3 m	Great Atlantic	3
Sandy Hook, NJ	2012	2.7 m	Sandy	3
Battery, NY	2012	2.7 m	Sandy	3
Kings Point, NY	1938	2.7 m	New England	3
New London, CT	1938	2.3 m	New England	3
	1954	2.0 m	Edna	3
Newport, RI	1938	2.9 m	New England	3
	1954	2.1 m	Edna	3
Providence, RI	1938	3.9 m	New England	3
Woods Hole, MA	1938	2.6 m	New England	3
	1954	2.4 m	Edna	3
Boston, MA	1978	1.5 m	---
	2018	1.5 m	---
Portland, ME	1978	1.3 m	---

Note: Stations are ordered from south to north along the coast. The dates and heights of 1/100 year surges come from [12]. The hurricanes are matched by date and location. Boston and Portland are the only stations where the highest tide was not caused by a hurricane. Bolded surge heights are well above the GEV predicted height.

provides a list of the 23 stations in this study. They stretch from Galveston, Texas, to Portland, Maine.

At each station, NOAA has estimated a GEV model using the maximum tide observed each year [8]. This leads to an accurate measure of the probability distribution of flooding for most common floods. For example, Figure 1 provides a scatter plot of the height of the storm surge versus the return rate of that surge for Charleston, South Carolina. A complete set of these figures for the entire sample are in the Supplementary Materials. The dots represent the annual maximum tide each year contrasting the height of the surge versus the return rate. The predicted value of the NOAA model is the central line in Figure 1, and the 95% confidence interval is the low and high lines. Most of the data fit tightly along the predicted value. However, the two highest measurements in Figure 1 are above the 95% confidence interval. Figure 1 shows that there have been two 100-year surges over the last 95 years in Charleston. The observed surge at 1.5 m has a return rate of 45 years, but the GEV model predicts that the return rate is 200 years. The observed surge at 2.1 m has an observed return rate of 90 years, but the GEV model predicts the return rate to be 400 years. The GEV probability surge model for Charleston seriously overestimates the return rate of the two largest surges. Given the fact that the highest surges lead to a large fraction of the damage from flooding, underestimating their frequency implies that the model will underestimate expected flood damage, fair insurance premiums for flood insurance, and the coastal damage from climate change. The underestimation of large surges illustrated in Figure 1 can be seen at most of the 23 stations, as shown in the Supplementary Materials.

An alternative perspective of this same problem comes from comparing actual surge height relative to the predicted surge height of the model for a specific probability (return rate). The predicted surge frequency of greatest interest in this paper is the 1% surge (the surge with a return rate of 100). Figure 2 presents the surge exceedance figure for Charleston, SC [10]. Similar figures for the other 23 sites are in the Supplementary Materials. The top red line reveals the predicted height of the 100-year surge. Figure 2 shows the same two extreme storms identified in Figure 1. The first surge in 1940 exceeded the 100-year surge by 0.3 m and the second surge in 1989 exceeded the 100-year surge by 0.8 m. Figure 2 shows that the GEV model underpredicts the height of the 100-year surge.

Using the extreme water levels (Figure 2) at each site [12], it is possible to identify all the surges that exceeded the 100-year predicted surge height. Table 1 is a list of all the 100-year surges gathered from the complete list of extreme water levels at all 23 sites in the Supplementary Materials. There are 46 occurrences of 100-year surges at the 23 tidal stations. The surge heights that far exceed the predicted 100-year surge height are shown in bold. There are 17 surges well above the predicted surge height of the 100-year storm.

If the GEV estimate of the 100-year surge was correct over 100 years, one would expect there to be 8.5 sites with none, 8.5 sites with one, 4.2 sites with two, 1.4 sites with three, and 0.4 sites with four 100-year surges for a total of 23 100-year surges in the 23 sites. In fact, there are nine sites with one, 11 sites with two, and four sites with four predicted 100-year surges for a total of 45 one-year surges. There are simply too many sites with two or more 100-year surges. The GEV model is predicting a return rate (a probability), which is twice (half) as high as the actual rate. This is an average outcome, which is six standard deviations too high.

The excess number of 100-year storms is particularly acute for the nine sites south of Virginia. Here, there should have been 3.3 sites with none, 3.3 sites with one, 1.7 sites with two, 0.6 sites with three, and 0.1 sites with four 100-year surges for a total of nine 100-year surges. In fact, the GEV model predicts there is one site with one, four sites with two, and four sites with four 100-year surges for a total of twenty-five 100-year surges. There are almost three times more 100-year surges in the southern sites than the GEM model predicts. The GEV model is predicting too high a return rate (too low a probability of major storms) in the south. This is an outcome that is ten standard deviations too high.

The hypothesis of the paper is that the phenomenon that generates most of the surge data is not the same phenomenon that generates the extreme surges. Specifically, the paper hypothesizes that the extreme surges are coming from major tropical cyclones. Given the date and location of each surge, we try to match all the 100-year surges with a major hurricane. The only three surges that were not associated with hurricanes occurred in Boston, Massachusetts, and Portland, Maine, where the highest observed tides came from winter storms occurring at high tide. Another three surges were caused by CAT2 hurricanes. All 41 of the remaining surges were caused by a major hurricane that was a CAT3+ during its lifetime (though not necessarily at the time of the strike). A CAT3+ hurricane implies sustained winds over 110 mph. Some of these surges across stations have been caused by the same storm striking multiple tidal stations. Eliminating this double counting reveals that 23 CAT3+ hurricanes led to most of the 100-year surges. So, the 100-year surges are mostly due to major hurricanes and are not just the tail end of the effect of common storms.

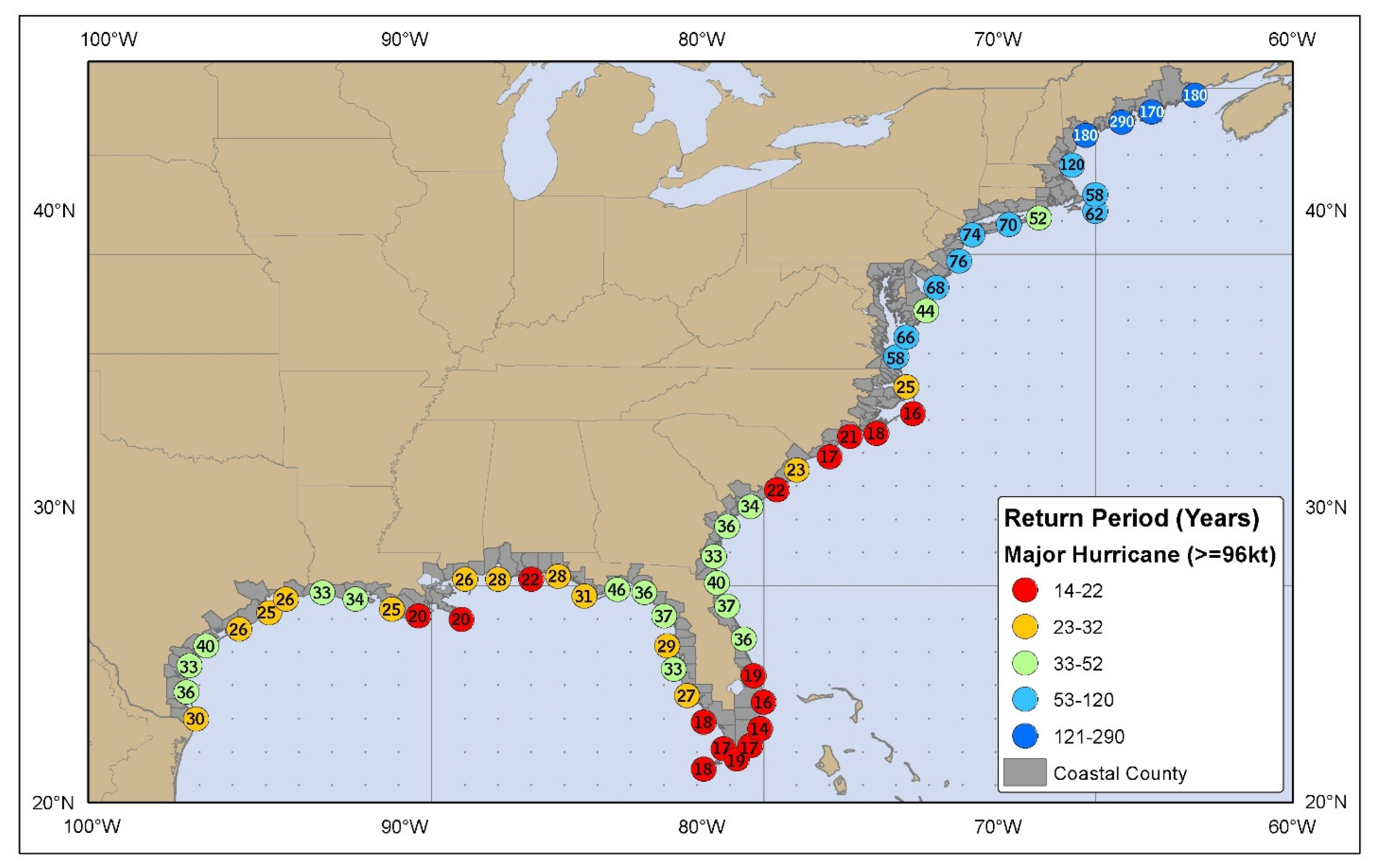
Examining the historic record of major hurricanes that have directly hit the tidal stations since 1930 suggests that each of these storms has caused an extraordinary tidal surge. The spatial distribution of the tropical cyclones also matches the undercounted high surges. Figure 3 shows the predicted probability of a CAT3+ storm striking the United States eastern coastline [12]. The probability is highest near New Orleans, southern Florida, South Carolina, and North Carolina. In contrast, there are far fewer major hurricane strikes predicted further north.

There are no long-standing tidal stations near New Orleans, so the data are missing for this region. However, southern Florida, South Carolina, and North Carolina stations all have multiple high surges that are consistent with the frequency of major hurricane strikes.

One strategy to fix the undercounting problem associated with using maximum tides from tidal stations is to drop the surges from major hurricanes from the GEV analysis. We used the GEV analysis to forecast the probability function of extreme tides from common storms. Then, we analyzed the surges from major hurricanes separately.

The return rate for CAT3+ storm surges has already been calculated by the National Hurricane Center, as shown in Figure 3 [12]. The figure presents the expected return rate of a major hurricane. In future research, hopefully the hurricane experts could also produce a 95% confidence interval around the expected return rate across the eastern United States.

One can combine the frequency of major hurricanes with the observed average surge height at each site when a major hurricane strikes. For example, we observe that Charleston has a major hurricane return rate of 22 years and that these hurricanes have caused an average surge of 1.7 m. Alternatively, one could also observe that the two major hurricanes caused a surge of 1.3 and 2.1 m. One could, therefore, also assume there is a hurricane with a return rate of 44 years that causes a surge of 1.3 m, and there is another hurricane with a return rate of 44 years that causes a surge of 2.1 m. With both methods, the return rate and average surge height would be an unbiased estimate of these observations. In both cases, the predicted frequency of these large surges would be a lot more frequent than the current GEV model predicts. The expected flood damage from major hurricane surges could then be added to the expected damage from common storms.

The revised expected damage would be well above the original NOAA GEV estimate, because the revision would properly assess the impact of major hurricanes. The effect of correcting for major tropical cyclones would be especially important for the southeast United States, where the climatologists predict that the return rate for major tropical cyclones is low. The areas marked in red and yellow in Figure 3 are struck frequently by major storms.

One way to test this new procedure is to calibrate the model on the data before 1980 and then use the calibrated model to predict the outcomes from 1980 to the present. Focusing on the problem, the 100-year surges, we compare in

Table 2. Simulation of new forecasting method.

	Height (m) Pre-1980	Height (m) Post-1980	Hurricane Actual Frequency	Hurricane Predicted Frequency	GEV Predicted Frequency
Whole Sample	1.82	1.92	1.85%	1.83%	0.41%
South	1.39	1.71	3.33%	3.50%	0.41%
North	2.22	2.19	0.89%	1.30%	0.41%

, the prediction of the GEV model, the new tropical cyclone model, and the actual data.

Using past heights of tropical cyclones provides a reasonable measure of future surge heights both for the sample as a whole and also by region. The big change in the new model concerns estimating the frequency one would see a surge from a major hurricane. The observed rate of major hurricane surges across the 23 sites since 1980 has been 1.8%. This is also close to the predictions of hurricane modelers. However, according to the GEV model, the predicted number of these surges is just 0.4%. That is the GEV model severely underestimates the probability that one would see the surge from a major tropical cyclone.

As shown in Table 2, the new method also reveals some important differences by region. The actual number of major hurricanes in the sites south of Virginia have occurred 3.3% of the time since 1980, whereas the actual rate in the northern sites was 0.9% of the time. The new model predicts that the southern sites would be hit 3.5% of the time, whereas the northern sites would be hit 1.3% of the time. In contrast, the GEV model predicts both the northern and southern sites would face the same 0.4% probability of a major surge. The new method corrects for the significant undercount of major surges and captures important spatial detail concerning where major surges are likely to occur.

4. Discussion

NOAA has done an excellent job of collecting tidal data across many sites over a long period of time. NOAA has also done a commendable job of analyzing that data to estimate a surge height probability distribution for decision makers. Their model predicts the return rate–surge height of common surges with remarkable accuracy and lack of bias.

This paper is concerned with a single issue. The NOAA model and the GEV approach tend to underestimate the frequency and height of the largest surges. The first part of this paper focuses on demonstrating that there is a problem. Whether one examines the exceedance probability curve or extreme water levels, large surges actually happen more frequently than the GEV model predicts. Over the last 90+ years, there have been 46 surges across the 23 sites that the GEV model identified as 100-year storms. This is about twice as often as one would expect. It is exceedingly likely this is an error.

The second part of the paper tests a hypothesis that these 100-year surges are being caused by major tropical cyclones, not common storms. The NOAA methodology is based on annual maximum tides. The data are dominated by the surges from common storms (including frequent small hurricanes). These storms simply cannot generate large surges. The model might, therefore, underestimate the surges that a large tropical cyclone can generate.

To test this hypothesis, we look at the date and location of the 47 100-year surges. We try to match these dates with hurricanes that have struck each station. The surges at the two northern most stations were not caused by hurricanes. However, the remaining 44 surges were all caused by a hurricane. Three were caused by a CAT2 hurricane. The remaining 41 surges were all caused by major hurricanes. The analysis supports the hypothesis that the overabundance of predicted 100-year surges is coming from major hurricanes. The GEV model predicts that surges of major hurricanes have an average return rate of over 200 years. The observed average return rate of major hurricanes across the sample is 50 years. The average predicted return rate of major hurricanes is 55 years. Over the last 90 years, the GEV model predicts that one would see 10 surges from major hurricanes; the actual number of surges from major hurricanes was 39, and the predicted number of surges from major hurricanes was 38.

The paper makes a simple suggestion to fix this issue. The GEV analysis of common surges should drop surges from major hurricanes and simply focus on accurately estimating common surges alone. The surges from major hurricanes should be estimated separately using the return rate of major hurricanes along the coast and the observed surge height from these storms. Using the predicted return rate of major hurricanes instead of the GEV estimated return rate would dramatically improve the model of major surges.

A simple experiment was conducted to test the model. Data from before 1980 were used to calibrate the new model. Data since 1980 were used to test it. The experiment revealed that earlier heights of major hurricane surges provide an unbiased estimate of future surge height (adjusting for sea level rise). However, analysis of return rates revealed that the new method did a much better job of capturing the observed frequency of major hurricanes and major surges than the GEV method. Over the recent 40-year period, the model predicted that the frequency of major surges would be 1.83%, and the actual frequency was 1.85%. In contrast, the GEV model predicted the frequency of major surges would be just 0.4%. The new model was also able to detect important spatial differences, because the probability of a major hurricane is much higher in the southeastern United States.

There remain challenges concerning estimating surge probability distributions along the coast. The coastal surges depend on the specific shape of the coast. The 23 sites used in this study are not sufficiently spatially dispersed to capture all this spatial detail. There are more tidal stations that have been created since 1930, and these stations need to be added to the analysis. There is a tradeoff between the length of time these stations have been in operation and the additional spatial information each one provides. More research is needed to explore how one can combine the information across more recent stations to achieve better estimates of what is likely to occur between the stations.

A second challenge concerns obtaining better information on the surge heights that major hurricanes are likely to cause. This study simply used the average of past surge heights caused by major hurricanes to predict future heights. However, more sophisticated modeling of surge heights could start to predict which sites would have relatively low surge heights and which sites would be struck by much higher surges. Future research could predict a range of surge heights that major hurricanes would cause along the coast.

A third challenge concerns forecasting surges into the future in order to estimate the effect of climate change. Using historic sea level rise and storm surges to forecast surges for the next decade or two might be reasonable. However, as one forecasts further into the future, the probability that sea level rise might accelerate becomes more likely. It is important to capture how climate change is likely to alter future sea level rise projections and include this in the surge analysis [14,15]. Climate change is also likely to affect the intensity of tropical cyclones [16] and especially the intensity of major tropical cyclones [17]. Capturing how climate change will affect the surge probability distribution is incredibly important given the likely flood damage that this will cause this century and for centuries to come.

A fourth unresolved issue is whether or not to combine smaller hurricanes with common storms, with major hurricanes, or to analyze them as a third group. There is clear evidence in the NOAA analyses that the very largest surges have been underestimated. There is a hint that possibly some other surges may have also been underestimated. Analyzing the return rate and surges from CAT1 and CAT2 hurricanes is worth exploring. Additional research on the return rate of CAT3+ storms is also warranted. This study relied on expected return rates along the eastern United States. It would also be helpful to know the range of possible return rates.

A final research question concerns the influence of the well-known North Atlantic Oscillation [18]. This study did not explore whether these oscillations might be affecting observed extreme water levels. This would be an interesting topic of further research as well.