An Urban Lagrangian Stochastic Dispersion Model for Simulating Traffic Particulate-Matter Concentration Fields
Abstract
:1. Introduction
2. Theory and Methods
2.1. The Lagrangian Stochastic Model
2.2. Inertia Effects
2.3. Canopy and Surface Layer Modeling
2.4. Backward Lagrangian Stochastic Modeling
2.5. Concentration Calculation Using LSM
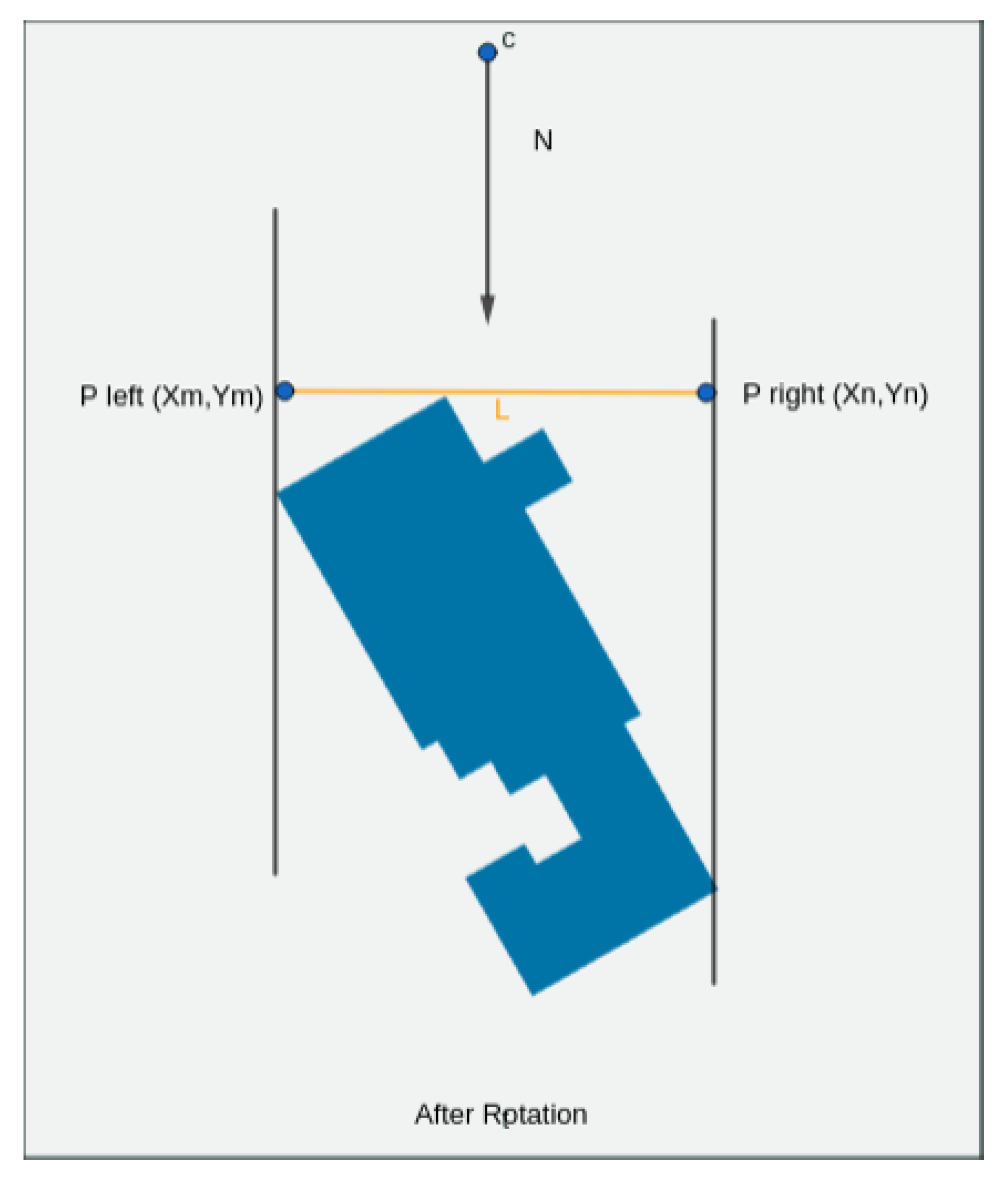
2.6. Source Structure and Footprint Screening
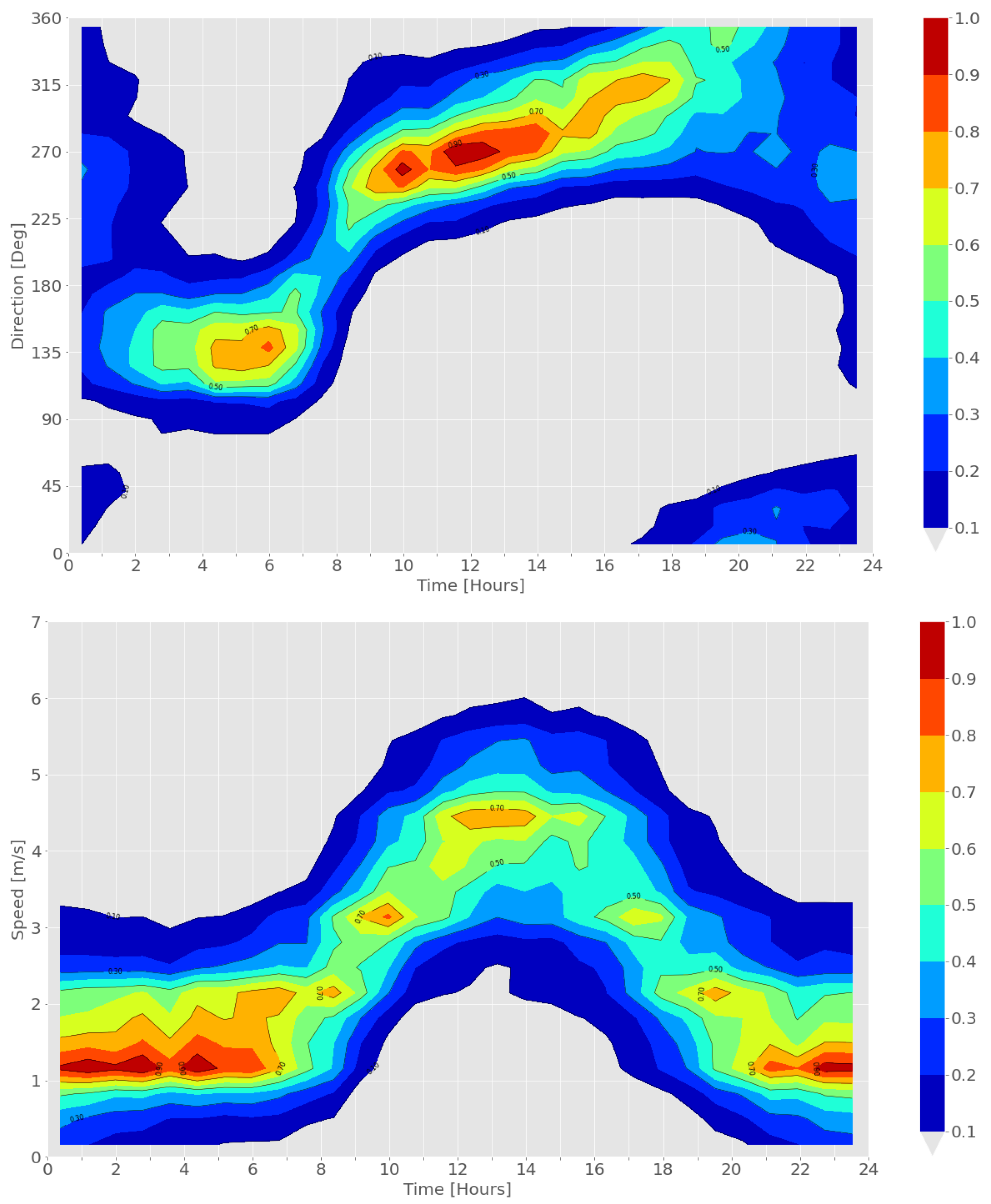
2.7. Wind Data and Climatological Analysis
3. Results and Discussion
3.1. Climatology
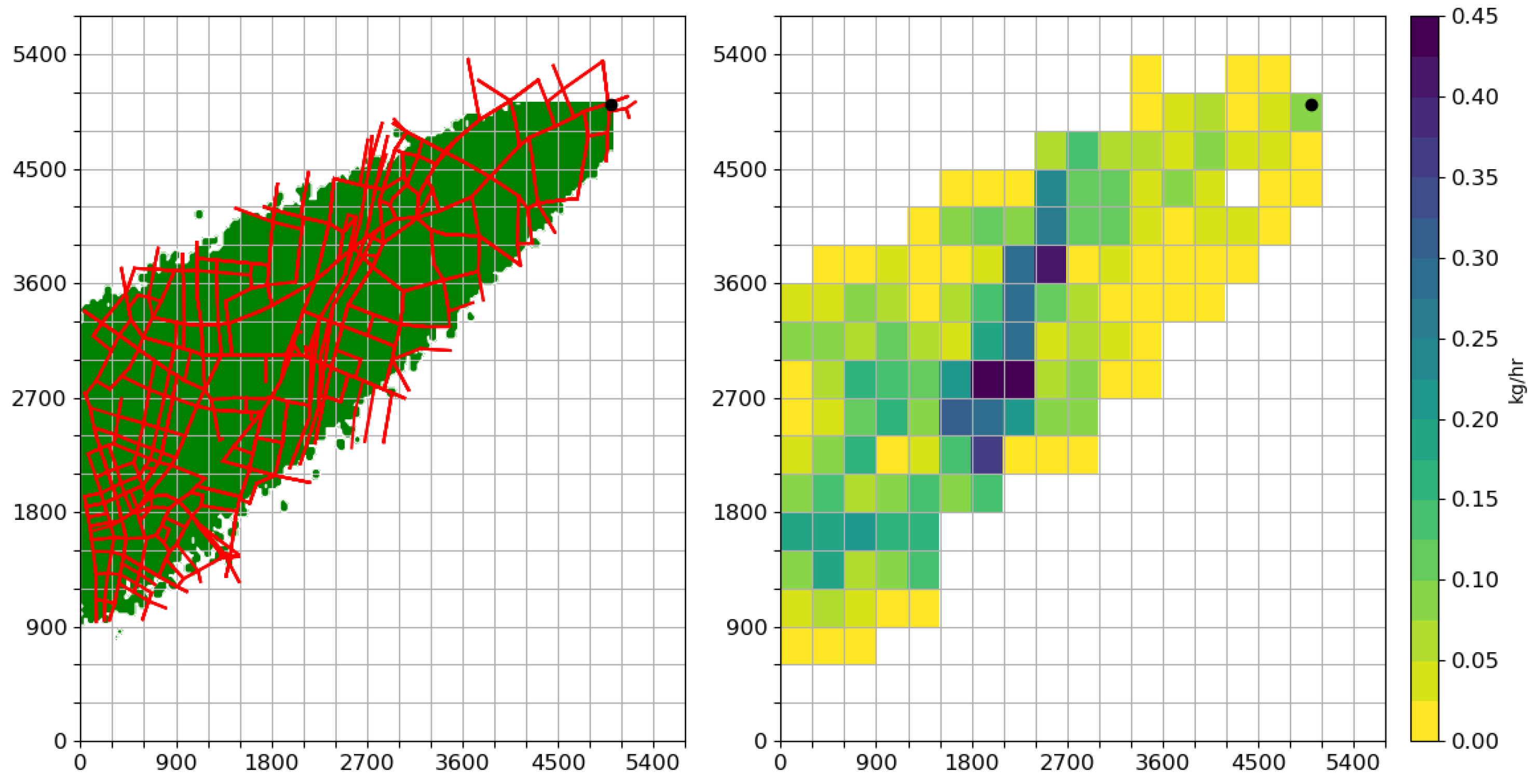
3.2. Morphology
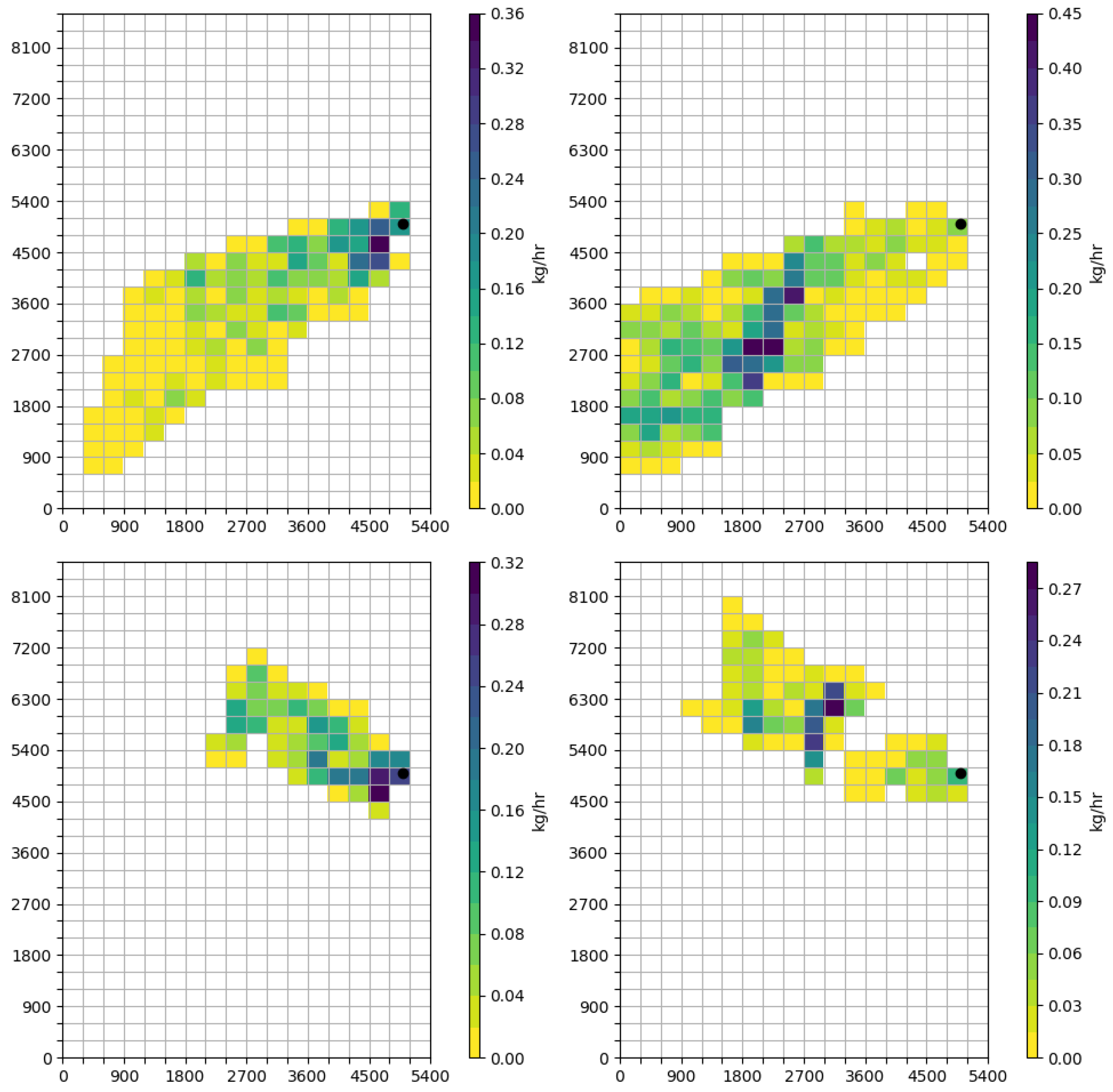
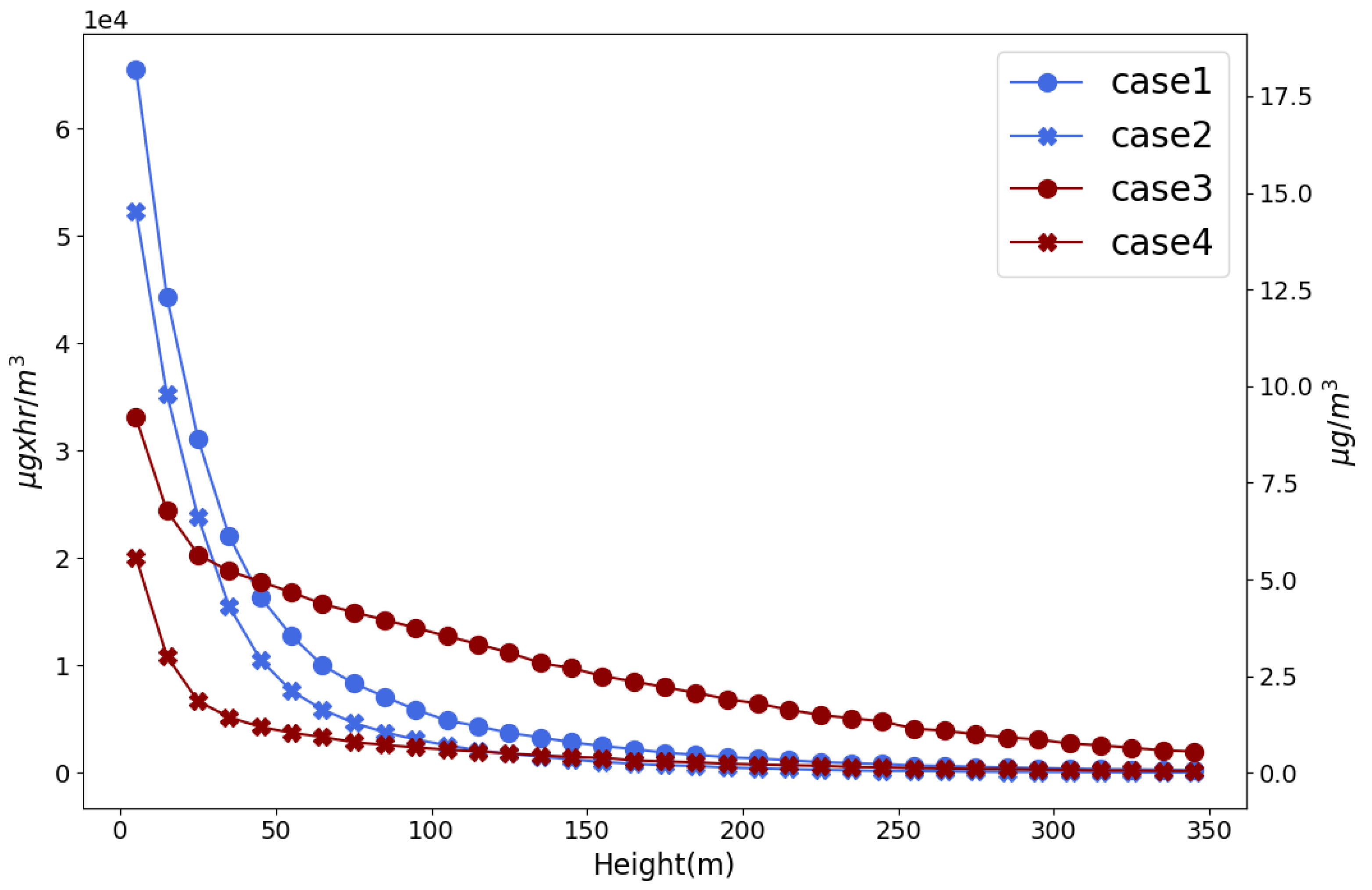
3.3. Analyzed Cases
3.4. Profile Calculation
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meier-Girard, D.; Delgado-Eckert, E.; Schaffner, E.; Schindler, C.; Künzli, N.; Adam, M.; Pichot, V.; Kronenberg, F.; Imboden, M.; Frey, U.; et al. Association of long-term exposure to traffic-related PM10 with heart rate variability and heart rate dynamics in healthy subjects. Environ. Int. 2019, 125, 4429–4439. [Google Scholar] [CrossRef] [PubMed]
- Khreis, H.; Kelly, C.; Tate, J.; Parslow, R.; Lucas, K.; Nieuwenhuijsen, M. Exposure to traffic-related air pollution and risk of development of childhood asthma: A systematic review and meta-analysis. Environ. Int. 2017, 100, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Eitan, O.; Barchana, M.; Dubnov, J.; Linn, S.; Carmel, Y.; Broday, D.M. Spatial analysis of air pollution and cancer incidence rates in Haifa Bay, Israel. Sci. Total Environ. 2010, 408, 4429–4439. [Google Scholar] [CrossRef] [PubMed]
- Yuval; Broday, D.M. High-resolution spatial patterns of long-term mean concentrations of air pollutants in Haifa Bay area. Atmos. Environ. 2006, 40, 3653–3664. [Google Scholar] [CrossRef]
- Sasaki, K.; Sakamoto, K. Vertical differences in the composition of PM10 and PM2.5 in the urban atmosphere of Osaka, Japanl. Atmos. Environ. 2005, 39, 7240–7250. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Xu, H.; Tian, Y.Z.; Shi, G.L.; Zeng, F.; Wu, J.H.; Zhang, X.Y.; Li, X.; Zhu, T.; Feng, Y.C. The study on vertical variability of PM10 and the possible sources on a 220 m tower, in Tianjin, China. Atmos. Environ. 2011, 45, 6133–6140. [Google Scholar] [CrossRef]
- Chan, C.Y.; Xu, X.D.; Li, Y.S.; Wong, K.H.; Ding, G.A.; Chan, L.Y.; Cheng, X.H. Characteristics of vertical profiles and sources of PM2.5, PM10 and carbonaceous species in Beijing. Atmos. Environ. 2005, 39, 5113–5124. [Google Scholar] [CrossRef]
- Pateraki, S.; Manousakas, M.; Bairachtari, K.; Kantarelou, V.; Eleftheriadis, K.; Vasilakos, C.; Assimakopoulos, V.D.; Maggos, T. The traffic signature on the vertical PM profile: Environmental and health risks within an urban roadside environment. Sci. Total Environ. 2019, 646, 448–459. [Google Scholar] [CrossRef]
- Roth, M. Review of atmospheric turbulence over cities. Q. J. R. Meteorol. Soc. 2000, 126, 941–990. [Google Scholar] [CrossRef]
- Belcher, S.E.; Finnigan, J.J.; Harman, I.N. Flows through forest canopies in complex terrain. Ecol. Appl. 2008, 18, 1436–1453. [Google Scholar] [CrossRef] [PubMed]
- Finnigan, J.J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Shaw, R.H.; Patton, E.G. Turbulence structure above a vegetation canopy. J. Fluid Mech. 2009, 637, 387. [Google Scholar] [CrossRef] [Green Version]
- Shnapp, R.; Bohbot-Raviv, Y.; Liberzon, A.; Fattal, E. Turbulence–Obstacle Interactions in the Lagrangian Framework: Applications for Stochastic Modeling in Canopy Flows. Phys. Rev. Fluids 2020, 5, 094601. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. Climatol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Belcher, S.E.; Jerram, N.; Hunt, J.C.R. Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 2003, 488, 369–398. [Google Scholar] [CrossRef] [Green Version]
- Wilson, D.J. Monin-Obukhov Functions for Standard Deviations of Velocity. Bound. Layer Meteorol. 2008, 129, 353–369. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound. Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Neophytou, M.; Gowardhan, A.; Brown, M. An inter-comparison of three urban wind models using Oklahoma City Joint Urban 2003 wind field measurements. J. Wind Eng. Ind. Aerodyn. 2011, 99, 357–368. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Wilson, D.J.; Sawford, B.L. Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound. Layer Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Gavze, E.; Fattal, E. A Semi-analytical Model for Short-Range Near-Ground Continuous Dispersion. Bound. Layer Meteorol. 2018, 169, 297–326. [Google Scholar] [CrossRef]
- Wilson, J.D. Turbulent transport within the plant canopy. Estim. Areal Evapotranspir. 1989, 177, 43–80. [Google Scholar]
- Hanna, S.R.; Brown, M.J.; Camelli, F.E.; Chan, S.T.; Coirier, W.J.; Hansen, O.R.; Huber, A.H.; Kim, S.; Reynolds, R.M. Detailed simulations of atmospheric flow and dispersion in downtown Manhattan: An applications of five computational fluid dynamics models. Bull. Am. Meteorol. Soc. 2006, 87, 1713–1726. [Google Scholar] [CrossRef] [Green Version]
- Wilson, D.J.; Yee, E.; Ek, N.; Amours, R. Lagrangian simulation of wind transport in the urban environment. Q. J. R. Meteorol. Soc. 2009, 1602, 1586–1602. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Wang, Z.H. Quantifying the impact of urban trees on passive pollutant dispersion using a coupled large-eddy simulation–Lagrangian stochastic model. Build. Environ. 2018, 145, 33–49. [Google Scholar] [CrossRef]
- Rockle, R. Bestimmung der Stomungsver-Haltnisse im Bereich Komplexer Bebauugsstruk-Turen. Ph.D. Thesis, Fachbereich Mechanik, der Technischen Hochschule Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
- Kaplan, H.; Dinar, N. A Lagrangian Dispersion Model for Calculating Concentrations Distribution Within a Built-up Domain. Atmos. Environ. 1996, 30, 4197–4207. [Google Scholar] [CrossRef]
- Pardyjak, E.R.; Brown, M.J. Fast response modeling of a two building urban street canyon. In Proceedings of the Fourth Symposium on the Urban Environment, American Meteorological Society, Atlanta, GA, USA, 20–24 May 2002; p. J1.4. [Google Scholar]
- Moussafir, J.; Oldrini, O.; Tinarelli, G.; Sontowski, J.; Catherine, M.D. A New Operational Approach to Deal with Dispersion Around Obstacles: The Mss (Micro Swift Spray) Software Suite. In Proceedings of the 9th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Garmisch-Partenkirchen, Germany, 1–4 June 2004; Volume 5.26. [Google Scholar]
- Fattal, E. A Non-Homogeneous Non-Gaussian Lagrangian-Stochastic Model for Pollutant Dispersion in Complex Terrain, and Its Comparison to Haifa 2009 Tracer Campaign (in Hebrew); 2014/56/53/5614; Israel Institute for Biological Research: Ness-Ziona, Israel, 2014.
- Coceal, O.; Belcher, S.E. Mean winds through an inhomogeneous urban canopy. Bound. Layer Meteorol. 2005, 115, 47–68. [Google Scholar] [CrossRef]
- Finnigan, J. The footprint concept in complex terrain. Agric. For. Meteorol. 2004, 127, 117–129. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.H.; Yang, J.; Li, Q. A Backward-Lagrangian-Stochastic Footprint Model for the Urban Environment. Bound. Layer Meteorol. 2018, 168, 59–80. [Google Scholar] [CrossRef]
- Fattal, E.; Gavze, E. Lagrangian-Stochastic Modeling of Pollutant Dispersion within the Urban Boundary-Layer over Complex Terrain-Israel, Haifa Campaign 2009. In Proceedings of the 2014 American Geophysical Union (AGU) Fall Meeting, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar] [CrossRef]
- Fattal, E.; Buchman, O.; Gavze, E. A Lagrangian Stochastic Model for Urban Area over Complex Terrain-Comparison with Haifa Campaigns. In Proceedings of the 23rd Symposium on Boundary Layers and Turbulence, Oklahoma City, OK, USA, 11–15 June 2018. [Google Scholar]
- Obukhov, A.M. Description of Turbulence in Terms of Lagrangian Variables. Adv. Geophys. 1959, 6, 113–116. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Flesch, T.K.; Wilson, J.D. A two-dimensional trajectory-simulation model for non-Gaussian, inhomogeneous turbulence within plant canopies. Bound. Layer Meteorol. 1992, 61, 349–374. [Google Scholar] [CrossRef]
- Weil, J.C. Linking a Lagrangian Particle Dispersion Model with Three-Dimensional Eulerian Wind Field Models. J. Appl. Meteorol. Climatol. 2008, 47, 2463–2467. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences; Springer: Berlin, Germany, 1997. [Google Scholar]
- Dinar, N. Mass consistent models for wind distribution in complex terrain-Fast algorithms for three dimensional problems. Bound. Layer Meteorol. 1984, 30, 177–199. [Google Scholar] [CrossRef]
- Bohbot-Raviv, Y.; Shnapp, R.; Liberzon, A.; Babin, V.; Fattal, E. Turbulence statistics of canopy-flows using novel Lagrangian measurements within an environmental wind tunnel. In Proceedings of the Physmod 2017—International Workshop on Physical Modelling of Flow and Dispersion Phenomena, École Centrale de Nantes, France, 23–25 August 2017. [Google Scholar]
- Shnapp, R.; Shapira, E.; Peri, D.; Bohbot-Raviv, Y.; Fattal, E.; Liberzon, A. Extended 3D-PTV for direct measurements of Lagrangian statistics of canopy turbulence in a wind tunnel. Sci. Rep. 2019, 9, 7405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shnapp, R. On small-scale and large-scale intermittency of Lagrangian statistics in canopy flow. J. Fluid Mech. 2021, 913, R2. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G.; Cassiani, M. On the anomalous behavior of the Lagrangian structure function similarity constant inside dense canopies. Atmos. Environ. 2008, 42, 4212–4231. [Google Scholar] [CrossRef]
- Du, S. Universality of the Lagrangian Velocity Stracture Function Constant (C0) Across Different kinds of Turbulence. Bound. Layer Meteorol. 1997, 83, 207–219. [Google Scholar] [CrossRef]
- Rizza, U.; Degrazia, G.A.; Mangia, C.; Filho, E.P.M. Estimation of the Kolmogorov constant for the Lagrangian velocity spectrum and structure function under different PBL stability regimes generated by LES. Phys. A Stat. Mech. Its Appl. 2010, 389, 4009–4017. [Google Scholar] [CrossRef]
- Christen, A.; Vogt, R.; Rotach, M.W. Profile measurements of selected turbulence parameters over different urban surfaces. In Proceedings of the 4th International Conference on Urban Air Quality, Prague, Czech Republic, 25–28 March 2003; pp. 408–411. [Google Scholar]
- Wilson, D.J.; Flesch, T.K. Trajectory curvature as a selection criterion for valid Lagrangian stochastic dispersion models. Bound. Layer Meteorol. 1997, 84, 411–425. [Google Scholar] [CrossRef]
- Sawford, B.L. Rotation of trajectories in lagrangian stochastic models of turbulent dispersion. Bound. Layer Meteorol. 1999, 93, 411–424. [Google Scholar] [CrossRef]
- Brouwers, J.J.H. Statistical description of turbulent dispersion. Phys. Rev. E 2012, 86, 066309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gloster, J.; Sellers, R.; Webster, H.; Valarcher, J.F. Assessing the risk of airborne spread of foot-and-mouth disease: A case study. Weather 2006, 61, 137–142. [Google Scholar] [CrossRef]
- Mayer, D.; Reiczigel, J.; Rubel, F. A Lagrangian particle model to predict the airborne spread of foot-and-mouth disease virus. Atmos. Environ. 2008, 42, 466–479. [Google Scholar] [CrossRef]
- Garner, M.G.; Hess, G.D.; Yang, X. An integrated modelling approach to assess the risk of wind-borne spread of foot-and-mouth disease virus from infected premises. Environ. Model. Assess. 2006, 11, 195–207. [Google Scholar] [CrossRef]
- Klausner, Z.; Klement, E.; Fattal, E. Modeling long distance dispersal of airborne foot-and-mouth disease virus as a polydisperse aerosol—Application to the emergence of a new strain from Egypt to Israel. Atmos. Environ. 2015, 122, 332–342. [Google Scholar] [CrossRef]
- Shi, J.P.; Mark, D.; Harrison, R.M. Characterization of particles from a current technology heavy-duty diesel engine. Environ. Sci. Technol. 2000, 34, 748–755. [Google Scholar] [CrossRef]
- Csanady, G.T. Turbulent Diffusion of Heavy Particles in the Atmosphere; D. Reidel Publishing: Dordrecht, The Netherlands, 1963. [Google Scholar] [CrossRef]
- Hanna, S.R.; Britter, R.E. Wind Flow and Vapor Cloud Dispersion at Industrial and Urban Sites; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology, 1st ed.; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Raupach, M.R.; Shaw, R.H. Averaging procedures for flow canopies. Bound. Layer Meteorol. 1982, 22, 79–90. [Google Scholar] [CrossRef]
- Coceal, O.; Belcher, S.E. A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 2004, 130, 1349–1372. [Google Scholar] [CrossRef] [Green Version]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Inoue, E. On the turbulent structure of airflow within crop canopies. J. Meteorol. Soc. Jpn. 1963, 41, 317–326. [Google Scholar] [CrossRef] [Green Version]
- Finnigan, J.; Harman, I.; Ross, A.; Belcher, S.E. First-order turbulence closure for modelling complex canopy flows. Q. J. R. Meteorol. Soc. 2015, 141, 2907–2916. [Google Scholar] [CrossRef] [Green Version]
- Harman, I.N.; Finnigan, J.J. A simple unified theory for flow in the canopy and roughness sublayer. Bound. Layer Meteorol. 2007, 123, 339–363. [Google Scholar] [CrossRef]
- Hicks, B.B.; Pendergrass, W.R.; Vogel, C.a.; Keener, R.N.; Leyton, S.M. On the Micrometeorology of the Southern Great Plains 1: Legacy Relationships Revisited. Bound. Layer Meteorol. 2014, 151, 389–405. [Google Scholar] [CrossRef]
- Hanna, S.R. Applications in air pollution modelling. In Atmospheric Turbulence and Air Pollution Modelling; Nieuwstadt, F.T.M., van Dop, H., Eds.; D. Reidel Publishing: Dordrecht, The Netherlands, 1982; p. 275. [Google Scholar] [CrossRef]
- Kastner-Klein, P.; Rotach, M.W. Mean flow and turbulence characteristics in an urban roughness sublayer. Bound. Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Mortarini, L.; Ferrero, E.; Richiardone, R.; Falabino, S.; Anfossi, D.; Trini Castelli, S.; Carretto, E. Assessment of dispersion parameterizations through wind data measured by three sonic anemometers in a urban canopy. Adv. Sci. Res. 2009, 3, 91–98. [Google Scholar] [CrossRef] [Green Version]
- Flesch, T.K.; Wilson, J.D.; Yee, E. Backward-time Lagrangian stochastic dispersion models and their application to estimate gaseous emissions. J. Appl. Meteorol. 1995, 34, 1320–1332. [Google Scholar] [CrossRef] [Green Version]
- Buchman, O.; Fattal, E. A Method for Source Location Estimation Based on Backward Lagrangian Stochastic Model. 2019/56/37/5614; Israel Institute for Biological Research: Ness-Ziona, Israel, 2019.
- Buchman, O.; Fattal, E. Adaptive degenerate space method for source term estimation using a backward Lagrangian stochastic model. arXiv 2020, arXiv:2004.06526. [Google Scholar]
- Sawford, B.L. Lagrangian Statistical Simulation of Concentration Mean and Fluctuation Fields. J. Clim. Appl. Meteorol. 1985, 24, 1152–1166. [Google Scholar] [CrossRef]
- Israel Ministry of Environmental Protection. Israel Road Traffic Emissions Inventory for the Year 2019; Received by Authors Request; Israel Ministry of Environmental Protection: Tel-Aviv, Israel, 2019.
- Wilson, J.D.; Swaters, G.E. The source area influencing a measurement in the Planetary Boundary Layer: The “footprint” and the “distribution of contact distance”. Bound. Layer Meteorol. 1991, 55, 25–46. [Google Scholar] [CrossRef]
- Schmid, H.P. Source areas for scalars and scalar fluxes. Bound. Layer Meteorol. 1994, 67, 293–318. [Google Scholar] [CrossRef]
- Alpert, P.; Osetinsky, I.; Ziv, B.; Shafir, H. A new seasons definition based on classified daily synoptic systems: An example for the eastern Mediterranean. Int. J. Climatol. 2004, 24, 1013–1021. [Google Scholar] [CrossRef]
- Klausner, Z.; Ben-efraim, M.; Arav, Y.; Tas, E.; Fattal, E. The micrometeorology of the Haifa bay area and Mount Carmel–Summer flow regimes. Atmosphere 2021, 12, 354. [Google Scholar] [CrossRef]
- Goldreich, Y. The Climate of Israel: Observation, Research and Application; Springer: New York, NY, USA, 1998; ISBN 9781461352006. [Google Scholar]
- Klausner, Z.; Fattal, E. An objective and automatic method for identification of pattern changes in wind direction time series. Int. J. Climatol. 2011, 31, 783–790. [Google Scholar] [CrossRef]
- Background_ENV_DATA; Ministry of Environmental Protection, Air Quality Division: Tel-Aviv, Israel, 2014. Available online: https://www.gov.il/BlobFolder/policy/guidelines_conducting_environmental_survey_air_pollution_transportation/he/transportation_airpollutants_by_land_area.pdf (accessed on 22 February 2021).

| Station Name | Location | Wind Sensor | Elevation ASL [m] | Owner |
|---|---|---|---|---|
| Bet Dagan | 32026 N 344850 E | Propeller-vane anemometer | 31 | IMS |
| Tel Aviv Coast | 32329 N 344532 E | Propeller-vane anemometer | 10 | IMS |
| Tel Aviv Kremenetski | 32359 N 344742 E | Cup anemometer + vane | 17 | MoAg |
| Tel Aviv university | 32484 N 345930 E | Cup anemometer + vane | 28 | MoEP |
| Case | Point | Speed (m/s) | Direction | ||
|---|---|---|---|---|---|
| 1 | Edgar Tower | 08:00 | 09:00 | 2 | 240 |
| 2 | Edgar Tower | 18:00 | 19:00 | 3 | 300 |
| 3 | Ben Gurion st. | 08:00 | 09:00 | 2 | 240 |
| 4 | Ben Gurion st. | 18:00 | 19:00 | 3 | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fattal, E.; David-Saroussi, H.; Klausner, Z.; Buchman, O. An Urban Lagrangian Stochastic Dispersion Model for Simulating Traffic Particulate-Matter Concentration Fields. Atmosphere 2021, 12, 580. https://doi.org/10.3390/atmos12050580
Fattal E, David-Saroussi H, Klausner Z, Buchman O. An Urban Lagrangian Stochastic Dispersion Model for Simulating Traffic Particulate-Matter Concentration Fields. Atmosphere. 2021; 12(5):580. https://doi.org/10.3390/atmos12050580
Chicago/Turabian StyleFattal, Eyal, Hadas David-Saroussi, Ziv Klausner, and Omri Buchman. 2021. "An Urban Lagrangian Stochastic Dispersion Model for Simulating Traffic Particulate-Matter Concentration Fields" Atmosphere 12, no. 5: 580. https://doi.org/10.3390/atmos12050580
APA StyleFattal, E., David-Saroussi, H., Klausner, Z., & Buchman, O. (2021). An Urban Lagrangian Stochastic Dispersion Model for Simulating Traffic Particulate-Matter Concentration Fields. Atmosphere, 12(5), 580. https://doi.org/10.3390/atmos12050580






