Identification of a Representative Stationary Period for Rainfall Variability Description in the Sudano-Sahelian Zone of West Africa during the 1901–2018 Period
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. Methods and Calculations
2.2.1. Criticism of the Gridded Datasets
2.2.2. Evaluation of the Changes and Trends in the Annual Rainfall Time Series
- Stationarity analysis;
- Breaks or shifts in the time series;
- Trends in the time series;
3. Results
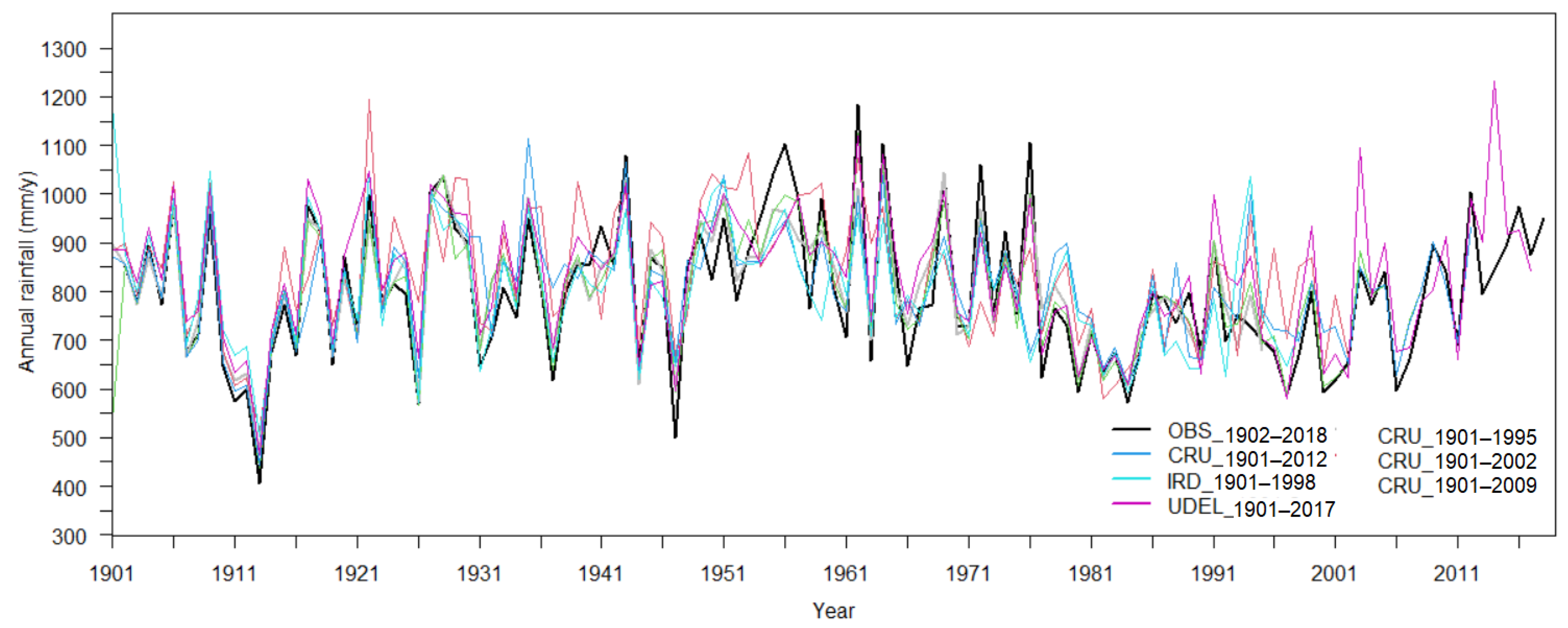
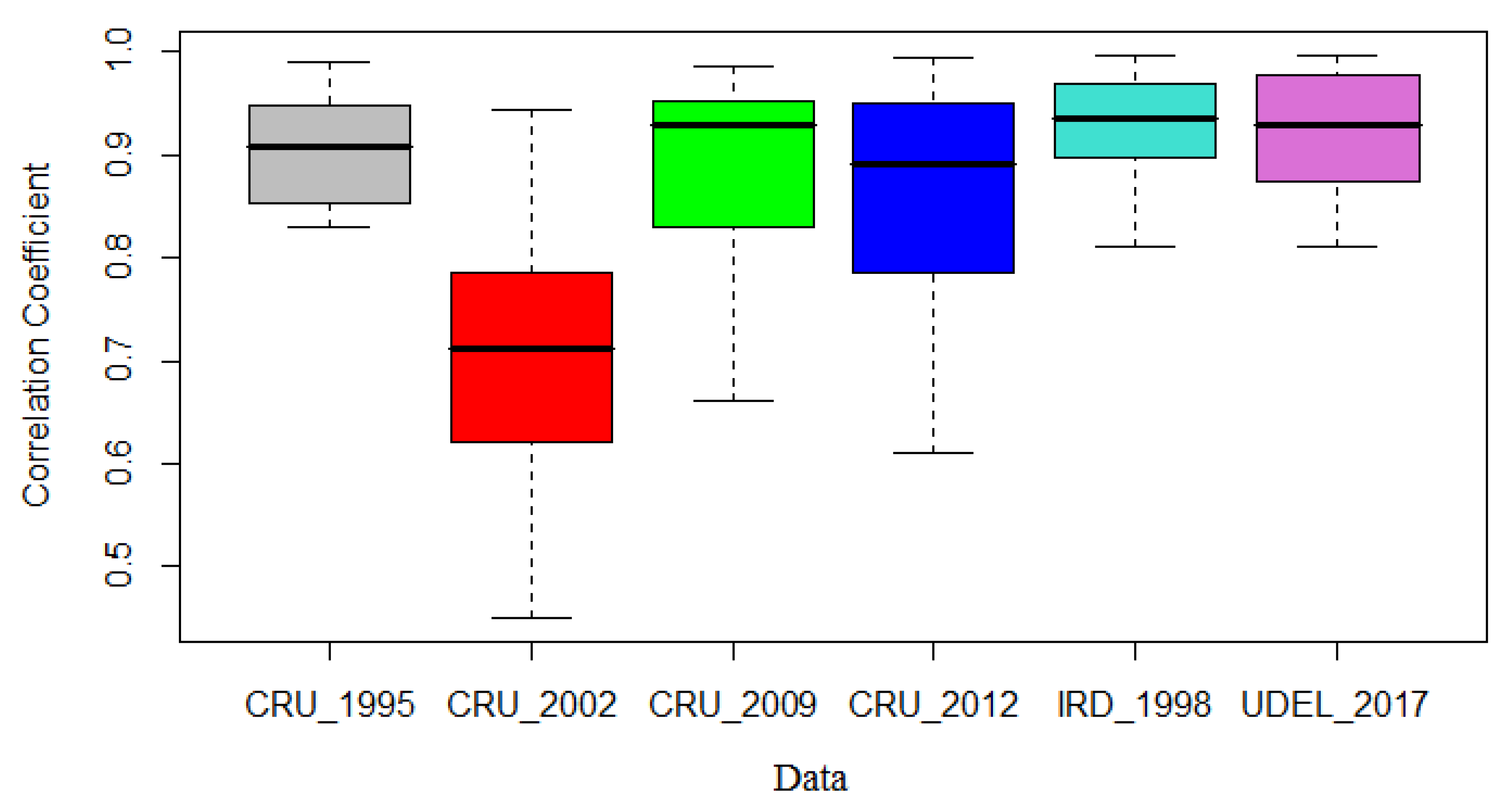
3.1. Comparison of Rainfall Data from the Different Sources
3.2. Identification of A Relevant Stationary Period for the Rainfall Regime
3.2.1. Assessment of the Stationarity in Rainfall Time Series
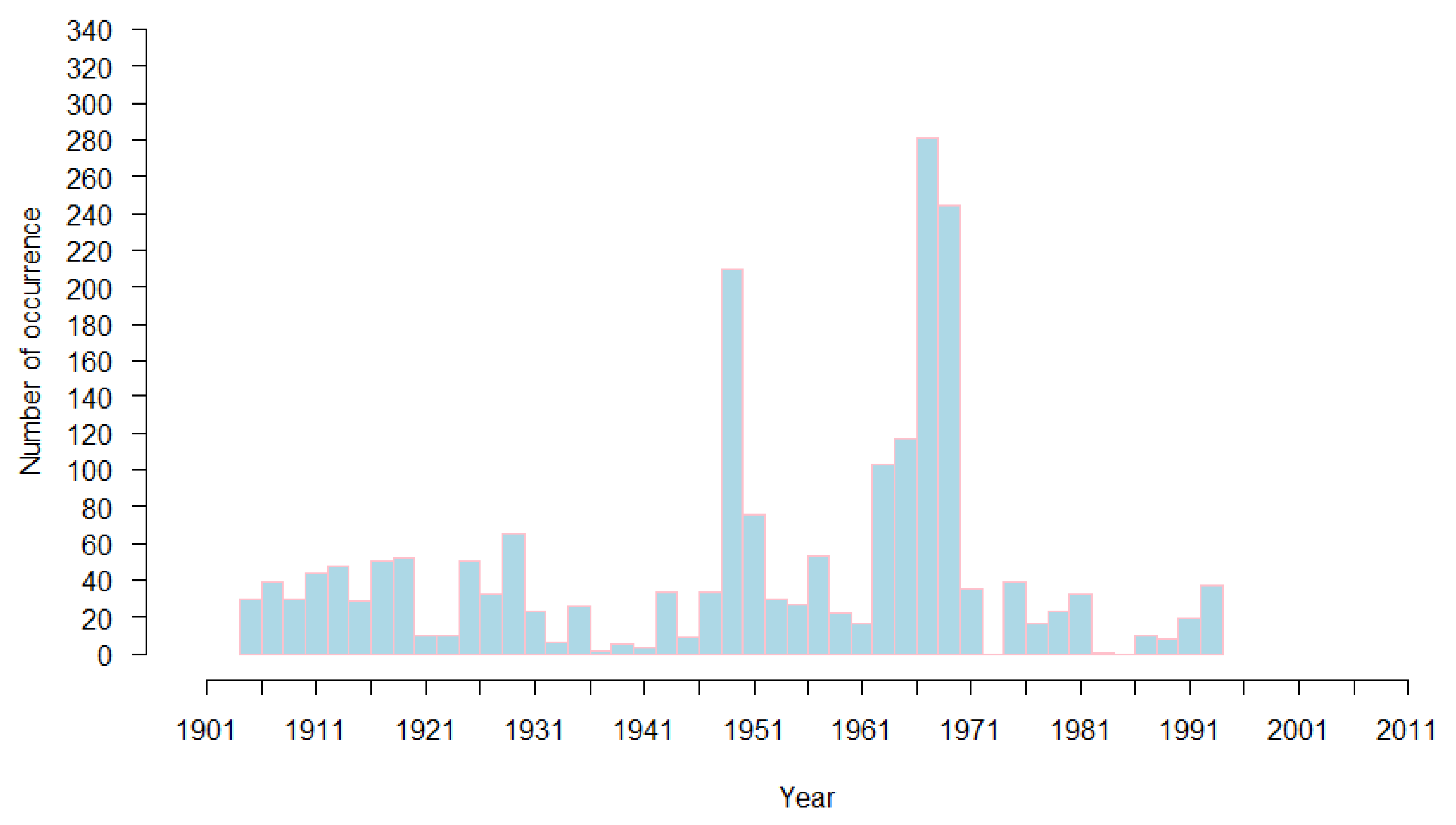
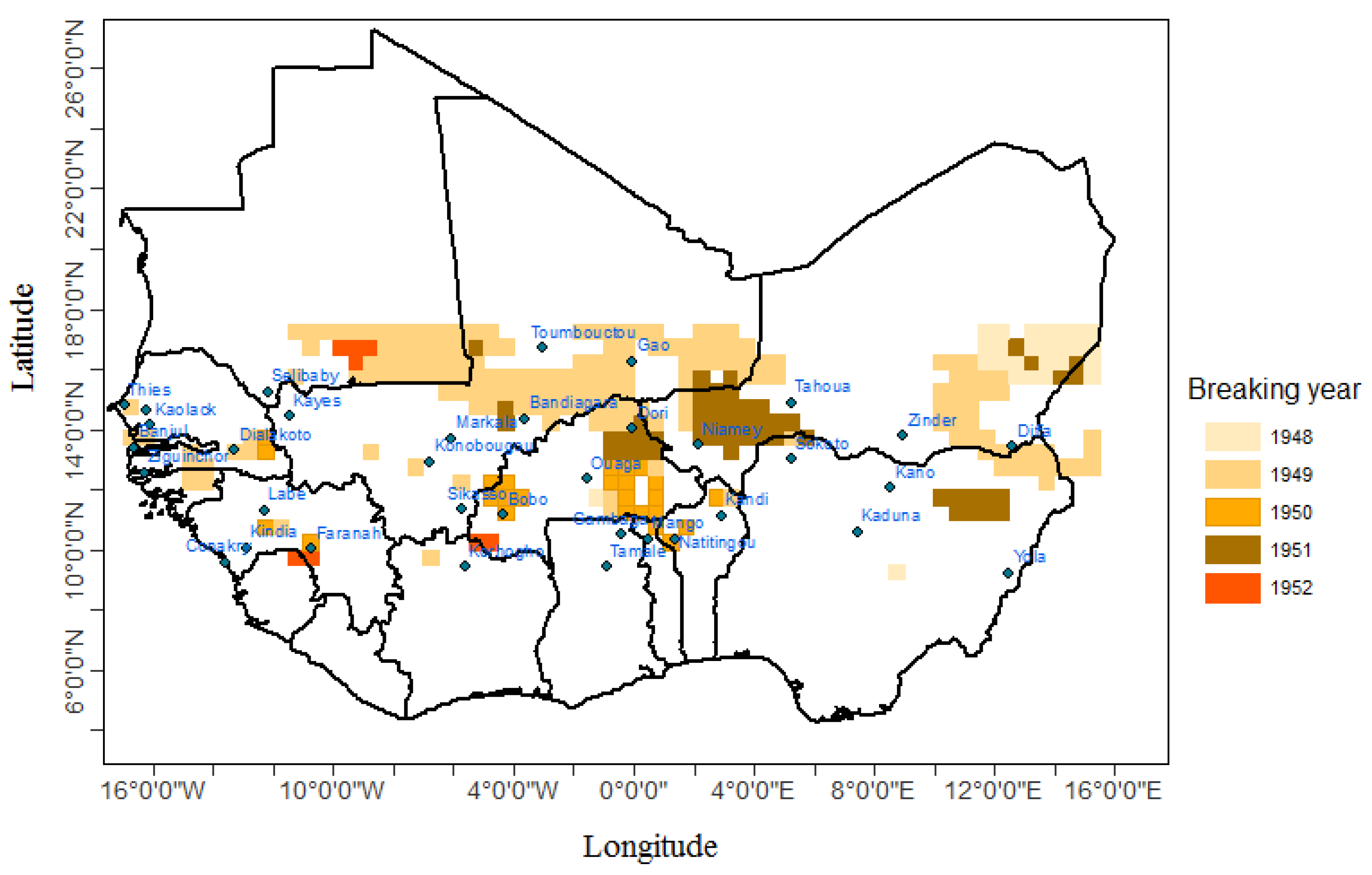
3.2.2. Identification of Breaks in the Annual Rainfall Time Series
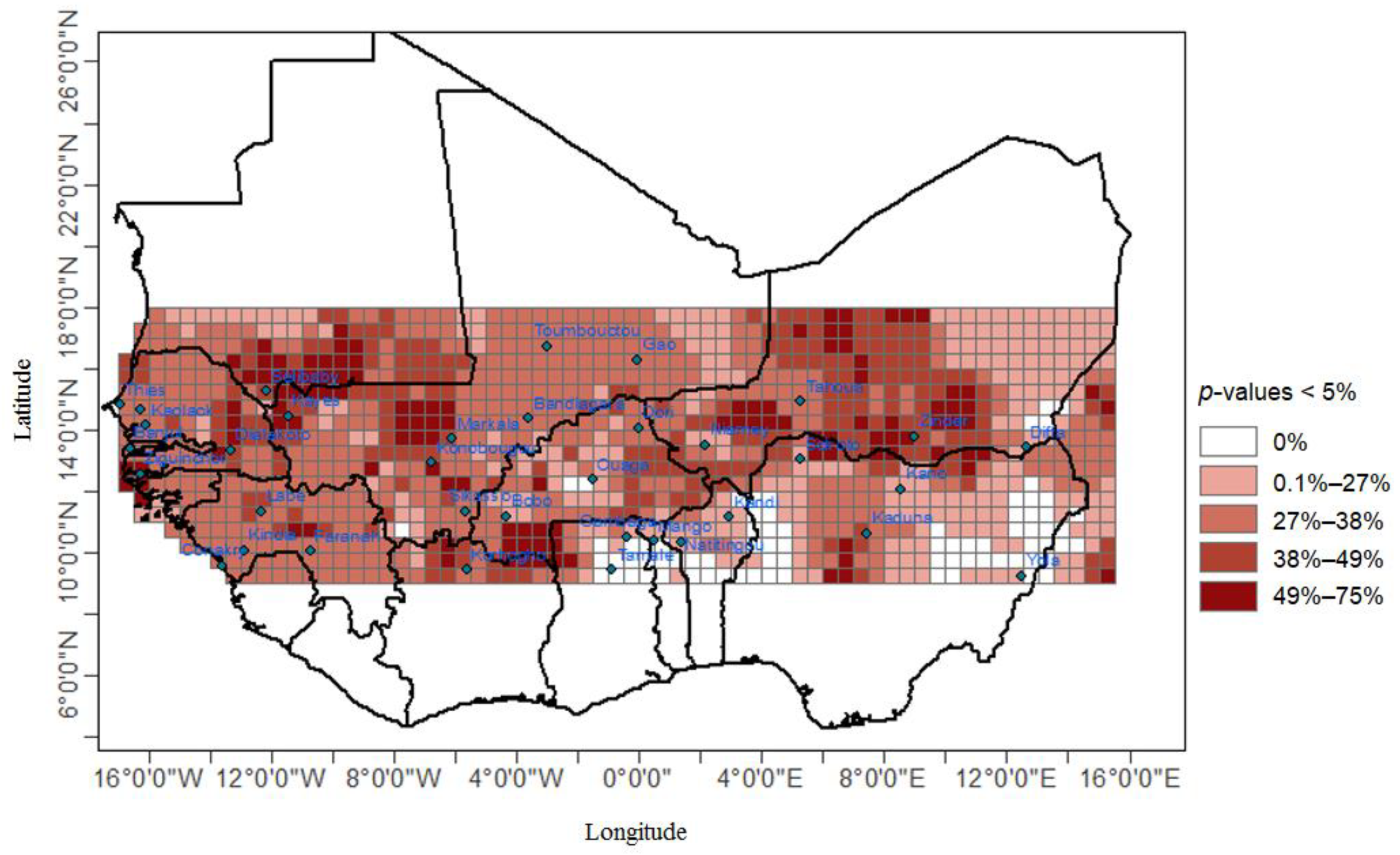
3.2.3. Assessment of the Breaks Significance
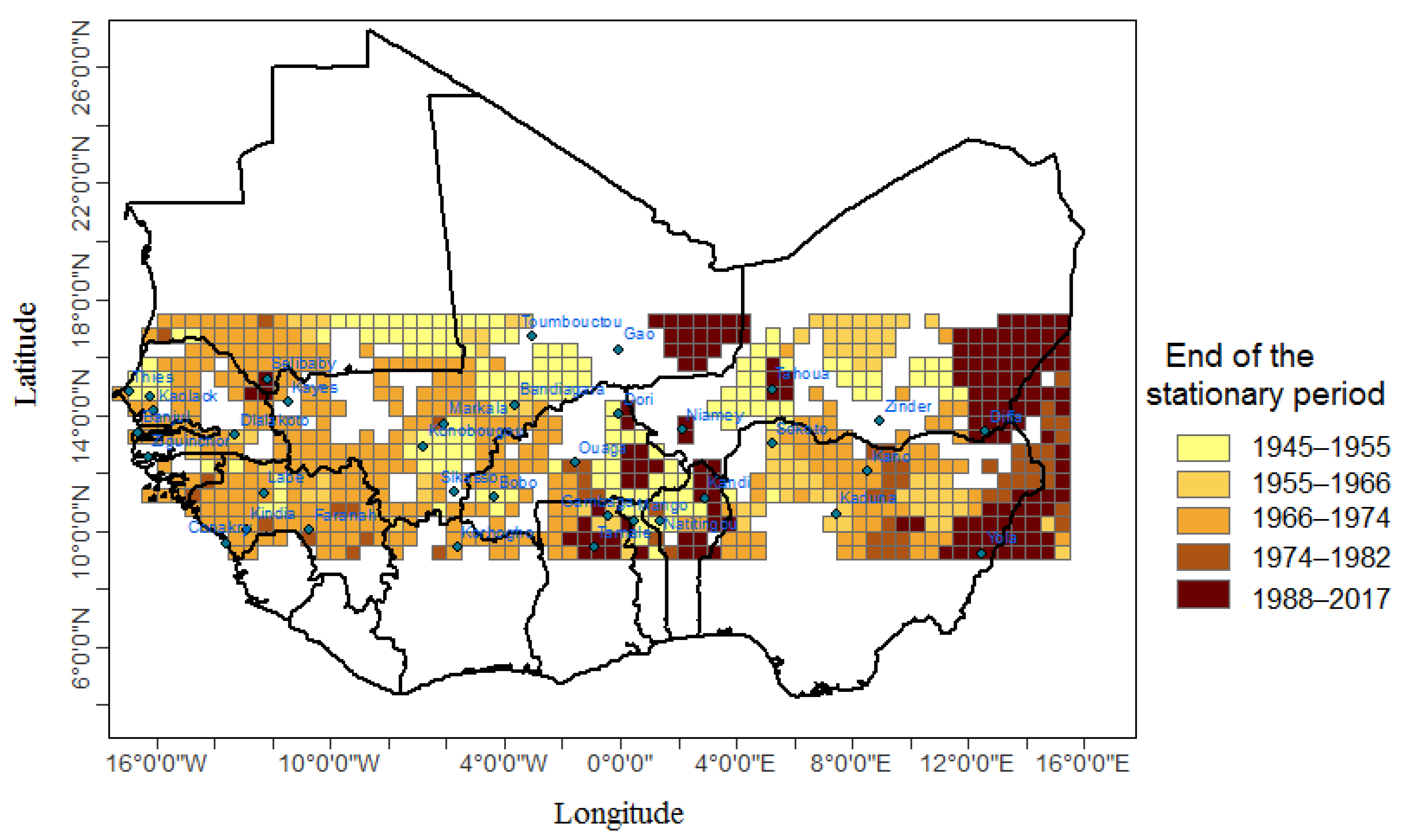
3.3. Identification of a Representative Stationary Period
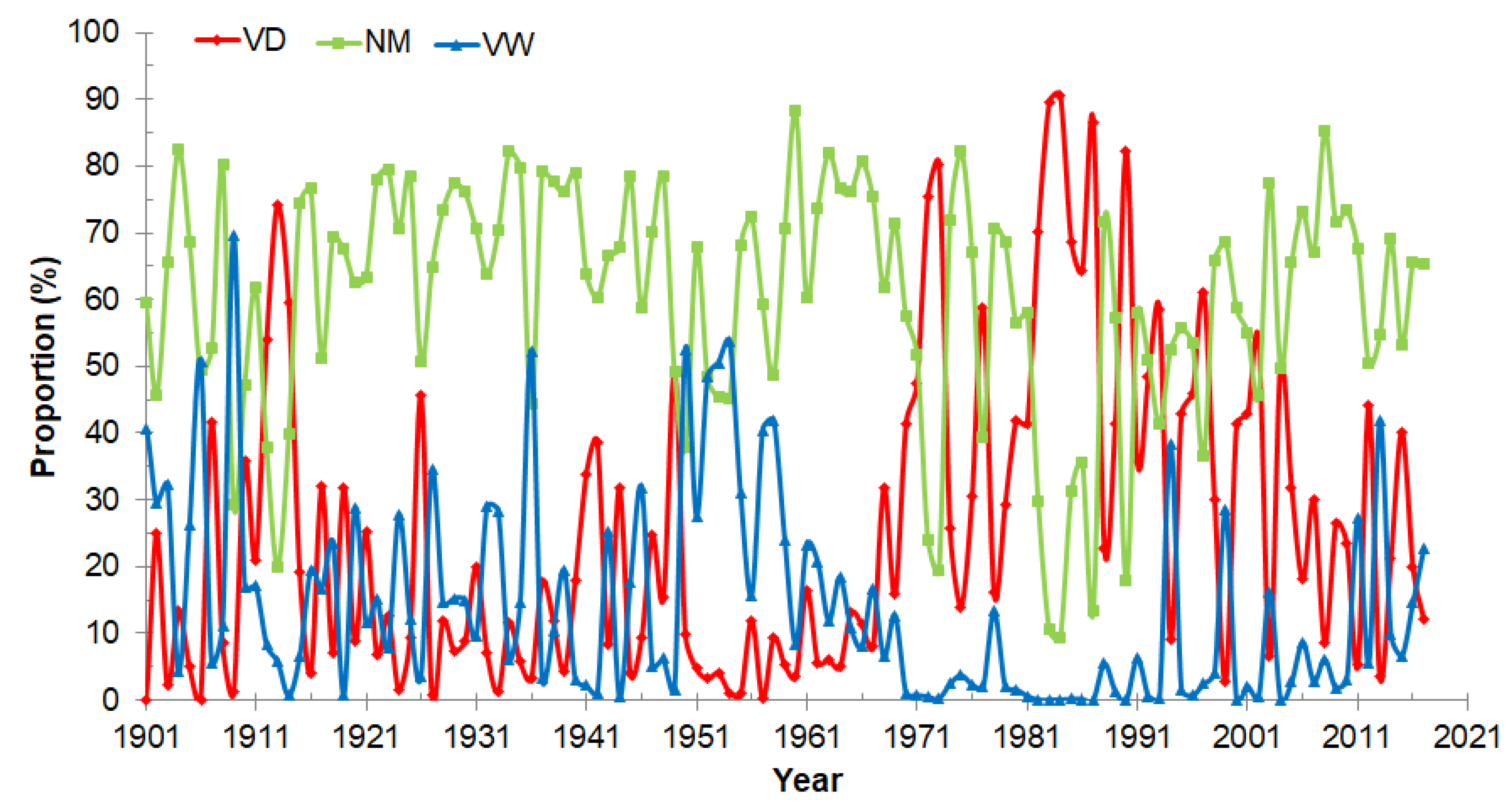
3.4. Determination of Wet and Dry Year with Regard to the Stationary Period
4. Summary and Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Breuer, L.; Huisman, J.A.; Willems, P.; Bormann, H.; Bronstert, A.; Croke, B.F.W.; Frede, H.-G.; Gräff, T.; Hubrechts, L.; Jakeman, A.J.; et al. Assessing the Impact of Land Use Change on Hydrology by Ensemble Modeling (LUCHEM). I: Model Intercomparison with Current Land Use. Adv. Water Resour. 2009, 32, 129–146. [Google Scholar] [CrossRef]
- Nikulin, G.; Jones, C.; Giorgi, F.; Asrar, G.; Büchner, M.; Cerezo-Mota, R.; Christensen, O.B.; Déqué, M.; Fernandez, J.; Hänsler, A.; et al. Precipitation Climatology in an Ensemble of CORDEX-Africa Regional Climate Simulations. J. Clim. 2012, 25, 6057–6078. [Google Scholar] [CrossRef] [Green Version]
- Gbobaniyi, E.; Sarr, A.; Sylla, M.B.; Diallo, I.; Lennard, C.; Dosio, A.; Dhiédiou, A.; Kamga, A.; Klutse, N.A.B.; Hewitson, B.; et al. Climatology, Annual Cycle and Interannual Variability of Precipitation and Temperature in CORDEX Simulations over West Africa. Int. J. Climatol. 2014, 34, 2241–2257. [Google Scholar] [CrossRef]
- Ibrahim, B.; Karambiri, H.; Polcher, J.; Yacouba, H.; Ribstein, P. Changes in Rainfall Regime over Burkina Faso under the Climate Change Conditions Simulated by 5 Regional Climate Models. Clim. Dyn. 2014, 42, 1363–1381. [Google Scholar] [CrossRef] [Green Version]
- Sultan, B.; Baron, C.; Dingkuhn, M.; Sarr, B.; Janicot, S. Agricultural Impacts of Large-Scale Variability of the West African Monsoon. Agric. For. Meteorol. 2005, 128, 93–110. [Google Scholar] [CrossRef]
- Sivakumar, M.V.K. Climate Change and Implications for Agriculture in Niger. Clim. Chang. 1992, 20, 297–312. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, S.E. Climatic and Environmental Change in Africa during the Last Two Centuries. Clim. Res. 2001, 17, 123–144. [Google Scholar] [CrossRef] [Green Version]
- Ouédraogo, E.; Mando, A.; Zombré, N.P. Use of Compost to Improve Soil Properties and Crop Productivity under Low Input Agricultural System in West Africa. Agric. Ecosyst. Environ. 2001, 84, 259–266. [Google Scholar] [CrossRef]
- Nicholson, S.E. The Nature of Rainfall Fluctuations in Subtropical West Africa. Mon. Weather Rev. 1980, 108, 473–487. [Google Scholar] [CrossRef] [Green Version]
- Sircoulon, J. Les Données Hydropluviométriques de La Sécheresse Récente En Afrique Intertropicale. Comparaison Avec Les Sécheresses «1913 et 1940». Cah Orstom Ser. Hydrol. XIIII2 1976, 13, 75–174. [Google Scholar]
- Ali, A.; Lebel, T. The Sahelian Standardized Rainfall Index Revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- Paturel, J.E.; Boubacar, I.; L’Aour, A.; Mahé, G. Analyses of Pluviometric Grids and Main Features of the Changes Occurring in West and Central Africa during the 20th Century. Hydrol. Sci. J. 2010, 55, 1281–1288. [Google Scholar] [CrossRef] [Green Version]
- L’Hôte, Y.; Mahé, G.; Somé, B.; Triboulet, J.P. Analysis of a Sahelian Annual Rainfall Index from 1896 to 2000; the Drought Continues. Hydrol. Sci. J. 2002, 47, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Mahé, G.; Paturel, J.-E. 1896–2006 Sahelian Annual Rainfall Variability and Runoff Increase of Sahelian Rivers. Comptes Rendus Geosci. 2009, 341, 538–546. [Google Scholar] [CrossRef]
- Livezey, R.E.; Vinnikov, K.Y.; Timofeyeva, M.M.; Tinker, R.; Dool, H.M. van den Estimation and Extrapolation of Climate Normals and Climatic Trends. J. Appl. Meteorol. Climatol. 2007, 46, 1759–1776. [Google Scholar] [CrossRef] [Green Version]
- Arguez, A.; Vose, R.S. The Definition of the Standard WMO Climate Normal: The Key to Deriving Alternative Climate Normals. Bull. Am. Meteorol. Soc. 2011, 92, 699–704. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated High-Resolution Grids of Monthly Climatic Observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Mahe, G.; Paturel, J.-E.; Servat, E.; Conway, D.; Dezetter, A. The Impact of Land Use Change on Soil Water Holding Capacity and River Flow Modelling in the Nakambe River, Burkina-Faso. J. Hydrol. 2005, 300, 33–43. [Google Scholar] [CrossRef]
- Paturel, J.E.; Barrau, C.; Mahé, G.; Dezetter, A.; Servat, E. Modelling the Impact of Climatic Variability on Water Resources in West and Central Africa from a Non-Calibrated Hydrological Model. Hydrol. Sci. J. 2007, 52, 38–48. [Google Scholar] [CrossRef]
- Ibrahim, B. Caractérisation des Saisons de Pluies au Burkina Faso Dans un Contexte de Changement Climatique et Evaluation des Impacts Hydrologiques sur le Bassin du Nakanbé. Ph.D. Thesis, Université Pierre et Marie Curie—Paris VI, Paris, France, 2012. [Google Scholar]
- Milot, G. Comprendre et Réaliser Les Tests Statistiques Avec R; De Boeck: Brussels, Belgium, 2009. [Google Scholar]
- Ansari, A.R.; Bradley, R.A. Rank-Sum Tests for Dispersions. Ann. Math. Stat. 1960, 31, 1174–1189. [Google Scholar] [CrossRef]
- Giorgi, F.; Bi, X.; Pal, J. Mean, Interannual Variability and Trends in a Regional Climate Change Experiment over Europe. II: Climate Change Scenarios (2071–2100). Clim. Dyn. 2004, 23, 839–858. [Google Scholar] [CrossRef]
- Dahmen, E.R.; Hall, M.J. Screening of Hydrological Data: Tests for Stationarity and Relative Consistency; ILRI: Wageningen, The Netherlands, 1990; ISBN 978-90-70754-23-5. [Google Scholar]
- Machiwal, D.; Jha, M.K. Time Series Analysis of Hydrologic Data for Water Resources Planning and Management: A Review. J. Hydrol. Hydromech. 2009, 54, 237–257. [Google Scholar]
- Kundzewicz, Z.W.; Robson, A.J. Change Detection in Hydrological Records—A Review of the Methodology/Revue Méthodologique de La Détection de Changements Dans Les Chroniques Hydrologiques. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Hubert, P. The Segmentation Procedure as a Tool for Discrete Modeling of Hydrometeorological Regimes. Stoch. Environ. Res. Risk Assess. 2000, 14, 297–304. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Hubert, P.; Servat, E.; Paturel, J.-E.; Kouame, B.; Bendjoudi, H.; Carbonnel, J.P.; Lubes-Niel, H. La Procédure de Segmentation, Dix Ans Après. IAHS Publ. 1998, 252, 267–274. [Google Scholar]
- Burn, D.H.; Hag Elnur, M.A. Detection of Hydrologic Trends and Variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s Rho Tests for Detecting Monotonic Trends in Hydrological Series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Paturel, J.E.; Ouédraogo, M.; Servat, E.; Mahé, G.; Dezetter, A.; Boyer, J.F. The Concept of Hydropluviometric Normal in West and Central Africa in a Context of Climatic Variability. Hydrol. Sci. J. 2003, 48, 125–137. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O.; Ajayi, V.O.; Adefisan, E.A.; Omotosho, J.A.; Sanogo, S. Comparison of Five Gridded Precipitation Products at Climatological Scales over West Africa. Meteorol. Atmos. Phys. 2017, 129, 669–689. [Google Scholar] [CrossRef]
- Cecinati, F.; Moreno-Ródenas, A.M.; Rico-Ramirez, M.A.; Ten Veldhuis, M.; Langeveld, J.G. Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data. Atmosphere 2018, 9, 446. [Google Scholar] [CrossRef] [Green Version]
- Dreaver, K.R.; Hutchinson, P. Random and Systematic Errors in Precipitation at an Exposed Site. J. Hydrol. N. Z. 1974, 13, 54–63. [Google Scholar]



| Stations | CRU_1995 | CRU_2002 | CRU_2009 | CRU_2012 | IRD_1998 | UDEL_2017 |
|---|---|---|---|---|---|---|
| Ouagadougou | 0.63 | 0.14 | 0.75 | 0.48 | 0.87 | 0.13 |
| Bobo-Dioulasso | 0.09 | 0.09 | 0.08 | 0.07 | 0.72 | 0.01 |
| Dori | 0.13 | 0.11 | 0.09 | 0.25 | 0.05 | 0.04 |
| Niamey | 0.04 | 0.09 | 0.03 | 0.03 | 0.04 | 0.36 |
| Tahoua | 0.37 | 0.06 | 0.37 | 0.25 | 0.46 | 0.40 |
| Zinder | 0.39 | 0.33 | 0.37 | 0.39 | 0.75 | 0.43 |
| Bandiagara | 0.24 | 0.57 | 0.14 | 0.15 | 0.38 | 0.99 |
| Toumbouctou | 0.76 | 0.91 | 0.62 | 0.80 | 0.96 | 0.70 |
| Diourbel | 0.95 | 0.57 | 0.81 | 0.96 | 0.37 | 0.86 |
| Thies | 0.41 | 0.12 | 0.23 | 0.21 | 0.78 | 0.22 |
| Ziguinchor | 0.33 | 0.60 | 0.49 | 0.54 | 0.07 | 1.00 |
| Banjul | 0.56 | 0.13 | 0.20 | 0.53 | 0.32 | 0.35 |
| Conakry | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Kindia | 0.00 | 0.00 | 0.00 | 0.00 | 0.81 | 0.64 |
| Labe | 0.06 | 0.08 | 0.04 | 0.10 | 0.63 | 0.50 |
| Korhogho | 0.46 | 0.37 | 0.64 | 0.47 | 0.62 | 0.92 |
| Gambaga | 0.81 | 0.83 | 0.51 | 0.73 | 0.55 | 0.34 |
| Tamale | 0.10 | 0.00 | 0.11 | 0.11 | 0.09 | 0.36 |
| Mango | 0.97 | 0.85 | 0.87 | 0.88 | 0.77 | 0.05 |
| Kandi | 0.01 | 0.04 | 0.01 | 0.01 | 0.40 | 0.72 |
| Natitingou | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 |
| Kano | 0.46 | 0.52 | 0.64 | 0.49 | 0.13 | 0.44 |
| Sokoto | 0.67 | 0.21 | 0.83 | 0.77 | 0.19 | 0.89 |
| Markala | 0.05 | 0.12 | 0.14 | 0.11 | 0.98 | 0.08 |
| Konobougou | 0.09 | 0.05 | 0.08 | 0.07 | 0.54 | 0.74 |
| Diffa | 0.02 | 0.04 | 0.04 | 0.01 | 0.04 | 0.04 |
| Kaduna | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.31 |
| Yola | 0.00 | 0.00 | 0.00 | 0.00 | 0.28 | 0.31 |
| Faranah | 0.00 | 0.00 | 0.00 | 0.00 | 0.78 | 0.94 |
| Gao | 0.06 | 0.02 | 0.06 | 0.09 | 0.90 | 0.99 |
| Dialakoto | 0.00 | 0.00 | 0.00 | 0.00 | 0.37 | 0.59 |
| Kaolack | 0.22 | 0.40 | 0.12 | 0.14 | 0.96 | 0.36 |
| Kayes | 0.01 | 0.00 | 0.00 | 0.00 | 0.08 | 0.00 |
| Selibaby | 0.15 | 0.60 | 0.13 | 1.00 | 0.50 | 0.01 |
| Number of Stations with Difference | 11 | 13 | 12 | 11 | 5 | 7 |
| 1929 | 1948 | 1952 | 1958 | 1969 | 1975 | 1979 | 1984 | 1987 | 1988 | Total | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Breaks | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 |
| Intervals | Ouagadougou | Zinder | Kano | Sokoto |
|---|---|---|---|---|
| PCI.90% | 30 | 23 | 27 | 13 |
| PCI.95% | 37 | 30 | 27 | 37 |
| PSD.100% | 67 | 73 | 70 | 73 |
| PSD.110% | 67 | 73 | 77 | 77 |
| PSD.150% | 87 | 87 | 87 | 83 |
| PSD.200% | 97 | 97 | 93 | 93 |
| PSD.210% | 100 | 97 | 97 | 93 |
| PSD.220% | 100 | 97 | 97 | 93 |
| PSD.230% | 100 | 97 | 97 | 100 |
| PSD.240% | 100 | 100 | 97 | 100 |
| PSD.250% | 100 | 100 | 97 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, B.; Nazoumou, Y.; Fowe, T.; Sidibe, M.; Barry, B.; Mahé, G.; Paturel, J.-E. Identification of a Representative Stationary Period for Rainfall Variability Description in the Sudano-Sahelian Zone of West Africa during the 1901–2018 Period. Atmosphere 2021, 12, 716. https://doi.org/10.3390/atmos12060716
Ibrahim B, Nazoumou Y, Fowe T, Sidibe M, Barry B, Mahé G, Paturel J-E. Identification of a Representative Stationary Period for Rainfall Variability Description in the Sudano-Sahelian Zone of West Africa during the 1901–2018 Period. Atmosphere. 2021; 12(6):716. https://doi.org/10.3390/atmos12060716
Chicago/Turabian StyleIbrahim, Boubacar, Yahaya Nazoumou, Tazen Fowe, Moussa Sidibe, Boubacar Barry, Gil Mahé, and Jean-Emmanuel Paturel. 2021. "Identification of a Representative Stationary Period for Rainfall Variability Description in the Sudano-Sahelian Zone of West Africa during the 1901–2018 Period" Atmosphere 12, no. 6: 716. https://doi.org/10.3390/atmos12060716
APA StyleIbrahim, B., Nazoumou, Y., Fowe, T., Sidibe, M., Barry, B., Mahé, G., & Paturel, J.-E. (2021). Identification of a Representative Stationary Period for Rainfall Variability Description in the Sudano-Sahelian Zone of West Africa during the 1901–2018 Period. Atmosphere, 12(6), 716. https://doi.org/10.3390/atmos12060716






