Understanding the Major Impact of Planetary Boundary Layer Schemes on Simulation of Vertical Wind Structure
Abstract
:1. Introduction
2. Methodology and Data
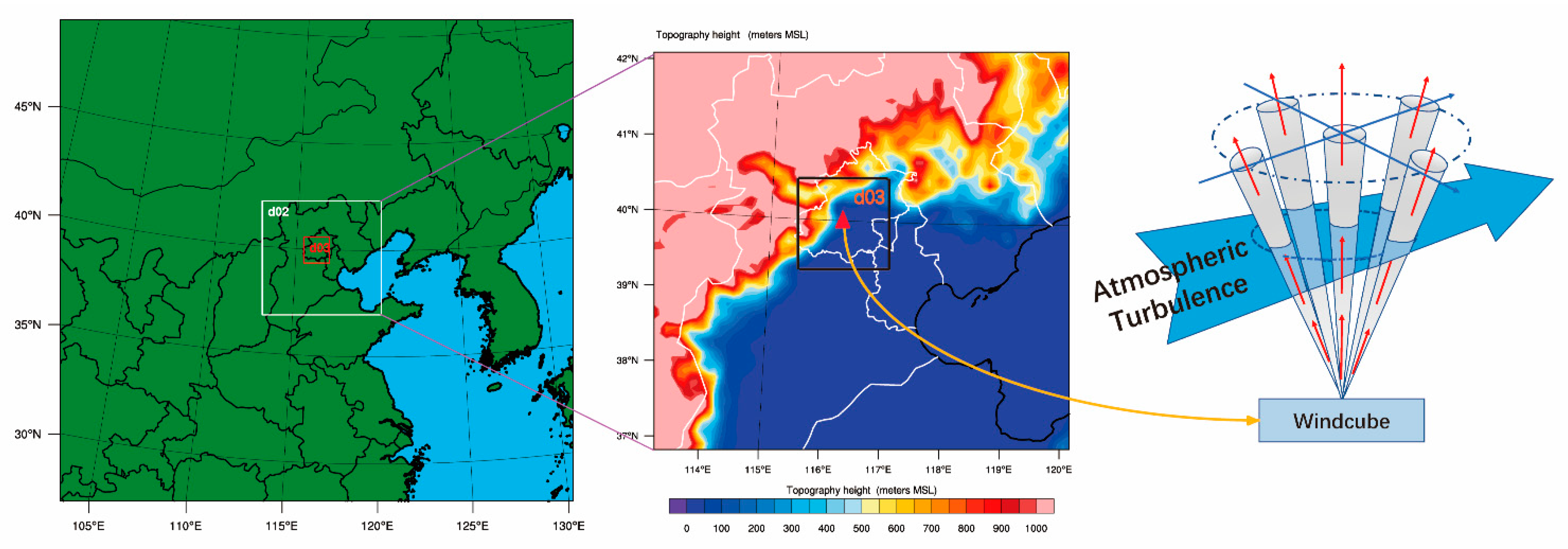
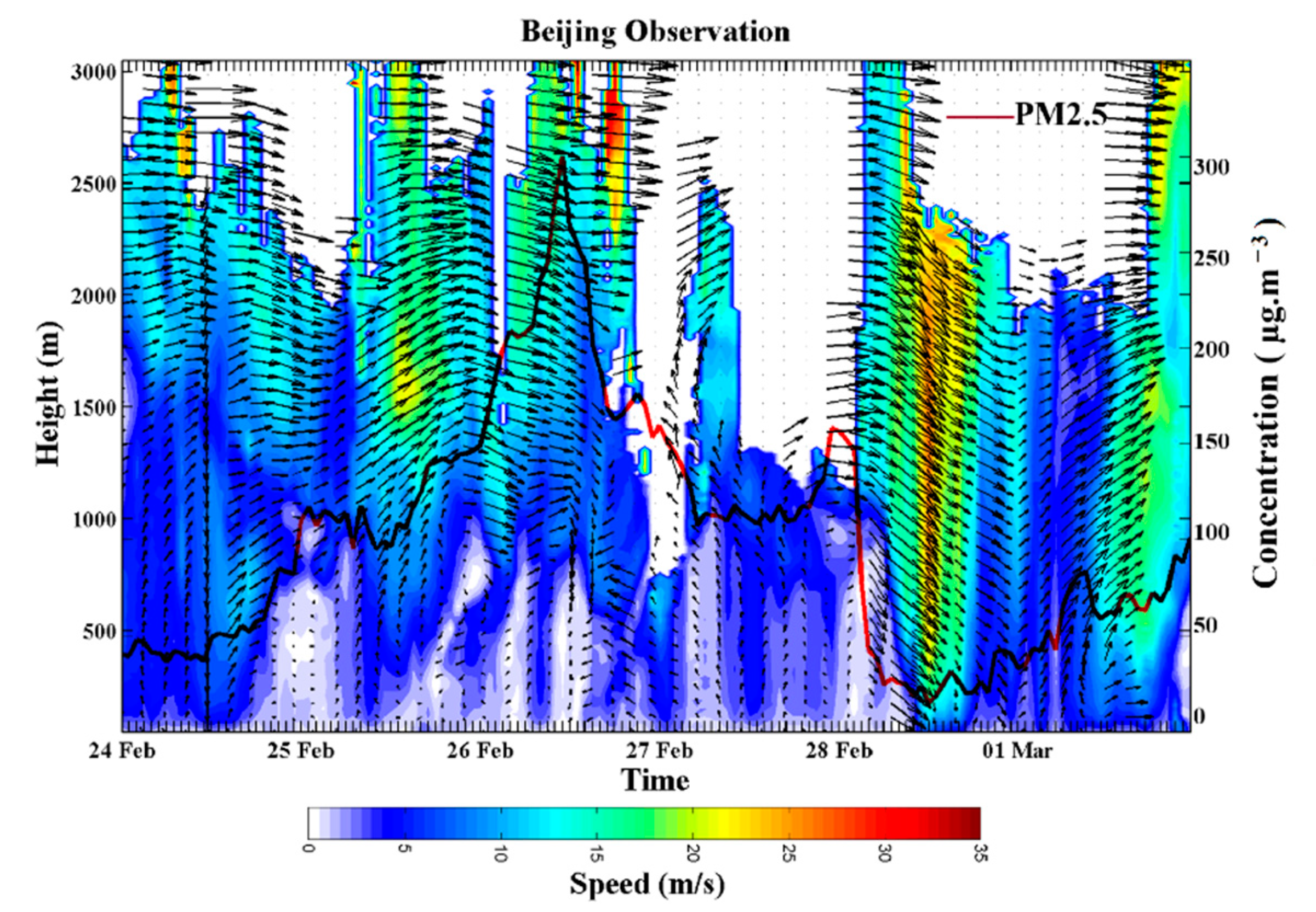
2.1. The DWL Observation
2.2. Experimental Design
| Options | Schemes | Closure Methods | Mixing Processes for Unstable Boundary Layers | Main Features |
|---|---|---|---|---|
| 1 | Yonsei University (YSU) | Nonlocal | K-Profile Method, First Order Closed Model | Considers the influence of the entrainment process at the top of the mixed layer on turbulent transport; the height of PBL depends only on the buoyancy profile [18] |
| 2 | Mellor-Yamada-Janjic Scheme (MYJ) | Local | Turbulent kinetic energy (TKE) closure scheme, 1.5-order closure model | It was suitable for studying fine PBL structure. The height of PBL was determined by the turbulent energy profile [19] |
| 3 | NCEP Global Forecast System (GFS) | Nonlocal | First-order vertical mixing scheme | The height of the PBL was determined by the iterative bulk Rechardson method from the surface up integration. The diffusion coefficient above the surface was a cubic function of the height of the PBL, and its coefficient value was obtained by the coupled surface flux [20] |
| 4 | Quasi-normal Scale Elimination (QNSE) | Local | TKE Closing Scheme, 1.5 Order Closing Model | The physical process was complex and suitable for the prediction and simulation of the PBL in the stable layer region [21] |
| 5 | Mellor-Yamada Nakanishi Niino (MYNN) Level 2.5 | Local | TKE Closing Scheme, 1.5 Order Closing Model | Improvement of MYNN3 limits the ratio between the main length scale and TKE [22] |
| 6 | Mellor-Yamada Nakanishi Niino (MYNN) Level 3 | Local | TKE Closing Scheme, 2 Order Closing Model | Considered the physical process of condensation, the prediction of mixed layer thickness was improved, the TKE magnitude decreased, and the time bias of fog formation and dissipation prediction was reduced [23] |
| 7 | Asymmetric Convection Model 2 Scheme (ACM2) | Nonlocal +Local | The upward and downward mixing process were local. First-order Closed Model | The thermal penetration and wind shear of the entrainment layer were considered in the PBL height under unstable conditions. The height of the PBL was determined by the Richardson number [24] |
| 8 | Bougeault-Lacarrere Scheme (BouLac) | Local | TKE Closing Scheme, 1.5 Order Closing Model | It could predict the intensity and location of clear-sky turbulence over steep terrain and provide a continuous prediction of turbulent energy intensity [25] |
| 9 | University of Washington (TKE) Boundary Layer | Local | TKE Closing Scheme, 1.5 Order Closing Model | The introduction of a water vapor conservation variable and explicit entrainment closure was suitable for the case of the dry convective PBL [26] |
| 10 | Shin-Hong Scale-aware | Local | TKE Closing Scheme, 1.5 Order Closing Model | Vertical mixing in a stable PBL and free atmosphere was similar to the YSU scheme, and it could also diagnose TKE and mixed length output [27] |
| 11 | Grenier-Bretherton-McCaa | Local | TKE Closing Scheme, 1.5 Order Closing Model | Considered the entrainment process at the top of the PBL, the cloud cover could be well simulated, and the height of the PBL could be calculated according to the grid point heat [28] |
3. Results
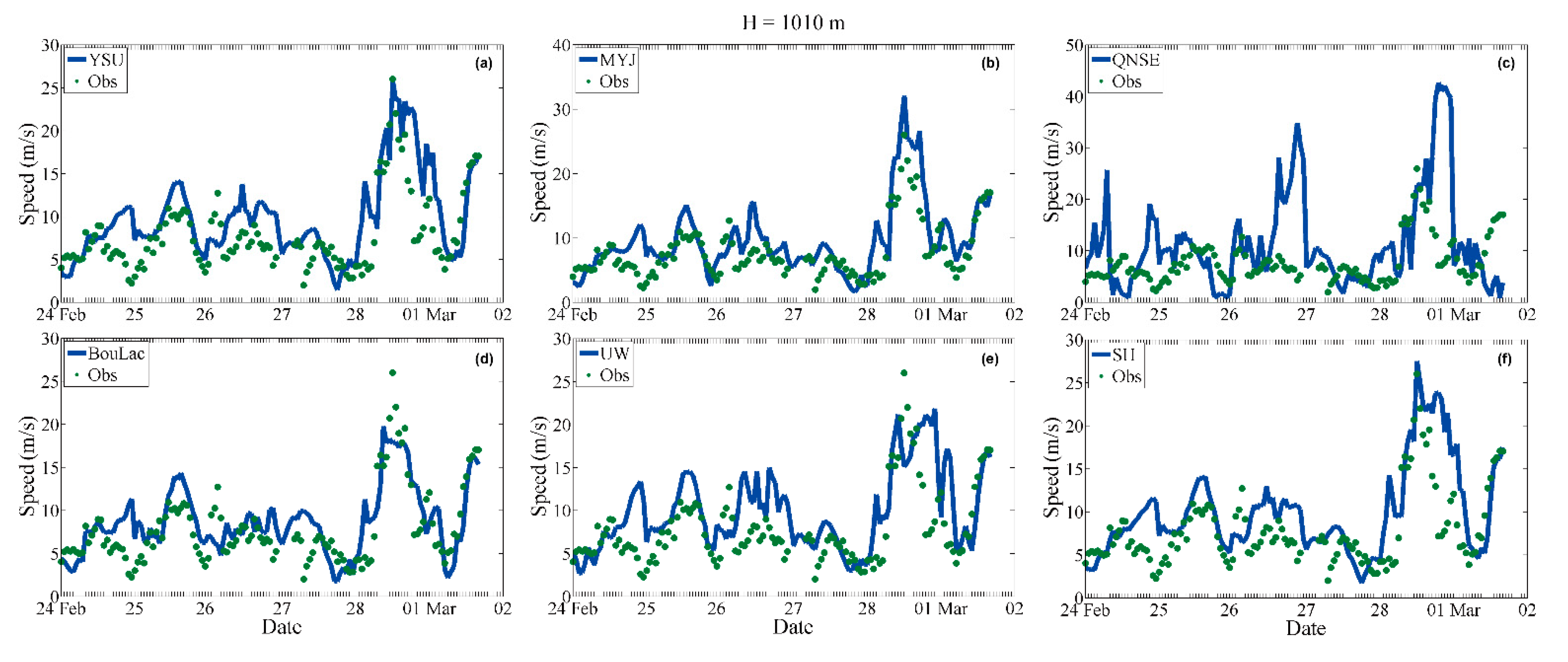
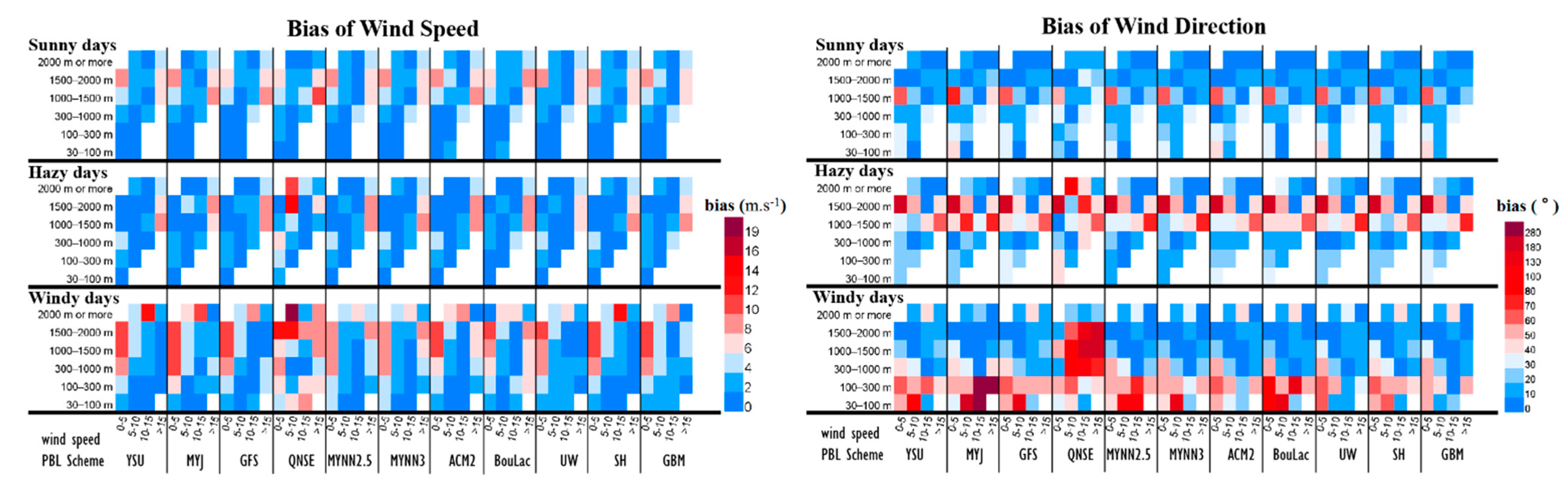
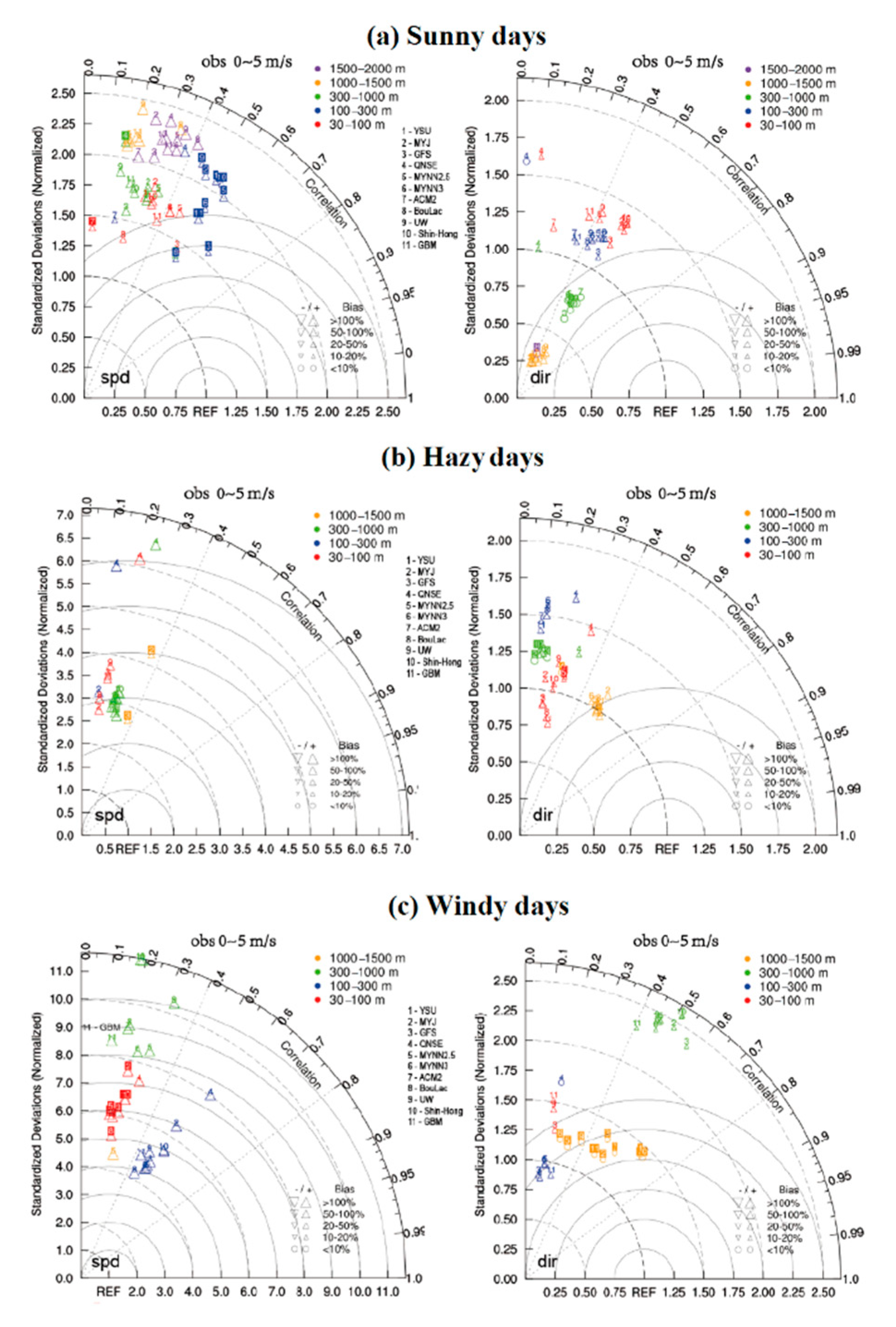
3.1. PBL Wind Speed Profile
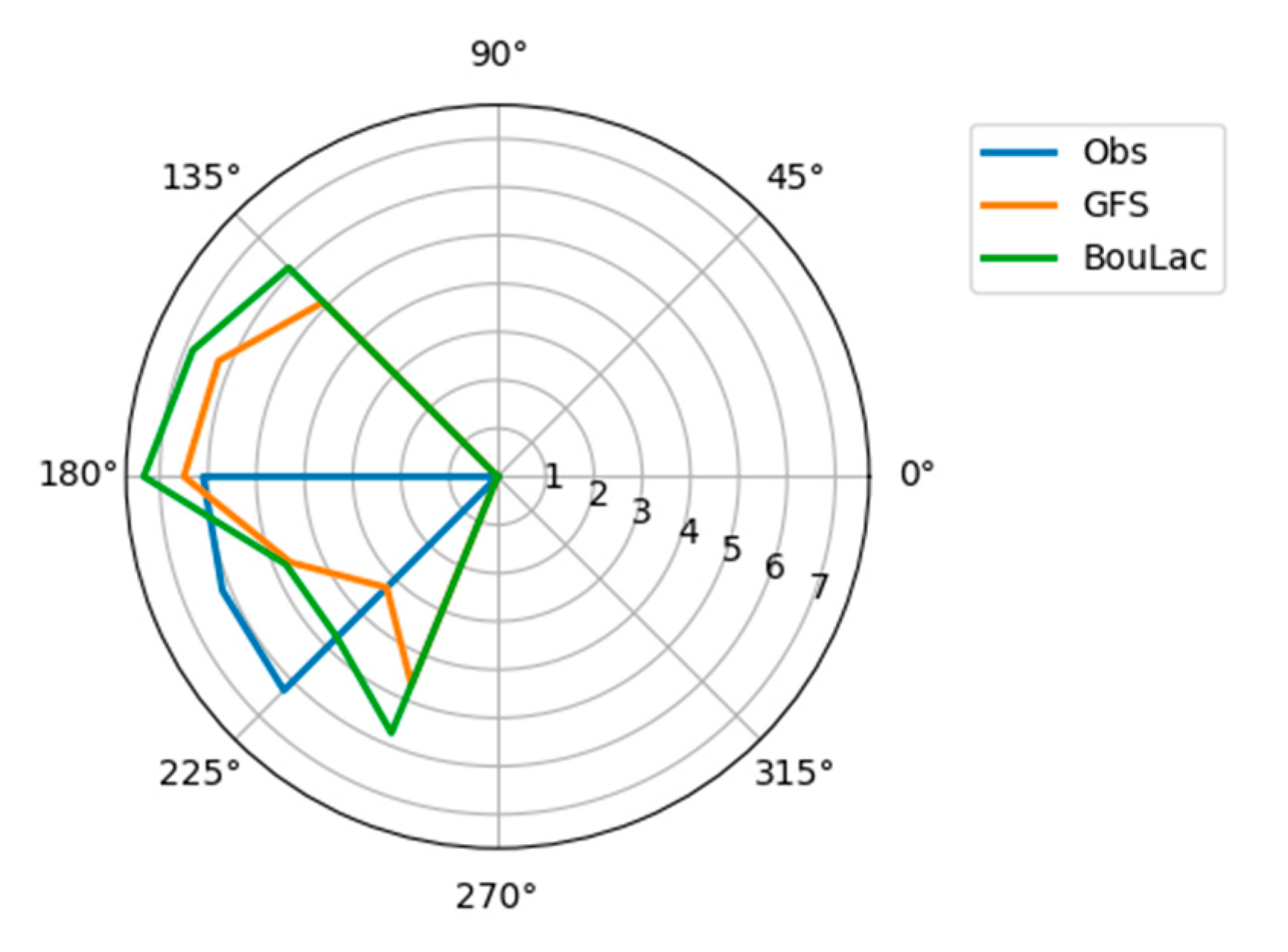
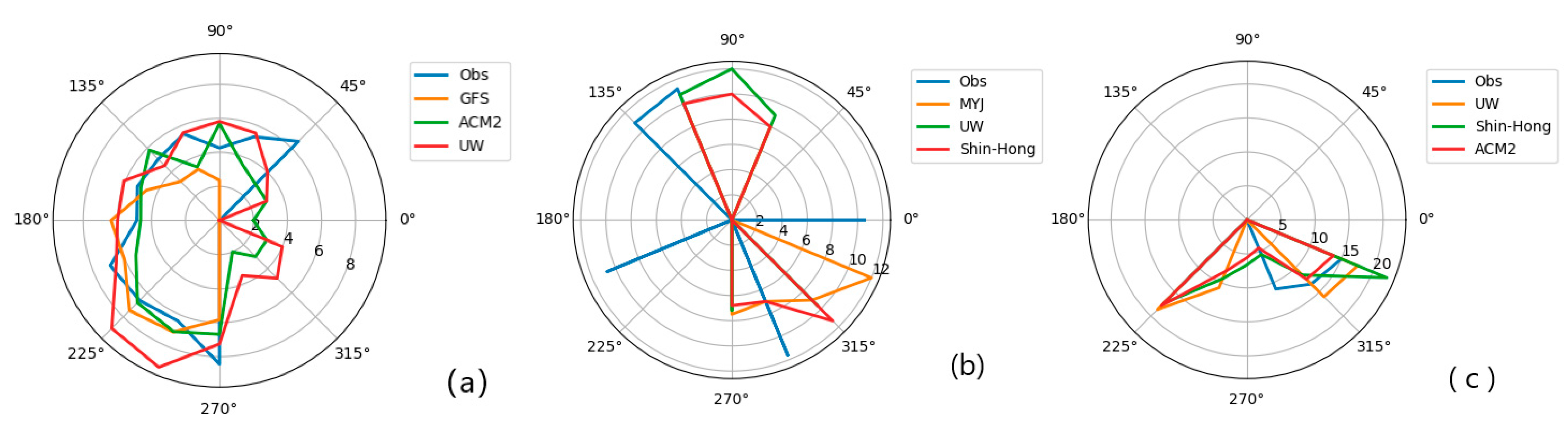
3.2. Horizontal Wind Component in PBL
3.3. Classical PBL Schemes
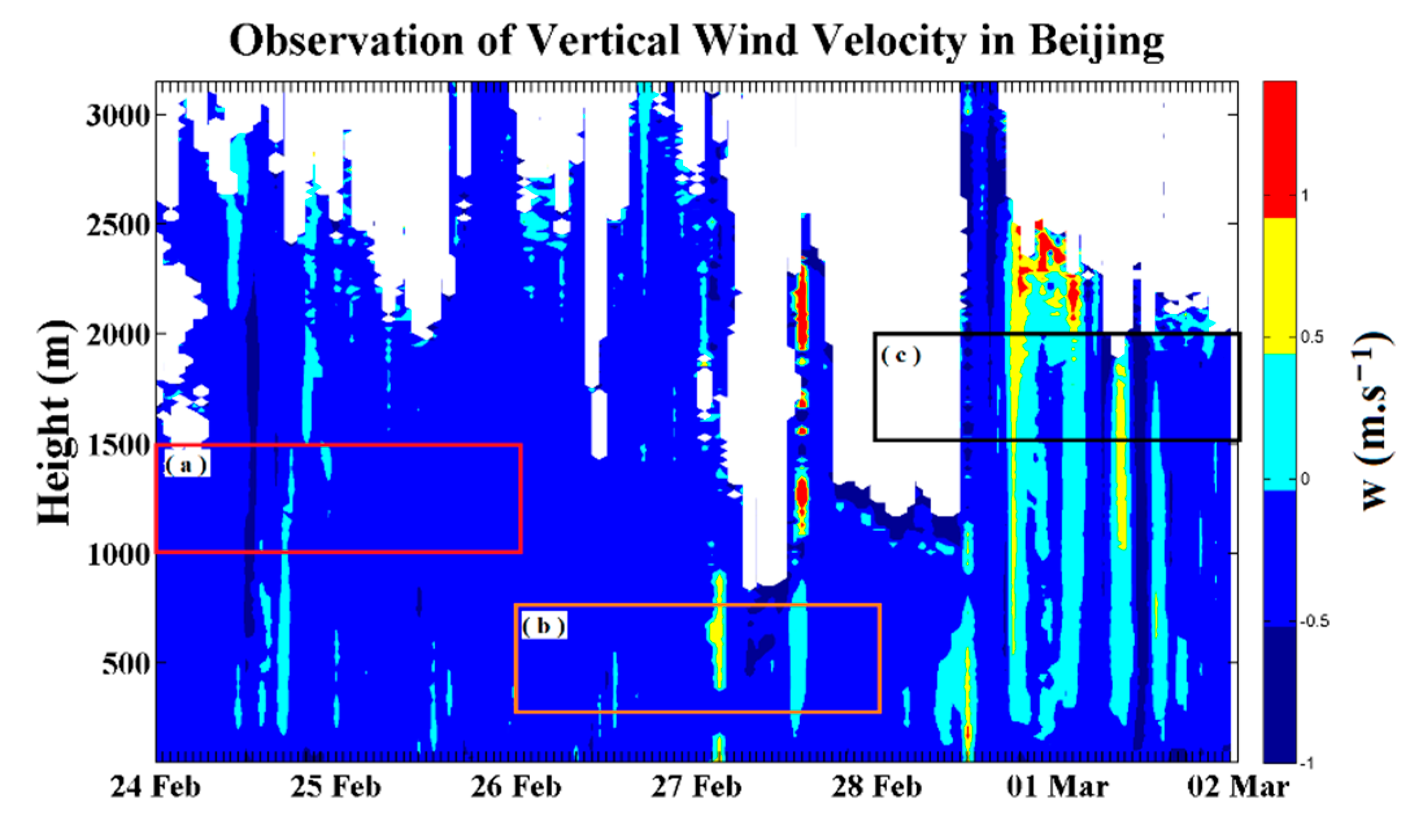
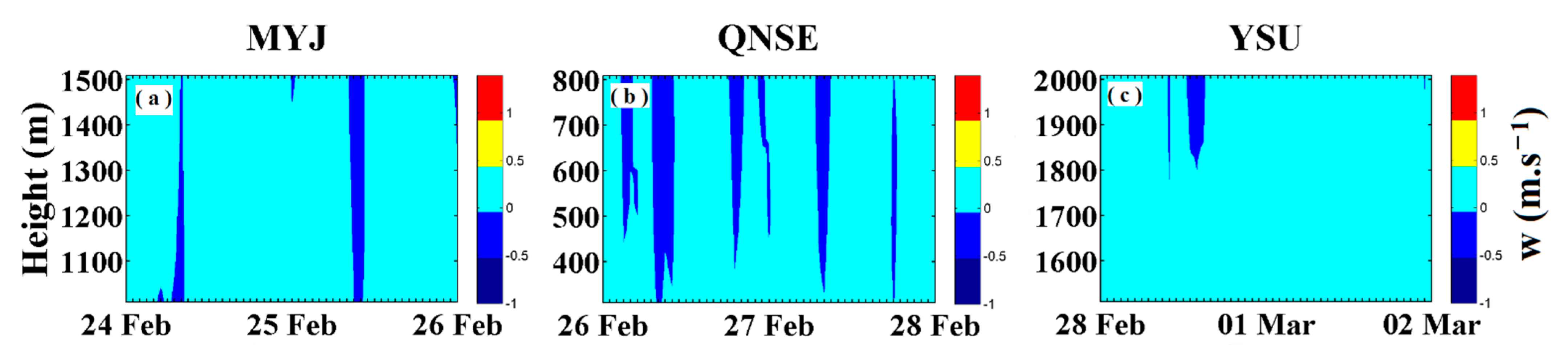
3.4. Vertical Wind Component in PBL
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Coantic, M.; Seguin, B. On the interaction of turbulent and radiative transfers in the surface layer. Bound. Layer Meteorol. 1971, 1, 245–263. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Chin, S.C.; Liu, T.H. The role of boundary layer schemes in meteorological and air quality simulations of the Taiwan area. Atmos. Environ. 2012, 54, 714–727. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, M.; An, J. Sensitivity of air quality model prediction to parameterization of vertical eddy diffusivity. Environ. Fluid Mech. 2008, 9, 73–89. [Google Scholar] [CrossRef]
- Wei, J.; Tang, G.; Zhu, X.; Wang, L.; Liu, Z.; Cheng, M.; Münkel, C.; Li, X.; Wang, Y. Thermal internal boundary layer and its effects on air pollutants during summer in a coastal city in North China. J. Environ. Sci. 2017, 70, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Cao, X.; Zhang, L.; Notholt, J.; Zhou, B.; Liu, R.; Zhang, B. Lidar measurement of planetary boundary layer height and comparison with microwave profiling radiometer observation. Atmos. Meas. Tech. 2012, 5, 1965–1972. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wang, D.; Gong, Y. Dynamic Modeling Study of Highly Resolved Near-Surface Wind Based on WRF/CALMET. Meteorol. Mon. 2015, 1, 34–44. [Google Scholar]
- Zhan, L.; Shu, J.; Chen, L. Distribution characteristics of wind and pollutant concentration fields in a parallel urban block. J. Meteorol. Environ. 2017, 33, 61–67. [Google Scholar]
- Hahmann, A.N.; Draxl, C.; Peña, A.; Nielsen, J.R. Simulating the Vertical Structure of the Wind with the Weather Research and Forecasting (WRF) Model; European Wind Energy Conference and Exhibition: EWEA 2011; Europe’s Premier Wind Energy Event: Brussels, Belgium, 2011; p. 153. [Google Scholar]
- Gholami, S.; Ghader, S.; Khaleghi-Zavareh, H.; Ghafarian, P. Sensitivity of WRF-simulated 10 m wind over the Persian Gulf to different boundary conditions and PBL parameterization schemes. Atmos. Res. 2020, 247, 105147. [Google Scholar] [CrossRef]
- Fekih, A.; Mohamed, A. Evaluation of the WRF model on simulating the vertical structure and diurnal cycle of the atmospheric boundary layer over Bordj Badji Mokhtar (southwestern Algeria). J. King Saud Univ. Sci. 2019, 31, 602–611. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Zecchetto, S.; De Biasio, F. WRF model and ASAR-retrieved 10 m wind field comparison in a case study over Eastern Mediterranean Sea. Adv. Sci. Res. 2010, 4, 83–88. [Google Scholar] [CrossRef]
- Shimada, S.; Ohsawa, T.; Chikaoka, S.; Kozai, K. Accuracy of the wind speed profile in the lower PBL as simulated by the WRF model. Sola 2011, 7, 109–112. [Google Scholar] [CrossRef] [Green Version]
- Banks, R.F.; Tiana-Alsina, J.; Rocadenbosch, F.; Baldasano, J.M. Performance Evaluation of the Boundary-Layer Height from Lidar and the Weather Research and Forecasting Model at an Urban Coastal Site in the North-East Iberian Peninsula. Bound. Layer Meteorol. 2015, 157, 265–292. [Google Scholar] [CrossRef] [Green Version]
- Banks, R.; Baldasano, J. Impact of WRF model PBL schemes on air quality simulations over Catalonia, Spain. Sci. Total Environ. 2016, 572, 98–113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muñoz-Esparza, D.; Cañadillas, B.; Neumann, T.; Beeck, J.V. Turbulent fluxes, stability and shear in the offshore environment: Mesoscale modelling and field observations at FINO1. J. Renew. Sustain. Energy 2012, 4, 063136. [Google Scholar] [CrossRef]
- Brewster, K.A. Profiler Training Manual #2: Quality Control of Wind Profiler Data; NOAA/ERL/FSL: Boulder, CO, USA; NOAA/NWS/OM: Silver Spring, MD, USA, 1989; p. 109. [Google Scholar]
- Clark, A.J.; Gallus, W.A.; Chen, T.C. Comparison of the Diurnal Precipitation Cycle in Convection-Resolving and Non-Convection-Resolving Mesoscale Models. Mon. Weather Rev. 2007, 135, 3456–3473. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather. Rev. 2005, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Janjic, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Pan, H.L. Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef] [Green Version]
- Sukoriansky, S.; Galperin, B.; Perov, V. Application of a New Spectral Theory of Stably Stratified Turbulence to the Atmospheric Boundary Layer over Sea Ice. Bound. Layer Meteorol. 2005, 117, 231–257. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An Improved Mellor–Yamada Level-3 Model: Its Numerical Stability and Application to a Regional Prediction of Advection Fog. Bound. Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Mikio, N.; Hiroshi, N. Development of an Improved Turbulence Closure Model for the Atmospheric Boundary Layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef] [Green Version]
- Pleim, J.E. A Combined Local and Nonlocal Closure Model for the Atmospheric Boundary Layer. Part I: Model Description and Testing. J. Appl. Meteorol. Clim. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of Orography-Induced Turbulence in a Mesobeta-Scale Model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A New Moist Turbulence Parameterization in the Community Atmosphere Model. J. Clim. 2009, 22, 3422–3448. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S. Representation of the Subgrid-Scale Turbulent Transport in Convective Boundary Layers at Gray-Zone Resolutions. Mon. Weather Rev. 2015, 143, 250–271. [Google Scholar] [CrossRef]
- Grenier, H.; Bretherton, C.S. A Moist PBL Parameterization for Large-Scale Models and Its Application to Subtropical Cloud-Topped Marine Boundary Layers. Mon. Weather Rev. 2001, 129, 357. [Google Scholar] [CrossRef] [Green Version]
- Sun, K.; Liu, H.; Wang, X.; Peng, Z.; Xiong, Z. The Aerosol Radiative Effect on a Severe Haze Episode in the Yangtze River Delta. J. Meteorol. Res. 2017, 31, 59–67. [Google Scholar] [CrossRef] [Green Version]


| Weather Conditions | Obs (m s−1) | 30–100 m | 100–300 m | 300–1000 m | 1000–1500 m | 1500–2000 m | 2000–3000 m |
|---|---|---|---|---|---|---|---|
| Sunny days | 0–5 | 239 | 342 | 653 | 249 | 87 | 0 |
| 5–10 | 1 | 90 | 923 | 719 | 403 | 72 | |
| 10–15 | 0 | 0 | 56 | 175 | 479 | 748 | |
| >15 | 0 | 0 | 0 | 34 | 131 | 261 | |
| Hazy days | 0–5 | 240 | 420 | 1056 | 44 | 3 | 0 |
| 5–10 | 0 | 0 | 480 | 13 | 96 | 28 | |
| 10–15 | 0 | 0 | 34 | 270 | 553 | 463 | |
| >15 | 0 | 0 | 0 | 27 | 142 | 424 | |
| Windy days | 0–5 | 205 | 257 | 607 | 135 | 86 | 0 |
| 5–10 | 34 | 110 | 493 | 314 | 146 | 8 | |
| 10–15 | 1 | 29 | 224 | 221 | 300 | 210 | |
| >15 | 0 | 2 | 308 | 357 | 324 | 271 |
| Wind Speed Simulation | |||||
| Height (m) | Obs (m·s−1) | ||||
| 0–5 | 5–10 | 10–15 | >15 | ||
| Sunny days | <100 | ③ | ③⑨ | — | — |
| 100–300 | ①③⑤⑥⑧⑩⑪ | ①②③④⑤⑥⑧⑨⑩⑪ | — | — | |
| 300–1000 | ⑦ | ②③④⑨ | ④ | — | |
| 1000–1500 | — | ③④ | ①⑤⑥⑧⑨⑩⑪ | — | |
| 1500–2000 | — | — | ⑦⑧⑪ | — | |
| >2000 | — | ④ | All | ④ | |
| Hazy days | <100 | ②⑧⑪ | — | — | — |
| 100–300 | ⑧ | All | — | — | |
| 300–1000 | ⑧ | ③⑧⑪ | ①②④⑨⑩ | — | |
| 1000–1500 | ②③ | ①⑤⑥⑦⑧⑨⑩⑪ | ② | — | |
| 1500–2000 | ②③④⑤⑥⑧⑨⑪ | ①⑥⑦⑩⑪ | ①④⑤⑥⑦⑧⑨⑩⑪ | — | |
| >2000 | — | ①②③⑤⑦⑧⑨⑩⑪ | ①②③⑤⑥⑦⑧⑨⑩⑪ | — | |
| Windy days | <100 | — | ①⑩ | ①⑤⑥⑩ | — |
| 100–300 | — | All | ①⑤⑥⑦⑩ | ①⑨⑩⑪ | |
| 300–1000 | — | ④⑧ | ②③⑤⑥⑦⑨⑩ | ⑩ | |
| 1000–1500 | ④⑤⑥ | ⑤⑥ | ③⑤⑥⑦⑧⑨⑪ | ①③⑨⑩ | |
| 1500–2000 | — | — | ③⑦⑧⑨⑪ | ①③⑨⑩ | |
| >2000 | — | — | — | ②⑦⑪ | |
| Wind Direction Simulation | |||||
| Height (m) | Obs (m·s−1) | ||||
| 0–5 | 5–10 | 10–15 | >15 | ||
| Sunny days | <100 | ③ | ①②④ | — | — |
| 100–300 | — | ①②③⑤⑥⑧⑨⑩⑪ | — | — | |
| 300–1000 | ①②③⑤⑥⑨⑩⑪ | All | — | — | |
| 1000–1500 | — | ④⑤⑧⑨⑪ | ①②③⑤⑥⑦⑧⑨⑩⑪ | ①⑤⑥⑧⑨⑩⑪ | |
| 1500–2000 | ①③⑧⑩⑪ | — | ⑦⑧⑪ | ①③⑤⑥⑦⑧⑨⑩⑪ | |
| >2000 | — | ①③⑦⑧⑨⑩⑪ | ①③⑤⑥⑦⑧⑨⑩⑪ | ①②③⑤⑥⑧⑨⑩ | |
| Hazy days | <100 | ⑤⑥ | — | — | — |
| 100 - 300 | ⑤⑥⑨ | ①②④⑤⑥⑧ | — | — | |
| 300 -1000 | ③⑧⑨ | ①③④⑤⑥⑦⑧⑨⑩⑪‘ | ①②③⑤⑥⑦⑧⑨⑩⑪ | — | |
| 1000–1500 | ① | — | — | — | |
| 1500–2000 | — | — | ①④⑤⑥⑦⑧⑨⑩⑪ | — | |
| >2000 | — | ② | ①②③⑤⑥⑦⑧⑨⑩⑪ | All | |
| Windy days | <100 | — | ⑨ | ①④⑨⑩ | — |
| 100–300 | — | — | ⑨ | — | |
| 300–1000 | ④ | ⑧ | ①②③⑤⑥⑦⑧⑨⑩⑪ | ①⑦⑩ | |
| 1000–1500 | — | ①②③⑤⑥⑦⑧⑨⑩⑪ | ①②③⑤⑥⑦⑧⑨⑩⑪ | ②⑤⑥⑦⑧ | |
| 1500–2000 | ①②③⑦⑩⑪ | ①⑧⑩ | ③⑧⑩⑪ | ②③⑤⑥⑦⑧⑨⑪ | |
| >2000 | — | ①③⑥⑦⑧⑩⑪ | ④ | ②⑨⑪ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Xin, J.; Yin, Y.; Chang, W.; Xue, M.; Jia, D.; Ma, Y. Understanding the Major Impact of Planetary Boundary Layer Schemes on Simulation of Vertical Wind Structure. Atmosphere 2021, 12, 777. https://doi.org/10.3390/atmos12060777
Zhang L, Xin J, Yin Y, Chang W, Xue M, Jia D, Ma Y. Understanding the Major Impact of Planetary Boundary Layer Schemes on Simulation of Vertical Wind Structure. Atmosphere. 2021; 12(6):777. https://doi.org/10.3390/atmos12060777
Chicago/Turabian StyleZhang, Lei, Jinyuan Xin, Yan Yin, Wenyuan Chang, Min Xue, Danjie Jia, and Yongjing Ma. 2021. "Understanding the Major Impact of Planetary Boundary Layer Schemes on Simulation of Vertical Wind Structure" Atmosphere 12, no. 6: 777. https://doi.org/10.3390/atmos12060777
APA StyleZhang, L., Xin, J., Yin, Y., Chang, W., Xue, M., Jia, D., & Ma, Y. (2021). Understanding the Major Impact of Planetary Boundary Layer Schemes on Simulation of Vertical Wind Structure. Atmosphere, 12(6), 777. https://doi.org/10.3390/atmos12060777








