Can a Warm Ocean Feature Cause a Typhoon to Intensify Rapidly?
Abstract
:1. Introduction
2. Methods
2.1. The Problem of Testing the WOF-RI Hypothesis
- (1)
- The warm eddy triggers RI while there is no RI in an otherwise identical model run without the warm eddy;
- (2)
- The number of RI events in a large ensemble of the model run with the warm eddy is statistically significantly more than the RI events for the corresponding twin runs without the warm eddy.
2.2. Modelling Strategy
2.3. The Atmosphere and Ocean Models
2.4. Model Parameters
2.5. Model Integration
3. Results
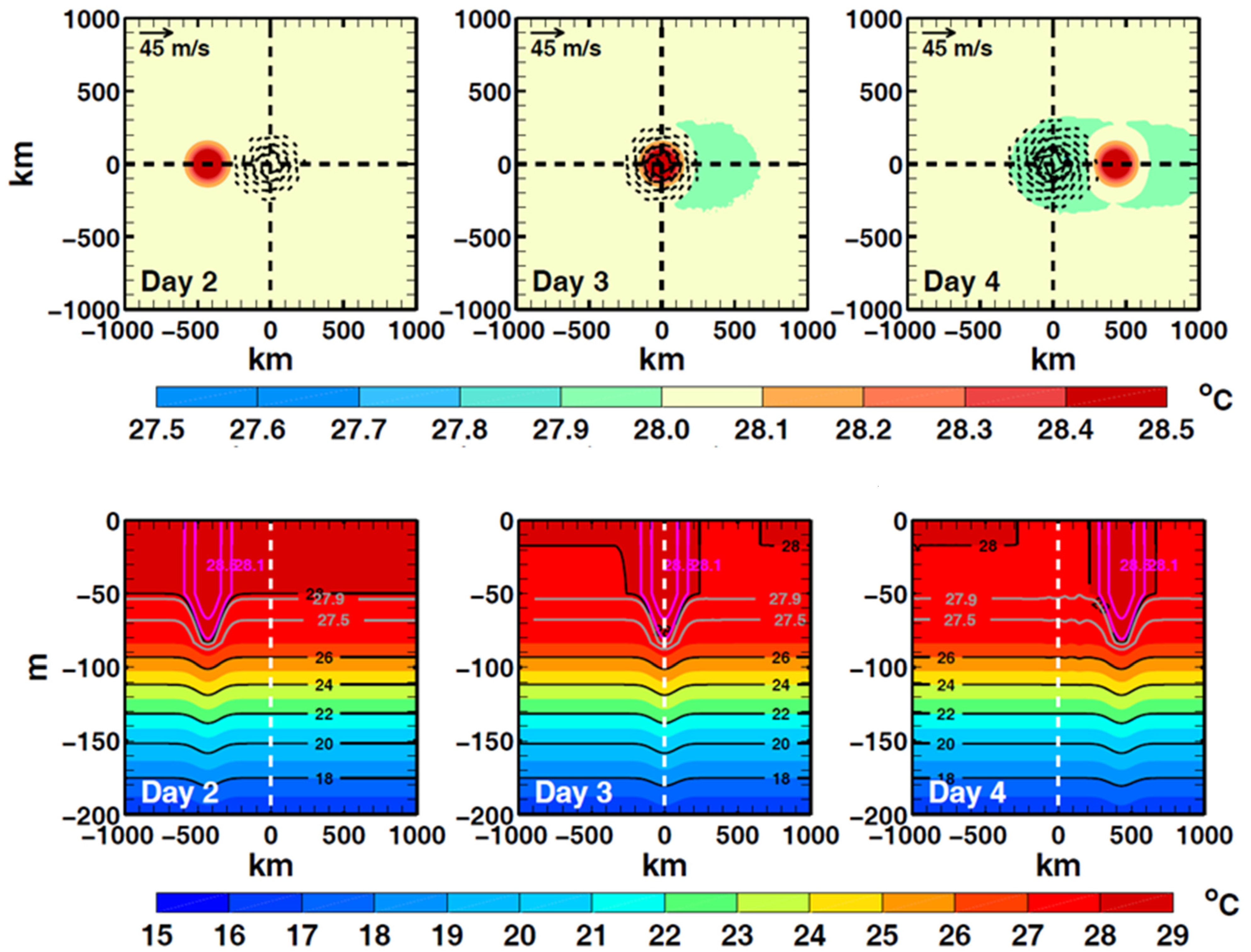
3.1. Model Response and Rapid Intensification
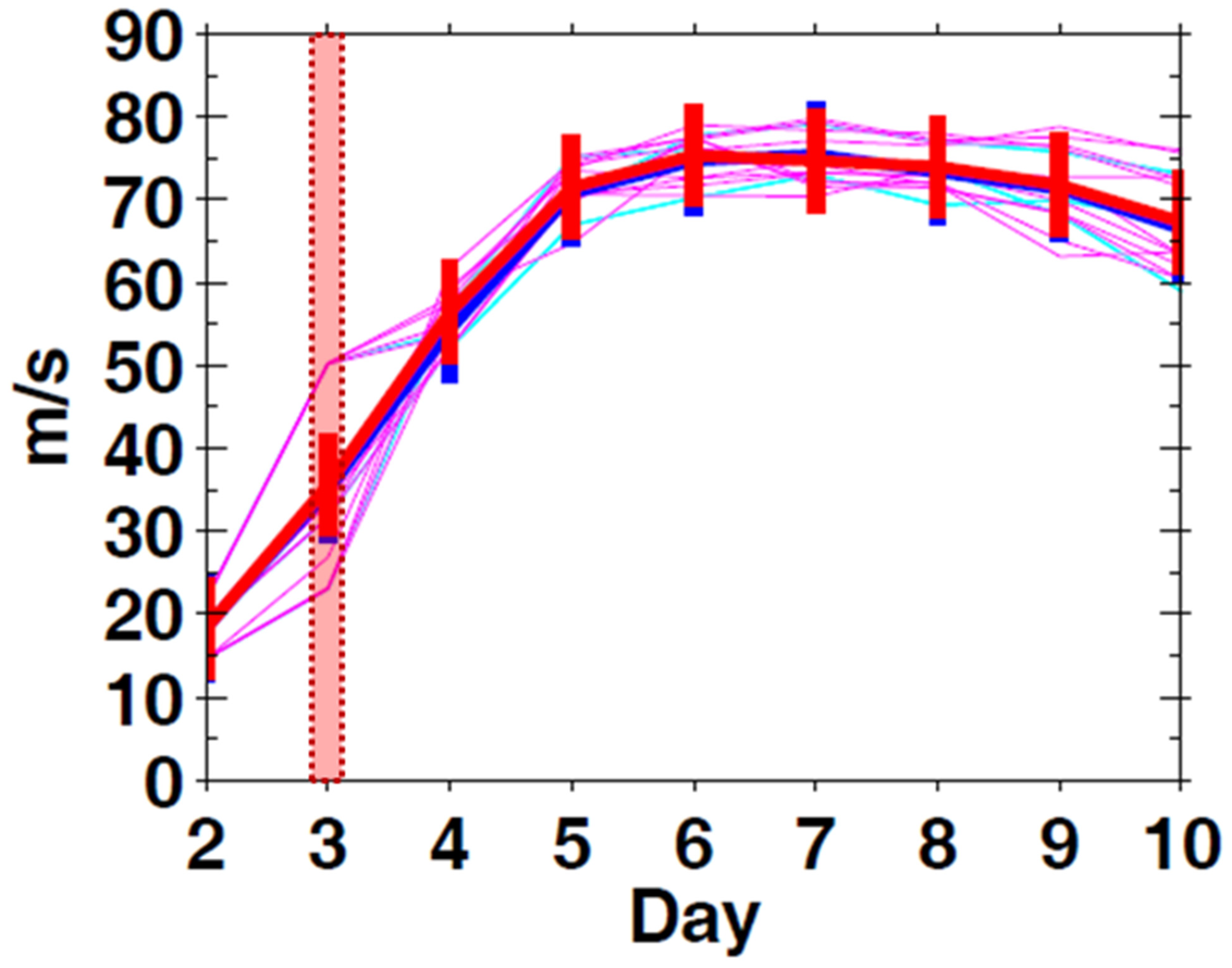
3.2. Large Ensemble
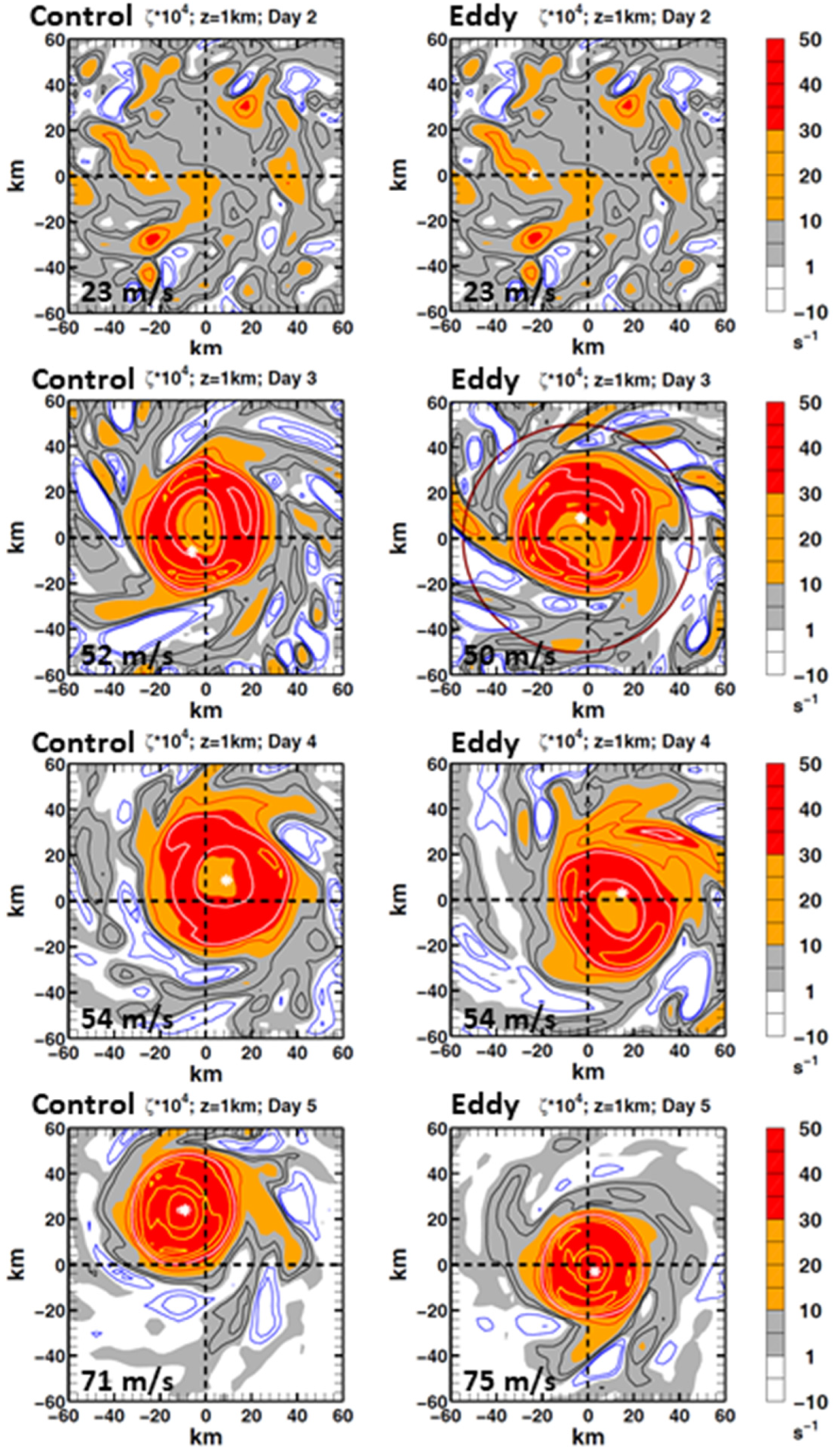
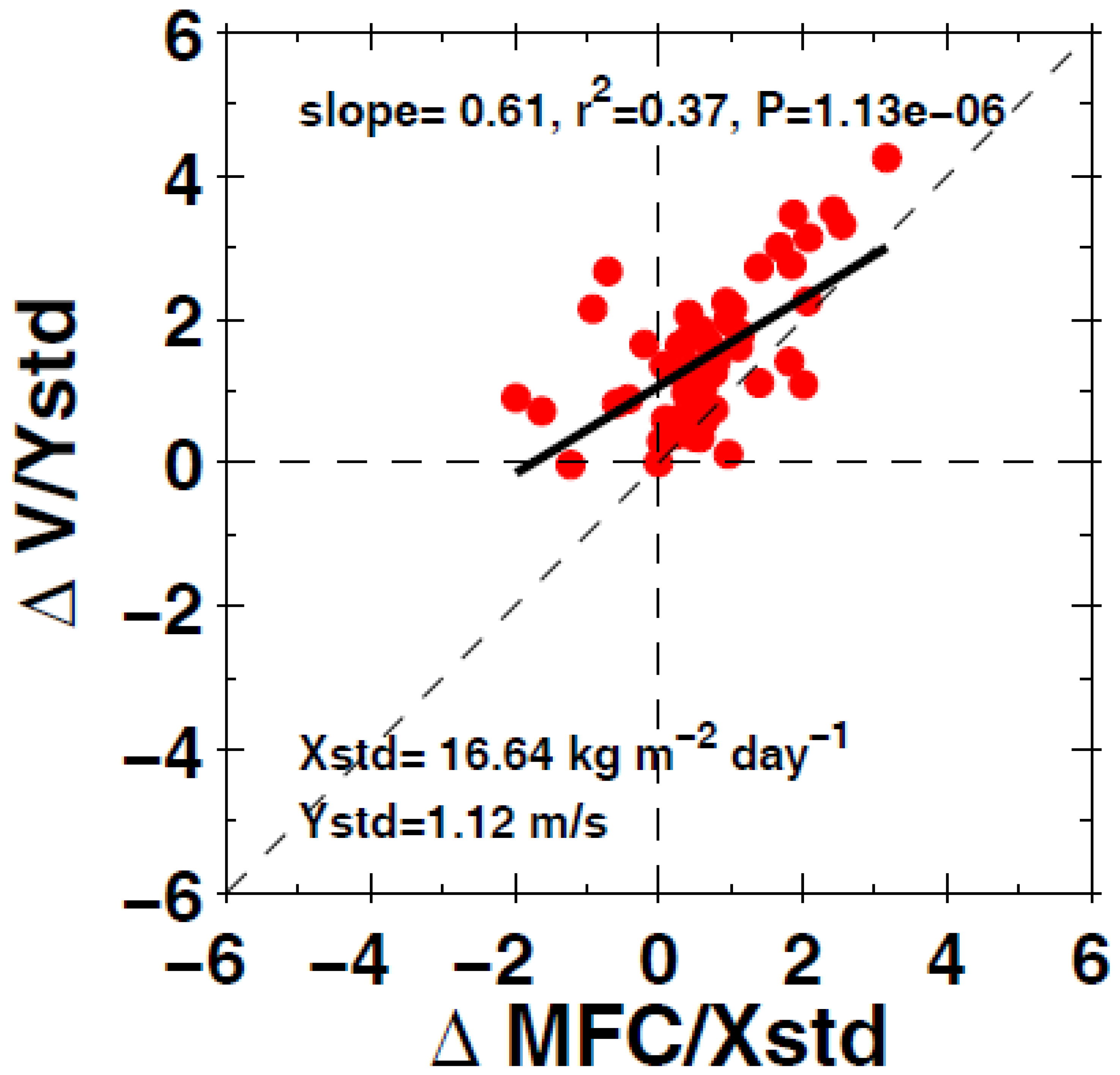
3.2.1. Warm-Eddy-Induced Amplified Circulation
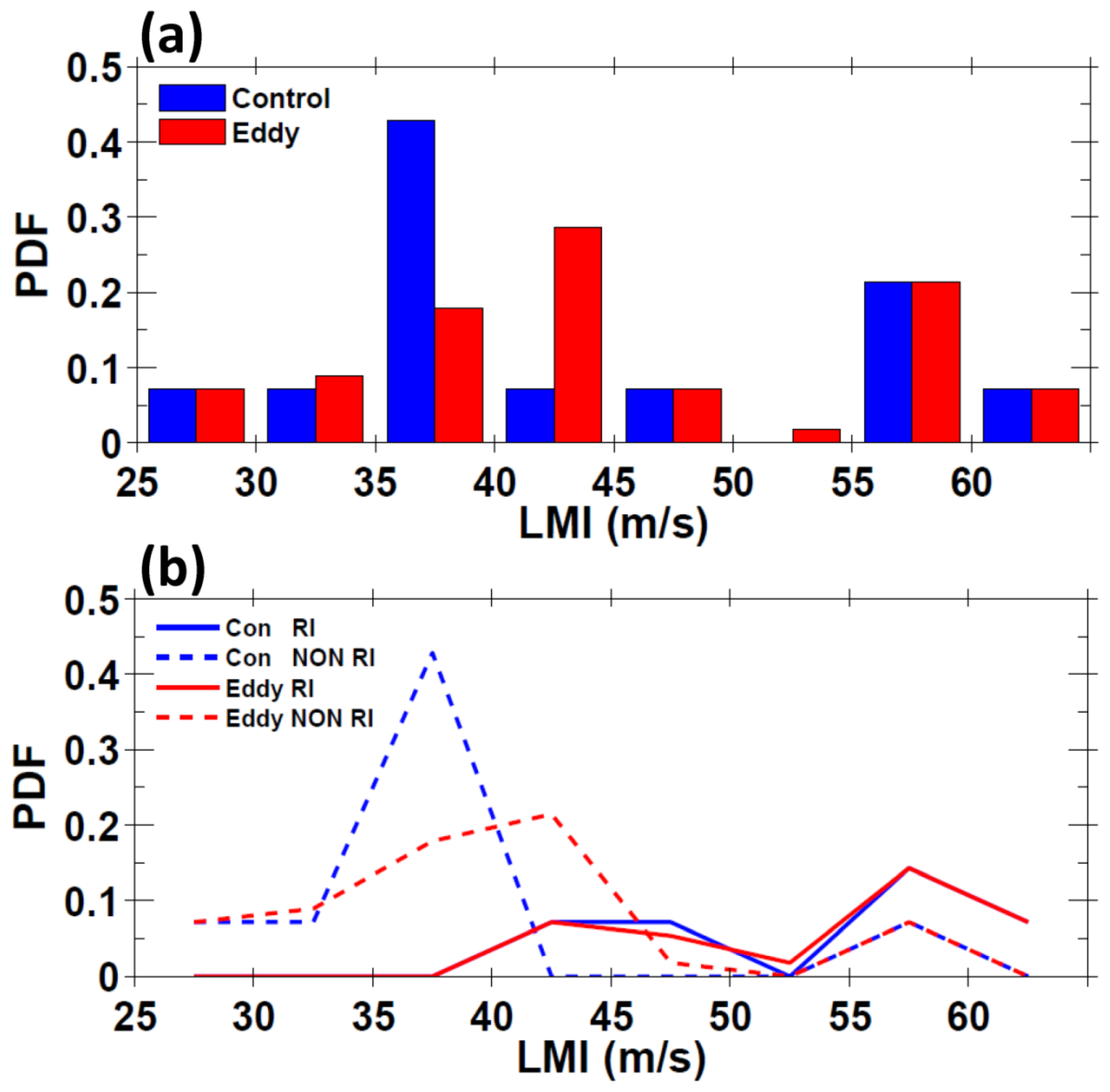
3.2.2. Probability Density Function of Lifetime Maximum Intensity
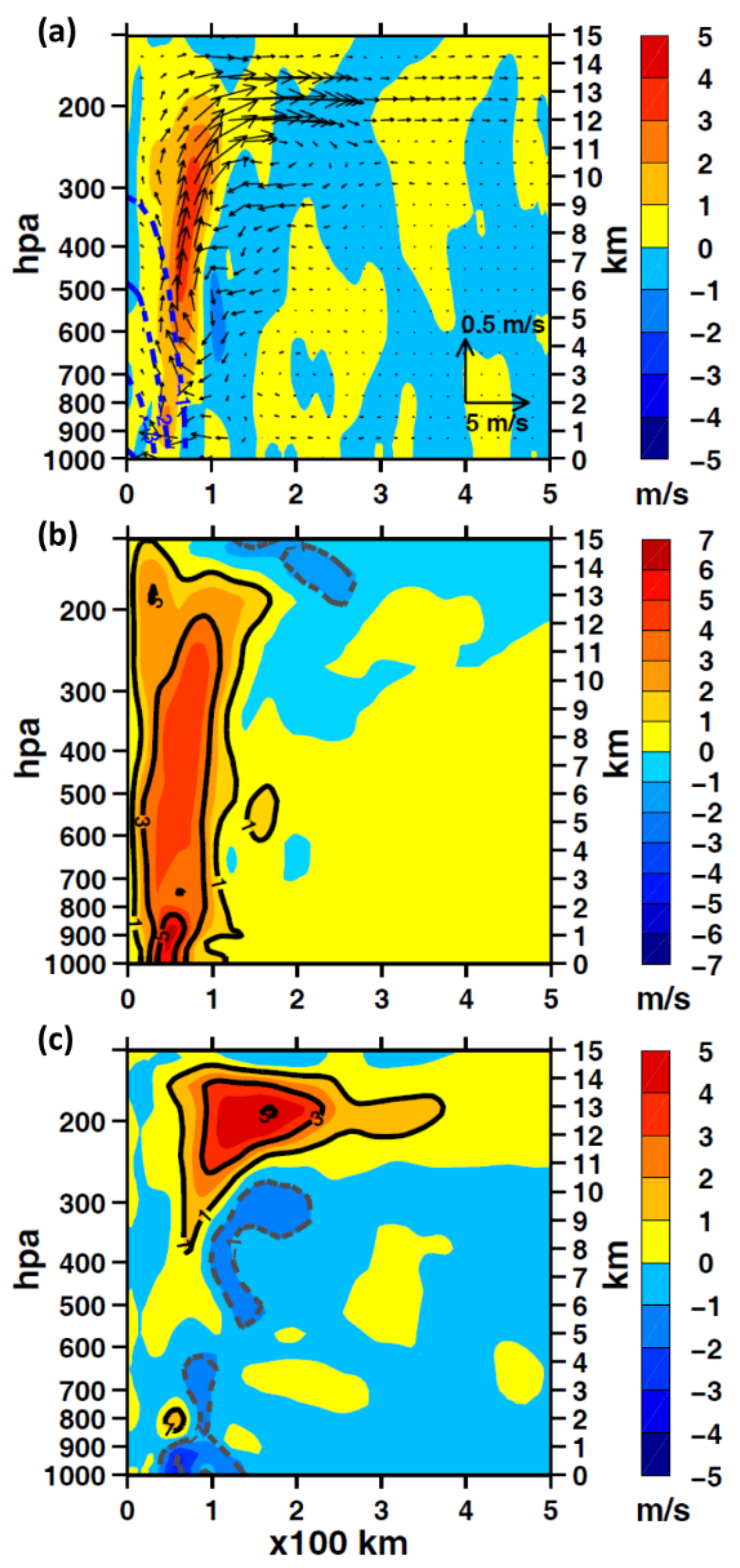
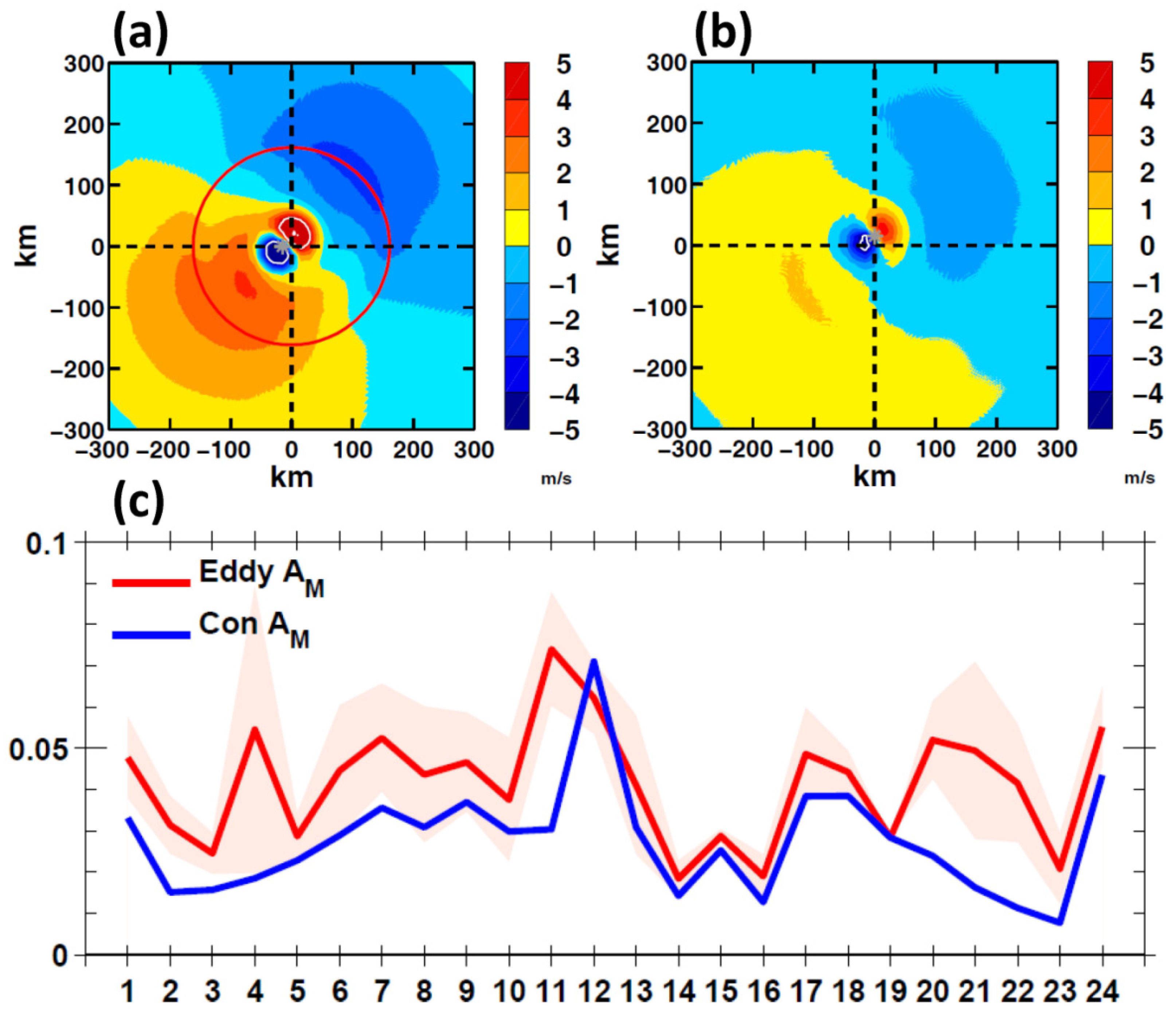
3.2.3. Vortex Asymmetry
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. An Analytical, Air-Sea Coupled Model of WOF-Induced Intensification
Appendix A.1. Increased Intensity Due to WOF
Appendix A.2. Ocean Cooling
Appendix A.3. The Coupling
References
- Kaplan, J.; DeMaria, M. Large-scale characteristics of rapidly intensifying tropical cyclones in the North Atlantic basin. Weather Forecast. 2003, 18, 1093–1108. [Google Scholar] [CrossRef] [Green Version]
- Kossin, J.P.; Olander, T.L.; Knapp, K.R. Trend analysis with a new global record of tropical cyclone intensity. J. Clim. 2013, 26, 9960–9976. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Tippett, M.K.; Sobel, A.H.; Camargo, S.J. Rapid intensification and the bimodal distribution of tropical cyclone intensity. Nat. Commun. 2016, 7, 10625. [Google Scholar] [CrossRef] [PubMed]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a warm oceanic feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Lin, I.I.; Wu, C.C.; Emanuel, K.; Lee, I.H.; Wu, C.R.; Pun, I.F. The interaction of Supertyphoon Maemi (2003) with a warm ocean eddy. Mon. Weather Rev. 2005, 2635–2649. [Google Scholar] [CrossRef]
- Ali, M.M.; Jagadeesh, P.V.; Jain, S. Effects of eddies on Bay of Bengal cyclone intensity. Eos Trans. Am. Geophys. Union 2007, 88, 93–95. [Google Scholar] [CrossRef]
- Mawren, D.; Reason, C.J.C. Variability of upper-ocean characteristics and tropical cyclones in the South West Indian Ocean. J. Geophys. Res. Oceans 2017, 122, 2012–2028. [Google Scholar] [CrossRef]
- Potter, H.; DiMarco, S.F.; Knap, A.H. Tropical Cyclone Heat Potential and the Rapid Intensification of Hurricane Harvey in the Texas Bight. J. Geophys. Res. Oceans 2019, 124, 2440–2451. [Google Scholar] [CrossRef]
- Gray, W.M. The formation of tropical cyclones. Meteor. Atmos. Phys. 1998, 67, 37–69. [Google Scholar] [CrossRef]
- Chang, Y.L.; Oey, L.Y. Interannual and seasonal variations of Kuroshio transport east of Taiwan inferred from 29 years of tide-gauge data. Geophys. Res. Lett. 2011, 38, L08603. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Sun, J.; Xu, F.H.; Oey, L.Y.; Lin, Y.L. Monthly variability of Luzon Strait tropical cyclone intensification over the Northern South China Sea in recent decades. Clim. Dyn. 2019, 52, 3631–3642. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Merrill, R.T. Environmental influences on hurricane intensification. J. Atmos. Sci. 1988, 45, 1678–1687. [Google Scholar] [CrossRef] [Green Version]
- DeMaria, M.; Kaplan, J.; Baik, J.J. Upper-level eddy angular momentum fluxes and tropical cyclone intensity change. J. Atmos. Sci. 1993, 50, 1133–1147. [Google Scholar] [CrossRef] [Green Version]
- Peng, M.S.; Jeng, B.; Williams, R.T. A numerical study on tropical cyclone intensification. Part I: Beta effect and mean flow effect. J. Atmos. Sci. 1999, 56, 1404–1423. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, Y.; Wu, C.C. Environmental dynamical control of tropical cyclone intensity—An observational study. Mon. Weather Rev. 2007, 135, 38–59. [Google Scholar] [CrossRef] [Green Version]
- Hendricks, E.A.; Peng, M.S.; Fu, B.; Li, T. Quantifying environmental control on tropical cyclone intensity change. Mon. Weather Rev. 2010, 138, 3243–3271. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, J.; DeMaria, M.; Knaff, J.A. A revised tropical cyclone rapid intensification index for the Atlantic and eastern North Pacific basins. Weather Forecast. 2010, 25, 220–241. [Google Scholar] [CrossRef]
- Wu, L.; Su, H.; Fovell, R.G.; Wang, B.; Shen, J.T.; Kahn, B.H.; Hristova-Veleva, S.M.; Lambrigtsen, B.H.; Fetzer, E.J.; Jiang, J.H. Relationship of environmental relative humidity with North Atlantic tropical cyclone intensity and intensification rate. Geophys. Res. Lett. 2012, 39, L20809. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Oey, L. Young ocean waves favor the rapid intensification of tropical cyclones—A global observational analysis. Mon. Weather Rev. 2019, 147, 311–328. [Google Scholar] [CrossRef]
- Rogers, R.; Aberson, S.; Black, M.; Black, P.; Cione, J.; Dodge, P.; Surgi, N. The intensity forecasting experiment: A NOAA multiyear field program for improving tropical cyclone intensity forecasts. Bull. Am. Meteorol. Soc. 2006, 87, 1523–1537. [Google Scholar] [CrossRef] [Green Version]
- Oey, L.; Lin, Y. The Influence of Environments on the Intensity Change of Typhoon Soudelor. Atmosphere 2021, 12, 162. [Google Scholar] [CrossRef]
- Mainelli, M.; DeMaria, M.; Shay, L.K.; Goni, G. Application of oceanic heat content estimation to operational forecasting of recent Atlantic category 5 hurricanes. Weather Forecast. 2008, 23, 3–16. [Google Scholar] [CrossRef]
- Balaguru, K.; Foltz, G.R.; Leung, L.R.; Hagos, S.M.; Judi, D.R. On the use of ocean dynamic temperature for hurricane intensity forecasting. Weather Forecast. 2018, 33, 411–418. [Google Scholar] [CrossRef]
- Frank, W.M.; Ritchie, E.A. Effects of vertical wind shear on the intensity and structure of numerically simulated hurricanes. Mon. Weather Rev. 2001, 129, 2249–2269. [Google Scholar] [CrossRef]
- Wu, L.G.; Braun, S.A. Effects of environmentally induced asymmetries on hurricane intensity: A numerical study. J. Atmos. Sci. 2004, 61, 3065–3081. [Google Scholar] [CrossRef]
- Fiorino, M.; Elsberry, R.L. Some aspects of vortex structure related to tropical cyclone motion. J. Atmos. Sci. 1989, 46, 975–990. [Google Scholar] [CrossRef] [Green Version]
- Oey, L.-Y. The formation and maintenance of density fronts on US southeastern continental shelf during winter. J. Phys. Oceanogr. 1986, 16, 1121–1135. [Google Scholar] [CrossRef] [Green Version]
- Chiang, T.L.; Wu, C.R.; Oey, L.Y. Typhoon Kai-Tak: A perfect ocean’s storm. J. Phys. Oceanogr. 2011, 41, 221–233. [Google Scholar] [CrossRef]
- Huang, S.M.; Oey, L.Y. Right-side cooling and phytoplankton bloom in the wake of a tropical cyclone. J. Geophys. Res. Oceans 2015, 120, 5735–5748. [Google Scholar] [CrossRef]
- Sun, J.; Oey, L.Y.; Chang, R.; Xu, F.; Huang, S.M. Ocean response to typhoon Nuri (2008) in western Pacific and South China Sea. Ocean Dyn. 2015, 65, 735–749. [Google Scholar] [CrossRef]
- Emanuel, K.A. Thermodynamic control of hurricane intensity. Nature 1999, 401, 665–669. [Google Scholar] [CrossRef]
- Michalakes, J.; Chen, S.-H.; Dudhia, J.; Hart, L.; Klemp, J.; Middlecoff, J.; Skamarock, W. Development of a next-generation regional weather research and forecast model. In Developments in Teracomputing, Proceedings of the Ninth ECMWF Workshop on the Use of High Performance Computing in Meteorology, Reading, UK, 13–17 Novmber 2000; Kreitz, N., Zwieflhofer, W., Eds.; World Scientific: London, UK, 2001; pp. 269–276. [Google Scholar]
- Mellor, G.L. Users Guide for a Three-Dimensional, Primitive Equation, Numerical Ocean Model; Princeton University: Princeton, NJ, USA, 2004; p. 56. Available online: http://jes.apl.washington.edu/modsims_two/usersguide0604.pdf (accessed on 18 June 2021).
- Oey, L.-Y.; Mellor, G.L.; Hires, R.I. A three-dimensional simulation of the Hudson-Raritan estuary. Part I: Description of the model and model simulations. J. Phys. Oceanogr. 1985, 15, 1676–1692. [Google Scholar] [CrossRef] [Green Version]
- Oey, L.; Chang, Y.; Lin, Y.-C.; Chang, M.-C.; Xu, F.-H.; Lu, H.-F. ATOP—The Advanced Taiwan Ocean Prediction System based on the mpiPOM. Part 1: Model descriptions, analyses and results. Terr. Atmos. Ocean. Sci. 2013, 24, 137–158. [Google Scholar] [CrossRef] [Green Version]
- Rotunno, R.; Emanuel, K.A. An Air–Sea Interaction Theory for Tropical Cyclones. Part II: Evolutionary Study Using a Nonhydrostatic Axisymmetric Numerical Model. J. Atmos. Sci. 1987, 44, 542–561. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, M.T.; Persing, J.; Smith, R.K. Putting to rest WISHE-ful misconceptions for tropical cyclone intensification. J. Adv. Model. Earth Syst. 2015, 7, 92–109. [Google Scholar] [CrossRef] [Green Version]
- Murthy, V.S.; Boos, W.R. Role of surface enthalpy fluxes in idealized simulations of tropical depression spinup. J. Atmos. Sci. 2018, 75, 1811–1831. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Kessler, E. On the Distribution and Continuity of Water Substance in Atmospheric Circulation. Meteor. Monogr. Am. Meteor. Soc. 1969, 32, 84. [Google Scholar]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). Asia Pac. J. Atmos. Sci. 2006, 42, 129–151. [Google Scholar]
- Mansell, E.R.; Ziegler, C.L.; Bruning, E.C. Simulated electrification of a small thunderstorm with two–moment bulk microphysics. J. Atmos. Sci. 2010, 67, 171–194. [Google Scholar] [CrossRef]
- Stensrud, D.J. Parameterization Schemes. Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007; p. 579. [Google Scholar]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef]
- Donelan, M.; Haus, B.; Reul, N.; Plant, W.; Stiassnie, M.; Graber, H.; Brown, O.; Saltzman, E. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2004, 31, L18306. [Google Scholar] [CrossRef] [Green Version]
- Davis, C.; Wang, W.; Chen, S.S.; Chen, Y.; Kristen, C.; Mark, D.M.; Jimy, D.; Greg, H.; Joe, K.; John, M. Prediction of landfalling hurricanes with the advanced hurricane WRF model. Mon. Weather Rev. 2008, 136, 1990–2005. [Google Scholar] [CrossRef] [Green Version]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Holliday, C.R.; Thompson, A.H. Climatological characteristics of rapidly intensifying typhoons. Mon. Weather Rev. 1979, 107, 1022–1034. [Google Scholar] [CrossRef]
- Wada, A. Unusually rapid intensification of Typhoon Man-yi in 2013 under preexisting warm-water conditions near the Kuroshio front south of Japan. J. Oceanogr. 2015, 131–156. [Google Scholar] [CrossRef]
- Sun, J.; Oey, L.; Xu, F.; Lin, Y.C. Sea level rise, surface warming, and the weakened buffering ability of South China Sea to strong typhoons in recent decades. Nature Sci. Rep. 2017, 7, 7418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Oey, L. An observational analysis of ocean surface waves in tropical cyclones in the western North Pacific Ocean. J. Geophys. Res. Oceans 2019, 124, 184–195. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Oey, L.Y. Rainfall-enhanced blooming in typhoon wakes. Nature Sci. Rep. 2016, 6, 31310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Oceanogr. 1981, 11, 153–175. [Google Scholar] [CrossRef] [Green Version]
- Oey, L.Y.; Ezer, T.; Wang, D.P.; Fan, S.J.; Yin, X.Q. Loop current warming by Hurricane Wilma. Geophys. Res. Lett. 2006, 33, L08613. [Google Scholar] [CrossRef] [Green Version]
- Oey, L.Y.; Ezer, T.; Wang, D.P.; Yin, X.Q.; Fan, S.J. Hurricane-induced motions and interaction with ocean currents. Cont. Shelf Res. 2007, 27, 1249–1263. [Google Scholar] [CrossRef]
- Xu, F.H.; Oey, L.Y. Seasonal SSH variability of the Northern South China Sea. J. Phys. Oceanogr. 2015, 45, 1595–1609. [Google Scholar] [CrossRef]
- Kowch, R.; Emanuel, K. Are special processes at work in the rapid intensification of tropical cyclones? Mon. Weather Rev. 2015, 143, 878–882. [Google Scholar] [CrossRef] [Green Version]
- Hong, X.; Chang, S.W.; Raman, S.; Shay, L.K.; Hodur, R. The interaction between Hurricane Opal (1995) and a warm core ring in the Gulf of Mexico. Mon. Weather Rev. 2000, 128, 1347–1365. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, G.; Peng, M.S.; Chen, J.H.; Lin, S.J. Predictability of Atlantic tropical cyclones in the GFDL HiRAM model. Geophys. Res. Lett. 2015, 42, 2547–2554. [Google Scholar] [CrossRef]
- Huang, S.-M.; Oey, L.Y. Malay Archipelago forest loss to cash crops and urban contributes to weaken the Asian summer monsoon: An atmospheric modeling study. J. Clim. 2019, 32, 3189–3205. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Oey, L.Y. Global trends of sea surface gravity wave, wind and coastal wave set-up. J. Clim. 2020, 32, 769–785. [Google Scholar] [CrossRef]
- Riehl, H. Some relations between wind and thermal structure of steady state hurricanes. J. Atmos. Sci. 1963, 20, 276–287. [Google Scholar] [CrossRef] [Green Version]
- Nolan, D.S.; Grasso, L.D. Three-dimensional perturbations to balanced, hurricane-like vortices. Part II: Symmetric response and nonlinear simulations. J. Atmos. Sci. 2003, 60, 2717–2745. [Google Scholar] [CrossRef] [Green Version]
- McCalpin, J.D. On the adjustment of azimuthally perturbed vortices. J. Geophys. Res. 1987, 92, 8213–8225. [Google Scholar] [CrossRef]
- Paterson, L.A.; Hanstrum, B.N.; Davidson, N.E.; Weber, H.C. Influence of Environmental Vertical Wind Shear on the Intensity of Hurricane-Strength Tropical Cyclones in the Australian Region. Mon. Weather Rev. 2005, 133, 3644–3660. [Google Scholar] [CrossRef]
- Bozart, L.E.; Velden, C.S.; Bracken, W.D.; Molinari, J.; Black, P.G. Environmental influences on the rapid intensification of Hurricane Opal (1995) over the Gulf of Mexico. Mon. Weather Rev. 2000, 128, 322–352. [Google Scholar] [CrossRef]
- DeMaria, M.; Kaplan, J. Sea surface temperature and the maximum intensity of Atlantic tropical cyclones. J. Clim. 1994, 7, 1325–1334. [Google Scholar] [CrossRef] [Green Version]
- Holland, G.J.; Belanger, J.I.; Fritz, A. A revised model for radial profiles of hurricane winds. Mon. Weather Rev. 2010, 138, 4393–4401. [Google Scholar] [CrossRef]
- Monismith, S.G.; Koseff, J.R.; White, B.L. Mixing efficiency in the presence of stratification: When is it constant? Geophys. Res. Lett. 2018, 45, 5627–5634. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean. Dynamics; Academic Press: Cambridge, MA, USA, 1982; p. 662. [Google Scholar]
- Etemad-Shahidi, A.; Imberger, J. Anatomy of turbulence in a narrow and strongly stratified estuary. J. Geophys. Res. 2002, 107, 3070. [Google Scholar] [CrossRef]
- Bouffard, D.; Boegman, L. A Diapycnal diffusivity model for stratified environmental flows. Dyn. Atmos. Oceans 2013, 61, 14–34. [Google Scholar] [CrossRef]
- Smyth, W.D. Marginal instability and the efficiency of ocean mixing. J. Phys. Oceanogr. 2020, 50, 2141–2150. [Google Scholar] [CrossRef]

| MP or CU | Descriptions |
|---|---|
| MP 1 | Kessler |
| MP 4 | WSM 5-class |
| MP 6 | WSM 6-class graupel |
| MP 18 | NSSL 2-moment 4-ice scheme with predicted CCN |
| MP 21 | NSSL 1-moment, (6-class) |
| CU 4 | Old GFS simplified Arakawa-Schubert scheme (SAS) |
| CU 14 | New GFS simplified Arakawa-Schubert scheme from YSU |
| CU 6 | Modified Tiedtke scheme |
| CU 16 | A newer Tiedtke scheme |
| CU 1 | Kain-Fritsch (new Eta) scheme (KF) |
| CU 11 | Multi-scale Kain-Fritsch scheme |
| CU 99 | Previous Kain-Fritsch scheme |
| CU 2 | Betts-Miller-Janjic scheme (BMJ) |
| CU 5 | Grell-3D ensemble scheme (G-3) |
| Parameters | Values | Meaning |
|---|---|---|
| Le | 106 and 212 km | radial scale of warm eddy |
| Tcon | 27, 28 and 29 °C | initial ambient SST (=control initial SST) |
| δT | 1 and 2 °C | initial eddy’s peak SST anomaly |
| Uh | 1 and 5 m/s | typhoon translation speed |
| Z26 | ∞, 90 m and 60 m | initial ambient depth of the 26 °C isotherm (=control initial Z26) |
| CU4 | CU14 | CU6 | CU16 | CU1 | CU11 | CU99 | CU2 | CU5 | |
|---|---|---|---|---|---|---|---|---|---|
| MP1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| MP4 | ✓ | ✓ | ✓ | ||||||
| MP6 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| MP18 | ✓ ☑ | ✓ | ✓ | ✓ | |||||
| MP21 | ✓ | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oey, L.; Huang, S. Can a Warm Ocean Feature Cause a Typhoon to Intensify Rapidly? Atmosphere 2021, 12, 797. https://doi.org/10.3390/atmos12060797
Oey L, Huang S. Can a Warm Ocean Feature Cause a Typhoon to Intensify Rapidly? Atmosphere. 2021; 12(6):797. https://doi.org/10.3390/atmos12060797
Chicago/Turabian StyleOey, Leo, and Shimin Huang. 2021. "Can a Warm Ocean Feature Cause a Typhoon to Intensify Rapidly?" Atmosphere 12, no. 6: 797. https://doi.org/10.3390/atmos12060797
APA StyleOey, L., & Huang, S. (2021). Can a Warm Ocean Feature Cause a Typhoon to Intensify Rapidly? Atmosphere, 12(6), 797. https://doi.org/10.3390/atmos12060797






